Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reactive force field development for magnesium chloride hydrates and its application for seasonal heat storage†
Amar Deep
Pathak
*a,
Silvia
Nedea
a,
Adri C. T.
van Duin
b,
Herbert
Zondag
a,
Camilo
Rindt
a and
David
Smeulders
a
aEnergy Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: a.d.pathak@tue.nl
bDepartment of Mechanical and Nuclear Engineering, Pennsylvania State University, 240 Research East Building, University Park, PA 16802, USA
First published on 23rd May 2016
Abstract
MgCl2 hydrates are considered as high-potential candidates for seasonal heat storage materials. These materials have high storage capacity and fast dehydration kinetics. However, as a side reaction to dehydration, hydrolysis may occur. Hydrolysis is an irreversible reaction, which produces HCl gas thus affecting the durability of heat storage systems. In this study, we present the parameterization of a reactive force field (ReaxFF) for MgCl2 hydrates to study the dehydration and hydrolysis kinetics of MgCl2·H2O and MgCl2·2H2O. The ReaxFF parameters have been derived by training against quantum mechanics data obtained from Density Functional Theory (DFT) calculations consisting of bond dissociation curves, angle bending curves, reaction enthalpies, and equation of state. A single-parameter search algorithm in combination with a Metropolis Monte Carlo algorithm is successfully used for this ReaxFF parameterization. The newly developed force field is validated by examining the elastic properties of MgCl2 hydrates and the proton transfer reaction barrier, which is important for the hydrolysis reaction. The bulk moduli of MgCl2·H2O and MgCl2·2H2O obtained from ReaxFF are in close agreement with the bulk moduli obtained from DFT. A barrier of 20.24 kcal mol−1 for the proton transfer in MgCl2·2H2O is obtained, which is in good agreement with the barrier (19.55 kcal mol−1) obtained from DFT. Molecular dynamics simulations using the newly developed ReaxFF on 2D-periodic slabs of MgCl2·H2O and MgCl2·2H2O show that the dehydration rate increases more rapidly with temperature in MgCl2·H2O than in MgCl2·2H2O, in the temperature range 300–500 K. The onset temperature of HCl formation, a crucial design parameter in seasonal heat storage systems, is observed at 340 K for MgCl2·H2O, which is in agreement with experiments. The HCl formation is not observed for MgCl2·2H2O. The diffusion coefficient of H2O through MgCl2·H2O is lower than through MgCl2·2H2O, and can become a rate-limiting step. The diffusion coefficient increases with temperature and follows the Arrhenius law both for MgCl2·H2O and MgCl2·2H2O. These results indicate the validity of the ReaxFF approach for studying MgCl2 hydrates and provide important atomistic-scale insight of reaction kinetics and H2O transport in these materials.
1 Introduction
Thermal energy storage is necessary for the successful implementation of solar thermal energy.1 Solar thermal energy can be stored in three forms: sensible, latent, and thermochemical.2 Thermal storage is a proven concept but it is volume restricted. The energy storage density is higher in thermochemical form than in sensible or latent form. Therefore thermochemical materials (TCMs) may offer a compact seasonal heat storage solution.3Salt hydrates are one class of TCMs.1 These materials convert thermal energy (physical form of energy) into chemical form by decomposing into lower hydrate form or anhydrous form (charging cycle). Anhydrous and lower hydrates recombine with water vapor (present in moisture) to form hydrates again, thereby releasing energy (discharging cycle). The operating principle of TCM can be expressed with the following reaction:
| Salt·mH2O + Heat ↔ Salt·(m − n)H2O + nH2O. |
In addition to higher energy storage capacity, TCMs can store thermal energy with almost no heat loss, even for longer periods, making TCM a unique seasonal heat storage material.4,5 Selection of an appropriate salt hydrate is the key aspect in designing a thermochemical heat storage system.6 Halide based salt hydrates (CaX2·6H2O, MgX2·6H2O, and SrX2·6H2O, X = Cl/Br), sulphate based salt hydrates (LiSO4·H2O, MgSO4·7H2O), and nitrate based salt hydrates (LiNO3·3H2O, Zn(NO3)2·3H2O) are the major class of promising reversible TCMs.6 These hydrates have theoretical crystal storage capacities between 2–3 GJ m−3.6
Magnesium chloride hydrates (MgCl2·nH2O, n = 0, 1, 2, 4, and 6) have been investigated extensively as an appropriate candidates for solar thermal storage.7–13 MgCl2·6H2O (Bischofite) has been successfully tested for 1000 cycles for application in solar based cooking.11 Thermal dehydration of Bischofite is an important process in production of pure Mg, Mg alloys, MgO, and in heat storage applications.14–17 The dehydration kinetics for MgCl2 hydrates is faster than for other materials like MgSO4 hydrates,8,18 but a problem with this material is the presence of the hydrolysis along with the dehydration. Hydrolysis is an irreversible side reaction in the dehydration process, which produces HCl gas and affects the durability of the heat storage system. It was experimentally observed that the hydrolysis reaction could be avoided by use of external HCl pressure14 or by adding other halides.19 However, there is no fundamental understanding of the conditions for the hydrolysis.
Next to the dehydration, the HCl production is also a key aspect in designing the MgCl2 based heat storage system. Experimentally, thermal dehydration and hydrolysis of MgCl2 hydrates have been studied by thermogravimetric analysis (TGA),17 derivative thermogravimetry (DTG),20 TGA/Differential scanning calorimetry (DSC)10 and thermochemical analysis.14 Galwey et al.21 has experimentally observed the hydrolysis reaction in MgCl2·2H2O in the temperature range of 623–703 K.21 Kirsh et al.20 has not observed hydrolysis below 473 K for MgCl2 hydrates, but found 43.8% of chlorine released as HCl at 673 K. However, Huang et al.17 has reported the onset temperature of HCl formation at 440 K in MgCl2·2H2O. Kipouros et al.14 has reported hydrolysis at 417 K for MgCl2·2H2O and at 413 K for MgCl2·H2O for an equilibrium HCl pressure of 5 × 10−3 atm. The onset temperature of HCl formation is thus ambiguous from experiments. There is no theoretical study to determine the hydrolysis kinetics and the onset temperature of HCl formation.
Atomic and molecular level simulations turned to be useful tools to gain insight in the hydrolysis coupled dehydration reactions. Weck et al.12 has computed thermal properties from thermodynamical calculations of MgCl2·nH2O using Density Function Theory (DFT) under harmonic assumption. Wang et al.16 has considered MgCl2·H2O to be the potential candidate for hydrolysis and proposed a reaction path for thermolysis of MgCl2·H2O from DFT calculations. Smeets et al.8 has obtained the safety limit of hydrolysis reactions for all hydrates of MgCl2 from DFT calculations using equilibrium thermodynamic principles under the ideal poly-atomic gas assumption. The atomic scale calculations can simulate systems upto a system size of 100–1000 atoms and a time scale upto 200 picosecond over a week of high performance computing.22 To the best of our knowledge, no kinetic study was done on molecular level to investigate the hydrolysis and dehydration reactions of MgCl2·H2O and MgCl2·2H2O from first principle atomic level calculations, integrating the quantum level results to molecular level modeling under reactive force field (ReaxFF) formalism.
For an efficient TCM storage cycle, heat and mass transfer in the storage volume are essential.2 Experimentally it has been observed that water transport through the solid MgCl2 hydrate affects the dehydration rate and may become the rate limiting step under specific reaction conditions.23 To understand the complex reaction (hydration and dehydration) coupled with water transport, it is desirable to investigate the diffusive transport of water molecules, which are formed by the dehydration reaction. These water molecules have to diffuse to the surface of the solid salt hydrate. The diffusion path may vary from several atomic layers up to a few micrometer.24 The water transport through the solid salt hydrate, the temperature, the diffusion path length, the external H2O pressure and the crystal defects influence considerably the dehydration rate.25 To study the effect of these aspects on the complex dehydration reaction on molecular level, a force field is required that is able to capture both the chemical reactivity and the mass transport of H2O in MgCl2·H2O and MgCl2·2H2O crystals.
Chemical reactivity has been incorporated using bond order dependent ReaxFF.26,27 According to previous studies,28,29 a training set needs to be developed from quantum level DFT calculations consisting of the bond dissociation energy curves of Mg–Cl and Mg–O bonds, the angle bending energy curves of Cl–Mg–Cl, O–Mg–O, and O–Mg–Cl angles in gaseous hydrates, the reaction enthalpies of dehydration and hydrolysis reaction, and the condensed phase equation of state (EOS) of MgCl2, MgCl2·H2O and MgCl2·2H2O.27,30,31 To our knowledge, no DFT studies exist presenting this information of the MgCl2 hydrates. For this purpose, in this paper we obtained various molecular structures of MgCl2 hydrates, reaction enthalpies, bond dissociation energies, angle bending energies, and EOS from DFT. With this extended information, we parameterize a new force field for MgCl2 hydrates. Both a single-parameter search algorithm32 and a Metropolis Monte Carlo (MMC) algorithm33 are used to optimize the newly developed ReaxFF for investigated MgCl2 hydrates.
In the present study, we parameterize the ReaxFF to model the dehydration kinetics of MgCl2·H2O and MgCl2·2H2O, as these hydrates are prone to hydrolysis reactions. Proton transfer is an important step in the hydrolysis reaction. The energy barrier for proton transfer in MgCl2·2H2O is obtained from the ReaxFF simulations and validated against results from DFT. The extent of the reaction depends on the temperature of the solid and the vapor transport inside the solid. The new ReaxFF is used to study the effect of temperature on the dehydration in the temperature range of 300–500 K. This temperature range is the typical operating range of TCM based heat storage systems. The onset temperature of HCl formation is investigated in the same temperature range. The dependence of the diffusion coefficient (DC) on temperature is analyzed using the Green–Kubo (GK) method.
2 Computational methods
2.1 Quantum mechanics calculations
To accurately predict the dehydration and hydrolysis reaction in the condensed phase of MgCl2 hydrates, quantum mechanics (QM) calculations are performed in both periodic and non-periodic systems in order to generate a training set necessary to parameterize the new force field. DFT under the generalized gradient approximation (GGA) is used for the QM calculations. All the non-periodic MgCl2 hydrate clusters are relaxed in the framework of DFT implemented in Amsterdam Density Functional (ADF) program.34 The Perdew–Wang exchange and correlation functional (PW91) is used with a double polarized triple-ζ basis set. A similar GGA-DFT framework has been used to study the CaCl2, MgCl2, and MgSO4 hydrates.8,18,35 The bond dissociation energy for Mg–O and Mg–Cl bonds are obtained from GGA-DFT for MgCl2·H2O and MgCl2·2H2O as they are responsible for the hydrolysis and the dehydration reactions. Similarly, the angle bending energy curves in MgCl2 hydrates like O–Mg–O, Cl–Mg–Cl, H–O–Mg are also obtained from GGA-DFT.To simulate a reaction in solid phase of hydrates, the crystal structure of MgCl2, MgCl2·H2O, and MgCl2·2H2O are compressed or stretched uniformly upto 20–30% of their relaxed volume to obtain the EOS. The periodic systems are relaxed in the framework of GGA-DFT using the VASP package.36 The projector augmented wave (PAW) method37 along with the Perdew Burke Ernzerhof (PBE) exchange–correlation functional38 is used under the GGA approximation. The Monkhorst–Pack k-point mesh is used to integrate the Brillouin zone of MgCl2 (5 × 5 × 3), MgCl2·H2O (3 × 5 × 3), and MgCl2·2H2O (4 × 4 × 8). The unit cell of crystals are fully relaxed with break condition for ionic relaxation of 10−6 eV and plane wave cut off of 500 eV using tetrahedron method with Blöchl corrections.
2.2 Reactive force field and parameterization
ReaxFF is a general bond-order-dependent many body empirical potential with a polarizable charge model that dynamically predicts a bond formation and dissociation during a reaction without connecting step function potentials.39 ReaxFF formalism represents a continuous landscape of energy which is dependent on the bond order and the non-bonded distance. The bond order is obtained from the inter-atomic distance and energy contribution updated with time. In the ReaxFF formalism, the total energy of the system can be partitioned into the following terms:| Etotal = Ebond + Eval + Etor + Elp + Eover/under + Econj + EH-bond + Eothers + ECoulomb + EvDW. | (1) |
The ReaxFF parameters required to define the potential energy surface are optimized against the training set obtained from QM data. The initial O/H parameters are taken from the iron–oxyhydroxide force field.40 The O/H parameters are kept fixed while bond parameters of Mg–O, Mg–Cl and angle parameters associated with these Mg and Cl are optimized. The optimization is done in such a way that optimized parameters are able to reproduce the energy and structural data present in the training set. The data in the training set used for comparison include bond dissociation energy, angle bending curve, reaction enthalpy and EOS for MgCl2, MgCl2·H2O, and MgCl2·2H2O. In an optimization process, ReaxFF parameters are varied such that the cumulative error (Ξ) between the DFT data in the training set and their corresponding values obtained from ReaxFF is minimized. The cumulative error is defined as
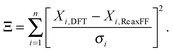 | (2) |
 | (3) |
2.3 Diffusion
The DC of H2O molecules through the MgCl2 hydrate crystal is obtained from the GK formulation described as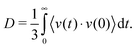 | (4) |
3 Results and discussion
3.1 Force field parameterization results
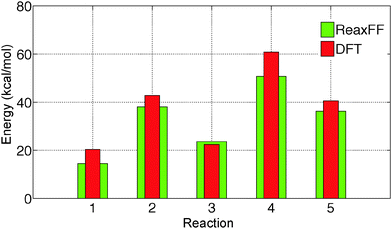
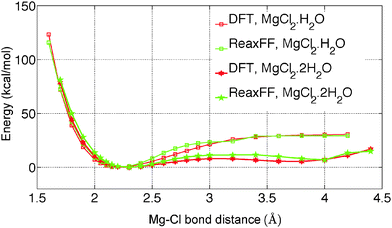
The initial force field parameters are optimized against hydrated Cl− ion and MgCl2 condensed phase data. The bond dissociation energies for Mg–Cl and Mg–O bonds present in MgCl2, MgCl2·H2O, and MgCl2·2H2O gas molecules are obtained from restrained GGA-DFT calculations. Bond dissociation energy is the relative energy of the constrained molecule (specific bond constrain) with respect to its relaxed geometry. Similarly, angle bending curves for Cl–Mg–Cl, O–Mg–O, O–Mg–Cl, and H–O–Mg are obtained from GGA-DFT. The single-parameter search algorithm32 approaches a global minimum when the initial ReaxFF parameters are chosen close to that minimum while the multi-parameter MMC algorithm33 approaches the global minimum irrespective of the initial guess. The bond and angle parameters are optimized with the single-parameter search32 followed by the multi-parameter MMC algorithm33 such that the trained parameters can reproduce the training set data accurately and the cumulative error attains a global minimum.The optimized ReaxFF parameters are able to reproduce the bond dissociation curve of Mg–O and Mg–Cl bond present in MgCl2·H2O and MgCl2·2H2O as shown in Fig. 1 and 2 remarkably well, particularly near the minimum. The shape of the Mg–O dissociation curve obtained from ReaxFF slightly differs from the DFT one. This discrepancy can be explained from the fact that there are many conformers of similar energy existing at the same Mg–O distance due to the weak bonded interaction of H2O with MgCl2 and to the relatively strong non-bonded interaction in MgCl2·H2O and MgCl2·2H2O. The optimized ReaxFF is also able to capture the angle bending energy curves for MgCl2·H2O and MgCl2·2H2O (see ESI†). The enthalpy change in the dehydration and in the hydrolysis reactions (gas phase) for MgCl2·H2O and MgCl2·2H2O are obtained from DFT. ReaxFF is also able to capture the enthalpy change in the dehydration and hydrolysis reaction of MgCl2·H2O and MgCl2·2H2O with a maximum difference of 5.5 kcal mol−1 (28% of DFT value) as shown in Fig. 3.
 | ||
| Fig. 1 Comparison of the Mg–Cl bond dissociation energy curve in MgCl2 hydrates obtained from DFT and ReaxFF. | ||
 | ||
| Fig. 2 Comparison of the Mg–O bond dissociation energy curve in MgCl2 hydrates obtained from DFT and ReaxFF. | ||
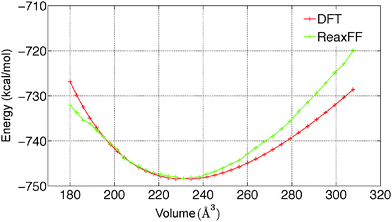
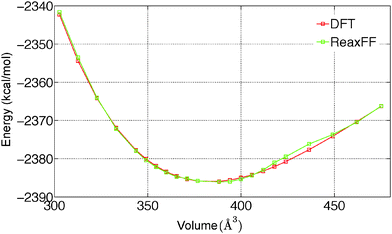
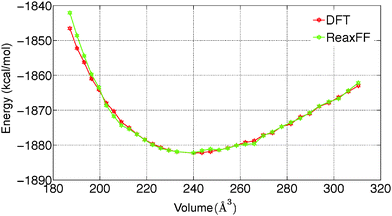
To predict the kinetics of solid MgCl2·H2O and MgCl2·2H2O, the EOS is essential. The optimized force field, which is able to describe the gas phase reactions accurately, is further optimized with a condensed phase EOS of MgCl2 hydrates obtained from DFT in VASP.36 The parameterized force field is also able to predict the experimentally observed crystal structures of MgCl2,42 MgCl2·H2O,43 and MgCl2·2H2O44 as shown in Table 1. In Table 1 (rows 1–6), it can be observed that ReaxFF reproduces the lattice parameters of the unit cell of MgCl2, MgCl2·H2O and MgCl2·2H2O with great accuracy. ReaxFF is also able to reproduce the EOS for MgCl2, MgCl2·H2O and MgCl2·2H2O as shown in Fig. 4–6.
| MgCl2 | MgCl2·H2O | MgCl2·2H2O | ||||
|---|---|---|---|---|---|---|
| ReaxFF | DFT | ReaxFF | DFT | ReaxFF | DFT | |
| a (Å) | 3.665 | 3.662 [3.596]42 | 8.936 | 8.936 [8.917]43 | 7.649 | 7.672 [7.389]44 |
| b (Å) | 3.665 | 3.666 [3.596]42 | 3.691 | 3.692 [3.634]43 | 8.491 | 8.516 [8.550]44 |
| c (Å) | 19.860 | 19.840 [17.589]42 | 11.592 | 11.593 [11.477]43 | 3.694 | 3.705 [3.648]44 |
| α (°) | 90 | 90 [90]42 | 90 | 90 [90]43 | 90 | 90 [90] |
| β (°) | 90 | 90 [90]42 | 90 | 90 [90]43 | 102.46 | 102.45 [98.96] |
| γ (°) | 120 | 120 [90]42 | 90 | 90 [90]43 | 90 | 90 [90] |
| B 0 (GPa) | 19.28 | 17.54 | 20.51 | 21.02 | 24.65 | 23.66 |
| B 0′ | 3.65 | 4.03 | 6.84 | 6.31 | 6.38 | 5.96 |
The bulk modulus is obtained from fitting the Birch–Murnaghan equation of state with the EOS obtained from DFT and ReaxFF. The bulk modulus (B0) and its first order derivative with respect to pressure (B0′) (rows 7 and 8 of Table 1) is obtained from ReaxFF and found to be in good agreement with DFT results for MgCl2, MgCl2·H2O and MgCl2·2H2O.
3.2 Proton transfer reaction
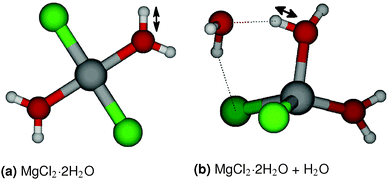
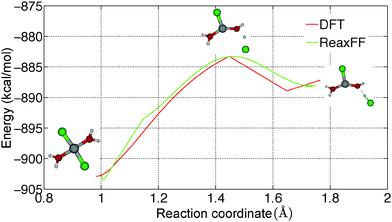
Hydrolysis is an irreversible reaction which is usually observed in MgCl2·H2O and MgCl2·2H2O. Wang and Chen16 have studied the thermolysis mechanism of MgCl2·H2O using a semi-empirical PM3 method. They observed that proton transfer is an important step in the hydrolysis reaction. To understand the reaction path for the proton transfer in MgCl2·2H2O, the relative energy of a MgCl2·2H2O molecule is obtained from GGA-DFT calculations by constraining the O–H bond lengths, which is shown in Fig. 7(a). We obtained a barrier of 19.55 kcal mol−1 for proton transfer in gaseous MgCl2·2H2O and a barrier of 8.31 kcal mol−1 for chloride ion (Cl−) formation, which indicates that proton transfer is a rate determining step in the hydrolysis reaction. To validate the applicability of the ReaxFF, we obtained the reaction path for proton transfer in gaseous MgCl2·2H2O from ReaxFF and compared it with DFT. From Fig. 8, it can be observed that ReaxFF is able to predict the barrier for proton transfer (20.24 kcal mol−1) and the reaction coordinate for proton transfer in MgCl2·2H2O.To understand the effect of a neighboring H2O molecule in proton transfer of MgCl2·2H2O, a H2O molecule is placed nearby as shown in Fig. 7(b). A barrier of 29.61 kcal mol−1 is obtained from DFT for proton transfer in MgCl2·2H2O surrounded by one H2O molecule. This explains the lower hydrolysis in the higher hydrates (tetra and hexa) of MgCl2, as the neighboring H2O molecule increases the barrier for proton transfer and inhibits the hydrolysis. A barrier of 26.54 kcal mol−1 for proton transfer is obtained from ReaxFF, which is in agreement with the DFT result (29.61 kcal mol−1). The position of the transition state predicted from ReaxFF differs by 0.5 Å because surrounding H2O molecule may form many structures of similar energy (see ESI†).
3.3 ReaxFF-MD simulations of MgCl2 hydrates
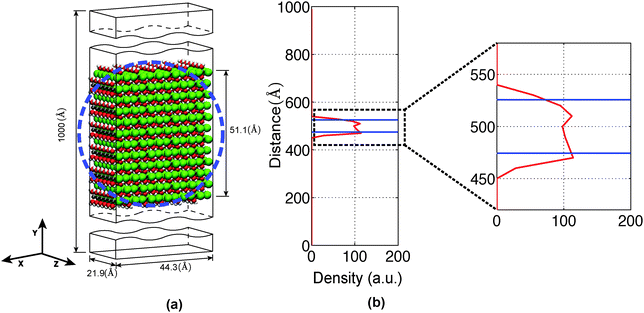
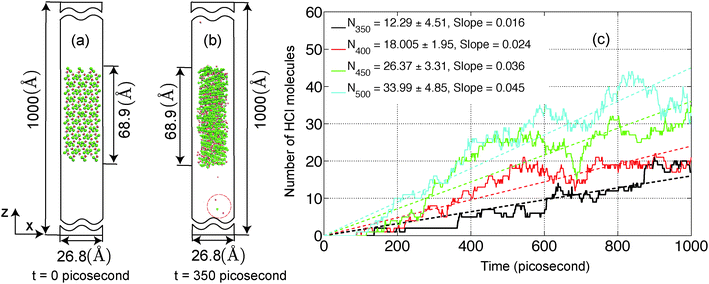
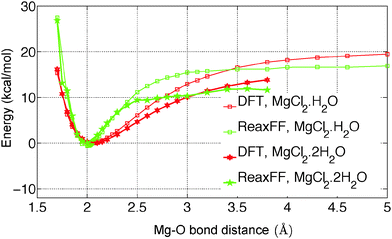
In the present study, we have investigated the kinetics of dehydration and hydrolysis reactions of solid MgCl2·H2O and MgCl2·2H2O. We created the 3 × 6 × 6 super-cell of MgCl2·H2O crystal43 and 6 × 6 × 6 super-cell of MgCl2·2H2O44 from their experimental crystallographic information file (CIF).45 2D-periodic slabs of 26.8 × 21.8 × 1000 Å for MgCl2·H2O (as shown in Fig. 13a) and 44.3 × 1000 × 21.9 Å for MgCl2·2H2O (as shown in Fig. 9a) are prepared from the super-cell by eliminating periodicity in the Z and Y direction respectively. The removal of periodicity is chosen is a direction parallel to the Mg–O bond as the Mg–O bond is weaker than the Mg–Cl bond. We carried out NVT-MD simulations at various temperatures using the Berendsen thermostat with a temperature damping constant of 100 femtosecond. The MD time step of 0.25 femtosecond is used for MgCl2·H2O and MgCl2·2H2O. All simulations are performed upto 1 nanosecond and average number of molecules are recorded from last 500 picosecond. | ||
| Fig. 10 Radial distribution functions of O–H, Mg–O, and Mg–Cl bond in MgCl2·H2O and MgCl2·2H2O obtained with newly developed ReaxFF parameters of MgCl2 hydrates at 300 K. The represents the corresponding distance in the experimental unit cell.43,44 | ||
The first peak location for the Mg–O pair is observed at 2.0 Å, which represents the Mg–O atomic bond as shown in Fig. 10. The corresponding distance in the experimental unit cell of MgCl2·2H2O is 2.0 Å.44 The second peak location for Mg–O pair is observed at 4.4 Å, which represents the non-bonded Mg attractions with the H2O molecule of the adjacent MgCl2 hydrate as shown in Fig. 10. The corresponding distance in the experimental unit cell of MgCl2·2H2O is 4.0 Å44 in this case.
The first peak location for Mg–Cl pair is observed at 2.3 Å which represents the Mg–Cl bond. The corresponding distances in the experimental unit cell of MgCl2·H2O and MgCl2·2H2O are 2.56 Å.43,44 The second peak is observed at 4.3 Å and 4.7 Å for MgCl2·H2O and MgCl2·2H2O which represents the Mg attraction with Cl of the adjacent MgCl2 hydrate molecule as shown in Fig. 10. The corresponding distances in the experimental unit cell of MgCl2·H2O and MgCl2·2H2O are 4.5 Å43 and 4.8 Å,44 respectively. We conclude that ReaxFF parameters obtained from the present study are consistent with DFT results and experimental results in representing the bonded and non-bonded interactions.
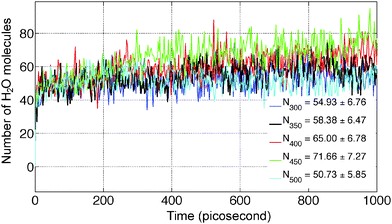
The average number of H2O molecules leaving the solid slab of MgCl2·2H2O (44.3 × 1000 × 21.9 Å) into the vacuum region (Y direction) is 51.17 ± 7.63 after 750 picosecond. The system is further equilibrated upto 1000 picosecond and H2O average increased by 4.61. The average density distribution of H2O molecules are obtained by diving the simulation box into the bins of 10 Å along the Y axis as shown in Fig. 9b. Blue lines represent the initial boundaries. The water molecules which escape from the solid slab accumulate on the surface at 300 K. There is a concentration gradient of H2O molecules present on the surface along the Y axis. Thereby, confirms the influence of water diffusion on the dehydration process. The average number of H2O molecules escaping from MgCl2·2H2O increases from 54.93 ± 6.76 to 71.66 ± 7.27 in the temperature range of 300 to 450 K as shown in Fig. 12. Further, increment in temperature leads to reduction in the number of H2O molecules escaping from MgCl2·2H2O to 50.73 ± 5.85 at 500 K as shown in Fig. 12. This reduction in number of water molecules escaping from solid slab of MgCl2·2H2O could be explained from the fact that existing water molecules present in the vacuum region are pushing them back into the crystal. The effect of temperature on the dehydration of MgCl2·H2O and MgCl2·2H2O is similar to experiments.47
To estimate the statistical error in the DC of H2O through 2D periodic slabs of MgCl2·H2O and MgCl2·2H2O, five repetitions of ReaxFF-MD simulations are performed with the same parameters at 300 K. The average diffusivity of H2O through MgCl2·H2O is 7.46 ± 0.77 × 10−11 m2 s−1 and 1.14 ± 0.15 × 10−10 m2 s−1 for MgCl2·2H2O. The DCs in MgCl2·H2O and MgCl2·2H2O are 0.03 and 0.04 times the DC of bulk water.48 In the lack of experimental study for the diffusion of H2O through MgCl2 hydrates, we compared with the H2O diffusivity through other TCM epsomite (MgSO4·7H2O).49 Zhang et al.49 has reported the same order of magnitude for the diffusivity of H2O in the center of the MgSO4.7H2O. Donkers et al.50 has measured the DC of water in epsomite using NMR. They reported the DC in range of 10−10 to 10−9 m2 s−1 in the temperature range of 293 to 413 K. In the light of their experimental and simulation results of water diffusion in other heat storage material (MgSO4·7H2O), we can conclude that the present ReaxFF-MD simulations could mimic the water transport in MgCl2 hydrates.
To investigate the effect of the temperature, the DC of H2O through 2D-periodic slabs of MgCl2·H2O and MgCl2·2H2O are obtained at various temperatures (300, 350, 400, 450, and 500 K). The rise in the temperature increased the thermal energy of H2O molecules and enhanced the water transport as shown in Table 2. The DC of H2O through 2D-periodic slabs at various temperatures follow the Arrhenius equation (D(T) = D0 × e−[E/RT]) with parameters given in Table 3. The activation energy and pre-exponential factor for H2O diffusion in MgCl2·H2O is higher than MgCl2·2H2O, thus the net effect of the temperature on DC of H2O through MgCl2·H2O is similar to MgCl2·2H2O. We have fitted the data on water-transport through the epsomite in the temperature range of 293 to 413 K.50 The DC follows the Arrhenius equation. The activation energy and pre-exponential factor are 5.7 × 10−4 m2 s−1 and 42.6 kcal mol−1. Thus, the strength of Mg–O bond in epsomite lies between the strength of Mg–O bond present in MgCl2·H2O and MgCl2·2H2O.
| Temperature, T, K | Diffusivity in MgCl2·H2O, m2 s−1 | Diffusivity in MgCl2·2H2O, m2 s−1 |
|---|---|---|
| 300 | 6.99 × 10−11 | 1.16 × 10−10 |
| 350 | 7.02 × 10−11 | 3.18 × 10−10 |
| 400 | 9.13 × 10−11 | 9.54 × 10−10 |
| 450 | 6.95 × 10−10 | 2.78 × 10−9 |
| 500 | 4.47 × 10−9 | 6.66 × 10−9 |
| Material | Pre exponential factor, D0 m2 s−1 | Activation energy, kJ mol−1 |
|---|---|---|
| MgCl2·H2O | 7.72 × 10−2 | 69.28 |
| MgCl2·2H2O | 1.55 × 10−5 | 32.22 |
4 Conclusions
To gain more insight into the reaction kinetics of MgCl2 hydrates on molecular level, the development of a new reactive force field (ReaxFF) is desirable. This force field is trained against an extensive set of quantum mechanics data. ReaxFF is optimized against a training set consisting of bond dissociation curve, angle bending curve, enthalpy change in hydrolysis and dehydration reactions and equation of state (EOS). A single-parameter search algorithm in combination with a Metropolis Monte Carlo algorithm is used. The optimized force field is able to reproduce the energy terms along with the computationally challenging EOS of solid crystals. Bulk moduli of MgCl2·H2O and MgCl2·2H2O obtained from DFT and ReaxFF simulations are in close agreement (∼4% deviation). ReaxFF parameters from the present study represent various chemical bonds like Mg–O, Mg–Cl, and O–H which are in agreement with the DFT and experimental structures.Barriers of 19.55 kcal mol−1 and 29.61 kcal mol−1 for proton transfer in MgCl2·2H2O and MgCl2·2H2O surrounded by a neighbor H2O molecule are obtained from DFT calculations. The ReaxFF parameters are able to reproduce the barrier obtained from DFT calculations for the proton transfer in MgCl2·2H2O (20.27 kcal mol−1) and MgCl2·2H2O surrounded by a neighbor H2O molecule (26.54 kcal mol−1). ReaxFF is also able to reproduce the reaction path for the proton transfer. This explains the lower hydrolysis in the higher hydrates (tetra and hexa) of MgCl2 as the neighboring H2O molecule in higher hydrates increases the barrier for proton transfer and inhibits the hydrolysis. The radial distribution functions for Mg–O, O–H, and Mg–Cl pairs confirm that the optimized force field is able to capture the bonded and non-bonded interactions in the MgCl2 hydrates.
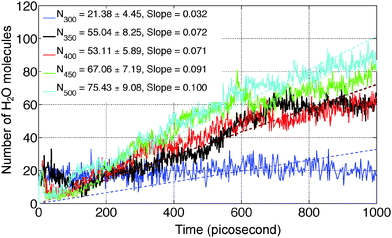
ReaxFF-MD simulations have been carried out on 2D periodic slabs of MgCl2·H2O and MgCl2·2H2O to investigate the dehydration and hydrolysis kinetics at various temperatures (300–500 K). The average number of H2O molecules escaping from the MgCl2·H2O slab (after 1 nanosecond) increased from 21.38 ± 4.45 to 75.43 ± 9.08 in the temperature range of 300 to 500 K. The dehydration rate increased 3.1 times in the same temperature range for MgCl2·H2O. The onset temperature of HCl formation in MgCl2·H2O is observed to be 340 K, which is in agreement with experiments. Increasing the temperature from 350 to 500 K, we observed that the average number of HCl molecules escaping from the MgCl2·H2O slab (after 1 nanosecond) increased from 12.29 ± 4.51 to 33.99 ± 4.85. The hydrolysis rate increased 2.8 times in the same temperature range for MgCl2·H2O. Increasing the temperatures from 300 to 450 K, the average number of H2O molecules escaping from the MgCl2·2H2O slab (after 1 nanosecond) increased from 54.93 ± 6.76 to 71.66 ± 7.27. Hydrolysis is not observed from the MgCl2·2H2O slab in the temperature range of 300–500 K.
The H2O transport through MgCl2·H2O and MgCl2·2H2O is investigated using ReaxFF-MD simulations. The diffusion coefficient (DC) of H2O through MgCl2 hydrates are reported from Green–Kubo method at various temperature ranging from 300–500 K. The DC of H2O in the present study is of the same order of magnitude as the DC of H2O in MgSO4·7H2O obtained both from MD simulations49 and experiments.50 The DC increases with temperature and follows the Arrhenius law for MgCl2·H2O and MgCl2·2H2O. The diffusivity of H2O through MgCl2·H2O at 500 K increases 64 times compared with diffusivity at 300 K. Similarly, the diffusivity of H2O through MgCl2·2H2O at 500 K increased 57 times compared to the 300 K. The diffusivity trend suggests that by increasing the temperature upto 500 K, the H2O transport (mass diffusion) can be improved. These results demonstrate the ability of ReaxFF to explore the molecular reaction rate for dehydration/hydrolysis of MgCl2 hydrates along with the water transport in the operational range of seasonal heat storage systems.
Acknowledgements
This work is part of the Industrial Partnership Programme (IPP) ‘Computational sciences for energy research’ of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organisation for Scientific Research (NWO). This research programme is co-financed by Shell Global Solutions International B. V.References
- K. E. N'Tsoukpoe, H. Liu, N. Le Pierrès and L. Luo, Renewable Sustainable Energy Rev., 2009, 13, 2385–2396 CrossRef.
- A. H. Abedin and M. A. Rosen, Open Renewable Energy J., 2011, 4, 42–46 CrossRef.
- J. Xu, R. Wang and Y. Li, Sol. Energy, 2014, 103, 610–638 CrossRef CAS.
- D. Aydin, S. P. Casey and S. Riffat, Renewable Sustainable Energy Rev., 2015, 41, 356–367 CrossRef CAS.
- A. J. Carrillo, D. Sastre, D. P. Serrano, P. Pizarro and J. M. Coronado, Phys. Chem. Chem. Phys., 2016, 18, 8039–8048 RSC.
- K. E. N'Tsoukpoe, T. Schmidt, H. U. Rammelberg, B. A. Watts and W. K. Ruck, Appl. Energy, 2014, 124, 1–16 CrossRef.
- H. Zondag, V. Van Essen, L. Bleijendaal, B. Kikkert and M. Bakker, Proceedings IRES 2010 conference, Berlin, 2010.
- B. Smeets, E. Iype, S. Nedea, H. Zondag and C. Rindt, J. Chem. Phys., 2013, 139, 124312 CrossRef CAS PubMed.
- A. El-Sebaii, S. Al-Amir, F. Al-Marzouki, A. S. Faidah, A. Al-Ghamdi and S. Al-Heniti, Energy Convers. Manage., 2009, 50, 3104–3111 CrossRef CAS.
- H. U. Rammelberg, T. Schmidt and W. Ruck, Energy Procedia, 2012, 30, 362–369 CrossRef CAS.
- A. El-Sebaii, S. Al-Heniti, F. Al-Agel, A. Al-Ghamdi and F. Al-Marzouki, Energy Convers. Manage., 2011, 52, 1771–1777 CrossRef CAS.
- P. F. Weck and E. Kim, J. Phys. Chem. C, 2014, 118, 4618–4625 CAS.
- R. Pilar, L. Svoboda, P. Honcova and L. Oravova, Thermochim. Acta, 2012, 546, 81–86 CrossRef CAS.
- G. J. Kipouros and D. R. Sadoway, J. Light Metals, 2001, 1, 111–117 CrossRef.
- L. Guangming, M. Peihua, W. Zhiming, L. Mingzhen and C. Minxong, Thermochim. Acta, 2004, 412, 149–153 CrossRef.
- W. Wang and S. Chen, Journal of Computational Science & Engineering, 2011, 2, 79–84 Search PubMed.
- Q. Huang, G. Lu, J. Wang and J. Yu, J. Anal. Appl. Pyrolysis, 2011, 91, 159–164 CrossRef CAS.
- E. Iype, S. V. Nedea, C. C. M. Rindt, A. A. van Steenhoven, H. A. Zondag and A. P. J. Jansen, J. Phys. Chem. C, 2012, 116, 18584–18590 CAS.
- S. Shoval, S. Yariv, Y. Kirsh and H. Peled, Thermochim. Acta, 1986, 109, 207–226 CrossRef CAS.
- Y. Kirsh, S. Yariv and S. Shoval, J. Therm. Anal., 1987, 32, 393–408 CrossRef CAS.
- A. K. Galwey and G. M. Laverty, Thermochim. Acta, 1989, 138, 115–127 CrossRef CAS.
- M. Dittner, J. Müller, H. M. Aktulga and B. Hartke, J. Comput. Chem., 2015, 36, 1550–1561 CrossRef CAS PubMed.
- C. Ferchaud, R. Scherpenborg, L. Scapino, J. Veldhuis, H. Zondag and R. D. Boer, Proceedings of the Advances in Thermal Energy Storage, Lleida, Spain, 2014.
- S. Lan, H. Zondag, A. van Steenhoven and C. Rindt, J. Therm. Anal. Calorim., 2016, 1–10 Search PubMed.
- A. Pathak, S. Nedea, C. Rindt, D. Smeulders and H. Zondag, Proceedings NEGF 2015 conference, Eindhoven, 2015.
- A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- K. Chenoweth, A. C. v. Duin, P. Persson, M.-J. Cheng, J. Oxgaard and W. A. Goddard, III, J. Phys. Chem. C, 2008, 112, 14645–14654 CAS.
- J. Ojwang, R. Van Santen, G. J. Kramer, A. C. van Duin and W. A. Goddard III, J. Chem. Phys., 2008, 128, 164714 CrossRef CAS PubMed.
- D. Raymand, A. C. van Duin, M. Baudin and K. Hermansson, Surf. Sci., 2008, 602, 1020–1031 CrossRef CAS.
- J. Ojwang, R. A. van Santen, G. J. Kramer, A. C. van Duin and W. A. Goddard III, J. Chem. Phys., 2009, 131, 044501 CrossRef CAS PubMed.
- K. Chenoweth, A. C. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053 CrossRef CAS PubMed.
- A. C. van Duin, J. M. Baas and B. van de Graaf, J. Chem. Soc., Faraday Trans., 1994, 90, 2881–2895 RSC.
- E. Iype, M. Hütter, A. Jansen, S. V. Nedea and C. Rindt, J. Comput. Chem., 2013, 34, 1143–1154 CrossRef CAS PubMed.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- A. D. Pathak, S. Nedea, H. Zondag, C. Rindt and D. Smeulders, Phys. Chem. Chem. Phys., 2016, 10059–10069 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- T. Liang, Y. K. Shin, Y.-T. Cheng, D. E. Yilmaz, K. G. Vishnu, O. Verners, C. Zou, S. R. Phillpot, S. B. Sinnott and A. C. van Duin, Annu. Rev. Mater. Res., 2013, 43, 109–129 CrossRef CAS.
- J. E. Mueller, A. C. T. van Duin and I. William A. Goddard, J. Phys. Chem. C, 2010, 114, 4939–4949 CAS.
- G. Mazenko, J. Banavar and R. Gomer, Surf. Sci., 1981, 107, 459–468 CrossRef CAS.
- R. Wyckoff, Cryst. Struct., 1963, 1, 239–444 Search PubMed.
- K. Sugimoto, R. E. Dinnebier and J. C. Hanson, Acta Crystallogr., Sect. B: Struct. Sci., 2007, 63, 235–242 CAS.
- J. A. Kaduk, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 370–379 Search PubMed.
- http://www.crystallography.net/ .
- A. L. Kaledin, A. C. van Duin, C. L. Hill and D. G. Musaev, J. Phys. Chem. A, 2013, 117, 6967–6974 CrossRef CAS PubMed.
- C. Ferchaud, PhD thesis, Eindhoven University of Technology, 2016.
- E. Chiavazzo, M. Fasano, P. Asinari and P. Decuzzi, Nat. Commun., 2014, 5 CAS.
- H. Zhang, E. Iype, S. V. Nedea and C. C. Rindt, Mol. Simul., 2014, 40, 1157–1166 CrossRef CAS.
- P. A. J. Donkers, S. Beckert, L. Pel, F. Stallmach, M. Steiger and O. C. G. Adan, J. Phys. Chem. C, 2015, 119, 28711–28720 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02762h |
| This journal is © the Owner Societies 2016 |