Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accurate force fields and methods for modelling organic molecular crystals at finite temperatures†
Jonas
Nyman
,
Orla Sheehan
Pundyke
and
Graeme M.
Day
 *
*
School of Chemistry, University of Southampton, Southampton, UK. E-mail: g.m.day@soton.ac.uk; Tel: +44(0) 2380599174
First published on 17th May 2016
Abstract
We present an assessment of the performance of several force fields for modelling intermolecular interactions in organic molecular crystals using the X23 benchmark set. The performance of the force fields is compared to several popular dispersion corrected density functional methods. In addition, we present our implementation of lattice vibrational free energy calculations in the quasi-harmonic approximation, using several methods to account for phonon dispersion. This allows us to also benchmark the force fields' reproduction of finite temperature crystal structures. The results demonstrate that anisotropic atom–atom multipole-based force fields can be as accurate as several popular DFT-D methods, but have errors 2–3 times larger than the current best DFT-D methods. The largest error in the examined force fields is a systematic underestimation of the (absolute) lattice energy.
1 Introduction
Intermolecular interactions are central to many fields of science,1 such as supramolecular chemistry, drug formulation and crystal engineering,2 for which computational methods have been developed with the aim of ab initio crystal structure prediction (CSP).3Computational modelling of molecular crystals with force fields has a long and rich history,4–8 but recently we have seen a trend favouring density functional theory (DFT) calculations, perhaps most notably in the latest blind tests of crystal structure prediction,9–11 where accurate lattice- and free energy calculations are a cornerstone of current prediction methods.9,12,13
Crystal structure prediction is, in part, motivated by the need to anticipate polymorphism, where a molecule adopts different crystal structures under different crystallisation conditions. Differences in crystal packing between polymorphs can have important impacts on physical properties. The lattice energy difference between most polymorph pairs is smaller than 2 kJ mol−1,14,15 so that many-body dispersion,16,17 induction,18,19 lattice vibrations14,20 and pressure21,22 can affect the relative stability of polymorphs, in principle necessitating a calculation of the Gibbs free energy and very intricate computational modelling. Also, since the relevant region of predicted crystal energy landscapes typically contain tens, or even hundreds of plausible polymorphs,23,24 the computational cost associated with evaluating each crystal structure must be kept reasonable.
Because of this, it is highly desirable to have an energy model for molecular crystals that is computationally affordable while also accurate, and benchmarking studies comparing the performance of different methods are common.25–31 However, it is difficult to develop and rigorously validate computational models for molecular crystals, because of the limited amount of available high-accuracy experimental reference data on the properties of molecular crystals. Experimental sublimation enthalpies are typically limited in accuracy to ±4.9 kJ mol−1.32 Consequently, the accuracy of computational methods cannot usually be assessed to better than this margin of error.
The benchmark study by Otero-de-la-Roza and Johnson33 compared several common periodic DFT-D methods and a recently developed exchange-hole dipole moment dispersion correction method (XDM) using a set of 21 crystal structures (C21) of small organic molecules for which accurate crystal structures and sublimation enthalpies are known. Temperature-free benchmark lattice energies were obtained by calculating and subtracting thermal contributions.
The C21 benchmark set was corrected and extended by Reilly and Tkatchenko to form the X23 benchmark,34 which has rapidly become quite popular. The benchmark set is currently restricted to single component crystal structures of small organic molecules; a future extension to multi-component crystals, such as salts and co-crystals would be useful to test methods on these systems, which have industrial relevance and where a different balance of interactions might be present.
Several DFT methods and dispersion correction schemes have been assessed using the X23 set. These include the GGA functional PBE, the hybrid functionals PBE0, HSE06, B3LYP and M06-2X, two non-local van der Waals functionals and the meta-GGA functional TPSS in combination with dispersion corrections such as the Tkatchenko–Scheffler (TS), Grimme's D2/D3 and many-body dispersion (MBD) models.34–37 In addition, the PBEh-3c functional and density functional tight binding (DFTB) have been benchmarked against X23.37,38
Since the interactions between organic molecules are relatively weak, temperature changes can have a significant influence on crystal structures and their properties. Therefore, it is desirable to be able to model molecular crystals at specific temperatures. The quasi-harmonic approximation39 is commonly used to this end. However, when using force fields fitted to reproduce experimental structures, the intermolecular interaction parameters absorb some of the effects of lattice dynamics. Thus, including temperature explicitly can result in a double-counting of the thermal expansion and zero-point energy. In an effort to determine how large this error is, we also compare computationally thermally expanded crystal structures to finite-temperature experimental data.
In this study we use the X23 benchmark to assess the performance of several closely related empirically parameterised intermolecular atom–atom force fields, all derived from the work of Donald Williams,40–44 when coupled with a DFT description of intramolecular energies. In essence, we present computationally very efficient methods for modelling crystal structures at finite temperatures with highly accurate force fields.
2 Methods
2.1 Force fields and crystal structures
In this benchmark study we have assessed the performance of the following force fields in reproducing the X23 benchmark lattice energies:• FIT: the FIT force field,41 which is used with electrostatics described by distributed, atomic multipoles.
• W99_ESP: the W99 force field,42,43,44 with atomic partial charges fitted to the molecular electrostatic potential.
• W99_DMA: the W99 force field with distributed atomic multipoles.
• W99rev6311: a revised version of the W99 force field,45 which was parameterised to improve hydrogen bonding when using atomic multipolar electrostatics.
• W99rev6311P3: a revised W99 force field,45 parameterised to be used with multipoles from a charge density calculated within a polarisable continuum model (PCM) with dielectric constant εr = 3.0.
• W99rev6311P5: the same as W99rev6311P3, but using εr = 5.0 during the PCM calculation for the electrostatic model.
The force fields we benchmark here are all hybrid models that utilise a DFT model for the molecular geometry and energy, along with an intermolecular atom–atom model potential. The different force fields are strongly related and have the same functional form; an exp-6 potential for non-electrostatic intermolecular interactions and a separate treatment of electrostatics; either with atomic point charges or atomic multipoles.
All force fields included here use transferable, empirically parameterised repulsion–dispersion models. Thus, no re-parameterisation of the non-electrostatic interaction model is required when applied to a new molecule. The electrostatic model is generated from a quantum chemical calculation through either fitting to the molecular electrostatic potential or partitioning of distributed multipoles. In their original forms, FIT, W99 and W99rev provide repulsion–dispersion parameters for carbon, hydrogen, oxygen and nitrogen, though they have been used successfully with sulfur and halogen parameters taken from other sources.46
The original W99 force field, published in 2001,44 was parameterised using an atomic partial charge electrostatic model, but is often applied using an atomic multipole description of electrostatics.47–49 Therefore, we have tested W99 with both multipoles (DMA) and molecular electrostatic potential derived atomic charges (ESP).
The newer revised versions of the W99 force field were partially re-parameterised to perform optimally with distributed multipoles.45 Parameterisation was performed against a large set of low temperature crystal structures to produce a force field whose parameters have absorbed as little thermal expansion as possible. Different versions of the force field were parameterised for use with multipoles derived either from a ground state charge density of the isolated molecule (W99rev6311), or from a polarised charge density obtained by embedding the molecular calculation in a polarising environment (W99rev6311P). It has been suggested19 that the molecular DFT calculations should be performed within a polarisable continuum model50,51 (PCM) with a dielectric constant of about 3, which is a typical permittivity of organic crystals. This should to some extent model an average polarisation of the molecular electron density in the crystal structure, and the accompanying induction energy. Polarised multipoles can then be derived from the polarised charge density. We can think of this as a mean field approximation of molecular polarisation in crystals, ignoring the local polarisation of functional groups arising from specific intermolecular interactions, particularly around hydrogen bonds. If a force field is parameterised specifically to be used with PCM-derived multipoles, the localized polarisation will be partly absorbed in the repulsion–dispersion parameters. This approach was attempted in parameterising the W99rev6311P force field. A relative permittivity of 3.0 was used in the parameterisation, but in our experience higher values can lead to improvements. Here we present results for εr = 3.0 and 5.0.
We also include the older FIT potential,41 which is a revision of the W84 force field,40 again re-parameterised to perform optimally with atomic multipole electrostatics.
The force fields investigated here were parameterised with foreshortened hydrogen positions. Foreshortening moves the interaction centre of hydrogen atoms off the nucleus, along the bond towards the heavy atom to which the hydrogen is bonded. The FIT force field did not foreshorten hydrogen atom positions during parameterisation, but we find that foreshortening nevertheless improves its performance. We have therefore foreshortened the hydrogen positions of the DFT geometries by 0.1 Å during lattice energy calculations. The distributed multipoles and point charges were determined at the foreshortened H positions.
The X23 benchmark consists of 23 crystals of small organic molecules. The crystal structures were obtained from the Cambridge Structure Database (CSD),52 the supplementary data of previous articles33,34 or from primary sources.53–55 The X23 hexamine structure corresponds to the experimental structure HXMTAM0956 and the succinic acid structure is the monoclinic β polymorph, best represented by SUCACB02.57 For compatibility with the lattice energy minimiser DMACRYS, the symmetries of crystal structures with Z′ < 1 were modified to obtain whole molecules in the asymmetric unit.
2.2 Lattice energy calculations
The lattice energy consists of the intermolecular cohesive energy and an intramolecular relaxation energy, i.e. the difference in energy of the in-crystal molecular geometry and electronic structure relative to the gas phase ground state geometry.| Elatt = Eatom–atominter + EDFTintra | (1) |
The intermolecular cohesive energy between any two molecules N and M is calculated as a sum over atom–atom pair interactions:
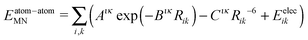 | (2) |
Atomic partial charges were fitted to the molecular electrostatic potential using the program MULFIT 2.1.60 Distributed multipoles61 were derived from the molecular charge density using GDMA 2.2.06.62
The crystal structures (except carbon dioxide) were first lattice energy-minimised using the program CrystalOptimizer 2.4.2,63,64 using the W99rev6311 force field. CrystalOptimizer minimises the sum of intra- and intermolecular energies with respect to crystal packing degrees of freedom and a set of selected intramolecular degrees of freedom (dihedrals and bond angles), chosen automatically as described previously.14 The optimised structures were then re-optimised with the different intermolecular force fields, using DMACRYS 2.0.4,46 keeping the molecular geometries rigid.
For the W99rev6311P3 and W99rev6311P5 force fields, we re-calculated the multipoles from a charge density obtained in an external-iteration polarisable continuum model with isotropic relative permittivity of 3.0 and 5.0, respectively.
Carbon dioxide was treated specially. A molecular geometry optimisation was performed in Gaussian 09 and partial charges were calculated with the CHelpG routine.65 Multipoles and a molecular local axis system were constructed by manually adding non-interacting dummy atoms.
Charge–charge, charge–dipole and dipole–dipole interactions were calculated using Ewald summation, while repulsion–dispersion interactions and all higher multipole–multipole interactions were calculated between whole molecules to a center of mass cutoff distance of 20 Å.
2.3 Modelling thermal effects
All lattice dynamics calculations were performed in the rigid-molecule approximation, as implemented in DMACRYS,46,66,67 with the FIT and W99rev6311P5 force fields. The theory of rigid molecule lattice dynamics has been described elsewhere.68–70 Our method for sampling phonon frequencies and calculating the resulting thermodynamic properties have also been described in our previous work on polymorph energy differences.14 However, recent improvements in the treatment of phonon dispersion will be described here in some detail.
A great challenge in lattice dynamics calculations lies in the convergence of the phonon density of states g(ω). The anisotropic phonon dispersion in molecular crystals necessitate that several k-points are included in the calculations, and preferably in some configuration that efficiently samples the first Brillouin zone.71,72 We sample k-points by forming several linear supercells, each elongated along one lattice vector. The supercell expansion in each direction is chosen such that the distance between the k-points is less than some target distance in reciprocal space, which we choose as 0.12 Å−1 in this work. This results in between 17 and 34 unique k-points being sampled for the crystals in the benchmark. However, sampling k-points close to the Γ-point is necessary to converge the lattice dynamical entropy and requires large supercells to yield long wavelength phonons at small k. Long supercells can be split into several shorter supercells with mutually co-prime expansion coefficients, which improves computational cost scaling, but does not improve the sampling near the Γ-point. To this end, we have implemented approximate methods to further improve the convergence, which we describe below. Results of convergence tests are included in the ESI.†
A Debye frequency ωD is calculated from the elastic stiffness tensor Cikjl obtained from DMACRYS.66 From the elastic tensor we then calculate 3 × 3 Christoffel matrices Γ for 13 direction vectors ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m in the Brillouin zone (see ESI†).
m in the Brillouin zone (see ESI†).
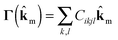 | (3) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m.
m.|Γ(![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m) − ρν2( m) − ρν2(![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m)I| = 0 m)I| = 0 | (4) |
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) (
(![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m). Assuming a sinusoidal phonon dispersion around Γ, we calculate the Debye frequency ωD(
m). Assuming a sinusoidal phonon dispersion around Γ, we calculate the Debye frequency ωD(![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m) as
m) as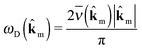 | (5) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) m we obtain the Debye frequency ωD, which is an approximation of the average phonon frequency on an ellipsoid around the Γ-point.
m we obtain the Debye frequency ωD, which is an approximation of the average phonon frequency on an ellipsoid around the Γ-point.
Adding the Debye approximation to the long wavelength acoustic phonon contributions (see eqn (8)) improves the convergence of calculated thermodynamic properties with respect to the number of sampled k-points, see Fig. S1–S4 (ESI†).
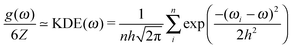 | (6) |
The choice of the kernel bandwidth h in eqn (6) is somewhat arbitrary, but by testing we have found that a suitable bandwidth can be chosen as a fraction of the standard deviation of the phonon frequencies, h = std(ωi)/20, for the k-point sampling used here. The calculated vibrational energy varies negligibly with respect to the denominator in the range 10–100, see Fig. S5 and S6 (ESI†). The kernel density estimate is not intended to smooth the density of states; we use it to model a small phonon dispersion around each explicitly sampled k-point.
The Helmholtz free energy is
| A(T) = Elatt + Fvib(T) | (7) |
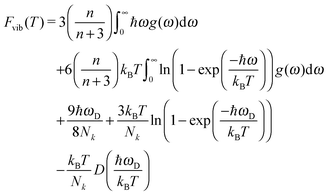 | (8) |
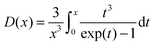 | (9) |
Naturally, carbon dioxide has only 5 intermolecular degrees of freedom, and was treated separately.
We believe that an isotropic scaling of the unit cell for the thermal pressure calculation could lead to errors, since molecular crystals can have strongly anisotropic thermal expansion. One option is to change the unit cell dimensions by directly scaling the lattice vectors in proportion to the elastic compliance constant in each direction. However, we found that the most consistent approach is to instead expand the unit cells by geometry optimising the crystal structure at a pressure different from the ambient pressure P0. We have chosen −300 MPa, taking a negative pressure as this should result in a crystal structure that is as similar to a thermally expanded structure as possible. The negative pressure causes a volume expansion between 2.4 and 7.7% in the benchmark crystal structures.
Provided that the same k-points are sampled in both the unexpanded and expanded structures, the vibrational energy varies linearly for volume changes up to about 15%, so the thermal pressure can be calculated as a finite difference between only two unit cells. The thermal pressure is then77
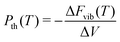 | (10) |
Again geometry optimising to minimise Elatt + PV at P = P0 − Pth results in a crystal structure close to the Gibbs free energy minimum at ambient pressure. The Gibbs free energy can then be calculated as
| G(P0,T) = Elatt(P) + Fvib(P,T) + P0V(P) | (11) |
3 Results and discussion
3.1 Lattice energies
In Fig. 2 we show a comparison of the performance of the different force fields in reproducing the X23 benchmark lattice energies. Table 1 shows the mean absolute deviation (MAD), mean absolute relative deviation (MA%D), the systematic mean error (ME) and the random error as one standard deviation (SD).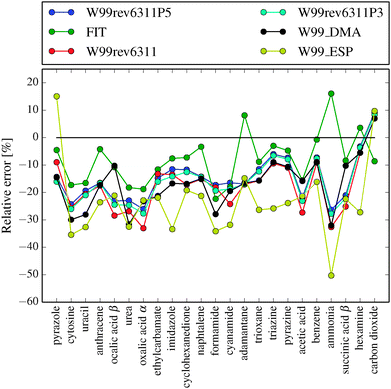 | ||
| Fig. 2 Relative errors in lattice energies for the X23 set of crystal structures calculated with six different intermolecular force fields. Negative values represent underbinding of the crystal. | ||
| Energy model | MA%D | MAD | ME | SD |
|---|---|---|---|---|
| FIT | 10.27 | 9.22 | −7.95 | 8.63 |
| W99rev6311P5 | 15.72 | 14.19 | −13.97 | 9.58 |
| W99rev6311P3 | 16.79 | 15.20 | −14.99 | 10.18 |
| W99_DMA | 17.47 | 15.70 | −15.52 | 11.27 |
| W99rev6311 | 18.28 | 16.38 | −16.21 | 10.70 |
| W99_ESP | 25.27 | 22.01 | −20.75 | 13.92 |
The force fields all systematically underbind the crystals. This is expected since the force fields were parameterised to thermally expanded experimental structures and sublimation enthalpies. Expressed as a percentage mean signed error, we have −7.9% for the FIT and −23.3% for the W99_ESP force field and the others in between.
The multipole electrostatics of W99_DMA improves on the point charge model in W99_ESP significantly, reducing errors by about a third. As was observed when re-parameterising W99,45 W99rev6311 does not significantly improve the accuracy of lattice energies compared to W99_DMA; the improvement was largely seen in how well the geometries of the structures were reproduced.
The revised force fields utilizing polarised multipoles perform better than the non-polarised version since the polarisation generally increases the strength of directional electrostatic interactions, principally hydrogen bonds, and this reduces the systematic underbinding. It is clear that the PCM method improves both the systematic and random errors. The use of a dielectric constant in the PCM calculation of 5 rather than the value 3 applied during parameterisation improves the energies further and is still in the range of reasonable dielectric constants for organic materials, so can be physically justified.
The best models in terms of lattice energy are the revised force fields with multipoles derived from a PCM model with a dielectric constant of 5 (W99rev6311P5) and the FIT force field. The latter is the most accurate of the tested force fields, and it performs remarkably well both with respect to systematic and random errors.
The accuracy of the force field results depends partly on the level of theory used for the intramolecular energies. However, apart from oxalic acid, where the crystalline geometry is calculated to be between 14.7 and 16.4 kJ mol−1 above the gas phase minimum, the molecular relaxation energies are small (less than 3.2 kJ mol−1 in the unpolarised models and up to 6.8 kJ mol−1 with PCM, εr = 5.0). Given these magnitudes, we expect that errors in the intramolecular energies are a small contribution to overall errors.
In Table 2 and Fig. 3 we compare the two best force fields with several DFT-D methods previously benchmarked against the X23 or C21 sets. For published C21 results, we have recalculated the errors relative to the X23 benchmark lattice energies and we have performed PBE-XDM and PBE-D2 calculations on hexamine and succinic acid using QuantumEspresso.78
| Energy model | MA%D | MAD | ME | SD |
|---|---|---|---|---|
| a Anthracene and naphthalene not included. | ||||
| TPSS-D335 | 5.21 | 3.84 | 0.71 | 5.13 |
| PBE-D335 | 5.75 | 4.47 | 1.63 | 5.65 |
| HSE06-D335 | 6.29 | 4.80 | 2.67 | 4.11 |
| PBE0-D335 | 6.43 | 4.67 | 2.20 | 5.85 |
| PBE-XDM33 | 7.68 | 6.51 | −2.54 | 8.67 |
PBEh-3c37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
7.8 | 5.4 | 0.4 | 7.0 |
| PBE-MBD34 | 8.05 | 5.92 | 4.73 | 5.14 |
| PBE-D233 | 9.96 | 7.83 | 6.24 | 8.15 |
| FIT | 10.27 | 9.22 | −7.95 | 8.63 |
| DFTB-D338 | 11.92 | 9.86 | −0.32 | 12.22 |
| W99rev6311P5 | 15.72 | 14.19 | −13.97 | 9.58 |
| PBE-TS34 | 17.22 | 13.40 | 13.13 | 8.62 |
| B3LYP37 | 34.7 | 27.2 | −24.6 | 28.0 |
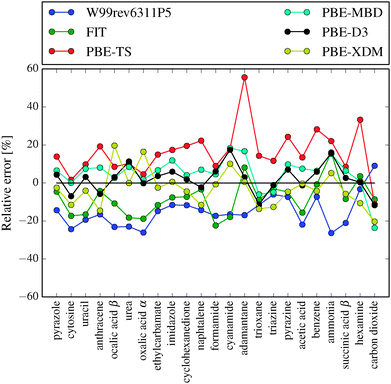 | ||
| Fig. 3 Relative error in lattice energies calculated with FIT, W99rev6311P5 and several PBE-D methods. PBE-D results reproduced from Reilly and Tkatchenko34 and Otero-de-la-Roza and Johnson.33 Negative values represent underbinding. | ||
The FIT and W99rev6311P5 force fields reproduce lattice energies better than PBE-TS and B3LYP (without dispersion correction). The random error is of the same magnitude for most of the benchmarked methods.
Most solid state calculations on molecular crystals are performed using GGA functionals, such as PBE. This is due to the cost of evaluating exact exchange, which is necessary for hybrid functionals, using plane-wave basis sets. Only with the most accurate dispersion correction methods: exchange-hole dipole (XDM), many-body dispersion (MBD) and Grimme's D3 method, is the PBE functional significantly better than the force fields we have tested here. We note that the force field-like dispersion correction used in these DFT methods has a more complex form than what is used in the current force fields: XDM uses a sum of C6, C8 and C10 dispersion terms, while MBD includes non-pairwise additive dispersion contributions. It seems reasonable to expect that the future development of force fields including such terms could reduce the gap between the current force fields and the best DFT-D methods.
The hybrid functionals HSE06 and PBE0 and the meta-GGA functional TPSS together with D3 or many-body dispersion methods are also significantly better than the force fields.35 However, even using the best DFT-D methods, the errors are only about 2 or 3 times smaller than the force field methods.
3.2 Lattice parameters and geometries
In Table 3 we compare the performance of the force fields in reproducing experimental lattice parameters, without any thermal adjustments. Symmetry-independent lattice vector lengths for 22 of the crystal structures are used, excluding urea. With the force field models, we find that the experimental tetragonal P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 21m urea structure (UREAXX02) is a vibrationally averaged structure corresponding to a saddle point on the potential energy surface.66 Breaking the symmetry results in a stable orthogonal P21212 structure. This prevents a direct comparison of lattice parameters for this structure.
21m urea structure (UREAXX02) is a vibrationally averaged structure corresponding to a saddle point on the potential energy surface.66 Breaking the symmetry results in a stable orthogonal P21212 structure. This prevents a direct comparison of lattice parameters for this structure.
The FIT force field performs very well in reproducing the experimental lattice parameters. It is comparable in accuracy to PBE-XDM. The B86b-XDM functional, PBE-TS and PBE-D2 are better than the force field methods in reproducing lattice parameters. The W99rev6311P5 force field also reproduces the crystal structures well, with the exception of benzene and naphthalene. The W99-based force fields do not perform well for crystals with aromatic ring systems in T-stacked configuration,31 see Table S3 (ESI†). However, systems in π-stacked configurations are well reproduced.28 The point charge force field W99_ESP performs significantly worse than the other methods and the errors in lattice parameters are about twice as large as the multipole-based force fields.
The errors are not systematic; the mean errors in lattice vector lengths are merely −0.03 Å and +0.04 Å for the FIT and W99rev6311P5 force fields respectively.
PBE-TS reproduces crystal geometries very well,27,33 but not lattice energies.34 Of course, an energy model must perform well on both energies and geometries to be useful and a benchmark study really should consider both. Unfortunately, this is not always done.
A common way to specify crystal structure similarity is the root mean square deviation in atomic coordinates in a cluster of molecules taken from a crystal structure.9,79 Taking 20-molecule cluster comparisons (RMSD20), the FIT and W99rev6311P5 force fields reproduce the experimental crystal structures with an average RMSD20 of 0.234 Å and 0.258 Å, respectively, see Table S3 (ESI†).
3.3 Vibrational free energies
An accurate method should reproduce the shape of the lattice energy surface well enough to give accurate vibrational energy contributions and thermal expansion. Therefore, for benchmarking purposes, we argue that these contributions should be calculated with the method being benchmarked.Lattice dynamics calculations involve a much higher computational cost than lattice energy minimisation. We and others have previously shown that it is crucially important to adequately sample phonons across the Brillouin zone to achieve reliable free energy contributions.14,20 Given the high computational expense of some of the methods currently being developed for lattice energy calculations, methods for accelerating the convergence of vibrational energies with respect to reciprocal space sampling could enable otherwise impractical free energy calculations. Furthermore, even using computationally efficient force field methods, free energy calculations can become the computational bottleneck in large studies of polymorphism or crystal structure prediction, where many hundreds of structures sometimes need to be evaluated.
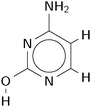
Fig. 4 shows the convergence of the calculated vibrational energy, Fvib, with respect to the target distance between sampled k-points for two of the benchmark crystal structures, benzene and acetic acid (results for urea and cyanamide are shown in the ESI†). For the purposes of testing, we treat calculations with a maximum k-point spacing of 0.1 Å−1 as converged. This corresponds to between 25 and 37 unique k-points for these four crystal structures.
The magnitude of Fvib increases (Fvib becomes more negative) as the k-point sampling density is increased, which is mainly due to including the contributions of the low frequency acoustic vibrations. For this reason, adding a Debye approximation of the acoustic modes between the Brillouin zone centre and the nearest sampled k-point improves the convergence significantly.
The KDE approach to approximating phonon dispersion around each sampled k-point also reduces errors in Fvib (Fig. 4), but by less than the Debye correction. While the energetic correction when using the KDE is sometimes small, its use has the effect of smoothing the convergence of Fvib by reducing the quantization effects resulting from discrete sampling of k-points (e.g. near 0.8 Å−1 in the benzene results and 1.0 Å−1 for acetic acid).
Used together, the Debye and KDE approximations improve the Fvib calculations dramatically, allowing accurate calculations of the vibrational energy contributions at much lower computational cost; in the cases studied here, sampling only a few k-points explicitly is sufficient.
3.4 Thermal pressures
Calculating the thermal expansion when using empirically fitted force fields could double-count the expansion, as some thermal effects have already been absorbed by the parameters of the force field. However, since modelling of thermal expansion can be important, we compare computationally thermally expanded crystal structures to the benchmark data, to see how large the errors are from this double-counting.In this work, we have used the computational efficient approach of modelling thermal expansion by including a thermal pressure during lattice energy minimization. Thermal pressures using FIT and W99rev6311P5 are reported in Table 4. Our results do not agree with the values reported by Otero-de-la-Roza and Johnson.33 The discrepancy is most likely due to the different k-point sampling, the unit cell expansion method, and our methods for improving convergence of the vibrational contributions to the free energy. We find that including phonon frequencies from a single k-point leads to inaccurate thermodynamic properties.14
| Structure | Temp. [K] | FIT | W99rev6311P5 |
|---|---|---|---|
| a Supercells of carbon dioxide were unstable during thermal expansion with FIT. | |||
| Cyclohexanedione | 133.15 | 254.3 | 239.9 |
| Acetic acid | 40.0 | 166.8 | 156.5 |
| Adamantane | 188.0 | 361.9 | 343.8 |
| Ammonia | 160.0 | 868.7 | 480.6 |
| Anthracene | 94.0 | 154.2 | 144.6 |
| Benzene | 218.15 | 192.2 | 301.5 |
| Carbon dioxide | 150.0 | —a | 991.4 |
| Cyanamide | 108.0 | 181.8 | 354.4 |
| Cytosine | 298.15 | 272.9 | 355.3 |
| Ethylcarbamine | 168.15 | 258.8 | 266.2 |
| Formamide | 90.0 | 216.9 | 241.5 |
| Imidazole | 123.15 | 286.8 | 251.9 |
| Naphtalene | 10.0 | 93.0 | 83.5 |
| Oxalic acid α | 298.15 | 629.9 | 607.9 |
| Oxalic acid β | 298.15 | 705.2 | 606.0 |
| Pyrazine | 184.0 | 371.3 | 332.9 |
| Pyrazole | 108.0 | 407.0 | 369.0 |
| Triazine | 298.15 | 825.4 | 788.9 |
| Trioxane | 103.15 | 277.5 | 262.7 |
| Uracil | 298.15 | 487.2 | 457.4 |
| Urea | 298.15 | 650.2 | 155.9 |
| Hexamine | 120.0 | 244.3 | 229.3 |
| Succinic acid β | 298.15 | 498.3 | 477.5 |
For the FIT force field, the deviations in lattice vector lengths for the thermally expanded structures are MAD = 0.188 Å and MA%D = 2.82%. The W99rev6311P5 force field yields MAD = 0.264 Å and MA%D = 3.89%. After thermal expansion, experimental crystal structure geometries are reproduced with an average RMSD20 of 0.234 Å and 0.314 Å for the two force fields respectively.
Since the force fields were parameterised to reproduce experimental crystal structures, the explicit modelling of thermal expansion here constitutes a double counting of some of the thermal expansion, although low temperature (<100 K) crystal structures were deliberately chosen in re-parameterising W99 to minimise this effect. This should cause a systematic positive error in the lattice vector lengths. However, the mean errors are only +0.14 Å and +0.05 Å for the W99rev6311P5 and the FIT force fields respectively. Again the FIT force field performs very well and does not have a large systematic overestimation of unit cell sizes.
These results confirm the soundness of the computationally very efficient thermal pressure method and that the error caused by the double-counting of implicit and explicit thermal expansion is negligible.
4 Conclusions
The FIT and W99rev6311P5 force fields perform very well for molecular crystals. Both have a relatively large systematic error in that they underestimate absolute intermolecular energies by 8 and 15% respectively, while the mean absolute deviations and random errors are comparable to several popular GGA DFT-D methods. The performance of force fields with atomic multipole electrostatics greatly reduces errors compared to an atomic partial charge model.For the application of crystal structure prediction, or other computational studies of polymorphs, the systematic error is less of a concern, as it is the stability difference between polymorphs that must be reproduced accurately. The force fields described here have random errors comparable to PBE-XDM, PBE-D2 and PBE-TS. In fact, only hybrid or meta-GGA functionals, or PBE with sophisticated (many-body or XDM) dispersion corrections outperform the force fields in reproducing experimental lattice energies and geometries. Even then, the errors are only 2 or 3 times smaller. These findings could help guide the development of better force fields, where developments in the functional form have thus-far focused largely on accurate electrostatics. More elaborate forms of dispersion in intermolecular force fields should be developed along the lines of the successful DFT dispersion correction schemes.
We have implemented methods by which it is possible to very rapidly model the thermal expansion of molecular crystals. This allows us to estimate Gibbs lattice vibrational free energies of crystals of small rigid molecules in a matter of a few CPU-hours. The accuracy of vibrational energy contributions is improved by including a Debye correction to the phonon density of states, along with a kernel density estimate of phonon dispersion around each sampled k-point. The error caused by the double-counting of some thermal contributions in empirical force fields is very small, and accurate modelling of crystals at finite temperatures can be performed with these force fields.
For future benchmarks, we encourage the consideration of both lattice energies and crystal geometries, since generally useful methods must give good accuracy in both. This must be done with care: thermal effects are large enough to significantly affect benchmarking results. In particular, 0 K calculated geometries cannot be directly compared to experimental crystal structures. Thermal pressures can be used to correct for this, but the thermal pressure (or any other method chosen to model thermal expansion) should be calculated with the method being benchmarked and phonon dispersion must be accounted for sufficiently well for accurate vibrational energies. We have described efficient methods for Brillouin zone integration that makes the calculated thermodynamic properties virtually independent of the exact choice of sampled k-points.
Since the impressive crystal structure prediction results by Neumann et al.11 in the fourth and fifth crystal structure prediction blind tests9,12 there has been a major focus on DFT-D methods in the computational crystallography community. However, other DFT-D methods have performed less well and there is little correlation between computational expense and predictive ability in currently used methods.13 One should not assume that density functional methods are always more accurate than intermolecular force fields, so long as the force field is constructed with a respect for the necessary functional form to describe the required physical interactions. When it comes to large-scale studies of organic molecular crystals, particularly crystal structure prediction, anisotropic atomic multipole based force fields are competitive with the best alternatives and should continue to be developed.
Acknowledgements
We thank Professor Neil Allan at the University of Bristol for pointing us to the work of Karo, Hardy and Gilat.71,76 The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 307358 (ERC-stG-2012-ANGLE). The authors acknowledge the use of the IRIDIS High Performance Computing Facility at the University of Southampton.References
- A. Stone, The Theory of Intermolecular Forces, Oxford University Press, 2nd edn, 2013 Search PubMed.
- G. R. Desiraju, Angew. Chem., Int. Ed., 2007, 46, 8342–8356 CrossRef CAS PubMed.
- G. M. Day, Crystallogr. Rev., 2011, 17, 3–52 CrossRef.
- A. Pertsin and A. Kitaigorodskii, The Atom–Atom Potential Method: Applications to Organic Molecular Solids, 1987 Search PubMed.
- D. E. Williams, Science, 1965, 147, 605–606 CAS.
- D. E. Williams, J. Chem. Phys., 1966, 45, 3770–3778 CrossRef CAS.
- A. Warshel and S. Lifson, J. Chem. Phys., 1970, 53, 582–594 CrossRef CAS.
- A. Gavezzotti, Molecular Aggregation, Oxford University Press, 2007 Search PubMed.
- D. A. Bardwell, C. S. Adjiman, Y. A. Arnautova, E. Bartashevich, S. X. M. Boerrigter, D. E. Braun, A. J. Cruz-Cabeza, G. M. Day, R. G. Della Valle, G. R. Desiraju, B. P. van Eijck, J. C. Facelli, M. B. Ferraro, D. Grillo, M. Habgood, D. W. M. Hofmann, F. Hofmann, K. V. J. Jose, P. G. Karamertzanis, A. V. Kazantsev, J. Kendrick, L. N. Kuleshova, F. J. J. Leusen, A. V. Maleev, A. J. Misquitta, S. Mohamed, R. J. Needs, M. A. Neumann, D. Nikylov, A. M. Orendt, R. Pal, C. C. Pantelides, C. J. Pickard, L. S. Price, S. L. Price, H. A. Scheraga, J. van de Streek, T. S. Thakur, S. Tiwari, E. Venuti and I. K. Zhitkov, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 535–551 CAS.
- M. A. Neumann, J. Phys. Chem. B, 2008, 112, 9810–9829 CrossRef CAS PubMed.
- M. A. Neumann, F. J. Leusen and J. Kendrick, Angew. Chem., Int. Ed., 2008, 47, 2427–2430 CrossRef CAS PubMed.
- G. M. Day, T. G. Cooper, A. J. Cruz-Cabeza, K. E. Hejczyk, H. L. Ammon, S. X. M. Boerrigter, J. S. Tan, R. G. Della Valle, E. Venuti, J. Jose, S. R. Gadre, G. R. Desiraju, T. S. Thakur, B. P. van Eijck, J. C. Facelli, V. E. Bazterra, M. B. Ferraro, D. W. M. Hofmann, M. A. Neumann, F. J. J. Leusen, J. Kendrick, S. L. Price, A. J. Misquitta, P. G. Karamertzanis, G. W. A. Welch, H. A. Scheraga, Y. A. Arnautova, M. U. Schmidt, J. van de Streek, A. K. Wolf and B. Schweizer, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 107–125 CAS.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadna, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. DiStasio Jr, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C.-A. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H.-Y. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vazquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu and C. R. Groom, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016 Search PubMed , in press.
- J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Chem. Soc. Rev., 2015, 44, 8619–8635 RSC.
- T. Risthaus and S. Grimme, J. Chem. Theory Comput., 2013, 9, 1580–1591 CrossRef CAS PubMed.
- N. Marom, R. A. DiStasio, V. Atalla, S. Levchenko, A. M. Reilly, J. R. Chelikowsky, L. Leiserowitz and A. Tkatchenko, Angew. Chem., Int. Ed., 2013, 52, 6629–6632 CrossRef CAS PubMed.
- G. W. A. Welch, P. G. Karamertzanis, A. J. Misquitta, A. J. Stone and S. L. Price, J. Chem. Theory Comput., 2008, 4, 522–532 CrossRef CAS PubMed.
- T. G. Cooper, K. E. Hejczyk, W. Jones and G. M. Day, J. Chem. Theory Comput., 2008, 4, 1795–1805 CrossRef CAS PubMed.
- B. P. van Eijck, J. Comput. Chem., 2001, 22, 816–826 CrossRef CAS.
- E. Boldyreva, Cryst. Growth Des., 2007, 7, 1662–1668 CAS.
- R. D. L. Johnstone, M. Ieva, A. R. Lennie, H. McNab, E. Pidcock, J. E. Warren and S. Parsons, CrystEngComm, 2010, 12, 2520–2523 RSC.
- G. M. Day, J. Chisholm, N. Shan, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2004, 4, 1327–1340 CAS.
- S. L. Price, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 313–328 CrossRef CAS PubMed.
- D. J. Carter and A. L. Rohl, J. Chem. Theory Comput., 2014, 10, 3423–3437 CrossRef CAS PubMed.
- G. J. O. Beran and K. Nanda, J. Phys. Chem. Lett., 2010, 1, 3480–3487 CrossRef CAS.
- J. Binns, M. R. Healy, S. Parsons and C. A. Morrison, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2014, 70, 259–267 CAS.
- T. S. Totton, A. J. Misquitta and M. Kraft, J. Chem. Theory Comput., 2010, 6, 683–695 CrossRef CAS PubMed.
- J. G. Brandenburg and S. Grimme, Prediction and Calculation of Crystal Structures, Springer, 2014, pp. 1–23 Search PubMed.
- C. E. S. Bernardes and A. Joseph, J. Phys. Chem. A, 2015, 119, 3023–3034 CrossRef CAS PubMed.
- P. Grančič, R. Bylsma, H. Meekes and H. M. Cuppen, Cryst. Growth Des., 2015, 15, 1625–1633 Search PubMed.
- J. S. Chickos and W. E. Acree, J. Phys. Chem. Ref. Data, 2002, 31, 537–698 CrossRef CAS.
- A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 137, 054103 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, J. Chem. Phys., 2013, 139, 024705 CrossRef PubMed.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CAS.
- R. Sure, J. G. Brandenburg and S. Grimme, ChemistryOpen, 2016, 5, 94–109 CrossRef CAS.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- J. G. Brandenburg and S. Grimme, J. Phys. Chem. Lett., 2014, 5, 1785–1789 CrossRef CAS PubMed.
- M. T. Dove, Structure and Dynamics: an atomic view of materials, Oxford University Press, 2003 Search PubMed.
- D. E. Williams and S. R. Cox, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 404–417 CrossRef.
- D. S. Coombes, S. L. Price, D. J. Willock and M. Leslie, J. Phys. Chem., 1996, 100, 7352–7360 CrossRef CAS.
- D. Williams, J. Mol. Struct., 1999, 485, 321–347 CrossRef.
- D. E. Williams, J. Comput. Chem., 2001, 22, 1154–1166 CrossRef CAS.
- D. E. Williams, J. Comput. Chem., 2001, 22, 1–20 CrossRef CAS.
- E. O. Pyzer-Knapp, H. P. G. Thompson and G. M. Day, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016 Search PubMed , in press.
- S. L. Price, M. Leslie, G. W. A. Welch, M. Habgood, L. S. Price, P. G. Karamertzanis and G. M. Day, Phys. Chem. Chem. Phys., 2010, 12, 8478–8490 RSC.
- E. O. Pyzer-Knapp, H. P. G. Thompson, F. Schiffmann, K. E. Jelfs, S. Y. Chong, M. A. Little, A. I. Cooper and G. M. Day, Chem. Sci., 2014, 5, 2235–2245 RSC.
- K. Hoxha, D. H. Case, G. M. Day and T. J. Prior, CrystEngComm, 2015, 17, 7130–7141 RSC.
- D. H. Case, J. E. Campbell, P. J. Bygrave and G. M. Day, J. Chem. Theory Comput., 2016, 12, 910–924 CrossRef CAS PubMed.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43–54 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef.
- R. Boese, D. Bläser, R. Latz and A. Bäumen, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1999, 55, IUC9900001 Search PubMed.
- R. Boese, N. Niederprüm, D. Bläser, A. Maulitz, M. Y. Antipin and P. R. Mallinson, J. Phys. Chem. B, 1997, 101, 5794–5799 CrossRef CAS.
- A. Simon and K. Peters, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2750–2751 CrossRef.
- S. P. Kampermann, J. R. Ruble and B. M. Craven, Acta Crystallogr., Sect. B: Struct. Sci., 1994, 50, 737–741 Search PubMed.
- J.-L. Leviel, G. Auvert and J.-M. Savariault, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1981, 37, 2185–2189 CrossRef.
- G. Fogarasi, J. Phys. Chem. A, 2002, 106, 1381–1390 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision D.01, Gaussian Inc, Wallingford CT, 2009 Search PubMed.
- G. Ferenczy, C. Reynolds, P. Winn and A. Stone, MULFIT: a program for calculating electrostatic potential-fitted charges, 1998 Search PubMed.
- A. Stone and M. Alderton, Mol. Phys., 2002, 100, 221–233 CrossRef.
- A. J. Stone, Distributed Multipole Analysis of Gaussian wavefunctions, GDMA version 2.2.02 Search PubMed.
- A. Kazantsev, P. Karamertzanis, C. Pantelides and C. Adjiman, CrystalOptimizer: An Efficient Algorithm for Lattice Energy Minimization of Organic Crystals Using Isolated-Molecule Quantum Mechanical Calculations, 2010 Search PubMed.
- A. V. Kazantsev, P. G. Karamertzanis, C. S. Adjiman and C. C. Pantelides, J. Chem. Theory Comput., 2011, 7, 1998–2016 CrossRef CAS PubMed.
- C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- G. M. Day, S. L. Price and M. Leslie, Cryst. Growth Des., 2001, 1, 13–27 CAS.
- G. M. Day, S. L. Price and M. Leslie, J. Phys. Chem. B, 2003, 107, 10919–10933 CrossRef CAS.
- M. Born and K. Huang, Dynamical theory of crystal lattices, Clarendon Press Oxford, 1954, vol. 188 Search PubMed.
- N. Neto, R. Righini, S. Califano and S. Walmsley, Chem. Phys., 1978, 29, 167–179 CrossRef CAS.
- S. Califano, V. Schettino and N. Neto, Lattice dynamics of molecular crystals, Springer-Verlag, Berlin, 1981, vol. 26 Search PubMed.
- G. Gilat and G. Dolling, Phys. Lett., 1964, 8, 304–306 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef.
- G. M. Day, PhD thesis, University College London, 2003.
- E. Parzen, Ann. Math. Stat., 1962, 1065–1076 CrossRef.
- M. Rosenblatt, Ann. Math. Stat., 1956, 27, 832–837 CrossRef.
- A. M. Karo and J. R. Hardy, Phys. Rev., 1969, 181, 1272 CrossRef CAS.
- O. L. Anderson, Equations of state of solids for geophysics and ceramic science, Oxford university press, 1995 Search PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. A. Chisholm and S. Motherwell, J. Appl. Crystallogr., 2005, 38, 228–231 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Additional results, a description of co-prime splitting and Debye calculations, expressions for thermodynamic properties and phonon densities of states. See DOI: 10.1039/c6cp02261h |
| This journal is © the Owner Societies 2016 |