Dynamics of internally functionalized dendrimers†
Received
11th April 2016
, Accepted 16th June 2016
First published on 16th June 2016
Abstract
The internally functionalized dendrimers are novel polymers that differ from conventional dendrimers by having additional functional units which do not branch out further. We investigate the dynamics of these structures with the inclusion of local semiflexibility and analyze their eigenmodes. The functionalized units clearly manifest themselves leading to a group of eigenvalues which are not present for homogeneous dendrimers. This part of the spectrum reveals itself in the local relaxation, leading to a corresponding process in the imaginary part of the complex dielectric susceptibility.
1 Introduction
Dendrimers are hyperbranched polymers with a very high symmetry. Due to their perfectly branched structure, dendrimers are promising materials in the fields of chemistry, biology, and medicine, see e.g., ref. 1–3. While the conventional dendrimers were synthesized several decades ago,4–7 recently new types of dendrimers have been created, see ref. 8 for review. Among them the internally functionalized dendrimers are of special interest.9–14 Their structure differs from homogeneous dendrimers: the internally functionalized dendrimers possess additional functional groups at each branching point (apart from the core). These functional units have distinct chemical properties so that they do not branch out further. As it has been highlighted in ref. 10, there are two major pathways to achieve functionalized dendrimers: premodification (i.e., functionalization before the construction of the macromolecule) or postmodification (i.e., functionalization after the construction of the macromolecule). With respect to these strategies one uses orthogonal protecting groups or groups that can be selectively activated.10 In particular, as has been recently shown,13,14 the use of orthogonal click reactions based on epoxy–amine and thiol–ene chemistry is very efficient for the introduction of functional groups at each dendritic layer. The advantage of these compounds is that the attachment of drugs or imaging agents to the internal groups can lead to good solubility and biocompatibility properties in comparison to conventional dendrimers.15 Moreover, internally functionalized dendrimers can be used as multichromophoric light-harvesting systems, in which the internal functionalization helps to establish complex energy gradients.11 Furthermore, the layers with different polarities allow the internally functionalized dendrimers to operate as unimolecular catalytic nanosytems.9
In this paper we investigate the dynamics of internally functionalized dendrimers. For their description we use the model of semiflexible treelike polymers (STPs) which includes semiflexibility by restrictions on the bonds' orientation.16 As has been shown previously for dendritic structures, such orientational restrictions are an important parameter for the characterization of dendrimers.17–21 In particular, for the local dynamics, which can be investigated by means of the dielectric or NMR relaxation,22–25 the orientational correlations cannot be disregarded.26–28 However, the STP framework leads to a higher computational effort stemming from the next-nearest neighboring interactions in the dynamical matrix. Nevertheless, due to the high symmetry of dendrimers, one can block-diagonalize the dynamical matrices very effectively as it has been shown for regular dendrimers.29 But, in contrast to regular semiflexible dendrimers,29 for which the set of eigenmodes of ref. 30 can be readily transferred, for internally functionalized dendrimers the set of eigenmodes of ref. 30 is not straightforwardly applicable. The reason for this feature lies in the symmetry breaking due to the functional units, for which the corresponding degrees of freedom have to be consecutively included. These fundamental degrees of freedom for internally functionalized dendrimers lead to an additional group of eigenvalues, which is not present for regular dendrimers. The ensuing relaxation spectrum leaves its fingerprints on the dynamic properties of the macromolecules. Here we focus on the mechanical and dielectric relaxation, and investigate, in particular, the role of the functional beads.
The paper is structured as follows: in Section 2 we recall briefly the STP-model16 and its formulas for dynamic quantities. In Section 3 we apply the STP-model to the internally functionalized dendrimers. Then, we introduce a complete set of eigenmodes which is used for the diagonalization of dynamic matrices. (The recursive construction of the resulting reduced matrices is relegated to Appendix A). We close Section 3 by analysis of the dynamics of internally functionalized dendrimers. Finally, Section 4 presents an overview of the most important results.
2 Theoretical methods
2.1 The model
The dynamics of internally functionalized dendrimers is modeled in the STP framework,16 which we recall here briefly.
The STP model describes polymers as treelike structures of N beads that are connected by springs. Moreover, the bond variables (i.e. springs) {da} are constrained to have: (i) fixed mean-square lengths, 〈da·da〉 = l2; (ii) two adjacent bonds da and db, connected by bead i, fulfilling 〈da·db〉 = ±l2qi, where qi denotes the stiffness parameter of bead i, the plus sign applies for a head-to-tail orientation of da and db and the minus sign for all other configurations of da and db; (iii) for two non-adjacent bonds da and dc, connected by the path (b1, b2,…, bk−1, bk), one has 〈da·da〉 = 〈da·db1〉〈db1·db2〉⋯〈dbk·dc〉l−2k.
As has been shown in ref. 16, the above listed restrictions (i)–(iii) on bonds {da} lead to the potential energy V({da}),
| |  | (1) |
where
K is the spring constant that is related to temperature
T and the mean-squared bond length
l2 by
K = 3
kBT/
l2. In
eqn (1) the matrix
W = (
Wab) is very sparse; its nonzero elements are either diagonal or related to adjacent bonds. It was shown in
ref. 16 that the restriction (iii) follows from maximizing entropy under constraints (i) and (ii) and therefore no Lagrange multipliers associated with restriction (iii) are needed,
i.e., the corresponding entries of
W are zeros.
We note that the vectors {ri} labeling the beads' positions are related to the bonds' vectors {da} through
| |  | (2) |
where
G is the so-called incidence matrix
31 and T denotes the transposition. Each line of
GT is related to a bond and contains only two nonzero entries (+1 and −1) on the places related to the beads connected by the bond.
31 Transforming
eqn (1) to bead variables (using
eqn (2)) yields the matrix
ASTP ≡
GWGT. Given that
W couples only adjacent bonds and that the nonvanishing elements of
G are related only to beads directly connected by a bond, the nonzero elements of
ASTP are either diagonal or related to the nearest neighboring (NN) and to the next-nearest neighboring (NNN) beads,
vide infra.
The dynamics of a polymer is described by a set of 3N Langevin equations. The equation for the x-component of vector ri labeling the position of the ith bead reads
| | 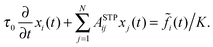 | (3) |
Here
τ0 =
ζ/
K, where
ζ is the friction coefficient and
K is the spring constant. Moreover,
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) i
i(
t) is the
x-component of the stochastic force obeying white noise relations. Furthermore, the structure of a polymer (connectivity and local stiffness) is coded through the matrix
ASTP = (
ASTPij), whose elements are known in a closed form.
16 To introduce them,
Fig. 1 shows the NN and NNN of a bead
i of a treelike structure. The NN beads of
i are denoted by
ik and the NNN ones by
iks. With this notation, the elements of the matrix
ASTP read as follows:
| |  | (4) |
| |  | (5) |
and
| | 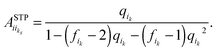 | (6) |
Here,
fi and
fik or
qi and
qik denote the functionality or the stiffness of the beads
i and
ik, respectively. All other elements of the matrix
ASTP vanish.
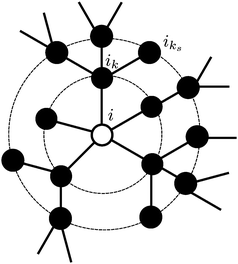 |
| | Fig. 1 Nearest (e.g., ik) and next-nearest (e.g., iks) neighbors of a bead i of a treelike network. | |
2.2 Dynamic quantities
The properties of the matrix ASTP are fundamental for the dynamics of STP.32,33 Using the eigenvalue spectrum of the matrix ASTP one can compute the complex shear modulus G*(ω) = G′(ω) + iG′′(ω).34G′(ω) denotes the storage modulus and G′′(ω) the loss modulus. Using dimensionless variables one can obtain the reduced moduli33| |  | (7) |
and| | 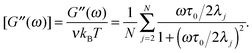 | (8) |
The sum includes all non-vanishing eigenvalues {λj}. The eigenvalue λ1 = 0 and its corresponding eigenvector describe the translation of the whole macromolecule.
Using additionally the eigenvectors of the matrix ASTP one can compute further quantities like the autocorrelation function
| | | Ma1(t) ≡ 〈da(t)·da(0)〉/l2 | (9) |
which turns out to read
27,35| |  | (10) |
Here the matrix
Q is constructed from the eigenvectors and the sum runs over all non-vanishing eigenvalues. As we proceed to show in Section 3.2 the eigenvalues {
λj} are usually very degenerate for symmetric hyperbranched structures. Denoting the amount of different nonvanishing eigenvalues by
χ(
G),
eqn (10) can be rewritten as
| |  | (11) |
with
τk ≡
τ0/
λk. The coefficient
Cak stands for
| |  | (12) |
where the sum runs over all eigenvectors belonging to the eigenvalue
λk. Using this coefficient one can determine through the Fourier–Laplace transform the complex dielectric susceptibility
ε*(
ω) =
ε′(
ω) − i
ε′′(
ω) for any segment
da.
36 The real and complex parts read
37| | 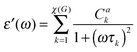 | (13) |
and
| |  | (14) |
respectively, where the sums run over the distinct nonvanishing eigenvalues.
3 Results and discussion
3.1 Analysis of ASTP for SFDs
In this subsection we analyze the matrix ASTP for semiflexible, internally functionalized dendrimers (SFDs).
First of all, we recall the topology of these structures. The internally functionalized dendrimers differ from homogenous dendrimers by having additional functional beads which do not branch out further. The construction of a functionalized dendrimer is analogous to the homogeneous ones wherein the core bead is connected to fC beads and all the other beads to f beads. Therefore, the difference r = f − fC gives the number of functional beads attached to each bead except the core. Thus, setting fC = f leads to a homogeneous dendrimer of functionality fC. The number of beads of an SFD is hence given by the number of beads of a homogeneous dendrimer38 plus the number of functional beads,
| |  | (15) |
Fig. 2 shows the topology of an internally functionalized dendrimer of functionalities
fC = 3 and
f = 4 and generation
G = 3.
 |
| | Fig. 2 Schematic drawing of an internally functionalized dendrimer of functionalities fC = 3 and f = 4 and generation G = 3. The different shells g = 1, g = 2, and g = 3 are indicated by dashed circles. The functional beads are depicted in red. | |
Based on the SFD structure, the matrix elements of ASTP, which for an SFD we will call in the following by ASFD, can be readily constructed. We assume a homogeneous situation which means that all internal beads except the core have the stiffness value q. The core being different from all other beads has a stiffness value qC. First, we present the diagonal elements {ASFDii}, then the NN elements  , and at last the NNN elements
, and at last the NNN elements  .
.
For the diagonal elements one obtains eight different situations (for visualization, see Fig. 3, where the open circles mark the beads corresponding to the discussed matrix element):
(a) If i is a peripheral or functional bead, one has fi = 1. Moreover, i has exactly one neighbor with functionality f (for G ≥ 2). Using eqn (4), the element ASFDii, denoted by μ1, equals
| | 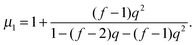 | (16) |
(b) For
G = 2, a bead in the first shell has functionality
f and possesses (
f − 1) peripheral neighbors. The core is its inner neighbor with functionality
fC. With this, the matrix element reads
| |  | (17) |
(c) For
G > 2, a bead adjacent to a peripheral bead has functionality
f. Its (
f − 1) neighbors are peripheral and the remaining one inner neighbor has functionality
f. It follows
| |  | (18) |
(d) A bead adjacent to the core has functionality
f for
G > 2. Hence, one of its neighbors (namely, the core) has functionality
fC,
r neighbors have functionality 1 and (
fC − 1) neighbors have functionality
f. Therefore, one has
| |  | (19) |
(e) A bead well inside the dendrimer of
G > 2 has functionality
f and possesses
fC neighbors with functionality
f and
r neighbors with functionality 1. Therefore, the matrix element reads
| |  | (20) |
(f) The core has functionality
fC and (for
G ≥ 2)
fC neighbors with functionality
f. This leads to
| |  | (21) |
(g) For
G = 1, the core has
fC neighbors with functionality 1, so the matrix element reads
| |  | (22) |
(h) For
G = 1, a peripheral bead has one neighbor with functionality
fC, therefore, one has
| |  | (23) |
 |
| | Fig. 3 Schematic drawing represents the diagonal elements of the matrix ASFD. The core is depicted in orange, the other internal beads in black, the functional beads in red, and the peripheral beads in blue. Open circles mark the beads which are related to the elements {μi}. | |
Next, we turn to the NN elements, the corresponding interactions are depicted in Fig. 4 by wavy lines. There are four different elements:(i) If one of the beads is peripheral or functional, the other bead has functionality f (for G ≥ 2). Eqn (5) then leads to the matrix element, denoted by ν1,
| |  | (24) |
(j) If one of the beads is the core, the other bead has functionality
f (if
G ≥ 2). Therefore, one gets
| |  | (25) |
(k) If both beads are inside the dendrimer, but none of them is the core, they have functionality
f, which leads to
| |  | (26) |
(l) For
G = 1, the element related to the core and to a peripheral bead reads
| |  | (27) |
 |
| | Fig. 4 Schematic drawing of the nonvanishing nondiagonal elements of the matrix ASFD, where the corresponding interactions are indicated by wavy lines. The color scheme is as in Fig. 3. | |
The NNN elements  depend only on the bead between the two considered beads, see eqn (6). Therefore, there are two possible distinct elements (the corresponding situations are exemplarily shown in Fig. 4):
depend only on the bead between the two considered beads, see eqn (6). Therefore, there are two possible distinct elements (the corresponding situations are exemplarily shown in Fig. 4):
(m) If the middle bead is the core, eqn (6) leads to
| |  | (28) |
(n) If the middle bead is an inner bead with functionality
f, one has
| |  | (29) |
All other elements of the matrix
ASFD vanish.
3.2 Eigenmodes
In this subsection, we present a complete set of eigenvectors of the matrix ASFD. The construction of the set is based on the fundamental procedure which was first introduced for flexible, homogeneous dendrimers30 (of functionality f = 3) and later generalized for other flexible dendritic structures.38–40 In ref. 29 it was shown that the same construction of eigenvectors is valid also in the semiflexible case. Here, we extend these methods to examine SFDs of functionalities f and fC and generation G.
Using the symmetry and the SFD structure, the set of eigenvectors can be divided into (G + 1) groups. The first group consists of all eigenmodes in which only peripheral beads are moving. The second group consists of the eigenmodes in which the peripheral and their NN are moving. This scheme continues until the group (G + 1) is reached in which all the beads including the core are moving, see Fig. 6 and 7 for an illustration.
To be able to describe the eigenmotions of the SFD more accurately, we introduce the notation of the subwedge. A subwedge is a part of the dendrimer which starts with another bead rather than the core. Fig. 5 depicts subwedges ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (G
(G![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ) of different generations G
) of different generations G![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) .
.
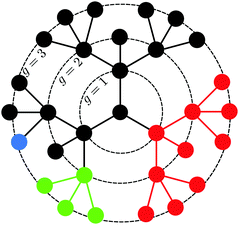 |
| | Fig. 5 Functionalized dendrimer of generation G = 3 with functionalities fC = 3 and f = 4. The color codes different subwedges ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (G (G![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ): ): ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (1) (blue), (1) (blue), ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2) (green), and (2) (green), and ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (3) (red). (3) (red). | |
As discussed in Section 2.1, the dynamics of SFDs is given by a set of Langevin equations, eqn (3). The corresponding set of homogeneous differential equations reads
| |  | (30) |
By choosing convenient eigenmodes, the system of equations can be simplified to a few nontrivial equations.
The first group of eigenmodes consists of eigenvectors which describe the movement of two NNN peripheral beads, see Fig. 6. Denoting the two moving beads as i and j, the amplitudes xl in eqn (30) read
| | | xl = 0 for i ≠ l ≠ j. | (32) |
Here,
x1 labels the single nonvanishing amplitude. Using the respective matrix elements, the single nontrivial equation of motion reads
| | | −τ0ẋ1 = μ1x1 − ρ2x1 = (μ1 − ρ2)x1. | (33) |
All other equations of motion are trivial. For the NN and NNN of the beads
i and
j, the terms of the two moving beads cancel each other because they move with the same amplitude but in the opposite direction. This is sufficient to leave the rest of the dendrimers in rest as well. Therefore, there is one eigenvalue belonging to the first group of eigenmodes, denoted by
λ(1). The described motion involves any two NNN peripheral beads. Each subwedge
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2)
(2) contains (
f − 1) peripheral beads which leads to (
f − 2) different, linear independent eigenvectors. Given that the number of
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2)
(2) subwedges is equal to
fC(
fC − 1)
G−2, the eigenvalue
λ(1) for
r ≤ 1 is
fC(
fC − 1)
G−2(
f − 2)-fold degenerate.
 |
| | Fig. 6 (a) A sketch of a possible motion related to the first group. (b) A sketch of a possible motion related to the first group involving two functional beads of an SFD of functionalities fC = 3 and f = 5. The moving beads i and j are highlighted by color. See text for details. | |
In the case of generation G = 1 one has to use different matrix elements which leads to the equation of motion
Furthermore, having r ≥ 2, the movement of two functional NN beads (see Fig. 6(b)) exactly leads to the same equation of motion as eqn (33) and therefore to the same eigenvalue. Hence, the eigenvalue λ(1) is additionally  -fold degenerate. Altogether, the degeneracy of the eigenvalue connected to the first group is
-fold degenerate. Altogether, the degeneracy of the eigenvalue connected to the first group is
| |  | (35) |
The second group consists of eigenvectors which describe the motion of two subwedges
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2)
(2) against each other, see
Fig. 7(a). Because of symmetry, all topologically equivalent beads of one subwedge move with the same amplitude, the respective beads of the other subwedge with the same amplitude in the opposite direction. There are two eigenvalues belonging to this group, denoted by
λ(2)1 and
λ(2)2. Following an analogous discussion as above, the degeneracy of each of the eigenvalue is
| | | D2 = fC(fC − 1)G−3(fC − 2). | (36) |
 |
| | Fig. 7 (a) A sketch of a possible motion related to the second group. (b) A sketch of a possible motion related to the third group. The involved subwedges are colored in green and orange. See text for details. | |
The third group of eigenmodes describes the motion of two subwedges ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (3), see Fig. 7(b). Here appears the first structural difference to the homogeneous dendrimer29 because the subwedge
(3), see Fig. 7(b). Here appears the first structural difference to the homogeneous dendrimer29 because the subwedge ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (3) includes r nonperipheral functional beads. These beads are described by another matrix element than the internal beads in the same shell. Therefore, an extra equation of motion is required. This means that the change in the topology leads to an extra degree of freedom. Hence, there are four eigenvalues connected to the third group of eigenmodes instead of three as it is in the case of homogeneous dendrimers. The respective degeneracy is given by
(3) includes r nonperipheral functional beads. These beads are described by another matrix element than the internal beads in the same shell. Therefore, an extra equation of motion is required. This means that the change in the topology leads to an extra degree of freedom. Hence, there are four eigenvalues connected to the third group of eigenmodes instead of three as it is in the case of homogeneous dendrimers. The respective degeneracy is given by
| | | D3 = fC(fC − 1)G−4(fC − 2). | (37) |
Now, one additional degree of freedom appears in each iteration from one group to the next one. That means, continuing the procedure leads to two new degrees of freedom for each transition, one for the internal beads of the new involved shell and one for its functionalized beads. Therefore, to the n-th group of eigenmodes (n = 2,…,G) belongs 2(n − 1) eigenvalues. The degeneracy is given by
| | | Dn = fC(fC − 1)G−n−1(fC − 2) | (38) |
for
n = 2,…, (
G − 1) and by
DG =
fC − 1 for the
G-th group.
In the group (G + 1) all beads including the core are moving. All topologically equivalent beads move with the same amplitude which leads to (2G − 1) degrees of freedom and therefore to (2G − 1) nondegenerate eigenvalues.
To verify that this set of eigenmodes is complete one has to show that their number is equal to the number of beads N. The number of eigenmodes is given by
| |  | (39) |
Here we used
eqn (15) giving the number of beads of an SFD.
3.3 Reduced matrices
The knowledge of eigenmodes presented in Section 3.2 allows formulating the respective reduced Langevin equations for each group. The eigenvalues can be then determined by diagonalizing the corresponding reduced matrices.
In the first group of eigenmodes, two peripheral NNN beads move against each other. The Langevin equation is given by
| | | −τ0ẋ1 = μ1x1 − ρ2x1 = (μ1 − ρ2)x1. | (40) |
Hence, the respective eigenvalue reads
| |  | (41) |
for
G ≥ 2. For
G = 1,
q has to be replaced by
qC.
The second group leads to the system of equations (G ≥ 3)
| | 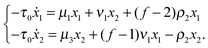 | (42) |
For
G = 2, the second equation of set
(42) changes to
| | | −τ0ẋ2 = μ2x2 + (f − 1)ν1x1 − ρ1x2. | (43) |
The coefficient matrix for these two cases (
G ≥ 3 and
G = 2) reads
| |  | (44) |
Here and in the following, the first index in the last matrix entry has to be used in the case
n <
G and the second index in the case
n =
G, where
n denotes the discussed group of eigenmodes.
For the third group of eigenmodes, one gets the reduced matrix
| |  | (45) |
Here, different from homogeneous dendrimers, one observes the additional row and column, as discussed in Section 3.2.
By following this procedure one can construct iteratively the matrices up to group G. These matrices are relegated to the Appendix.
Next, we discuss the group (G + 1). In this group, all beads including the core are mobile. All beads which are topologically equivalent move with the same amplitude. For a dendrimer of generation G = 1 the system of equations of motion for the second group reads
| |  | (46) |
Therefore, the corresponding reduced matrix is given by
| | 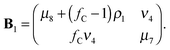 | (47) |
For generations two and three one gets
| |  | (48) |
and
| | 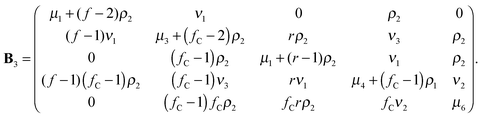 | (49) |
The Bn-matrices for n > 3 can be constructed iteratively from the matrices of an SFD of the previous generations. As for An, these matrices can be found in the Appendix.
3.4 Dynamics of SFDs
We start the discussion of dynamic properties of an SFD by the analysis of the eigenvalue spectrum of ASFD. Using the reduced matrices of Section 3.3, one can easily compute the eigenvalue spectrum of a very large SFD.
Fig. 8(a) shows the eigenvalue spectra of an SFD of generation G = 10. The core's functionality is fC = 3, its stiffness parameter is qC = 0.49. The functionality of the inner beads is f = fC + r, their stiffness parameter follows  . Such choice of q ensures that both stiffness parameters reach the two limiting cases at the same time.33,41,42 One can observe in Fig. 8(a) that the eigenvalue
. Such choice of q ensures that both stiffness parameters reach the two limiting cases at the same time.33,41,42 One can observe in Fig. 8(a) that the eigenvalue  takes a larger part of the spectrum with increasing amount of functional beads. This is obvious since this eigenvalue describes the motion of two peripheral beads against each other. The number of such beads increases for growing r. On the left-hand side of this plateau there is a difference between the cases r = 0 and r ≠ 0. While the plateau of eigenvalue
takes a larger part of the spectrum with increasing amount of functional beads. This is obvious since this eigenvalue describes the motion of two peripheral beads against each other. The number of such beads increases for growing r. On the left-hand side of this plateau there is a difference between the cases r = 0 and r ≠ 0. While the plateau of eigenvalue  for r = 0 is preceded by a jump from another (smaller) plateau, for r ≠ 0, the transition to this plateau is rather steady. The corresponding in-between eigenvalues (which do not exist for the homogeneous dendrimer, r = 0) originate from the additional degrees of freedom due to the functional beads. As discussed in Sections 3.2 and 3.3 these degrees of freedom appear starting from the third group, i.e. they exist for dendrimers of G ≥ 3.
for r = 0 is preceded by a jump from another (smaller) plateau, for r ≠ 0, the transition to this plateau is rather steady. The corresponding in-between eigenvalues (which do not exist for the homogeneous dendrimer, r = 0) originate from the additional degrees of freedom due to the functional beads. As discussed in Sections 3.2 and 3.3 these degrees of freedom appear starting from the third group, i.e. they exist for dendrimers of G ≥ 3.
 |
| | Fig. 8 (a) Eigenvalue spectra and (b) the corresponding reduced loss moduli of an SFD of generation G = 10 and functionality fC = 3 with different amounts of functional beads, r = f − fC, see text for details. In (a) the highlighted area indicates the eigenvalues of an SFD (r ≥ 1) that originate from the additional degrees of freedom due to the functional beads. | |
Based on the spectra of Fig. 8(a) we compute the reduced loss moduli [G′′(ω)] which we show in Fig. 8(b). (We focus on the loss modulus because it typically displays a richer structure than the corresponding storage modulus.33) As can be inferred from Fig. 8(b), the increasing influence of the eigenvalue  manifests itself in increasing significance of the left maximum. The growth of the jump after this eigenvalue with a larger amount of functional beads squeezes the region of higher eigenvalues; consequently leading to a shift of the right maximum to higher frequencies.
manifests itself in increasing significance of the left maximum. The growth of the jump after this eigenvalue with a larger amount of functional beads squeezes the region of higher eigenvalues; consequently leading to a shift of the right maximum to higher frequencies.
Now, holding the functionality of the core fixed and varying the amount of functional beads leads to a different functionality of all other beads. Thus, it is also interesting to compare a homogeneous dendrimer of functionality f = 4 (r = 0) and stiffness parameter q = 0.32 with an SFD of functionalities fC = 3 and f = 4 and stiffness parameters qC = 0.48 and q = 0.32. Therefore, we have a comparable setup concerning the functionalities and stiffness, while the number of beads of the two dendrimers differs. Fig. 9(a) shows the eigenvalue spectra of the considered dendrimers (and the corresponding SFD spectrum, rescaled with the number of beads). One can see that the spectra look similar after rescaling. The significant difference is the absence of a jump for SFDs in front of the longest plateau as discussed above. There are also minor differences in some of the eigenvalues and in their degeneracy, but they are rather insignificant. Therefore, these two spectra lead to very similar loss moduli as shown in Fig. 9(b). This feature can be traced back to the fact that the periphery of the dendrimers contains a large part of the molecular mass, so that it influences very much the mechanical relaxation, what has been also observed for heterogeneous dendrimers.43
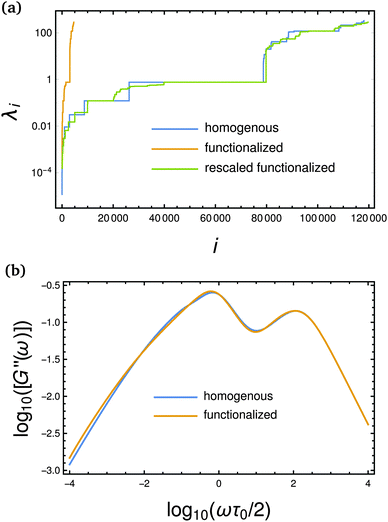 |
| | Fig. 9 (a) Eigenvalue spectra of a homogeneous dendrimer (f = 4, q = 0.32) and an SFD (fC = 3, qC = 0.48, f = 4, q = 0.32) of generation G = 10. The green line represents the rescaled spectrum of the SFD. (b) Reduced loss moduli computed based on the spectra of figure (a). See text for details. | |
Since one can find a homogeneous counterpart to SFDs which lead to similar mechanical relaxation moduli, we are going to look at local properties of such counterparts. The relaxation of single segments is described by the correlation function Ma1(t) (see eqn (10)). This quantity requires the knowledge of coefficients involving eigenvectors. Although one can do rigorous calculations of these coefficients by means of projection operator44 or reduced description42 techniques, here for investigation of the local properties it is enough to perform brute-force computations for an SFD of a smaller generation. Hence in the following we discuss dendrimers of generation G = 5 and the setup of Fig. 9.
Fig. 10(a) shows the autocorrelation function Ma1 for different segments of a homogeneous dendrimer and of an SFD as a function of time. Due to the symmetry, for homogeneous dendrimers the segments belonging to the same shell g have the same dynamics. For SFDs there are two types of segments (functionalized and non-functionalized) in each shell g > 1, see Fig. 2. In order to have a direct correspondence to the homogeneous dendrimer, we consider for the SFD non-functionalized segments only. One can see that the relaxation of the segments of the homogeneous dendrimer is slower than that of the corresponding ones of the SFD. The difference is smaller for the more peripheral segments. To understand this behaviour we look at the amplitudes Cak of the relaxation decays given by eqn (12) for different relaxation times τk = τ0/λk, see Fig. 10(b). As is known,27 homogeneous semiflexible dendrimers have one dominating coefficient Cak for each shell. The same behaviour we find for the SFD, as can be observed in Fig. 10(b). However, in the case of SFDs the dominating coefficient has a smaller influence than for the homogeneous dendrimer. Moreover, for SFDs there are some additional amplitudes in the region between τ0 and 10τ0. These amplitudes arise from the eigenvalues in front of the plateau  in the eigenvalue spectrum, as it was observed in Fig. 8. Furthermore, for each shell g > 1 the most significant relaxation time of SFDs is smaller than that of the homogeneous dendrimer. These two facts lead to faster decaying correlation functions for higher g.
in the eigenvalue spectrum, as it was observed in Fig. 8. Furthermore, for each shell g > 1 the most significant relaxation time of SFDs is smaller than that of the homogeneous dendrimer. These two facts lead to faster decaying correlation functions for higher g.
 |
| | Fig. 10 (a) Autocorrelation function Ma1(t) and (b) the corresponding amplitude Cak of the relaxation decays of different segments of a homogeneous (f = 4) and a functionalized (fC = 3, f = 4) dendrimer of generation G = 5. In (a) the solid lines are related to segments of the homogeneous dendrimer, while the dashed lines represent the results of the corresponding non-functional segments of the SFD. In (b) the dots indicate the amplitude Cak for the homogeneous dendrimer and the triangles for the SFD. The dendrimers' shells are numbered by g in an ascending order, starting from the core shell, as indicated in Fig. 2. | |
Now, using the amplitude Cak one can compute the real part ε′(ω) and the imaginary part ε′′(ω) of the complex dielectric susceptibility, see eqn (13) and (14). Here we focus on the ε′′(ω) since it displays more emphasized differences. Fig. 11 shows the ε′′(ω) computed based on the amplitudes of Fig. 10(b). As can be inferred from the figure, ε′′(ω) is dominated by two processes. The right maximum originates from the large eigenvalues, i.e. from the relaxation times τk < τ0. This maximum is less pronounced since the corresponding amplitudes Cak are small in this region. The left maximum originates mostly from the dominating, very large amplitude. Moreover, for lower g the left maximum appears for the SFD at a bit higher frequencies than for the corresponding shells of the homogeneous dendrimer. This indicates that the viscosity and the gyration radius of the SFD is a bit lower than those of the corresponding homogeneous dendrimer, because the behavior of these characteristics is dominated by lower eigenvalues, see the ESI† for details. Now, for functionalized dendrimers there is an additional shoulder in the intermediate frequency region, which is significantly developed especially for internal shells (i.e. for lower g). This additional process in the ε′′(ω) arises from the relaxation times between τ0 and 10τ0, see Fig. 10(b). Thus the presence of functional beads is clearly manifested in the local dynamics of the non-functionalized segments on intermediate frequencies. We note that for fully-flexible structures the presence of the additional process in ε′′(ω) is hardly pronounced, i.e., the semiflexibility highlights the presence of functionalized units, see the ESI† for details.
 |
| | Fig. 11 Imaginary part of the complex dielectric susceptibility corresponding to the structures of Fig. 10. The lines and the color code are the same as in Fig. 10. | |
We close this section by discussing the role of the dendrimers' generation G. In Fig. 12 we display the autocorrelation function Ma1(t) and the corresponding imaginary part of the complex dielectric susceptibility ε′′(ω) for different shells g of an SFD of generations G = 5 and G = 7. As it was observed for homogeneous dendrimers,27 for higher g the curves overlap each other: the corresponding segments feel the size of the branches which originated from them, but not the total size of the dendrimer, i.e., G. The behavior of the core segments is somewhat different. Here the difference between the core beads and all other beads is also revealed. In particular, the similarity of neighborhood for core segments of both dendrimers (G = 5 and G = 7) is reflected in the initial decay of Ma1(t) or at higher frequencies of ε′′(ω).
 |
| | Fig. 12 (a) Autocorrelation function Ma1(t) and (b) the corresponding imaginary part of the complex dielectric susceptibility ε′′(ω) for functionalized (fC = 3, f = 4) dendrimers of generations G = 5 (dashed lines) and G = 7 (solid lines). The dendrimers' shells are numbered by g in an ascending order, starting from the core shell, as indicated in Fig. 2. | |
4 Conclusions
In this work we studied the dynamics of semiflexible, internally functionalized dendrimers (SFDs). Based on their symmetry we have block-diagonalized the dynamical matrix stemming from the STP framework. The ensuing reduced matrices grow linearly with the generation G of the dendrimer, whose molecular mass has an exponential dependence on G. The reduced scheme provides not only the computational effort, but also gives a better understanding of the SFD's eigenmotions. Starting from generation G = 3 the SFD eigenmodes become distinct from those of a homogeneous dendrimer. These differences come from the functional beads inside the SFD, resulting in the group of new relaxation times close to the segmental relaxation time. While the mechanical relaxation of SFDs is mostly determined by the peripheral shells, and hence one can find for each SFD a homogeneous counterpart with a similar behavior, the local dynamic properties allow uncovering the presence of functional units. These lead to an additional process (related to the group of new relaxation times close to the segmental relaxation time) in the imaginary part of the complex dielectric susceptibility in the intermediate frequency region.
A Appendix
Here we present reduced matrices An and Bn for n > 3.
The fourth and fifth groups of eigenmodes lead to the matrices
| |  | (50) |
and
| |  | (51) |
For higher groups the matrices can be constructed iteratively. The matrix
An is a 2(
n − 1) × 2(
n − 1)-matrix and it reads
| |  | (52) |
where the matrix
Ãn−1 is obtained by crossing out the last row and the last column of the matrix
An−1.
The B-matrices of generations four and five read
| |  | (53) |
and
| |  | (54) |
For higher generations, the matrix can be given in an iterative form. The matrix
Bn (
n = 6,…,
G) is of the dimension (2
n − 1) × (2
n − 1) and reads
| |  | (55) |
where the matrix
![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) n−1
n−1 is obtained by crossing out the last row and the last column of the matrix
Bn−1 and replacing its last entry (
i.e. (
Bn−1)
2n−4,2n−4) by
μ5 + (
fC − 2)
ρ2.
Acknowledgements
The authors appreciate the fruitful discussions with Alexander Blumen and Florian Fürstenberg. M. D. acknowledges the support of the Deutsche Forschungsgemeinschaft (Grant No. GRK 1642/1).
References
- D. Astruc, E. Boisselier and C. Ornelas, Chem. Rev., 2010, 110, 1857–1959 CrossRef CAS PubMed.
- K. Inoue, Prog. Polym. Sci., 2000, 25, 453–571 CrossRef CAS.
- F. Vögtle, S. Gestermann, R. Hesse, H. Schwierz and B. Windisch, Prog. Polym. Sci., 2000, 25, 987–1041 CrossRef.
- E. Buhleier, W. Wehner and F. Vögtle, Synthesis, 1978, 155–158 CrossRef CAS.
- G. R. Newkome, Z. Yao, G. R. Baker and V. K. Gupta, J. Org. Chem., 1985, 50, 2003–2004 CrossRef CAS.
- D. A. Tomalia, H. Baker, J. Dewald, M. Hall, G. Kallos, S. Martin, J. Roeck, J. Ryder and P. Smith, Polym. J., 1985, 17, 117–132 CrossRef CAS.
- C. J. Hawker and J. M. J. Fréchet, J. Am. Chem. Soc., 1990, 112, 7638–7647 CrossRef CAS.
- M. Sowinska and Z. Urbanczyk-Lipkowska, New J. Chem., 2014, 38, 2147–2708 RSC.
- M. E. Piotti, F. Rivera, R. Bond, C. J. Hawker and J. M. J. Fréchet, J. Am. Chem. Soc., 1999, 121, 9471–9472 CrossRef CAS.
- S. Hecht, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 1047–1058 CrossRef CAS.
- W. R. Dichtel, S. Hecht and J. M. Fréchet, Org. Lett., 2005, 7, 4451–4454 CrossRef CAS PubMed.
- P. Antoni, Y. Hed, A. Nordberg, D. Nyström, H. von Holst, A. Hult and M. Malkoch, Angew. Chem., 2009, 121, 2160–2164 CrossRef.
- T. Kang, R. J. Amir, A. Khan, K. Ohshimizu, J. N. Hunt, K. Sivanandan, M. I. Montañez, M. Malkoch, M. Ueda and C. J. Hawker, Chem. Commun., 2010, 46, 1556–1558 RSC.
- I. Gadwal and A. Khan, RSC Adv., 2015, 5, 43961–43964 RSC.
- E. Lallana, F. Fernandez-Trillo, A. Sousa-Herves, R. Riguera and E. Fernandez-Megia, Pharm. Res., 2012, 29, 902–921 CrossRef CAS PubMed.
- M. Dolgushev and A. Blumen, J. Chem. Phys., 2009, 131, 044905 CrossRef PubMed.
- R. La Ferla, J. Chem. Phys., 1997, 106, 688–700 CrossRef CAS.
- A. Kumar and P. Biswas, Macromolecules, 2010, 43, 7378–7385 CrossRef CAS.
- A. Kumar and P. Biswas, J. Chem. Phys., 2012, 137, 124903 CrossRef PubMed.
- A. Kumar and P. Biswas, Soft Matter, 2013, 9, 2375–2379 RSC.
- G. J. Rai, A. Kumar and P. Biswas, J. Rheol., 2016, 60, 111–120 CrossRef CAS.
- L. F. Pinto, J. Correa, M. Martin-Pastor, R. Riguera and E. Fernandez-Megia, J. Am. Chem. Soc., 2013, 135, 1972–1977 CrossRef CAS PubMed.
- L. F. Pinto, R. Riguera and E. Fernandez-Megia, J. Am. Chem. Soc., 2013, 135, 11513–11516 CrossRef CAS PubMed.
- F. Mohamed, M. Hofmann, B. Pötzschner, N. Fatkullin and E. A. Rössler, Macromolecules, 2015, 48, 3294–3302 CrossRef CAS.
- M. Hofmann, C. Gainaru, B. Cetinkaya, R. Valiullin, N. Fatkullin and E. A. Rössler, Macromolecules, 2015, 48, 7521–7534 CrossRef CAS.
- A. Kumar and P. Biswas, Phys. Chem. Chem. Phys., 2013, 15, 20294–20302 RSC.
- D. A. Markelov, M. Dolgushev, Y. Y. Gotlib and A. Blumen, J. Chem. Phys., 2014, 140, 244904 CrossRef PubMed.
- D. A. Markelov, S. G. Falkovich, I. M. Neelov, M. Y. Ilyash, V. V. Matveev, E. Lähderanta, P. Ingman and A. A. Darinskii, Phys. Chem. Chem. Phys., 2015, 17, 3214–3226 RSC.
- F. Fürstenberg, M. Dolgushev and A. Blumen, J. Chem. Phys., 2012, 136, 154904 CrossRef PubMed.
- C. Cai and Z. Y. Chen, Macromolecules, 1997, 30, 5104–5117 CrossRef CAS.
-
N. L. Biggs, Algebraic graph theory, Cambridge university press, 1993 Search PubMed.
- A. A. Gurtovenko and A. Blumen, Adv. Polym. Sci., 2005, 182, 171 CrossRef CAS.
- M. Dolgushev and A. Blumen, Macromolecules, 2009, 42, 5378–5387 CrossRef CAS.
-
M. Doi, Introduction to polymer physics, Oxford university press, 1996 Search PubMed.
- A. Perico and M. Guenza, J. Chem. Phys., 1985, 83, 3103–3109 CrossRef CAS.
- S. H. Glarum, J. Chem. Phys., 1960, 33, 1371–1375 CrossRef CAS.
- Y. Y. Gotlib and D. A. Markelov, Polym. Sci., Ser. A, 2007, 49, 1137–1154 CrossRef.
- A. A. Gurtovenko, D. A. Markelov, Y. Y. Gotlib and A. Blumen, J. Chem. Phys., 2003, 119, 7579 CrossRef CAS.
- Y. Y. Gotlib and D. A. Markelov, Polym. Sci., Ser. A, 2002, 44, 1341–1350 Search PubMed.
- A. A. Gurtovenko, Y. Y. Gotlib and A. Blumen, Macromolecules, 2002, 35, 7481–7491 CrossRef CAS.
- M. L. Mansfield and W. H. Stockmayer, Macromolecules, 1980, 13, 1713–1715 CrossRef CAS.
- M. Guenza and A. Perico, Macromolecules, 1992, 25, 5942–5949 CrossRef CAS.
- M. Dolgushev and A. Blumen, J. Chem. Phys., 2010, 132, 124905 CrossRef PubMed.
- M. Dolgushev, T. Guérin, A. Blumen, O. Bénichou and R. Voituriez, Phys. Rev. Lett., 2015, 115, 208301 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6cp02406h |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

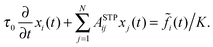
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) i(t) is the x-component of the stochastic force obeying white noise relations. Furthermore, the structure of a polymer (connectivity and local stiffness) is coded through the matrix ASTP = (ASTPij), whose elements are known in a closed form.16 To introduce them, Fig. 1 shows the NN and NNN of a bead i of a treelike structure. The NN beads of i are denoted by ik and the NNN ones by iks. With this notation, the elements of the matrix ASTP read as follows:
i(t) is the x-component of the stochastic force obeying white noise relations. Furthermore, the structure of a polymer (connectivity and local stiffness) is coded through the matrix ASTP = (ASTPij), whose elements are known in a closed form.16 To introduce them, Fig. 1 shows the NN and NNN of a bead i of a treelike structure. The NN beads of i are denoted by ik and the NNN ones by iks. With this notation, the elements of the matrix ASTP read as follows:

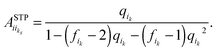

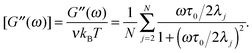



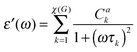


 , and at last the NNN elements
, and at last the NNN elements  .
.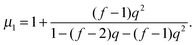












 depend only on the bead between the two considered beads, see eqn (6). Therefore, there are two possible distinct elements (the corresponding situations are exemplarily shown in Fig. 4):
depend only on the bead between the two considered beads, see eqn (6). Therefore, there are two possible distinct elements (the corresponding situations are exemplarily shown in Fig. 4):

![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (G
(G![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ) of different generations G
) of different generations G![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) .
.
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (G
(G![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) ):
): ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (1) (blue),
(1) (blue), ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2) (green), and
(2) (green), and ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (3) (red).
(3) (red).
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2) contains (f − 1) peripheral beads which leads to (f − 2) different, linear independent eigenvectors. Given that the number of
(2) contains (f − 1) peripheral beads which leads to (f − 2) different, linear independent eigenvectors. Given that the number of ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2) subwedges is equal to fC(fC − 1)G−2, the eigenvalue λ(1) for r ≤ 1 is fC(fC − 1)G−2(f − 2)-fold degenerate.
(2) subwedges is equal to fC(fC − 1)G−2, the eigenvalue λ(1) for r ≤ 1 is fC(fC − 1)G−2(f − 2)-fold degenerate.
 -fold degenerate. Altogether, the degeneracy of the eigenvalue connected to the first group is
-fold degenerate. Altogether, the degeneracy of the eigenvalue connected to the first group is
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (2) against each other, see Fig. 7(a). Because of symmetry, all topologically equivalent beads of one subwedge move with the same amplitude, the respective beads of the other subwedge with the same amplitude in the opposite direction. There are two eigenvalues belonging to this group, denoted by λ(2)1 and λ(2)2. Following an analogous discussion as above, the degeneracy of each of the eigenvalue is
(2) against each other, see Fig. 7(a). Because of symmetry, all topologically equivalent beads of one subwedge move with the same amplitude, the respective beads of the other subwedge with the same amplitude in the opposite direction. There are two eigenvalues belonging to this group, denoted by λ(2)1 and λ(2)2. Following an analogous discussion as above, the degeneracy of each of the eigenvalue is![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (3), see Fig. 7(b). Here appears the first structural difference to the homogeneous dendrimer29 because the subwedge
(3), see Fig. 7(b). Here appears the first structural difference to the homogeneous dendrimer29 because the subwedge ![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) (3) includes r nonperipheral functional beads. These beads are described by another matrix element than the internal beads in the same shell. Therefore, an extra equation of motion is required. This means that the change in the topology leads to an extra degree of freedom. Hence, there are four eigenvalues connected to the third group of eigenmodes instead of three as it is in the case of homogeneous dendrimers. The respective degeneracy is given by
(3) includes r nonperipheral functional beads. These beads are described by another matrix element than the internal beads in the same shell. Therefore, an extra equation of motion is required. This means that the change in the topology leads to an extra degree of freedom. Hence, there are four eigenvalues connected to the third group of eigenmodes instead of three as it is in the case of homogeneous dendrimers. The respective degeneracy is given by

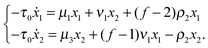



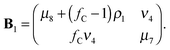

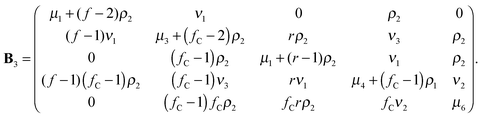
 . Such choice of q ensures that both stiffness parameters reach the two limiting cases at the same time.33,41,42 One can observe in Fig. 8(a) that the eigenvalue
. Such choice of q ensures that both stiffness parameters reach the two limiting cases at the same time.33,41,42 One can observe in Fig. 8(a) that the eigenvalue  takes a larger part of the spectrum with increasing amount of functional beads. This is obvious since this eigenvalue describes the motion of two peripheral beads against each other. The number of such beads increases for growing r. On the left-hand side of this plateau there is a difference between the cases r = 0 and r ≠ 0. While the plateau of eigenvalue
takes a larger part of the spectrum with increasing amount of functional beads. This is obvious since this eigenvalue describes the motion of two peripheral beads against each other. The number of such beads increases for growing r. On the left-hand side of this plateau there is a difference between the cases r = 0 and r ≠ 0. While the plateau of eigenvalue  for r = 0 is preceded by a jump from another (smaller) plateau, for r ≠ 0, the transition to this plateau is rather steady. The corresponding in-between eigenvalues (which do not exist for the homogeneous dendrimer, r = 0) originate from the additional degrees of freedom due to the functional beads. As discussed in Sections 3.2 and 3.3 these degrees of freedom appear starting from the third group, i.e. they exist for dendrimers of G ≥ 3.
for r = 0 is preceded by a jump from another (smaller) plateau, for r ≠ 0, the transition to this plateau is rather steady. The corresponding in-between eigenvalues (which do not exist for the homogeneous dendrimer, r = 0) originate from the additional degrees of freedom due to the functional beads. As discussed in Sections 3.2 and 3.3 these degrees of freedom appear starting from the third group, i.e. they exist for dendrimers of G ≥ 3. manifests itself in increasing significance of the left maximum. The growth of the jump after this eigenvalue with a larger amount of functional beads squeezes the region of higher eigenvalues; consequently leading to a shift of the right maximum to higher frequencies.
manifests itself in increasing significance of the left maximum. The growth of the jump after this eigenvalue with a larger amount of functional beads squeezes the region of higher eigenvalues; consequently leading to a shift of the right maximum to higher frequencies. in the eigenvalue spectrum, as it was observed in Fig. 8. Furthermore, for each shell g > 1 the most significant relaxation time of SFDs is smaller than that of the homogeneous dendrimer. These two facts lead to faster decaying correlation functions for higher g.
in the eigenvalue spectrum, as it was observed in Fig. 8. Furthermore, for each shell g > 1 the most significant relaxation time of SFDs is smaller than that of the homogeneous dendrimer. These two facts lead to faster decaying correlation functions for higher g.








![[B with combining tilde]](https://www.rsc.org/images/entities/b_char_0042_0303.gif) n−1 is obtained by crossing out the last row and the last column of the matrix Bn−1 and replacing its last entry (i.e. (Bn−1)2n−4,2n−4) by μ5 + (fC − 2)ρ2.
n−1 is obtained by crossing out the last row and the last column of the matrix Bn−1 and replacing its last entry (i.e. (Bn−1)2n−4,2n−4) by μ5 + (fC − 2)ρ2.







