RIDME distance measurements using Gd(III) tags with a narrow central transition

Abstract

Methods based on pulse electron paramagnetic resonance allow measurement of the electron–electron dipolar coupling between two spin labels. Here we compare the most popular technique, Double Electron–Electron Resonance (DEER or PELDOR), with the dead-time free 5-pulse Relaxation-Induced Dipolar Modulation Enhancement (RIDME) method for Gd(III)–Gd(III) distance measurements at W-band (94.9 GHz, ≈3.5 T) using Gd(III) tags with a small zero field splitting (ZFS). Such tags are important because of their high EPR sensitivity arising from their narrow central transition. Two systems were investigated: (i) a rigid model compound with an inter-spin distance of 2.35 nm, and (ii) two mutants of a homodimeric protein, both labeled with a DOTA-based Gd(III) chelate and characterized by an inter-spin distance of around 6 nm, one having a narrow distance distribution and the other a broad distribution. Measurements on the model compound show that RIDME is less sensitive to the complications arising from the failure of the weak coupling approximation which affect DEER measurements on systems characterized by short inter-spin distances between Gd(III) tags having a narrow central transition. Measurements on the protein samples, which are characterized by a long inter-spin distance, emphasize the complications due to the appearance of harmonics of the dipolar interaction frequency in the RIDME traces for S > 1/2 spin systems, as well as enhanced uncertainties in the background subtraction. In both cases the sensitivity of RIDME was found to be significantly better than DEER. The effects of the experimental parameters on the RIDME trace are discussed.

---

1. Introduction

Distance measurements between two spin labels in biological macromolecules such as proteins and nucleic acids have become an important tool in Structural Biology, complementing the widely used X-ray crystallography and NMR methods. The spin labels are usually introduced via site-directed spin labeling either through engineered cysteine residues¹ or via the introduction of unnatural amino acids.^2,3 The most commonly used spin labels are based on the nitroxide group, and recently transition metal ions such as Cu(II),⁴ Mn(II)^5,6 and Gd(III)^7,8 have also been used. Among the metal ions, Gd(III) complexes feature the highest sensitivity, particularly at W-band (95 GHz), although they perform well also at Q-band (34 GHz).^9–11 The main motivation for their development is their high sensitivity, the lack of orientation selection at high fields, which allows simple data analysis and straightforward extraction of the distance distribution from the experimental data,^3,12–15 the low sensitivity to multi-spin effects in oligomeric proteins,¹⁶ and their chemical stability in the reducing environment of the cellular cytosol, which renders them suitable for in-cell measurements.^17–19 Combined with nitroxide radicals, Gd(III) labels offer the option of orthogonal labeling and multi-distance measurements.^20–22

So far, double electron–electron resonance (DEER, called also PELDOR; Fig. 1a) has been the most commonly used method for distance measurements.^23,25 DEER requires the application of pulses having two different frequencies, where the first frequency is used to observe one set of spins, referred to as A spins, and the other frequency is used to pump another set of spins called B spins. The analysis of DEER data for a pair of S = 1/2 spins, such as nitroxide spin labels, is well-established, and different software packages are available for extracting distance distributions.^26,27 It has been shown that DEER measurements with pairs of Gd(III) ions can be analyzed using the same software packages, as if Gd(III) had an effective spin S = 1/2.^10,12 This, however, requires some caution, as we shall discuss later. It was recently demonstrated that chirped pump pulses can increase considerably the Gd(III)–Gd(III) DEER effect (the modulation depth of the dipolar oscillations), and consequently also the sensitivity the experiment.²⁸ Further combination with a pre-polarization sequence, which transfers populations to maximize the polarization of the |−1/2〉 → |1/2〉 EPR transition, resulted in an additional increase in sensitivity for Gd(III)–Gd(III) DEER measurements.²⁹ These new developments, which have so far been demonstrated on model compounds, hold a great promise for broadening the scope of structural studies of biomolecules by DEER.

Fig. 1 Pulse sequences of the 4-pulse DEER²³ (a) and 5-pulse RIDME²⁴ (b) experiments. In the 4-pulse DEER experiment the intensity of the refocused echo (RE) is modulated by the electron–electron dipolar interaction as a function of the time t, which defines the position of the π pulse at the second MW frequency ν₂. PE is the primary echo. In the 5-pulse RIDME experiment the intensity of the refocused virtual echo (RVE) is modulated by the electron–electron dipolar interaction as a function of the time t, which defines the position of the third and fourth pulses. VE, SE and RSE are the virtual, stimulated and refocused stimulated echoes, respectively.

Another method for measuring distances between paramagnetic centers is the RIDME (Relaxation-Induced Dipolar Modulation Enhancement) experiment (Fig. 1b).²⁴ RIDME is a single frequency technique, where the action of the pump pulse in the DEER experiment is replaced by relaxation-induced flips of the B electron spins. The RIDME experiment, first demonstrated for a pair of nitroxides,^30,31 has been shown to be highly effective for spin pairs containing a nitroxide and a paramagnetic transition metal ion, using the nitroxide as the observe spin and the transition metal ion as the “relaxing” partner.^32–35 Whereas DEER is limited by the bandwidth of the pump pulse, no restrictions apply to the frequency spectrum of the B spins in RIDME, resulting in a larger modulation depth. Recently it has been demonstrated that the RIDME experiment carried out at W-band can be very effective for a Gd(III)–Gd(III) pair because the modulation depth is much greater than in DEER experiments.³⁶ An additional signal gain arises from the fact that RIDME, being a single frequency technique, can be performed using a narrowband, high-Q cavity as opposed to DEER, where a broadband cavity is usually required. As a drawback, the high spin of Gd(III) leads to the appearance of harmonics of the dipolar interaction frequency arising from multiple quantum (mainly double and triple quantum) relaxation pathways. This results in extra contributions in the distance distribution extracted using standard data analysis software that assumes a weakly coupled S = 1/2 pair. This effect has been observed earlier for the analogous experiment in NMR, Dipolar Exchange-Assisted Recoupling (DEAR), performed on L-alanine to extract the ¹³C_α–¹⁴N dipolar spectrum.^37,38

The present work explores the applicability of the RIDME experiment to Gd(III)–Gd(III) distance measurements for two types of samples: (i) a rigid model compound, referred to as Gd(III)–DOTA ruler (Fig. 2a), with a mean Gd(III)–Gd(III) distance of 2.35 nm and a small zero field splitting (ZFS), to assess the sensitivity of the experiment with respect to the contribution of the pseudo-secular terms of the dipolar interaction, and (ii) two mutants of a homodimeric protein, ERp29,^39,40 both labeled with a DOTA-based Gd(III) tag with a small ZFS and characterized by Gd(III)–Gd(III) distances of ∼6 nm, to assess the influence of the harmonics of the dipolar interaction frequency on the determination of the inter-spin distance. One of the mutants exhibits a narrow distance distribution, whereas the other has a broad distance distribution. For both systems the results of the RIDME experiments are compared with DEER measurements performed on the same samples under standard conditions.

Fig. 2 Molecular structure of the Gd(III)–DOTA ruler (a) and W-band ED-EPR spectra (b). The spectra were recorded at 5 K (black), 10 K (red), and 25 K (blue). The inset shows a magnification of the central transition region (T = 10 K). The “p” and “o” labels denote the positions of the pump (p) and observe (o) pulses in the DEER experiment. Gray dashed lines and circles highlight the field positions at which RIDME experiments were performed. The two upper traces were plotted with vertical displacements by 0.15 and 0.30, respectively for improved visibility.

A small ZFS parameter, D < 800 MHz, is associated with high sensitivity due to the D²/ν₀ dependence of the width of the central transition (where ν₀ is the spectrometer frequency), but a few caveats have to be taken into account when deriving Gd(III)–Gd(III) distance distributions. For Gd(III) with such small D values and distances below 4 nm, the common data analysis procedure leads to artificial broadening of the distance distribution due to the failure of the underlying assumption that the electron–electron dipolar interaction can be described in the framework of the weak coupling approximation, as in the case of a pair of nitroxides, where the pseudo-secular terms of the dipolar Hamiltonian are ignored.^6,12,41 Under typical Gd(III)–Gd(III) DEER conditions, the pump pulse is positioned at the peak of the Gd(III) spectrum, which is dominated by the central, |−1/2〉 → |1/2〉 transition, and the detection pulses are positioned 90–100 MHz away, such that the main contribution to the detected signal is primarily from the |−3/2〉 → |−1/2〉 transition for the case of a small ZFS at W-band. Alternatively, the observe pulses are set to the maximum of the central transition and the pump pulse is set 90–100 MHz away, at a field position where the |−3/2〉 → |−1/2〉 transition dominates. It has been shown that, under either of these conditions, the Fourier transform (FT) of the DEER trace for short distances (2–4 nm) deviates considerably from the expected Pake pattern.^10,12,41 Simulations indicated that the distortions are a result of contributions from the pseudo-secular terms of the dipolar Hamiltonian.^12,41 The central transitions of the two dipolar interacting spins are separated due to a different contribution of the second order ZFS to the m_S = ±1/2 spin levels because of differences in the ZFS D values for the two spins, arising from the distribution of D values or from a different orientation of the ZFS principal frames with respect to the magnetic field. When the separation between the central transitions is small compared with the magnitude of the electron–electron dipolar interaction the weak coupling approximation no longer applies, and the pseudo-secular terms lead to a shift of the m_S = ±1/2 levels of the two spins.^8,12 This, in turn affects the frequency of the |−3/2〉 → |−1/2〉 transitions, as they share a common level with the |−1/2〉 → |−1/2〉 transitions. As a consequence, data analysis with the commonly used DeerAnalysis software,²⁶ which is based on the weak coupling approximation, yields distance distributions that are artificially broadened and include spurious peaks to fit the distorted Pake pattern. The theory also predicts that these undesirable effects increase with decreasing D values, and that they are not significant when detecting the higher m_S transitions.

We have recently shown that such artificial broadening can be minimized by choosing a large frequency difference between the pump and observed pulses, typically Δν = 600–1000 MHz, depending on the D value.⁴¹ In the RIDME experiment, where there is no bandwidth limitation on the B spins, all B spins are potential contributors to the dipolar modulation, and therefore the contribution of the |−3/2〉 → |−1/2〉 transition will not be dominant, hence diminishing the effect of the pseudo-secular terms. Accordingly, the derived width of distance distribution should be close to the real one. Employing the Gd(III)–DOTA ruler (Fig. 2a) we show that RIDME is indeed much less sensitive to the effect of the pseudo-secular terms than DEER. We also explore the experimental conditions that yield the best RIDME sensitivity.

For the protein samples with a long Gd(III)–Gd(III) distance (∼6 nm), which represent conditions under which the DEER trace is unaffected by the pseudo-secular terms, we found that the RIDME sensitivity is considerably higher than for the DEER experiment, but the appearance of harmonics of the dipolar interaction frequencies is of a major concern. Moreover, the uncertainty in the background subtraction results in distortions of the distance distribution related to the fundamental dipolar interaction frequency, particularly when the distance distribution is broad.

2. Experimental

2.1 Sample preparation

The Gd(III)–DOTA ruler (Fig. 2a) was prepared as described previously.⁴¹ The compound was dissolved to a concentration of 50 μM in a 1 : 1 v/v mixture of D₂O and DMSO-d₆. The C157S/S114C (henceforth S114C) and C157S/G147C (henceforth G147C) mutants of the ERp29 protein were expressed and labeled with the C9–Gd(III) tag as reported earlier.¹⁵ Unless stated otherwise, the protein samples were dissolved to a concentration of 100 μM in 20 mM MES buffer in D₂O, pD 4.9, containing 20% volume of glycerol-d₈.

2.2 Spectroscopic measurements

All measurements were performed on a home-built W-band (94.9 GHz, 3.5 T) EPR spectrometer.^42,43 Unless stated otherwise, all experiments used pulse durations t_π/2 and t_π of 15 ns and 30 ns, respectively. The temperature was set to 10 K and the shot repetition time was set to 800 μs unless stated otherwise.

Echo-detected EPR (ED-EPR) spectra were recorded using the pulse sequence π/2 − τ − π − τ − echo and measuring the echo amplitude while sweeping the magnetic field at a rate of 0.27 mT s⁻¹. The inter-pulse delay was τ = 160 ns and the echo was integrated over its full width. A 2-step phase cycle (+x, −x) was applied to the π/2 microwave (MW) pulse. The same sequence was used to measure phase relaxation measuring the echo amplitude while increasing τ. The pulse lengths were as above and the minimum inter-pulse delay τ_min was set to 120 ns. The echo was integrated over its full width at half maximum.

Saturation recovery (SR) experiments for the evaluation of the longitudinal spin–lattice relaxation time were recorded by measuring the echo generated by the pulse sequence t_sat − T − π/2 − τ − π − τ − echo with increasing time delay T. The length of the saturation pulse, t_sat, was chosen such that a further increase did not vary the echo recovery trace. t_sat pulse lengths were 800 μs, 600 μs, and 100 μs for the Gd(III)–DOTA ruler at 5 K, 10 K and 25 K, respectively, and 1 ms for both mutants of the ERp29 dimer at 10 K. The repetition rate was chosen to allow recording of the full SR trace and to avoid temperature-related artifacts, yielding 50 ms, 25 ms and 5 ms for the Gd(III)–DOTA ruler at 5 K, 10 K and 25 K, respectively, and 25 ms for both ERp29 mutants at 10 K. For all samples in all conditions, the echo delay τ was set to 500 ns. The minimum delay T was set to 1 μs and the echo was integrated over its full width at half maximum. Unless otherwise specified, the experiments were performed with the magnetic field set to the maximum of the Gd(III) EPR spectrum. A 2-step phase cycle (+x, −x) was applied to the π/2 MW pulse of the detection sequence.

DEER traces were recorded using the 4-pulse dead-time free sequence²³ π/2 (ν₁) − τ₁ − π (ν₁) − τ₁ + t − π (ν₂) − τ₂ − t − π (ν₁) − τ₂ − echo (Fig. 1a), in which the intensity of the refocused primary echo at the frequency ν₁ is monitored as the timing t of the pump pulse at ν₂ is incremented while keeping the intervals τ₁ and τ₂ constant so as to keep the overall evolution time of the transverse magnetization equal to 2τ₁ + 2τ₂. 2-Step phase cycles were applied to the first two observe pulses and to the pump pulse resulting in an overall 8-step phase cycle (ϕ₁ = (x, −x)₄; ϕ₂ = (x, x, −x, −x)₂; ϕ₃ = (x)₄, (−x)₄; receiver = (x, −x)₄). The frequency of the pump pulse, ν₂, was set to the maximum of the Gd(III) spectrum and the observe frequency, ν₁, was set 100 MHz higher. The frequencies were set in a symmetric way with respect to the resonant mode of the cavity (centered at 94.9 GHz), with ν₁ = 94.95 GHz and ν₂ = 94.85 GHz. The pump pulse length t_π(ν₂) was 15 ns. The separation between the two π pulses, τ₁ + τ₂, was set to 2.5 μs, 7.9 μs, and 8.9 μs for the Gd(III)–DOTA ruler, ERp29–G147C–C9–Gd(III), and ERp29–S114C–C9–Gd(III), respectively, with τ₁ = 375 ns for all samples. The variable delay t was incremented in steps of 10 ns for the Gd(III)–DOTA ruler and in steps of 75 ns for both mutants of ERp29, always starting from an initial value of −225 ns. Overall acquisition times were 1 hour for the Gd(III)–DOTA ruler and 5–6 hours for the protein samples.

RIDME traces were recorded using the 5-pulse dead-time free sequence²⁴ π/2 − τ₁ − π − τ₁ + t − π/2 − T_mix − π/2 − τ₂ − t − π − τ₂ − echo (Fig. 1b), in which the intensity of the refocused virtual echo is monitored as the delay t, which defines the positions of the third and fourth pulses, is incremented, while the intervals τ₁, τ₂, and T_mix are kept constant to keep the overall evolution time of the magnetization equal to 2τ₁ + 2τ₂ + T_mix, with evolution of transverse magnetization during 2τ₁ + 2τ₂. A 2-step phase cycle was applied to the first MW pulse and a 4-step phase cycle was applied to the third and fourth MW pulses, resulting in an overall 8-step phase cycle (ϕ₁ = (x)₄, (−x)₄; ϕ₃ = ϕ₄ = (x, −x, y, −y)₂; receiver = (x)₄, (−x)₄).²⁴

The chosen phase cycling scheme required 90° and 180° phase shifts of the excitation pulses. The 180° phase shift was implemented using the standard phase shifter whereas the 90° phase shift was generated by a second MW channel where we inserted a variable phase shifter (ARRA 9424A) between the 7.3 GHz MW source and the ×13 multiplier. The receiver phase was optimized to detect a maximally positive signal of the echo generated by the pulses on channel 1, while the 90° phase shift of the π/2 pulse on channel 2 was determined by producing a symmetric dispersion-like echo shape. Unless stated otherwise, the magnetic field was set to the maximum of the Gd(III) spectrum.

For the Gd(III)–DOTA ruler, the delays τ₁ and τ₂ were set to 400 ns and 2.5 μs, respectively, and the variable delay t was stepped in increments of 5 ns starting from −300 ns. The total recording time of each trace was about 1–2 hours. For the C9–Gd(III)-labeled ERp29 mutants, the delays τ₁ and τ₂ were set to 400 ns and 8.5 μs, respectively, and the variable delay t was stepped in increments of 25 ns starting from −300 ns. Using a mixing time T_mix of 25 μs and a protein concentration of 100 μM, the experimental time was 2 hours and 4 hours for the S114C and G147C mutant, respectively. The measurement time for a 20 μM solution of the S114C mutant was 10 hours.

2.3 Data analysis

DEER and RIDME traces were analyzed and converted into distance probability distributions using the model-free Tikhonov regularization algorithm implemented in the DeerAnalysis 2015 software.²⁶ The background decay was fitted by a single exponential function

I(t) = e^−k·t (1)

for DEER traces, where it arises only from long-range intermolecular interactions, and to a stretched exponential function

I(t) = e^−k·td/3 (2)

for RIDME traces, where additional contributions from spectral diffusion processes are present.³² The parameters of the background decay function for all the recorded traces are reported in Table S1 (ESI†). In both cases, the choice of the fitting region relied on visual inspection of the Fourier transform of the background-subtracted dipolar evolution trace. The regularization parameter α was chosen according to the L curve criterion, resulting in values of α = 1000 for the DEER trace of the Gd(III)–DOTA ruler, α = 1 for the RIDME traces of the Gd(III)–DOTA ruler, and α = 10 and 100 for the S114C and G147C mutants of ERp29, respectively, for both the DEER and RIDME traces.

3. Results

3.1 Gd(III)–DOTA ruler

3.1.1 Comparison between DEER and RIDME. The W-band echo-detected EPR spectra of the Gd(III)–DOTA ruler (Fig. 2a) measured at 5, 10, and 25 K are shown in Fig. 2b. The Gd(III)–DOTA ruler is characterized by a narrow central transition arising from a highly distributed D value centered at 500 MHz.⁴¹ The phase memory time, T_M, and the spin–lattice relaxation time, T_1e, play an important role in the performance of the RIDME measurements and therefore we measured them at several temperatures. Fig. 3a shows the echo decay curves measured at 5, 10, and 25 K, revealing a considerable shortening of the phase memory time at 25 K, while the difference between the 5 and 10 K curves is smaller. These decay curves were fitted by a double stretched exponential function and the fit parameters are given in Table S2 in the ESI.†

Fig. 3 Echo decay traces (a) and SR traces (b) of the Gd(III)–DOTA ruler at 5 K (black), 10 K (red), and 25 K (blue). Circles on the SR traces mark the T_mix values used for RIDME experiments. The magnetic field was set to the maximum of the EPR spectrum for both experiments. (The curves presented in a logarithmic scale are shown in Fig. S1, ESI†).

The saturation recovery (SR) curves used to determine the longitudinal electron spin relaxation time T_1e at these three temperatures show the expected lengthening of T_1e as the temperature is reduced (Fig. 3b). The relaxation times derived from the relaxation measurements are listed in Table S3 (ESI†). In general for distance measurements a long T_M is desired for accessing long distances and for increasing sensitivity. In contrast, a short T_1e is desired to allow efficient signal averaging, therefore there is an optimal temperature that satisfies both requirements, which for Gd(III) at W-band is around 10 K.

The T_1e value is important for RIDME experiments, as the RIDME efficiency, and hence the observed modulation depth, is related to the fraction of B spins flipping an odd number of times during T_mix. T_1e of a Gd(III)–DOTA complex has previously been shown to be practically field independent at W-band,⁴⁴ and this was confirmed by additional measurements presented in Fig. S2 in the ESI,† and Table S3. Therefore, we took measurements on the central transition as indicative for the overall spin–lattice relaxation behavior of the B spins.

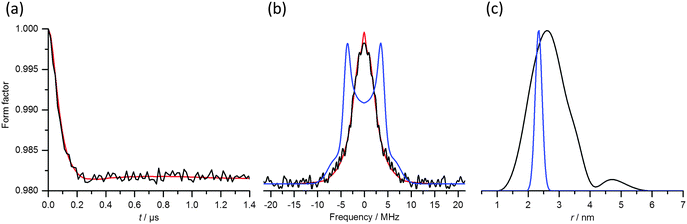
Fig. 4 presents W-band DEER data obtained from experiments carried out under the standard conditions, i.e. setting the pump pulse at the maximum of the EPR spectrum and using Δν = 100 MHz (Fig. 2b, inset). The form factor obtained after background removal (Fig. 4a) shows a pronounced damping of the dipolar oscillations. The Fourier transform of this trace yields a spectrum strongly deviating from the Pake pattern expected for an effective S = 1/2 spin system (Fig. 4b), as reported earlier.⁴¹ The distance probability distribution curve derived from these DEER data gives a very broad distribution (Fig. 4c). Fig. 4 also shows a comparison with the expected Pake pattern arising from a spin pair with a distance of 2.35 nm and a full distribution width at half height of 0.25 nm.⁴¹

Fig. 4 DEER measurements of the Gd(III)–DOTA ruler. (a) DEER form factor (black line) and fit (red line) obtained at T = 10 K with Δν = 100 MHz. (b) Comparison between the Fourier transforms of the experimental (black) and fitted (red) DEER form factor and the expected Pake pattern for a S = 1/2 spin system characterized by an inter-spin distance of 2.35 nm with a distance distribution width of 0.25 nm (blue). (c) Distance distribution obtained from Tikhonov regularization of the DEER form factor (α = 1000; black) and expected distance distribution (blue).

In contrast to the DEER data, the form factor obtained from RIDME measurements of the Gd(III)–DOTA ruler shows clear modulations of the dipolar evolution trace (Fig. 5a). The Fourier transform spectrum reveals a superposition of powder patterns with clear features at ±3.75 MHz (compare with the calculated spectrum in Fig. 4b) and the main narrow peak in the distance distribution is centered at 2.35 nm with a full width at half height of 0.25 nm, in agreement with the DEER results obtained with Δν = 1.09 GHz.⁴¹ Both the frequency spectrum and the distance distribution, however, display additional peaks corresponding to harmonics of the dipolar coupling frequency up to the 3rd order. These harmonics are expected, as already reported in the first applications of RIDME to Gd(III)–Gd(III) systems.³⁶Fig. 5b shows a decomposition of the Pake pattern into the three individual harmonics with weights f₁ = 0.66, f₂ = 0.15 and f₃ = 0.19. In agreement with the earlier report,³⁶ the modulation depth of the RIDME trace (10%) is clearly greater than that of the DEER trace (1.8%), which is a consequence of lifting the pump pulse bandwidth limitations that determine the modulation depth in the DEER experiment.

Fig. 5 RIDME measurements of the Gd(III)–DOTA ruler. (a) RIDME form factor (black) and fit (red) obtained at T = 10 K with T_mix = 150 μs. The ripple on the experimental trace arises from ²H modulations (ν_I ≈ 22.5 MHz; see Fig. S3b, ESI†). (b) Fourier transforms of the RIDME form factor (black) and fit (red). The magenta line shows the expected overall frequency spectrum, which can be decomposed into the spectrum expected for a S = 1/2 spin system characterized by an inter-spin distance of 2.35 nm with a distribution width of 0.25 nm (blue line; see Fig. 4b), and spectra arising from double (green) and triple (purple) harmonics of the electron–electron dipolar frequency. (c) Distance distribution (α = 1; black solid line). The distance distribution was validated by combining data from experiments performed on different days under the same conditions (red shaded area). The grey dashed lines denote, from right to left, the mean distances corresponding to the first (r₀), second and third harmonics of the electron–electron dipolar interaction. The small contribution at r = 3.2 nm arises from an impurity.⁴¹

While the impact of the pseudo-secular term on the DEER trace strongly affects the dipolar evolution trace, leading to a large apparent broadening of the distance probability distribution, this effect is minor in the RIDME experiment, though still apparent as manifested by the intensity around 0 MHz in the frequency spectrum and by the appearance of distances longer than 2.35 nm.

The contribution of the background decay is much stronger in the 5-pulse RIDME than in the 4-pulse DEER experiment (Fig. 6 and Table S1, ESI†), although both techniques employ a constant total phase-evolution time. This can be explained by spectral diffusion during the mixing time T_mix as the main mechanism for signal decay in RIDME.³² In RIDME the first three pulses, the effect of which is equivalent to the π/2 − t − π/2 sequence, produce a polarization grating with a frequency spacing inversely proportional to t, which is thus increasingly prone to destruction by spectral diffusion for longer t values. This is consistent with the observation that a longer mixing time leads to stronger background decay (see Fig. S4a, b, and Table S1, ESI†). The background decay in RIDME experiments is strong compared to the modulation depth and, furthermore, not exponential. Therefore, its removal is subjected to a greater uncertainty than in DEER experiments, which are usually associated with weak and mono-exponential background decay. While this is not a crucial issue when the distance distribution is narrow, namely when the form factor is characterized by clear modulations, the background removal can become problematic when the distance distribution is broad and the distance is long, as we will show later.

Fig. 6 Comparison of background decays in DEER and RIDME experiments for the Gd(III)–DOTA ruler. Normalized primary dipolar evolution traces of the DEER (black) and RIDME (red) traces of Fig. 4 and 5, respectively, are shown together with the background fits (grey lines).

Both DEER and RIDME experimental traces show small, yet clear modulations at around 22 MHz, assigned to ²H modulation from the solvent deuterons. As this frequency is outside the frequency span of the dipolar spectra (see Fig. S3b, ESI†) and of very small amplitude, we did not attempt to remove it. This constitutes an advantage over Q-band RIDME, where ²H modulation suppression techniques had to be devised to allow extraction of distances from the experimental traces.³³

We performed additional experiments to optimize the sensitivity of the RIDME trace by varying T_mix, the temperature, the field position with respect to the central transition, and the pulse excitation bandwidths. The results of these measurements are summarized in Table S1 (ESI†) in terms of background decay parameters, modulation depth (λ), echo intensity, and total RIDME signal-to-noise ratio (SNR), where the SNR is proportional to λV_echo and V_echo corresponds to the echo intensity at t = 0. These are discussed next.

3.1.2 Effect of mixing time. RIDME measurements were carried out with the mixing times marked by points on the recovery curves in Fig. 3b. For a given temperature, increasing the mixing time increased the slope of the background function and the modulation depth (Fig. S4a and Fig. 7a for T = 10 K; Fig. S4b and c (ESI†) for T = 25 K). The first finding is consistent with the proposed mechanism, where the decay of the refocused virtual echo signal during the constant-time 5-pulse RIDME sequence increases with longer mixing times due to spectral diffusion processes that affect the polarization grating.⁴⁵ The increase of the modulation depth is consistent with a higher probability of B spin flip events as reported earlier.³⁶ The combined effect of these two factors results in an optimal mixing time value for optimal SNR: an overly short mixing time will not allow enough time for the B spins to flip, whereas a too long mixing time is more prone to spectral diffusion reducing the SNR.

Fig. 7 10 K RIDME measurements of the Gd(III)–DOTA ruler with different T_mix values as indicated on the figure. (a) Form factors with corresponding fits (grey). (b) Corresponding Fourier transforms of the experimental data (colored) and fits (grey). (c) Distance distributions obtained by Tikhonov regularization of the RIDME form factors (α = 1). The grey dashed lines denote, from right to left, the mean distances corresponding to the first, second and third harmonic of the electron–electron dipolar interaction. The color codes are the same for all panels.

Although the relative weights of the frequency components of the form factor varied somewhat with temperature (see Fig. 7b and Fig. S4d (ESI†) for data at 10 and 25 K), the contribution from high harmonics seems to decrease with increasing T_mix. This change will not be discussed further as it may be within experimental error. A summary of these results in terms of RIDME SNR, modulation depth, and background decay parameters is given in Table S1 (ESI†).

3.1.3 Effect of temperature. Saturation recovery experiments performed on the central transition (Fig. 3b and Table S3, ESI†) showed a pronounced dependence of the longitudinal relaxation rate on temperature, with lower temperatures resulting in slower relaxation. Experiments performed under conditions of a similar degree of saturation recovery but at different mixing times (5 K: T_mix = 300 μs, I/I₀ = 89%; 10 K: T_mix = 150 μs, I/I₀ = 84%; 25 K: T_mix = 25 μs, I/I₀ = 82%, where I and I₀ are the echo intensities recorded with and without the saturation pulse, respectively) resulted in an increase of the modulation depth with decreasing temperature (Fig. S5, ESI†). We tentatively attribute this effect to the depopulation of the central transition at lower temperatures, which reduces the population of A spins and increases the populations of the B spins. No significant changes were observed either in the relative contributions of the harmonics of the dipolar interaction to the form factor (Fig. S5c, ESI†) or to the background decay (Table S1, ESI†).

3.1.4 Effect of field position with respect to the central transition. In contrast to the phase memory time, which is dependent on the field position⁴⁴ (Fig. S2a and c, Table S2, ESI†), the spin–lattice relaxation time for Gd(III) complexes is essentially field independent (Fig. S2b and d, Table S3, ESI†), as mentioned previously. Consequently, the fraction of B spins flipping during a given T_mix is independent of the magnetic field at which the RIDME sequence is performed. On the other hand, owing to the different widths of the |m_S〉 → |m_S + 1〉 transitions, different field positions correspond to different fractions of excited A spins and, consequently, a different composition of transitions exists for the B spins. For example setting the magnetic field to the maximum of the EPR spectrum produces the maximal fraction of A spins for a given pulse excitation bandwidth because the |−1/2〉 → |+1/2〉 transition is the narrowest transition. Experiments performed at several field positions (indicated in Fig. 2b) show that the modulation depth, which depends on relaxation-induced flips of the B spins, was systematically higher when the magnetic field was moved away from the maximum of the EPR spectrum (Fig. 8a and Table S1, ESI†). A potential simple minded explanation could be the decrease in the number of B spins as a result of the increase in the number of A spins when the field is set to the central transition. The effect however is larger than expected from the above argument and other factors, currently not understood, should be considered.

Fig. 8 RIDME measurements of the Gd(III)–DOTA ruler as a function of the magnetic field position within the EPR spectrum. (a) Form factors measured at ΔB₀ indicated on the figure, where ΔB₀ is the field offset with respect to the maximum of the EPR spectrum, with corresponding fits (grey). Measurements were performed at T = 10 K with T_mix = 150 μs. (b) Fourier transforms of the form factors and fits shown in (a). (c) Distance distributions obtained from Tikhonov regularization of the RIDME form factors (α = 1) in (a). The grey dashed lines denote, from right to left, the mean distances corresponding to the first, second, and third harmonic of the electron–electron dipolar interaction. Same color codes are used for all three panels.

Analysis of the EPR spectrum of the Gd(III)–DOTA ruler⁴¹ indicates comparable weights of the |−5/2〉 → |−3/2〉 and |−3/2〉 → |−1/2〉 transitions (which constitute approximately 70% of the observed signal) for all chosen off-central field positions. This result is consistent with the experimentally observed independence of the RIDME traces upon the specific value of the magnetic field offset with respect to the maximum of the central transition. Although the modulation depth is higher when the measurements are performed away from the central transition of the EPR spectrum, the sensitivity is influenced by three additional factors: (i) a lower spin echo signal; (ii) a shorter phase memory time (Fig. S2a and c, Table S2, ESI†),⁴⁴ and (iii) a steeper background decay (Table S1, Fig. S6, ESI†). We furthermore observed an increased contribution to the dipolar evolution trace from the higher harmonics of the dipolar interaction when RIDME experiments were performed away from the central transition, suggesting that spins with m_S = ±1/2 have a greater tendency to follow relaxation pathways which involve multiple quantum transitions.

3.1.5 Effect of pulse excitation bandwidth. Reducing the excitation bandwidth of the pulses had little effect on the observed dipolar evolution traces, neither for the modulated part nor for the background decay, provided that the MW excitation profile of the preparation sequence was wider than the dipolar spectrum, including the higher harmonics of the dipolar interaction (see Fig. S7, ESI†).³² If this condition is not met, distortions of the dipolar spectrum occur (Fig. S7c, ESI†), which may eventually result in an erroneous evaluation of the inter-spin distance (Fig. S7d, ESI†). Besides lower sensitivity stemming from a smaller excitation bandwidth, longer pulses also result in a less accurate definition of the zero time of the dipolar evolution trace (Fig. S7b, ESI†). All these effects are summarized in Table S1 (ESI†).

3.2 Gd(III)-spin labeled ERp29 homodimer

RIDME measurements were performed on two cysteine mutants of the homodimeric ERp29 protein (Fig. 9a and b) labeled with the C9–Gd(III) tag (Fig. 9c), which, like Gd(III)–DOTA, features a rather narrow central transition (Fig. S8, ESI†) and a D value of 800 MHz.⁴¹ Both mutants feature inter-spin distances around 6 nm, one having a narrow distance distribution (S114C) and the other a broad distance distribution (G147C). For this distance, the dipolar spectra are devoid of artifacts arising from the pseudosecular terms of the dipolar interaction Hamiltonian and therefore the comparison with DEER is straightforward, allowing a focus on SNR and the appearance of high order harmonics.

Fig. 9 Structures of the ERp29 homodimer with C9–Gd(III) tag.¹⁵ (a) Ribbon representation of the S114C mutant. (b) G147C mutant. (c) Molecular structure of the C9–Gd(III) tag.

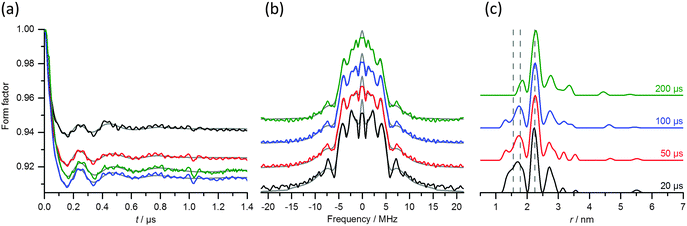
Fig. 10(a–c) compares the RIDME and DEER distance measurements of the S114C mutant (raw data are shown in Fig. S9, ESI†). Both experiments reveal a narrow distance distribution centered at distances of 5.8 nm for DEER and 5.7 nm for RIDME. For both experiments, the dipolar evolution trace had to be collected sufficiently long to encompass at least 1–2 periods of the dipolar oscillation with the lowest frequency. In the case of RIDME, which has steep background decay, this imposes a limit on the maximum acceptable mixing time (see Table S4, ESI†). Beyond this limit, the intensity of the refocused virtual echo signal decreases below a few percent of the signal at zero dipolar evolution time, causing excessive noise after the division of the raw data by the background function (see Fig. S10a and b, ESI†). In the present case, the optimal value of the mixing time T_mix proved to be 25 μs for a temperature of 10 K in a fully deuterated solvent.

Fig. 10 (a–c) RIDME and DEER experiments of ERp29 S114C–C9–Gd(III). (a) RIDME (red) and DEER (black) form factors and fits (grey) for experiments performed at T = 10 K, using Δν = 100 MHz in the DEER experiment and T_mix = 25 μs in the RIDME experiment. (b) Fourier transforms of the RIDME and DEER form factors (red and black, respectively) and fits (grey). (c) Distance distributions obtained from Tikhonov regularization of the RIDME and DEER form factors (α = 10). The grey dashed lines denote, from right to left, the mean distances corresponding to the first, second, and third harmonics of the electron–electron dipolar interaction. (d–f) RIDME and DEER experiments of ERp29 S147C–C9–Gd(III). The same measurement conditions and data analysis protocol were used as in (a)–(c).

The distance distribution derived from RIDME showed additional peaks at 4.7 and 4.4 nm that can be assigned to high harmonics of the dipolar modulation frequency, ω_dip. For r₀ = 5.7 nm these are expected at 4.5 and 3.95 nm, while for r₀ = 5.8 nm, obtained by DEER, these should appear at 4.6 and 4.0 nm, respectively. The experimental results showed clear evidence for the expected second harmonic peak. Unlike the case of the Gd(III)–DOTA ruler, the second harmonic of the dipolar interaction frequency contributed more strongly to the distance probability distribution than the first harmonic.

Fig. 10(d–f) compares the RIDME and DEER data for the G147C mutant (raw data are given in Fig. S9, ESI†). The Gd(III)–Gd(III) distance in this mutant is also close to 6 nm, but the distance distribution is significantly wider than in the S114C mutant.¹⁵ This choice of mutants thus allows assessing the effects of the higher harmonics of the dipolar interaction on narrow and broad distance distributions. In the RIDME experiment of the G147C mutant, the first harmonic peak appeared again shifted to lower distances with respect to the main peak in the distance distribution of the DEER trace. Furthermore, the former is considerably narrower than the latter. The distance distribution derived from RIDME once again showed a peak at 4.7 nm, which corresponds to the second harmonic of the dipolar interaction frequency and has a larger integral than the first harmonic peak. Furthermore, its maximum is slightly shifted with respect to the expected value of 4.5 nm. Both the DEER and RIDME experiments showed an additional small peak at around 3.5 nm, the origin of which is unknown and tentatively attributed to SNR limitations.

This example illustrates the main difficulties associated with RIDME experiments of samples characterized by long distances, where contributions originating from harmonics of the dipolar interaction can overlap with the signals arising from genuine inter-spin distances, which may arise from alternative protein conformations. This problem becomes even more prominent when the distance distribution is broad. In addition, the dipolar modulations are superimposed on a very strong background decay, which stems from the long dipolar evolution time required for detecting the long distance (see Fig. S9b, ESI†). Under these conditions, sensitivity to the background removal becomes a bigger problem than in DEER.

In DEER experiments, reducing the spin concentration extends the phase memory time and reduces the background decay. To evaluate the effect of spin concentration the background decay in RIDME we reduced the concentration of the S114C mutant 5-fold (from 100 μM to 20 μM). Unexpectedly, the background decay remained practically unchanged, showing only a 10% reduction in slope (see Fig. S10a and Table S4, ESI†). This indicates that for this concentration range (20–100 μM) the background decay is governed by spectral diffusion processes that are not due to electron spin–spin interactions. Interestingly, also the echo decay has not changed significantly (Fig. S11a and c, Table S5, ESI†), suggesting that the main source of phase relaxation is the interaction with the protein's protons. The modulation depth was similarly unaffected by the dilution (Fig. 10b and Table S4, ESI†), reflecting the insensitivity of the spin–lattice relaxation time with regard to concentration (Fig. S11b and d, Table S6, ESI†). The SNR normalized per unit time was reduced only by a factor of 2.15. Therefore, maintaining the SNR of the form factor achieved with the 100 μM sample requires an almost 5-fold increase in accumulation time. The distance probability distribution curves of the two experiments show overall the same behavior (Fig. S10d, ESI†).

Evaluation of the SNR per unit time allows for comparison of the DEER and RIDME techniques in terms of the lowest concentration that can be used with a given total recording time. Assuming that a minimum SNR of 5–10 is required for successful analysis of the form factor and considering that the SNR is proportional to the product of concentration and the square root of total recording time, this sets the minimal concentrations to 25–50 μM for DEER and 6.5–13.0 μM for RIDME for a 12 h collection time on our spectrometer for this sample. This assessment takes into account the fact that the t increment in the RIDME trace has to be set to 1/3 of the step used in the corresponding DEER experiment (namely requiring more data points) owing to the presence of harmonics of the dipolar interaction up to the 3rd order.

4. Discussion

In this work we explored the utility of W-band RIDME for Gd(III)–Gd(III) distance measurements. The first report on Gd(III)–Gd(III) RIDME was carried out on a ruler molecule with a distance of 3.4 nm and a PyMTA chelate,³⁶ which exhibits a relatively large D value (1150 MHz) corresponding to a rather wide central line (∼130 MHz)¹² Here we focused on Gd(III) tags based on the DOTA chelate, for which D is in the range of 500–800 MHz and the central line width (full width at half maximum) is correspondingly in the range of 30–48 MHz. This small ZFS is advantageous sensitivity wise, which is particularly important for measurements of long distances, but generates problems for short distances due to artificial broadening of the distance probability distribution arising from ignoring contributions of the pseudo-secular terms of the dipolar interaction in the data analysis. These considerations led us to examine two types of samples, one with a short Gd(III)–Gd(III) distance of 2.35 nm and the other with a longer distance of about 6 nm, where in both samples the Gd(III) tag was based on the DOTA macrocycle. For the longer distance, which is not compromised by the effects of the pseudo-secular terms, we compared the two limiting situations of narrow vs. broad distance distribution.

We start our discussion with the advantages of RIDME over DEER. As the first report clearly demonstrated,³⁶ RIDME is superior in terms of SNR as it generates a considerably larger modulation depth. This increased modulation depth has also been reported for cases of RIDME applied to a nitroxide-transition metal ion pair, where the transition metal ion has a large g anisotropy and exhibits faster relaxation than the nitroxide.^32,33 In this case also issues related to orientation selection were eliminated. Being a single frequency experiment is another advantage of RIDME, posing fewer demands on hardware than DEER. As a single frequency experiment RIDME does not require a broad cavity bandwidth that can accommodate two frequencies, allowing, in principle, the use of cavities with a higher quality factor Q, which will further increase the sensitivity compared with DEER. Measurements could be carried out in the temperature range of 5–25 K with relatively large values of T_mix for the sample with a short inter-spin distance. For the samples featuring long distances, the T_mix value was limited by the strong background decay. This will be discussed later. For the 5.8 nm Gd(III)–Gd(III) distance in the ERp29–S114C–C9–Gd(III) sample, the sensitivity of RIDME was about 3-fold higher compared with DEER on our spectrometer and this gain can probably be increased further with an optimized cavity. It was suggested that a high T_M/T_1e ratio improves the RIDME sensitivity.³⁶ We observed for the Gd(III)–DOTA ruler that this ratio decreases from 0.39 at 25 K to 0.15 at 5 K (Table S3, ESI†). For a particular temperature, 10 K, this ratio decreases as the observe field is further away from the central transition (see Table S3, ESI†). However, we did not observe a clear correlation with the SNR values presented in Table S1 (ESI†), but as the measurements where not targeted towards the elucidation of such a correlation the series compared may be incomplete. Finally, at 10 K this ratio was higher for Gd(III)–DOTA ruler (0.21) than for the protein samples (0.06–0.07) mainly because of faster phase relaxation the latter.

The RIDME experiment is significantly less sensitive to the effect of the pseudo secular terms at short distances because the flipping B spins involve all possible transitions. The distance distribution of the Gd(III)–DOTA ruler derived from the RIDME dipolar evolution trace gave the expected distance of 2.35 nm and the narrow distance distribution. In contrast, overcoming the artificial broadening in DEER requires a very large Δν of 600–1000 MHz between the pump and observe pulses,⁴¹ which can be obtained either with a dual mode cavity or with an extremely broadband resonator. Either of these approaches is detrimental for the SNR of the trace.

A major disadvantage of the RIDME experiment is the appearance of additional peaks in the distance distribution, arising from the presence of multiple harmonics of the dipolar interaction frequency in the dipolar evolution trace. In principle, the presence of the multiple quantum relaxation pathways can be taken into account by developing new data analysis tools. Unfortunately, the relaxation pathways in high-spin systems are currently not understood and such an analysis would have to treat the relative contributions of the various relaxation pathways as free parameters,³⁶ which would spoil the simplicity and uniqueness of the data analysis. It was shown for the NMR analog of the RIDME experiment^37,38 that the relative contributions of the different relaxation pathways simplify considerably in the limit of complete exchange, namely when the storage time T_mix is short with respect to the T_1e relaxation time of the observed spin and long compared with the T_1e of the relaxing spin. In this situation, the 2S + 1 states contribute with a coefficient (2S + 1)^−1/2 in room temperature measurements.³⁷ At low temperatures, as in our case, the relative contributions should be governed by the Boltzmann distribution. While this condition can likely be met for a Gd(III)–nitroxide sample, it clearly does not apply to the case of a Gd(III)–Gd(III) pair, where the two spins are of the same type and therefore have the same T_1e value. Unfortunately, we observed very fast background decay and poor SNR for longer T_mix values, which is particularly relevant for long distances that require long evolution times. We expect the relative contributions of the second and third dipolar harmonics to depend on the tag properties (ZFS) and on the field position in the EPR spectrum at which the RIDME experiment is conducted. For example, we noticed that observing outside the central transition increased the contribution of the high order harmonics, suggesting that the m_S = ±1/2 levels are more involved in multiple-quantum relaxation pathways than the other levels. Thus, high order harmonics may be identified by comparing measurements carried out at the center of the central transition and further away. A systematic study characterizing the various multiple-quantum relaxation pathways is required before RIDME can be turned into a robust, standalone distance measurement technique for high spin systems. Potentially, very long distances could be measured by RIDME by analyzing the multiple harmonics of the dipolar interaction. This may become of interest for distances that cannot be accessed by DEER due to phase memory time limitations. Such an analysis, however, would require unambiguous assignment of the harmonic rank, which could, in principle, be done by comparison with DEER for assurance. In the protein samples of the present study, however, we observed some significant shifts from the expected distance positions.

A second disadvantage of RIDME is the strong, non-exponential background decay for large T_mix values. Whereas the background decay of DEER is affected only by the spin concentration, the background decay of RIDME is affected also by spectral diffusion, which is a function of T_mix. This is particularly problematic for long distances with broad distributions, where the background subtraction becomes ambiguous and affects the reliability of the obtained distance distribution. Systematic studies which identify the parameters affecting the background decay are essential for further optimization of the RIDME experiment for Gd(III)–Gd(III) distance measurements.

A comparison between the results obtained for the Gd(III)–DOTA ruler those reported for a PyMTA-based Gd(III) ruler with an inter-spin distance of 3.4 nm³⁶ shows that for the latter RIDME modulation depths up to 50% could be obtained with the experiment performed at the maximum of the EPR spectrum, whereas in our case the highest achieved modulation depth at this field position is only on the order of 10% even at the longest values of T_mix. A contribution to the enhanced modulation depth for the PyMTA-based Gd(III) ruler can be attributed to the different width of the central transition, as the larger D of Gd(III)–PyMTA compared to Gd(III)–DOTA implies a smaller fraction of A spins, hence a larger fraction of B spins. Here it is relevant to consider that experiments performed on the Gd(III)–DOTA ruler outside the central transition, where the fraction of A spins is strongly reduced, allowed to reach a maximum modulation depth of approximately 22%. Hence this explanation accounts only partially for the difference. The different ZFS is also expected to affect the relaxation behavior as well. Considering that the PyMTA-based Gd(III) ruler was measured at a much higher concentration, namely 500 μM, 10 folds higher than the concentration of the Gd(III)–DOTA ruler, the increased RIDME effect may be rationalized in terms of an increased efficiency of spin flip-flop processes for higher concentrations. This may also account for the difference in the relative weights of the harmonics of the dipolar interaction frequency: whereas for the more diluted Gd(III)–DOTA ruler the higher harmonics make up to 34% of the overall signal, for the more concentrated PyMTA-based Gd(III) ruler, where the efficiency of spin flip-flop processes is expected to be increased, this contribution is as high as 56%.

In principle, RIDME should also be attractive for Gd(III)–nitroxide distance measurements, where the observation is set to the nitroxide. However, we expect the appearance of harmonics of the dipolar interaction in this case as well, as recently observed for a nitroxide–Mn(II) model compound.³⁵ Furthermore, the behavior of the background decay in these systems is yet to be explored.

To summarize, the current state of knowledge makes Gd(III)–Gd(III) RIDME a method complementary to DEER distance measurements, but not yet as a robust alternative. Our results demonstrate that RIDME is particularly useful for overcoming the complications arising in DEER experiments from the pseudo-secular terms of the dipolar interaction, which is a significant effect for distances below 4 nm and small ZFS values.⁴¹ Furthermore, the RIDME technique, having a better SNR, can be very useful to complement DEER measurements with insufficient SNR that still gave a rough idea about the distance distribution, so the harmonics peaks can be identified.

5. Conclusions

W-band 5-pulse RIDME can be used for reliably measuring Gd(III)–Gd(III) distances as short as 2.35 nm for DOTA-type tags that feature a narrow central transition. The technique yields a distance distribution without the artificial broadening that afflicts DEER due to the failure of the weak coupling approximation. Furthermore, it features a higher sensitivity than DEER because of the considerably larger modulation depth. The modulation depth in turn is directly influenced by the choice of mixing time, with a long T_mix value entailing an increased modulation depth at the expense of the echo intensity owing to increased z-magnetization recovery of the observed spins along with faster spectral diffusion rates. In contrast, a short T_mix value results in a strong echo signal at the expense of modulation depth. Therefore, there is an optimal T_mix value, which is essentially a function of the temperature-dependent longitudinal relaxation properties of the tag and of the dipolar evolution time needed for the RIDME trace. The major drawback of RIDME applied to high spin systems is the appearance of high harmonics of the dipolar interaction frequency, which currently cannot be controlled. These harmonics generate additional peaks in the distance probability distribution obtained using the standard data analysis tools, which can interfere with the detection of different coexisting conformations of the system under study. Such harmonics may be identified by carrying out measurements at different positions along the EPR powder pattern, as they are minimized by observing at the maximum of the EPR spectrum, where the contribution of the central transition is largest. The strong dependence of the background decay on T_mix poses a challenge for measurements of long distances. Finally, as the shape of the background decay in the RIDME experiment has not yet been modeled analytically, its removal may be ambiguous, mostly affecting long distances with broad distance distributions.

Acknowledgements

This research was supported by the Israeli Science Foundation (grant 334/14) and was made possible in part by the historic generosity of the Harold Perlman Family (D. G.). We also acknowledge the Australian Research Council for a Discovery grant to G. O. and B. G. (DP150100383) and a Future Fellowship to B. G. (FT130100838). D. G. holds the Erich Klieger professorial chair in Chemical Physics.

References

1. W. L. Hubbell, A. Gross, R. Langen and M. A. Lietzow, Curr. Opin. Struct. Biol., 1998, 8, 649–656.
2. M. R. Fleissner, E. M. Brustad, T. Kalai, C. Altenbach, D. Cascio, F. B. Peters, K. Hideg, S. Peuker, P. G. Schultz and W. L. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 21637–21642.
3. E. H. Abdelkader, A. Feintuch, X. Yao, L. A. Adams, L. Aurelio, B. Graham, D. Goldfarb and G. Otting, Chem. Commun., 2015, 51, 15898–15901.
4. T. F. Cunningham, M. R. Putterman, A. Desai, W. S. Horne and S. Saxena, Angew. Chem., Int. Ed., 2015, 54, 6330–6334.
5. D. Banerjee, H. Yagi, T. Huber, G. Otting and D. Goldfarb, J. Phys. Chem. Lett., 2012, 3, 157–160.
6. H. Y. Vincent Ching, P. Demay-Drouhard, H. C. Bertrand, C. Policar, L. C. Tabares and S. Un, Phys. Chem. Chem. Phys., 2015, 17, 23368–23377.
7. D. Goldfarb, Phys. Chem. Chem. Phys., 2014, 16, 9685–9699.
8. A. Feintuch, G. Otting and D. Goldfarb, Methods Enzymol., Academic Press, 2015, vol. 563, pp. 415–457.
9. A. M. Raitsimring, A. V. Astashkin, J. H. Enemark, I. Kaminker, D. Goldfarb, E. D. Walter, Y. Song and T. J. Meade, Appl. Magn. Reson., 2013, 44, 649–670.
10. A. M. Raitsimring, C. Gunanathan, A. Potapov, I. Efremenko, J. M. L. Martin, D. Milstein and D. Goldfarb, J. Am. Chem. Soc., 2007, 129, 14138–14140.
11. M. Yulikov, P. Lueders, M. F. Warsi, V. Chechik and G. Jeschke, Phys. Chem. Chem. Phys., 2012, 14, 10732–10746.
12. A. Dalaloyan, M. Qi, R. Ruthstein, S. Vega, A. Godt, A. Feintuch and D. Goldfarb, Phys. Chem. Chem. Phys., 2015, 17, 1464–18476.
13. H. Yagi, D. Banerjee, B. Graham, T. Huber, D. Goldfarb and G. Otting, J. Am. Chem. Soc., 2011, 133, 10418–10421.
14. A. Potapov, H. Yagi, T. Huber, S. Jergic, N. E. Dixon, G. Otting and D. Goldfarb, J. Am. Chem. Soc., 2010, 132, 9040–9048.
15. E. H. Abdelkader, M. D. Lee, A. Feintuch, M. R. Cohen, J. D. Swarbrick, G. Otting, B. Graham and D. Goldfarb, J. Phys. Chem. Lett., 2015, 6, 5016–5021.
16. D. T. Edwards, T. Huber, S. Hussain, K. M. Stone, M. Kinnebrew, I. Kaminker, E. Matalon, M. S. Sherwin, D. Goldfarb and S. Han, Structure, 2014, 22, 1677–1686.
17. F. X. Theillet, A. Binolfi, B. Bekei, A. Martorana, H. M. Rose, M. Stuiver, S. Verzini, D. Lorenz, D. Goldfarb and P. Selenko, Nature, 2016, 530, 45–50.
18. M. Qi, A. Gross, G. Jeschke, A. Godt and M. Drescher, J. Am. Chem. Soc., 2014, 136, 15366–15378.
19. A. Martorana, G. Bellapadrona, A. Feintuch, E. Di Gregorio, S. Aime and D. Goldfarb, J. Am. Chem. Soc., 2014, 136, 13458–13465.
20. M. Yulikov, in Electron Paramagnetic Resonance, ed. B. C. Gilbert, V. Chechik and D. M. Murphy, 2015, vol. 24, pp. 1–31.
21. I. Kaminker, H. Yagi, T. Huber, A. Feintuch, G. Otting and D. Goldfarb, Phys. Chem. Chem. Phys., 2012, 14, 4355–4358.
22. P. Lueders, H. Jager, M. A. Hemminga, G. Jeschke and M. Yulikov, J. Phys. Chem. B, 2013, 117, 2061–2068.
23. M. Pannier, S. Veit, A. Godt, G. Jeschke and H. W. Spiess, J. Magn. Reson., 2000, 142, 331–340.
24. S. Milikisyants, F. Scarpelli, M. G. Finiguerra, M. Ubbink and M. Huber, J. Magn. Reson., 2009, 201, 48–56.
25. A. D. Milov, A. B. Ponomarev and Y. D. Tsvetkov, Chem. Phys. Lett., 1984, 110, 67–72.
26. G. Jeschke, V. Chechik, P. Ionita, A. Godt, H. Zimmermann, J. Banham, C. R. Timmel, D. Hilger and H. Jung, Appl. Magn. Reson., 2006, 30, 473–498.
27. R. A. Stein, A. H. Beth and E. J. Hustedt, Methods Enzymol., 2015, 563, 531–567.
28. A. Doll, M. Qi, N. Wili, S. Pribitzer, A. Godt and G. Jeschke, J. Magn. Reson., 2015, 259, 153–162.
29. A. Doll, M. Qi, S. Pribitzer, N. Wili, M. Yulikov, A. Godt and G. Jeschke, Phys. Chem. Chem. Phys., 2015, 17, 7334–7344.
30. L. V. Kulik, S. V. Paschenko and S. A. Dzuba, J. Magn. Reson., 2002, 159, 237–241.
31. L. V. Kulik, S. A. Dzuba, I. A. Grigoryev and Y. D. Tsvetkov, Chem. Phys. Lett., 2001, 343, 315–324.
32. A. V. Astashkin, Methods Enzymol., 2015, 563, 251–284.
33. D. Abdullin, F. Duthie, A. Meyer, E. S. Mueller, G. Hagelueken and O. Schiemann, J. Phys. Chem. B, 2015, 119, 13534–13542.
34. A. V. Astashkin, B. O. Elmore, W. H. Fan, J. G. Guillemette and C. J. Feng, J. Am. Chem. Soc., 2010, 132, 12059–12067.
35. A. Meyer and O. Schiemann, J. Phys. Chem. A, 2016, 120, 3463–3472.
36. S. Razzaghi, M. Qi, A. I. Nalepa, A. Godt, G. Jeschke, A. Savitsky and M. Yulikov, J. Phys. Chem. Lett., 2014, 5, 3970–3975.
37. J. R. Sachleben, P. Beverwyk and L. Frydman, J. Magn. Reson., 2000, 144, 330–342.
38. J. R. Sachleben, V. Frydman and L. Frydman, J. Am. Chem. Soc., 1996, 118, 9786–9787.
39. N. N. Barak, P. Neumann, M. Sevvana, M. Schutkowski, K. Naumann, M. Malesevic, H. Reichardt, G. Fischer, M. T. Stubbs and D. M. Ferrari, J. Mol. Biol., 2009, 385, 1630–1642.
40. E. Liepinsh, M. Baryshev, A. Sharipo, M. Ingelman-Sundberg, G. Otting and S. Mkrtchian, Structure, 2001, 9, 457–471.
41. M. Ramirez Cohen, V. Frydman, P. Milko, M. A. Iron, E. H. Abdelkader, M. D. Lee, J. D. Swarbrick, A. Raitsimring, G. Otting, B. Graham, A. Feintuch and D. Goldfarb, Phys. Chem. Chem. Phys., 2016, 18, 12847–12859.
42. F. Mentink-Vigier, A. Collauto, A. Feintuch, I. Kaminker, V. Tarle and D. Goldfarb, J. Magn. Reson., 2013, 236, 117–125.
43. D. Goldfarb, Y. Lipkin, A. Potapov, Y. Gorodetsky, B. Epel, A. M. Raitsimring, M. Radoul and I. Kaminker, J. Magn. Reson., 2008, 194, 8–15.
44. A. Raitsimring, A. Dalaloyan, A. Collauto, A. A. Feintuch, T. Meade and D. Goldfarb, J. Magn. Reson., 2014, 248, 71–80.
45. W. B. Mims, K. Nassau and J. D. McGee, Phys. Rev., 1961, 123, 2059–2069.

---

Footnote

† Electronic supplementary information (ESI) available: Measurements of T_M and T_1e, analysis of background decay and SNR; field and temperature dependence of the phase memory and longitudinal relaxation times for the Gd(III)–DOTA ruler; analysis of the DEER and RIDME traces for the Gd(III)–DOTA ruler; effect of experimental parameters on the RIDME traces for the Gd(III)–DOTA ruler; field-swept echo-detected EPR spectrum of the C9–Gd(III) tag; dipolar evolution traces for the DEER and RIDME experiments on the mutants of the ERp29 homodimer labeled with the C9–Gd(III) tag; effect of the experimental parameters on the RIDME traces for the S114C mutant of the ERp29 homodimer labeled with the C9–Gd(III) tag; mutant and concentration dependence of the phase memory and longitudinal relaxation times for the C9–Gd(III)-labeled ERp29 samples. See DOI: 10.1039/c6cp03299k

---