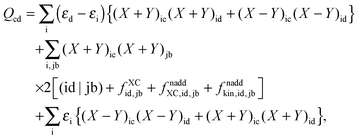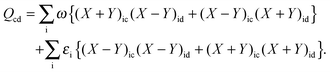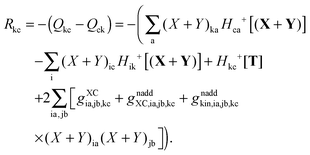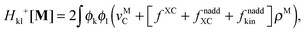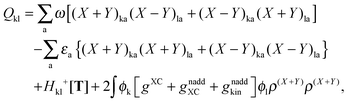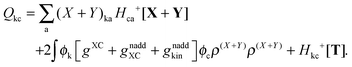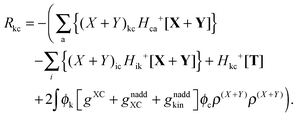Analytical gradients for excitation energies from frozen-density embedding†
Received
18th January 2016
, Accepted 3rd March 2016
First published on 21st March 2016
Abstract
The formulation of analytical excitation-energy gradients from time-dependent density functional theory within the frozen-density embedding framework is presented. In addition to a comprehensive mathematical derivation, we discuss details of the numerical implementation in the Slater-function based Amsterdam Density Functional (ADF) program. Particular emphasis is put on the consistency in the use of approximations for the evaluation of second- and third-order non-additive kinetic-energy and exchange–correlation functional derivatives appearing in the final expression for the excitation-energy gradient. We test the implementation for different chemical systems in which molecular excited-state potential-energy curves are affected by another subsystem. It is demonstrated that the analytical implementation for the evaluation of excitation-energy gradients yields results in close agreement with data from numerical differentiation. In addition, we show that our analytical results are numerically more stable and thus preferable over the numerical ones.
1 Introduction
A full interpretation of excited-state processes requires to have reliable theoretical models for the explanation of experimental data in terms of excited-state geometric and electronic structure at hand.1 The characterization of excited-state potential energy surfaces is important for understanding a variety of phenomena, such as photochemical reactions, vibrationally resolved UV-Vis spectra, resonance Raman spectra, excited-state dynamics etc. Efficient calculations of potential energy surfaces require an analytical approach for the evaluation of excited-state gradients. The main advantage of such an analytical calculation of gradients in contrast to a numerical approach is that the computational cost does not depend on the number of nuclear degrees of freedom. For a long time, the standard method to calculate nuclear derivatives of excited-state energies for large molecular systems has been the configuration interaction singles method.2 In 1994, Ortiz derived and implemented gradients of excited states within the random phase approximation.3 The first implementation of analytical excited-state gradients within Time-Dependent Density Functional Theory (TDDFT) was presented by Van Caillie and Amos.4 While in that work the expression for the gradients was obtained by straightforward differentiation, Furche and Ahlrichs employed5 a more convenient Lagrangian-based approach, similar to the one used in ref. 6 for configuration interaction methods. The same technique was used by Hutter in his work,7 where the calculation of analytical excited-state gradients from the Tamm–Dancoff approximation to TDDFT was implemented within a plane-wave-basis set framework. In 2005, Doltsinis extended8 plane-wave TDDFT excited-state gradient calculations beyond the Tamm–Dancoff approximation, where in addition, an active space approach9 and an implicit differentiation scheme were employed. Seth et al.10 implemented analytical gradients for spin–flip TDDFT excitation in the Amsterdam Density Functional program package (ADF),11,12 which uses Slater-type functions in contrast to most other quantum chemistry packages. These implementations provided a powerful toolbox for the theoretical characterization of excited-state potential-energy surfaces of large molecules. Embedding techniques like the Polarizable Continuum Model13 (PCM), Quantum Mechanics/Molecular Mechanics14 (QM/MM) or Frozen-Density Embedding (FDE)15 can increase the range of application for TDDFT gradients. Analytical gradients for the evaluation of excitation-energy gradients have been implemented, e.g. for PCM-TDDFT16 and QM/MM-TDDFT17 and other fragmentation or embedding strategies.18,19 However, no such analytical gradients are available so far for FDE, which partitions the total electron density of a large system into that of an active region and the frozen density of an environment. The TDDFT extension of FDE has been presented in ref. 20 and 21, and several challenging applications have been presented since then (see ref. 22–25 or the review in ref. 26 for some examples). Following the strict version of “frozen-density embedding”, we will assume here and in the following that the response of the system to an external perturbation is entirely localized in the active system. This corresponds to the case of “uncoupled FDE” (FDEu) for excited states in the nomenclature of ref. 27, which is also known as the “neglect of differential response of the environment” (NDRE).28 This can be relaxed in a full subsystem TDDFT treatment (see ref. 27 and the work by Casida and Wesolowski20). For recent reviews, see ref. 29 and 30. Note that analytical ground-state energy gradients for FDE have been reported before,31 and will thus not be considered here. The development of analytical excited-state gradient theory in TDDFT within FDE will give fast access to potential energy surfaces of the excited states of complex systems.
2 Theory
The excited-state gradient in TDDFT is calculated as the sum of the ground-state gradient and the gradient of the excitation energy, but since the former is established for FDE31 we focus here only on the latter part. In order to introduce the notation, the underlying theory of FDE and its TDDFT extension are briefly presented in Sections 2.1 and 2.2, respectively. The formulation of FDEu-TDDFT excitation-energy gradients is concisely established in Section 2.3, which is followed by a derivation of the Z-vector equation for FDEu-TDDFT gradients in Section 2.4. An in-depth derivation including all intermediate steps is presented in Appendix A. Note that our theoretical development is based on the formalism introduced in the work by Seth et al.10 as well as in that by Furche and Ahlrichs.5
2.1 Frozen-density embedding
The FDE theory15 is a fundamental framework for embedding schemes within DFT. The total density of the system in the FDE approach is partitioned into an active part and a frozen part| | | ρtot(r) = ρ(r) + ρf(r). | (1) |
The active electron density, ρ(r), can be expressed through the orbitals located in the active fragment of the molecular system,| | 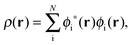 | (2) |
where N is the number of electrons in the active part. The molecular orbitals of this fragment are usually varied during the calculation, and hence its density as well. Contrarily, the density of the frozen part, ρf(r), is chosen to be constraint during the calculation. In the context of the related subsystem DFT method,32–34 it consists of orbitals located in the environment, ϕif,| | 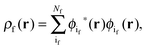 | (3) |
and both subsystem densities can be optimized. Please note that we do not use an extra label for indices of orbitals, densities, and potentials of the active fragment, while the terms for the frozen fragment are marked with “f” as a subscript (or, in the case of potentials, as a superscript).
In order to obtain the ground-state density of the active system, ρ(r), in the presence of the frozen density, the Kohn–Sham (KS) equations with Constrained Electron Density (KSCED)15 must be solved,
| | 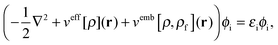 | (4) |
where
veff[
ρ](
r) has the same form as the effective potential for the standard Kohn–Sham equation of the isolated active system,
| | 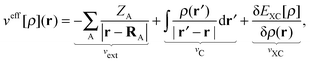 | (5) |
and
vemb[
ρ,
ρf](
r) is responsible for the interaction of the active part with the frozen environment density,
| | 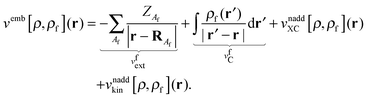 | (6) |
The last two terms represent the so-called non-additive XC potential and non-additive kinetic potential, which read
| | 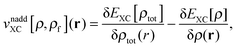 | (7) |
| | 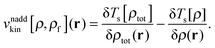 | (8) |
The term in parenthesis on the left hand-side of
eqn (4) is denoted as
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif)
and can be identified as the time-independent FDE-KS Hamiltonian.
2.2 Frozen-density embedding within TDDFT
The FDE formalism has been extended to excited states by Casida and Wesolowski,20 and a general subsystem TDDFT framework was established in ref. 27. The FDE approach can be considered as a special case of the subsystem-based TDDFT scheme in which local excitations are obtained under the influence of a given environment, e.g. a solvent. The matrix elements of the time-independent FDE-KS Hamiltonian are given as| | 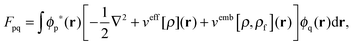 | (9) |
where ϕp are orbitals of the active part of the system. The convention that indices i,j, etc. correspond to occupied orbitals, a, b, etc. to virtual orbitals and p,q, etc. refer to general orbitals is adopted for the following derivations. Expanding the time-dependent one-electron functions, ϕp(r,t), in a linear combination of time-independent one-electron functions, ϕj(r) with time-dependent orbital coefficients, Kjp(t),| | 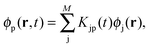 | (10) |
the Time-Dependent KS (TDKS) equations will take the following form35,36| | 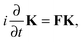 | (11) |
where the i-th column of the matrix K contains the expansion coefficients of ϕi(r,t). F is a matrix representation of the TDKS Hamiltonian operator in the basis of {ϕi(r)}. Assuming that a time-dependent external field is applied35 one can derive the main equation of linear-response TDDFT within the FDE approach from eqn (11),| | 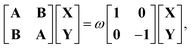 | (12) |
where the elements of A and B read (real orbitals are assumed),| | | Aia,jb = Fabδij − Fijδab + (ia|jb) + (ia|fXC|jb) + (ia|fnaddkin|jb) + (ia|fnaddXC|jb), | (13) |
| | | Bia,jb = (ia|bj) + (ia|fXC|bj) + (ia|fnaddkin|bj) + (ia|fnaddXC|bj). | (14) |
The response of the XC potential corresponds to the second functional derivative of the exchange–correlation energy, which is called XC kernel and given as| | 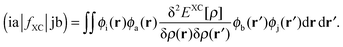 | (15) |
Only non-additive terms from the embedding potential, vemb[ρ,ρf](r), remain and they are represented as a second functional derivative of the corresponding non-additive energies, which are also called non-additive kernels,| | 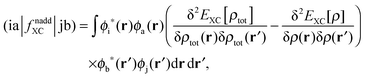 | (16) |
| | 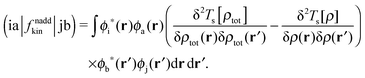 | (17) |
Using the fact that in the basis of canonical orbitals| | | Fab = Fabδab = εaδab, | (18) |
| | | Fij = Fijδij = εiδij, | (19) |
elements of matrices A and B change to| | | Aia,jb = δijδab(εa − εi) + (ia|jb) + (ia|fXC|jb) + (ia|fnaddkin|jb) + (ia|fnaddXC|jb), | (20) |
| | | Bia,jb = (ia|bj) + (ia|fXC|bj) + (ia|fnaddkin|bj) + (ia|fnaddXC|bj). | (21) |
In the ADF package XC, non-additive XC, and non-additive kinetic kernels in the equations above are by default evaluated within the adiabatic local density approximation (ALDA) for non-hybrid XC potentials. This gives a good compromise between accuracy and efficiency. Moreover, ALDA kernels show smoother behavior for the low density regions than adiabatic generalized gradient approximation (AGGA) kernels. The last statement can be explained by the absence of 1/|∇ρ(r)|β dependencies in kernels, where β is a positive exponent.
We note that it is sometimes useful to rearrange eqn (12) by means of the unitary transformation U,
| | 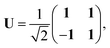 | (22) |
into the two coupled equations
| | | (A + B)(X + Y) = ω(X − Y), | (23) |
| | | (A − B)(X − Y) = ω(X + Y). | (24) |
2.3 TDDFT excitation-energy gradients within FDE
Having the concepts of excitation-energy gradients for regular TDDFT at hand,5,10 it is possible to establish the theory of FDEu-TDDFT excited-state gradients in a similar way (see Appendix A for a detailed derivation).
The Lagrangian for FDEu-TDDFT reads [see eqn (86) in Appendix A.2]
| | 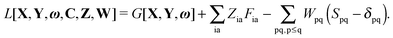 | (25) |
The quantity
G[
X,
Y,
ω] has the following form,
| | 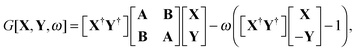 | (26) |
where
A and
B are the matrices specified in Section 2.2,
X and
Y are the solution vectors from
eqn (12),
C is the matrix of orbital coefficients.
Z and
W in
eqn (25) contain two additional sets of Lagrangian multipliers. The sum
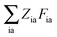
takes care of the conditions
Fia = 0 (which implies that KSCED equations are solved, but not necessarily in canonical orbitals) and
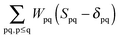
ensures orthonormality of the orbitals (
Spq is the overlap integral for orbitals p and q). Note that our definition of the vector
Z implies that only occupied–virtual components among all
Zrs are non-zero. The FDE-TDDFT eigenvalue problem can be expressed as
| | 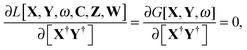 | (27) |
and the orthonormality constraint is given as
| | 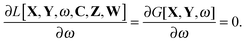 | (28) |
It is possible to rewrite the Lagrangian as (see Appendix A.3; for simplicity of notation the Lagrangian,
L[
X,
Y,
ω,
C,
Z,
W], will be written from now on as
L)
| | 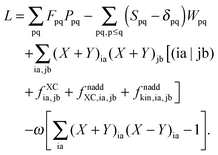 | (29) |
In the equation above, a relaxed difference density matrix
P was introduced (see Appendix A.6 for more details),
where
T is an unrelaxed difference density matrix with elements equal to
| | 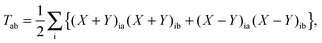 | (31) |
| | 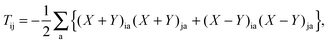 | (32) |
We now introduce some external perturbation
ξ. In our particular case,
ξ represents some nuclear coordinate
RAk (
i.e., component
k of the position vector of atom A). The derivatives of the Lagrangian with respect to all possible nuclear coordinates
ξ in the system constitute the gradient of the excitation energy with respect to the position of the nuclei. As stressed by Furche and Ahlrichs, the formalism is also valid if
ξ represents some general perturbation,
e.g. a component of a static electric field, which gives access to the excited-state dipole moment.
5 In order to differentiate the Lagrangian with respect to a perturbation
ξ, it is useful first to convert it to atomic orbital representation (see also Appendices A.4 and A.5). In comparison with the regular TDDFT case,
eqn (29) contains the additional terms
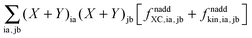
(which results from
G[
X,
Y,
ω]) and
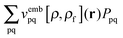
(which results from
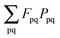
). The focus here will thus be mostly on these terms. For convenience, we will sometimes drop the notation
vemb[
ρ,
ρf],
veff[
ρ],
etc. and write
vemb,
veff instead. Converting
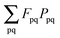
to atomic orbital basis, we get
| | 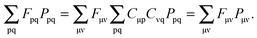 | (34) |
For convenience, we define the kinetic energy operator
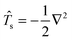
. Keeping the orbital coefficients constant and taking the derivative with respect to the perturbation
ξ [
ξ as a superscript indicates differentiation over
ξ, while (
ξ) means that MO coefficients are kept constant during differentiation], we get from the equation above,
| | 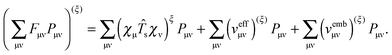 | (35) |
The first term reads
10| | 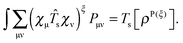 | (36) |
Here, we introduced the density
| | 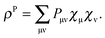 | (37) |
The second term
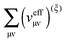
reads (here, we introduce a simplified notation in which the integration of a function
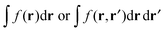
will be expressed as
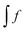
),
| | 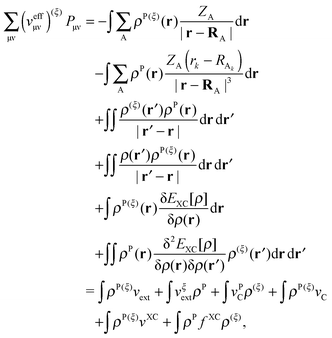 | (38) |
where
vC and
vPC are the Coulomb potentials due to
ρ and
ρP, respectively, and
| | 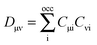 | (39) |
is an element of the ground-state density matrix. Similarly, we get for the third term
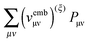
,
| |  | (40) |
where
vfC is the Coulomb potential due to
ρf. Converting the third term in
eqn (29) to the atomic basis representation and taking its derivative with respect to
ξ leads to
| | 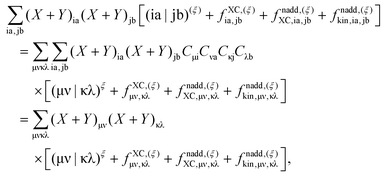 | (41) |
or, in terms of densities,
| | 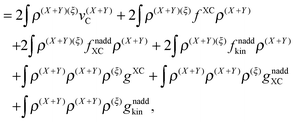 | (42) |
where
gXC,
gnaddXC, and
gnaddkin are given as functional derivatives of the kernels (third functional derivatives of the corresponding energy functionals with respect to the density).
The derivative of the last term in eqn (29) with respect to ξ gives zero. Summing up all the terms mentioned above together with 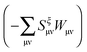 the expression for the Lagrangian derivative Lξ is
the expression for the Lagrangian derivative Lξ is
| | 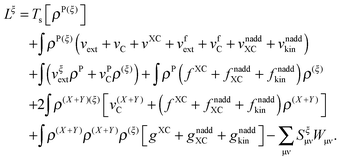 | (43) |
2.4
Z-vector equation for FDE-TDDFT
For the evaluation of Lξ, the corresponding vectors W and Z have to be known (P = Z + T, and T is already determined from the solution of FDE-TDDFT problem). These vectors can be obtained from the so-called Z-vector equation,5,37 which is derived using the condition,| | 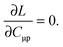 | (44) |
If eqn (44) is multiplied by Cμq and summed over index μ, we get the following relation,| | 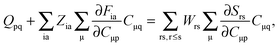 | (45) |
where Q stands for| | 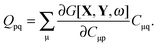 | (46) |
Introducing the abbreviation for some arbitrary M,| | 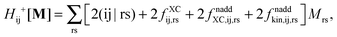 | (47) |
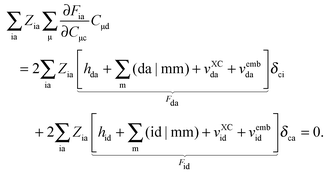
it is possible to derive the following equations (see ref. 5 and Appendix B),| | | Qij + Hij+[Z] = Wij(1 + δij), | (48) |
| | | Qia + εaZia + Hia+[Z] = Wia, | (49) |
where the explicit expressions for Qpq look like (four cases are distinguished),| | 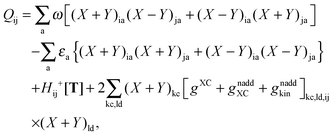 | (52) |
| | 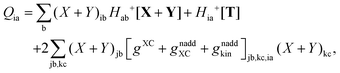 | (53) |
| | 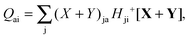 | (54) |
| | 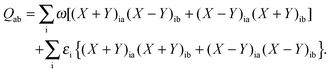 | (55) |
Subtracting eqn (50) from eqn (49) we get the Z-vector equation| | | (εa − εi)Zia + Hia+[Z] = − (Qia − Qai). | (56) |
This equation can be rewritten as| | 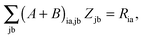 | (57) |
where Ria = −(Qia − Qai) reads| | 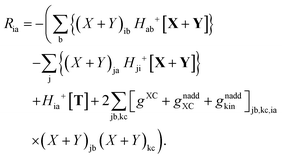 | (58) |
The matrix W is determined from the following equations| | 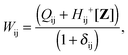 | (59) |
| | 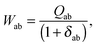 | (60) |
The Z-vector equation and all relevant variables can be rewritten in terms of densities.10 The corresponding quantities Hij+[M], Qij, and Qia then read,| | 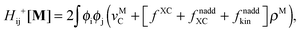 | (62) |
| | 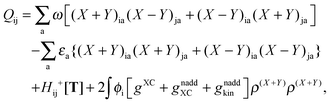 | (63) |
| | 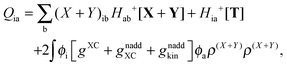 | (64) |
while Qai and Qab will remain the same. Note that ρM and ρ(X+Y) are defined in analogy to eqn (37). Finally, one can rewrite Ria in terms of densities| | 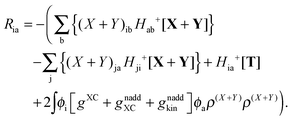 | (65) |
3 Details of the implementation
An algorithm for the evaluation of excitation-energy gradients within FDEu-TDDFT was implemented in ADF.11 Our implementation is based on the modules for the calculation of excitation-energy gradients in TDDFT, which were developed by Seth et al.10 In addition, we created modules for the evaluation of the second functional derivative of the non-additive kinetic energy using the AGGA (denoted as FULL in the formulas below to distinguish from the commonly used ALDA approximation), and the second and third functional derivatives of the non-additive kinetic energy using the Thomas Fermi approximation (denoted as TF in the formulas below). These modules make use of the XCFUN library.38 As was already mentioned in Section 2.2, the evaluation of the second functional derivative in response calculations is usually done within the ALDA in ADF, independently of the approximation used for the XC potential. This introduces some consistency issues in the evaluation of TDDFT gradients. Every kernel and potential term in the expression for the gradient which originates from the Fock matrix (XC potential and second XC functional derivative) have to be evaluated in the original approximation (LDA, GGA,…), while terms which result from the response part are always evaluated in the ALDA (which in the case of the non-additive kinetic energy is the TF approximation). Within the ADF setup, the ALDA-consistent expression for the excited-state gradients thus reads,| |  | (66) |
The difference in the approximations for the XC part has to be taken into account in the Z-vector equation, eqn (57), as well. Special attention should be paid to the elements Hij+[M]. Note that| | 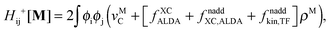 | (67) |
when M is (X + Y), and| | 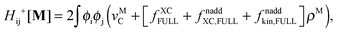 | (68) |
when M is T or Z.
An additional comment should be made on the evaluation of the non-additive XC kernels. One can significantly simplify the evaluation of the XC kernels and their functional derivatives if the expression for the non-additive XC potential, eqn (7) is recalled,
| | | fXC[ρ] + fnaddXC[ρtot,ρ] = fXC[ρ] + fXC[ρtot] − fXC[ρ] = fXC[ρtot], | (69) |
| | | gXC[ρ] + gnaddXC[ρtot,ρ] = gXC[ρ] + gXC[ρtot] − gXC[ρ] = gXC[ρtot]. | (70) |
This basically means that instead of the evaluation and summation of XC kernels for active and total densities, one needs to evaluate the XC kernels only for the total density
ρtot(
r).
Concerning the computational scaling of the FDEu-TDDFT gradient calculations, we note that only a small additional step in the calculation of embedding potentials and kernels is needed, compared to the effort in the standard TDDFT gradients. In particular, the orbital space is not increased in FDEu-TDDFT calculations when using monomer basis sets for the active system (which is the default in these types of calculations). The differences in timing and computational effort of the ground-state DFT step and in TDDFT excitation-energy calculations have been addressed in ref. 23, and we refer the interested reader to this reference for further details.
4 Computational details
A locally modified version of the ADF package11,12 was used for all calculations. For ground-state structure optimizations, the Becke–Perdew (BP86) XC functional39,40 in combination with the triple-ζ polarized Slater-type (TZP) basis set from the ADF basis set library was employed. The same basis set and the XC functional were used for the excitation energy calculations. For the FDE calculations, we employed the corresponding ADF implementation,41 making use of the so-called GGA97 generalized-gradient approximation (GGA) for the non-additive kinetic contribution to the embedding potential.42 This approximation is also known as PW91k, because it has the same functional form for the enhancement factor as used in the exchange functional of Perdew and Wang (PW91).43
5 Results and discussions
To test the analytical gradients for excitation energies within the FDEu approach, three different test systems were studied. A first test was performed on the complex of formaldehyde with a lithium ion (charge +1), where the density of the lithium ion was frozen. The structure of the system was obtained in the following way: at first, the formaldehyde structure was optimized with BP86/TZP; then the lithium ion was put on the axis along the CO bond (oriented along the z-axis). The structure is shown in Fig. 1. Such an orientation of the lithium ion was chosen to enforce a rather large effect of the embedding potential in this initial test. This system is thus highly polarized, and the effect of the classical electrostatic part of the embedding potential will be quite pronounced. But in addition, the non-additive kinetic-energy contributions can be important in such systems, because they are necessary to prevent over-polarization effects.
 |
| | Fig. 1 Structure of the CH2O⋯Li+ system and its orientation in coordinate space. | |
The excitation energy dominated by the HOMO → LUMO transition was chosen for the calculation of the gradient at different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances. Note that the C⋯Li+ distance is kept constant in our calculations, so that increasing C
O bond distances. Note that the C⋯Li+ distance is kept constant in our calculations, so that increasing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances correspond to decreasing O⋯Li+ distances. The HOMO of this system corresponds to a nonbonding (n) orbital, while the LUMO corresponds to a π* orbital. Isosurface plots of the orbitals involved in the transition are shown in Fig. 2.
O distances correspond to decreasing O⋯Li+ distances. The HOMO of this system corresponds to a nonbonding (n) orbital, while the LUMO corresponds to a π* orbital. Isosurface plots of the orbitals involved in the transition are shown in Fig. 2.
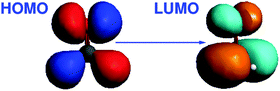 |
| | Fig. 2 Isosurface plots of the orbitals (BP86/TZP) involved in the dominant orbital transition of the excitation under study for CH2O⋯Li+ (lithium ion is not shown). | |
To check whether the embedding potential and all of its components affect the electronic transitions, the excitation energies for the CH2O⋯Li+ complex and for isolated formaldehyde were calculated for different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances. These results are shown in Fig. 3. One can see from this figure that the closer the oxygen atom is to the lithium ion, the more the excitation energy is affected by the embedding potential. Thus, the complex represents a good test system to check the implemented procedure.
O bond distances. These results are shown in Fig. 3. One can see from this figure that the closer the oxygen atom is to the lithium ion, the more the excitation energy is affected by the embedding potential. Thus, the complex represents a good test system to check the implemented procedure.
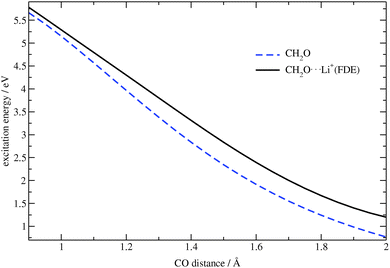 |
| | Fig. 3 Dependence of the excitation energy on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance in CH2O and CH2O⋯Li+ (TZP/BP86). O bond distance in CH2O and CH2O⋯Li+ (TZP/BP86). | |
The gradients of the excitation energies10 for isolated formaldehyde for different C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances were calculated analytically with BP86/TZP. Then for the same distances gradients were calculated numerically for the complex, where the lithium ion was described with FDEu. In addition, the analytical gradients of the excitation energy were calculated for the same system with FDEu. To compare the obtained results, the dependence of the z-component of the gradient for the oxygen atom on the C
O bond distances were calculated analytically with BP86/TZP. Then for the same distances gradients were calculated numerically for the complex, where the lithium ion was described with FDEu. In addition, the analytical gradients of the excitation energy were calculated for the same system with FDEu. To compare the obtained results, the dependence of the z-component of the gradient for the oxygen atom on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance is plotted for each calculation in Fig. 4.
O bond distance is plotted for each calculation in Fig. 4.
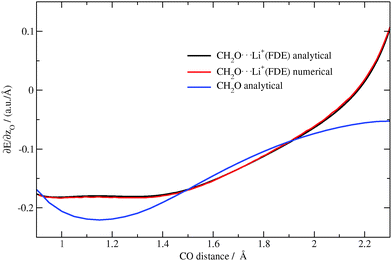 |
| | Fig. 4 Dependence of the z-component of the gradient of the excitation energy for the oxygen atom in CH2O (analytical) and CH2O⋯Li+(analytical/numerical) on the CO distance (TZP/BP86/PW91K). | |
One can see from the plot that the presence of the lithium ion is simulated very well by the embedding potential, and that it contributes significantly to the value of the excitation-energy gradient. For all displacements of the oxygen atom towards lithium, the values of the z-component of the gradient for oxygen are in perfect agreement.
In the second test system, the lithium ion was substituted by a helium atom, and the O⋯He distance was changed while keeping the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance fixed at 1.7 Å. This is significantly larger than the ground-state equilibrium C
O distance fixed at 1.7 Å. This is significantly larger than the ground-state equilibrium C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance of about 1.2 Å, and was selected in order to observe a significant effect of the embedding contribution (at the equilibrium distance, this effect is rather small). Contrary to the first, the second test system has a small contribution of the classical electrostatic part to the embedding potential. The same excitation as in the previous case was considered, see Fig. 2. The effect of the FDE potential on the excitation energy under study can clearly be seen in Fig. 5.
O distance of about 1.2 Å, and was selected in order to observe a significant effect of the embedding contribution (at the equilibrium distance, this effect is rather small). Contrary to the first, the second test system has a small contribution of the classical electrostatic part to the embedding potential. The same excitation as in the previous case was considered, see Fig. 2. The effect of the FDE potential on the excitation energy under study can clearly be seen in Fig. 5.
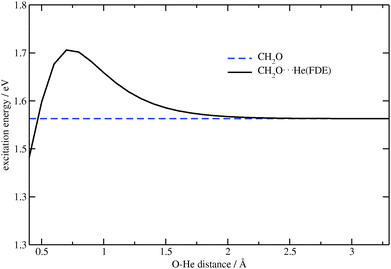 |
| | Fig. 5 Dependence of the excitation energy on the O⋯He distance for CH2O⋯He (TZP/BP86). The excitation energy for CH2O (constant in this plot) is shown for comparison. | |
Again, as in the previous case, the dependence of the z-component of the gradient for the oxygen atom on the O⋯He distance is plotted in Fig. 6 for the CH2O molecule alone as well as for the CH2O⋯He system (analytical/numerical). We observe a very good agreement between numerical and analytical results. The small remaining discrepancies can be attributed to inaccuracies of the numerical gradient. This can be seen by considering the region from 3.1 Å to 3.3 Å (see inset in Fig. 6). In this region the influence of the He atom on the gradient should vanish and the result should be very close to the one for the isolated molecule. While the analytical FDE gradient approaches the result for the isolated molecule with good accuracy, the numerical one underestimates the z-component of the gradient by roughly 0.0005 a.u. Å−1. This shows the advantages of the analytical approach over the numerical one. Note that the error for the numerical approach might be larger in regions where the gradient changes faster, e.g. near 0.4 Å, see Fig. 6.
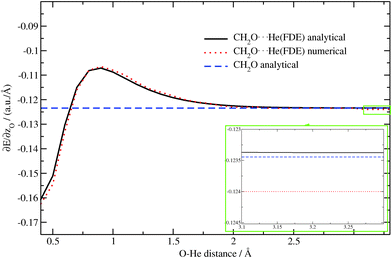 |
| | Fig. 6 Dependence of the z-component of the gradient of the excitation energy for the oxygen atom in CH2O⋯He (analytical/numerical) and in CH2O (analytical) on the O⋯He distance (TZP/BP86/PW91K). The region from 3.1 Å to 3.3 Å is magnified in the inset. | |
The third test system consists of an acetone molecule and water treated with FDE. We take this system from our previous work on frozen density embedding.44 The system was optimized with BP86/TZP imposing Cs symmetry, see Fig. 7. Here, we studied the excitation dominated by the HOMO → LUMO (n → π*) orbital transition. The orbital composition of the excitation considered for the gradient calculation is shown in Fig. 8.
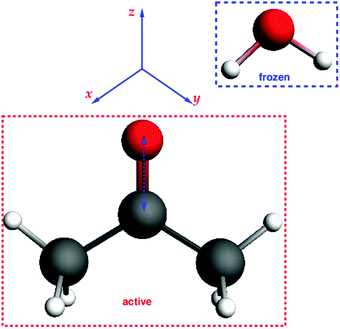 |
| | Fig. 7 Structure of the acetone⋯water system and its orientation in coordinate space. | |
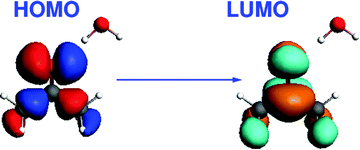 |
| | Fig. 8 Isosurface plots of the orbitals (BP86/TZP) involved in the dominant orbital transition of the excitation studied for the acetone⋯water system. | |
In comparison to the previous tests where only single atoms were considered as frozen systems within FDE, here we deal with a frozen molecule. In this case, both electrostatic and non-additive kinetic parts of the FDE potential are significant. Structures in which the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance in acetone was varied from 1.2 Å to 2 Å were generated for the comparison of numerical and analytical gradients. Similar to our first test system, the carbon–water distance was kept fixed, i.e., longer C
O bond distance in acetone was varied from 1.2 Å to 2 Å were generated for the comparison of numerical and analytical gradients. Similar to our first test system, the carbon–water distance was kept fixed, i.e., longer C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances correspond to shorter O⋯H2O contacts. In Fig. 9 the dependence of the excitation energy on the C
O distances correspond to shorter O⋯H2O contacts. In Fig. 9 the dependence of the excitation energy on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance for isolated acetone and for the acetone⋯water system are plotted. One can see that the FDE potential has a slight effect on the excitation energy.
O bond distance for isolated acetone and for the acetone⋯water system are plotted. One can see that the FDE potential has a slight effect on the excitation energy.
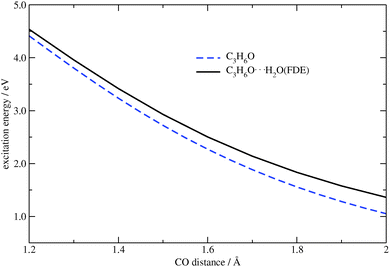 |
| | Fig. 9 Dependence of the excitation energy on the CO distance in C3H6O and C3H6O⋯H2O (TZP/BP86). | |
The analytical and numerical excitation energy gradients for C3H6O⋯H2O as well as for isolated acetone were calculated for the above-mentioned structures. The z-component of the excitation energy gradient for the oxygen atom in acetone (analytical) and in acetone⋯water (analytical/numerical) are shown in Fig. 10. Again, the results from the analytical approach are in good agreement with the numerical ones.
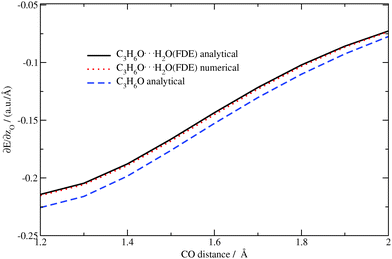 |
| | Fig. 10 Dependence of the z-component of the gradient of the excitation energy for the (acetone–)oxygen atom in the acetone⋯water system on the CO distance in acetone (TZP/BP86/PW91K). | |
6 Summary and conclusions
In this paper we have, for the first time, presented the formulation of analytical excitation-energy gradients in FDE-TDDFT. Furthermore, an algorithm and an implementation for the analytical evaluation of excitation-energy gradients within the FDEu approximation were developed and discussed in detail. We have shown how to incorporate the contributions from the embedding potential into the final expression for excitation-energy gradients consistently with the non-FDE implementation in ADF by Seth et al.10 Special care has to be taken concerning approximations for non-additive kinetic and XC kernel and their functional derivatives in order to be consistent with the previous ALDA implementation. The kernels arising from the Fock operator should be evaluated in the original approximation, while terms originating from the response part are evaluated in the ALDA. Of course, the implementation is flexible and allows for an extension beyond the ALDA in future work.
The implemented procedure was successfully tested and yields very good agreement with numerical reference results. Three different test systems were considered, which were chosen according to the expected contribution of different parts of the FDE embedding potential. In particular, the correct behavior of the gradient was tested on formaldehyde with a lithium ion as the frozen part and on formaldehyde with a frozen helium atom. The former has a large contribution from classical electrostatics in the FDE potential, while in the latter system the contribution from the non-additive kinetic potential is more important. As another test with a frozen molecular environment system, an acetone⋯water complex was chosen. All calculations on the above-mentioned systems showed good agreement between analytical and numerical results. Moreover, it was demonstrated that results of analytical FDEu-TDDFT gradients are more accurate and thus preferable to the ones obtained by numerical differentiation.
The whole formalism was successfully implemented into the ADF package. In future work, we plan to address more complicated test systems to optimize the performance of the implementation and make FDE calculations beyond the ALDA possible. Also extensions beyond the approximation of a response localized on the active system are desirable if subsystem-based descriptions of excitonically coupled chromophores45 or explicit solvent response effects46 are of interest.
A Detailed derivation of the excitation-energy gradients
A.1 Introduction
In this appendix, we provide an in-depth derivation of the expression for excitation-energy gradients in FDE-TDDFT, based on the studies of Furche and Ahlrichs5 as well as Seth et al.10 The latter directly focuses on aspects relevant for the Slater-based ADF framework and thus provides the basis for the derivation of excited-state gradients in FDE-TDDFT, which is established here in Sections 2.3 and 2.4.
A.2 Excited state gradients for TDDFT
In FDE-TDDFT, the excited-state energy is represented as a sum of the ground-state energy and the excitation energy. If the gradient of the excited-state energy has to be evaluated, one has to consider the derivatives of these two terms. The derivatives of the former are formulated in ref. 31, and the derivative of the latter can be established in a similar way using Lagrangian techniques. We will only be concerned with the latter here. The variational formulation of FDE-TDDFT (by analogy to TDDFT case5,47,48) reads| | 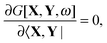 | (71) |
| | 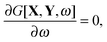 | (72) |
where the Lagrangian G[X,Y,ω] for the excitation energy has the following form| | | G[X,Y,ω] = 〈X,Y|Λ|X,Y〉 − ω(〈X,Y|Δ|X,Y〉 − 1). | (73) |
The quantities Λ and Δ are super-matrices,| | 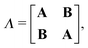 | (74) |
| | 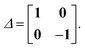 | (75) |
The |X,Y〉 vector in Dirac notation is| | 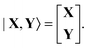 | (76) |
After differentiation and elementary manipulations, eqn (71) leads to a set of two matrix-vector equations, eqn (23) and (24) given in Section 2.2. The first term of the Lagrangian in eqn (73), 〈X,Y|Λ|X,Y〉, can be rewritten in the following way,| | 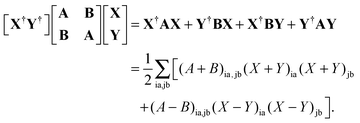 | (77) |
After substitution of this result into eqn (73) and writing the second term in an explicit way, the Lagrangian will take the following form| | 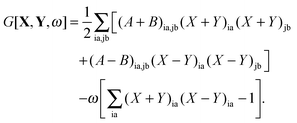 | (78) |
If G[X,Y,ω] is expressed in this way, then the requirement of eqn (71) can equivalently be expressed in terms of two conditions48| | 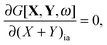 | (79) |
| | 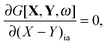 | (80) |
for every combination ia, since one can use (X + Y)ia and (X − Y)ia instead of Xia and Yia as free variables. These two equations lead to eqn (23) and (24). If the TDDFT eigenvalue problem is solved, then the Lagrangian is stationary with respect to (X + Y)ia and (X − Y)ia but not with respect to the molecular orbital coefficients Cμp. This introduces difficulties if one studies the derivative of the Lagrangian with respect to some perturbation ξ,| | 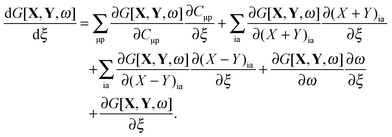 | (81) |
The implicit dependence of G[X,Y,ω] on ξ through (X + Y)ia, (X − Y)ia, and ω can be dropped using the conditions from eqn (72), (79) and (80). Thus, the derivative of G[X,Y,ω] can be simplified to| | 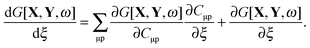 | (82) |
The derivative of G[X,Y,ω] with respect to molecular orbital coefficients has the following form,| | 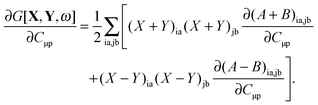 | (83) |
Since| | 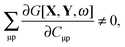 | (84) |
or, in other words, since the orbitals in the excited state are unrelaxed, the implicit dependence of G[X,Y,ω] on ξ through the molecular orbital coefficients Cμp cannot be dropped. Thus the derivatives ∂Cμp/∂ξ must be evaluated, which requires the solution of the 3M Coupled-Perturbed Kohn–Sham (CPKS) equations if gradients shall be calculated (M is the number of atoms). These equations can be derived from the relation| | 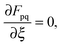 | (85) |
substituting ξ with each coordinate of every atom in the system. This is a rather inefficient way to calculate the gradient of the excitation energy. But in 1984, Handy and Schaefer37 suggested an efficient method to avoid solving these 3M equations, which instead requires to solve only one equation with the same dimension as the CPKS equation. This approach is called the Z-vector method49 and it is set up in such a way that it does not require derivatives of molecular orbital coefficients.5,37 It introduces the so-called relaxed difference density matrices5P (discussed in detail in Section A.6) and removes any implicit dependence of the Lagrangian on the molecular orbital coefficients. This can be done by introducing a new Lagrangian for the calculation of excitation energies in FDE-TDDFT (in analogy to TDDFT5),| | 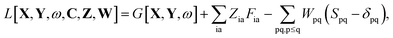 | (86) |
and requiring it to be stationary with respect to the all molecular orbital coefficients Cμp (for simplicity of notation the Lagrangian, L[X,Y,ω,C,Z,W], will be written from now on as L),| | 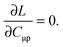 | (87) |
The Lagrangian multipliers Zia and Wpq ensure implicit relaxation of the ground-state density and also enforce the relaxed density to be a solution of the KS equation. In particular, 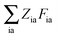 takes care of the conditions Fia = 0 (which implies that the KS equations are solved),
takes care of the conditions Fia = 0 (which implies that the KS equations are solved),| | 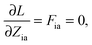 | (88) |
and 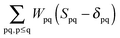 ensures orthonormality of the orbitals,
ensures orthonormality of the orbitals,| | 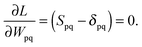 | (89) |
The relations below require that the Lagrangian satisfies the TDDFT eigenvalue problem| | 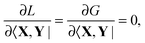 | (90) |
| | 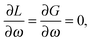 | (91) |
where eqn (90) is the usual TDDFT eigenvalue problem and eqn (91) is the orthonormality constraint for the eigenvectors |X,Y〉.
A.3 Expression for the Lagrangian in terms of MO integrals
Substituting the results of eqn (13) and (14) into eqn (78), the expression for G[X,Y,ω] reads| | 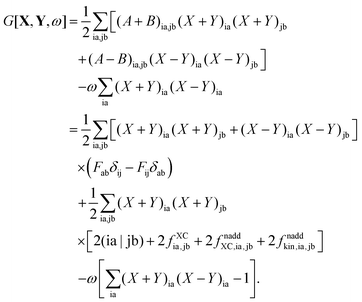 | (92) |
For ease of notation the unrelaxed difference density matrix T is introduced,| | 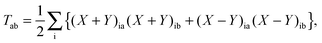 | (93) |
| | 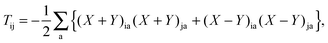 | (94) |
where the last equality holds due to the properties of (X + Y) and (X − Y),| | | (X + Y)ab = (X + Y)ij = 0, | (96) |
| | | (X − Y)ab = (X − Y)ij = 0. | (97) |
In eqn (92) the sum of terms containing Fab over two indexes i, j collapses to a sum over one index i because of δij, which is then absorbed into Tab, see eqn (93). In the same way, the sum of terms containing Fij over two indexes a, b collapses to a sum over one index a (because of δab), which is included in the definition of Tij, see eqn (94). Considering eqn (95), the terms with Fij and Fab can be unified as terms with Fpq (since Fia = Fai = 0) and eqn (92) can be simplified to| | 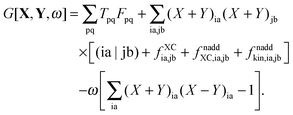 | (98) |
Using this form of G[X,Y,ω], eqn (86) takes the form,| | 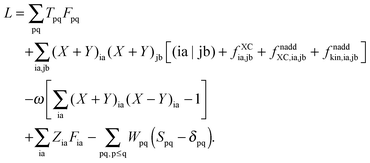 | (99) |
After the introduction of the relaxed difference density matrix P = T + Z, the Lagrangian can be rewritten as| | 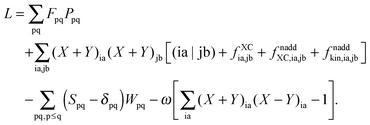 | (100) |
Recalling the Fock matrix, eqn (9), and using the definition of the core hamiltonian 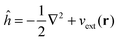 , we get
, we get| | 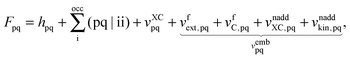 | (101) |
and we can finally transform the Lagrangian to the following form,| | 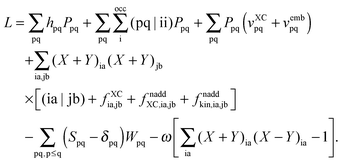 | (102) |
A.4 Expression for the Lagrangian in terms of AO integrals
The imposed requirement for the Lagrangian to be stationary with respect to the elements of C,| | 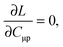 | (103) |
cancels out the implicit dependence of L on a perturbation ξ through the MO coefficients Cμp. Hence it is more convenient to convert all terms to atomic orbitals by means of the relation,| | 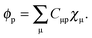 | (104) |
Noting that| | 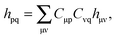 | (105) |
and defining,| | 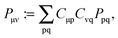 | (106) |
the first term in eqn (102) results in,| | 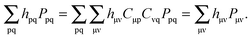 | (107) |
From the second term, we obtain,| | 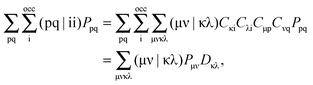 | (108) |
where| | 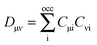 | (109) |
is an element of the ground-state density matrix. The third term reads| | 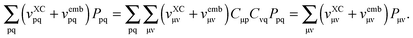 | (110) |
Similarly, the first part of the fifth term can be re-written as| | 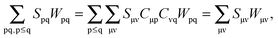 | (111) |
where the last equality defines Wμν. For the fourth term, involving the double sum, we get| | 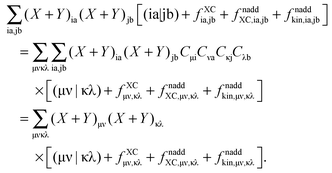 | (112) |
Grouping everything together, the Lagrangian in terms of atomic integrals is established (except for the last two terms, which will not survive the differentiation as shown in the following section),| | 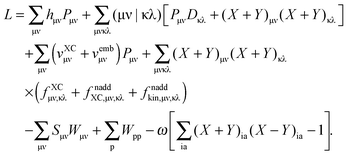 | (113) |
A.5 Derivative of the Lagrangian in terms of AO integrals and densities
At this point the dependency of the Lagrangian, L, on ξ has been clearly established, and it is apparent that only atomic-basis-function integrals are involved in the differentiation with respect to ξ, i.e., Lξ = L(ξ) by means of the conditions in eqn (103). Then, after taking the derivative with respect to ξ, the following result occurs [ξ as a superscript indicates differentiation over ξ, while (ξ) means that MO coefficients are kept constant during differentiation]| | 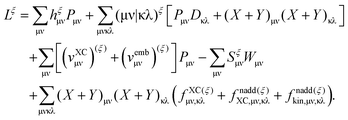 | (114) |
In the context of a DFT framework, it is more convenient to write this expression in terms of densities, in particular, for the purpose of implementation in the ADF code. Using the definition 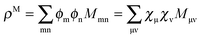 , eqn (114) can be rewritten in terms of densities.10 The Coulomb potential based on this density takes the following form (for ease of notation the integration of a function
, eqn (114) can be rewritten in terms of densities.10 The Coulomb potential based on this density takes the following form (for ease of notation the integration of a function 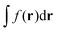 will be defined as
will be defined as 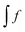 ),
),| | 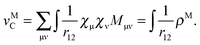 | (115) |
Eqn (114) will be analyzed term by term. Defining the kinetic energy operator as 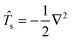 the first term from eqn (114) will take the following form:
the first term from eqn (114) will take the following form:
| | 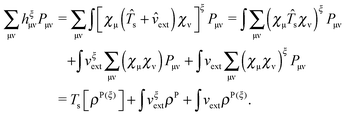 | (116) |
The sum containing derivatives of the matrix elements of the XC potential read
| | 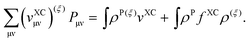 | (117) |
In the same way one can transform the sum with the derivatives of the embedding potential matrix elements
| | 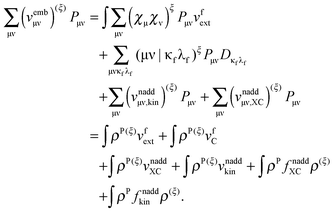 | (118) |
Here, we have explicitly assumed that the external potential from the frozen region does not change,
i.e., no perturbations in the positions of frozen atoms are included (although this can easily be generalized). The derivative of the term containing the kernels in
eqn (114) takes the following form:
| | 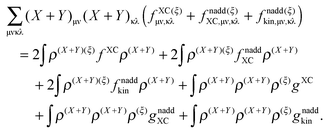 | (119) |
The term with the Coulomb integrals which originates from the Fock matrix and from the TDDFT part can be transformed as follows:
| | 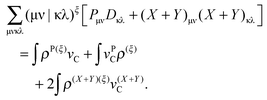 | (120) |
Grouping together all the terms mentioned above, it is finally possible to write the derivative of the Lagrangian in terms of densities
| | 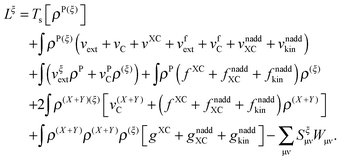 | (121) |
A.6 Derivation of the Z-vector equation
For the calculation of the Lagrangian derivative, eqn (114) and (121), the elements of W and Z have to be known. The matrix P contains the difference between the excited- and ground-state density matriceswhere T is the unrelaxed difference density matrix (“unrelaxed” part) and is already determined once the TDDFT eigenvalue problem has been solved, since it contains products of transition density matrices (excitation vectors, TDDFT solution factors). The matrix Z takes care of the relaxation of the ground-state orbitals and can be of the same order of magnitude as T.47 The information in P is complementary to the information contained in the transition vector |X,Y〉 (the transition density matrix).47P is related to the difference of expectation values for excited states and the ground state, while the transition vector is related to mixed matrix elements between the ground and excited states. P can give insight into the re-distribution of the electronic charge due to the excitation process.47
These Lagrangian multipliers can be obtained from the so-called Z-vector equation,5,37 which can be derived from the following condition:
| | 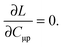 | (123) |
If
eqn (123) is multiplied by
Cμq and summed over index μ, it leads to the following equation:
| | 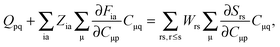 | (124) |
where
Q is a matrix with elements,
| | 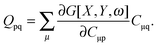 | (125) |
Four possible cases for the orbitals p and q in
eqn (124) have to be considered at this point. The first case corresponds to occupied orbitals for p and q, so that we can set p = k ≤ q = l. The right hand-side of
eqn (124) can be expanded as follows:
| |  | (126) |
Taking into account that
Wrs =
Wsr, the following equation holds for any k,
| | 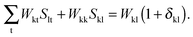 | (127) |
The last equality holds because of
Stk =
δtk. The second term of the left hand-side of
eqn (124) can be transformed by analogy with the derivation mentioned above
| |  | (128) |
The first sum on the right hand-side of
eqn (128) is zero due to the condition
Fla = 0. Since
δka = 0 for every a, the second term of
eqn (128) also vanishes, and finally
eqn (124) changes to
| | | Qkl + Hkl+[Z] = Wkl(1 + δkl). | (129) |
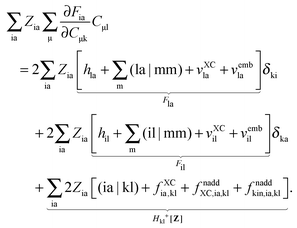
For the second case, where only virtual orbitals are considered for p and q, p = c ≤ q = d in
eqn (124), the result for the terms containing
Wrs will be similar to the previous case, namely
Wcd(1 +
δcd). The second term of the left-hand side in
eqn (124) transforms as follows in this case:
| |  | (130) |
Since
δci = 0 for every i, the first term on the right-hand side of
eqn (130) vanishes and the second term is zero due to the condition
Fid = 0. Then
eqn (124) can be simplified for the case p = c ≤ q = d to
The third case concerns the combination of virtual (c) and occupied (k) orbitals, so that p = k, q = c in
eqn (124),
| | 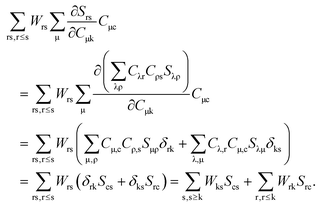 | (132) |
Taking into account that
Wrs =
Wsr, the following equation holds for a given k
| | 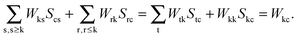 | (133) |
The last equality holds true since
Stc =
δtc and k ≠ c. The second term on the left-hand side of
eqn (124) can then be rewritten in the following way:
| |  | (134) |
Since
δka = 0 for every a, the second term vanishes. In terms of canonical orbitals, the equation above changes to,
| | 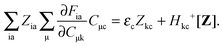 | (135) |
Eqn (124) will change to
| | | Qkc + εcZkc + Hkc+[Z] = Wkc. | (136) |
Finally, the fourth case concerns the combination of occupied and virtual orbitals by making the choice p = c, q = k. The right-hand side of
eqn (124) will give the same result as in the case above (
Wkc), while the second term on the left hand side will take the form
| |  | (137) |
The last step holds after making use of canonical orbitals and realizing that
δic = 0 for every i (the first term vanishes). Finally
eqn (124) takes the form
Thus, the following set of equations has to be solved in order to get the vectors
Z and
W,
| | | Qkl + Hkl+[Z] = Wkl(1 + δkl), | (139) |
| | | Qkc + εcZkc + Hkc+[Z] = Wkc, | (140) |
Subtracting
eqn (141) from
eqn (140), we get
| | | (εa − εi)Zia + Hia+[Z] = Ria, | (143) |
where
Ria = −(
Qia −
Qai). It is common to call
eqn (143) the
Z-vector equation in the context of TDDFT, and it is usually written in the following form
| | 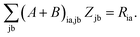 | (144) |
Once this equation is solved with respect to
Z, it is possible to determine
W from the following equations:
| | 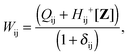 | (145) |
| | 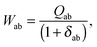 | (146) |
To solve the
Z-vector equation,
eqn (144), explicit expressions for the elements of the vector
Q have to be established:
| | 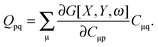 | (148) |
These expressions are derived in Section B.
B Elements of the vector Q
Here we present a derivation of the expressions for elements of the vector Q. First, two auxiliary relations will be derived in Section B.1 and then the necessary expressions will be obtained in Section B.2.
B.1 Auxiliary relation for the derivation of elements Qpq
If differentiation of eqn (78) with respect to (X + Y)la [note that (X + Y)ia and (X − Y)ia are considered as independent variables] is followed by multiplication with (X + Y)ka and summation over a, then due to the condition in eqn (79), the following equation is valid:| | 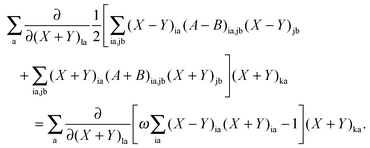 | (149) |
After some manipulation, the previous equation can be transformed to| | 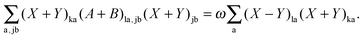 | (150) |
Using eqn (13) and (14), this can be rewritten as| | 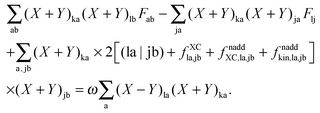 | (151) |
The differentiation of eqn (78) can also be carried out with respect to (X − Y)la. If the result is multiplied by (X − Y)ka and summed over a, the following equation can be established using eqn (80),| | 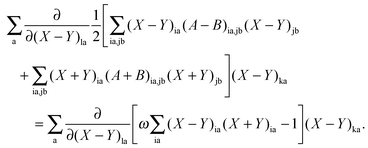 | (152) |
After some further manipulations, this can be transformed to| | 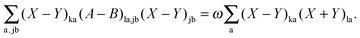 | (153) |
Using eqn (13) and (14), this equation can further be rewritten as| | 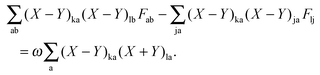 | (154) |
If now eqn (151) and (154) are summed up, it is possible to derive the equality,| | 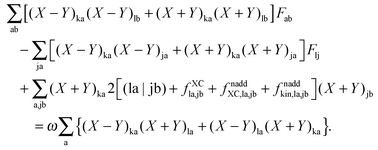 | (155) |
Representing the Fock matrix in canonical orbitals and substituting the diagonal elements by their corresponding orbital energies, the equation above changes to| | 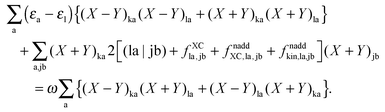 | (156) |
With the same strategy as before, but only differentiating eqn (78) first with respect to (X + Y)ic and then with respect to (X − Y)ic, each time multiplying the equation with the corresponding (X + Y)id or (X − Y)id and summing over i, it is possible to get a second important relation:| | 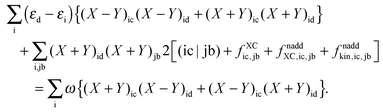 | (157) |
B.2 Derivation of elements Qpq
In order to evaluate the matrix elements Qpq in Section A.6, eqn (148), we repeat the equation for G[X,Y,ω], eqn (98), at this point,| | 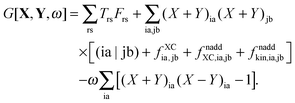 | (158) |
Recalling the fact that only [(ia|jb) + fXCia,jb + fnaddXC,ia,jb + fnaddkin,ia,jb] and Frs will be affected by differentiation [see eqn (83)], again (as in Section A.6) four cases must be considered. The first case considers only occupied orbitals p and q for Qpq, so that p = k ≤ q = l. Recalling that the terms like vXC[ρ](r) and fXC[ρ](r) implicitly depend on Cμk through the density ρ, it is possible to write| | 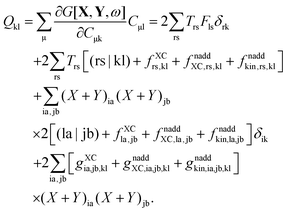 | (159) |
Using the nature of the matrices T and F (Tia = 0, Fia = 0), and the definition of Hkl+[M], the elements Qkl can be rewritten as| | 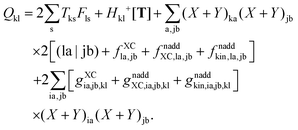 | (160) |
If one uses canonical orbitals and expands Tkl according to eqn (94), then Qkl reads| | 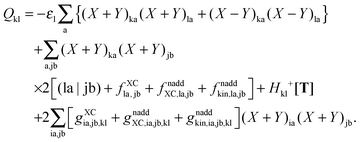 | (161) |
Now one can notice that if 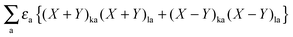 is added and subtracted from the expression for element Qkl,
is added and subtracted from the expression for element Qkl,| | 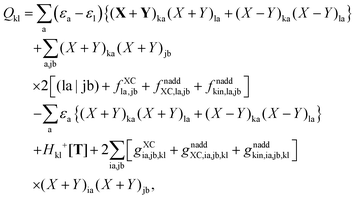 | (162) |
then the first two terms are identical to the left-hand side of eqn (156) (see Section B.1), and Qkl finally reads| | 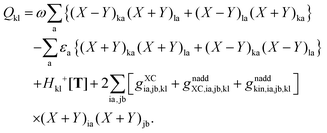 | (163) |
The second case, in which occupied and virtual orbitals are used, i.e. p = k, q = c, reads,| | 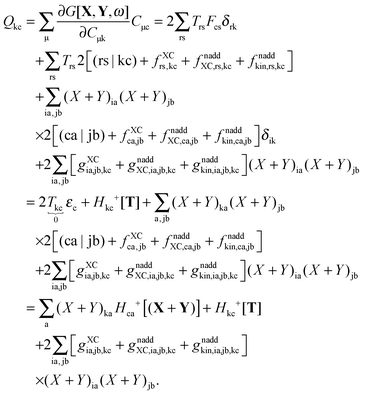 | (164) |
The transformation made in the last step is valid due to the nature of X and Y (Xaa = Yaa = Xii = Yii = 0) in spite of the fact that the sum is not over pq as in the definition Hca+[M], eqn (47), but over jb. The third case is p = c, q = k,| | 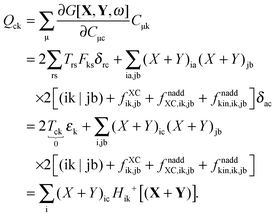 | (165) |
The last case corresponds to p = c ≤ q = d, and results in| | 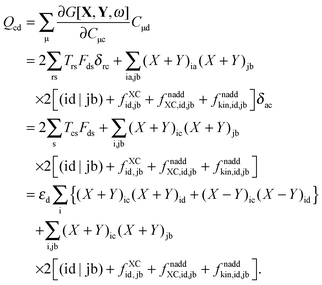 | (166) |
Now one can notice that if 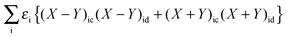 is added and subtracted from the expression for element Qcd,
is added and subtracted from the expression for element Qcd,| | 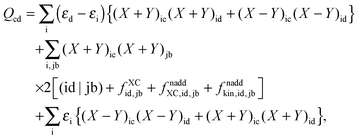 | (167) |
then the first two terms are identical to the left-hand side of eqn (157) (see Section B.1), and Qcd finally reads| | 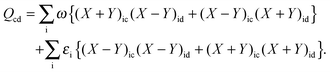 | (168) |
At this point, all elements of the Q vector are determined, and the elements of vector R from the Z-vector equation, eqn (144), can be expressed in the following way| | 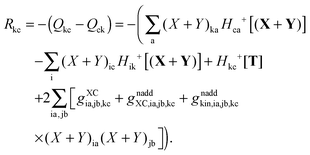 | (169) |
The form of the elements of matrices Q and R presented here is most convenient for practical calculations and was first presented in ref. 5. The Z-vector equation and all relevant variables can also be rewritten in terms of densities.10 For that purpose, the quantities Hkl+[M], Qkl, and Qkc should be expressed as| | 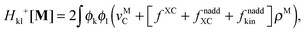 | (170) |
| | 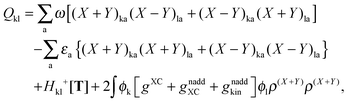 | (171) |
| | 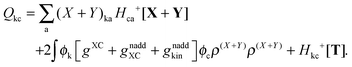 | (172) |
Qck and Qcd will stay the same, while Ria can be rewritten as| | 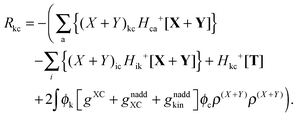 | (173) |
Acknowledgements
This work was supported by a VIDI grant (700.59.422) of the Netherlands Organization for Scientific Research (NWO). Helpful discussions with the late Tom Ziegler are gratefully acknowledged.
References
-
Computational Photochemistry, ed. M. Olivucci, Elsevier, Amsterdam, 2005 Search PubMed.
- J. B. Foresman, M. Head-Gordon, J. A. Pople and M. J. Frisch, Toward a Systematic Molecular Orbital Theory for Excited States, J. Phys. Chem., 1992, 96, 135–149 CrossRef CAS.
- J. V. Ortiz, One-electron density matrices and energy gradients in the random phase approximation, J. Chem. Phys., 1994, 101, 6743–6749 CrossRef.
- C. Van Caillie and R. D. Amos, Geometric derivatives of excitation energies using SCF and DFT, Chem. Phys. Lett., 1999, 308, 249–255 CrossRef CAS.
- F. Furche and R. Ahlrichs, Adiabatic time-dependent density functional methods for excited state properties, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- T. Helgaker and P. Jørgenson, Configuration-interaction energy derivatives in a fully variational formulation, Theor. Chim. Acta, 1989, 75, 111–127 CrossRef CAS.
- J. Hutter, Excited-state nuclear forces from the Tamm–Dancoff approximation to time-dependent density functional theory within the plane wave basis set framework, J. Chem. Phys., 2003, 118, 3928–3934 CrossRef CAS.
- N. L. Doltsinis and D. S. Kosov, Plane wave/pseudopotential implementation of excited state gradients in density functional linear response theory: A new route via implicit differentiation, J. Chem. Phys., 2005, 122, 144101 CrossRef PubMed.
- N. L. Doltsinis and M. Sprik, Electronic excitation spectra from time-dependent density functional response theory using plane-wave methods, Chem. Phys. Lett., 2000, 330, 563–569 CrossRef CAS.
- M. Seth, G. Mazur and T. Ziegler, Time-dependent density functional theory gradients in the Amsterdam density functional package: geometry optimizations of spin–flip excitations, Theor. Chem. Acc., 2011, 129, 331–342 CrossRef CAS.
- Amsterdam density functional program. Theoretical Chemistry, Vrije Universiteit, Amsterdam. URL: http://www.scm.com.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, S. J. A. van Gisbergen, C. Fonseca Guerra, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- D. Bakowies and W. Thiel, Hybrid Models for Combined Quantum Mechanical and Molecular Mechanical Approaches, J. Phys. Chem., 1996, 100, 10580–10594 CrossRef CAS.
- T. A. Wesolowski and A. Warshel, Frozen Density Functional Approach for ab Initio Calculations of Solvated Molecules, J. Phys. Chem., 1993, 97, 8050 CrossRef CAS.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, Geometries and properties of excited states in the gas phase and in solution: Theory and application of a time-dependent density functional theory polarizable continuum model, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- D. Si and H. Li, Analytic energy gradient in combined time-dependent density functional theory and polarizable force field calculation, J. Chem. Phys., 2010, 133(14), 144112 CrossRef PubMed.
- N. Minezawa, N. De Silva, F. Zahariev and M. S. Gordon, Implementation of the analytic energy gradient for the combined time-dependent density functional theory/effective fragment potential method: Application to excited-state molecular dynamics simulations, J. Chem. Phys., 2011, 134, 054111 CrossRef PubMed.
- M. Chiba, D. G. Fedorov, T. Nagata and K. Kitaura, Excited state geometry optimizations by time-dependent density functional theory based on the fragment molecular orbital method, Chem. Phys. Lett., 2009, 474, 227–232 CrossRef CAS.
- M. E. Casida and T. A. Wesolowski, Generalization of the Kohn–Sham Equations with Constrained Electron Density Formalism and Its Time-Dependent Response Theory Formulation, Int. J. Quantum Chem., 2004, 96, 577–588 CrossRef CAS.
- T. A. Wesolowski, Hydrogen-bonding induced shifts of the excitation energies in nucleic acid bases: an interplay between electrostatic and electron density overlap effects, J. Am. Chem. Soc., 2004, 126, 11444–11445 CrossRef CAS PubMed.
- J. Neugebauer, M. J. Louwerse, E. J. Baerends and T. A. Wesolowski, The merits of the frozen-density embedding scheme to model solvatochromic shifts, J. Chem. Phys., 2005, 122, 094115 CrossRef PubMed.
- J. Neugebauer, C. R. Jacob, T. A. Wesolowski and E. J. Baerends, An Explicit Quantum Chemical Method for Modeling Large Solvation Shells Applied to Aminocoumarin C151, J. Phys. Chem. A, 2005, 109, 7805–7814 CrossRef CAS PubMed.
- X. Zhou, J. W. Kaminski and T. A. Wesołowski, Multi-scale modelling of solvatochromic shifts from frozen-density embedding theory with non-uniform continuum model of the solvent: the coumarin 153 case, Phys. Chem. Chem. Phys., 2011, 13, 10565–10576 RSC.
- M. Humbert-Droz, X. Zhou, S. V. Shedge and T. A. Wesolowski, How to choose the frozen density in Frozen-Density Embedding Theory-based numerical simulations of local excitations, Theor. Chem. Acc., 2013, 132, 1405 Search PubMed.
-
J. Neugebauer, Orbital-Free Embedding Calculations of Electronic Spectra, in Recent Progress in Orbital-Free Density Functional Theory, ed. T. A. Wesolowski and Y. A. Wang, World Scientific, Singapore, 2013, pp. 325–356 Search PubMed.
- J. Neugebauer, Couplings between electronic transitions in a subsystem formulation of time-dependent density functional theory, J. Chem. Phys., 2007, 126, 134116 CrossRef PubMed.
- G. Fradelos, J. W. Kaminski, T. A. Wesołowski and S. Leutwyler, Cooperative Effect of Hydrogen-Bonded Chains in the Environment of a π → π* Chromophore, J. Phys. Chem. A, 2009, 113, 9766–9771 CrossRef CAS PubMed.
- C. R. Jacob and J. Neugebauer, Subsystem Density-Functional Theory, WIREs Comput. Mol. Sci., 2014, 4, 325–362 CrossRef CAS.
- T. A. Wesolowski, S. Shedge and X. Zhou, Frozen-density embedding strategy for multilevel simulations of electronic structure, Chem. Rev., 2015, 115, 5891–5928 CrossRef CAS PubMed.
- M. Dułak, J. W. Kamiński and T. A. Wesołowski, Equilibrium Geometries of Noncovalently Bound Intermolecular Complexes Derived from Subsystem Formulation of Density Functional Theory, J. Chem. Theory Comput., 2007, 3, 735–745 CrossRef PubMed.
- G. Senatore and K. R. Subbaswamy, Density dependence of the dielectric constant of rare-gas crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5754 CrossRef CAS.
- P. Cortona, Self-consistently determined properties of solids without band-structure calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 8454 CrossRef.
- T. A. Wesolowski and J. Weber, Kohn–Sham equations with constrained electron density: an iterative evaluation of the ground-state electron density of interacting molecules, Chem. Phys. Lett., 1996, 248, 71–76 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- C. König, N. Schlüter and J. Neugebauer, Direct determination of exciton couplings from subsystem time-dependent density-functional theory within the tamm–dancoff approximation, J. Chem. Phys., 2013, 138, 034104 CrossRef PubMed.
- N. C. Handy and H. F. Schaefer, III, On the evaluation of analytic energy derivatives for correlated wave functions, J. Chem. Phys., 1984, 81, 5031–5033 CrossRef CAS.
- U. Ekström, L. Visscher, R. Bast, A. J. Thorvaldsen and K. Ruud, Arbitrary-Order Density Functional Response Theory from Automatic Differentiation, J. Chem. Theory Comput., 2010, 6, 1971–1980 CrossRef PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38(6), 3098–3100 CrossRef CAS.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef.
- C. R. Jacob, J. Neugebauer and L. Visscher, A flexible implementation of frozen-density embedding for use in multilevel simulations, J. Comput. Chem., 2008, 29, 1011–1018 CrossRef CAS PubMed.
- T. A. Wesolowski, Density functional theory with approximate kinetic energy functionals applied to hydrogen bonds, J. Chem. Phys., 1997, 106, 8516–8526 CrossRef CAS.
-
J. P. Perdew, in Electronic Structure of Solids ′91, ed. P. Ziesche and H. Eschrig, Akademie Verlag, Berlin, 1991, p. 11 Search PubMed.
- A. Kovyrshin and J. Neugebauer, Potential-Energy
Surfaces of Local Excited States from Subsystem- and Selective Kohn-Sham-TDDFT, Chem. Phys., 2011, 391, 147 CrossRef CAS.
- J. Neugebauer, Photophysical Properties of Natural Light-Harvesting Complexes Studied by Subsystem Density Functional Theory, J. Phys. Chem. B, 2008, 112, 2207–2217 CrossRef CAS PubMed.
- J. Neugebauer, C. Curutchet, A. Muños-Losa and B. Mennucci, A Subsystem TDDFT Approach for Solvent Screening Effects on Excitation Energy Transfer Couplings, J. Chem. Theory Comput., 2010, 6, 1843–1851 CrossRef CAS PubMed.
-
F. Furche and D. Rappoport, Density Functional Methods for Excited States: Equilibrium Structure and Electronic Spectra, in Computational Photochemistry, Volume 16 of Theoretical and Computational Chemistry, ed. M. Olivucci, Elsevier, Amsterdam, 2005, pp. 93–128 Search PubMed.
- D. Rappoport and F. Furche, Analytical time-dependent density functional derivative methods within the RI-J approximation, an approach to excited states of large molecules, J. Chem. Phys., 2005, 122, 064105 CrossRef PubMed.
-
Y. Yamaguchi, Y. Osamura, J. D. Goddard and H. F. Schaefer III, A New Dimension to Quantum Chemistry: Analytical Derivative Methods in Ab Initio Molecular Electronic Structure Theory, Oxford University Press, Oxford, 1994 Search PubMed.
Footnote |
| † Dedicated to Professor Evert Jan Baerends on the occasion of his 70th birthday. |
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article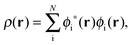
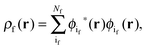
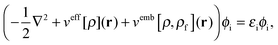
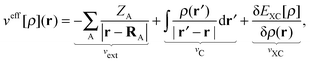
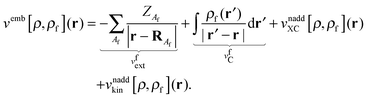
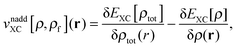
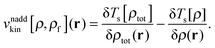
![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) and can be identified as the time-independent FDE-KS Hamiltonian.
and can be identified as the time-independent FDE-KS Hamiltonian.
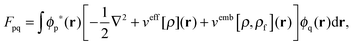
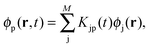
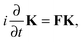
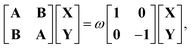
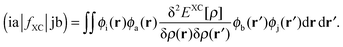
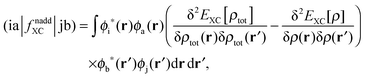
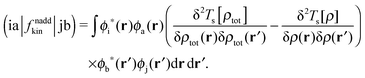
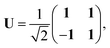
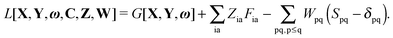
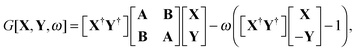
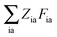 takes care of the conditions Fia = 0 (which implies that KSCED equations are solved, but not necessarily in canonical orbitals) and
takes care of the conditions Fia = 0 (which implies that KSCED equations are solved, but not necessarily in canonical orbitals) and 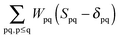 ensures orthonormality of the orbitals (Spq is the overlap integral for orbitals p and q). Note that our definition of the vector Z implies that only occupied–virtual components among all Zrs are non-zero. The FDE-TDDFT eigenvalue problem can be expressed as
ensures orthonormality of the orbitals (Spq is the overlap integral for orbitals p and q). Note that our definition of the vector Z implies that only occupied–virtual components among all Zrs are non-zero. The FDE-TDDFT eigenvalue problem can be expressed as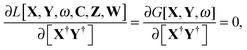
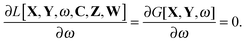
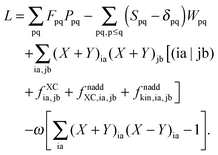
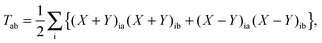
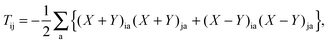
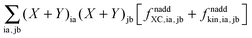 (which results from G[X,Y,ω]) and
(which results from G[X,Y,ω]) and 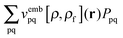 (which results from
(which results from 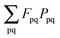 ). The focus here will thus be mostly on these terms. For convenience, we will sometimes drop the notation vemb[ρ,ρf], veff[ρ], etc. and write vemb, veff instead. Converting
). The focus here will thus be mostly on these terms. For convenience, we will sometimes drop the notation vemb[ρ,ρf], veff[ρ], etc. and write vemb, veff instead. Converting 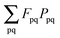 to atomic orbital basis, we get
to atomic orbital basis, we get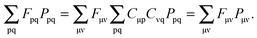
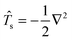 . Keeping the orbital coefficients constant and taking the derivative with respect to the perturbation ξ [ξ as a superscript indicates differentiation over ξ, while (ξ) means that MO coefficients are kept constant during differentiation], we get from the equation above,
. Keeping the orbital coefficients constant and taking the derivative with respect to the perturbation ξ [ξ as a superscript indicates differentiation over ξ, while (ξ) means that MO coefficients are kept constant during differentiation], we get from the equation above,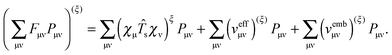
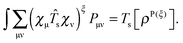
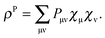
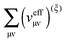 reads (here, we introduce a simplified notation in which the integration of a function
reads (here, we introduce a simplified notation in which the integration of a function 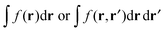 will be expressed as
will be expressed as  ),
),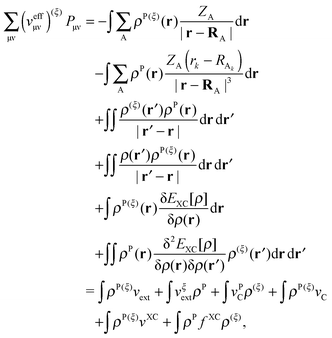
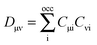
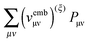 ,
,
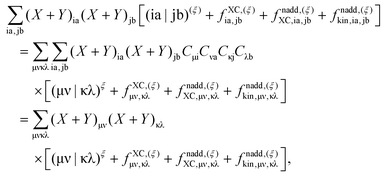
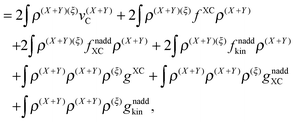
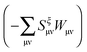 the expression for the Lagrangian derivative Lξ is
the expression for the Lagrangian derivative Lξ is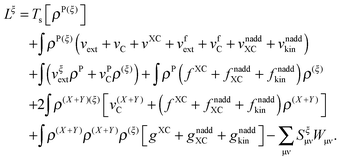
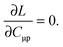
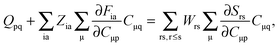
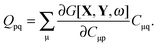
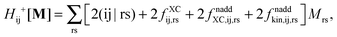
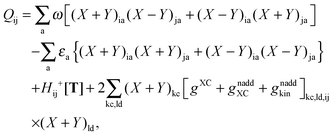
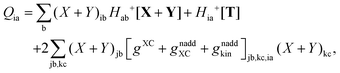
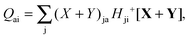
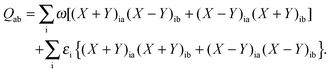
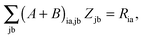
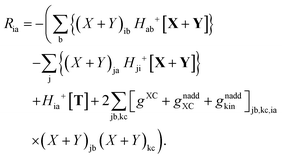
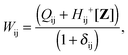
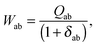
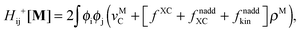
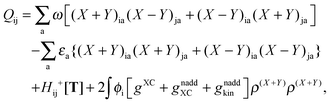
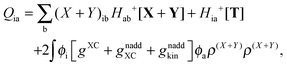
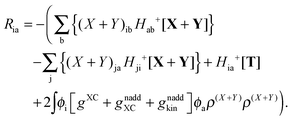

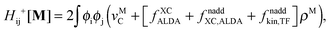
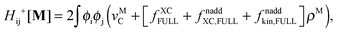
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances. Note that the C⋯Li+ distance is kept constant in our calculations, so that increasing C
O bond distances. Note that the C⋯Li+ distance is kept constant in our calculations, so that increasing C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances correspond to decreasing O⋯Li+ distances. The HOMO of this system corresponds to a nonbonding (n) orbital, while the LUMO corresponds to a π* orbital. Isosurface plots of the orbitals involved in the transition are shown in Fig. 2.
O distances correspond to decreasing O⋯Li+ distances. The HOMO of this system corresponds to a nonbonding (n) orbital, while the LUMO corresponds to a π* orbital. Isosurface plots of the orbitals involved in the transition are shown in Fig. 2.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances. These results are shown in Fig. 3. One can see from this figure that the closer the oxygen atom is to the lithium ion, the more the excitation energy is affected by the embedding potential. Thus, the complex represents a good test system to check the implemented procedure.
O bond distances. These results are shown in Fig. 3. One can see from this figure that the closer the oxygen atom is to the lithium ion, the more the excitation energy is affected by the embedding potential. Thus, the complex represents a good test system to check the implemented procedure.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distances were calculated analytically with BP86/TZP. Then for the same distances gradients were calculated numerically for the complex, where the lithium ion was described with FDEu. In addition, the analytical gradients of the excitation energy were calculated for the same system with FDEu. To compare the obtained results, the dependence of the z-component of the gradient for the oxygen atom on the C
O bond distances were calculated analytically with BP86/TZP. Then for the same distances gradients were calculated numerically for the complex, where the lithium ion was described with FDEu. In addition, the analytical gradients of the excitation energy were calculated for the same system with FDEu. To compare the obtained results, the dependence of the z-component of the gradient for the oxygen atom on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance is plotted for each calculation in Fig. 4.
O bond distance is plotted for each calculation in Fig. 4.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance fixed at 1.7 Å. This is significantly larger than the ground-state equilibrium C
O distance fixed at 1.7 Å. This is significantly larger than the ground-state equilibrium C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distance of about 1.2 Å, and was selected in order to observe a significant effect of the embedding contribution (at the equilibrium distance, this effect is rather small). Contrary to the first, the second test system has a small contribution of the classical electrostatic part to the embedding potential. The same excitation as in the previous case was considered, see Fig. 2. The effect of the FDE potential on the excitation energy under study can clearly be seen in Fig. 5.
O distance of about 1.2 Å, and was selected in order to observe a significant effect of the embedding contribution (at the equilibrium distance, this effect is rather small). Contrary to the first, the second test system has a small contribution of the classical electrostatic part to the embedding potential. The same excitation as in the previous case was considered, see Fig. 2. The effect of the FDE potential on the excitation energy under study can clearly be seen in Fig. 5.
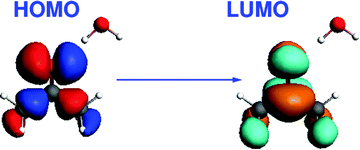
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance in acetone was varied from 1.2 Å to 2 Å were generated for the comparison of numerical and analytical gradients. Similar to our first test system, the carbon–water distance was kept fixed, i.e., longer C
O bond distance in acetone was varied from 1.2 Å to 2 Å were generated for the comparison of numerical and analytical gradients. Similar to our first test system, the carbon–water distance was kept fixed, i.e., longer C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O distances correspond to shorter O⋯H2O contacts. In Fig. 9 the dependence of the excitation energy on the C
O distances correspond to shorter O⋯H2O contacts. In Fig. 9 the dependence of the excitation energy on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond distance for isolated acetone and for the acetone⋯water system are plotted. One can see that the FDE potential has a slight effect on the excitation energy.
O bond distance for isolated acetone and for the acetone⋯water system are plotted. One can see that the FDE potential has a slight effect on the excitation energy.
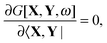
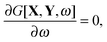
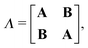
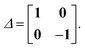
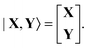
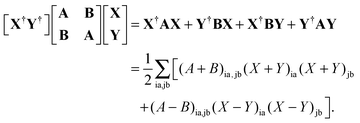
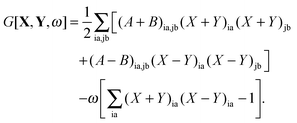
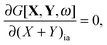
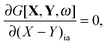
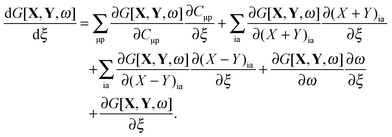
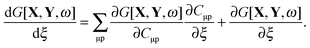
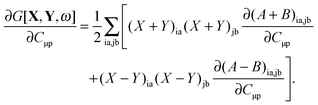
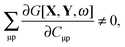
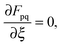
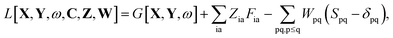
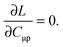
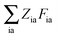 takes care of the conditions Fia = 0 (which implies that the KS equations are solved),
takes care of the conditions Fia = 0 (which implies that the KS equations are solved),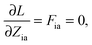
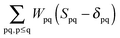 ensures orthonormality of the orbitals,
ensures orthonormality of the orbitals,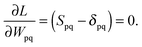
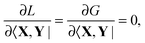
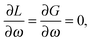
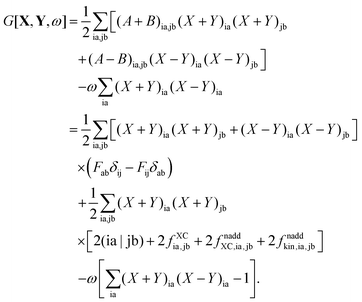
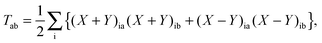
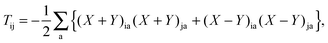
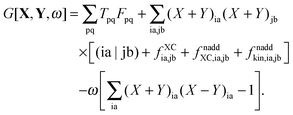
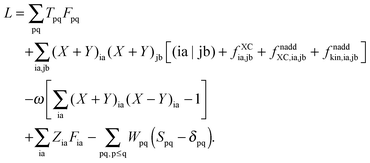
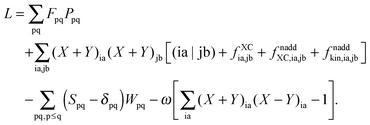
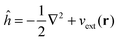 , we get
, we get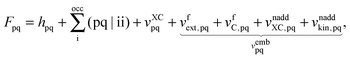
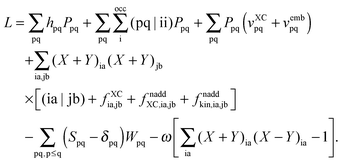
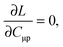
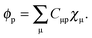
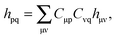
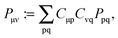
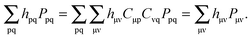
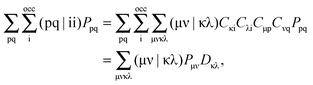
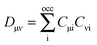
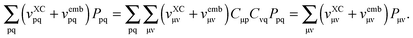
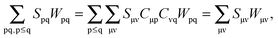
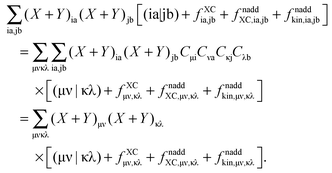
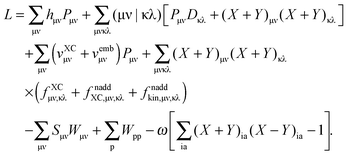
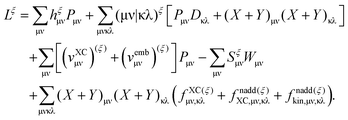
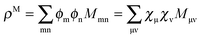 , eqn (114) can be rewritten in terms of densities.10 The Coulomb potential based on this density takes the following form (for ease of notation the integration of a function
, eqn (114) can be rewritten in terms of densities.10 The Coulomb potential based on this density takes the following form (for ease of notation the integration of a function 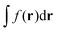 will be defined as
will be defined as 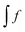 ),
),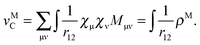
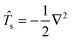 the first term from eqn (114) will take the following form:
the first term from eqn (114) will take the following form: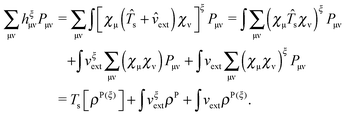
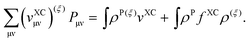
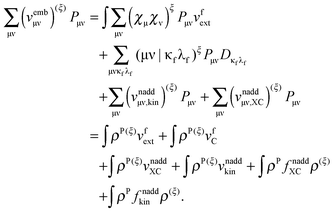
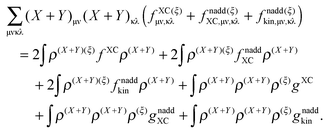
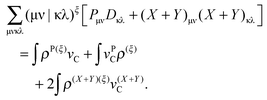
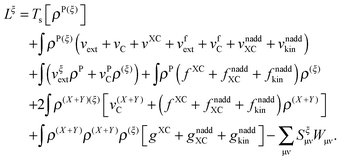
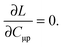
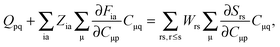
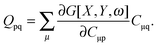

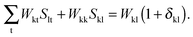


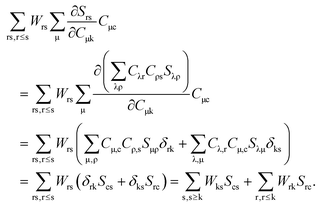
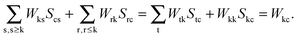

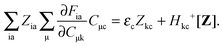

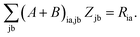
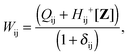
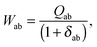
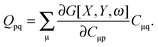
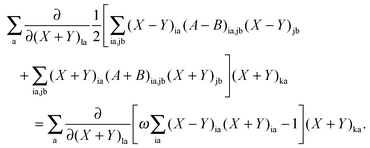
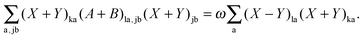
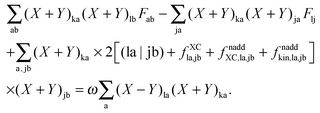
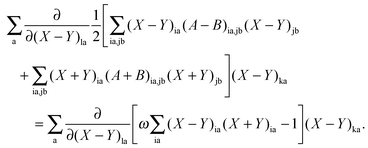
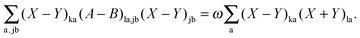
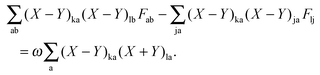
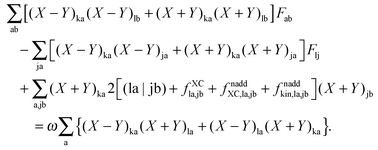
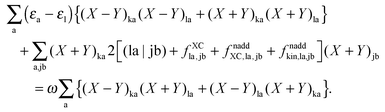
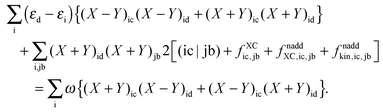
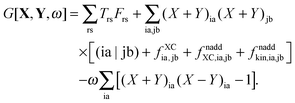
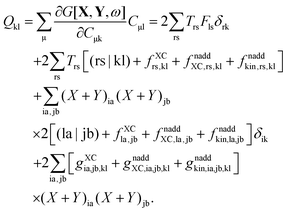
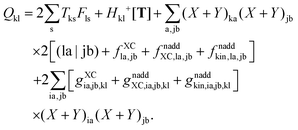
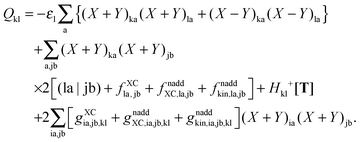
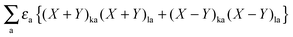 is added and subtracted from the expression for element Qkl,
is added and subtracted from the expression for element Qkl,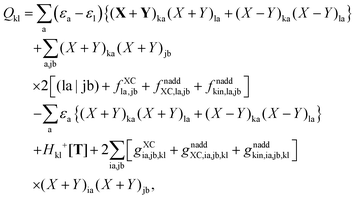
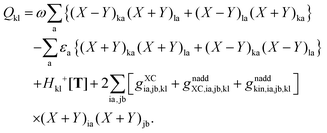
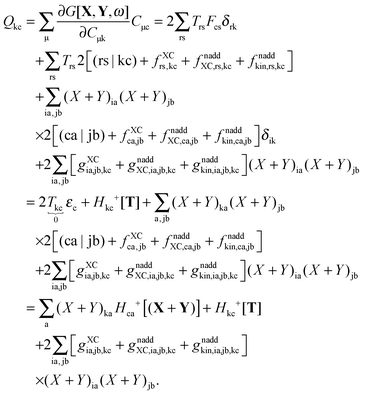
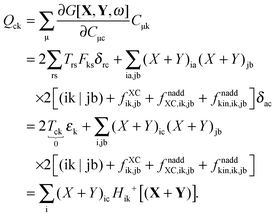
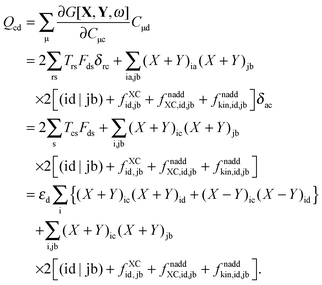
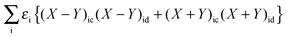 is added and subtracted from the expression for element Qcd,
is added and subtracted from the expression for element Qcd,