Time-dependent Dyson orbital theory
Received
8th February 2016
, Accepted 7th March 2016
First published on 18th March 2016
Abstract
Although time-dependent density functional theory (TDDFT) has become the tool of choice for real-time propagation of the electron density ρN(t) of N-electron systems, it also encounters problems in this application. The first problem is the neglect of memory effects stemming from the, in TDDFT virtually unavoidable, adiabatic approximation, the second problem is the reliable evaluation of the probabilities Pn(t) of multiple photoinduced ionization, while the third problem (which TDDFT shares with other approaches) is the reliable description of continuum states of the electrons ejected in the process of ionization. In this paper time-dependent Dyson orbital theory (TDDOT) is proposed. Exact TDDOT equations of motion (EOMs) for time-dependent Dyson orbitals are derived, which are linear differential equations with just static, feasible potentials of the electron–electron interaction. No adiabatic approximation is used, which formally resolves the first TDDFT problem. TDDOT offers formally exact expressions for the complete evolution in time of the wavefunction of the outgoing electron. This leads to the correlated probability of single ionization P1(t) as well as the probabilities of no ionization (P0(t)) and multiple ionization of n electrons, Pn(t), which formally solves the second problem of TDDFT. For two-electron systems a proper description of the required continuum states appears to be rather straightforward, and both P1(t) and P2(t) can be calculated. Because of the exact formulation, TDDOT is expected to reproduce a notorious memory effect, the “knee structure” of the non-sequential double ionization of the He atom.
I. Introduction
Real-time propagation of the electron density ρN(x1,t) provides valuable information about dynamics of N-electron systems in strong rapidly changing electric fields. It is applied to simulate multiphoton ionization of atoms,1–4 while the related power spectrum |μ(ω)|2 of the dipole moment 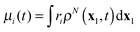 describes high-harmonic generation in atomic systems.4,5 Electronic dynamics with fixed nuclei serves as a first stage of the simulation of similar processes in molecules.4,6 Coupling to nuclear dynamics provides not only more complete simulation of the electronic dynamics but also the description of photoinduced molecular dissociation7 and isomerisation.8
describes high-harmonic generation in atomic systems.4,5 Electronic dynamics with fixed nuclei serves as a first stage of the simulation of similar processes in molecules.4,6 Coupling to nuclear dynamics provides not only more complete simulation of the electronic dynamics but also the description of photoinduced molecular dissociation7 and isomerisation.8
For real-time propagation of ρN(x1,t) a dynamical orbital approach, time-dependent density functional theory (TDDFT)3,9–15 has become the tool of choice. In TDDFT ρN(x1,t) is expressed as the sum
| | 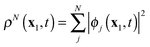 | (1) |
of the densities of the occupied Kohn–Sham (KS) orbitals
ϕj(
x1,
t), which are obtained from the TDDFT equations of motion (EOMs)
| | 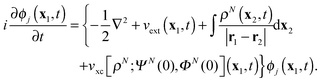 | (2) |
The driving force of evolution in
(2) is the external potential
vext(
x1,
t), which includes the contribution from the applied electric field, while the third term in the figure brackets is the Hartree potential. The fourth term is the local exchange–correlation potential, which is a functional of the density, the initial state
ΨN(0) of the interacting system with the density
ρN(
x1,0), and the initial state
ΦN(0) of the KS non-interacting system with the same density.
16–18 At present, direct construction of the complicated functional
vxc[
ρN;
ΨN(0),
ΦN(0)] appears to be not feasible. Then, in order to make the propagation with the EOMs
(2) possible, the adiabatic approximation is employed, in which the xc potential is evaluated instantaneously as the ground-state functional
v0xc[{
ϕj(
t)}] of the density
ρN(
t) or the orbitals {
ϕj(
t)} at the time
t| | | vxc[ρN;ΨN(0),ΦN(0)](x1,t) ≈ v0xc[{ϕj(t)}](x1,t). | (3) |
Since not even for the ground state the exact functional
v0xc[{
ϕj}] is known, it itself is, usually, replaced with an approximate functional
v0,apprxc({
ϕj}) of some DFT approximation. The resultant adiabatic EOMs
| | 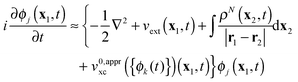 | (4) |
are coupled non-linear differential equations with respect to the time-dependent KS orbitals {
ϕj(
t)}, which are solved with one of the standard or especially designed techniques of numerical integration.
19
The first problem of standard TDDFT is the lack of the so-called memory effects. The memory effect is the influence on the dynamics of an electronic system of the dependence of vxc[ρN;ΨN(0),ΦN(0)](x1,t1) evaluated at t1 on the densities ρN(t) obtained at earlier times t < t1. What is called the adiabatic approximation (4), is essentially ignoring this dependence on t < t1 and just using ρ(t1). This can seriously affect the quality of simulated electronic dynamics.3,18,20,21 The paradigmatic memory effect is the famous “helium knee” indicating an enhancement of the non-sequential double ionization of the He atom by several orders of magnitude over what sequential ionization models would predict.3,4 A second problem TDDFT is facing here is the reliable evaluation of the correlated time-dependent probabilities Pn(t) of multiple ionizations, which in the case of He reduces to estimation of the probabilities P1(t) and P2(t) of single and double ionization, respectively. Usually, these probabilities are estimated in TDDFT in a rather crude independent-particle approximation. Note, that time-dependent Hartree–Fock (TDHF) theory, which has been also applied to real-time simulation of electronic dynamics,22–26 has these two problems as well. Then, because of this, standard TDDFT and TDHF approaches fail to reproduce the knee structure of P2(t) as a function of the intensity of an applied field.3,4 There is also a third problem with the application of TDDFT to photoionization, which it shares with all other theoretical approaches to photoionization. This is the important problem of reliable representation of continuum states of ejected electrons. This can be solved completely by using grid based techniques,12,14,19 which become very cumbersome in more dimensions, or by choosing sufficiently flexible basis functions, such as provided by angular momentum expansion around the nuclei and the molecular centre and B-spline functions for the radial functions,6,27 or by choosing mixed basis set representations of Gaussians or Slaters at the nuclear centres and plane waves or Coulomb waves for the outgoing electron.28–32
In spite of all these problems, useful information about electronic dynamics can be obtained already in a rather crude single-active-electron (SAE) approximation,1,2,6 which provides a considerable simplification of the EOMs (4). SAE employs frozen static Hartree and xc potentials
| | 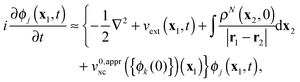 | (5) |
which turn
(4) into uncoupled linear differential
eqn (5) with respect to the time-dependent KS orbitals {
ϕj(
t)}, so that in SAE individual KS orbitals are propagated independently.
In this paper time-dependent Dyson orbitals are introduced and it is shown that these orbitals provide both a theoretically appealing description of the time-evolution of the one-electron state of the electron that is ejected and a practical means of simulating this process. The time-dependent Dyson orbital theory (TDDOT) formally resolves the memory and multiple ionization problems (first and second of the above mentioned TDDFT problems) in the general N-electron case. In the special two-electron case of the He atom the formalism becomes particularly simple and allows investigation of truncation errors (in the limitation of summations over the ion states) and progressive uncoupling approximations in the spirit of the SAE approximation, e.g. uncoupling the propagation of a specific DO, e.g. the DO d0 corresponding to the ion ground state ΨN−10 (which at t ≈ 0 is practically the 1s orbital) from other DOs. Note, that in the physics literature DOs (or Feynman-Dyson amplitudes) are introduced as the residues in the spectral expansion of the electron propagator.33–35 Applications in chemistry have concentrated on momentum densities and ionization phenomena.36–43 We note that these calculations were concerned with the static Dyson orbitals, the amplitudes of the overlap between the ground-state N-electron wave function ΨN and the cationic ground- and excited-state (N − 1)-electron wave functions Ψ(N−1)j
| | 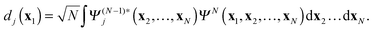 | (6) |
They can be obtained from one-electron equations (the “orbital Dyson equations”), which feature the energy-dependent self-energy, but they can also be calculated straightforwardly from good wavefunctions for the neutral starting system and the ionized system according to
eqn (6). Katriel and Davidson
44 derived energy-independent but coupled equations for the static Dyson orbitals. These static Dyson orbitals are actually very close to the occupied Hartree–Fock and Kohn–Sham orbitals.
45 We stress that we are dealing in this paper with time-dependent one-electron states, which only at
t = 0 coincide with the familiar Dyson orbitals. In Section II the time-dependent DOs
dj(
x1,
t) are introduced, with the sum of the DO densities giving the time-dependent electron density
ρN(
t). The EOMs of TDDOT are derived with the projection and partial integration of the time-dependent Schrödinger equation for an
N-electron wave function
ΨN(
t), which is expanded in terms of the eigenstates of the time-independent (
N − 1)-electron Hamiltonian and the time-dependent DOs
dj(
x1,
t). In spite of being exact, these EOMs (similar to the SAE EOMs
(5)) contain just static potentials of the electron–electron interaction, and this solves the memory problem mentioned above. In the case of a time-independent Hamiltonian the EOMs describe stationary temporal oscillations of the DOs with frequencies equal to the corresponding vertical ionization potentials (VIPs). The TDDOT EOMs reduce in this case to the static one-electron equations for the ground-state DOs.
44 In Section III application of TDDOT to real-time simulation of electronic dynamics is discussed and the matrix form of the TDDOT EOMs is presented. The matrix elements of their static electron–electron potentials can be precalculated and later used at all times during propagation, which offers an efficient propagation technique. A particularly promising application of TDDOT is the simulation of the dynamics of photoinduced ionization. In the general
N-electron case TDDOT offers a method for the calculation of the time-dependent correlated probability of single ionization
P1(
t) as well as the probabilities
Pn(
t) of multiple ionization of
n electrons, the second problem mentioned above. In the case of a two-electron system (the He atom) the calculation of
P1(
t) and
P2(
t) appears to be particularly straightforward. The cation states of the DO expansion reduce to hydrogenic orbitals, which could be extended with the well-known hydrogenic continuum states of the He
2+ ion to obtain a set of cation states that affords the simulation of double ionisation. Then, TDDOT is expected to successfully reproduce the “helium knee” in the experimental ion yield curves.
46
II. EOMs of TDDOT
The main ingredient of TDDOT proposed in this paper, the time-dependent DO dj(x1,t), is introduced in analogy to the stationary case39,44,45 as the amplitude of the overlap| | 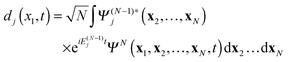 | (7) |
between the time-dependent state ΨN(t) and 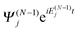 , the latter describes temporal oscillations of an eigenstate of the time-independent (N − 1)-electron Hamiltonian
, the latter describes temporal oscillations of an eigenstate of the time-independent (N − 1)-electron Hamiltonian| | 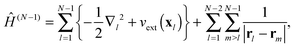 | (8) |
with Ψ(N−1)j being the stationary cation state with the energy E(N−1)j. In (7) the wave function ΨN(t) is the solution of the time-dependent Schrödinger equation for the N-electron system| | 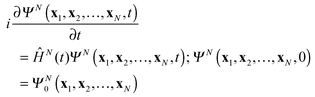 | (9) |
with as initial state at t = 0 the time-independent ground state ΨN0 with the energy EN0. The Hamiltonian ĤN(t) in (9) contains the time-dependent external potentials vext(xl,t)| | 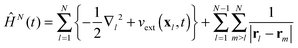 | (10) |
together with the kinetic operators in its first sum, while its third sum combines the electron–electron interaction operators.
We derive the TDDOT EOMs for the DOs (7) from the N-electron Schrödinger eqn (9) with the expansion of ΨN(t) in terms of the stationary cation states 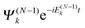 and the DOs dk(x1,t)
and the DOs dk(x1,t)
| | 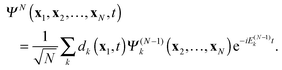 | (11) |
At
t = 0 this is the familiar time-independent “Dyson expansion” of the ground state wavefunction in ion states times Dyson amplitudes.
44 When
t → ∞ the propagation of the wavefunction in time will lead to a superposition of ion states times the one-electron state (orbital) describing the emitted electron, which is by definition the time-dependent DO
dk(
x1,
t). The probability to find the system (atom or molecule) ionized at time
t to the stationary ion state
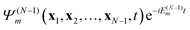
is proportional to the norm of
dm(
x1,
t),
| | 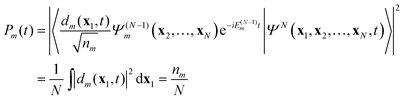 | (12) |
where
nm is the norm of the DO
dm. One often considers the probability of finding the system in ion state
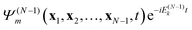
times a “free” electron in a plane wave (or orthogonalized plane wave, or Coulomb wave)
ψk(
x1,
t) with wavevector
k (energy |
k|
2/2),
| | 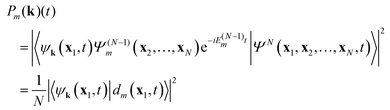 | (13) |
When we are just interested in the appearance of ion state
ΨN−1m we have to integrate over all possible one-electron states {
ψk(
x1,
t)} which gives the same result as
(12)| | 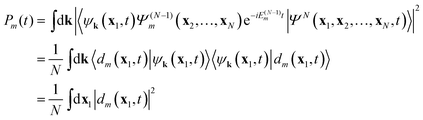 | (14) |
where completeness of the set {
ψk(
x1,
t)} has been used. The time-dependence of the
dm(
x1,
t) and their relative amplitudes, and thus the relative probabilities, are determined by the shape and magnitude of the applied perturbing field. In the so-called “sudden approximation” the probability of ionization to ion state
ΨN−1m is taken proportional to the norm of the corresponding Dyson orbital at
t = 0,
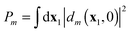
.
37 This approximation is applied with high-energy ionization, but it would be possible, according to
eqn (12), to obtain probabilities without such approximation, as a function of time and of the nature of the applied field, if we could describe the time-dynamics of the time-dependent Dyson orbital we have defined. Suppose we have a system that is reasonably well described by an independent particle model both in the ground state and in the ionized state (a good Hartree–Fock molecule and simple orbital ionization to a frozen orbital (Koopmans) ion state or relaxed orbital ion state). In that case the
t = 0 DO are just the occupied orbitals in the ground state determinant, and in the correlated wavefunction they will still be approximately equal to those orbitals.
45 Then the time evolution of the time-dependent DO would describe the photoionization process as the evolution of a one-electron state from a ground state orbital, to the fully propagated orthogonalized continuum state
dm(
x1,
t → ∞) for the emitted electron. We will consider in the Discussion section how to treat multiple (or no) ionization probabilities.
In order to develop solvable equations for the time evolution of the DO {dk(x1,t)} we introduce the following partitioning of the Hamiltonian (10)
| | 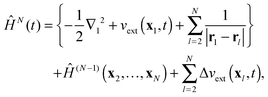 | (15) |
where
ĤN−1 is the time-independent (
N − 1)-particle Hamiltonian with the time-independent potentials
vext(
xl),
l = 2…
N and eigenfunctions
ΨN−1k. The figure brackets in
(15) contain all operators acting on the first electron, while Δ
vext(
t) is the time-dependent change of the external potential
| | | Δvext(x,t) = vext(x,t) − vext(x). | (16) |
Inserting the expansion
(11) and the partitioning
(15) in
(9), multiplying by
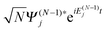
, and integrating over the coordinates
x2,…,
xN, one obtains the following equations
| | 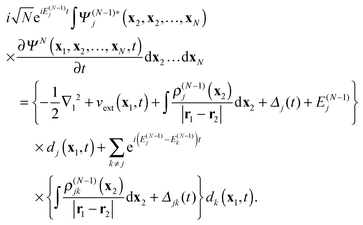 | (17) |
Substituting expansion
(11) into the left hand side, these equations can be written in the form of EOMs for the DOs
dj(
t) with static potentials for the electron–electron interaction
| | 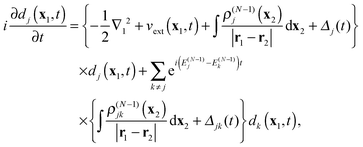 | (18) |
where
Δj(
t) and
Δjk(
t) are the time-dependent scalar functions coming from interaction of Δ
vext(
t) with
ρ(N−1)j and
ρ(N−1)jk| | 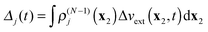 | (19) |
and
| | 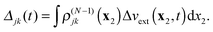 | (20) |
In
(18)–(20)ρ(N−1)j is the electron density of the cation state
Ψ(N−1)j| | 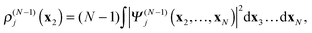 | (21) |
while
ρ(N−1)jk is the transition density between the cation states
Ψ(N−1)j and
Ψ(N−1)k| | 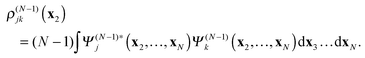 | (22) |
From
(7) and (11) follows, that the sum of the densities of the DOs
dj(
t) yields the total electron density
ρN(
x1,
t) of the wave function
ΨN(
t)
| | 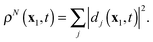 | (23) |
Note the principal difference between the derivation of the EOMs in the proposed TDDOT and the TDDFT EOMs
(2).
9 The Kohn–Sham (KS) orbitals of TDDFT represent the corresponding non-interacting system, which is introduced through the action functional. Then, the stationary action principle is applied
9 and the orbital EOMs are obtained with the functional differentiation of the action with respect to the time-dependent density. In contrast to this, the time-dependent DOs are defined in
(7) through the wave functions of the time-dependent
N-electron and time-independent (
N − 1)-electron interacting systems, so that no auxiliary non-interacting system is required. Then, the EOMs of TDDOT are obtained directly in
(9)–(18) from the corresponding projected and partially integrated
N-electron time-dependent Schrödinger equation, in which the wave function is expanded according to
(11) and the Hamiltonian is partitioned according to
(15).
In the special case of the time-dependent Schrödinger equation with a time-independent Hamiltonian
| | 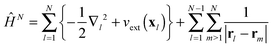 | (24) |
its solution
ΨN(
t) exhibits temporal oscillations with the exponential prefactor only
| | 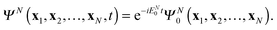 | (25) |
Then, from the DO definition
(7) follows that
dj(
t) acquires in this case the simple complex exponential for the oscillations in time
| | | dj(x1,t) = dj(x1)eiIjt | (26) |
The frequency
Ij is equal to the vertical ionization potential (VIP),
Ij =
E(N−1)j −
EN0. In
(26)dj(
x1) is the conventional stationary DO
(6). Insertion of
(26) in
eqn (18), in which the scalar functions
Δj(
t) and
Δjk(
t) are absent because the Hamiltonian is time-independent in this case, yields the stationary equations for the static DOs
dj(
x1)
44| | 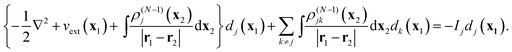 | (27) |
This provides an energy-independent potential instead of the energy-dependent self-energy operator in the traditional Dyson equation. It does couple, as do the time-dependent
eqn (18), the different DOs by the coupling terms with
ρ(N−1)jk.
The EOMs (18) are the key equations of TDDOT and they constitute the main result of the paper. Their remarkable feature is that they contain just static potentials of the electron–electron interaction and they could be classified as coupled homogeneous linear partial differential equations. Contrary to the TDDFT EOMs (3), no adiabatic approximation is employed. Thus, the memory problem of standard TDDFT mentioned in the Introduction is not present in TDDOT. We also note that the equations not only hold for primary ion states (resulting from orbital ionizations), as in the case of (the SAE to) the time-dependent KS orbital eqn (5), but are just as well applicable for Dyson orbitals corresponding to satellite ion states, resulting from an orbital ionization plus an excitation. The eqn (18) are completely general, the DOs that result are only determined by the applied field (the potential vext(x,t)). An intriguing possibility is to study the relative probabilities of ionization to specific ion states as a function of the frequency of the applied radiation, which may sweep through resonance with the subsequent ion states, or alternatively to study the relative probabilities of the first set of ionizations (valence and subvalence) as a function of the energy of the radiation, e.g. ranging from UPS energies to typical XPS energies. A prerequisite is of course an accurate solution method (see Section III).
One may also consider simplification of the full set of eqn (18). For instance, one could work towards a type of SAE approximation by first simplifying the present TDDOT EOMs by replacing in eqn (18) for a particular dj(t), all other DOs dk(t), k ≠ j with the time-independent DOs dk(x1)eiIkt, which correspond to the initial time-independent potential (retaining of course the exponential time factor of the stationary orbital). With this, eqn (18) are simplified to
| | 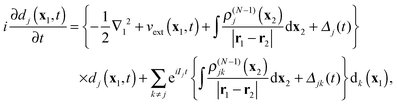 | (28) |
which are uncoupled inhomogeneous linear partial differential differential equations with the last sum representing the free terms. We may also call them single active electron (SAE) equations, like
(5), but note that they are for the time-dependent Dyson orbital and incorporate the Coulomb potential of the density of the corresponding ion state
ΨN−1j, not the Coulomb potential of the ground state density
ρN(
x). They also retain time-dependent potentials
vext(
x1,
t) and
Δj(
t). Possible application of the TDDOT EOMs to real-time simulation of the electronic dynamics will be discussed in the next section.
III. Discussion
For applications, propagation of the one-electron functions {dk(x1,t)} on a 3D grid would give complete flexibility to the evolving Dyson orbitals. It is also possible to operate with the matrix form of the proposed TDDOT EOMs, which is obtained with the expansion of the time-dependent DOs dj(t) in a convenient time-independent orthonormal basis {ϕν}| | 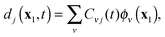 | (29) |
where Cνj(t) are the elements of the DO evolution matrix C(t). This introduces the well known problem of the representation of a continuum wavefunction, into which the DOs evolve in the course of time, with a suitable basis. Solutions for continuum electron wavefunctions have been obtained with mixed basis sets of atom based functions (Gaussians or Slater-type orbitals) and plane waves,28–32 and rather successfully, for small molecules, with very flexible B-spline representation of the radial part of spherical harmonic expansions.6,27 Inserting the expansion (29) in the TDDOT EOMs (18) and integrating it with ϕμ*, one obtains their matrix form| | 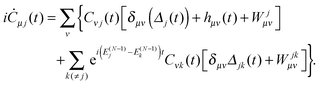 | (30) |
Here, hμν(t) are the matrix elements of the time-dependent one-electron operator| | 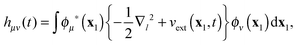 | (31) |
Wjμν are the elements of the static potential of ρ(N−1)j| | 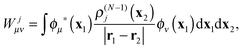 | (32) |
and Wjkμν are those of the static potential of ρ(N−1)jk| | 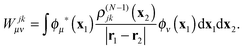 | (33) |
With (23) and (29), the matrix form ρNμν(t) of the time-dependent density reads| | 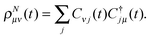 | (34) |
The form of the linear matrix EOMs (30) provides a perspective on the application of TDDOT to real-time simulation of electronic dynamics. This simulation includes the following stages:
(1) At the preliminary stage the N-electron ground state ΨN0 and a chosen number M > N of the ground and excited stationary (N − 1)-electron states Ψ(N−1)j and their energies EN0 and E(N−1)j are obtained with a standard ab initio configuration interaction (CI) or coupled cluster (CC) calculation. Also, the orbitals to be used in the propagation eqn (30) are to be determined. The actual basis to be used may be the {ϕν} of the chosen static basis set, that has for instance been used in the ab initio calculations, or it may be a basis of linear combinations of the primitive basis that diagonalizes a convenient one-electron hamiltonian (Hartree–Fock or Kohn–Sham), plus some set of continuum functions. The quantities obtained are used to calculate the initial evolution matrix C(0), the cation electron density ρ(N−1)j and transition densities ρ(N−1)jk as well as the matrix elements Wjμν and Wjkμν of the static electron–electron interaction potential.
(2) At the real-time propagation stage the evolution matrix C(t) is propagated through a number of time steps tn with a numerical solution of the matrix TDDOT EOMs (30). In order to accomplish this, the one-electron elements hμν(tn), the phase factors 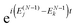 , and the scalar functions Δj(tn), Δjk(tn) are evaluated at the time tn, while the pre-calculated matrix elements Wjμν and Wjkμν are used in (30).
, and the scalar functions Δj(tn), Δjk(tn) are evaluated at the time tn, while the pre-calculated matrix elements Wjμν and Wjkμν are used in (30).
With this, the present TDDOT offers a viable computational scheme. Indeed, the expensive ab initio approach is employed only in the preliminary stage. Also, during the bottleneck real-time simulation of electronic dynamics only relatively inexpensive orbital propagation is performed, which requires re-calculation of simple one-electron integrals with the external potential, while the same pre-calculated matrix elements of the static electron–electron interaction potentials are used at all time steps tn. Since the EOMs (30) are linear equations for the evolution matrix elements Cνj(t), one can expect a rather stable propagation according to these equations. Obviously, the exact TDDOT requires the full expansion (11) with an infinite number of time-dependent DOs dj(t). Of course, the application of the TDDOT scheme would be particularly profitable, if for a reasonably accurate simulation only a fairly small number M of the DOs would have to be retained.
The TDDOT EOMs (30) can be further simplified with the SAE approximation of eqn (28). Inserting the expansion (29) in (28), one obtains the following inhomogeneous TDDOT-SAE matrix equations
| | 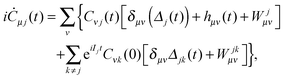 | (35) |
where the last sum represents their free terms. Because the generic TDDOT-SAE
eqn (28) are uncoupled, the matrix TDDOT-SAE EOMS
(35) are partitioned into uncoupled sub-sets of equations for the independent propagation of the expansion coefficients of individual DOs
dj(
t).
Coupled to nuclear dynamics, the matrix TDDOT EOMs could be applied to simulate photoinduced molecular dissociation and isomerisation. In particular, such simulation of the induced dissociation of the H2 molecule and isomerisation of the diimide N2H2 molecule could be compared with the corresponding TDHF and TDDFT simulations of ref. 7 and 8. Note, that in the case of a two-electron system X (for instance, X = H2) the TDDOT EOMs (30) are especially simple. Indeed, in this case the static cation state Ψ(N−1)j in the DO expansion (11) reduces to the ground-state wave function (orbital) ψj(x1) of the one-electron cation X+. Then, the cation density ρ(N−1)j in the matrix element Wjμν of (32) reduces to the density of the orbital ψj(x1), while the transition density ρ(N−1)jk in the matrix element Wjkμν of (33) turns to the product of the corresponding orbitals.
The very structure of TDDOT provides an especially interesting perspective on its application to real-time simulation of the electron dynamics of ionization induced by a strong rapidly changing electric field. Indeed, the expansion (11) can be rewritten as a weighted sum of normalized functions ΘNj(t)
| | 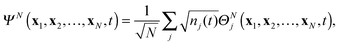 | (36) |
which are the products of the normalized DO
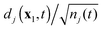
and
Ψ(N−1)j| | 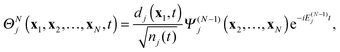 | (37) |
where
nj(
t) is the DO norm
| | 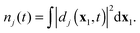 | (38) |
The expansion
(36) can be interpreted as the partitioning of
ΨN(
t) into “channels” of ionization to various cation states
Ψ(N−1)j. In its turn, the normalized DO
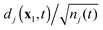
can be interpreted as the state of the electron that is being ejected during ionization to the ion state
Ψ(N−1)j. In the course of the simulated ionization, the DOs experience gradual delocalization, with diminishing norm for the DOs starting out at
t = 0 as practically Hartree–Fock or Kohn–Sham orbitals (we mentioned the identity of the DOs at
t = 0 with the orbitals if the wavefunction is approximated as a determinant). For satellites the DOs start out with very low norm (norm zero within the determinantal approximation
45), and will acquire increasing norm. For long-time simulation the inclusion of sufficient continuum states of various energies in the basis set expansion
(29) (the third problem mentioned in the Introduction) will be mandatory. We have mentioned the alternative option of representation of the TDDOT EOMs
(18) on a three-dimensional grid in 3D physical space with the fully numerical solution of these equations.
Note, that simulation of multiple ionization will require also the inclusion of unbound cation states in the DO expansion (11). The present TDDOT allows in the first place evaluation of the correlated probability P1(t) of a single ionization of an N-electron system at the time t. The expression for P1(t) reads4
| | 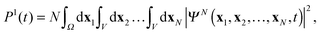 | (39) |
where the entire physical space
R is subdivided into a chosen finite volume
V and the outside space
Ω,
R =
V +
Ω. The electrons in the region
Ω are assumed to be ejected, while those inside the volume
V are considered to be bound. Inserting the expansion
(11) in
(39), one obtains the TDDOT expression for
P1(
t)
| | 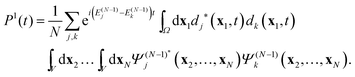 | (40) |
The cation states
Ψ(N−1)j in
(40) are available from the above mentioned stage (1) of the calculations, while the DOs
d(
t) are obtained with their propagation at the stage (2). If the cation states are continuum states,
i.e. bound states of the +2 ion times a free electron wavefunction, corresponding to two-fold ionization (and similar for multiple ionization), they would at least have one electron in a continuum state with negligible amplitude in the volume
V, so the integrals over
V will yield zero. So with
V a limited volume, sufficient to practically fully contain the bound ion states, the summation over cation states
ΨN−1j reduces to one over bound cation states. This is also implied when we are considering the probability of single ionization, where the cation remains behind in a bound state. Orthogonality between the bound cation states is obtained by integration over the volume
V, and the probabilities of single ionization (
P1), no ionization (
P0), and multiple ionization (
P>1) become
| | 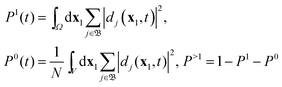 | (41) |
where
j runs over the set of bound singly ionized (+1) ion states. Note that the outer space
Ω in
eqn (41) has to be the space complementary to a space
V in which the bound states are fully contained, at least to the extent that the integrals over the bound states in
eqn (40) yield orthogonality to high precision. The present formalism then naturally covers the traditional photoelectron experiment which measures single ionization events. We may ask at any time
t for the probability to detect an emitted electron in some free electron state
ψk (a plane wave or, more accurately, an orthogonalized Coulomb wave in the +1 field of the cation left behind), and the cation in some state
ΨN−1j,
i.e. the system in state
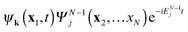
. The inner product
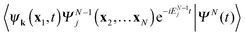
yields with expansion
(11) 〈
ψk(
x1,
t)|
dj(
x1,
t)〉. Of course, depending on the frequency (energy) of the ionizing radiation and the energy of the ion state,
dj(
x1,
t) will develop into free electron states of specific energy, and only corresponding
ψk will give a finite matrix element. We have noted that the total probability of finding the system in cation state
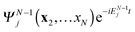
regardless of the state of the ejected electron is obtained by summing (integrating) over all free electron states, giving
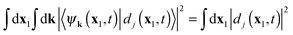
on account of the completeness of the set of free electron states {
ψk}. In the traditional sudden approximation this is already evaluated at time
t = 0,
i.e. for the initial Dyson orbital, and provides an estimate of the relative intensities of the various peaks in the spectrum in the case of very high energy radiation. Taking into consideration the different types DOs, this affords the differentiation between primary ionizations and satellites. A primary ionization is an “orbital ionization” characterized by an ion wavefunction which can be reasonably approximated by a single determinant with a single orbital removed and the others possibly relaxed but recognizable. Its DO resembles closely the Hartree–Fock orbital that is vacated (the Hartree–Fock orbitals are the Dyson orbitals in a frozen-orbital approximation to the ion states). For satellites (primary ion states plus an excitation which are close in energy to some other primary ion state) the Dyson orbital at
t = 0 has, for correlated wavefunctions, the same shape as the orbital corresponding to the main peak to which it is a satellite, but with (much) reduced amplitude (the DOs are not normalized), see
ref. 45 for discussion. It would be zero in the frozen orbital determinantal approximation for ground state and ion (there are no satellites in the Koopmans' approximation) but will be different from zero in a relaxed orbital and in particular in a correlated treatment of the ion state. The present formalism affords a study of these features in a photoionization spectrum either without approximation or with limitations of the number of ion states included in the coupling (
eqn (18)) or in the free terms of the uncoupled treatment (
eqn (28)). Also the effect of more or less sophistication in the treatment of the ion states (Koopmans' approximation, SCF with orbital relaxation, correlated) can be investigated.
The present TDDOT formalism also covers the simulation of the modern very short and strong laser pulse experiments which allow for multiple ionization. Note, that the total number Ne of electrons ejected from the volume V because of all kinds of single and multiple ionizations is given by the integral of the electron density ρ(x1,t) over the outer region Ω.4 Using the probabilities Pn(t) of ejection of n electrons, we have for the expectation value of Ne
| | 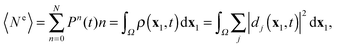 | (42) |
which is the integral over the outer space of the standard expression of the electron density written as a sum of squares of Dyson orbitals, now time-dependent. The electron density in the outer space can be larger than 1 if the summation over
j in
(42) includes ion states which are continuum states,
i.e. ion states that describe a doubly (or higher) ionized bound ion and one (or more) outgoing electrons. The norms of the Dyson orbitals belonging to such continuum ion states give the probability to find doubly (or higher) ionized ions and two (or more) electrons in the outer space. Then, from
(40) and (42) follows that TDDOT allows also the evaluation of the number
N>1 of electrons ejected in multiple ionizations
| | 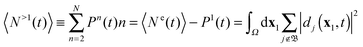 | (43) |
The summation over
j (in fact, an integration) runs over all the unbound +1 ion states,
i.e. states that have a bound multiply charged ion (
n-fold ionized atom or molecule,
n = 2…(
N − 1)) and
n − 1 other free electrons (the
n-th outgoing electron is the one already described by
dj(
x1,
t)). We can also focus on one individual multiple ionization yield
Pn, with
n one of the numbers in the range 2…(
N − 1). TDDOT at least formally resolves for the general
N-electron case the problem of the evaluation of such an individual multiple ionization yield, one of the problems mentioned in the Introduction. For such a specific probability
Pn,
n > 1 we need to take those terms in the sum over
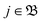
in
eqn (43) which refer to states with (
n − 1) free electrons and a bound atomic or molecular ion state of (
N −
n) electrons, with charge +
n. We call this the set (+
n) of unbound ion states and write
| | 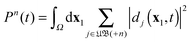 | (44) |
With this differentiation of the summation over the unbound states in
eqn (43) into subsets we formally solve the problem of obtaining individual
Pns.
In the special case of two-electron systems eqn (43) reduces to the expression for the individual probability P2 (and P0 can be obtained from the sum rule 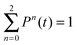 ). As was mentioned earlier in this Section, the cation states Ψ(N−1)j reduce in this case to the one-electron states (orbitals) of the cation, ψj(x1). In the basis set expansion for the DO we would then need, as always, functions that can represent continuum wave functions, e.g. by inclusion of unbound orbitals in the basis set expansion (29), which should be Coulomb waves in the +1/r field of the cation. Grid-based propagation of the DOs would obviate this basis set problem, of course. For the multiple ionization a second set of continuum states are needed, namely the continuum states of the cation have to be included in the expansion (11). In e.g. the He case these are the well known unbound states of the one-electron hydrogenic system,47,48i.e. the Coulomb waves in the +2/r field of the bare nucleus. This will be sufficient for the rigorous description of electron ejection in the process of non-sequential double ionization. Since there is no adiabatic approximation, there is not a memory problem (the first problem mentioned in the Introduction for applications of TDDFT) and TDDOT is expected to correctly reproduce the “helium knee” structure.
). As was mentioned earlier in this Section, the cation states Ψ(N−1)j reduce in this case to the one-electron states (orbitals) of the cation, ψj(x1). In the basis set expansion for the DO we would then need, as always, functions that can represent continuum wave functions, e.g. by inclusion of unbound orbitals in the basis set expansion (29), which should be Coulomb waves in the +1/r field of the cation. Grid-based propagation of the DOs would obviate this basis set problem, of course. For the multiple ionization a second set of continuum states are needed, namely the continuum states of the cation have to be included in the expansion (11). In e.g. the He case these are the well known unbound states of the one-electron hydrogenic system,47,48i.e. the Coulomb waves in the +2/r field of the bare nucleus. This will be sufficient for the rigorous description of electron ejection in the process of non-sequential double ionization. Since there is no adiabatic approximation, there is not a memory problem (the first problem mentioned in the Introduction for applications of TDDFT) and TDDOT is expected to correctly reproduce the “helium knee” structure.
IV. Conclusions
In this paper time-dependent Dyson orbital theory (TDDOT) has been proposed for real-time simulation of the photoionization process, i.e. the full dynamics of electron ejection from an atom or molecule. To this end a time-dependent extension of the Dyson orbital (DO) concept is introduced. The time-dependent DOs are defined by projection of the generic time-dependent wavefunction ΨN(t) onto the the stationary cation states Ψ(N−1)j. The defining formula (7) for the time-dependent DOs dj(x1,t) leads to the master equations of motion for the DOs, the TDDOT EOMs (18), which describe the evolution in the course of time of the one-electron state of the electron being ejected from the initial static Dyson orbital (very similar to a Hartree–Fock or Kohn–Sham orbital) into the plane wave like state of the final ionized electron. Remarkably, the equations of motion only require static electron–electron interaction potentials, but the price to be paid is coupling of the various one-electron equations, and therefore accurate solutions of the different ion states that are included in the coupled equations are required. Importantly, the present TDDOT fully covers the memory effects and does not resort to the adiabatic approximation, thus resolving the first of the mentioned problems of conventional TDDFT.
The master eqn (18) have been cast into the convenient form (30) of the EOMs for the evolution matrix C(t) in a basis, which can readily include the continuum functions. This ensures the adequate representation in TDDOT of continuum wave functions, into which the DOs evolve in the course of time. The linear form of the TDDOT EOMs suggests a stable propagation of the DO evolution matrix elements Cνj(t).
Partitioning (36) of the generic function ΨN(t) into ionization “channels” makes the application of TDDOT to real-time simulation of the electron dynamics of ionization by a strong rapidly changing electric field especially promising. The present formalism covers the single ionization events of traditional photoelectron spectroscopy. The total probabilities P1(t) and P0(t) (eqn (41)) of single ionization and no ionization at a particular time t as well as the probabilities of individual primary ionizations and satellites are evaluated from the densities |dj(x1,t)|2 of the propagated DOs associated with the corresponding bound cation states. The TDDOT formalism also covers multiple ionizations by very short and strong laser pulses. The total number (43) of electrons ejected in all multiple ionizations and the individual probabilities Pn(t) (eqn (44)) of n-tuple ionization are evaluated from the densities of the DOs associated with the relevant unbound cation states. This resolves the second of the above mentioned TDDFT problems.
Real-time simulation of the paradigmatic non-sequential double ionization of the He atom offers an efficient simple test for the present TDDOT formalism. In this two-electron case all wave functions employed in TDDOT reduce to well-known orbitals. These are the the orbitals of the discrete spectrum of the He+ ion as well as the unbound Coulomb waves in the +1/r field of He+ and those in the +2/r field of the bare helium nucleus. Due to the above mentioned resolution of the memory problem, TDDOT is expected to reproduce a notorious memory effect, the “knee structure” of P2(t) as a function of the intensity of an applied field.
References
- K. C. Kulander, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 778 CrossRef CAS.
- K. C. Kulander, K. J. Schafer and J. L. Krause, Int. J. Quantum Chem., Symp., 1991, 25, 415 CrossRef CAS.
- D. Lappas and R. van Leeuwen, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, L249 CrossRef CAS.
-
C. A. Ullrich and A. D. Bandrauk, in Fundamentals of Time-Dependent Density Functional Theory, Lecture Notes in Physics, ed., M. A. L. Marques, N. T. Maitra, F. Nogueira, E. K. U. Gross and A. Rubio, Springer, 2012, ch. 18, vol. 837, p. 351 Search PubMed.
- X. Chu and S.-I. Chu, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 70, 063404 CrossRef.
- M. Awasthi, Y. V. Vanne, A. Saenz, A. Castro and P. Decleva, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 063403 CrossRef.
- M. Uhlmann, T. Kunert and R. Schmidt, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 72, 045402 CrossRef.
- J. Handt, T. Kunert and R. Schmidt, Chem. Phys. Lett., 2006, 428, 220 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997 CrossRef CAS.
- R. van Leeuwen, Phys. Rev. Lett., 1998, 80, 1280 CrossRef CAS.
- T. Kunert and R. Schmidt, Eur. Phys. J. D, 2003, 25, 15 CrossRef CAS.
- M. A. L. Marques, A. Castro, G. F. Bertsch and A. Rubio, Comput. Phys. Commun., 2003, 151, 60 CrossRef CAS.
- C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001 CrossRef PubMed.
- A. Castro, H. Appel, M. Oliveira, C. A. Rozzi, X. Andrade, F. Lorenzen, M. A. L. Marques, E. K. U. Gross and A. Rubio, Phys. Status Solidi B, 2006, 243, 2465 CrossRef CAS.
- N. T. Maitra, J. Chem. Phys., 2006, 125, 184111 CrossRef PubMed.
- R. van Leeuwen, Phys. Rev. Lett., 1999, 82, 3863 CrossRef CAS.
- M. Ruggenthaler, M. Penz and R. van Leeuwen, J. Phys.: Condens. Matter, 2015, 27, 203202 CrossRef PubMed.
-
N. T. Maitra, in Fundamentals of Time-Dependent Density Functional Theory, Lecture Notes in Physics, ed., M. A. L. Marques, N. T. Maitra, F. Nogueira, E. K. U. Gross and A. Rubio, Springer, 2012, ch. 8, vol. 837, p. 167 Search PubMed.
- A. Castro, M. A. L. Marques and A. Rubio, J. Chem. Phys., 2004, 121, 3425 CrossRef CAS PubMed.
- J. F. Dobson, Phys. Rev. Lett., 1994, 73, 2244 CrossRef CAS PubMed.
- G. Vignale, Phys. Rev. Lett., 1995, 74, 3233 CrossRef CAS PubMed.
- K. C. Kulander, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 35, 445 CrossRef CAS.
- M. Lein, T. Kreibich, E. K. U. Gross and V. Engel, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 033403 CrossRef.
- X. S. Li, S. M. M. Smith, A. N. Markevitch, D. A. Romanov, R. J. Levis and H. B. Schlegel, Phys. Chem. Chem. Phys., 2005, 7, 233 RSC.
- H. B. Schlegel, S. M. Smith and X. Li, J. Chem. Phys., 2007, 126, 244110 CrossRef PubMed.
- H. Eshuis, G. Balint-Kurti and F. Manby, J. Chem. Phys., 2008, 128, 114113 CrossRef PubMed.
- M. Brosolo and P. Decleva, Chem. Phys., 1992, 159, 15 CrossRef.
- K. Ladanyi and T. Szondy, Nuovo Cimento B, 1971, 5, 70 CrossRef.
- I. Cacelli and V. Carravetta, J. Phys. B: At., Mol. Opt. Phys., 1996, 29, 3363 CrossRef CAS.
- A. P. P. Natalense and R. R. Lucchese, J. Chem. Phys., 1999, 111, 5344 CrossRef CAS.
- V. Carravetta and I. Cacelli, Chem. Phys., 1999, 77, 243 Search PubMed.
- V. P. Osinga, B. C. Oostenbrink, E. van Lenthe, C. Fonseca Guerra and E. J. Baerends, Chem. Phys., 2002, 284, 565 CrossRef CAS.
- G. Csanak, H. S. Taylor and R. Yaris, Adv. At. Mol. Phys., 1971, 7, 287 Search PubMed.
-
A. L. Fetter and J. D. Walecka, Quantum Theory of Many-Particle Systems, Dover Publiations, Inc., 2003 Search PubMed.
-
J. W. Negele and H. Orland, Quantum Many-Particle Systems, of Frontiers in Physics, Addison-Wesley, 1988, vol. 68 Search PubMed.
- L. S. Cederbaum, Theor. Chim. Acta, 1973, 31, 239 CrossRef CAS.
- B. T. Pickup, Chem. Phys., 1977, 19, 193 CrossRef CAS.
- R. J. Williams, I. E. McCarthy and E. Weigold, Chem. Phys., 1977, 22, 281 CrossRef.
- A. O. Bawagan, C. E. Brion, E. R. Davidson and D. Feller, Chem. Phys., 1987, 113, 19 CrossRef CAS.
- Y. Zheng, C. E. Brion, M. J. Brunger, K. Zhao, A. M. Grisogono, S. Braidwood, E. Weigold, S. J. Chakravorty, E. R. Davidson and A. Sgamelotti,
et al.
, Chem. Phys., 1996, 212, 269 CrossRef CAS.
- O. Doulgounitcheva, V. G. Zakrzewski and J. V. Ortiz, J. Phys. Chem. A, 2002, 106, 8411 CrossRef.
- J. V. Ortiz, Int. J. Quantum Chem., 2004, 100, 1131 CrossRef CAS.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- J. Katriel and E. R. Davidson, Proc. Natl. Acad. Sci. U. S. A., 1980, 77, 4403 CrossRef CAS.
- O. V. Gritsenko, B. Braïda and E. J. Baerends, J. Chem. Phys., 2003, 119, 1937 CrossRef CAS.
- B. Walker, B. Sheeny, L. F. Di Mauro, P. Agostini, K. J. Schafer and K. C. Kulander, Phys. Rev. Lett., 1994, 73, 1227 CrossRef CAS PubMed.
-
H. A. Bethe and E. E. Salpeter, Quantum mechanics of one- and two-electron systems, Plenum, 1957 Search PubMed.
-
A. Messiah, Quantum Mechanics, North-Holland Publ. Co, Amsterdam, 1961 Search PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article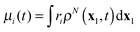 describes high-harmonic generation in atomic systems.4,5 Electronic dynamics with fixed nuclei serves as a first stage of the simulation of similar processes in molecules.4,6 Coupling to nuclear dynamics provides not only more complete simulation of the electronic dynamics but also the description of photoinduced molecular dissociation7 and isomerisation.8
describes high-harmonic generation in atomic systems.4,5 Electronic dynamics with fixed nuclei serves as a first stage of the simulation of similar processes in molecules.4,6 Coupling to nuclear dynamics provides not only more complete simulation of the electronic dynamics but also the description of photoinduced molecular dissociation7 and isomerisation.8
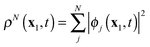
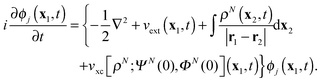
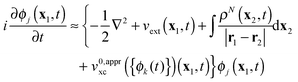
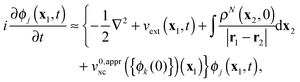
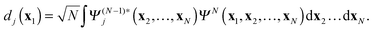
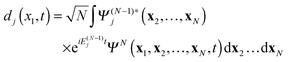
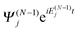 , the latter describes temporal oscillations of an eigenstate of the time-independent (N − 1)-electron Hamiltonian
, the latter describes temporal oscillations of an eigenstate of the time-independent (N − 1)-electron Hamiltonian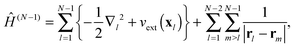
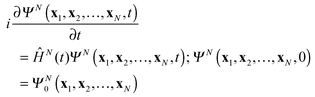
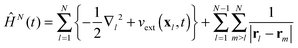
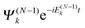 and the DOs dk(x1,t)
and the DOs dk(x1,t)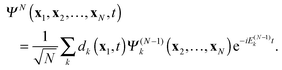
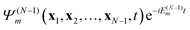 is proportional to the norm of dm(x1,t),
is proportional to the norm of dm(x1,t),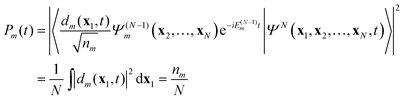
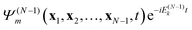 times a “free” electron in a plane wave (or orthogonalized plane wave, or Coulomb wave) ψk(x1,t) with wavevector k (energy |k|2/2),
times a “free” electron in a plane wave (or orthogonalized plane wave, or Coulomb wave) ψk(x1,t) with wavevector k (energy |k|2/2),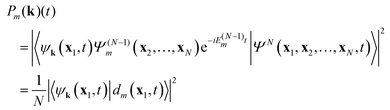
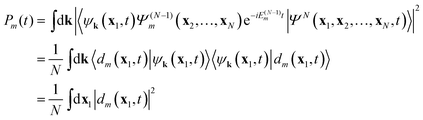
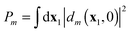 .37 This approximation is applied with high-energy ionization, but it would be possible, according to eqn (12), to obtain probabilities without such approximation, as a function of time and of the nature of the applied field, if we could describe the time-dynamics of the time-dependent Dyson orbital we have defined. Suppose we have a system that is reasonably well described by an independent particle model both in the ground state and in the ionized state (a good Hartree–Fock molecule and simple orbital ionization to a frozen orbital (Koopmans) ion state or relaxed orbital ion state). In that case the t = 0 DO are just the occupied orbitals in the ground state determinant, and in the correlated wavefunction they will still be approximately equal to those orbitals.45 Then the time evolution of the time-dependent DO would describe the photoionization process as the evolution of a one-electron state from a ground state orbital, to the fully propagated orthogonalized continuum state dm(x1,t → ∞) for the emitted electron. We will consider in the Discussion section how to treat multiple (or no) ionization probabilities.
.37 This approximation is applied with high-energy ionization, but it would be possible, according to eqn (12), to obtain probabilities without such approximation, as a function of time and of the nature of the applied field, if we could describe the time-dynamics of the time-dependent Dyson orbital we have defined. Suppose we have a system that is reasonably well described by an independent particle model both in the ground state and in the ionized state (a good Hartree–Fock molecule and simple orbital ionization to a frozen orbital (Koopmans) ion state or relaxed orbital ion state). In that case the t = 0 DO are just the occupied orbitals in the ground state determinant, and in the correlated wavefunction they will still be approximately equal to those orbitals.45 Then the time evolution of the time-dependent DO would describe the photoionization process as the evolution of a one-electron state from a ground state orbital, to the fully propagated orthogonalized continuum state dm(x1,t → ∞) for the emitted electron. We will consider in the Discussion section how to treat multiple (or no) ionization probabilities.
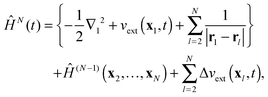
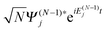 , and integrating over the coordinates x2,…,xN, one obtains the following equations
, and integrating over the coordinates x2,…,xN, one obtains the following equations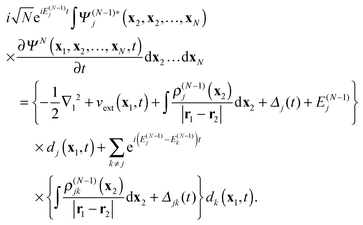
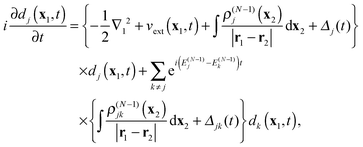
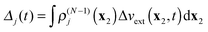
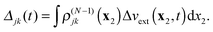
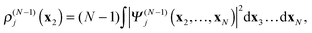
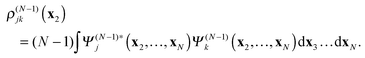
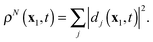
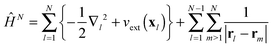
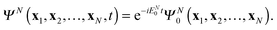
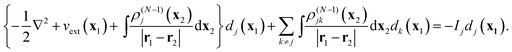
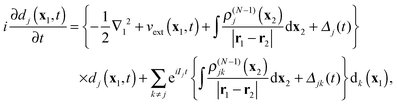
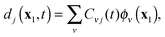
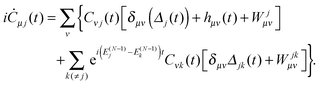
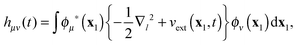
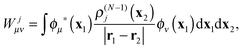
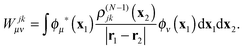
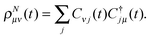
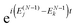 , and the scalar functions Δj(tn), Δjk(tn) are evaluated at the time tn, while the pre-calculated matrix elements Wjμν and Wjkμν are used in (30).
, and the scalar functions Δj(tn), Δjk(tn) are evaluated at the time tn, while the pre-calculated matrix elements Wjμν and Wjkμν are used in (30).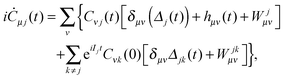
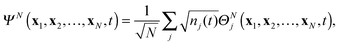
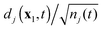 and Ψ(N−1)j
and Ψ(N−1)j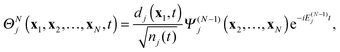
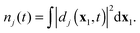
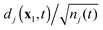 can be interpreted as the state of the electron that is being ejected during ionization to the ion state Ψ(N−1)j. In the course of the simulated ionization, the DOs experience gradual delocalization, with diminishing norm for the DOs starting out at t = 0 as practically Hartree–Fock or Kohn–Sham orbitals (we mentioned the identity of the DOs at t = 0 with the orbitals if the wavefunction is approximated as a determinant). For satellites the DOs start out with very low norm (norm zero within the determinantal approximation45), and will acquire increasing norm. For long-time simulation the inclusion of sufficient continuum states of various energies in the basis set expansion (29) (the third problem mentioned in the Introduction) will be mandatory. We have mentioned the alternative option of representation of the TDDOT EOMs (18) on a three-dimensional grid in 3D physical space with the fully numerical solution of these equations.
can be interpreted as the state of the electron that is being ejected during ionization to the ion state Ψ(N−1)j. In the course of the simulated ionization, the DOs experience gradual delocalization, with diminishing norm for the DOs starting out at t = 0 as practically Hartree–Fock or Kohn–Sham orbitals (we mentioned the identity of the DOs at t = 0 with the orbitals if the wavefunction is approximated as a determinant). For satellites the DOs start out with very low norm (norm zero within the determinantal approximation45), and will acquire increasing norm. For long-time simulation the inclusion of sufficient continuum states of various energies in the basis set expansion (29) (the third problem mentioned in the Introduction) will be mandatory. We have mentioned the alternative option of representation of the TDDOT EOMs (18) on a three-dimensional grid in 3D physical space with the fully numerical solution of these equations.
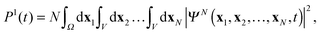
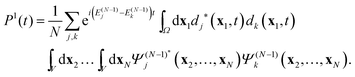
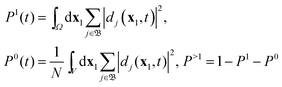
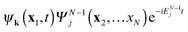 . The inner product
. The inner product 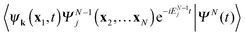 yields with expansion (11) 〈ψk(x1,t)|dj(x1,t)〉. Of course, depending on the frequency (energy) of the ionizing radiation and the energy of the ion state, dj(x1,t) will develop into free electron states of specific energy, and only corresponding ψk will give a finite matrix element. We have noted that the total probability of finding the system in cation state
yields with expansion (11) 〈ψk(x1,t)|dj(x1,t)〉. Of course, depending on the frequency (energy) of the ionizing radiation and the energy of the ion state, dj(x1,t) will develop into free electron states of specific energy, and only corresponding ψk will give a finite matrix element. We have noted that the total probability of finding the system in cation state 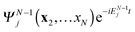 regardless of the state of the ejected electron is obtained by summing (integrating) over all free electron states, giving
regardless of the state of the ejected electron is obtained by summing (integrating) over all free electron states, giving 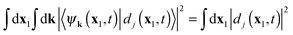 on account of the completeness of the set of free electron states {ψk}. In the traditional sudden approximation this is already evaluated at time t = 0, i.e. for the initial Dyson orbital, and provides an estimate of the relative intensities of the various peaks in the spectrum in the case of very high energy radiation. Taking into consideration the different types DOs, this affords the differentiation between primary ionizations and satellites. A primary ionization is an “orbital ionization” characterized by an ion wavefunction which can be reasonably approximated by a single determinant with a single orbital removed and the others possibly relaxed but recognizable. Its DO resembles closely the Hartree–Fock orbital that is vacated (the Hartree–Fock orbitals are the Dyson orbitals in a frozen-orbital approximation to the ion states). For satellites (primary ion states plus an excitation which are close in energy to some other primary ion state) the Dyson orbital at t = 0 has, for correlated wavefunctions, the same shape as the orbital corresponding to the main peak to which it is a satellite, but with (much) reduced amplitude (the DOs are not normalized), see ref. 45 for discussion. It would be zero in the frozen orbital determinantal approximation for ground state and ion (there are no satellites in the Koopmans' approximation) but will be different from zero in a relaxed orbital and in particular in a correlated treatment of the ion state. The present formalism affords a study of these features in a photoionization spectrum either without approximation or with limitations of the number of ion states included in the coupling (eqn (18)) or in the free terms of the uncoupled treatment (eqn (28)). Also the effect of more or less sophistication in the treatment of the ion states (Koopmans' approximation, SCF with orbital relaxation, correlated) can be investigated.
on account of the completeness of the set of free electron states {ψk}. In the traditional sudden approximation this is already evaluated at time t = 0, i.e. for the initial Dyson orbital, and provides an estimate of the relative intensities of the various peaks in the spectrum in the case of very high energy radiation. Taking into consideration the different types DOs, this affords the differentiation between primary ionizations and satellites. A primary ionization is an “orbital ionization” characterized by an ion wavefunction which can be reasonably approximated by a single determinant with a single orbital removed and the others possibly relaxed but recognizable. Its DO resembles closely the Hartree–Fock orbital that is vacated (the Hartree–Fock orbitals are the Dyson orbitals in a frozen-orbital approximation to the ion states). For satellites (primary ion states plus an excitation which are close in energy to some other primary ion state) the Dyson orbital at t = 0 has, for correlated wavefunctions, the same shape as the orbital corresponding to the main peak to which it is a satellite, but with (much) reduced amplitude (the DOs are not normalized), see ref. 45 for discussion. It would be zero in the frozen orbital determinantal approximation for ground state and ion (there are no satellites in the Koopmans' approximation) but will be different from zero in a relaxed orbital and in particular in a correlated treatment of the ion state. The present formalism affords a study of these features in a photoionization spectrum either without approximation or with limitations of the number of ion states included in the coupling (eqn (18)) or in the free terms of the uncoupled treatment (eqn (28)). Also the effect of more or less sophistication in the treatment of the ion states (Koopmans' approximation, SCF with orbital relaxation, correlated) can be investigated.
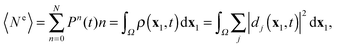
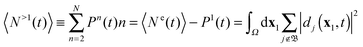
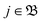 in eqn (43) which refer to states with (n − 1) free electrons and a bound atomic or molecular ion state of (N − n) electrons, with charge +n. We call this the set (+n) of unbound ion states and write
in eqn (43) which refer to states with (n − 1) free electrons and a bound atomic or molecular ion state of (N − n) electrons, with charge +n. We call this the set (+n) of unbound ion states and write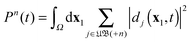
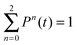 ). As was mentioned earlier in this Section, the cation states Ψ(N−1)j reduce in this case to the one-electron states (orbitals) of the cation, ψj(x1). In the basis set expansion for the DO we would then need, as always, functions that can represent continuum wave functions, e.g. by inclusion of unbound orbitals in the basis set expansion (29), which should be Coulomb waves in the +1/r field of the cation. Grid-based propagation of the DOs would obviate this basis set problem, of course. For the multiple ionization a second set of continuum states are needed, namely the continuum states of the cation have to be included in the expansion (11). In e.g. the He case these are the well known unbound states of the one-electron hydrogenic system,47,48i.e. the Coulomb waves in the +2/r field of the bare nucleus. This will be sufficient for the rigorous description of electron ejection in the process of non-sequential double ionization. Since there is no adiabatic approximation, there is not a memory problem (the first problem mentioned in the Introduction for applications of TDDFT) and TDDOT is expected to correctly reproduce the “helium knee” structure.
). As was mentioned earlier in this Section, the cation states Ψ(N−1)j reduce in this case to the one-electron states (orbitals) of the cation, ψj(x1). In the basis set expansion for the DO we would then need, as always, functions that can represent continuum wave functions, e.g. by inclusion of unbound orbitals in the basis set expansion (29), which should be Coulomb waves in the +1/r field of the cation. Grid-based propagation of the DOs would obviate this basis set problem, of course. For the multiple ionization a second set of continuum states are needed, namely the continuum states of the cation have to be included in the expansion (11). In e.g. the He case these are the well known unbound states of the one-electron hydrogenic system,47,48i.e. the Coulomb waves in the +2/r field of the bare nucleus. This will be sufficient for the rigorous description of electron ejection in the process of non-sequential double ionization. Since there is no adiabatic approximation, there is not a memory problem (the first problem mentioned in the Introduction for applications of TDDFT) and TDDOT is expected to correctly reproduce the “helium knee” structure.