Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thioxanthone in apolar solvents: ultrafast internal conversion precedes fast intersystem crossing
Ramona
Mundt†
a,
Torben
Villnow†
a,
Christian Torres
Ziegenbein
a,
Peter
Gilch
*a,
Christel
Marian
b and
Vidisha
Rai-Constapel
b
aInstitut für Physikalische Chemie, Heinrich-Heine-Universität Düsseldorf, Universitätstr. 1, D-40225 Düsseldorf, Germany. E-mail: gilch@hhu.de
bInstitut für Theoretische Chemie und Computerchemie, Heinrich-Heine-Universität Düsseldorf, Universitätstr. 1, D-40225 Düsseldorf, Germany
First published on 12th February 2016
Abstract
The photophysics of thioxanthone dissolved in cyclohexane was studied by femtosecond fluorescence and transient absorption spectroscopy. From these experiments two time constants of ∼400 fs and ∼4 ps were retrieved. With the aid of quantum chemically computed spectral signatures and rate constants for intersystem crossing, the time constants were assigned to the underlying processes. Ultrafast internal conversion depletes the primarily excited 1ππ* state within ∼400 fs. The 1nπ* state populated thereby undergoes fast intersystem crossing (∼4 ps) yielding the lowest triplet state of 3ππ* character.
1 Introduction
Long-lived triplet states of organic molecules play a key role in the photoreactivity or photostability of organic molecules. Triplet states are, for instance, relevant in the photo-degradation of polymers1 or in the formation of some photo-lesions in DNA.2 Reactions initiated by triplet states are utilized in UV curing,3i.e., light-triggered polymerization, and photodynamic therapy.4The principles underlying the population of triplet states are thus of great importance for photochemistry. In organic molecules with singlet ground states, transitions from the singlet ground state to a triplet excited state are spin-forbidden, exhibiting small oscillator strengths f of the order of 10−9–10−5.5 Hence, triplet states are usually populated by radiationless transitions ensuing excitation to a higher-lying singlet state. Such transitions are termed intersystem crossing (ISC) and are mediated by spin–orbit coupling (SOC).6
The presence of nπ* excitations in organic carbonyl compounds leads to significant SOC and consequently large ISC rate constants. Thioxanthone (TX) is prototypical for such compounds. It has been a subject of numerous spectroscopic7–17 and quantum chemical studies18–21 which aimed at a quantitative understanding of the ISC processes. The geometry of TX being planar,19 a clear distinction between n- and π-orbitals is possible. This allows for a clear designation of the electronic character of the excited states for the application of El-Sayed's rules5,22,23 to ISC. The optical transition of TX, lowest in energy, peaks around 377 nm.18 Because of the favourable spectral location of this peak, all contributions to transient signals such as ground-state bleach (GSB), stimulated emission (SE) and excited-state absorption (ESA) can be conveniently recorded.
Fluorescence properties (lifetimes τfl10 and quantum yields ϕfl7) of TX are strongly solvent dependent. For TX in 2,2,2-trifluoroethanol, the yield ϕfl equals 0.46,7 whereas in cyclohexane (cH) a value as low as 2 × 10−4 was reported.15 Since the depletion of the singlet excited state by fluorescence or IC is expected to compete with ISC, this large variance in ϕfl should be mirrored in ISC rate constants. Such effects are commonly attributed to solvent-induced shifts of excitation energies.24
In our earlier studies on ISC in TX, we recorded spectroscopic signatures and rate parameters by time-resolved spectroscopy and compared those with predictions from quantum chemistry. With this approach, we could elucidate the peculiar photophysical behavior of TX in alcohols (methanol and 2,2,2-trifluoroethanol). In alcohols, the photo-excited TX simultaneously emits fluorescence and donates triplet energy.25 Experiments17 and computations21 ascribe this to an accidental (near) degeneracy of the primarily excited 1ππ* state and a 3nπ* one (Fig. 1). Because of the fast ISC and reverse ISC, the two states equilibrate within ∼5 ps. The equilibrium persists for ∼2 ns. Depletion of the two equilibrated states results in the population of the lowest triplet state of 3ππ* character. For the photophysical relaxation processes in alcohols, it is crucial that the 1nπ* state lies energetically above the aforementioned ones.
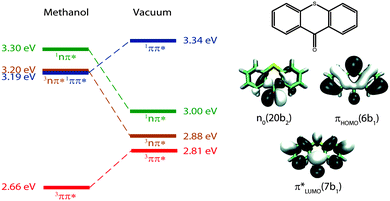 | ||
| Fig. 1 Adiabatic energies in eV of the four lowest excited states of TX in methanol and in vacuum as determined by quantum chemistry.20,21 Molecular orbitals involved predominately in the excitations are sketched on the right. Adapted from ref. 20. | ||
In vacuum and presumably also in apolar solvents, the 1nπ* state should be energetically accessible from the primarily excited 1ππ* state. This has been shown by the computations of Rai-Constapel et al.20 In the following, we investigate the kinetic consequences of this accessibility. Femtosecond (fs) transient absorption spectroscopy has already been applied to TX in cH.15 In that study, a time constant of ∼5 ps was observed and ascribed to the depletion of the primary 1ππ* excitation. Based on SE signatures in fs-transient absorption data as well as fs-fluorescence spectroscopy, we will show that in this study15 a process on the time scale of 100 fs was missed. With the aid of quantum chemistry, we will analyze and assign this transition to the proper deactivation channel.
2 Results
2.1 Steady-state spectroscopy
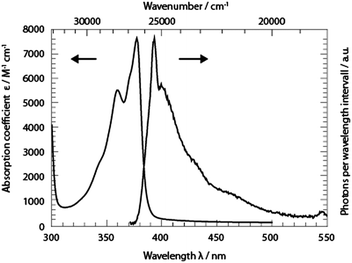
The absorption band of TX in cH, lowest in energy, peaks at 377 nm (26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 cm−1) (Fig. 2). A vibronic progression is partially resolved and its spacing is ∼1330 cm−1. This pattern recurs in the fluorescence emission spectrum which approximately obeys the mirror image rule.26 The fluorescence maximum lies at 393 nm (25
530 cm−1) (Fig. 2). A vibronic progression is partially resolved and its spacing is ∼1330 cm−1. This pattern recurs in the fluorescence emission spectrum which approximately obeys the mirror image rule.26 The fluorescence maximum lies at 393 nm (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 cm−1). With this spectral input, the 0–0 transition energy was estimated.26,27 Spectra corrected for the frequency dependence of the absorption and emission26 were normalized. From the crossing point of the two normalized spectra a 0–0 transition energy of 26
450 cm−1). With this spectral input, the 0–0 transition energy was estimated.26,27 Spectra corrected for the frequency dependence of the absorption and emission26 were normalized. From the crossing point of the two normalized spectra a 0–0 transition energy of 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 was determined. In relation to these corrected spectra, the Stokes shift amounts to 1090 cm−1. The fluorescence quantum yield ϕfl of TX in cH was determined relative to a reference (coumarin 102 in ethanol, 0.9528). The yield was determined to be 3 × 10−5 s−1. This is nearly an order of magnitude smaller than a value reported earlier.15 The lower value reported here will find support from the time-resolved fluorescence described below. An average fluorescence lifetime 〈τfl〉sb can be obtained from the value viaeqn (1):27
100 cm−1 was determined. In relation to these corrected spectra, the Stokes shift amounts to 1090 cm−1. The fluorescence quantum yield ϕfl of TX in cH was determined relative to a reference (coumarin 102 in ethanol, 0.9528). The yield was determined to be 3 × 10−5 s−1. This is nearly an order of magnitude smaller than a value reported earlier.15 The lower value reported here will find support from the time-resolved fluorescence described below. An average fluorescence lifetime 〈τfl〉sb can be obtained from the value viaeqn (1):27| ϕfl = 〈τfl〉sbkrad. | (1) |
Based on the Strickler–Berg analysis26,29 and the spectra in Fig. 2, the radiative rate constant krad was determined to be 4.4 × 107 s−1. This translates into a lifetime 〈τfl〉sb of 0.7 ps.
2.2 Transient fluorescence spectroscopy
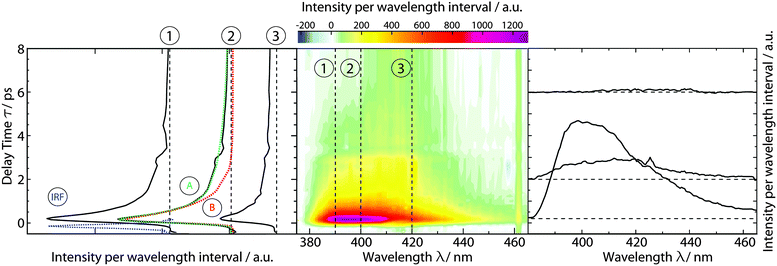
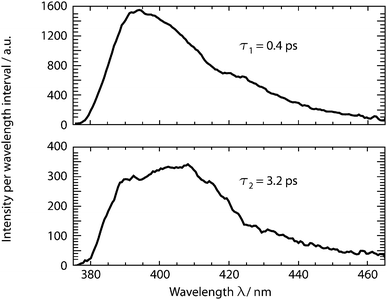
Time-resolved fluorescence spectroscopy gives more details on the decay of the primary excitation. In the experiment, the pump pulse was tuned to 370 nm and thereby in resonance with the first vibronic peak of the 1ππ* transition. The resulting fluorescence was time resolved relying on the optical Kerr effect. Here, care was taken to cover fluorescence signals close to the excitation wavelength. Fluorescence with wavelengths larger than 385 nm should be detectable using the set-up. In the spectral region of the steady-state fluorescence, a signal is seen to rise within the instrumental response time of 210 fs (Fig. 3). At its temporal maximum, the spectrum resembles the stationary one, except for the sharp peak at ∼395 nm. This peak is only observable in the stationary spectrum (cf.Fig. 2) due to a higher spectral resolution. Within a few 100 fs, the signal magnitude drops to roughly one-fifth of its initial value. The spectrum recorded thereafter is similar in spectral shape and position to the one at time zero. The peak at 395 nm observed in the earlier one is, however, now missing. The initial ultrafast decay is followed by one on the time scale of 1–10 ps. This becomes most apparent in the time traces plotted in Fig. 3. These traces also show that the amplitude of this slower process is much smaller than the one of the faster process.The dataset was analyzed relying on a global fitting procedure which yields time constants and decay-associated spectra (see DAS, Materials and methods). Analyzing the data with only one kinetic component results in a systematic deviation between the data and the fit (cf.Fig. 3, left). Visual inspection suggests that a bi-exponential trial function yields a much better agreement. Indeed, the total χ2 value30 is reduced by 82% upon adding a second exponential. With a third exponential the reduction with respect to a single exponential fit is only marginally larger (84%). Hence considering the principle of parsimony,31 it is reasonable to perform the fit procedure with two exponentials. The time constants obtained are τ1 = 0.42+0.02−0.06 ps and τ2 = 3.2+0.48−1.20 ps. The respective DAS ΔF1,2(λ) are both similar to the steady-state fluorescence (Fig. 4). In the second one, ΔF2(λ), the hint of a peak at 395 nm is missing. The similarity of the two DAS points to some type of delayed fluorescence. This will be further discussed below. The DAS ΔF1(λ) is larger in amplitude than the DAS ΔF2(λ) by a factor of ∼5. To ensure that the comparison is not affected by the differences in the shapes of the two spectra, the normalized spectral integrals were computed26
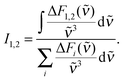 | (2) |
| 〈τfl〉 = I1τ1 + I2τ2. | (3) |
 | ||
| Fig. 4 DAS retrieved from the fs-transient fluorescence data given in Fig. 3. | ||
2.3 Transient absorption spectroscopy
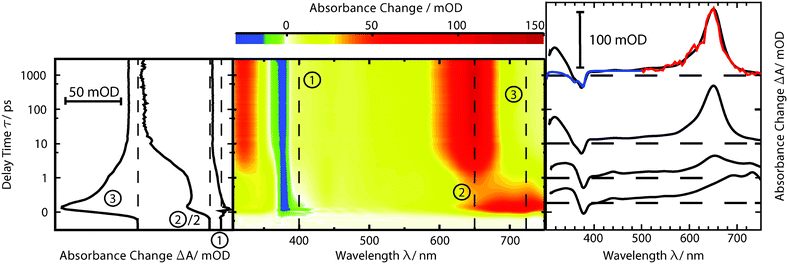
fs-transient absorption spectroscopy was used to identify the electronic states accessed after the depletion of the bright 1ππ* excitation (Fig. 5). TX in cH was excited with fs-pulses (∼100 fs duration, 370 nm) with similar properties as in the fs-fluorescence experiment. Absorption changes ΔA(λ) induced by those pulses were probed with a white-light continuum. At time zero, a strong ESA band peaking around 700 nm is present. The band exhibits some structure presumably due to a vibronic progression. Moving towards shorter wavelengths, weaker ESA contributions are observed. At about 400 nm, the signal turns negative. With reference to the steady-state spectra (cf.Fig. 2), this can be assigned to SE and GSB. For even shorter wavelengths, another ESA contribution is seen. Within a couple of 100 fs, the band around 700 nm and the SE decay. The time traces (3) and (1) in Fig. 5 highlight this. The decay leads to a difference spectrum which is weaker in magnitude throughout the covered range. It is dominated by a flat ESA contribution except for the GSB at 380 nm and a peak at 650 nm. This peak grows in amplitude on the time scale of 10 ps (cf. time trace (2)) and remains constant thereafter. Concomitant with this increase, an ESA band around 330 nm also increases. The spectra recorded from ∼10 ps to 3 ns after excitation are identical within the noise level and resemble the ones already reported for the lowest TX triplet state in cH.9,32 In a nanosecond laser flash experiment on TX in cH, a transient with a lifetime τ3 of 64 μs is observed in a nitrogen purged solution. The presence of oxygen (1 atm) reduces the lifetime to 1 μs. This value agrees with a published one.32 The spectrum ΔA3(λ) associated with the microsecond decay superimposes with the late spectra of the fs-experiment (Fig. 5). Hence, it may safely be stated that the processes populating the lowest triplet state of 3ππ* character are terminated after ∼10 ps.As for the fluorescence data, a global fitting procedure was used to obtain quantitative information on the kinetics. From the above description of the fluorescence and absorption data, it follows that at least three kinetic components—including the offset—are required to describe the kinetics. Indeed, with three components, a satisfactory description of the data is possible. The resulting time constants are τ1 = 0.36 ± 0.05 ps and τ2 = 3.6 ± 0.36 ps. The values are in accordance with those obtained by fluorescence. In the corresponding DAS ΔA1,2,∞(λ) (Fig. 6), the qualitative features described above are clearly discernible. The spectrum ΔA1(λ) features strong positive contributions around 700 nm which represent the rapid initial decay in that region. The negative signature in the range 390–500 nm overlaps with the fluorescence spectrum (cf.Fig. 2) and can therefore be assigned to SE (see also fs-fluorescence data described above). The dominant characteristic of the spectrum ΔA2(λ) is a strong negative band peaking at 650 nm. Since this band is the inverse of the corresponding one in the offset spectrum ΔA∞(λ), it can safely be assigned to the increase of the carrier of this offset spectrum—the 3ππ* state. Also a negative signature around 320 nm in the spectrum ΔA2(λ) finds a positive counterpart in the DAS ΔA∞(λ). Two positive bands at 360 and 720 nm represent signal reductions due to the decay of the precursor of the 3ππ* state. Finally, a weak negative signature in the SE region is observed (see also fs-fluorescence data described above). The offset spectrum ΔA∞(λ) is identical to the spectra recorded for late (≳10 ps) delay times. This spectral signature has already been assigned to the 3ππ* state.
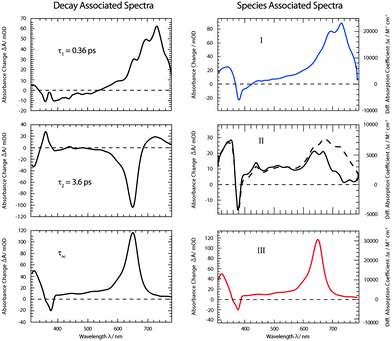 | ||
| Fig. 6 DAS (left) and SAS (right) derived from the dataset depicted in Fig. 5. For the SAS the experimental absorbance changes (left axis) were converted into difference absorption coefficients Δε (right axis). For species II SAS relating to two models (i (dashed line) and ii (solid line)) were computed. | ||
From the offset spectrum and measurements on a reference compound, the quantum yield ϕisc can be derived. A description of the approach is given in ref. 17. It amounts to 0.95 ± 0.05. This is somewhat larger than the reported value of 0.85 determined by thermal lens spectroscopy.33 The analysis of species-associated spectra (SAS) below is in favor of the larger value.
For a comparison of the experimental spectra with the computed ones, the DAS described above were transformed into SAS34,35 (see Materials and methods). This transformation requires a kinetic model. Transformations were performed relying on two models. Computations for both models rely on the same fit data (time constants and DAS). It is, thus, not possible to make a statistical statement on which model is more reliable.
In the first model (i), simple consecutive kinetics
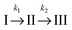 | (4) |
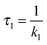 | (5) |
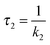 | (6) |
In the second model (ii), the reverse process of the first transition (rate constant k−1) is considered as well.
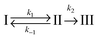 | (7) |
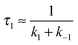 | (8) |
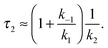 | (9) |
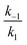 was set to
was set to 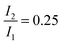 (see below). The SAS of species I and III are identical for either model. The spectrum of species I is further given by the sum of the three DAS. The spectrum of species III is identical to the DAS ΔA∞(λ). By trimming the inverted ground-state spectrum into the SAS for species I and III (the procedure is illustrated in Fig. 5), the respective magnitudes of GSB can be determined. The absorption changes ΔA at 377 nm amount to −29 (I), −24 (II), and −27 mOD (III). These values underline that little or no ground state recovery has occurred and lend support to the above finding of a quantum yield ϕisc equal to ∼1. The GSB contribution is also used to compute difference absorption coefficients ΔεI,II,III(λ) for the three species. To this end, the GSB contribution is scaled to match the absorption coefficient of TX in its ground state (cf.Fig. 2).
(see below). The SAS of species I and III are identical for either model. The spectrum of species I is further given by the sum of the three DAS. The spectrum of species III is identical to the DAS ΔA∞(λ). By trimming the inverted ground-state spectrum into the SAS for species I and III (the procedure is illustrated in Fig. 5), the respective magnitudes of GSB can be determined. The absorption changes ΔA at 377 nm amount to −29 (I), −24 (II), and −27 mOD (III). These values underline that little or no ground state recovery has occurred and lend support to the above finding of a quantum yield ϕisc equal to ∼1. The GSB contribution is also used to compute difference absorption coefficients ΔεI,II,III(λ) for the three species. To this end, the GSB contribution is scaled to match the absorption coefficient of TX in its ground state (cf.Fig. 2).
2.4 Quantum-chemical computations
For the assignment of spectroscopic signatures and kinetic processes, quantum-chemical computations were performed. These yielded energy profiles of electronic states along the potential energy paths of the involved electronic states, their transient absorption spectra, and rate constants for ISC processes. The computations built on previous results by the Marian group.19–21 Properties have already been computed for vacuum conditions as well as polar and protic solvents. Here, these results are augmented by computations in the apolar solvent cH.The computations confirm the notion made in the Introduction that four excited states could be accessible. For these states, vertical and adiabatic energies as well as energies for linear interpolation were calculated. The starting points for these interpolations were the respective adiabatic minima. These energy profiles are depicted in Fig. 7. They resemble the ones for TX in vacuum (cf. Fig. 7 in ref. 20). Increasing polarity of the medium surrounding thioxanthone affects the states with nπ* character to a larger extent than those with ππ* character. For cH, the blue shift undergone by the nπ* states is about 0.08 eV which is four times larger than the energy stabilization experienced by the 1,3ππ* states relevant in the photophysics. This shift causes the energy gaps between the 1ππ* minimum and the 1,3nπ* minima to be lowered. According to the computation, the adiabatic excitation energy of the 1ππ* state amounts to 3.32 eV. As described above, a 0–0 energy of 3.24 eV can be derived from the experimental spectra depicted in Fig. 2. Approximating the adiabatic transition energy with the 0–0 one, this is an excellent agreement. A second point of the profiles which can be compared with experimental data is the minimum of the 3ππ* state. According to the computation, this minimum lies at 2.79 eV. For TX in CH2Cl2, a value of 2.75 eV was deduced from phosphorescence spectroscopy.36 The agreement for the two reference points lends credibility to the complete set of energy profiles. The reproduction of the accidental degeneracy of 1ππ* and 3nπ* states for TX in protic solvents17,21 by the computations further demonstrates the power of the method to predict nπ* excitations. These excitation energies are difficult to access directly in an experiment. The profiles (Fig. 7) show that, starting from the 1ππ* state, both nπ* excitations (singlet and triplet) are accessible in downhill processes. Furthermore, the nπ* energy profiles cross the one of the 1ππ* state close to its minimum. This implies small or vanishing barriers for transitions to these states. So, according to these profiles, the 1ππ* state might deplete via an IC process populating the 1nπ* or an ISC process yielding the 3nπ* one.
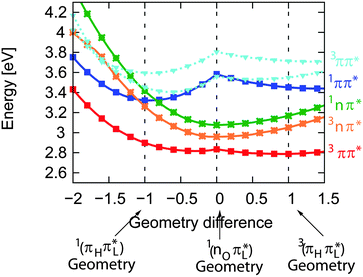 | ||
| Fig. 7 DFT/MRCI energy profiles along the linearly interpolated path between the equilibrium geometries of the 1ππ* (−1), 1,3nπ* (0) and 3ππ* (1) states. The path was extrapolated on both sides. | ||
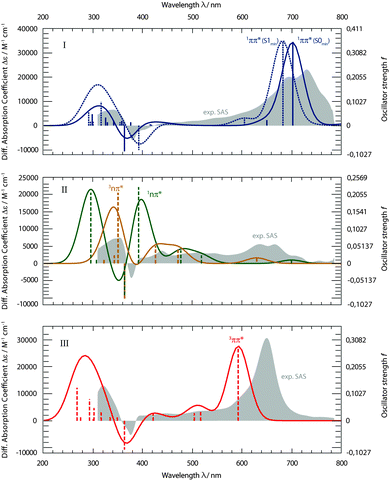
With the aim to distinguish between those two pathways, the transient spectra for these states were computed and compared with the experimental ones (Fig. 8). Starting from respective states and geometries, vertical excitation energies and oscillator strengths f were computed. Up to 50 states were included in the calculations for both singlet and triplet manifolds to cover the spectral range of the experiment. For the sake of comparison with the experimental SAS, stick spectra were convoluted with Gaussians of 50 nm FWHM. The convoluted spectra were transformed to obtain absorption coefficients ε as a function of the wavelength λ, using the definition of the oscillator strength f (see e.g.ref. 26). Thus, the absolute band heights may be compared with the experimental absorption coefficients.
The computed spectra for the 1ππ* state (Fig. 8, I) reproduce the experimental one well. Two spectra were computed. For the first one, the equilibrium geometry of the ground state S0 was used. This corresponds to transitions starting from the Franck–Condon (FC) point. The second spectrum refers to the equilibrium geometry of the 1ππ* state. Since the lifetime of the 1ππ* excitation is short with respect to vibrational relaxation37,38 and dielectric relaxation39 is of minor importance in cH, the FC computation seems more to the point. The computation reproduces the strong ESA band around 700 nm. In the experiment, this band shows a vibronic progression which the present computational method cannot yield. The computation also predicts the window of weak absorption between 600 and 400 nm. ESA and GSB as well as the positive signature at 340 nm are also recovered by the computation. The computation, thus, agrees with assigning the SAS I to the 1ππ* state.
The experimental SAS II features flat ESA contributions in the visible range (Fig. 8, II). Maximal absorption coefficients ε are of the order of 5000 M−1 cm−1. In the SAS I and III, values up to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1 are measured. Computations for both nπ* states result in such a pattern. However, for wavelengths shorter than 400 nm, the computations predict strong transitions (oscillator strengths f of ∼0.2) for either state. In the experiment, a much weaker one is seen. Apart from this deviation, computations for the 1nπ* as well as 3nπ* state concur with the rather indistinct experimental pattern. Furthermore, both computed nπ* spectra feature weak absorptions around 700 nm. This is in favor of kinetic model II, as for model I the absorption strength is expected to be higher there (see Fig. 6).
000 M−1 cm−1 are measured. Computations for both nπ* states result in such a pattern. However, for wavelengths shorter than 400 nm, the computations predict strong transitions (oscillator strengths f of ∼0.2) for either state. In the experiment, a much weaker one is seen. Apart from this deviation, computations for the 1nπ* as well as 3nπ* state concur with the rather indistinct experimental pattern. Furthermore, both computed nπ* spectra feature weak absorptions around 700 nm. This is in favor of kinetic model II, as for model I the absorption strength is expected to be higher there (see Fig. 6).
The experimental SAS III features a very distinct and strong band at 650 nm (Fig. 8, III). The computation places this band at a somewhat shorter wavelength of 600 nm and nearly matches the experimental absorption coefficient ε of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 cm−1. The slight discrepancy concerning the wavelength is within the computational error limit. The flat signature in between 600 and 400 nm, the GSB and the positive signature around 320 nm are very well reproduced.
000 M−1 cm−1. The slight discrepancy concerning the wavelength is within the computational error limit. The flat signature in between 600 and 400 nm, the GSB and the positive signature around 320 nm are very well reproduced.
The computed spectra are supportive of the intermediacy of an nπ* excitation in the decay of photo-excited TX in cH. They are not conclusive concerning the multiplicity of this state. In this respect, computations of ISC rate constants will be helpful. The methodology for the evaluation of the rate constants is identical to the one described in ref. 21. In the computations, thermal excitations are taken into account. The temperature was set to 298 K. The two El-Sayed allowed (1ππ* → 3nπ* and 1nπ* → 3ππ*) as well as El-Sayed forbidden (1ππ* → 3ππ* and 1nπ* → 3nπ*) transitions were considered. The values obtained (see Table 1) are of the order of 1010–1011 s−1 for the El-Sayed allowed processes and an order of magnitude smaller for the forbidden ones. The latter are non-zero due to vibronic effects which are known to be rather important in the photophysics of organic molecules.40,41 The rate constant kisc for the depletion of the 1ππ* excitation due to ISC (1ππ* → 3nπ*) translates into a time constant of 30 ps. This is nearly two orders of magnitude longer than the experimental decay time of τ1 ≈ 400 fs. Considering vibrational excitation does not mitigate this discrepancy. To model this effect, rate constants kisc for increased temperature (29 ps at 323 K) were computed. The rate constant kisc is hardly affected. This is in line with the fact that the energy profile of the 3nπ* state crosses that of the 1ππ* close to its minimum. The computed rate constant kisc is, thus, too small to explain the ultrafast 1ππ* decay. This also applies for the El-Sayed forbidden transitions (1ππ* → 3ππ*). We therefore assign this time constant to an IC process yielding the 1nπ* state. Fig. 7 shows that this process should be very fast, since the involved singlet states cross each other very close to the minimum of the bright state. The computed rate constant kisc for the ensuing ISC process (1nπ* → 3ππ*) is very supportive of this assignment. The value corresponds to a time constant of 6 ps which compares favorably with the experimental value of τ2 ≈ 4 ps.
| Transition | Rate constant kisc (s−1) at 298 K |
|---|---|
| 1ππ* → 3nπ* | 3.0 × 1010 |
| 1nπ* → 3ππ* | 1.8 × 1011 |
| 1ππ* → 3ππ* | ≈109 |
| 1nπ* → 3nπ* | ≈1010 |
3 Discussion
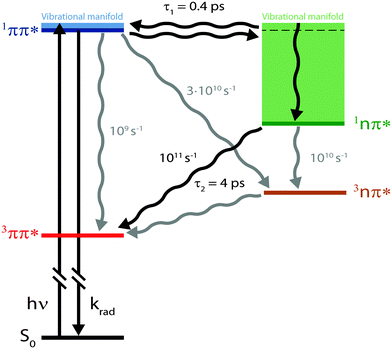
fs-fluorescence and transient absorption experiments were carried out on the photophysics of TX in cH. They give clear indications that starting in the 1ππ* state, two transitions with time constants of τ1 ≈ 400 fs and τ2 ≈ 4 ps result in the population of its lowest triplet state of 3ππ* character. In an earlier fs-study,15 only one time constant of ∼5 ps was reported. The fact that the shorter one was missed might be due to the fact that the SE region was not covered. In this region and in time-resolved fluorescence, this time constant is clearly seen.Computed spectral signatures and rate constants allow us to characterize the two processes and to devise the following kinetic scheme (Fig. 9). The initial 1ππ* excitation features a lifetime of τ1 ≈ 400 fs. The computed rate constant kisc for the depletion of this state by ISC translates into a lifetime of 30 ps. The efficiency of the channel is, thus, expected to be of the order of 0.01 and cannot explain the overall triplet yield ϕisc close to unity. The ultrafast decay of the 1ππ* state proceeds via IC and yields the 1nπ* state. This state in turn undergoes ISC, yielding the lowest triplet state, the 3ππ* state. The measured time constant τ2 ≈ 4 ps for this El-Sayed allowed transition is in excellent agreement with the quantum chemical computation (6 ps). The fast formation of this state is in line with its high quantum yield. A rate constant of about 1010 s−1 has been computed for the vibronic ISC from 1nπ* → 3nπ*, which is an order of magnitude smaller than the direct ISC to the 3ππ* state.
What remains to be explained is the bi-phasic decay of the fluorescence. We have assigned the time constant τ1 to the transition from the bright 1ππ* state to the dark 1nπ* one. Still, the second time constant τ2 attributed to the decay of this dark state shows up in the fs-fluorescence data, albeit with a small amplitude. The similarity of the spectra associated with the two time constants (cf.Fig. 4) suggests that the fluorescence indeed originates from one state. E-type delayed fluorescence22 can render this possible. The crucial parameter in E-type delayed fluorescence is the energy gap ΔE between the bright and the dark state. Equating this gap with the adiabatic energy difference ΔEad obtained in the computations (cf.Fig. 7) leads to a value of −0.24 eV (negative implies that the dark state is below the bright one). With this an equilibrium constant K can be estimated,
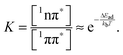 | (10) |
Equating the thermal energy kbT with its room temperature value yields a constant K of ∼104. Thus, in equilibrium only one out of 104 ought to populate the bright state. The fluorescence amplitude I1 “lost” during the initial process with the time constant τ1 should populate the dark state; therefore [1nπ*] ∝ I1. The remaining amplitude I2 should be proportional to [1ππ*] and the equilibrium constant should be given by K = I1/I2 = 4. Obviously, the experimental value is much smaller than the above prediction for K. A somewhat better agreement is obtained with an expression considering entropy and zero point energies,
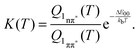 | (11) |
Obviously, when applying the above expressions one assumes thermal equilibrium. As already stated above, the vibrational relaxation occurs on somewhat longer time scales (10–20 ps)43–45 than characteristic times encountered here. Thus, to some part the vibrational energy generated by photo-excitation above the 0–0 origin of the 1ππ* state, as well as the vibrational energy generated in the IC process, is still in the molecule. We used two approaches to obtain crude estimates of the consequences. In the first approach, we assume complete intramolecular vibration redistribution (IVR)46 but no transfer of vibrational energy. Based on this assumption an effective temperature Teff can be computed. To this end, the vibrational contribution to the internal energy E1nπ* of the 1nπ* state was computed according to (see ref. 42)
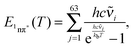 | (12) |
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/char_e0e1.gif) i are the wavenumbers of the 63 normal modes of TX. These were obtained by quantum chemistry. Equating this internal energy with the difference in 0–0 energy ΔE00 plus the thermal energy at RT yields an effective temperature Teff of 375 K. Inserting this temperature into eqn (11) yields a constant K of around 30. Working with the photoenergy minus the 0–0 energy of the 1nπ* state (0.24 eV) yields an effective temperature Teff of 389 K and a similar K value of 27 results. The value is still much larger than the experimental ones. However, the value is of course very sensitive to the computed energy difference. Changing this difference by less than 0.1 eV, an agreement with the experiment can be reached.
i are the wavenumbers of the 63 normal modes of TX. These were obtained by quantum chemistry. Equating this internal energy with the difference in 0–0 energy ΔE00 plus the thermal energy at RT yields an effective temperature Teff of 375 K. Inserting this temperature into eqn (11) yields a constant K of around 30. Working with the photoenergy minus the 0–0 energy of the 1nπ* state (0.24 eV) yields an effective temperature Teff of 389 K and a similar K value of 27 results. The value is still much larger than the experimental ones. However, the value is of course very sensitive to the computed energy difference. Changing this difference by less than 0.1 eV, an agreement with the experiment can be reached.
Presumably, the more realistic assumption is that IVR is not completed. In the limiting case of no IVR, only vibrational states of the 1nπ* state isoenergetic with the initial ones of the 1ππ* state (cf.Fig. 9) need to be considered. Further assuming that all vibrational states within an energy band roughly equal to the thermal energy are accessible, the ratio 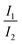 should depend on the number of vibrational states. For the 1ππ* state this number may be approximated by the partition function Q1ππ*. For room temperature it amounts to 4000 and refers to an energy width of ∼kbT ≙ 200 cm−1. The respective number of vibrational states in the 1nπ* state and the same width was determined to be ∼13
should depend on the number of vibrational states. For the 1ππ* state this number may be approximated by the partition function Q1ππ*. For room temperature it amounts to 4000 and refers to an energy width of ∼kbT ≙ 200 cm−1. The respective number of vibrational states in the 1nπ* state and the same width was determined to be ∼13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. For this computation the step function width 2η was set to 800 cm−1 (see Materials and methods). The ratio of ∼3 fits with the experimental one. The exact numerical values aside, the bi-phasic fluorescence behavior observed gives clear evidence that the accepting state in the IC process must be energetically close by—just as the computations predict.
000. For this computation the step function width 2η was set to 800 cm−1 (see Materials and methods). The ratio of ∼3 fits with the experimental one. The exact numerical values aside, the bi-phasic fluorescence behavior observed gives clear evidence that the accepting state in the IC process must be energetically close by—just as the computations predict.
4 Conclusions
With the aid of femtosecond spectroscopy and quantum chemical calculations, the photophysics of TX in cH was elucidated. The primary bright photo-excitation decays via an ultrafast IC process (400 fs), ensued by fast ISC (4 ps). The calculated ISC time constant (6 ps) is very close to the experimental one. The computations also concur with the experiment concerning the energetic vicinity (∼0.1 eV) of the two states involved in the IC process.Concerning solvent dependent photophysics, our results stress that quantitative and qualitative effects ought to be considered. Solvents may alter energy gaps and thereby the rate constants of non-radiative processes. In addition to such quantitative effects, qualitative ones may occur because different states may be energetically accessible. As a consequence, the nature of the initial non-radiative process may change. For TX in alcohols, the initial process is a fast ISC transition. An IC one cannot occur since the pertinent 1nπ* state is out of energetic reach. In apolar solvents, that state is accessible and the primary process is an ultrafast IC transition. Notably, in both solvents a bi-phasic fluorescence decay is observed, albeit on very different time scales and for very different reasons.
5 Materials and methods
5.1 Samples
TX (≥97%) was obtained from Sigma-Aldrich and cyclohexane (cH) (99.5%, HPLC grade) from VWR. Both were used as supplied without further purification. For fs-measurements sample solutions with a concentration of ∼1 mM were prepared. This corresponded to optical densities at an excitation wavelength of ∼0.5–1. All measurements were performed at room temperature (21 °C). In all time resolved experiments sample solutions were flown through optical cells. The overall amount of sample (>10−4 mol TX) was large enough to ensure that contributions of potential photoproducts could be neglected. In addition the flow rate in the sample cell was large enough that the solution in the excitation volume was exchanged for each laser shot.5.2 Steady-state measurements
The steady-state absorption spectrum was obtained using a two-beam absorption spectrometer (Perkin Elmer, Lambda 19) and a 1 cm quartz cuvette (Hellma Analytics). The steady-state fluorescence spectrum was recorded using a Kerr gate set-up with parallel polarizers, i.e. in the open state. The sample solution was guided through a flow cell (Hellma, suprasil, pathlength 1 mm). The same flow system was used for time resolved measurements. The fluorescence spectrum was corrected for the offset and spectral sensitivity of the instrument.5.3 Transient fluorescence measurements
Fluorescence was time resolved using a set-up based on the optical Kerr effect. The instrument is an upgrade of the design described by Schmidt et al.47 As it contains two major modifications, a complete description of the set-up ensues.The output of a Ti:Sa laser amplifier system (Coherent Libra, 1 kHz, 100 fs, 800 nm) was split and fed into a NOPA (Light Conversion, TOPAS white) and a home-built OPA.47,48 The NOPA output (740 nm, <50 fs) was frequency doubled to obtain pump pulses at 370 nm. They had an energy of 0.9 J and a focal diameter of 120 μm at the sample position. The focusing lens (f = 300 mm) and all other lenses were made of fused silica. The fluorescence light was collected and focused by identical cassegrainian objectives (Davin 5002-000, NA 0.5, focal length 13.41 mm). To increase the transmission in the UV-region, UV-enhanced wire-grid polarizers (ProFlux UBB01A, 0.7 mm thickness, range 300–2800 nm) were used to extinguish the fluorescence. As the first major modification of the set-up, they were positioned in the collimated beam path instead of directly enclosing the Kerr medium KM (1.2 mm fused silica) as described by Schmidt et al.47 It was found that this configuration increases the extinction of the polarizers by a factor of two. The gate pulse, which is the output of the OPA (1230 nm, 70 fs, 11 J), was also focused onto the KM (f = 350 nm, 140 μm) where it induces the Kerr effect and opens the gate. The transmitted fluorescence was filtered (Asahi ZUL0385) to suppress scattered excitation light and focused (focal diameter 170 μm) into the detection unit (Andor Shamrock 303 spectrograph, grating 150 l mm−1, Andor iDus 420bu detector cooled down to −70 °C) using a triplet apochromat (Lens-Optics, fused silica/CaF2/fused silica, NA 0.114). This setup features a spectral resolution of ∼5 nm and a time resolution of 210 fs.
The second major modification was the implementation of two reference diodes. To record intensity fluctuations of both the pump and the gate, the beams were guided to integrating photodiodes (Hamamatsu S1226-8BQ (pump) and Thorlabs FDG50 (gate)) after transmitting the sample (pump) or the Kerr medium (gate). They were connected to a digital integrator (WieserLabs, WL-IDP4A). With the recorded intensity traces the following correction procedure is possible.
The instrument provides raw fluorescence spectra Fr(λ,td) depending on the detection wavelength λ and delay time td. Background signals contribute to these spectra which need to be subtracted. To this end, pump only Bp(λ) and gate only Bg(λ) background spectra were recorded. The pump only spectrum Bp(λ) is dominated by fluorescence leaking through the crossed polarizers.49 It scales linearly with the pump intensity P. This intensity is recorded using a photodiode for the pump only condition (P0) as well as for every delay time (P(td)). Third harmonic generation in the Kerr medium50 causes the overwhelming contribution to the gate only spectrum Bg(λ). Its signal grows with the third power of the gate intensity. This intensity was also recorded using a photodiode for the gate only condition (G0) and for each delay time (G(td)). The correction for these background contributions is given by the term in square brackets in eqn (13).
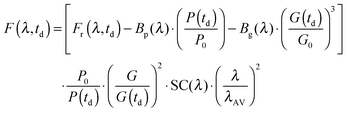 | (13) |
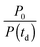 for the pump intensity and the term
for the pump intensity and the term 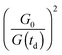 for the gate intensity. Note that the gate efficiency is quadratic in the gate intensity.49 The spectral sensitivity of the complete instrument is corrected by multiplying with a correction function SC(λ). Multiplying by λ2 compensates the wavelength dependence of the gate efficiency.51 Finally the data were corrected for the time zero dispersion,47 with the values taken from ref. 52 and 53.
for the gate intensity. Note that the gate efficiency is quadratic in the gate intensity.49 The spectral sensitivity of the complete instrument is corrected by multiplying with a correction function SC(λ). Multiplying by λ2 compensates the wavelength dependence of the gate efficiency.51 Finally the data were corrected for the time zero dispersion,47 with the values taken from ref. 52 and 53.
To record one raw spectrum, 20 spectra (0.5 s integration time) were averaged. Between −1 and 2 ps the delay time was varied linearly in 60 steps. Up to 20 ps equidistant steps on a logarithmic scale were set. 60 scans were averaged. Datasets for the neat solvent and TX solutions were recorded. The solvent contribution was subtracted after proper scaling which accounts for the inner filter effect of the solute.
5.4 Femtosecond transient absorption
The femtosecond transient absorption set-up used is described in depth elsewhere.17,54,55 Here the pertinent parameters are listed. The energy of the pump pulses at 370 nm was ∼1 μJ. At the sample the diameter of the pump beam amounted to ∼160 μm. The white light probe featured pulse energies of some tens of nanojoules and a beam diameter of ∼40 μm. The relative polarization of pump and probe light was set to the magic angle. The instrumental response function (IRF) had a temporal width of ∼160 fs (FWHM). For every setting of the delay line, signal contributions of 4000 laser pulses (1000 pump and probe on) were averaged. By operating with two choppers stray light contributions could be corrected.54,56 For the measurement a total of 4 scans were averaged. Each scan consisted of 164 steps, 75 being equidistant from −2 to 1 ps and 89 on a logarithmic scale up to 3.3 ns. Datasets for the neat solvent and TX solutions were recorded. The solvent contribution was subtracted after proper scaling which accounts for the inner filter effect of the solute.5.5 Nanosecond flash photolysis
Nanosecond transient absorption spectra were acquired using an LSK 6.0 spectrometer (Applied Photophysics) with a cross-beam configuration.57 Frequency tripled (355 nm) pulses from a Nd:YAG laser (Innolas, Spitlight 600, 1 Hz repetition rate) served as the excitation. Their energy was attenuated to 2 mJ and the duration was 7 ns (FWHM). A pulsed xenon lamp (L2273, Hamamatsu) provided the probe light. After passing the sample the probe light was monochromatized using a grating spectrometer (bandwidth 4.7 nm) and detected using a photomultiplier (R5108, Hamamatsu). Its signal was digitized using an oscilloscope (Agilent Infiniium) and transferred to a computer. Time traces were recorded for detection wavelengths ranging from 500 nm to 855 nm in 5 nm steps. For each measured wavelength 10 successive laser shots were averaged. The sample concentration was of the order of ∼80 M to ensure a uniform excitation along the cuvette path (sealed 111-QS, Hellma Analytics). Samples purged with nitrogen as well as oxygen were investigated. The ambient temperature of 20 °C was controlled using a thermostat.5.6 Data analysis
The measurements of both the time-resolved fluorescence and the transient absorption were analyzed using a global fitting routine. The signal S(λ,td) as a function of detection wavelength λ and delay time td is expressed by decay-associated spectra (DAS) Si(λ) and the associated time constants τi as given in the below trial function:58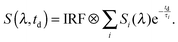 | (14) |
5.7 Quantum chemistry
The ground- and excited-state geometries have been optimized at the density functional theory (DFT) and time-dependent DFT (TDDFT) level with the B3-LYP functional using the Turbomole program package.59 The TZVP basis set has been used to describe the C, H and O centers and the TZVPP basis describes the S center in accordance with the previous theoretical studies carried out on thioxanthone by the Marian group.19–21 A cyclohexane (dielectric constant, ε = 2) environment was hereby treated as a continuum using the conductor-like screening model (COSMO) approach.60,61 Vertical electronic excitation energies, dipole (transition) moments and oscillator strengths were obtained from subsequent single-point calculations using the combined density functional theory/multi-reference configuration interaction (DFT/MRCI) method of Grimme and Waletzke.62 The linearly interpolated paths (LIPs) for the qualitative discussion have been determined between the minima of relevant electronic states using the program package DISTORT.63 At each of the geometries obtained along the path, a single point DFT/MRCI calculation was carried out in order to determine the electronic state energy profiles.The vibrational modes, required for the computation of the rate constants, have been obtained using SNF program package.64 The rate constants have been determined using the time dependent version of the VIBES program developed in the laboratory of the Marian group.65 This method also allows for the temperature dependency in the rate constant calculation. For the discussion of the photophysics, the vibrational density of states of the 1nπ* state around the minimum of the bright singlet state was also determined. To this end, the time independent branch of the VIBES program was made use of.63 In this ansatz the δ-function ensuring energy conservation is replaced by a step function of finite width 2η centered at the minimum of the initial state. The density of states between the involved states is estimated using the analytical expression given by Haarhoff.66 This number increases exponentially with the number of degrees of freedom available and the energy difference between the two states. One may, however, reduce the computational burden by exploiting the symmetry of the molecule and taking into consideration only those states which would give a strong coupling. The effect of temperature may be simulated by allowing the vibrational modes to be excited by more than one quantum. Hence, the number of states found within this interval depends upon how large a value is assigned to η, the number of quanta with which each vibrational mode is excited and how many active modes are considered in the calculation. In the present calculations we allowed excitation by 10 quanta and all 63 modes were included.
Acknowledgements
Financial support by the Deutsche Forschungsgemeinschaft (projects GI349/5-1 and MA 1051/12-1) is gratefully acknowledged.References
- J. Rabek, Photodegradation of Polymers: Physical Characteristics and Applications, Springer, Berlin Heidelberg, 2012 Search PubMed.
- M. C. Cuquerella, V. Lhiaubet-Vallet, F. Bosca and M. A. Miranda, Chem. Sci., 2011, 2, 1219–1232 RSC.
- J. Fouassier and J. Rabek, Radiation Curing in Polymer Science and Technology: Practical Aspects and Applications, Springer, 1993 Search PubMed.
- D. E. J. G. J. Dolmans, D. Fukumura and R. K. Jain, Nat. Rev. Cancer, 2003, 3, 380–387 CrossRef CAS PubMed.
- N. Turro, V. Ramamurthy and J. Scaiano, Modern Molecular Photochemistry of Organic Molecules, University Sciences Books, Sausalito, California, 2010 Search PubMed.
- C. M. Marian, Rev. Comput. Chem., 2001, 17, 99–204 CAS.
- J. C. Dalton and F. C. Montgomery, J. Am. Chem. Soc., 1974, 96, 6230–6232 CrossRef CAS.
- T. Lai and E. Lim, Chem. Phys. Lett., 1980, 73, 244–248 CrossRef CAS.
- K. A. Abdullah and T. J. Kemp, J. Photochem., 1986, 32, 49–57 CrossRef CAS.
- D. Burget and P. Jacques, J. Lumin., 1992, 54, 177–181 CrossRef CAS.
- F. Morlet-Savary, C. Ley, P. Jacques, F. Wieder and J. P. Fouassier, J. Photochem. Photobiol., A, 1999, 126, 7–14 CrossRef CAS.
- C. Ley, F. Morlet-Savary, P. Jacques and J. P. Fouassier, Chem. Phys., 2000, 255, 335–346 CrossRef CAS.
- E. Krystkowiak, A. Maciejewski and J. Kubicki, ChemPhysChem, 2006, 7, 597–606 CrossRef CAS PubMed.
- G. C. Ferreira, C. C. Schmitt and M. G. Neumann, J. Braz. Chem. Soc., 2006, 17, 905–909 CrossRef CAS.
- G. Angulo, J. Grilj, E. Vauthey, L. Serrano-Andrés, Ò. Rubio-Pons and P. Jacques, ChemPhysChem, 2010, 11, 480–488 CrossRef CAS PubMed.
- R. Pandey and S. Umapathy, J. Phys. Chem. A, 2012, 116, 8484–8489 CrossRef CAS PubMed.
- T. Villnow, G. Ryseck, V. Rai-Constapel, C. M. Marian and P. Gilch, J. Phys. Chem. A, 2014, 11696–11707 CrossRef CAS PubMed.
- Ò. Rubio-Pons, L. Serrano-Andrés, D. Burget and P. Jacques, J. Photochem. Photobiol., A, 2006, 179, 298–304 CrossRef.
- V. Rai-Constapel, M. Kleinschmidt, S. Salzmann, L. Serrano-Andrés and C. M. Marian, Phys. Chem. Chem. Phys., 2010, 12, 9320–9327 RSC.
- V. Rai-Constapel, S. Salzmann and C. M. Marian, J. Phys. Chem. A, 2011, 115, 8589–8596 CrossRef CAS PubMed.
- V. Rai-Constapel, T. Villnow, G. Ryseck, P. Gilch and C. M. Marian, J. Phys. Chem. A, 2014, 11708–11717 CrossRef CAS PubMed.
- P. Klán and J. Wirz, Photochemistry of organic compounds: From concepts to practice, John Wiley & Sons, 2009 Search PubMed.
- M. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- J. Cavaleri, K. Prater and R. Bowman, Chem. Phys. Lett., 1996, 259, 495–502 CrossRef CAS.
- D. Wöll, S. Laimgruber, M. Galetskaya, J. Smirnova, W. Pfleiderer, B. Heinz, P. Gilch and U. E. Steiner, J. Am. Chem. Soc., 2007, 129, 12148–12158 CrossRef PubMed.
- W. W. Parson, Modern Optical Spectroscopy, With Exercises and Examples from Biophysics and Biochemistry, Student Edition, Springer, Verlag 2009 Search PubMed.
- J. Lakowicz, Principles of Fluorescence Spectroscopy, 3rd edn, Springer, New York, 2006 Search PubMed.
- G. Jones, W. Jackson and C.-Y. Choi, J. Phys. Chem., 1985, 89, 294–300 CrossRef CAS.
- S. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822 CrossRef CAS.
- J. C. Earnshaw, Eur. J. Phys., 1990, 11, 338 CrossRef.
- A. A. Istratov and O. F. Vyvenko, Rev. Sci. Instrum., 1999, 70, 1233–1257 CrossRef CAS.
- J. F. Rodrigues, F. de Assis da Silva and J. C. Netto-Ferreira, J. Braz. Chem. Soc., 2010, 21, 960–965 CrossRef CAS.
- X. Allonas, C. Ley, C. Bibaut, P. Jacques and J. Fouassier, Chem. Phys. Lett., 2000, 322, 483–490 CrossRef CAS.
- J. E. Loefroth, J. Phys. Chem., 1986, 90, 1160–1168 CrossRef CAS.
- I. H. van Stokkum, D. S. Larsen and R. van Grondelle, Biochim. Biophys. Acta, Bioenerg., 2004, 1657, 82–104 CrossRef CAS PubMed.
- K. Meier and H. Zweifel, J. Photochem., 1986, 35, 353–366 CrossRef CAS.
- T. Elsaesser and W. Kaiser, Annu. Rev. Phys. Chem., 1991, 42, 83–107 CrossRef CAS.
- S. Kovalenko, S. Schanz, H. Hennig and N. Ernsting, J. Chem. Phys., 2001, 115, 3256–3273 CrossRef CAS.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337 CrossRef CAS.
- A. Rodriguez-Serrano, V. Rai-Constapel, M. C. Daza, M. Doerr and C. M. Marian, Photochem. Photobiol. Sci., 2012, 11, 1860–1867 CAS.
- C. M. Marian, M. Etinski and V. Rai-Constapel, J. Phys. Chem. A, 2014, 118, 6985–6990 CrossRef CAS PubMed.
- P. Atkins and J. De Paula, Atkins' Physical Chemistry, Oxford University Press, Oxford, 2010 Search PubMed.
- M. Lee and C. B. Harris, J. Am. Chem. Soc., 1989, 111, 8963–8965 CrossRef CAS.
- D. L. Phillips, J.-M. Rodier and A. B. Myers, Chem. Phys., 1993, 175, 1–12 CrossRef CAS.
- S. H. Pullen, N. A. Anderson, L. A. Walker II and R. J. Sension, J. Chem. Phys., 1998, 108, 556–563 CrossRef CAS.
- Ultrafast Infrared and Raman Spectroscopy, ed. M. Fayer, Marcel Dekker, Inc., New York, 2001 Search PubMed.
- B. Schmidt, S. Laimgruber, W. Zinth and P. Gilch, Appl. Phys. B: Lasers Opt., 2003, 76, 809–814 CrossRef CAS.
- G. Cerullo and S. De Silvestri, Rev. Sci. Instrum., 2003, 74, 1–18 CrossRef CAS.
- S. Arzhantsev and M. Maroncelli, Appl. Spectrosc., 2005, 59, 206–220 CrossRef CAS PubMed.
- T. Y. F. Tsang, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 4116–4125 CrossRef CAS.
- J. Takeda, K. Nakajima, S. Kurita, S. Tomimoto, S. Saito and T. Suemoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 10083–10087 CrossRef CAS.
- I. H. Malitson, J. Opt. Soc. Am., 1965, 55, 1205–1208 CrossRef CAS.
- J. Rheims, J. Köser and T. Wriedt, Meas. Sci. Technol., 1997, 8, 601 CrossRef CAS.
- S. Laimgruber, H. Schachenmayr, B. Schmidt, W. Zinth and P. Gilch, Appl. Phys. B: Lasers Opt., 2006, 85, 557–564 CrossRef CAS.
- S. Bay, T. Villnow, G. Ryseck, V. Rai-Constapel, P. Gilch and T. J. J. Müller, ChemPlusChem, 2013, 78(2), 137–141 CrossRef CAS.
- S. Laimgruber, T. Schmierer, P. Gilch, K. Kiewisch and J. Neugebauer, Phys. Chem. Chem. Phys., 2008, 10, 3872–3881 RSC.
- S. Fröbel, L. Buschhaus, T. Villnow, O. Weingart and P. Gilch, Phys. Chem. Chem. Phys., 2015, 17, 376–386 RSC.
- H. Satzger and W. Zinth, Chem. Phys., 2003, 295, 287–295 CrossRef CAS.
- TURBOMOLE V6.3 2011, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from E-mail: http://www.turbomole.com.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Schäfer, A. Klamt, D. Sattel, J. C. Lohrenz and F. Eckert, Phys. Chem. Chem. Phys., 2000, 2, 2187–2193 RSC.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- J. Tatchen, PhD thesis, Heinrich Heine Universität Düsseldorf, 2006.
- J. Neugebauer, M. Reiher, C. Kind and B. A. Hess, J. Comput. Chem., 2002, 23, 895–910 CrossRef CAS PubMed.
- M. Etinski, V. Rai-Constapel and C. M. Marian, J. Chem. Phys., 2014, 140, 114104 CrossRef PubMed.
- P. Haarhoff, Mol. Phys., 1964, 7, 101–117 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2016 |