The magnetocaloric effect with critical behavior of a periodic Anderson-like organic polymer
Received
12th October 2015
, Accepted 18th November 2015
First published on 19th November 2015
Abstract
We study the magnetocaloric effect and the critical behavior of a periodic Anderson-like organic polymer using Green's function theory, in which the localized f orbitals hybridize with the conduction orbitals at even sites. The field-induced metal–insulator transitions with the magnetic Grüneisen parameter showing |Γh| ∼ T−1 power-law critical behaviour are revealed, which provides a new thermodynamic means for probing quantum phase transitions. It is found that the competition of up-spin and down-spin hole excitations is responsible for the double peak structure of magnetic entropy change (−ΔS) for the dominant Kondo coupling case, implying a double magnetic cooling process via demagnetization, which follows a power law dependence of the magnetic field h: −ΔS ∼ hn. The local exponent n tends to 1 and 2 below and above TC, while has a minimum of 0.648 at TC, which is in accordance with the experimental observation of perovskite manganites Pr0.55Sr0.45MnO3 and Nd0.55Sr0.45MnO3 (J. Y. Fan et al., Appl. Phys. Lett., 2011, 98, 072508; Europhys. Lett., 2015, 112, 17005) corresponding to the conventional ferromagnets within the mean field theory −ΔS ∼ h2/3. At TC, the −ΔS ∼ h curves with a convex curvature superpose each other for small V values, which are separated by the large V case, distinguishing the RKKY interaction and Kondo coupling explicitly. Furthermore, the critical scaling law n(TC) = 1 + (β − 1)/(β + γ) = 1 + 1/δ(1 − 1/β) is related to the critical exponents (β, γ, and δ) extracted from the Arrott–Noakes equation of state and the Kouvel–Fisher method, which fulfill the Widom scaling relation δ = 1 + γβ−1, indicating the self-consistency and reliability of the obtained results. In addition, based on the scaling hypothesis through checking the scaling analysis of magnetization, the M–T–h curves collapse into two independent universal branches below and above TC.
1. Introduction
Recently the magnetocaloric effect (MCE) has been intensively studied in a great number of magnetic materials due to their potential application in magnetic refrigeration,1–11 which was proposed as an environmentally friendly and energy-efficient cooling technique. In a magnetic cooling cycle, the magnetic material is a crucial part of system design, because heat is pumped in and out through the material and cooling performance is dependent on its ability to generate and reverse heat. One important issue related to magnetic refrigeration is to understand how the MCE evolves with the magnetic field and temperature, which is helpful for the deeper understanding of magnetic phase transitions.12,13 Usually, the MCE was used as a powerful tool for the investigation of magnetic phase transitions accompanying spin structure transformations. In particular, a class of magnetic materials is governed by pronounced quantum many-body effects, in which the MCE has been used to study the quantum criticality arising from quantum fluctuations. A map of the entropy landscape can identify various quantum phases.14 Moreover, the magnetic Grüneisen parameter Γh, related to the cooling rate, displays a sign change close to the quantum critical point (QCP) signaling an accumulation of entropy, which was regarded as an important tool to identify and classify a QCP by its divergence near a field-induced quantum phase transition (QPT), giving a very direct way to extract the critical exponents of the QCP.13,15 Meanwhile, the underlying QPT manifests itself at finite temperatures in an unusual sensitivity of thermodynamics under different fields. Additionally, the MCE is an intrinsic property for all magnetic materials wherein the entropy changes with the magnetic field. Accordingly, the isothermal entropy change (−ΔS) plays a crucial role in the performance of magnetic cooling. In contrast to inorganic magnets, organic magnets are drawing attention in light of their lightness, flexibility and unbreakability.6–11,16,17 To pursue large −ΔS, recently, many explorations focused on constructing various clusters or coordination polymers through selecting suitable metal ions and ligands. Some compounds were obtained such as [{Gd(OAc)3(H2O)2}2]·4H2O, Gd(OH)CO3, [Na2Mn3(SO4)3(μ3-OH)2(μ2-OH2)2]n and so on.8–10 It is worth noting that in the triangular [Mn3] cluster-based ferrimagnet,10 the competition of the ferromagnetic and antiferromagnetic interactions plays a crucial role in enhancing the MCE, which obeys the Lieb–Mattis theory.18
In addition, it has been shown that the field dependence of magnetocaloric parameters was associated with the intricate nature of magnetic phase transition and parametrized by critical exponents governing the transitions.19,23 The analysis of the critical behavior can also provide significant information about the thermodynamic observations near the transition temperature TC. For a continuous ferromagnetic transition, the critical behavior near TC is characterized by a set of critical exponents β, γ, and δ.19,20,22,23 The Arrott plot is the most straightforward approach in the form of M2versus h/M with parallel lines signaling the mean-field values β = 0.5 and γ = 1.0. To further refine the critical exponents, the isotherms are extrapolated to the M2 = 0 and h/M = 0 axes to obtain the spontaneous magnetization Ms(T) and χ0(T), respectively, a power law fitting which will yield the values of β and γ.24 By using the critical exponents as a starting point, we can obtain a modified Arrott plot M1/βversus (h/M)1/γ with iteration procedures to restore parallel straight isotherm lines and get correct critical exponents, until β and γ converge.
Based on the Lieb–Mattis theory, Ovchinnikov25 firstly proposed a synthesis of alternate hydrocarbon with the high-spin ground state, as schematically illustrated in Fig. 1(a). The spin gap and magnon excitations were investigated by employing the Hubbard model.26,27 Likewise, it was developed as a periodic Anderson-like model (PALM).28,29 The f electrons are strongly localized, while the conduction electrons form a conduction sea distributing throughout the main zigzag chain, which presents a Fermi liquid coupling with localized spins, wherein two interactions compete for dominance. One interaction is the Kondo coupling for the localized spins screened by the conduction sea; the other is the superexchange, i.e., the indirect Ruderman–Kittel–Kasuya–Yosida (RKKY) interaction between the neighboring localized spins mediated by the conduction sea.30,31 For the symmetrical case, the Kondo coupling JK ∼ V2/U gives rise to the fact that the behavior of the system is controlled by two parameters: the hybridization V between the conduction and localized f orbitals, and the Hubbard repulsion U on the localized f orbital.32 Thus, the competition between Kondo coupling and RKKY interaction is attributed to the consequence of interplay between Coulomb interaction and hybridization. For this PALM, the ground state, ferrimagnetic and metal-insulator phase transitions were studied in detail.28,29 However, in a magnetic field, the competition between Kondo coupling and RKKY interaction responsible for enhancing the MCE will shed light on the critical behavior of the strong correlation electron system. Simultaneously, a systematic study of scaling analysis of the temperature and field dependence of magnetization will be carried out. A double peak structure in the magnetic entropy change manifests a double magnetic cooling process. Thus, it is quite necessary to carry out a deeper investigation on the MCE and critical behavior for this PALM. In the forthcoming section, the model Hamiltonian and many-body Green's function method are presented. In Section 3, the field-induced phase diagram associated with quantum criticality is explored; the MCE and critical scaling behavior are also analyzed and discussed. Finally, we draw a conclusion in Section 4.
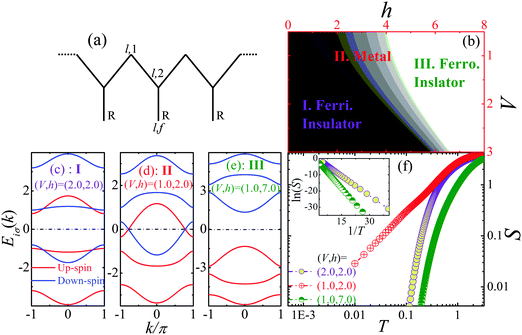 |
| | Fig. 1 (a) Schematic illustration of a quasi-one-dimensional periodic Anderson-like organic polymer chain; (b) the h–V phase diagram with (I) ferrimagnetic insulator, (II) metal and (III) ferromagnetic insulator phases, which are demonstrated by the energy bands in (c), (d) and (e), respectively; (f) the temperature dependence of entropy S, ln(S)–1/T curve is plotted in the inset. | |
2. Model and method
The organic polymer illustrated in Fig. 1(a) is described as a quasi-one-dimensional PALM, wherein the conduction electrons with uncorrelated orbitals reside in the main zigzag chain forming a conduction sea, while a correlated localized f orbital locates at the side radical R. In an external magnetic field, it is governed by the following Hamiltonian,| | 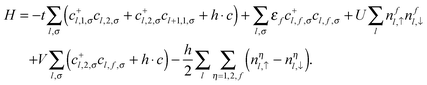 | (1) |
Herein, t denotes the hopping integral between the nearest-neighboring conduction orbitals, and c+l,η,σ(cl,η,σ), nηl,σ = c+l,η,σcl,η,σ(η = 1, 2) are the creation (annihilation) and number operators with spin σ = ↑, ↓ for conduction electrons. Nevertheless, c+l,f,σ(cl,f,σ) denotes the creation (annihilation) operator of localized f electrons in the side radical R with bare energy εf and Coulomb repulsion U. In addition, V is the hybridization strength of the localized f electron with the conduction orbital (l,2), and h = gμBB is the reduced magnetic field (Zeeman energy).
Now, the Green's function method33 is employed to decouple the Hamiltonian (1), which is defined as
| | | Gσij(t1 − t2) = 〈〈ci,σ(t1);c+j,σ(t2)〉〉= −iθ(t1 − t2)〈ci,σc+j,σ + c+j,σci,σ〉, | (2) |
where the subscripts
i and
j number the lattice sites. After the time Fourier transformation, it is put into the equation of motion,
| | |
ω〈〈ci,σ;c+j,σ〉〉 = 〈[ci,σ,c+j,σ]+〉 + 〈〈[ci,σ,H];c+j,σ〉〉.
| (3) |
By performing the equation of motion analogous to
eqn (3) for the high-order Green's function 〈〈[
ci,σ,
H];
c+j,σ〉〉, a higher-order Green's function will appear on the right side, resulting in an infinite set of coupled equations. In terms of Wick's theorem, we adopt the decoupling scheme for the four-operator Green's functions,
34| | | 〈〈A+BC;D+〉〉 ≈ 〈A+B〉〈〈C;D+〉〉 − 〈A+C〉〈〈B;D+〉〉. | (4) |
Meanwhile, it is important to introduce the Green's functions for each spin channel (up-spin and down-spin), respectively,
i.e., the Green's functions are diagonal in spin space
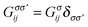
. For further Fourier transformation into
k-space, the Green's function can be expressed as
| | 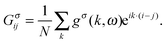 | (5) |
The integral of the wavevector k extends over the first Brillouin zone. So, the momentum space Green's function gσ(k,ω) can be described as a function of wavevector k and the elementary excitation spectrum ω = ω(k).
According to the standard spectral theorem, the correlation function of the product of the electron operators can be calculated through the corresponding Green's function gσ(k, w)
| | 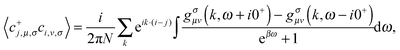 | (6) |
where
β = 1/
kBT,
kB is the Boltzman constant, and
T is the absolute temperature.
The spin density (sublattice magnetization) at one site is defined as
| | 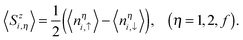 | (7) |
Then the average magnetization of the unit cell
M and magnetic susceptibility
χ are expressed as
| | 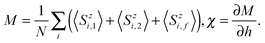 | (8) |
Likewise, the specific heat can be attained as
| | 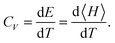 | (9) |
Accordingly, we can get the entropy,
| | 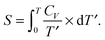 | (10) |
The magnetic entropy change is obtained as
1,2| | 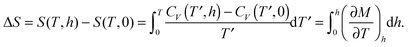 | (11) |
Likewise, the magnetic Grüneisen parameter is expressed as
12,13| | 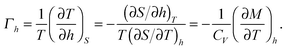 | (12) |
Thereby, the above equations can be solved self-consistently. In calculations, an initial state, composed of a set of electron numbers and spin density of the f orbital, is put into the equations to produce resultant values. The iteration goes on until convergence is reached.
3. Results and discussion
In what follows, we set the hopping integral t = 1.0, and all parameters are in units of it. We consider the symmetrical case U + 2εf = 0 without charge fluctuations. As an external magnetic field is turned on, it may undergo insulator–metal and magnetic phase transitions. Fig. 1(b) presents the field-induced ground state phase diagram, wherein the ferrimagnetic insulator, metal and ferromagnetic insulator phases are unveiled. As V ascends, the metallic region becomes narrower, which is ascribed to the enhancement of Kondo coupling. In order to identify the electric and magnetic states, the energy bands are plotted in Fig. 1(c)–(e). The Fermi level is located at EF = 0. At low fields, Fig. 1(c) shows that two up-spin and one down-spin bands are occupied with an energy gap for large V, indicating that the ground state lies in the ferrimagnetic insulating state because of the dominant Kondo coupling. As V decreases, the insulating behavior becomes weaker and it undergoes a transition into the metallic state, as shown in Fig. 1(d), wherein one up-spin and one down-spin bands transverse the Fermi level, as a result of the enhanced RKKY interaction. However, as the field is very large, all the up-spin bands are pulled down into the Fermi sea with an energy gap opened up (see Fig. 1(e)), resulting in the spin polarized ferromagnetic insulating state. Furthermore, the gapless and gapped low-lying excitations are also identified by the temperature dependence of entropy S, as shown in Fig. 1(f). One can find that the entropy asymptote presents activated behaviour because of the existence of the finite energy gap between the ground and excited states for insulating phases, which is clearly manifested by the ln(S)–1/T curve at low temperature in the inset, wherein ln(S) behaves linearly with 1/T, giving rise to S ∝ e−Δ/kBT, the slope of which reflects the magnitude of the energy gap (−Δ). However, for the metallic phase, the entropy behaves T-linearly at ultra-low temperature, implying a gapless ground state.
In order to present the competition between Kondo coupling and RKKY interaction responsible for the ferrimagnetic nature, the spin density (sublattice magnetization) for V = 1.0 and 2.0 is performed and plotted in Fig. 2(a). One can find that for weak hybridization V, the localized f spin mainly contributes to the ferrimagnetism with relatively high transition temperature TC, because the RKKY interaction is dominant. Nevertheless, as V ascends, the transition temperature TC decreases with the ferrimagnetism mainly coming from the orbital (l,1). It is ascribed to the more and more dominant Kondo screening between orbitals (l,2) and (l,f). However, in a magnetic field, it presents a 1/3 magnetization plateau with two transition fields (see Fig. 2(b)), suggesting a ferrimagnetic ground state and metal–insulator transitions. Furthermore, we anticipate that the QPTs will be reflected by the magnetocaloric properties at finite temperatures. From Fig. 2(c), one can clearly see that the quantum criticality can be identified explicitly for the entropy contour plots with a sufficiently small value, and the QPTs are demonstrated by the dips of isoentropes. The accumulation of the entropy close to the transition fields indicates that the system is maximally undetermined which ground state to choose. Besides, the field dependence of the Grüneisen ratio Γh proportional to the magnetic cooling rate for different temperatures is plotted in Fig. 2(d), which presents the very sharp and pronounced positive peaks and negative valleys around the transition points at ultra-low temperature. Making contact with the argumentation of Garst,13 the Grüneisen ratio Γh displays a characteristic divergent behaviour close to the transition point and changes the sign as the field crosses it. However, with temperature ascending, all features become broader with the peaks reduced, and last will be washed out attributed to the strong thermal fluctuations that drive the system to the excited state without QPTs.
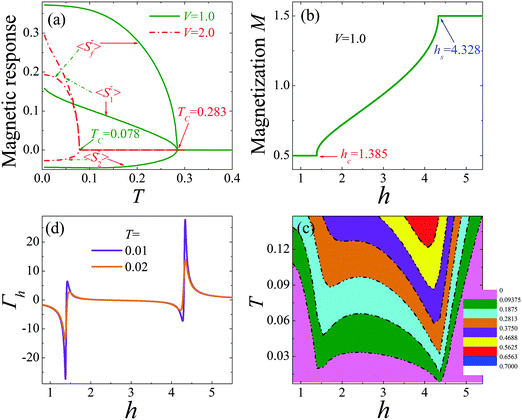 |
| | Fig. 2 (a) The temperature dependence of sublattice magnetization; (b) the field dependence of magnetization for V = 1.0; (c) the isoentropes for V = 1.0; (d) the field dependence of the Grüneisen parameter Γh at different temperatures. | |
At different phases, the thermodynamics behave diversely, especially at the QCPs. Fig. 3(a) shows the magnetization against T1/2 under different fields. One can find that the entrance into the gapless metal state is marked with a minimum or a maximum (see the arrow) in the magnetization, which provides a simple way to feature the phase boundary of the gapless metal phase at finite temperature well. It is notable that the magnetization develops a T1/2 behavior (linear relation of the M–T1/2 curve) as h approaches hc. When h is close to hs, we obtain a characteristic decrease M ∼ −T1/2. Besides, the temperature dependence of the entropy at critical fields is presented in Fig. 3(b). It behaves T1/2-linearly, different from that in the gapped and gapless phases. More generally, the results emphasize that the Grüneisen ratio Γh provides a novel thermodynamic means for probing QPTs. Fig. 3(c) shows that with decreasing temperature, Γh changes its sign in the gapless phase. Nevertheless, its absolute value increases gradually in the gapped state for h < hc and h > hs. It is worth noting that when h approaches hc or hs, Γh diverges rapidly upon cooling down to zero temperature, which provides a new way to explore QCPs. The double-logarithmic scale is plotted in Fig. 3(d) to demonstrate the occurring |Γh| ∼ T−1 power-law critical behaviour, which has been observed in the spin ladder system experimentally.15
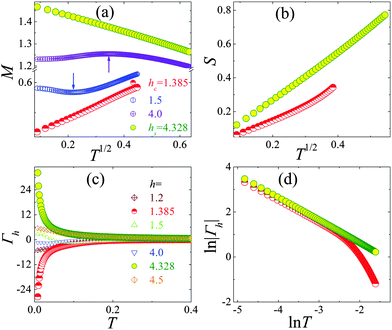 |
| | Fig. 3 (a) The magnetization M and (b) entropy S as a function of T1/2 under different fields; (c) the temperature dependence of the Grüneisen parameter Γh under different fields; (d) ln|Γh| versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T at the critical fields. T at the critical fields. | |
At finite temperature, the system will manifest the MCE under different magnetic fields. In Fig. 4(a) and (b), the magnetic entropy change against temperature is plotted for V = 1.0 and 2.0, respectively. Recalling Fig. 1(d), as the field extends hc but is nearby, the intermediate down-spin and up-spin energy bands cross the Fermi level slightly, making the excitations with minus energies become the hole type.29 Thus, the magnetic entropy change −ΔS is closely related to the competition of the down-spin and up-spin hole excitations. For h < hc, the magnetic field can open up the energy gap, and then close it. First, the energy gap is washed out by thermal fluctuations at low temperature, after that, the up-spin hole excitation crossover into the down-spin one occurs, giving rise to only a sharp peak in −ΔS at TC with the broadened temperature region. Nevertheless, it is worth noting that the maximum of −ΔS is larger for the larger V value due to the larger hole density of states resulting from the dispersion relation of energy bands, which indicates that strong Kondo coupling is beneficial for low temperature cooling at low fields. As h exceeds hc, the up-spin band above EF is pulled down into the Fermi sea partially, while the down-spin one below EF is pushed up partially. At this time, after a few up-spin holes are occupied, the down-spin ones will be excited, giving rise to a shoulder in −ΔS at high temperature. However, as the field gets across (hc + hs)/2, −ΔS presents a double-peak structure for strong Kondo coupling (V = 2.0) (see Fig. 4(b)), implying the double magnetic refrigeration process at moderate fields. In this case, the density of states of down-spin holes is larger than that of the up-spin ones near the Fermi level, yielding more down-spin holes excited at low temperature firstly, which contributes to the first peak of −ΔS. After that, the up-spin holes will be excited, responsible for the high temperature peak. While for the strong RKKY interaction (V = 1.0) case, the strong dispersion relation of the down-spin band (see Fig. 1(d)) yields less down-spin hole excitations at low temperature, thus resulting in the first peak of −ΔS that collapses into a shoulder (see Fig. 4(a)). For the field high enough (h > hs), the low temperature peak vanishes gradually and the high temperature peak becomes higher with a wider temperature region, because the energy gap becomes larger and only the up-spin holes will be excited.
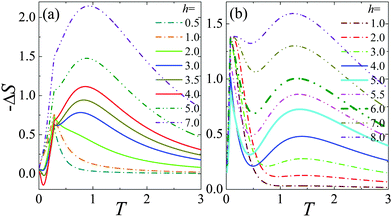 |
| | Fig. 4 The temperature dependence of the magnetic entropy change (−ΔS) for (a) V = 1.0 and (b) V = 2.0. | |
Furthermore, it should be pointed out that −ΔS follows a power-law dependence of h: −ΔS ∼ hn (see the insets in Fig. 5(a) and (c)) with n being the local exponent, which can be calculated via the relation: 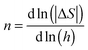 .21 Different from the antiferromagnets, wherein n is ∼2 for the entire temperature range at low fields,21 one can find that the local exponent n is strongly dependent on temperature as shown in Fig. 5(a) and (c), demonstrated by the linear relation of ln(|ΔS|) versus ln(h) with different slopes for different temperatures. At low temperatures well below TC, n tends to 1 for a ferrimagnetic system, while tends to 2 at temperatures above TC as a consequence of the Curie–Weiss law (see the insets in Fig. 5(b) and (d)). This scaling behavior is similar to that occurred in ferromagnetic materials.19,35 In addition, n has a minimum value at the transition temperature TC, which is clearly illustrated in Fig. 5(b) and (d).
.21 Different from the antiferromagnets, wherein n is ∼2 for the entire temperature range at low fields,21 one can find that the local exponent n is strongly dependent on temperature as shown in Fig. 5(a) and (c), demonstrated by the linear relation of ln(|ΔS|) versus ln(h) with different slopes for different temperatures. At low temperatures well below TC, n tends to 1 for a ferrimagnetic system, while tends to 2 at temperatures above TC as a consequence of the Curie–Weiss law (see the insets in Fig. 5(b) and (d)). This scaling behavior is similar to that occurred in ferromagnetic materials.19,35 In addition, n has a minimum value at the transition temperature TC, which is clearly illustrated in Fig. 5(b) and (d).
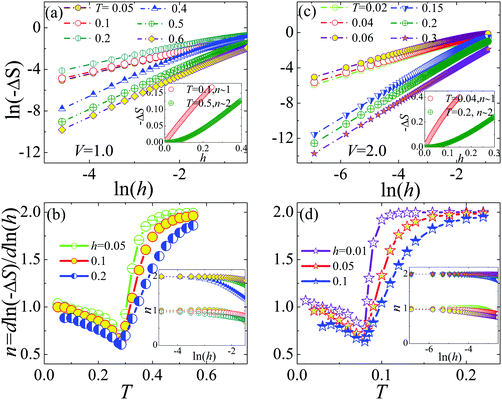 |
| | Fig. 5 ln(−ΔS) versus ln(h) at different temperatures for (a) V = 1.0 and (b) V = 2.0; the insets are the field dependencies of −ΔS for the temperature below and above TC; The corresponding local exponent n = d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(−ΔS)/d ln(−ΔS)/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(h) as a function of temperature in (c) and (d), respectively; the insets show the local exponent n against ln(h) for the temperature below and above TC, respectively. ln(h) as a function of temperature in (c) and (d), respectively; the insets show the local exponent n against ln(h) for the temperature below and above TC, respectively. | |
In order to explore the minimum of local exponent n and distinguish the domination of RKKY interaction and Kondo coupling, we plot the field dependence of −ΔS for different V values at TC in Fig. 6(a). It is clearly seen that the −ΔS–h curve presents a convex curvature, indicating n < 1, which is unlike the case below or above TC. Interestingly, for small V values, the curves superpose each other, separated with the large V case, which provides a new thermodynamic means to distinguish RKKY interaction and Kondo coupling in strong correlation electron systems. Fig. 6(b) presents a nearly parallel linear relation of the ln(−ΔS)–ln(h) curve at TC with n = 0.648 for different V values, which is basically consistent with the experimental observation of perovskite manganites Pr0.55Sr0.45MnO3 and Nd0.55Sr0.45MnO3 corresponding to the conventional ferromagnets taking the mean field value 2/3.22,23,36,37 The linear fits in Fig. 6(c) demonstrate the validity of the relationship −ΔS ∝ h0.648 at around TC that characterizes a second order phase transition, which is close to −ΔS ∝ h2/3 for conventional ferromagnets obeying the mean field theory.36,37
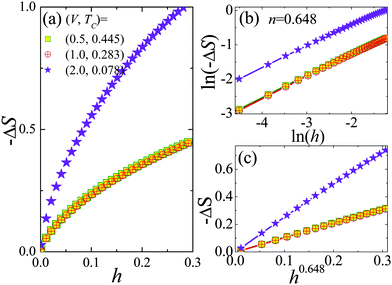 |
| | Fig. 6 (a) The field dependence of −ΔS for T = TC with different V values; (b) double-logarithm of −ΔS − h curves for T = TC; (c) the linear behaviour of −ΔS − h0.648. | |
Of particular interest is the scaling law related to the critical exponent β, γ, and δ, which obey the following relation at T = TC:19,20,22,23
| | | n(TC) = 1 + (β − 1)/(β + γ) = 1 + 1/δ(1 − 1/β). | (13) |
Herein, the critical exponents (
β,
γ, and
δ) are determined by a detailed scaling analysis based on the Arrott–Noakes equation of state,
38 which are defined for the spontaneous magnetization
Ms(
T), inverse initial susceptibility
χ0−1, and critical isotherm (
M(
h)) at
TC with the reduced temperature
t = (
T −
TC)/
TC as follows:
20,24,38–41| | | χ0−1(T) ∝ |t|γT > TC, | (15) |
Thus, we can know that the critical behavior is determined by the critical exponents, but not by the critical temperature. For
V = 1.0, from the temperature dependence of
Ms and
χ0−1, we can get
β = 0.473 and
γ = 0.99 with
TC = 0.283, as shown in
Fig. 7(a) and (b), respectively. Accurately, the critical exponent
β and
γ can be determined by the Kouvel–Fisher (KF) method:
42| | 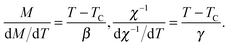 | (17) |
Accordingly, the temperature dependence of
M/(d
M/d
T) and
χ−1/(d
χ−1/d
T) will yield straight lines with slopes 1/
β and 1/
γ, as plotted in the insets in
Fig. 7(a) and (b), respectively. It gives us the critical exponents
β = 0.482 and
γ = 0.976 at
TC by the KF method, which are close to those deduced from the Arrott–Noakes equation of state. Besides, according to
eqn (16), we plot the double-logarithm of the
h–
M curve in
Fig. 7(c), which shows a straight line with slope
δ at
TC. Thus, we can obtain
δ = 3.041. According to the statistic theory, these critical exponents should fulfill the Widom scaling relation:
43 As a result,
δ = 3.093 and
δ = 3.025 are obtained from the Arrott–Noakes equation of state and the KF method, which are close to those obtained from the critical isotherm analysis. It is demonstrated that these critical exponents are reliable and unambiguous for their self-consistency. Furthermore, from
eqn (13), we can get
n(
TC) = 0.64 and
n(
TC) = 0.645 from the Arrott–Noakes and KF methods, respectively, which approach the MCE measurement. For
V = 2.0, one can get (
β,
γ) = (0.479, 1.001) and (
β,
γ) = (0.481, 0.995) with
TC = 0.078 from the Arrott–Noakes and KF methods (see
Fig. 7(d) and (e) associated with the insets), respectively. According to the Widom scaling relation, we obtain
δ = 3.089 and
δ = 3.068, which agree with the critical isotherm measurement
δ = 2.997, as shown in
Fig. 7(f). Meanwhile, the local exponent
n(
TC) = 0.648 is obtained from both the Arrott–Noakes and KF methods, which coincides with the MCE value. Note that the critical exponents we obtained are close to the mean field prediction (
n(
TC) = 2/3,
β = 0.5,
γ = 1.0 and
δ = 3.0).
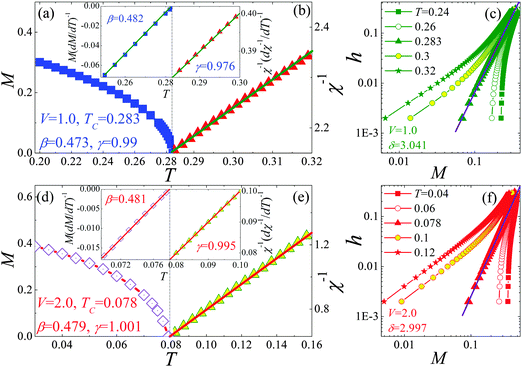 |
| | Fig. 7 For V = 1.0, the temperature dependence of (a) magnetization M and (b) inverse initial susceptibility χ−1; For V = 2.0 the temperature dependence of (d) magnetization M and (e) inverse initial susceptibility χ−1; the insets are the KF plots; the lg–lg scale of h–M curves for (c) V = 1.0 and (f) V = 2.0. | |
These critical exponents can also be further confirmed by the scaling equation. First, we turn our attention to the Modified Arrott plots, plotting M1/βversus (h/M)1/γ with the critical exponents obtained by the KF method, as shown in Fig. 8(a) and (b). The lines are parallel and spaced linearly in temperature. Notably, the M1/βversus (h/M)1/γ line goes through the origin at TC. In addition, in the asymptotic critical region, the critical exponents can also be confirmed by the magnetic scaling equation:39–41
| | | M(h,t) = tβf±(h/tβ+γ), | (19) |
where
f± are regular functions denoted as
f+ for
T >
TC and
f− for
T <
TC. It indicates that
M|
t|
−βversus h|
t|
−(β+γ) forms two universal curves for
T >
TC and
T <
TC, respectively. Based on the scaling equation, the lg–lg scales of isothermal magnetization around the critical temperatures are plotted in
Fig. 8(c) and (d) for
V = 1.0 and 2.0, wherein the data points fall on two independent branches. The last confirmation of validity of the obtained critical exponents would come from checking the scaling of the magnetization curves, which takes the form,
44,45| | 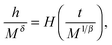 | (20) |
with
H(
x) being a scaling function. Therefore, based on the above equation, if the critical exponent values are appropriate, the plot of
M/
h1/δversus t/
h1/(β+γ) should correspond to a universal curve with all data points collapsing. Herein, we still adopt the values obtained from the KF method, and the scaled data are plotted in the insets of
Fig. 8(c) and (d). It presents an excellent overlap of data points, indicating that the obtained critical exponent values are in good agreement with the scaling hypothesis. On the whole, the obedience of the scaling equation over the entire range of normalized variables confirms the reliability of the obtained critical exponents.
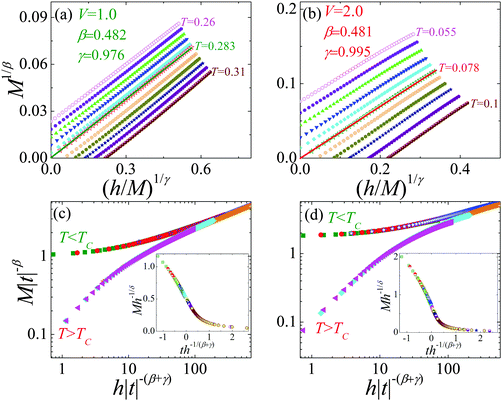 |
| | Fig. 8 The isotherms M1/βvs. (h/M)1/γ for (a) V = 1.0 and (b) V = 2.0; scaling plots at around TC for (c) V = 1.0 and (d) V = 2.0; the insets are the normalized isotherms below and above TC using the values of β and γ determined by the KF method. | |
4. Conclusions
In conclusion, the magnetocaloric effect and critical behavior of a periodic Anderson-like organic polymer are investigated by means of Green's function theory, in which the localized f orbitals hybridize with the conduction orbitals at even sites. We explore the field-induced ground state phase diagram with ferrimagnetic insulator, metal and ferromagnetic insulator states unveiled. The quantum criticality is clearly demonstrated by the Grüneisen parameter which shows |Γh| ∼ T−1 power-law critical behaviour and diverges rapidly upon cooling down to zero temperature as h approaches the critical fields, providing a novel thermodynamic means for probing QPTs.
At finite temperatures, the magnetic entropy change (−ΔS) presents a double peak structure for the dominant Kondo coupling case as a result of the competition of up-spin and down-spin hole excitations, implying a double magnetic cooling process via demagnetization. Meanwhile, the magnetic entropy change follows a power law dependence of the magnetic field h: −ΔS ∼ hn. The local exponent n tends to 1 and 2 below and above TC, while reaches a minimum of 0.648 at TC, which is consistent with the experimental observation of perovskite manganites Pr0.55Sr0.45MnO3 and Nd0.55Sr0.45MnO3 corresponding to the conventional ferromagnets within the mean field theory −ΔS ∼ h2/3. At TC, the −ΔS ∼ h curves with convex curvature superpose each other for small V values, which are separated by the large V case, distinguishing the RKKY interaction and Kondo coupling explicitly. Furthermore, the critical scaling law n(TC) = 1 + (β − 1)/(β + γ) = 1 + 1/δ(1 − 1/β) is related to the critical exponents (β, γ, and δ) extracted from the Arrott–Noakes equation of state and the Kouvel–Fisher method, which fulfill the Widom scaling relation δ = 1 + γβ−1, indicating the self-consistency and reliability of the obtained results. In addition, based on the scaling hypothesis through checking the scaling analysis of magnetization, the lg–lg scales of M|t|−βversus h|t|−(β+γ) collapse into two independent universal branches for T > TC and T < TC, respectively, while the plot of M/h1/δversus t/h1/(β+γ) forms one universal curve with all data points collapsing, which further confirms the reliability of the obtained critical exponents over the entire range of normalized variables.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant no. 11204157, 11174179 and 11247020.
References
-
A. M. Tishin and Y. I. Spichkin, The magnetocaloric effect and its applications, Institute of Physics Publishing, Bristol and Philadelphia, 2003 Search PubMed.
- N. A. de Oliveira and P. J. von Ranke, Phys. Rep., 2010, 489, 89 CrossRef CAS.
- E. Brück, J. Phys. D: Appl. Phys., 2005, 38, R381 CrossRef.
- L. Mañosa, A. Planes and M. Acet, J. Mater. Chem. A, 2013, 1, 4925 Search PubMed.
- Y. Y. Gong, D. H. Wang, Q. Q. Cao, E. K. Liu, J. Liu and Y. W. Du, Adv. Mater., 2015, 27, 801 CrossRef CAS PubMed.
- S. Nayak, M. Evangelisti, A. K. Powell and J. Reedijk, Chem. – Eur. J., 2010, 16, 12865 CrossRef CAS PubMed.
- J. L. Liu, W. Q. Lin, Y. C. Chen, S. Gómez-Coca, D. Aravena, E. Ruiz, J. D. Leng and M. L. Tong, Chem. – Eur. J., 2013, 19, 17567 CrossRef CAS PubMed.
- M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606 CrossRef CAS PubMed.
- Y. C. Chen, L. Qin, Z. S. Meng, D. F. Yang, C. Wu, Z. D. Fu, Y. Z. Zheng, J. L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M. L. Tong, J. Mater. Chem. A, 2014, 2, 9851 CAS.
- H. C. Hu, C. S. Cao, Y. Yang, P. Cheng and B. Zhao, J. Mater. Chem. C, 2015, 3, 3494 RSC.
- H. C. Hu, X. M. Kang, C. S. Cao, P. Cheng and B. Zhao, Chem. Commun., 2015, 51, 10850 RSC.
- B. Wolfa, Y. Tsuia, D. Jaiswal-Nagara, U. Tutscha, A. Honeckerb, K. Remović-Langera, G. Hofmanna, A. Prokofievc, W. Assmusa, G. Donathd and M. Langa, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6862 CrossRef.
- M. Garst and A. Rosch, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 205129 CrossRef.
- A. W. Rost, R. S. Perry, J. F. Mercure, A. P. Mackenzie and S. A. Grigera, Science, 2009, 325, 1360 CrossRef CAS PubMed.
- H. Ryll, K. Kiefer, C. Rüegg, S. Ward, K. W. Krämer, D. Biner, P. Bouillot, E. Coira, T. Giamarchi and C. Kollath, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 144416 CrossRef.
- J. S. Miller, Adv. Mater., 2002, 14, 1105 CrossRef CAS.
- W. Fujita, K. Kikuchi and K. Awaga, Angew. Chem., Int. Ed., 2008, 47, 9480 CrossRef CAS PubMed.
- E. Lieb, T. Schultz and D. Mattis, Ann. Phys., 1961, 16, 407 Search PubMed.
- V. Franco and A. Conde, Int. J. Refrig., 2010, 33, 465 CrossRef CAS.
- Y. T. Su, Y. Sui, J. G. Cheng, J. S. Zhou, X. J. Wang, Y. Wang and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195102 CrossRef.
- A. Biswas, S. Chandra, T. Samanta, B. Ghosh, S. Datta, M. H. Phan, A. K. Raychaudhuri, I. Das and H. Srikanth, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134420 CrossRef.
- J. Y. Fan, L. Pi, L. Zhang, W. Tong, L. S. Ling, B. Hong, Y. G. Shi, W. C. Zhang, D. Lu and Y. H. Zhang, Appl. Phys. Lett., 2011, 98, 072508 CrossRef.
- L. S. Xu, J. Y. Fan, Y. G. Shi, Y. Zhu, K. Bärner, C. P. Yang and D. N. Shi, Europhys. Lett., 2015, 112, 17005 CrossRef.
- S. N. Kaul, J. Magn. Magn. Mater., 1985, 53, 5 CrossRef CAS.
- A. A. Ovchinnikov, Theor. Chim. Acta, 1978, 47, 297 CrossRef CAS.
- M. A. Hajj and J. P. Malrieu, J. Chem. Phys., 2007, 127, 144902 CrossRef PubMed.
- L. Zhao, K. L. Yao and Y. F. Duan, Phys. Chem. Chem. Phys., 2000, 2, 4001 RSC.
- W. Z. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 035118 CrossRef.
- L. J. Ding, K. L. Yao and H. H. Fu, Phys. Chem. Chem. Phys., 2011, 13, 328 RSC.
- M. F. Crommie, Science, 2005, 309, 1501 CrossRef CAS PubMed.
- C. A. Hooley and A. P. Mackenzie, Science, 2007, 137, 1332 CrossRef PubMed.
- H. Tsunetsugu, M. Sigrist and K. Ueda, Rev. Mod. Phys., 1997, 69, 809 CrossRef CAS.
- P. Fröbrich and P. J. Kuntz, Phys. Rep., 2006, 432, 223 CrossRef.
- N. A. Zimbovskaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 035331 CrossRef.
- V. Franco, J. S. Blázquez and A. Conde, Appl. Phys. Lett., 2006, 89, 222512 CrossRef.
- H. Oesterreicher and F. T. Parker, J. Appl. Phys., 1984, 55, 4334 CrossRef CAS.
- L. A. Burrola-Gándara, C. R. Santillan-Rodriguez, F. J. Rivera-Gomez, R. J. Saenz-Hernandez, M. E. Botello-Zubiate and J. A. Matutes-Aquino, J. Appl. Phys., 2015, 117, 17D144 CrossRef.
- A. Arrott and J. E. Noakes, Phys. Rev. Lett., 1967, 19, 786 CrossRef CAS.
- L. Zhang, J. Fang, J. Y. Fan, M. Ge, L. S. Ling, C. J. Zhang, L. Pi, S. Tan and Y. H. Zhang, J. Alloys Compd., 2014, 588, 294–299 CrossRef CAS.
- L. Zhang, D. Menzel, C. M. Jin, H. F. Du, M. Ge, C. J. Zhang, L. Pi, M. L. Tian and Y. H. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 024403 CrossRef.
- E. Svanidze, L. Liu, B. Frandsen, B. D. White, T. Besara, T. Goko, T. Medina, T. J. S. Munsie, G. M. Luke, D. Zheng, C. Q. Jin, T. Siegrist, M. B. Maple, Y. J. Uemura and E. Morosan, Phys. Rev. X, 2015, 5, 011026 Search PubMed.
- J. S. Kouvkl and M. E. Fisher, Phys. Rev., 1964, 136, A1626 CrossRef.
- B. Widom, J. Chem. Phys., 1965, 43, 3898 CrossRef.
- M. H. Phan, V. Franco, A. Chaturvedi, S. Stefanoski, G. S. Nolas and H. Srikanth, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 054436 CrossRef.
- V. Franco, R. Caballero-Flores, A. Conde, K. E. Knipling and M. A. Willard, J. Appl. Phys., 2011, 109, 07A905 Search PubMed.
|
| This journal is © the Owner Societies 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 
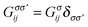 . For further Fourier transformation into k-space, the Green's function can be expressed as
. For further Fourier transformation into k-space, the Green's function can be expressed as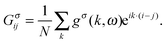
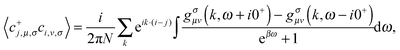
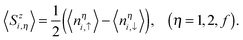
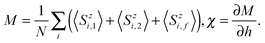
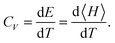
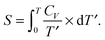
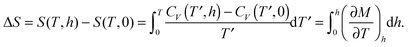
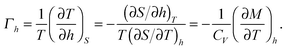

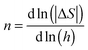 .21 Different from the antiferromagnets, wherein n is ∼2 for the entire temperature range at low fields,21 one can find that the local exponent n is strongly dependent on temperature as shown in Fig. 5(a) and (c), demonstrated by the linear relation of ln(|ΔS|) versus ln(h) with different slopes for different temperatures. At low temperatures well below TC, n tends to 1 for a ferrimagnetic system, while tends to 2 at temperatures above TC as a consequence of the Curie–Weiss law (see the insets in Fig. 5(b) and (d)). This scaling behavior is similar to that occurred in ferromagnetic materials.19,35 In addition, n has a minimum value at the transition temperature TC, which is clearly illustrated in Fig. 5(b) and (d).
.21 Different from the antiferromagnets, wherein n is ∼2 for the entire temperature range at low fields,21 one can find that the local exponent n is strongly dependent on temperature as shown in Fig. 5(a) and (c), demonstrated by the linear relation of ln(|ΔS|) versus ln(h) with different slopes for different temperatures. At low temperatures well below TC, n tends to 1 for a ferrimagnetic system, while tends to 2 at temperatures above TC as a consequence of the Curie–Weiss law (see the insets in Fig. 5(b) and (d)). This scaling behavior is similar to that occurred in ferromagnetic materials.19,35 In addition, n has a minimum value at the transition temperature TC, which is clearly illustrated in Fig. 5(b) and (d).
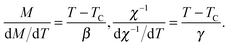
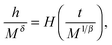




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)


