Gas-phase structure of 2,2,2-trichloroethyl chloroformate studied by electron diffraction and quantum-chemical calculations

Abstract

The molecular structure and conformational properties of 2,2,2-trichloroethyl chloroformate, ClC(O)OCH₂CCl₃ were determined experimentally using gas-phase electron diffraction (GED) and theoretically based on quantum-chemical calculations at the MP2 and DFT levels of theory. Further experimental measurements such as UV-visible, IR and Raman spectroscopy were complemented with the corresponding theoretical studies. All experimental results and calculations confirm the presence of two conformers namely anti–gauche (C₁ symmetry) and anti–anti (C_s symmetry). The conformational preference was rationalised by NBO and AIM analyses. Molecular properties such as ionisation potential, electronegativity, chemical potential, chemical hardness and softness were deduced from HOMO–LUMO analyses. The TD-DFT approach was applied to assign the electronic transitions observed in the UV-visible spectrum. A detailed interpretation of the infrared and Raman spectra of the title compound are reported. Using calculated frequencies as a guide, IR and Raman spectra also provide evidence for the presence of both C₁ and C_s conformers.

---

1. Introduction

The compound 2,2,2-trichloroethyl chloroformate, ClC(O)OCH₂CCl₃, is a derivative of 2,2,2-trichloroethanol and is a stable reagent which is capable of acylating different aliphatic and aromatic hydroxyl and amino groups under mild conditions. This reagent has been widely used in regio-, chemo- and stereoselective synthesis.¹ Montzka et al. have found the reaction of tertiary methylamines with ClC(O)OCH₂CCl₃ to afford the corresponding demethylated trichloroethyl carbamate derivatives in excellent yields. These carbamates are in general crystalline materials and readily purified by crystallisation. They are easily cleaved by reduction with zinc in acetic acid or methanol.² Several methods of removal of the C(O)OCH₂CCl₃ moiety have been described, leaving a wide variety of other functional groups unaffected.^3,4 Chloroformates are useful as catalysts for the polymerisation of unsaturated compounds and in the preparation of polycarbonates, polyesters and formaldehyde polymers.⁵

The compound ClC(O)OCH₂CCl₃ is commercially available, but its molecular structure has not yet been studied. In this contribution we report on the gas-phase structure of the title compound determined by gas-phase electron diffraction (GED) and on infrared and Raman spectra recorded in the liquid phase. We compare these experimental data to results of quantum-chemical calculations. Further quantum-chemical exploration of structure and bonding properties concern the internal rotation about the O–CH₂ bond indicating that the most stable conformation is anti–anti (C_s symmetry), natural bond orbital (NBO) and AIM analyses to rationalise these results as well as exploration of the HOMO and LUMO frontier molecular orbitals that results in information on ionisation potential (IP), electron affinity (EA), electronegativity (χ), electrophilicity index (ω), hardness (η) and chemical potential (μ). These findings are compared to those previously reported for different acetates^6–9 and chloroformates.^10–12

2. Experimental section

Sample preparation

2,2,2-Trichloroethyl chloroformate was obtained as a commercial product (Sigma-Aldrich) and was used without further purification. All handling was performed under dry nitrogen in order to protect the sample from atmospheric humidity. The purity of the sample was checked using ¹H-NMR and vibrational spectroscopy. The compound shows a sharp and characteristic singlet in the ¹H NMR spectrum at δ = 4.68–4.89 ppm; its presence or absence makes the compound easily detectable.

Gas-phase electron diffraction

Electron diffraction patterns were recorded using the KD-G2 gas diffractometer at Bielefeld University¹³ with an accelerating voltage of 60 kV at two nozzle-to-plate distances (250 and 500 mm). The samples as well as the inlet system and nozzle tip were heated to 55 °C throughout the GED experiments. Details of these are summarised in Table S1 (ESI†). The electron wavelength was determined from diffraction patterns of carbon tetrachloride standard measurements, carried out at room temperature.¹⁴ Molecular intensities I_mol(s) were obtained in the s-range from 3.0–28.0 Å⁻¹. Molecular structure refinements were performed using the UNEX program.¹⁵ Starting parameters, fixed differences as well as relative potential energies for all pseudo conformers were based on quantum chemical calculations at MP2/6-311G(d,p) level of theory and are summarised in Table S3 (ESI†).

Vibrational spectra

Infrared spectra for ClC(O)OCH₂CCl₃ in the liquid phase were recorded in the range of 4000–400 cm⁻¹ at room temperature (RT) using a Perkin-Elmer GX1 Fourier transform infrared instrument. KBr windows were used to record the IR spectrum of the substance in the liquid state. The resolution achievable with this equipment was 1 cm⁻¹. A total of 64 scans were recorded under each condition. Raman spectra of the liquid at RT in the range of 3500–50 cm⁻¹ were measured on a Thermo Scientific DXR Smart Raman instrument. Data were collected using a diode-pump, solid state laser of 780 nm (5 cm⁻¹ spectral resolution). In order to achieve a sufficient signal to noise, 100 expositions of 2 s were accumulated for the sample. The laser power was maintained at 5 mW during data collection.

UV-visible measurements

The UV-visible spectra were recorded using quartz cells (1 mm optical path length) on a Beckman/DU 7500 spectrometer. For this purpose, a 10⁻⁴ M solution of ClC(O)OCH₂CCl₃ in methanol was prepared.

3. Computational details

Quantum-chemical calculations were performed using the Gaussian 03 program package.¹⁶ Geometry optimisations were performed using MP2¹⁷ and DFT functionals. Pople's 6-311G(d,p), 6-311++G(d,p) and 6-311G(3df,2pd) basis sets were used throughout.^18–21 DFT calculations were performed using Becke's three-parameter hybrid exchange functional (B3) combined with both the Lee–Yang–Parr gradient-corrected correlation functional (LYP).^22,23 The second DFT method used, mPW1PW91 applies a modified Perdew–Wang exchange functional and Perdew–Wang 91 correlation functional.²⁴ The gradient-corrected correlation functional of Perdew, Burke and Ernzerhof (PBEPBE) was also used in the geometry optimisations.^25,26 All calculations were performed using standard gradient techniques and default convergence criteria. The calculated geometries showed no imaginary frequencies and consequently proved to be minima on the potential hyper surface. Relaxed potential energy scans of the C(1)–O(3)–C(4)–C(5) dihedral angle were performed at MP2, B3LYP and mPW1PW91 methods using 6-311++G(d,p) as well as 6-311G (d,p) basis sets using a step size of 10° and default convergence criteria. The vibrational modes were assigned by means of visual inspection using the GAUSSVIEW 05 program.²⁷ Quantum-chemically calculated frequencies were compared with the experimentally measured ones. The calculated frequencies were found to be slightly shifted to higher wavenumbers than the fundamental frequencies. Using the optimised geometries from B3LYP/6-311++G(d,p) the thermodynamic properties at 298.15 K were evaluated.

Raman intensities were predicted by the procedure outlined below. The Raman activities (S_i) were calculated by GAUSSIAN 03 and converted into relative Raman intensity (I_i) using the following relation from the basic theory of Raman scattering:²⁸

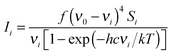where ν₀ is the laser exciting wavenumber in cm⁻¹ (in this work, we have used the excitation wavenumber ν₀ = 12820.5 cm⁻¹, which corresponds to the wavelength of 780 nm of the solid state laser), ν_i the vibrational wavenumber of the ith normal mode (in cm⁻¹), h, c and k are universal constants and f is the suitably chosen common scaling factor for all the peaks intensities (10⁻¹²).

Natural bond orbital (NBO) calculations were performed at the B3LYP/6-311++G(d,p) level using the NBO 3.1 program²⁹ as implemented in GAUSSIAN 03. These analyses were performed in order to understand various second order interactions between the filled orbitals of one subsystem and vacant orbitals of another subsystem to consequently obtain a measure of intramolecular delocalisation and hyperconjugation. In addition, analyses of the reactivity of the compound was done within Bader's Quantum Theory of Atoms in Molecules (QTAIM) by using the AIM2000 code.^30,31

Molecular properties such as ionisation potential, electronegativity, chemical potential, chemical hardness and softness have been deduced from HOMO–LUMO-analysis employing B3LYP/6-311++G(d,p) and PBEPBE/6-311G(3df,2pd) methods. The electronic absorption spectra for the optimised structures were calculated using time dependent DFT (TD-DFT) at PBEPBE/6-311G(3df,2pd) level for the free molecules as well as within the polarisable continuum model (PCM) with methanol as solvent.

4. Results and discussion

4.1 Quantum-chemical calculations

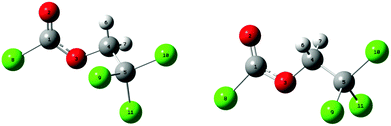
Fig. 1 shows the potential energy curves for the internal rotation around the C(1)–O(3)–C(4)–C(5) dihedral angle at the B3LYP, mPW1PW91 and MP2 levels using the 6-311++G(d,p) basis sets as well as 6-311G(d,p) for MP2. An overall good agreement between these methods can be observed. All curves show two minima; one of these corresponds to the conformer with C₁ symmetry (anti–gauche) and the other to the one with C_s symmetry (anti–anti). The anti–gauche conformation is characterised by an anti-orientation of the O(3)–C(4) single bond relative to the C(1)–Cl bond and the C(1)–O(3)–C(4)–C(5) dihedral angle is about 120°. The anti–anti conformation is defined as an anti-orientation of the O(3)–C(4) single bond relative to the C(1)–Cl bond and the C(1)–O(3)–C(4)–C(5) dihedral angle is 180°. From the potential energy curves, the differences in total energy between the two minima is very small (0–2 kJ mol⁻¹) indicating that the title compound may be present as a mixture of anti–gauche (C₁ symmetry) and anti–anti (C_s symmetry) conformations in the gas-phase. The structures of all possible conformers were quantum-chemically optimised to identify the energetically and thermodynamically most stable conformation of the compound. In the C₁ conformer, the CCl₃ group is staggered with respect to the CH₂ group with a dihedral angle C(1)–O(3)–C(4)–C(5) of 112.9° (MP2/6-311++G(d,p)). This angle is very sensitive to the change of substituents as can be seen in related molecules.^6–9 The anti–anti conformer is almost planar, where the dihedral angles Cl(8)–C(1)–O(3)–C(4) and C(1)–O(3)–C(4)–C(5) are 179.9° and 180°, respectively. The optimised structures of the two possible conformers are shown in Fig. 2. While all DFT calculations predict the anti–anti to be energetically more stable than anti–gauche conformer by 0.1–1 kJ mol⁻¹, the MP2 calculations estimate the C₁ conformer to be more favourable by 1–2 kJ mol⁻¹. These results are nearly independent from the choice of basis set.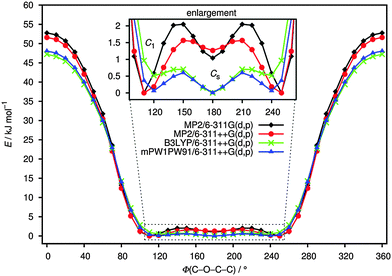

Fig. 1 Torsional potential around O(3)–C(4) bond of ClC(O)OCH₂CCl₃ calculated at B3LYP, mPW1PW91 and MP2 levels of theory using 6-311++G(d,p) and 6-311G(d,p) basis sets.

Fig. 2 Optimised molecular structures with numbering of atoms for anti–gauche conformer with C₁ symmetry (left) and anti–anti conformer with C_s symmetry (right) for ClC(O)OCH₂CCl₃ calculated at the B3LYP/6-311++G(d,p) approximation.

The difference of free B3LYP/6-311++G(d,p) energies, is 1.5 kJ mol⁻¹ indicating the C_s conformation to be more stable than C₁. These results agree well with those reported for different compounds of similar structure.^6–9 Using the Boltzmann distribution and this difference in free energy, the conformational composition was estimated to be 0.52 : 0.48 (C₁ : C_s) at room temperature, taking into account a multiplicity of 2 for the C₁ conformer.

The quantum-chemically optimised structural parameters for both conformers of ClC(O)OCH₂CCl₃ are listed in Table 1. The experimental parameters obtained by gas-phase electron diffraction (GED) are also presented in Table 1 for comparison; they are described in Section 4.3. According to Table 1, structural parameters calculated at the MP2/6-311++G(d,p) level reproduce most experimental gas-phase parameters within experimental error. Some differences between calculated and experimental parameters are observed for the C=O, C–O and C–Cl bond lengths. The theoretical description of molecules containing chlorine atoms requires the use of highly polarised basis functions. As was found for related compounds containing sulfonate groups,^32–34 the inclusion of extra polarisation functions (beyond a single d function) is necessary to predict the bond lengths in these types of molecules accurately. Table S2 (ESI†) lists the structural parameters obtained using the PBEPBE and MP2 methods with 6-311G(3df,2pd) basis set. These calculations produce a structure close to the experimental one observed in related molecules.^8,12,35,36 However, a better match of bond lengths and angles experimentally determined from GED measurements was achieved by the MP2/6-311G(3df,2pd) estimates.

Table 1 Optimised structural parameters (bond lengths, bond angles and selected dihedral angles) for both conformers of ClC(O)OCH₂CCl₃ calculated with different levels of theory (basis set always 6-311++G(d,p)) as well as experimental ones obtained from gas electron diffraction data

Parameter^a	C 1 conformer (re)			C s conformer (re)			GED (re)^b
	B3LYP	mPW1PW91	MP2	B3LYP	mPW1PW91	MP2
a Bond lengths in Å, angles in degrees. See Fig. 2 for numbering of atoms. b Values for conformer of Cs symmetry, standard deviations given as 3σLS, superscript numbers indicate the regularisation coefficient, subscript letters state if parameters were refined in groups with fixed differences in between. The O(2)=C(1)–O(3) angle was not refined explicitly, but results from O(2)=C(1)–Cl(8), Cl(8)–C(1)–O(3) and the assumed planarity of the Cl(8)–C(1)–O(2)–O(3) moiety.
C(4)–H (mean)	1.089	1.089	1.090	1.090	1.090	1.092	1.090(15)^5.0
C(1)–Cl(8)	1.764	1.744	1.738	1.764	1.745	1.738	1.744(2)^a
C(1)=O(2)	1.187	1.184	1.195	1.189	1.186	1.197	1.184(8)^5.0
C(1)–O(3)	1.339	1.332	1.346	1.334	1.327	1.338	1.327(9)^5.0
O(3)–C(4)	1.437	1.423	1.428	1.439	1.426	1.432	1.422(10)^5.0
C(4)–C(5)	1.531	1.524	1.525	1.527	1.519	1.520	1.535(10)^5.0
C(5)–Cl	1.795	1.777	1.771	1.795	1.777	1.771	1.772(2)^a
O(2)=C(1)–Cl(8)	123.5	123.6	124.2	123.9	123.9	124.5	124.9(17)^0.5
O(2)=C(1)–O(3)	128.1	127.8	127.7	127.3	127.0	126.7	126.2(9)
Cl(8)–C(1)–O(3)	108.4	108.5	108.0	108.9	109.0	108.7	108.9(14)^0.5
C(1)–O(3)–C(4)	116.9	116.7	115.7	114.8	114.4	112.9	110.6(23)^0.5
O(3)–C(4)–C(5)	110.1	110.1	109.3	108.1	108.1	107.1	105.1(10)^0.5
Cl–C(5)–Cl	109.8	109.9	110.4	109.7	109.9	110.3	109.2(9)^0.5
Cl8–C1–O3–C4	178.7	178.4	176.2	179.9	179.9	179.9	179.1(24)^0.5
C1–O3–C4–C5	121.3	119.2	112.9	179.9	179.9	179.9	Fixed to 180.0

---

Thermodynamic parameters of both conformations of ClC(O)OCH₂CCl₃ were also computed. These calculations were performed in order to get reliable data from which relations among energy, structure and reactivity characteristics of the molecule can be obtained. Table S4 (ESI†) shows values of some calculated thermodynamic parameters (such as thermal energy, heat capacity, entropy, zero-point vibrational energies (ZPVEs), rotational constants and rotational temperatures) of both conformers of ClC(O)OCH₂CCl₃ (B3LYP/6-311++G(d,p)). All values agree well with literature data.^6–9 All thermodynamic parameters are smaller in magnitude for the C_s than for the C₁ conformer. Dipole moments of C₁ and C_s conformers are 1.75 and 1.11 Debye, respectively. Fig. S1 (ESI†) shows a representation of the two conformers with the corresponding directions of dipole moments.

Natural bond orbital (NBO) analyses is a useful tool for understanding delocalisation of electron density from occupied Lewis-type (donor) NBOs into unoccupied non-Lewis type (acceptor) NBOs within a molecule. Table 2 shows the most relevant hyperconjugation interactions for both conformers of ClC(O)OCH₂CCl₃ (NBO: B3LYP/6-311++G(d,p)). According to the NBO analyses, the stabilising character of the hyperconjugation interactions is more pronounced in the C_s than in the C₁ conformer. These results suggest a higher stability of C_s over C₁. Similar results were obtained for the related compound CH₃C(O)OCH₂CCl₃.⁶ The entries of Table 2 demonstrate the hyperconjugative effect LP(O(3)) → σ*(C(4)–C(5)) to be stronger in the anti–gauche than in the anti–anti conformer, indicating that this interaction is important for stabilising the C₁ conformer. This interaction helps to rationalise the large dipole moment of the C₁ compared with the C_s conformer. In both conformers the lone pair LP(Cl(8)) participates in LP(Cl(8)) → σ*(C(1)–O(2)) and LP(Cl(8)) → σ*(C(1)–O(3)) type interactions. Also in both, the LP(Cl(8)) → σ*(C(1)–O(2)) delocalisation strongly stabilises the molecule. Another strongly stabilising interaction is LP(O(3)) → σ*(C(1)–O(2)) with 229 and 233 kJ mol⁻¹ for conformers C₁ and C_s, respectively. Anomeric interactions promoted by electron donation from in-plane (σ) oxygen lone pairs directly affect the bond length of the carbonyl group, mainly in the C_s conformer. A longer bond is expected when the interaction between lone pairs and the antibonding orbital of the carbonyl group increases. As shown in Tables 1 and 2, the C=O bond of the C_s conformer is longer than in the C₁ one, a fact attributed to the strong LP(O(3)) → σ*(C(1)–O(2)) interaction. The relation between the electron occupation of the σ*(C(4)–O(3)), σ*(C(4)–C(5)) as well as σ*(C(1)–O(2)) and the bond lengths C–C, C–O and C=O was investigated in both conformers (results see Table S5, ESI†). The C(4)–O(3) bond in the anti–anti conformer is longer than that of the anti–gauche conformer, which is in agreement with the high occupation of the σ*(C(4)–O(3)) orbital in the C_s conformer. The strength of the LP(O(3)) → σ*(C(4)–C(5)) interaction in the C₁ conformer (see Table 2) causes a lengthening of the C–C bond and a shortening of the C–O bond. The latter is attributed to the lower occupation of the σ*(C(4)–O(3)) orbital.

Table 2 Important hyperconjugation type interactions in kJ mol⁻¹ for C₁ and C_s conformers of ClC(O)OCH₂CCl₃ calculated at the B3LYP/6-311++G(d,p) approximation

Interaction (donor → acceptor)^a	anti–gauche (C1)	anti–anti (Cs)
a LP indicates electron lone pair on the specified atom (see Fig. 2 for numbering of atoms).
LP(O(2)) → σ*(C(1)–Cl(8))	170	175
LP(O(2)) → σ*(C(1)–O(3))	132	131
LP(O(3)) → σ*(C(1)–O(2))	229	233
LP(O(3)) → σ*(C(4)–C(5))	17	5
LP(O(3)) → σ*(C(1)–Cl(8))	5	5
LP(O(3)) → σ*(C(4)–H(6))	11	22
LP(O(3)) → σ*(C(4)–H(7))	19	22
LP(Cl(8)) → σ*(C(1)–O(2))	116	117
LP(Cl(8)) → σ*(C(1)–O(3))	25	25
LP(Cl(9)) → σ*(C(4)–C(5))	19	20
LP(Cl(10)) → σ*(C(4)–C(5))	16	16
LP(Cl(11)) → σ*(C(4)–C(5))	20	20
Total	781	790

---

Atomic charges affect molecular polarisabilities, dipole moments, electronic structures and even more molecular properties. Here we use Mulliken charge calculations to investigate them. The charge distributions of C₁ and C_s conformers of the title compound were calculated at the B3LYP/6-311++G(d,p) level of theory; they are listed in Table S6 (ESI†). In both conformers the atomic charges for the three different carbon atoms C(1), C(4) and C(5) are found to be +0.76 e, −0.09 e and −0.18 e, respectively. For the oxygen and chlorine atoms there is no significant difference in atomic charges between the two conformers, either. When changing from the anti–anti to anti–gauche, the hydrogen atoms become chemically inequivalent. Hence, their atomic charges differ marginally at +0.22 e and +0.24 e in the C₁ conformer, whereas in the C_s conformer they are the same (+0.22 e). The negative charges on O(2) and O(3) makes C(1) positively charged and therefore a preferred site for nucleophilic attack. The negative charges are mainly located on O(2) and O(3). Hence, these atoms are supposed to interact with the positive part of a receptor.

The Quantum Theory of Atoms in Molecules (QTAIM) is used to characterise bonding interactions through a topological analysis of the electron densities.³⁰ In QTAIM the nature of bonding interactions is determined by the charge density ρ and its Laplacian ∇²(ρ) at the bond critical points (BCPs). Atomic charges within molecules are obtained by integrating the charge density over atomic basins defined by charge density topology.³⁰Table 3 lists characteristic QTAIM parameters and Fig. S2 (ESI†) shows the molecular graphs consisting of atomic interactions lines (also called bond paths) and bond critical points for both conformers of ClC(O)OCH₂CCl₃. The charge densities at the BCP along C(1)–O(3) are relatively high for both conformers and the corresponding Laplacians of the electron densities are negative. This means the charge density is located in the internuclear region and indicates highly covalent character for these bonds. The charge density at the BCP in the C_s (0.312 e a₀⁻³) and the C₁ conformer (0.309 e a₀⁻³) vary only insignificantly. The electron density at the C=O BCPs in the C₁ conformer (0.435 e a₀⁻³) and the C_s conformer (0.434 e a₀⁻³) are also the same and the Laplacian of the charge density is negative, too. These results agree with the NBO data (see Table 2) that give similar values for the interaction LP(O(3)) → σ*(C(1)–O(2)) in both conformers.

Table 3 Details of QTAIM analyses based on B3LYP/6-311++G(d,p) electron densities. If not stated otherwise, all parameters in a.u.

	anti–gauche	anti–anti
C(1)–O(3)
ρ	0.309	0.312
∇^2(ρ)	−0.57	−0.54
d(BCP–C(1))	0.886	0.877
d(BCP–O(3))	1.646	1.645
d/Å	1.339	1.334
q(C(1))	−0.364	−0.277
q(O(3))	0.134	0.125
ν/cm^−1	1143	1167
C(1)=O(2)
ρ	0.435	0.434
∇^2(ρ)	−0.04	−0.05
d(BCP–C(1))	0.767	0.768
d(BCP–O(2))	1.476	1.478
d/Å	1.187	1.189
q(C(1))	−0.364	−0.277
q(O(2))	−0.143	−0.152
ν/cm^−1	1847	1840
O(3)–C(4)
ρ	0.239	0.239
∇^2(ρ)	−0.354	−0.378
d(BCP–O(3))	1.773	1.771
d(BCP–C(4))	0.945	0.949
d/Å	1.437	1.439
q(O(3))	0.134	0.125
q(C(4))	−0.421	−0.577
ν/cm^−1	985	1002

---

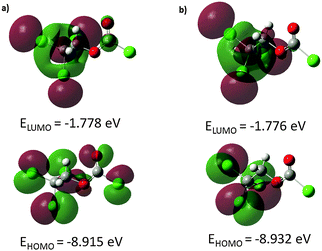
The energies and topologies of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) are important parameters for predicting chemical reactivity. The HOMO acts primarily as an electron donor and the LUMO as electron acceptor and their energies correspond to the ionisation potential (IP) and the electron affinity (EA): IP = −E_HOMO; EA = −E_LUMO. The energy difference between HOMO and LUMO (ΔE_HOMO–LUMO) is an important parameter to estimate the molecular chemical stability as well as electrical transport by means of electron conductivity.³⁷ In order to understand biological properties including drug design and the possible eco-toxicological characteristics of drug molecules, several new chemical reactivity descriptors have been proposed. Conceptual DFT based descriptors have helped in many ways to understand the structure of molecules and their reactivity by calculating the chemical potential, global hardness and electrophilicity index. Using HOMO and LUMO energy values for both conformers, the electronegativity (χ), chemical potential (μ), chemical hardness (η), chemical softness (S) and global electrophilicity index (ω) can be calculated by using the following equations: χ = (IP + EA)/2, μ = −(IP + EA)/2, η = (IP − EA)/2, S = 1/(2η), ω = μ²/(2η), where IP and EA are the ionisation potential and electron affinity, respectively.³⁸ The above-mentioned parameters were calculated at B3LYP/6-311++G(d,p) and PBEPBE/6-311G(3df,2pd) levels of theory and are listed in Table 4. Using the B3LYP method, the HOMO–LUMO energy gap is predicted to be 7.14 and 7.16 eV for C₁ and C_s conformers, respectively. The energy gaps obtained from the PBEPBE calculations are comparable but slightly lower. The energy gap of both conformers is relatively large indicating that both exhibit high chemical stability and lower reactivity. The global electrophilicity index measures the stabilisation energy when the system acquires an additional electronic charge from the environment. Electrophilicity encompasses both, the ability of an electrophile to acquire additional electronic charge and the resistance of the system to exchange electronic charge with the environment. It contains information about electron transfer (chemical potential) as well as the stability (hardness) and is the better descriptor of global chemical reactivity. The hardness signifies the resistance towards deformation of the electronic cloud of chemical systems under small perturbations encountered during chemical processes. Molecules with large HOMO–LUMO gap are considered hard, those with small HOMO–LUMO gap soft. This concept relates molecular stability to hardness in a way that smaller HOMO–LUMO gaps are associated with more reactive species.

Table 4 Calculated physicochemical properties for C₁ and C_s conformers of ClC(O)OCH₂CCl₃ correlated with molecular orbital theory at different levels of theory

Parameter	C 1 conformer		C s conformer
	B3LYP^a	PBEPBE^b	B3LYP	PBEPBE
a B3LYP/6-311++G(d,p). b PBEPBE/6-311G(3df,2pd).
E HOMO/eV	−8.915	−7.558	−8.932	−7.544
E LUMO/eV	−1.778	−2.445	−1.776	−2.454
ΔEHOMO–LUMO/eV	7.137	5.113	7.156	5.090
Electronegativity χ/eV	5.346	5.001	5.354	4.999
Chemical potential μ	−5.346	−5.001	−5.354	−4.999
Chemical hardness η/eV	3.569	2.556	3.578	2.545
Chemical softness, S/eV	0.140	0.196	0.139	0.196
Global electrophilicity index, ω/eV^−1	4.004	4.892	4.006	4.909
Dipole moment, μ/D	1.755	1.598	1.112	0.995

---

Molecular orbitals are defined as Eigen-functions of the Fock operator, which exhibits the full symmetry of the nuclear point group. They necessarily from a basis for irreducible representations of full point-group symmetry. The pictorial illustration of the frontier molecular orbitals and their respective positive and negative regions for both conformers of the title compound is shown in Fig. 3. Both HOMO and LUMO frontier molecular orbitals play an important role in the electrical and optical properties, as well as in the UV-visible spectra and chemical reactions. The HOMO of the anti–gauche conformer (Fig. 3a) is primarily composed of p-type orbitals located on oxygen and chlorine atoms. The LUMO is spread over the entire molecule except the chloroformate group. The HOMO of the anti–anti conformer (Fig. 3b) is composed of p-type orbitals located on the CCl₃ moiety. The LUMO plot reveals that this molecular orbital is mostly spread over the CH₂CCl₃ group.

Fig. 3 The frontier molecular orbitals for both conformers of ClC(O)OCH₂CCl₃ calculated at B3LYP/6-311++G(d,p) level: (a) C₁ conformer, (b) C_s conformer. The positive and negative phase is represented in red and green colours, respectively.

4.2 UV-visible analysis

Electronic absorption spectra of the title compound were recorded in the gas phase and in CH₃OH solution. On the basis of fully optimised ground-state structures, TD-DFT calculations were used in order to determine the low-lying excited states of the title compound. The calculations were performed using B3LYP with 6-311++G(d,p) and 6-311G(3df,2pd) basis sets. Additionally, PBEPBE with a 6-311G (3df,2pd) basis set was applied. These results were compared with the experimental counterpart. The data obtained using PBEPBE/6-311G(3df,2pd) turned out to reproduce the experimental results better than those derived from B3LYP calculations. In this case, the choice of the DFT functional seems to be more influential on the quality of the results than the basis set.

Fig. 4 shows the experimental UV-visible spectrum measured in methanol solution and the calculated ones for both conformations of ClC(O)OCH₂CCl₃. Over all a good agreement between calculated and experimental spectra is observed. Absorption bands for a HOMO−2 → LUMO transition calculated including a PCM model for solvation in methanol appear at 215 nm for the C₁ conformer and at 213 nm for the conformer with C_s symmetry. According to these calculations, we can assign the experimentally observed absorptions at 211 nm and 209 nm to the C₁ and C_s conformers, respectively. Other transitions were obtained in quantum-chemical calculations corresponding to the HOMO → LUMO and HOMO−1 → LUMO transitions but they were not observed experimentally, probably due to the smaller oscillator strengths (f) calculated for both conformers.

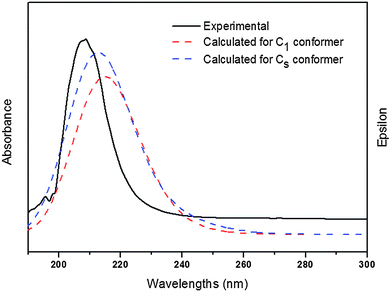Fig. 4 UV-visible spectrum measured in methanol as well as the calculated ones for both conformations of ClC(O)OCH₂CCl₃ (PBEPBE/6-311G(3df,2pd)/PCM(methanol)).

4.3 Experimental gas-phase structure by electron diffraction

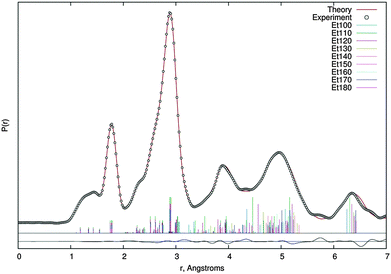
Based on the above-mentioned quantum chemical calculations a two conformer model including anti–anti and anti–gauche conformers was used to describe the experimental electron scattering intensities. During structure refinement this model as well as the single-conformer model turned out to be non-satisfying by means of obtained R-factors (for radial distribution and sM(s) curves, see Fig. S3–S7, ESI†). This is probably due to the very low rotational barrier separating the two conformers (see Fig. 1) and hence a large population of torsional states between the two minimum geometries. To overcome this issue dynamic models based on MP2/6-311G(d,p) as well as MP2/6-311++G(d,p) relaxed potential energy surface scans were applied. Differences in geometric parameters caused by the choice of potential turned out to be negligible. Nevertheless, all of the following results were obtained by using the MP2/6-311G(d,p) potential energy curve.

Nine pseudo conformers with C(1)–O(3)–C(4)–C(5) dihedral angles in the range of 100°–180° in steps of 10° were used and weighted by means of their relative energy via a Boltzmann distribution at the temperature of experiment (328 K). Differences in parameters between the pseudo conformers were kept fixed to their computed values. Thus, sixteen independent geometrical parameters were refined during the least-squares procedure. Refinement of most of these was supported by flexible restraints along the ideas of Bartell et al.³⁹ and the SARACEN⁴⁰ method as are implemented in the UNEX program.⁴¹

Quadratic and cubic force fields were calculated at the MP2/6-311G(d,p) level of theory for both conformers and, using the SHRINK program,⁴² two sets of amplitudes and anharmonic vibrational corrections were obtained. Each of these was used for a certain range of pseudo conformers (anti–anti: 150° ≤ Φ ≤ 180°, anti–gauche: 100° ≤ Φ ≤ 140°). Scale factors of vibrational amplitudes were refined in groups corresponding to distinct peaks on the radial distribution curve, whereas the ones of the C(1)–O(2), C(1)–O(3), O(3)–C(4) and C(4)–C(5) bond lengths had to be refined individually with weak restraints. Experimental structural data are summarised in Table 1 and the radial distribution curve is shown in Fig. 5. The finally achieved R-factor was R_G = 5.0%.

Fig. 5 Theoretical (dots) and experimental (line) radial distribution curve as well as delta curve (below) and geometrical terms (vertical coloured lines) from GED data refinement using the dynamic model based on MP2/6-311G(d,p) calculations.

The C(1)–O(3)–C(4) angle, 110.6(23)° (for C_s) in GED, exhibits the most significant difference between the experiment and the different levels of theory, as the latter yield it at least 2° wider. Despite the sterically demanding CCl₃ group, this angle is smaller than in the ethyl esters F₃CC(O)OCH₂CF₃ (114.4°),⁷ H₃CC(O)OCH₂CH₃ (115.7°)⁴³ and in the methyl esters H₃CC(O)OCH₃ (116.4°)⁴⁴ as well as F₃CC(O)OCH₃. Structure refinement of the latter was done with a small-amplitude motion model for the rotation of the CF₃ group⁸ as well as with a dynamic model,⁴⁵ resulting in a C–O–C angle of 114.2° and 116.3°, respectively. Surprisingly this angle is wider for molecules bearing sterically less demanding substituents at O(3). This effect can be neglected within the error limit for ethyl acetate but is of higher significance for F₃CC(O)OCH₂CF₃ and ClC(O)OCH₂CCl₃. Additionally, this angle is found at 117.6° in ClC(O)OCF₃.⁴⁶ So, one can conclude that the electronic effect of the chlorine substituent at C(1) on this angle is quite small and, if at all, widens it. Therefore, the narrow C–O–C angle in ClC(O)OCH₂CCl₃ could be attributed to an attractive interplay between the CCl₃ or CF₃ groups and the carbonyl group, however, NBO analyses did not provide any indication for this in our case.

The C(1)–O(3) and O(3)–C(4) bond lengths depend on the strength of the electron-withdrawing nature of the substituents at C(1) and – if present – C(5), as one can see for the above-mentioned molecules. The shortest C(1)–O(3) bond can be observed in F₃CC(O)OCH₃⁷ and ClC(O)OCH₂CCl₃ with 1.326 Å and 1.327 Å, respectively. The unsubstituted molecules show significantly longer C(=O)–O bond lengths of 1.345 Å (H₃CC(O)OCH₂CH₃)⁴³ and 1.360 Å (H₃CC(O)OCH₃).⁴⁵ The same applies to the O(3)–C(4) bond, which is determined to 1.421 Å in F₃CC(O)OCH₃ and ClC(O)OCH₂CCl₃, but is longer in methyl and ethyl acetate with 1.443 Å and 1.448 Å, respectively. Interestingly these bonds are shorter in the title compound than in F₃CC(O)OCH₂CF₃ (C(=O)–O: 1.336 Å, O–C: 1.423 Å), which one could expect to show a similar or even stronger electron-with drawing effect of the substituents.

Additionally it should be noted that in all quantum-chemical calculations the O(3)–C(4)–C(5) angle is 2–3° larger than in the GED structure refinement at 105.1(10)°. In contrast to the above-mentioned C(1)–O(3)–C(4) angle, the O(3)–C(4)–C(5) angle is in good compliance with those determined for other ethyl esters, namely CH₃C(O)OCH₂CH₃ (108.2°)⁴³ and CF₃C(O)OCH₂CF₃ (107.8°).⁷ Note, that for this angle we observe significant differences between theory and experiment for all ethyl esters investigated to date.

Due to the complex shape and low height of the potential energy profile, it was not possible to find a parameterised function suitable for refining its parameters and, hence, the rotational barrier itself. Therefore the refinement of GED data did not allow providing an experimental ratio of conformers, however, the failure of one- and two-conformer models proves the existence of both, anti–anti and anti–gauche conformers in the gas-phase and justifies the description by a dynamic model. Regarding the potential used to describe the populations of the pseudo conformers we conclude that both of them supply a good description of the gas-phase composition, since they yield the same structural parameters as well as R-factors.

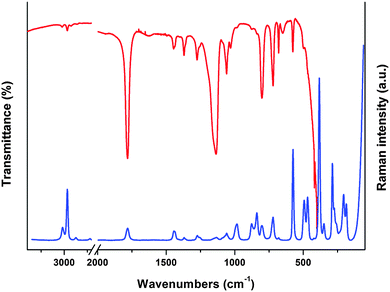
4.4 Vibrational analysis

The assignment of the experimental infrared absorption and Raman dispersion bands to the normal modes of vibration of ClC(O)OCH₂CCl₃ was based on the comparison of related molecules^6–12,32 and assisted by the theoretical calculations performed in this work at B3LYP/6-311++G(d,p) level of theory. The FTIR and Raman spectra of the liquid substance are shown in Fig. 6. The simulated Raman spectra of both conformers are shown in Fig. S8 (ESI†). The wavenumbers of the observed spectra and the approximate descriptions of the modes of both conformers of ClC(O)OCH₂CCl₃ are given in Table 5. At room temperature, most of the bands are attributable to the same fundamentals for both conformations. The predicted conformational splitting for the modes agrees well with that in the IR and Raman spectrum of the liquid substance and therefore proves the existence of both conformers in the gas-phase.

Fig. 6 Infrared and Raman spectra of ClC(O)OCH₂CCl₃ in liquid phase.

Table 5 Observed and calculated wavenumbers (in cm⁻¹) and tentative assignments for the C₁ and C_s conformers of ClC(O)OCH₂CCl₃

Mode	Experimental		B3LYP/6-311++G(d,p)^c		Approximate description of mode^d
	IR (liq.)^a	Raman (liq.)^b	C 1 conf.	C s conf.
a sh, shoulder; s, strong; w, weak; m, medium; v, very. b Relative band heights in parentheses. c IR intensities are shown in parenthesis. d ν, stretching; δ, bending; ρ, rocking; ω, wagging; τω, twisting; τ, torsion. See Fig. 2 for numbering of atoms.
1	3022 w	3018 (8)	3158 (3)	3142 (<1)	ν a CH2
2	2967 w	2966 (31)	3092 (11)	3081 (6)	ν s CH2
3	1782 vs	1781 (7)	1847 (376)	1840 (412)	ν C=O
4	1445 w (Cs)	1444 (6)	1478 (14)	1482 (13)	δ CH2
	1440 sh (C1)	1439 (5)
5	1370 w (Cs)	1370 (2)	1402 (17)	1405 (13)	ω CH2
	1362 sh (C1)	1360 sh
6	1276 w (C1)	1274 (3)	1305 (38)	1278 (16)	τω CH2
	1257 sh (Cs)	1256 (2)
7	1156 sh (Cs)	1153 sh	1143 (728)	1167 (857)	ν C(1)–O(3)
	1136 s (C1)	1135 (2)
8	1068 sh (Cs)	1067 sh	1077 (154)	1094 (35)	ν C(4)–C(5)
	1060 w (C1)	1060 (4)
9	1050 sh (C1)	—	1072 (18)	1055 (30)	ρ CH2
	1031 vw (Cs)
10	983 vw	984 (10)	985 (9)	1002 (3)	ν O(3)–C(4)
11	878 vw (Cs)	877 (10)	845 (36)	883 (32)	ν C(1)–Cl(8)
	839 vw (C1)	839 (17)
12	802 m	803 (9)	777 (173)	765 (209)	ν a CCl3
13	721 m	721 (14)	695 (122)	701 (136)	ν a CCl3
14	680 w	680 (1)	682 (15)	685 (8)	δ out-of-plane C=O
15	576 w	575 (56)	564 (32)	568 (41)	ν s CCl3
16	498 vvw	494 (24)	489 (40)	482 (14)	δ out-of-plane C=O + O(2)–C(1)–Cl(8)
17	467 vvw	468 (26)	471 (11)	457 (14)	δ Cl(8)–C(1)–O(3)
18	—	383 (100)	382 (4)	377 (5)	δ s CCl3
19	—	349 (10)	347 (2)	347 (2)	δ a CCl3
20	—	287 (47)	287 (<1)	287 (<1)	δ a CCl3
21	—	260 (10) (C1)	272 (1)	255 (1)	δ C(1)–O(3)–C(4)
		247 (20) (Cs)
22	—	231 (6)	229 (<1)	207 (2)	δ O(3)–C(4)–C(5)
23	—	206 (28)	204 (1)	201 (<1)	ρ CCl3
24	—	186 (22)	181 (1)	175 (<1)	τ C(4)–C(5)
25	—	—	67 (1)	86 (1)	ρ CCl3
26	—	—	48 (<1)	48 (0)	τ CCl3
27	—	—	32 (1)	23 (2)	τ C(4)–O(3)

---

4.4.1 Assignment of bands.
Methylene group modes. Two IR bands at 3022 and 2967 cm⁻¹ (3018 and 2966 cm⁻¹ in Raman) are assigned to the anti-symmetric and symmetric stretching modes of the methylene group, respectively. These values agree with the calculated ones for both conformers. The IR band observed at 1445 cm⁻¹ and the shoulder located at 1440 cm⁻¹ are assigned to the CH₂ bending modes of C_s and C₁ conformers, respectively. These bands appear at 1444 and 1439 cm⁻¹ in the Raman spectrum. The location of these bands correlates well with those obtained for similar compounds.^6–9,32 The weak IR bands located at 1370 and 1362 cm⁻¹ (1370 and 1360 cm⁻¹ in Raman) are assigned to the CH₂ wagging mode. The observed splitting clearly indicates the presence of two conformers in the sample. Two IR bands at 1276 and 1257 cm⁻¹ are assigned to the CH₂ twisting mode of C₁ and C_s conformers, respectively. The same splitting of the band corresponding to the twisting mode was observed in the Raman spectrum of the liquid substance. All these observations are in good agreement with quantum-chemical calculations as seen in Table 5. The very weak IR band and the shoulder at 1050 and 1031 cm⁻¹ are assigned to the CH₂ rocking mode for C₁ and C_s conformers, respectively.
Carbonyl group modes. A very strong IR band located at 1782 cm⁻¹ is assigned to the C=O stretching mode. A corresponding Raman band is found at 1781 cm⁻¹. Both are in agreement with values predicted by calculations performed at B3LYP/6-311++G(d,p) level. The calculated wavenumber for the anti–gauche conformer is 1847 cm⁻¹ and for the anti–anti conformer 1840 cm⁻¹. The C=O stretching mode is extremely sensitive to substitutions. In compounds with the general formula F₃CC(O)OX the ν(C=O) band appears at 1789 cm⁻¹ in the IR spectrum.⁸ A shift towards lower wavenumbers occurs when the CF₃ group is replaced by Cl and CH₃. This is in accordance with the decreasing group electronegativity. The corresponding C=O stretching bands of ClC(O)OCH₂CCl₃ and CH₃C(O)OCH₂CCl₃⁶ are at 1782 and 1763 cm⁻¹, respectively. Weak bands observed at 680 cm⁻¹ in both, IR and Raman spectra, are assigned to the C=O out-of-plane bending mode. A very weak IR band at 494 cm⁻¹ belongs to the C=O in-plane bending mode. These values agree well with the calculated ones (see Table 5).
Trichloromethyl group modes. The assignment of the bands corresponding to the CCl₃ group was made by comparison with related molecules^6,11,12,32 and with quantum-chemical calculations. Two IR bands of medium intensity at 802 and 721 cm⁻¹ (803 and 721 cm⁻¹ in Raman) are assigned to the CCl₃ anti-symmetric stretching modes. The weak IR band at 576 cm⁻¹ is assigned to the CCl₃ symmetric stretching vibration. This mode corresponds to an intense Raman band at 575 cm⁻¹. For CH₃C(O)OCH₂CCl₃, this mode appears as a weak band at 567 cm⁻¹.⁶ The most intense Raman band at 383 cm⁻¹ is assigned to the CCl₃ symmetric deformation; quantum-chemically predicted values are at 382 and 377 cm⁻¹ for the C₁ and C_s conformers, respectively. The Raman bands observed at 349 and 287 cm⁻¹ are assigned to CCl₃ anti-symmetric bending modes. The Raman spectrum shows only one band corresponding to the rocking of CCl₃ observed at 206 cm⁻¹.
Skeletal modes. Fig. 7 shows the calculated IR spectra of both conformers of the title compound in the range of 1300–1000 cm⁻¹ with the corresponding experimental spectrum. This band was deconvoluted and compared with those calculated for the C₁ and C_s conformers. As shown in Fig. 7, the IR band corresponding the C(1)–O(3) stretching mode appears split into two components at 1156 and 1136 cm⁻¹ indicating the presence of the two conformers identified above. A corresponding splitting is observed in the Raman spectrum at 1153 and 1135 cm⁻¹. The quantum-chemically predicted values are 1167 and 1143 cm⁻¹ for C_s and C₁ conformers, respectively. A very weak IR band at 983 cm⁻¹ could be assigned to the O(3)–C(4) stretching mode in agreement with quantum-chemical calculations and values reported for related molecules. The shoulder located at 1068 cm⁻¹ and the weak band at 1060 cm⁻¹ in the IR spectrum (1067 and 1060 cm⁻¹ in Raman) are assigned to the C(4)–C(5) stretching modes of both conformers and the IR bands at 878 and 839 cm⁻¹ (877 and 839 cm⁻¹ in Raman) are assigned to the C(1)–Cl(8) stretching modes of C_s and C₁ conformers, respectively. This assignment is in agreement with the calculated wavenumbers. The very weak IR band at 498 cm⁻¹ (494 cm⁻¹ in Raman) corresponds to the O(2)–C(1)–Cl(8) bending mode and the IR band at 467 cm⁻¹ is assigned to the Cl(8)–C(1)–O(3) bending mode. The band corresponding to the C(1)–O(3)–C(4) bending mode appears split in the Raman spectrum at 274 and 260 cm⁻¹, the first corresponding to the C₁ and the latter to the C_s conformer.

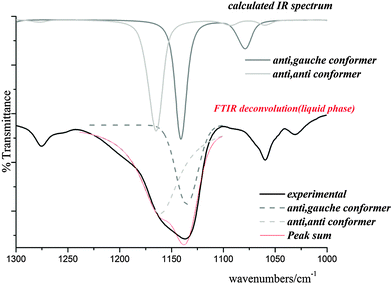Fig. 7 IR spectrum calculated for both conformers of ClC(O)OCH₂CCl₃ with the experimental one in the range of 1300–1000 cm⁻¹.

Torsional modes. The Raman band at 186 cm⁻¹ is assigned to the C(4)–C(5) torsional mode. Other bands corresponding to torsional modes were not observed in the Raman spectrum of the liquid.

5. Conclusions

The optimised molecular geometries and the conformational evaluation for ClC(O)OCH₂CCl₃ were investigated using MP2 and DFT quantum-chemical methods and different basis sets. Two conformers separated by a low rotational barrier were identified, namely anti–anti of C_s symmetry and anti–gauche of C₁ symmetry. The structural results indicate that the anti–anti conformation (C_s symmetry) is the most stable form according to the differences of free energies, but MP2 energies suggest that the C₁ conformer is more stable. The calculated geometrical parameters obtained by the different methods are in good agreement with the experimental values from gas-phase electron diffraction experiments and structure refinement. For the latter only the application of a dynamic model based on quantum-chemically calculated potential energy curves provided reliable parameters and therefore indirectly proved the existence of the two conformers as well as the large amplitude vibrational motion connecting them. NBO analyses were performed in order to elucidate the preferred conformation of ClC(O)OCH₂CCl₃. Stabilisation by hyperconjugation is stronger in the C_s than in the C₁ conformer. These results were confirmed by QTAIM analyses. Calculations on both conformations gave a relatively large HOMO–LUMO energy-gap indicating the molecule to show relatively high chemical stability and therefore reduced chemical reactivity. Electronic transitions in the UV-visible spectrum were assigned by the TD-DFT approach. The IR and Raman spectra of ClC(O)OCH₂CCl₃ in the liquid phase agree with the presence of C₁ and C_s conformers and 24 out of the 27 expected normal modes of vibration were assigned.

Acknowledgements

D. M. G., M. E. T. and A. B. A. thank CIUNT, CONICET (PIP 0205) and ANPCyT (PICT-2013-0697) for financial support. D. M. G. thanks CONICET for a postdoctoral fellowship. This work was supported by Deutsche Forschungsgemeinschaft (core facility GED@BI, Mi477/25-1). Authors thank HPC facilities at the UniversitätzuKöln (CHEOPS@RRZK) for providing computational time and programs.

References

1. T. B. Windholz, D. B. R. Johnston and M. Sharp, Tetrahedron Lett., 1967, 27, 2555.
2. T. A. Montzka, J. D. Metiskella and R. A. Partyka, Tetrahedron Lett., 1974, 14, 1325.
3. T. Doi, Y. Numajori, A. Munakata and T. Takahashi, Org. Lett., 2006, 8, 531.
4. T. Itoh, Y. Matsuya, Y. Enomoto, K. Nagata, M. Miyazaki and A. Ohsawa, Synlett, 1999, 1799.
5. D. E. Gould L. R. Anderson and W. B. Fox, US Pat., 3769312, Chem. Abstr., 19737254743.
6. D. M. Gil, M. E. Tuttolomondo and A. Ben Altabef, Spectrochim. Acta, Part A, 2014, 123, 290.
7. M. E. DefonsiLestard, M. E. Tuttolomondo, E. L. Varetti, D. A. Wann, H. E. Robertson, D. W. H. Rankin and A. Ben Altabef, J. Mol. Struct., 2009, 917, 183.
8. M. E. Defonsi Lestard, M. E. Tuttolomondo, D. A. Wann, H. E. Robertson, D. W. H. Rankin and A. Ben Altabef, J. Raman Spectrosc., 2009, 40, 2053.
9. M. E. DefonsiLestard, R. A. Cobos Picot, M. E. Tuttolomondo and A. Ben Altabef, Vib. Spectrosc., 2013, 65, 124.
10. S. E. Ulic, E. M. Coyanis, R. M. Romano and C. O. Della Védova, Spectrochim. Acta, Part A, 1986, 54, 695.
11. M. F. Erben, C. O. Della Védova, R. Boese, H. Willner and H. Oberhammer, J. Phys. Chem. A, 2004, 108, 699.
12. V. B. Arce, C. O. Della Védova, A. J. Downs, S. Parsons and R. M. Romano, J. Org. Chem., 2006, 71, 3423.
13. R. J. F. Berger, M. Hoffmann, S. A. Hayes and N. W. Mitzel, Z. Naturforsch., 2010, 64b, 1259.
14. S. Shibata, K. Iijima, R. Tani and I. Nakamura, Rep. Fac. Sci., Shizuoka Univ., 1974, 9, 33.
15. (a) Yu. V. Vishnevskiy, UNEX, v. 1.6.0, 2013, http://unexprog.org; (b) Yu. V. Vishnevskiy, J. Mol. Struct., 2007, 833, 30.
16. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265; M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr., T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. González and J. A. Pople, Gaussian 03, revision C.02, Gaussian, Inc., Wallingford, CT, 2004.
17. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618.
18. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
19. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639.
20. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265.
21. W. J. Hehre, P. V. R. Schleyer and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
23. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
24. C. Alamo and B. Barone, J. Chem. Phys., 1998, 108, 664.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
27. M. J. Frisch, A. B. Nielsen and A. J. Holder, GaussView User Manual, Gaussian, Pittsburgh, 2008.
28. V. Krishnakumar, G. Keresztury, T. Sundius and R. Ramanamy, J. Mol. Struct., 2004, 702, 9.
29. E. D. Glendening, J. K. Badenhoop, A. D. Reed, J. E. Carpenter and F. F. Weinhold, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 1996.
30. R. F. W. Bader, Atoms in Molecules, A Quantum Theory, Clarendon Press, Oxford, 1990.
31. F. Biegler-Köning, J. Schönnbohn and D. Bayles, J. Comput. Chem., 2001, 22, 545.
32. D. M. Gil, O. E. Piro, G. A. Echeverría, M. E. Tuttolomondo and A. Ben Altabef, Spectrochim. Acta, Part A, 2013, 116, 122.
33. M. E. DefonsiLestard, M. E. Tuttolomondo, D. A. Wann, H. E. Robertson, D. W. H. Rankin and A. Ben Altabef, J. Chem. Phys., 2009, 131, 214303.
34. M. E. Tuttolomondo, A. Navarro, T. P. Ruiz, E. L. Varetti, S. A. Hayes, D. A. Wann, H. E. Robertson, D. W. Rankin and A. Ben Altabef, J. Phys. Chem. A, 2007, 111, 9952.
35. M. Cuaquira Reina, R. Boese, M. Ge, S. E. Ulic, H. Beckers, H. Willner and C. O. Della Védova, J. Phys. Chem. A, 2008, 112, 7939.
36. J. R. Durig and M. G. Griffin, J. Mol. Spectrosc., 1977, 64, 252.
37. T. S. Xavier, I. Hubert Joe, M. A. Palafox, S. Kumar and V. K. Rastogi, Spectrochim. Acta, Part A, 2013, 114, 502.
38. H. Pir, N. Günay, Ö. Tamer, D. Avci and Y. Atalay, Spectrochim. Acta, Part A, 2013, 112, 331.
39. L. S. Bartell, D. J. Romanesko and T. C. Wong, in Molecular Structure by Diffraction Methods, ed. G. A. Sims and L. E. Sutton, The Chemical Society, London, 1975, vol. 3, p. 72.
40. N. W. Mitzel and D. W. H. Rankin, Dalton Trans., 2003, 3650.
41. Yu. V. Vishnevskiy, M. A. Abaev, A. N. Rykov, M. E. Gurskii, P. A. Belyakov, S. Yu. Erdyakov, Yu. N. Bubnov and N. W. Mitzel, Chem. – Eur. J., 2012, 18, 10585.
42. (a) V. A. Sipachev, J. Mol. Struct., 1985, 121, 143; (b) V. A. Sipachev, Struct. Chem., 2000, 11, 167; (c) V. A. Sipachev, J. Mol. Struct., 2001, 67, 567.
43. M. Sugino, H. Takeuchi, T. Egawa and S. Konaka, J. Mol. Struct., 1991, 245, 357.
44. W. Pyckhout, C. Van Alsenoy and H. J. Geise, J. Mol. Struct., 1986, 144, 265.
45. N. Kuze, A. Ishikawa, M. Kono, T. Kobayashi, N. Fuchisawa, T. Tsuji and H. Takeuchi, J. Phys. Chem. A, 2015, 119, 1774.
46. M. F. Erben, C. O. Della Védova, R. Boese, H. Willner and H. Oberhammer, J. Phys. Chem. A, 2004, 108, 699.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5cp05295e

‡ Member of the Research Career of CONICET, Argentina.

---