Photophysics of Auramine-O: electronic structure calculations and nonadiabatic dynamics simulations

Abstract

Diphenylmethane dyes are very useful photoinduced molecular rotors; however, their photophysical mechanisms are still elusive until now. In this work, we adopted combined static electronic structure calculations (MS-CASPT2//CASSCF) and trajectory-based surface-hopping dynamics simulations (OM2/MRCI) to study the S₁ excited-state relaxation mechanism of a representative diphenylmethane dye Auramine-O. On the basis of the optimized S₁ minima and the computed emission bands, we have for the first time assigned experimentally proposed three transient states (i.e. S1-LE, S1-I1 or S1-I2, and S1-II). Mechanistically, upon irradiation to the S₁ state, the system first relaxes to the locally excited S₁ minimum (S1-LE). Starting from this point, there exist two kinds of relaxation paths to S1-II. In the sequential path, the system first evolves into S1-I1 or S1-I2 and then runs into S1-II; in the concerted one, the system, bypassing S1-I1 and S1-I2, directly runs into S1-II. In addition, the system can decay to the S₀ state in the vicinity of three S₁/S₀ conical intersections i.e. S1S0-I1, S1S0-I2, and S1S0-II. In the S₁ dynamic simulations, 54% trajectories decay to the S₀ state via S1S0-II; the remaining trajectories are de-excited to the S₀ state via S1S0-I1 (11%) and S1S0-I2 (35%). Our present theoretical investigation does not support the experimentally proposed S₁ excited-state hypothesis that the intramolecular rotation of the two dimethyl groups around the C–N bond is responsible for the rapid decay of the emission band at about 500 nm; instead, it should be heavily interrelated with the rotation of the two dimethylanilino groups. Finally, this work provides important mechanistic insights into similar diphenylmethane dyes.

---

Introduction

Due to their utility as molecular rotors, di- and tri-phenylmethane dyes such as malachite green, crystal violet, ethyl violet, and brilliant green have attracted a lot of experimental attention on their photophysical and photochemical properties.^1–25 In comparison, theoretical studies on these molecular rotors were rarely reported in the past decades.

Auramine-O, a representative diphenylmethane dye in Fig. 1, shows similar excited-state relaxation dynamics as has been reported for tri-phenylmethane dyes, especially its ultrafast photoinduced intramolecular conformational changes.^26–36 In the beginning, three important but different models were separately postulated by Oster and Nishijima,³⁷ Forster and Hoffmann,³⁸ and Bagchi, Fleming, and Oxtoby³⁹ to study the effect of viscosity on quantum yields and the barrierless torsional motion of phenyl groups that leads to radiationless decay to the ground state. However, all these models can only describe a single-exponential excited-state relaxation behavior. Later, Martine and Glasbeek questioned the single-exponential models on the basis of observing nonexponential excited-state behavior and proposed an adiabatic coupling model involving a locally emissive excited state and a nonemissive excited state.^40,41 Hirose et al. believed that not only solvent viscosity but also solvation dynamics affect the excited-state relaxation dynamics of Auramine-O.⁴² Meech and coworkers proposed that in aqueous solutions, solvation rather than solvent viscosity promotes a facile barrierless formation of a charge-transfer state and decides the excited-state relaxation.^43,44 Singh et al. investigated Auramine-O using sub-picosecond time-resolved absorption spectroscopic techniques in aprotic and alcoholic solvents.^45,46 They found two different stimulated emission bands at ca. 715 and 830 nm and suggested that there are two transition states involved in the excited-state relaxation. These findings are opposite to the widely accepted barrierless models. This is as well supported by Sen and Rafiq using time resolved femtosecond fluorescence measurements, in which an unexpectedly large fluorescence lifetime and multi-exponential transients in chloroform are observed.⁴⁷ They also found that Auramine-O has eight times larger fluorescence quantum yield in chloroform than in methanol and that the torsional motion of the dimethylanilino groups occurs in 1.5 ps in methanol and 14.2 ps in chloroform. More recently, Erez et al. employed steady-state and time-resolved optical techniques to study the short-time excited-state decay dynamics of Auramine-O with a duration of about 150–300 fs in several solutions at room temperature.^48,49 They found that its excited-state behavior could be divided into three time steps. The shortest decay time constant is associated with a strong emission with a band maximum at about 500 nm, which is attributed to the twisted motion of the dimethylamino group of the two anilines of Auramine-O. The second time constant is attributed to the rapid decay of the fluorescence band, which can be further red-shifted from about 510 nm to 550 nm in hydrogen-bonding solvents. The third time constant is related to a rather long decay of a dark state, about 10–20 ps in hydrogen-bonding liquids with medium viscosity. To summarize, experimentally, there exist a few ambiguous even paradoxical viewpoints on the photophysical mechanism of Auramine-O. For example, whether the torsional motion of the dimethylanilino groups is barrierless in the S₁ state? What are the geometric and electronic structures for the transient states observed in experiments? What are the intrinsic S₁ excited-state deactivation paths? Obviously, answering these atomistic mechanistic details calls for high-level ab initio electronic structure calculations, even the reliable nonadiabatic dynamics simulations.

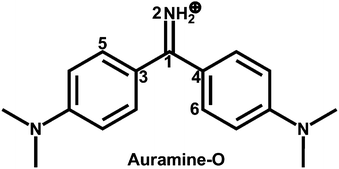Fig. 1 Molecular structure of the diphenylmethane dye Auramine-O. Also shown are the atomic labeling and the dihedral angles ϕ₁(N2C1C3C5), ϕ₂(N2C1C4C6), and ϕ₃(C3C1C4N2).

However, to the best of our knowledge, there are only few theoretical studies reported until now for excited-state properties of Auramine-O. Olsen proposed a four-electron, three-orbital model for low-energy electronic structures of several di- and tri-phenylmethane dyes including Auramine-O.³¹ Using DFT and TDDFT methods, Singh et al. obtained a ground state minimum and a transient state with the emission maximum at 831 nm.⁴⁵ But, they did not obtain the other transient states proposed experimentally. Sen and Pafiq employed the same computational methods to scan the S₁ and S₀ potential energy surfaces of Auramine-O with respect to the rotation of the dimethylanilino rings.⁴⁷ In addition, they suggested a funnel for the S₁ excited-state radiationless decay to the ground state taking into account of the small S₁–S₀ energy gap.

In this work, we first employed the complete active space self-consistent field (CASSCF) and its second-order perturbation (CASPT2) methods to explore the S₁ excited-state minima, conical intersections, and potential energy profiles relevant to the excited-state decay. On the basis of the results, we propose our S₁ excited-state deactivation model. Finally, we use the semiempirical OM2/MRCI-based nonadiabatic dynamics simulations to verify our physical model. This work presents the first effort to systematically study the S₁ excited-state deactivation pathways of Auramine-O using combined high-level electronic structure calculations and nonadiabatic dynamics simulations, setting the stage for studying the photophysics of other similar diphenylmethane dyes in near future.

Simulation details

Ab initio calculations

The ground-state conformer of Auramine-O is first optimized using the DFT method⁵⁰ with the B3LYP exchange–correlation functional.^51–54 Minima, conical intersections, and linearly interpolated internal coordinate (LIIC) paths are computed using the state-averaged complete active space self-consistent field (SA-CASSCF) method in which equal state weights are used for the S₁ and S₀ states. In the SA-CASSCF computations, the active space of 10 electrons in 8 orbitals is employed, which is referred to as SA-CASSCF(10,8) hereinafter. Since CASSCF theory is unable to provide sufficient correlation energy, the multi-state complete active space 2nd-order perturbation approach (MS-CASPT2)^55,56 is exploited to re-evaluate the energies of all optimized structures and LIIC paths. In the MS-CASPT2 computations, the Cholesky decomposition technique with unbiased auxiliary basis sets is used for accurate two-electron integral approximations;⁵⁷ the ionization potential-electron affinity (IPEA) shift of 0.0 is used;⁵⁸ the imaginary shift technique (0.2 au) is employed to avoid intruder-state issues.⁵⁹

Vertical excitation energies at Franck–Condon points are also calculated using the MS-CASPT2, TD-B3LYP, and TD-CAM-B3LYP methods.^60,61 6-31G and 6-31G* basis sets are employed for all geometry optimizations and single-point energy computations, respectively.^62–65 DFT and TD-DFT calculations are carried out using GAUSSIAN09;^50,60,66 SA-CASSCF optimizations for conical intersections are performed using MOLPRO2012;⁶⁷ all SA-CASSCF computations for minima and LIIC paths and MS-CASPT2 computations are conducted using MOLCAS8.0.^68,69

Semiempirical methods

All semiempirical calculations were performed using the OM2/MRCI method as implemented in the MNDO99 code.^70–73 During geometry optimizations and dynamics simulations, all required energies, gradients and nonadiabatic coupling elements were computed analytically. Minimum-energy conical intersections were optimized using the Lagrange–Newton approach.^74,75

In the OM2/MRCI calculations, the restricted open-shell HF formalism was applied in the self-consistent field (SCF) treatment. The active space in the MRCI calculations included 12 electrons in 12 orbitals (see ESI,† Fig. S1). In terms of the SCF configuration it comprised five highest doubly occupied orbitals, two singly occupied orbitals, and five lowest unoccupied orbitals. For the MRCI treatment, three configuration state functions were chosen as references, namely the SCF configuration and the two closed-shell configurations derived therefrom (i.e., all singlet configurations that can be generated from the HOMO and the LUMO of the closed-shell ground state). The MRCI wavefunction was built by allowing all single and double excitations from these three references.

Nonadiabatic dynamics

The S₁ nonadiabatic dynamics were studied by performing 1 ps OM2/MRCI trajectory surface-hopping simulations. The initial atomic coordinates and velocities for the S₁ photodynamics simulations were randomly selected from a 5 ps NVT (T = 300 K) ground-state trajectory. The excited state dynamic runs were then chosen according to the computed S₀–S₁ transition probabilities; configurations with very small S₀–S₁ transition dipole moments were not sampled. A total of 200 surface-hopping trajectories were run for the S₁ photodynamics, with all relevant energies, gradients, and nonadiabatic coupling vectors being computed on-the-fly as needed. For points with an energy gap of less than 10 kcal mol⁻¹, the fewest-switches criterion was applied to decide whether to hop. The time step was chosen to be 0.1 fs for the nuclear motion and 0.0005 fs for the electronic propagation. The unitary propagator evaluated at mid-point was used to propagate the electronic motion. The translational and rotational motions were removed in each step. The empirical decoherence correction (0.1 au) proposed by Granucci et al. was employed.⁷⁶ The final evaluations were done for 186 trajectories that finished successfully in the S₁ photodynamics and that satisfied our energy continuity criterion (no change greater than 30 kcal mol⁻¹ between any two consecutive MD steps). Further technical details were given in previous publications.^25,77–98

Results and discussion

S₀ structure and vertical excitation energies

By using the OM2/MRCI and SA-CASSCF methods, we have optimized the ground-state conformers of Auramine-O. All these computations give a similar equilibrium structure shown in Fig. 3. The stable S₀ conformer is almost in C₂ symmetry. Its C1–C3 and C1–C4 bond lengths are 1.439 and 1.440 Å at the SA-CASSCF level, its two dihedral angles ϕ₁(N2C1C3C5) and ϕ₂(N2C1C4C6) are computed to be 29.8° and 29.2° at the same computational level as well.

Table 1 collects the computed vertical excitation energies to S₁ at the S₀ minimum S0. Compared with the experimental value measured in methanol solution,⁴⁹ TD-CAM-B3LYP and MS-CASPT2 computations overestimate and underestimate the S₀ → S₁ vertical excitation energy, respectively; but, TD-B3LYP computations fortuitously give very good agreement. Our current OM2/MRCI computations give a reasonably accurate number: the vertical excitation energy to the S₁ state is 0.4 eV lower than the experimental value.⁴⁹

Table 1 Vertical excitation energies (in eV) of the S₁ state; experimental value are measured in methanol⁴⁹

	OM2/MRCI^a	MS-CASPT2^b	Exp.
a OM2/MRCI optimized S0 minimum structure. b SA-CASSCF optimized S0 minimum structure.
S1	2.6	2.6	3.0

---

Analysis of electronic configuration states in the CASPT2 computations illustrates that the S₁ vertical electronic excitation mainly originates from HOMO → LUMO as shown in Fig. 2 (weight: 0.67) and HOMO−1 → LUMO (0.16). The S₁ electronic state at the Franck–Condon point has clear charge-transfer character from the phenyl to methaniminium group. Charge-transfer electronic transition is usually associated with the remarkable change in the permanent electronic dipole moments, in either magnitudes or directions. In our OM2/MRCI computations, electronic dipole moments at the S₀ minimum S0 are computed to be 2.2 Debye for the S₀ state and 1.2 Debye for the S₁ state; thus, the S₁ state is of charge-transfer character. It is in line with the point of view proposed by Singh et al.⁴⁵ that the emissive state is expected to be less polar than the ground state due to the neutralization of the positive charge of the nitrogen atom as a result of intramolecular charge transfer from the dimethylanilino to methaniminium or imidocarbonyl group.

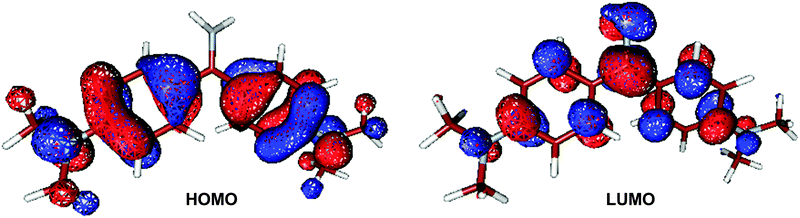Fig. 2 Canonical molecular orbitals related to the S₀ → S₁ (HOMO → LUMO) electronic transition at the Franck–Condon point at the OM2/MRCI level.

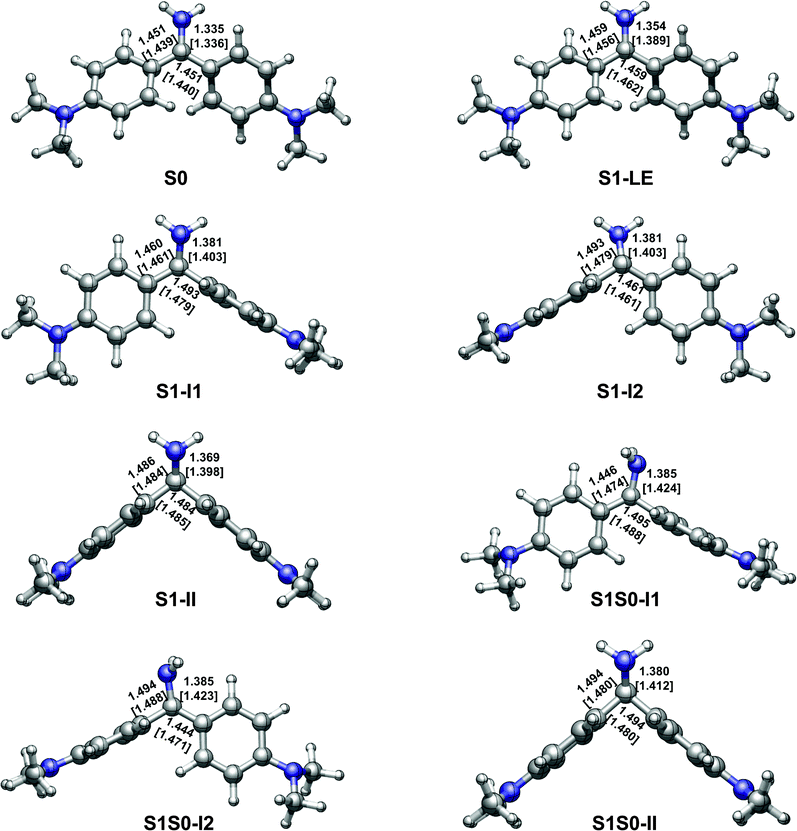Fig. 3 OM2/MRCI [SA-CASSCF] optimized S₀ and S₁ minima and S₁/S₀ conical intersections. See Table 2 for their relative energies and Fig. 1 for the dihedral angles ϕ₁(N2C1C3C5), ϕ₂(N2C1C4C6), and ϕ₃(C3C1C4 N2).

S₁ minima

With the OM2/MRCI and SA-CASSCF methods, three kinds of minima are optimized in the S₁ state, which are referred to as S1-LE, S1-I1, S1-I2, and S1-II in Fig. 3. Overall, S1-LE is structurally similar to the S₀ minimum S0 except for a little different bond lengths and dihedral angles. In comparison, S1-II changes a lot in structure. At the OM2/MRCI and SA-CASSCF levels, the corresponding ϕ₁ and ϕ₂ dihedral angles are ϕ₁ = 127.8° and 128.1°, and ϕ₂ = 33.9° and 34.9°; the C1–C3 and C1–C4 bond lengths are nearly same as each other, 1.486 and 1.484 Å…, and 1.484 and 1.485 Å…, respectively. Its dihedral angle ϕ₃ is also rotated to about 137.0° and 138.9° as the central carbon atom changes its hybridization pattern from sp² to sp³. In addition, we have also optimized another pair of S₁ minima i.e. S1-I1 and S1-I2 in Fig. 3. In these two structures, one aminophenyl group is almost perpendicular to the other aminophenyl and amino groups, for example, ϕ₂ = 103.6° (101.1°) for S1-I1 and ϕ₁ = 74.6° (77.2°) for S1-I2 at the OM2/MRCI (SA-CASSCF) level. Energetically, these four S₁ minima are close to each other in the order of S1-LE, S1-I1, S1-I2, and S1-II, they are 62.5 (60.0), 62.2 (68.1), 62.2 (68.1), and 60.4 (64.5) kcal mol⁻¹ at the OM2/MRCI (MS-CASPT2) level. However, their importance in the photodynamics of Auramine-O is very different due to the ease of access to these structures (see the following).

In experiments of steady-state absorption and emission spectra in different solutions, Palit and coworkers found an important spectroscopic feature that there is a weak but long tail in the main fluorescence band, which is beyond 800 nm.⁴⁵ The main intense emission band centered at 495 nm was experimentally assigned to a locally excited electronic state; the weak one to a relaxed weakly emissive excited state. In addition, on the basis of time-resolved absorption-stimulated emission spectra, Palit et al. also suggested that the relaxation process proceeds via the formation of at least two transient states, which are geometrical conformers and consecutively formed following the decay of the local excited state. The steady-state fluorescence spectra show three emission bands centered at 510 nm, 710 nm and 870 nm, respectively. All experimental information implies that there exist at least three S₁ minima. However, only a transient state was obtained computationally at the TD-DFT level to date.⁴⁵ The electronic and geometric structures of the other emissive states are not known. Here we have for the first time assigned these three emission bands. The emission band at S1-LE is computed to be at 523 nm with an oscillator strength of 0.84 at the MS-CASPT2 level. This should correspond to the intense emission band of the locally excited electronic state observed in experiments (510 nm). Similarly, emission bands of both S1-I1 and S1-I2 are calculated to be at 721 nm with an oscillator strengths of 0.10, which match very well with the weak emission bands at 710 nm. The emission band of S1-II is predicted to be at 884 nm with an oscillator strength of 0.06 at the MS-CASPT2 level, which should correspond to the weakest emission band at around 870 nm in experiments.⁴⁵

S₁/S₀ conical intersections

In addition, we have obtained three S₁/S₀ conical intersections, which are labeled as S1S0-I1, S1S0-I2, and S1S0-II in Fig. 3. Structurally, they are, respectively, close to their corresponding S₁ minima, for example, S1S0-I1 is close to S1-I1. Energetically, S1S0-II is the lowest among these three conical intersections: it is about 4.0 (4.8) and 4.7 (5.1) kcal mol⁻¹ lower than S1S0-I1 and S1S0-I2 at the OM2/MRCI (MS-CASPT2) level. All these three S₁/S₀ conical intersections are energetically accessible because they are just ca. 5 kcal mol⁻¹ higher than their related S₁ minima in energy. On the other hand, the computed LIIC paths also show that S1S0-I1, S1S0-I2, and S1S0-II can be approached readily from the corresponding S₁ minima (see panels a, b, and c in Fig. 4).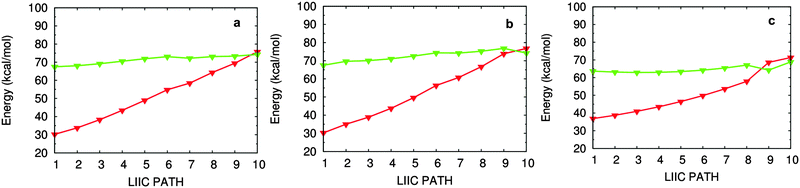

Fig. 4 Linearly interpolated internal coordinate (LIIC) paths connecting (a) S1-I2 and S1S0-I2; (b) S1-I1 and S1S0-I1; and (c) S1-II and S1S0-II.

Nonadiabatic dynamics

On the basis of the results of static electronic structure computations, one can see that the chosen OM2/MRCI method gives reasonably accurate S₁ excited-state electronic and geometric structures in comparison to those computed by the SA-CASSCF method. More important for photodynamics simulations is that the OM2/MRCI method can accurately describe the conical intersections among the lowest two singlet states of Auramine-O, i.e. S₀ and S₁. In the following, the OM2/MRCI method is exploited to simulate the photodynamics of Auramine-O starting from the initial S₁ excited state.

Among the 186 trajectories in the S₁ nonadiabatic dynamics simulations, 46 trajectories decay to the S₀ state at the end of 1 ps; while, 140 trajectories survive in the S₁ state. Fig. 5 shows the time-dependent S₁ and S₀ state populations. In the first 260 fs, both state populations do not change at all. This period of time should correspond to the initial relaxation time from the S₁ Franck–Condon point via the S₁ minima to the S₁/S₀ conical intersections. This process takes a relatively long time because such a process involves a marked conformational change, e.g. ϕ₁ changes from 28.6° of S0 to 135.6° of S1S0-II. After this relaxation, the S₁ system starts to decay gradually to the S₀ state until the end of simulations.

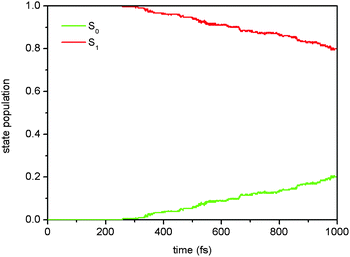Fig. 5 Time-dependent S₁ and S₀ state populations in the two-state (S₁ and S₀) photodynamics simulations.

If the S₁ excited-state decay is treated as a first-order process, we can estimate the S₁ excited-state lifetime τ to be about 3.6 ps according to the single-exponential fitting equation of p = exp(− (t − t₀)/τ) + p₀, in which the initial delay time t₀ and the residual S₁ state population p₀ are assigned to 258.8 fs and 0.8, respectively.

The distribution of the selected dihedral angles ϕ₁ and ϕ₂ at all S₁ → S₀ hopping points in the S₁ photodynamics is shown in Fig. 6. The dihedral angles ϕ₁(N2C1C3C5) and ϕ₂(N2C1C4C6) are mainly distributed around 40–70° and 110–140°, respectively. Such distribution is consistent with the S₁ excited-state topological structures computed in the preceding static electronic structure calculations (see above). S1S0-II is energetically the lowest among the three S₁/S₀ conical intersections: it is about 5.0 kcal mol⁻¹ lower than the other two at the OM2/MRCI and MS-CASPT2 levels (see Table 2). In addition, in our case, along the ϕ₁ and ϕ₂ dihedral angles, the S₁–S₀ energy gap is very small; the S₁ potential energy surface is very flat and forms an extended conical intersection seam with the S₀ state. Therefore, the distribution of these two angles at the hopping points is much spread.

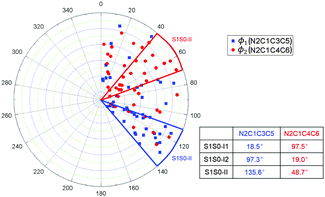Fig. 6 Distribution of the dihedral angles ϕ₁(N2C1C3C5) and ϕ₂(N2C1C4C6) at the S₁ → S₀ hopping points.

Table 2 OM2/MRCI [MS-CASPT2] computed relative energies (in kcal mol⁻¹) of all OM2/MRCI [CASSCF] optimized structures

Structure	S0	S1-LE	S1-I1	S1-I2
OM2/MRCI	0.0	62.5	62.2	62.2
MS-CASPT2	0.0	60.0	68.1	68.1

---

Structure	S1-II	S1S0-I1	S1S0-I2	S1S0-II
OM2/MRCI	60.4	66.5	67.2	62.5
MS-CASPT2	64.5	74.0	74.3	69.2

---

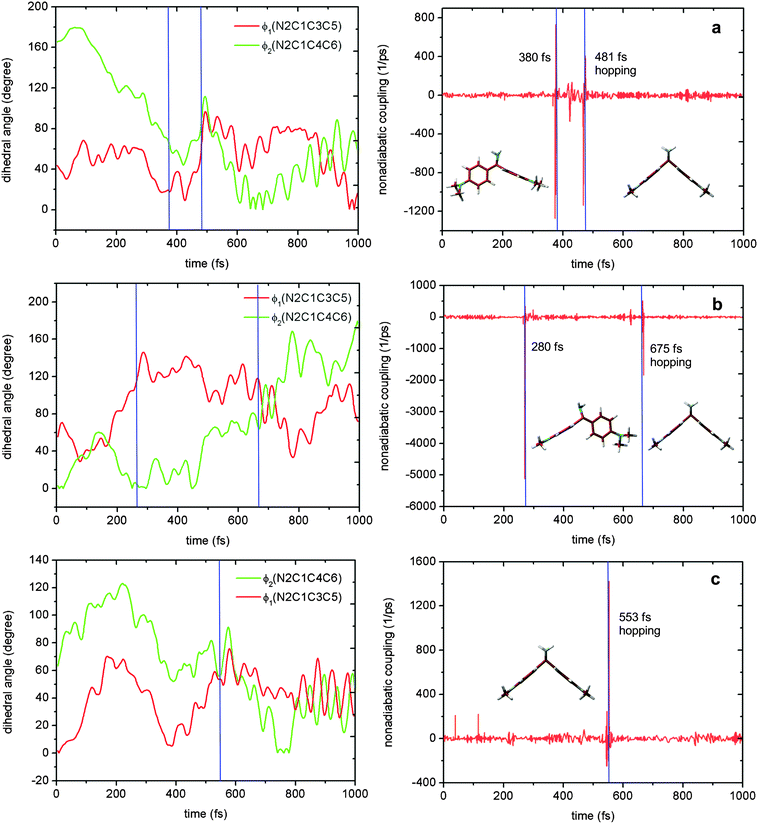
It is found from Fig. 7 that 54% hopping-trajectories decay to the S₀ state via S1S0-II; and, 11% and 35% hopping-trajectories do via S1S0-I1 and S1S0-I2. How to understand this distribution? First, energetically, S1S0-II is the lowest one among the three S₁/S₀ conical intersections; the former is computed to be about 5.0 kcal mol⁻¹ lower than the latter two at both OM2/MRCI and MS-CASPT2 levels. Thus, we can understand very well that the preferred S₁ → S₀ hopping region is close to S1S0-II. Second, why is S1S0-I2 superior to S1S0-I1 for the S₁ excited-state deactivation although both conical intersections have nearly same potential energies? It is clear that upon irradiation to the S₁ state, the lowest S₁ minimum S1-LE is first populated because S1-LE is structurally more close to the Franck–Condon point i.e. the S₀ minimum S0 (see Fig. 3). At this point, except proceeding to S1-II, there still exist two other excited-state relaxation paths, first to S1-I1 and second to S1-I2. However, as shown in Fig. 8, the conformational change from S1-LE to S1-I2 is significantly smaller than that from S1-LE to S1-I1. Therefore, more trajectories will decay to the S₀ state around S1-I2 via S1S0-I2. In addition, we have computed the averaged S₁ → S₀ hopping times via S1S0-I1, S1S0-I2, and S1S0-II, which are 441, 597, and 716 fs, respectively, (Table 3).

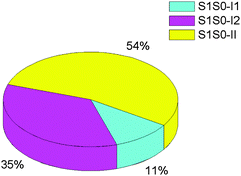Fig. 7 Percentage distribution of the S₁ → S₀ hoppings via S1S0-I1, S1S0-I2, and S1S0-II conical intersections in the photodynamics of Auramine-O.

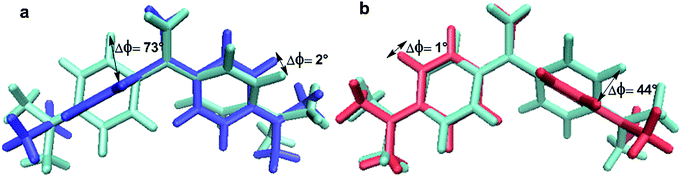Fig. 8 Spatial overlap of the three different S₁ geometric structures produced using the VMD1.9.1 package:⁹⁹ (a) S1-LE and S1-I1 and (b) S1-LE and S1-I2.

Table 3 Averaged S₁ → S₀ hopping times (unit: fs) via S1S0-I1, S1S0-I2, and S1S0-II

	S1S0-I1	S1S0-I2	S1S0-II
t	441	597	716

---

Typical trajectories

It is noteworthy that starting from the locally excited S₁ minimum S1-LE, there exist three competitive S₁ relaxation processes (two sequential and one concerted paths; see panal a of Fig. 9).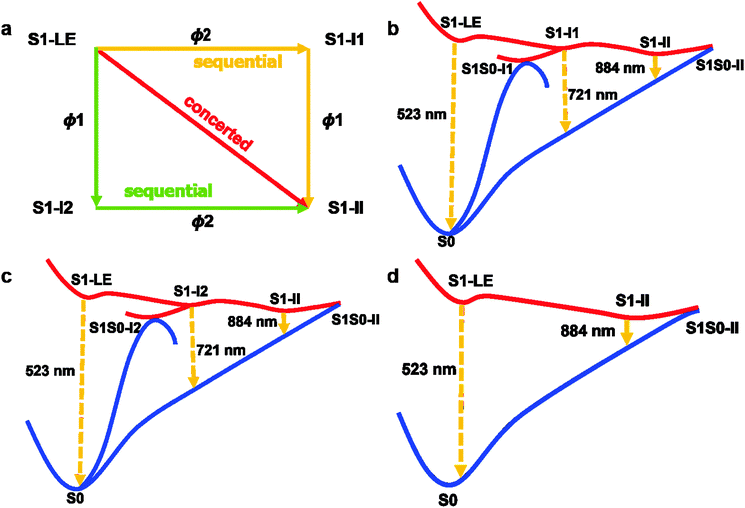

Fig. 9 Concerted and sequential deactivation channels proposed based on the present electronic structure calculations and nonadiabatic dynamics simulations. See text for discussion.

The first two relaxation processes are related to the rotation of two dimethylanilino groups (ϕ₁ and ϕ₂), as shown in panels b and c of Fig. 9. In these two paths, the system near the locally excited S₁ minimum first proceeds into a transient excited-state intermediate S1-I1 or S1-I2 via a simple rotation of a dimethylanilino group. These two intermediates S1-I1 and S1-I2 are spectroscopically observed in experiments (see the above discussion). After arriving at S1-I1 or S1-I2, the system not only can decay to the S₀ state via the nearby S₁/S₀ conical intersections S1S0-I1 or S1S0-I2 but also can further evolve into the S₁ minimum S1-II by rotating the remaining dimethylanilino group (transient state II in experiments). Finally, the system is de-excited via another S₁/S₀ conical intersection S1S0-II returning back the S₀ state. Certainly, in addition to the sequential paths to S1-II, from the locally S₁ excited-state minimum S1-LE the system can also, bypassing S1-I1 and S1-I2, concertedly proceed into the final transient S₁ excited-state minimum S1-II.

Fig. 10 shows the time-dependent evolution of the two dihedral angles ϕ₁ and ϕ₂ and the S₁–S₀ nonadiabatic coupling in three trajectories that support the sketch in Fig. 9. Panels a and b represent the sequential S₁ relaxation paths. As shown in panel a, in the first 380 fs, the ϕ₂ dihedral angle gradually decreases to about 70° from the initial 160°; while, the corresponding ϕ₁ dihedral angle just oscillates around its equilibrium value. At that time, the system still encounters a conical intersection region with large nonadiabatic coupling. However, the system does not hop to the S₀ state; instead, it continues to evolve into the S1-II region through rotating the ϕ₁ dihedral angle. Near this region, the S₁ system jumps to the ground state at 481 fs. The dynamic bahavior of the trajectory in panel b of Fig. 10 is similar to that in panel a, except for rotating the two dihedral angles ϕ₁ and ϕ₂ in a different order. In contrast, in panel c, the rotations of these two dihedral angles proceed in a synchronous means; hence, the system in this trajectory directly runs into the S1-II region, near which the S₀ state is populated at 553 fs as a result of the S₁ → S₀ internal conversion. Finally, it must be stressed that in our simulations, most of the trajectories decay to the ground state using the concerted way and only a few ones decay to S₀via the sequential means.

Fig. 10 Three representative trajectories. In panels a and b, the S₁ system first evolves to the transient intermediates S1-I1 or S1-I2 and then to the final transient state S1-II; in panel c, the system concertedly, bypassing S1-I1 and S1-I2, proceeds into the final transient S₁ excited-state minimum S1-II.

Correlation with experiments

On the basis of the results of present static electronic structure calculations and dynamics simulations, we have gained several new mechanistic insights into the photophysics of Auramine-O.

First, we have for the first time computationally characterized the three S₁ excited-state transient states observed in the subpicosecond time-resolved spectroscopic experiments of Singh et al.⁴⁵ (see above; Fig. 9).

Second, the emission band at ca. 500 nm observed in the steay-state and time-resolved experiments of Erez et al.,⁴⁹ in terms of our computational results, should be assigned to the locally excited transient state.

Third, in addition to the experimentally proposed sequential S₁ relaxation process leading to the transient intermediate S1-II (referred to as TS II in experiments), we have observed a concerted S₁ relaxation path to S1-II. This explains why the S₁ relaxation process exhibits a multi-exponential excited-state dynamics behavior.⁴⁵

Fourth, the S₁ excited-state decay is experimentally proposed to occur primarily near S1-II.⁴⁵ However, the corresponding S₁/S₀ conical intersection is not characterized computationally until now. Here, we not only optimized this conical intersection but also found the other two S₁/S₀ conical intersections in the vicinity of S1-I1 and S1-I2. The importance of these three conical intersections in the S₁ excited-state decay of Auramine-O has been proved in our nonadiabatic dynamics simulations. It is found that S1S0-II plays a major role in the S₁ excited-state decay; but, the significance of the other two conical intersections S1S0-I1 and S1S0-I2 cannot be excluded as well, which accounts for 46% of all trajectories that decay to the S₀ state.

Fifth, in a recent experimental study, Erez et al. proposed an S₁ excited-state deactivation mechanism: the intramolecular rotation of the dimethyl groups around the C–N bond is responsible for the rapid decay (150–300 fs) of the emission band at about 500 nm.⁴⁹ This mechanism is not supported by our present electronic structure calculations and nonadiabatic dynamics simulations; instead, the S₁ excited-state decay should be heavily interrelated with the rotation of the dimethylanilino groups, which is consistent with experiments of Rafiq et al.⁴⁷ and Singh et al.⁴⁵

Conclusions

With the use of high-level MS-CASPT2//CASSCF electronic structure calculations and semi-empirical OM2/MRCI nonadiabatic dynamics simulations, we have for the first time theoretically explored the S₁ excited-state deactivation mechanism of Auramine-O. First, the S₁ excited-state minima, the S₁/S₀ conical intersections, and the relevant S₁ excited-state potential energy profiles are computed at the MS-CASPT2//CASSCF and OM2/MRCI levels. On the basis of these static electronic structure calculations, we have assigned all three transient states proposed in experiments⁴⁵ and suggested an S₁ excited-state decay mechanism involving three S₁ transient intermediate states and three S₁/S₀ conical intersections. Our proposed S₁ decay mechanism is immediately verified by our following OM2/MRCI-based surface-hopping dynamics simulations. In addition, we have found that the S₁ relaxation process to the final transient state can proceed either sequentially or concertedly. This work represents the first theoretical effort to explore the S₁ excited-state deactivation processes of diphenylmethane dyes.

Acknowledgements

This work was supported by National Natural Science Foundation of China (21421003); G.C. is also grateful for financial support from “Recruitment Program of Global Youth Experts” and “Fundamental Research Funds for Central Universities”.

References

1. W. Yu, F. Pellegrino, M. Grant and R. R. Alfano, J. Chem. Phys., 1977, 67, 1766–1773.
2. J. M. Grzybowski, S. E. Sugamori, D. F. Williams and R. W. Yip, Chem. Phys. Lett., 1979, 65, 456–460.
3. D. A. Cremers and M. W. Windsor, Chem. Phys. Lett., 1980, 71, 27–32.
4. R. Menzel, C. W. Hoganson and M. W. Windsor, Chem. Phys. Lett., 1985, 120, 29–34.
5. M. Vogel and W. Rettig, Ber. Bunsen-Ges. Phys. Chem., 1985, 89, 962–968.
6. A. Mokhtari, L. Fini and J. Chesnoy, J. Chem. Phys., 1987, 87, 3429–3435.
7. F. W. Wise, M. J. Rosker and C. L. Tang, J. Chem. Phys., 1987, 86, 2827–2832.
8. M. Canva, G. Le Saux, P. Georges, A. Brun, F. Chaput and J. P. Boilot, Chem. Phys. Lett., 1991, 176, 495–498.
9. M. Ishikawa and Y. Maruyama, Chem. Phys. Lett., 1994, 219, 416–420.
10. K. M. Abedin, J. Y. Ye, H. Inouye, T. Hattori, H. Sumi and H. Nakatsuka, J. Chem. Phys., 1995, 103, 6414–6425.
11. Y. Maruyama, M. Ishikawa and H. Satozono, J. Am. Chem. Soc., 1996, 118, 6257–6263.
12. J. Y. Ye, T. Hattori, H. Inouye, H. Ueta, H. Nakatsuka, Y. Maruyama and M. Ishikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 8349–8353.
13. J. Y. Ye, T. Hattori, H. Nakatsuka, Y. Maruyama and M. Ishikawa, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 5286–5296.
14. B. Strehmel, H. Seifert and W. Rettig, J. Phys. Chem. B, 1997, 101, 2232–2243.
15. A. C. Bhasikuttan, L. V. Shastri, A. V. Sapre and J. P. Mittal, J. Photochem. Photobiol., A, 1998, 112, 179–185.
16. J. Y. Ye, M. Ishikawa, O. Yogi, T. Okada and Y. Maruyama, Chem. Phys. Lett., 1998, 288, 885–890.
17. M. Ishikawa, J. Y. Ye, Y. Maruyama and H. Nakatsuka, J. Phys. Chem. A, 1999, 103, 4319–4331.
18. M. Jurczok, P. Plaza, M. M. Martin and W. Rettig, J. Phys. Chem. A, 1999, 103, 3372–3377.
19. Y. Maruyama, O. Magnin, H. Satozono and M. Ishikawa, J. Phys. Chem. A, 1999, 103, 5629–5635.
20. Y. Kanematsu, H. Ozawa, I. Tanaka and S. Kinoshita, J. Lumin., 2000, 87–89, 917–919.
21. M. Glasbeek and H. Zhang, Chem. Rev., 2004, 104, 1929–1954.
22. M. Kondo, I. A. Heisler, J. Conyard, J. P. H. Rivett and S. R. Meech, J. Phys. Chem. B, 2009, 113, 1632–1639.
23. M. Kondo, I. A. Heisler and S. R. Meech, Faraday Discuss., 2010, 145, 185–203.
24. S. Rafiq, B. K. Rajbongshi, N. N. Nair, P. Sen and G. Ramanathan, J. Phys. Chem. A, 2011, 115, 13733–13742.
25. B. B. Xie, S. H. Xia, L. H. Liu and G. L. Cui, J. Phys. Chem. A, 2015, 119, 5607–5617.
26. P. Changenet, H. Zhang, M. J. Van Der Meer, M. Glasbeek, P. Plaza and M. M. Martin, J. Phys. Chem. A, 1998, 102, 6716–6721.
27. P. Changenet, H. Zhang, M. J. van der Meer, M. Glasbeek, P. Plaza and M. M. Martin, J. Fluoresc., 2000, 10, 155–160.
28. N. Forsberg and P. A. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204.
29. M. Hasegawa, T. Sugimura, Y. Suzaki, Y. Shindo and A. Kitahara, J. Phys. Chem., 1994, 98, 2120–2124.
30. N. T. Hunt, A. A. Jaye and S. R. Meech, Chem. Phys. Lett., 2005, 416, 89–93.
31. S. Olsen, J. Phys. Chem. A, 2012, 116, 1486–1492.
32. P. Prosposito, H. Zhang and M. Glasbeek, J. Sol-Gel Sci. Technol., 2011, 60, 347–351.
33. R. F. Steiner, S. Albaugh, E. Nenortas and L. Norris, Biopolymers, 1992, 32, 73–83.
34. S. R. Valandro, A. L. Poli, M. G. Neumann and C. C. Schmitt, J. Lumin., 2015, 161, 209–213.
35. Y. Wang and H. Morawetz, Macromolecules, 1986, 19, 1925–1930.
36. J. G. Weers and A. H. Maki, Biochemistry, 1986, 25, 2897–2904.
37. G. Oster and Y. Nishijima, J. Am. Chem. Soc., 1956, 78, 1581–1584.
38. T. Förster and G. Hoffmann, Z. Phys. Chem., Neue Folge, 1971, 75, 63–76.
39. B. Bagchi, G. R. Fleming and D. W. Oxtoby, J. Chem. Phys., 1983, 78, 7375–7385.
40. M. Glasbeek, H. Zhang and M. J. Van der Meer, J. Mol. Liq., 2000, 86, 123–126.
41. M. J. Van Der Meer, H. Zhang and M. Glasbeek, J. Chem. Phys., 2000, 112, 2878–2887.
42. Y. Hirose, H. Yui and T. Sawada, J. Phys. Chem. B, 2004, 108, 9070–9076.
43. I. A. Heisler, M. Kondo and S. R. Meech, J. Phys. Chem. B, 2009, 113, 1623–1631.
44. M. Kondo, I. A. Heisler and S. R. Meech, J. Mol. Liq., 2012, 176, 17–21.
45. C. Singh, B. Modak, J. A. Mondal and D. K. Palit, J. Phys. Chem. A, 2011, 115, 8183–8196.
46. P. K. Singh, A. K. Mora, S. Murudkar and S. Nath, RSC Adv., 2014, 4, 34992–35002.
47. S. Rafiq and P. Sen, J. Chem. Phys., 2013, 139, 124302.
48. Y. Erez, N. Amdursky, R. Gepshtein and D. Huppert, J. Phys. Chem. A, 2012, 116, 12056–12064.
49. Y. Erez, R. Simkovitch, K. Akulov, R. Gepshtein, T. Schwartz and D. Huppert, J. Phys. Chem. C, 2014, 118, 27063–27073.
50. R. G. Parr and W. T. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, USA, 1994.
51. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
52. C. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
53. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
54. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
55. K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
56. K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
57. F. Aquilante, R. Lindh and T. Bondo Pedersen, J. Chem. Phys., 2007, 127, 114107.
58. G. Ghigo, B. O. Roos and P. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149.
59. N. Försberg and P. Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204.
60. M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. K. U. Gross, Time-dependent Density Functional, Springer, 2006.
61. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
62. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 54, 724–728.
63. M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665.
64. G. L. Cui, P. J. Guan and W.-H. Fang, J. Phys. Chem. A, 2014, 118, 4732–4739.
65. P. J. Guan, G. L. Cui and Q. Fang, ChemPhysChem, 2015, 16, 805–811.
66. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheesem, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
67. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012, see http://www.molpro.net.
68. G. Karlström, R. Lindh, P. Å. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P. O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–229.
69. F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247.
70. W. Weber, PhD thesis, University of Zürich, 1996.
71. W. Weber and W. Thiel, Theor. Chem. Acc., 2000, 103, 495–506.
72. A. Koslowski, M. E. Beck and W. Thiel, J. Comput. Chem., 2003, 24, 714–726.
73. W. Thiel, MNDO99 program, version 6.1, Max-Planck-Institut für Kohlenforschung, Mülheim, Germany, 2007.
74. D. R. Yarkony, J. Chem. Phys., 2001, 114, 2601–2613.
75. T. W. Keal, A. Koslowski and W. Thiel, Theor. Chem. Acc., 2007, 118, 837–844.
76. G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111.
77. M. R. Silva-Junior and W. Thiel, J. Chem. Theory Comput., 2010, 6, 1546–1564.
78. M. Barbatti, A. J. A. Aquino, J. J. Szymczak, D. Nachtigallova, P. Hobza and H. Lischka, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 21453–21458.
79. D. Nachtigallova, T. Zeleny, M. Ruckenbauer, T. Müller, M. Barbatti, P. Hobza and H. Lischka, J. Am. Chem. Soc., 2010, 132, 8261–8263.
80. T. Zelený, M. Ruckenbauer, A. J. A. Aquino, T. Müller, F. Lankaš, T. Dršata, W. L. Hase, D. Nachtigallova and H. Lischka, J. Am. Chem. Soc., 2012, 134, 13662–13669.
81. H. L. Tao, B. G. Levine and T. J. Martinez, J. Phys. Chem. A, 2009, 113, 13656–13662.
82. M. Richter, P. Marquetand, J. González-Vázquez, I. Sola and L. González, J. Phys. Chem. Lett., 2012, 3, 3090–3095.
83. L. Martnez-Fernández, I. Corral, G. Granucci and M. Persico, Chem. Sci., 2014, 5, 1336–1347.
84. G. L. Cui and W. Thiel, J. Chem. Phys., 2014, 141, 124101.
85. G. L. Cui and W. Thiel, Angew. Chem., Int. Ed., 2013, 52, 433–436.
86. G. L. Cui, Z. G. Lan and W. Thiel, J. Am. Chem. Soc., 2012, 134, 1662–1672.
87. G. L. Cui and W. Thiel, Phys. Chem. Chem. Phys., 2012, 14, 12378–12384.
88. L. Spörkel, G. L. Cui, A. Koslowski and W. Thiel, J. Phys. Chem. A, 2013, 118, 152–157.
89. L. Spörkel, G. L. Cui and W. Thiel, J. Phys. Chem. A, 2013, 117, 4574–4583.
90. O. Weingart, Z. G. Lan, A. Koslowski and W. Thiel, J. Phys. Chem. Lett., 2011, 2, 1506–1509.
91. A. Kazaryan, Z. G. Lan, L. V. Schafer, W. Thiel and M. Filatov, J. Chem. Theory Comput., 2011, 7, 2189–2199.
92. Y. Lu, Z. G. Lan and W. Thiel, Angew. Chem., Int. Ed., 2011, 50, 6864–6867.
93. E. Fabiano, T. W. Keal and W. Thiel, Chem. Phys., 2008, 349, 334–347.
94. J. B. Schönborn, A. Koslowski, W. Thiel and B. Hartke, Phys. Chem. Chem. Phys., 2012, 14, 12193–12201.
95. J. B. Schönborn and B. Hartke, Phys. Chem. Chem. Phys., 2014, 16, 2483–2490.
96. R. B. Gerber, D. Shemesh, M. E. Varner, J. Kalinowski and B. Hirshberg, Phys. Chem. Chem. Phys., 2014, 16, 9760–9775.
97. D. Shemesh, S. L. Blair, S. A. Nizkorodov and R. B. Gerber, Phys. Chem. Chem. Phys., 2014, 16, 23861–23868.
98. S.-H. Xia, B.-B. Xie, Q. Fang, G. Cui and W. Thiel, Phys. Chem. Chem. Phys., 2015, 17, 9687–9697.
99. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.

---

Footnote

† Electronic supplementary information (ESI) available: Active orbitals in the OM2/MRCI and CASSCF computations and Cartesian coordinates of all optimized structures and paths. See DOI: 10.1039/c5cp05312a

---