Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
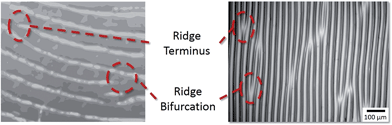
Hierarchical line-defect patterns in wrinkled surfaces†
Bernhard A.
Glatz
a,
Moritz
Tebbe
a,
Badr
Kaoui
b,
Roland
Aichele
b,
Christian
Kuttner
a,
Andreas E.
Schedl
c,
Hans-Werner
Schmidt
c,
Walter
Zimmermann
b and
Andreas
Fery
*a
aDepartment of Physical Chemistry II, University of Bayreuth, 95440 Bayreuth, Germany. E-mail: andreas.fery@uni-bayreuth.de
bTheoretical Physics I, University of Bayreuth, 95440, Bayreuth, Germany. E-mail: walter.zimmermann@uni-bayreuth.de
cDepartment of Macromolecular Chemistry I, University of Bayreuth, 95440, Bayreuth, Germany. E-mail: hans-werner.schmidt@uni-bayreuth.de
First published on 11th March 2015
Abstract
We demonstrate a novel approach for controlling the formation of line-defects in wrinkling patterns by introducing step-like changes in the Young's modulus of elastomeric substrates supporting thin, stiff layers. Wrinkles are formed upon treating the poly(dimethylsiloxane) (PDMS) substrates by UV/Ozone (UVO) exposure in a uniaxially stretched state and subsequent relaxation. Line defects such as minutiae known from fingerprints are a typical feature in wrinkling patterns. The position where these defects occur is random for homogenous substrate elasticity and film thickness. However, we show that they can be predetermined by using PDMS substrates consisting of areas with different cross-linking densities. While changing the cross-linking density is well known to influence the wrinkling wavelength, we use this parameter in this study to force defect formation. The defect formation is monitored in situ using light microscopy and the mechanical parameters/film thicknesses are determined using imaging AFM indentation measurements. Thus the observed wrinkle-wavelengths can be compared to theoretical predictions. We study the density and morphology of defects for different changes in elasticity and compare our findings with theoretical considerations based on a generalized Swift–Hohenberg-equation to simply emulate the observed pattern-formation process, finding good agreement. The fact that for suitable changes in elasticity, well-ordered defect patterns are observed is discussed with respect to formation of hierarchical structures for applications in optics and nanotechnology.
Introduction
Wrinkling is a mechanical instability phenomenon of thin films. Wrinkles form, if a laminar system consisting of a stiff, thin layer in strong adhesive contact with a soft, macroscopic elastomer is subject to in-plane compression. Under these conditions, the well-known buckling instability results in periodic surface corrugations. Due to its generic nature, wrinkling can be found in biological,1,2 geomorphological3,4 as well as artificial structures.5,6 In the framework of surface patterning and structuring, controlled formation of wrinkles has been investigated and characterized intensively in the last two decades.7–12 Importantly, permanent wrinkle patterns can be formed, if the thin layer is created while an elastomeric substrate is under strain and subsequently relaxed. Possible preparation methods are in situ oxidation of poly(dimethylsiloxane) (PDMS) substrates by treatment with plasma,13,14 UVO,15–17 wet chemicals18 or coating of these substrates with metals19 and polymers,20 respectively. Besides, other methods are employed, e.g. the utilization of distortion effects of elastomers at an water–substrate-interface that lead to sinusoidal bending21 or the coating of an elastomer with a UV-curable material instead of attaching two layers to each other.22Wrinkle patterns display always deviations from an ideal structure, even in the simplest case of uni-axial strain, yielding parallel oriented wrinkles. These defects can be classified into two categories, cracks and line defects, respectively. Most work has been done on the investigation of cracks, which are mechanically induced film fractures.23–25 Recently, some publications report on specific applications of thin-film-cracking where the evolving channels are filled with metals and consequently utilized as conducting 2D-networks.26,27 In contrast our work focuses on the second defect type – the line defects that are known as minutiae in fingerprints. Their evolution in random fingerprint-like structures with defects has been simulated lately.28 Line defects are characterized by two adjacent ridges merging into one single ridge or by a termination of a ridge, as illustrated in Fig. 1 for fingerprints, where the term minutiae is used for the line defects, and for wrinkle patterns formed using the method presented in this study.
For ideal homogenous, infinite systems line defect nucleation is a homogenous nucleation process. However, in real systems line defects are frequently found to nucleate at heterogeneities in elastic constants or film thicknesses or at boundaries. In many applications, these line defects are considered a nuisance since they appear stochastically and thus limit the structural perfection and long range order of wrinkling patterns. However, they as well present an interesting example of symmetry breaking and harnessing the position at which line defects occur might pave the road to control symmetry breaking and formation of complex hierarchical structures.
Following this rationale, we present a method to generate patterned defects in a controlled fashion. We introduce a novel method for the preparation of PDMS with steep local changes in the Young's modulus and study permanent wrinkle formation in these systems. We investigate the mechanical properties of the system using nanomechanical AFM techniques. Furthermore, we employ light microscopy for in situ investigation of wrinkle and line-defect formation. These studies are the basis to elucidate the underlying structure formation mechanism. We investigate the spatial distribution of line defects and long range ordering effects. Finally, we discuss potential applications in optics, particle alignment or microfluidics.29,30
Results and discussion
Wrinkled samples were prepared from commercially available PDMS system Sylgard 184 (Dow Corning Ltd., Midland, USA). PDMS samples were treated with UVO in uni-axially stretched state to induce wrinkle formation upon relaxation. A buckling instability caused by mechanical mismatch between the applied thin oxide layer and the elastic substrate leads to wrinkle formation perpendicular to the strain direction (see Fig. 2). The resulting wavelengths of the buckling instability can be calculated for small strains according to the well-known eqn (1)–(3)31,32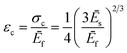 | (1) |
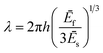 | (2) |
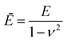 | (3) |
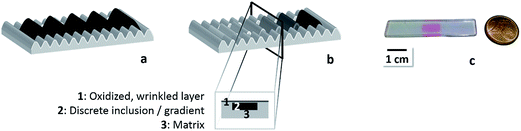
Herein, εc represents the critical uniaxial strain necessary to induce wrinkling, while λ describes the wavelength of the buckling instability, h is denoted as layer thickness and Ēf and Ēs are the plane-strain-moduli of the layer and substrate respectively that can be calculated with the according Poisson's ratio ν. Modifying the ratio of the pre-polymer to curing-agent results in a stiffness variation of the resulting silicone from 0.24 MPa to 1.82 MPa. To create a sample that features two different wrinkling wavelengths and a small, defined crossover area in between, we combined these materials displaying large differences in stiffness.
Sample preparation
The samples were prepared sequentially in three steps: (1) a matrix containing the highest cross-linker content was prepared, (2) fluid soft PDMS being discrete or gradient-like was cast into the matrix presenting one side and (3) the matrix was cross-linked thermally, ensuring a covalent linkage between both phases. The process is depicted in the ESI schematically in Fig. S1.† Thus, PDMS of adjustable Young's modulus was embedded in a matrix of hard PDMS. Consequently, the interface between both materials displayed a sharp mechanical transition between the different phases of PDMS. According to eqn (2) a change of substrate elasticity is directly correlated with a change in wavelength for constant film elasticity and thickness. To investigate wrinkling of substrates with different Young's moduli focusing on the defect formation process two different sample types were prepared (Fig. 2). One sample type was prepared casting soft PDMS into a mold consisting of only hard PDMS (Fig. 2a) giving a composite consisting of two pure materials. The other sample type was prepared by casting a soft-to-hard-gradient into a mold of hard PDMS using a modified method of Claussen et al.33 (Fig. 2b). The line-defects are expected to preferentially nucleate at the interface of hard-to-soft material. This is due to a difference in substrate stiffness, which forces a local change of preferred wavelength that goes along with formation of line branches. Additionally, the speed of relaxation has an impact on their number and shape,34 that is why the samples were allowed to relax with highest possible rate after oxidation to create as many line defects as possible. Furthermore, according to eqn (1) the wrinkle evolution is not simultaneous in both phases, but will occur when the critical strain εc is reached, depending on the respective Young's moduli. In order to analyze this predicted behavior, we used a custom-built in situ setup (see also Fig. S2†) based on optical microscopy to study wrinkle and defect formation along the stiffness modification lines.Qualitative analysis
The stretched and oxidized samples were released with a defined speed. The wrinkle evolution was tracked in situ via reflected light microscopy focused at the oxidized surface layer in order to capture changes in the surface morphology. Fig. 3 shows representative results for a homogeneous sample with a discrete step in substrate elasticity: After focusing the interface between hard and soft polymer the wrinkle evolution was induced by slowly decreasing the strain from an elongation of ε = 50% (15 mm initial sample length and 22.5 mm strained state) with 6.1 mm min−1. For a ε of 41% the first wrinkles can be observed in the soft phase (Fig. 3b). They were entirely shaped at a ε of 39% (Fig. 3c), meaning the amount of waves and line-defects remains constant. For a ε of 35% buckling is induced within the hard phase (Fig. 3d). The wrinkle evolution is completed at a ε of 30% resulting in a fully wrinkle-covered surface (Fig. 3e). The corrugations on the soft phase slightly protrude into the unwrinkled hard phase (Fig. 3c). It is caused by different boundary conditions of the two phases which results in a singularity within the interphase that consequently induces line-defect formation close to the interface. Here the critical strain as well as the final wavelength changes dramatically. Thus, line defects caused by singularity are pinned to the interface transition or nucleate in close proximity. Further strain release afterwards only leads to a compression of the waves, which results in increasing amplitudes and reduced wavelengths. The underlying wrinkle formation process can be divided into two different steps. First the waves emerge within domains with sizes of a few buckling periods, followed by a rapid growth with decreasing strain resulting in wrinkle joining. The latter is accompanied by the appearance of line-defects.35 Furthermore, the buckling period depends on the stiffness (Young's modulus) of the underlying substrate following a third root law, in consistence with eqn (2). The results observed for low strains are shown in Fig. 3e. As expected a large wavelength is obtained on substrates with low stiffness values. | ||
| Fig. 3 Same-spot in situ observation of the release process, focused on the crossover line from hard to soft PDMS. The soft discrete inclusion is present at the bottom each, the hard at the top. In the beginning the substrate is pre-strained to 50% of its initial length (a), the oxidized layer on top is unstrained. Upon strain release wrinkles do form first within the soft inclusion (b and c) followed by the hard matrix (d and e). For a video capture of this process, see ESI.† | ||
Quantitative parameter analysis
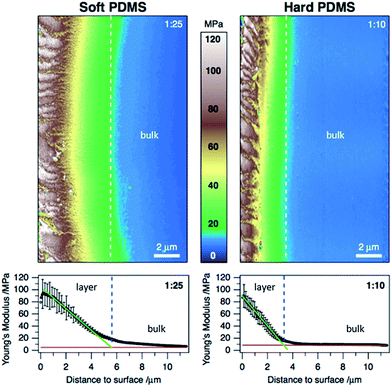
To compare our experimental results with theory we quantitatively determined all relevant parameters. According to eqn (2) the required parameters are the Young's moduli ĒS and ĒF respectively, and the layer height hF of homogenous (non-embedded) hard and soft PDMS. The data for the substrate moduli of hard and soft phase were taken from Claussen et al.33 They determined 1.82 ± 0.04 MPa for hard and 0.24 ± 0.01 MPa for soft PDMS. Additionally, we performed indentation measurements to check for the mechanical uniformity of the individual phases. Therefore the samples were analyzed prior to oxidation with a sapphire sphere (400 μm radius) along the line of previous publications.15,36 For statistical reasons every sample was measured five times on different spots. For hard PDMS the averaged Young's modulus was determined to be 2.9 ± 0.31 MPa and for soft 0.65 ± 0.14 MPa. These results are higher compared to the data taken from Claussen et al. obtained for bulk measurements.33 Other groups showed that this effect is due to general differences between the mechanical testing setups.37–39 Consequently we relied on the data of bulk tensile tests for further calculations. However, based on the performed indentation measurements we could not identify any stiffness gradient at the interface between soft and hard phase, as the modulus abruptly changes.Next peak force tapping atomic force microscopy (AFM) allows for quantitative nanomechanical mapping (QNM) at nanometer lateral resolutions.40–42 Consequently, this technique was applied to determine the Young's modulus and thickness of the oxide layer present on PDMS after UVO treatment. UVO-oxidized surfaces are assumed to show a vertical gradient in stiffness from the hard film to the soft substrate. Consequently, there is no distinct borderline but a declining interphase between layer and substrate.43 This method enabled us to map areas of 20 μm × 20 μm at the interphase of bulk and oxidized PDMS. For this we took an oxidized and wrinkled sample and cut a cross profile at the layer edge from the sample middle with a scalpel. Afterwards a cryo-microtome was used to smoothen the surface (subsequent roughness: ∼5 nm) followed by peak-force QNM measurements (for detailed sample preparation see ESI†). The local maxima of Young's moduli for both hard and soft oxidized PDMS are found to be in the range of 90–100 MPa (Fig. 4). The effective layer thickness of the oxide-films was determined as the intersection of a linear fit of the gradient slope (green lines in Fig. 4) and the baseline of the profile (red lines). The resulting film thickness was determined to be 4.9 μm for hard and 5.7 μm for soft PDMS, respectively. Averaging the elastic constants allowed for estimation of the wrinkling wavelengths of the UVO oxidized samples. The averaging was performed by calculating the arithmetic mean of all Young's moduli from the layer top to its bottom. Doing so the average Young's modulus was determined to be 54.0 MPa for the oxidized layer on hard PDMS and 55.3 MPa on soft PDMS, respectively, which is compatible with the range found in literature.44 The linear-like slope of hard PDMS is slightly steeper for soft PDMS. Most likely the less dense polymer network facilitates the ozone to penetrate deeper into the substrate. In general UVO results in a low degree of oxidation compared to plasma treated PDMS (0.4 GPa < E < 7.1 GPa)44 or to glass (E ∼ 73 GPa).45
Wrinkled surfaces were analyzed using a profilometer in order to determine the wavelengths of λhard = 46 μm and λsoft = 72 μm. From the above discussed values the theoretical wavelength for the homogeneous samples were calculated according to eqn (2) (in first order approximation) and compared to the experimentally determined wavelengths. Besides all known variables the Poisson's ratios used in eqn (3) were set to 0.5 for PDMS and 0.17 for the oxidized, glassy film. Here, theory predicts wavelengths that are 30% above our experimental results. Furthermore, we performed calculations based on a higher order approximation introduced by Jiang et al46 (Table 1). This approach also considers the effect of the applied strain on the wrinkle wavelength and amplitude as described in eqn (4). Wrinkles always evolve at the same compression, if the stiffness values of layer and substrate are not modified. Nevertheless, further compression reduces the wavelength and increases the amplitude.
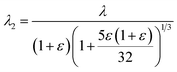 | (4) |
Calculations based on eqn (4) yields wavelengths of 39 μm for hard and 90 μm for soft PDMS (Table 2). In comparison to the simple approximation (eqn (2)), which significantly overestimates the wavelength, eqn (4) yields wavelengths that are slightly reduced compared to the values determined experimentally. Thus the measured data are in better agreement with higher order approximation. We assume that the applied strain is well-above the critical value resulting in creeping at least for the hard PDMS, causing better agreement with the Jiang's equation (eqn (4)).
| λ 2 theoretical,homogenous/μm | λ heterogeneous/μm | Deviation/% | |
|---|---|---|---|
| Matrix (hard PDMS) | 38.96 | 35.26 ± 0.96 | −9.50 |
| Discrete inclusion (soft PDMS) | 89.74 | 45.60 ± 2.63 | −49.19 |
After this complete analysis of homogenous PDMS systems, we applied the results to the more complex embedded situation as sketched in Fig. 2a. Table 2 compares the calculations according to Jiang and the values of elastic constants and layer thicknesses determined for the homogenous samples and experimental results performed for the composite sample. Both, hard matrix and discrete inclusion show smaller wavelengths (35 μm and 45 μm, respectively) than the equally stiff homogenous materials. However, the deviation in the hard matrix is not as pronounced as for the soft discrete inclusion. This difference is mainly caused by the complex stress/strain situation in the embedded sample: for the homogenous sample, the strain can be considered to be homogenous and directly related to the elongation of the sample in stretching direction. As defined by Hook's law stress is directly related to strain. The composite nature of the embedded sample however causes heterogeneity of the stress and strain. Neither can the local strain be inferred from the elongation of the sample, nor can stress be considered to be homogenous.
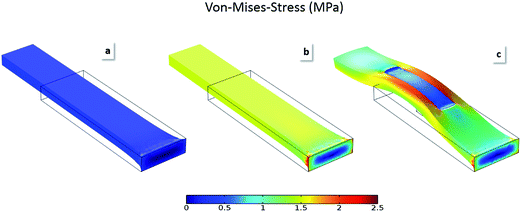
To gain a more quantitative picture of the stress/strain situation, mechanical finite element modelling was performed to understand the underlying mechanisms and distortions of the composite sample compared to homogenous PDMS. In a block of homogenous hard or soft PDMS the stress upon compression is distributed homogenously within the sample, as depicted in Fig. 5a. In contrast the stress is not uniformly distributed for soft PDMS embedded in hard PDMS. The stress within the soft discrete inclusion is much lower than for the surrounding hard PDMS (Fig. 5a and c). Furthermore, the stress within the hard matrix is focused at the sides of the inclusion leading to an increase from ∼1.6 MPa (Fig. 5b) to ∼2.4 MPa (Fig. 5c). Stress and strain correlate over the Young's modulus according to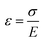 , as a consequence an increase of the applied stress leads to smaller wrinkle wavelengths when considering eqn (4). This finding fits to our experimentally found data.
, as a consequence an increase of the applied stress leads to smaller wrinkle wavelengths when considering eqn (4). This finding fits to our experimentally found data.
Nevertheless it does not explain the shrinkage in wavelength for the soft PDMS. We identified two other potential reason for this observation: (1) an inhomogeneous stress distribution within the asymmetric matrix of soft PDMS (from all sides but one) causes a vertical distortion of the compressed sample, (2) changes in sample composition have however larger effects. Indentation measurements on unwrinkled composite substrates revealed differences in the Young's modulus compared to the neat samples. The soft phase is hardened from 0.65 to 0.8 MPa while at the same time the hard phase is slightly weakened from 2.9 to 2.5 MPa. These changes are most likely caused by diffusion of the Pt-catalyst from the hard into the soft phase either while gelation at room temperature and during thermal curing, respectively. In combination with the increase of stress within the matrix that is indicated by simulations the drastic changes in wavelength for both matrix and inner part can be explained.
Defect formation in gradient structures
The observed effects at the border between discrete inclusion and surrounding revealed that defects preferentially nucleate in close proximity to the mechanical transition. In order to study the underlying processes in more detail we substituted the discrete soft inclusion with a lateral, defined gradient in Young's modulus33 and embedded it as before in a matrix of hard PDMS. Thus, the crossover from inclusion to matrix within this composite material is no longer at a fixed ratio between two stiffness values but changes gradually along the substrate. The initial Young's modulus ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and it decreases to a ratio of 1
5 and it decreases to a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at the hard end.
1 at the hard end.
At the interface bearing a Young's modulus ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 a similar wrinkle wavelength developed in both areas and no line-defects were observed (see Fig. 6a). For the other cases, we defined a defect density by counting the number of waves in both areas from one to the next defect (eqn (5)). Dividing the counted number derived from the gradient by this of the matrix gives a defect density ratio σd defined by the number of waves in one repetitive unit ni for the gradient and nm for the matrix.
1 a similar wrinkle wavelength developed in both areas and no line-defects were observed (see Fig. 6a). For the other cases, we defined a defect density by counting the number of waves in both areas from one to the next defect (eqn (5)). Dividing the counted number derived from the gradient by this of the matrix gives a defect density ratio σd defined by the number of waves in one repetitive unit ni for the gradient and nm for the matrix.
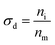 | (5) |
So at the center of the composite material the defect density from microscopy images is 0.83 (5 gradient waves divided by 6 matrix waves), with a measured modulus ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
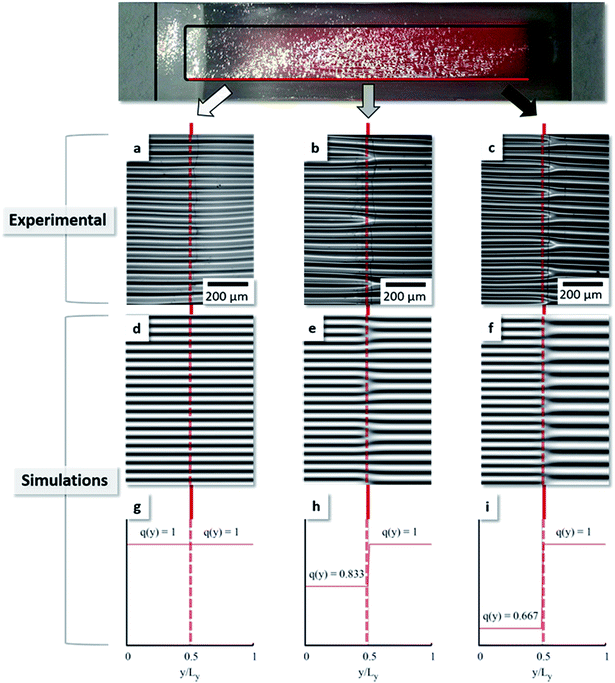
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Fig. 6b). The measured difference in wavelength by profilometry at the sample middle is as high as 43 ± 3 μm to 56 ± 2 μm, giving an average ratio of 0.77, so slightly lower. For the soft end however the defect density was determined to be 0.66 (Fig. 6c) compared to 0.67 for profilometry, so in perfect agreement. These values are directly correlated with the change in wavelength and consequently the branching period. Furthermore, a drastic but uniform change of wavelength again indicates that no stiffness gradient perpendicular to the interface is present. Using numerical simulations for samples with a step-like transition function recover the same features and pinning of the line defects to the interface as observed experimentally. Fig. 6d–f show patterns obtained by solving a generalized version of the Swift–Hohenberg equation47 that includes both anisotropy48 and a spatially periodic inhomogeneity (eqn (6))49 using the pseudo-spectral method and considering a flat surface with small noise as initial condition.
2 (Fig. 6b). The measured difference in wavelength by profilometry at the sample middle is as high as 43 ± 3 μm to 56 ± 2 μm, giving an average ratio of 0.77, so slightly lower. For the soft end however the defect density was determined to be 0.66 (Fig. 6c) compared to 0.67 for profilometry, so in perfect agreement. These values are directly correlated with the change in wavelength and consequently the branching period. Furthermore, a drastic but uniform change of wavelength again indicates that no stiffness gradient perpendicular to the interface is present. Using numerical simulations for samples with a step-like transition function recover the same features and pinning of the line defects to the interface as observed experimentally. Fig. 6d–f show patterns obtained by solving a generalized version of the Swift–Hohenberg equation47 that includes both anisotropy48 and a spatially periodic inhomogeneity (eqn (6))49 using the pseudo-spectral method and considering a flat surface with small noise as initial condition.
| ∂tu = [ε − (q2(y) + Δ)2]u − W∂x2∂y2u − c∂y4u − u3 − 2(∂yu)∂y[q2(y)] − u∂y2[q2(y)] | (6) |
u mimics the local height of the surface, ε is the dimensionless strain and the parameters W and c control the anisotropy of the system. We chose W = 1 and c = 0.5. The spatially varying “natural” wavelength was set to be 2π/q(y). Perfectly aligned straight wrinkles (Fig. 6d) are obtained for constant natural wavenumber q (Fig. 6g). For a steep transition in wavenumber (Fig. 6h) branching defects emerge (Fig. 6e). The periodicity of these line-defects is further decreased resulting in higher branching density (Fig. 6f) for increased values of the wavenumber jump (Fig. 6i). Here, all the branching-defects are stationary and emerge spontaneously along the contact line between the two domains with different preferred wavenumbers. Those correspond well to the ratios determined experimentally at the middle end the soft end of the gradient, respectively.
The presented method has high potential for the systematic production of gradients and so not only for the aimed generation and understanding of ordered line branching structures. Beyond this the presented results might find application within the field of particle alignment. Controlled induction of line-defects can be used to break the symmetry within particle assemblies by generating Y-shaped particle lines. Furthermore, microfluidics might benefit from well-defined size- and angle-tunable channel junctions.
Conclusion
The objective of this work was the investigation of line defects observed in wrinkled substrates. Composite PDMS samples consisting of two covalently attached PDMS phases with different mechanical properties were prepared, wrinkled and analyzed. The predetermined change of substrate stiffness along the phase border resulted in different wavelengths caused by the buckling instability and so reinforced the wrinkles to branch more frequently here. Consequently the branches had a main orientation at the border, pointing from the soft side with large waves to the hard side, where shorter waves were found. The gradient sample showed an interesting behavior of oriented, patterned defects. We concluded that the stiffness difference of both substrate phases did match a value here that induced a whole-number ratio of the buckling instability. This was not observed in the sample with discrete, soft PDMS in the inclusion. In order to confront empirical wrinkling theories with our results, we had to measure hF and EF of the UVO-oxidized layer. Via Peak Force QNM we gained values of hF = 4.9–5.7 μm and EF = 54.0 MPa and 55.3 MPa, respectively. Wavelengths and amplitudes of the wrinkles were determined via profilometry resulting in 46 μm and 73 μm for the homogeneous samples, 35 μm and 45 μm in the heterogeneous system with just hard and soft PDMS respectively 51 μm and 63 μm in the gradient system. A mechanical stress simulation revealed an increase in the surface stress distribution around the embedded discrete inclusion that induces a wave shortage. In the wider dimensioned gradient sample this problem was less pronounced. Summarized the system presented in this paper has a high potential for ordering defects in a patterned way and beyond to keep the adjacent wrinkled areas defect-free. Our findings increase the understanding of the formation of defects in controlled wrinkling systems. One application that may use line defects of adjustable number and direction is the generation of size- and angle-tunable channel junctions for microfluidic devices. Two waves terminating into one act as the micro-channel junction that may be sealed on top with another layer of PDMS or glass. Another application might be the organization of nanoparticles onto well-defined, equi-distant Y-shaped templates. Stamping these assemblies onto a flat substrate creates lines of particles that split on predefined positions. This might be useful for light management in nanophotonics.Acknowledgements
We thank M. Lehmann for Peak Force QNM measurements as well as M. P. Neubauer for indentation measurements. Also we thank the European Research Council for financing this work within the Starting Grant Project ERC-2012-StG 306686 METAMECH. M. Tebbe was supported by the Elite Network Bavaria in the frame of the Elite Study Program “Macromolecular Science” and funded via a grant for PhD candidates according to Bavarian elite promotion law (BayEFG).References
- P. Yamato, B. J. P. Kaus, F. Mouthereau and S. Castelltort, Geology, 2011, 39(9), 815–818 CrossRef.
- B. Prüm, H. Florian Bohn, R. Seidel, S. Rubach and T. Speck, Acta Biomater., 2013, 9, 6360–6368 CrossRef PubMed.
- C.-D. Reuther, Grundlagen der Tektonik, Springer Publishing, Berlin, Heidelberg, 2012 Search PubMed.
- A. Mohamed, Die Krusten der Raender der Fayoum-Depression, Ludwig-Maximilians-Universitaet Muenchen, Muenchen, 2003 Search PubMed.
- M. Berneburg, H. Plettenberg and J. Krutmann, Photodermatol., Photoimmunol. Photomed., 2000, 16, 239–244 CAS.
- H. Vandeparre, M. Piñeirua, F. Brau, B. Roman, J. Bico, C. Gay, W. Bao, C. N. Lau, P. M. Reis and P. Damman, Phys. Rev. Lett., 2011, 106, 224301 CrossRef PubMed.
- J. Genzer and J. Groenewold, Soft Matter, 2006, 2, 310–323 RSC.
- C. Jiang, S. Singamaneni, E. Merrick and V. V. Tsukruk, Nano Lett., 2006, 6, 2254–2259 CrossRef CAS PubMed.
- D.-Y. Khang, J. A. Rogers and H. H. Lee, Adv. Funct. Mater., 2009, 19, 1526–1536 CrossRef CAS.
- A. Schweikart and A. Fery, Microchim. Acta, 2009, 165, 249–263 CrossRef CAS.
- S. Singamaneni and V. V. Tsukruk, Soft Matter, 2010, 6, 5681–5692 RSC.
- J. Y. Chung, A. J. Nolte and C. M. Stafford, Adv. Mater., 2011, 23, 349–368 CrossRef CAS PubMed.
- M. Pretzl, A. Schweikart, C. Hanske, A. Chiche, U. Zettl, A. Horn, A. Böker and A. Fery, Langmuir, 2008, 24, 12748–12753 CrossRef CAS PubMed.
- F. A. Bayley, J. L. Liao, P. N. Stavrinou, A. Chiche and J. T. Cabral, Soft Matter, 2014, 10, 1155–1166 RSC.
- K. Efimenko, M. Rackaitis, E. Manias, A. Vaziri, L. Mahadevan and J. Genzer, Nat. Mater., 2005, 4, 293–297 CrossRef CAS PubMed.
- C. J. Rand, R. Sweeney, M. Morrissey, L. Hazel and A. J. Crosby, Soft Matter, 2008, 4, 1805–1807 RSC.
- J. Rodríguez-Hernández and A. Del Campo, J. Appl. Polym. Sci., 2015, 132(17) DOI:10.1002/app.41863.
- M. Watanabe and K. Mizukami, Macromolecules, 2012, 45, 7128–7134 CrossRef CAS.
- H. Vandeparre, J. Léopoldès, C. Poulard, S. Desprez, G. Derue, C. Gay and P. Damman, Phys. Rev. Lett., 2007, 99, 188302 CrossRef PubMed.
- D. U. Ahn, Z. Wang, R. Yang and Y. Ding, Soft Matter, 2010, 6, 4900–4907 RSC.
- G. Miquelard-Garnier, A. B. Croll, C. S. Davis and A. J. Crosby, Soft Matter, 2010, 6, 5789–5794 RSC.
- Y. Xuan, X. Guo, Y. Cui, C. Yuan, H. Ge, B. Cui and Y. Chen, Soft Matter, 2012, 8, 9603–9609 RSC.
- W. P. Lee and A. F. Routh, Langmuir, 2004, 20, 9885–9888 CrossRef CAS PubMed.
- S. Frank, U. A. Handge, S. Olliges and R. Spolenak, Acta Mater., 2009, 57, 1442–1453 CrossRef CAS.
- J. Y. Chung, J.-H. Lee, K. L. Beers and C. M. Stafford, Nano Lett., 2011, 11, 3361–3365 CrossRef CAS PubMed.
- J. Gao, K. Pei, T. Sun, Y. Wang, L. Zhang, W. Peng, Q. Lin, M. Giersig, K. Kempa, Z. Ren and Y. Wang, Small, 2013, 9, 732 CrossRef CAS.
- B. Han, K. Pei, Y. Huang, X. Zhang, Q. Rong, Q. Lin, Y. Guo, T. Sun, C. Guo, D. Carnahan, M. Giersig, Y. Wang, J. Gao, Z. Ren and K. Kempa, Adv. Mater., 2014, 26, 873–877 CrossRef CAS PubMed.
- N. Stoop, R. Lagrange, D. Terwagne, P. M. Reis and J. Dunkel, Nat. Mater., 2015, 14, 337–342 CrossRef CAS PubMed.
- A. Ahmadivand and S. Golmohammadi, Opt. Commun., 2014, 310, 1–11 CrossRef CAS.
- C. P. Ody, C. N. Baroud and E. de Langre, J. Colloid Interface Sci., 2007, 308, 231–238 CrossRef CAS PubMed.
- N. Bowden, W. T. S. Huck, K. E. Paul and G. M. Whitesides, Appl. Phys. Lett., 1999, 75, 2557–2559 CrossRef CAS.
- R. Huang, J. Mech. Phys. Solids, 2005, 53, 63–89 CrossRef.
- K. U. Claussen, M. Tebbe, R. Giesa, A. Schweikart, A. Fery and H.-W. Schmidt, RSC Adv., 2012, 2, 10185–10188 RSC.
- P. Ball, Branches, Oxford University Press, Oxford, 2009 Search PubMed.
- Z. Li, S. Zhang, P. Zhang, D. Yang, G. Jin and H. Ma, Polym. Adv. Technol., 2012, 23, 1240–1245 CrossRef CAS.
- C. M. Stafford, C. Harrison, K. L. Beers, A. Karim, E. J. Amis, M. R. VanLandingham, H.-C. Kim, W. Volksen, R. D. Miller and E. E. Simonyi, Nat. Mater., 2004, 3, 545–550 CrossRef CAS PubMed.
- A. Mata, A. Fleischman and S. Roy, Biomed. Microdevices, 2005, 7, 281–293 CrossRef CAS PubMed.
- C. C. White, M. R. VanLandingham, P. L. Drzal, N. K. Chang and S. H. Chang, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 1812–1824 CrossRef CAS.
- J.-H. Seo, K. Sakai and N. Yui, Acta Biomater., 2013, 9, 5493–5501 CrossRef CAS PubMed.
- B. Foster, Am. Lab., 2012, 42, 215–221 Search PubMed.
- P. Trtik, J. Kaufmann and U. Volz, Cem. Concr. Res., 2012, 42, 215–221 CrossRef CAS.
- C. Kuttner, M. Tebbe, H. Schlaad, I. Burgert and A. Fery, ACS Appl. Mater. Interfaces, 2012, 4, 3484–3492 CAS.
- C. Kuttner, A. Hanisch, H. Schmalz, M. Eder, H. Schlaad, I. Burgert and A. Fery, ACS Appl. Mater. Interfaces, 2013, 5, 2469–2478 CAS.
- S. p. Béfahy, P. Lipnik, T. Pardoen, C. Nascimento, B. Patris, P. Bertrand and S. Yunus, Langmuir, 2009, 26, 3372–3375 CrossRef PubMed.
- S. Inaba, S. Fujino and K. Morinaga, J. Am. Ceram. Soc., 1999, 82, 3501–3507 CrossRef CAS.
- H. Jiang, D.-Y. Khang, J. Song, Y. Sun, Y. Huang and J. A. Rogers, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15607–15612 CrossRef CAS PubMed.
- J. Swift and P. Hohenberg, Phys. Rev. A, 1977, 15, 319–328 CrossRef.
- W. Pesch and L. Kramer, Z. Phys. B, 1986, 63, 121–130 CrossRef.
- B. Kaoui, A. Guckenberger, F. Ziebert, A. Krekhov and W. Zimmermann, 2015, ArXiv: 1503.04234.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5sm00318k |
| This journal is © The Royal Society of Chemistry 2015 |