Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cluster coarsening on drops exhibits strong and sudden size-selectivity
Aidan I.
Brown
and
Andrew D.
Rutenberg
*
Department of Physics and Atmospheric Science, Dalhousie University, Halifax, NS, Canada B3H 4R2. E-mail: andrew.rutenberg@dal.ca
First published on 27th March 2015
Abstract
Autophagy, an important process for degradation of cellular components, requires the targeting of autophagy receptor proteins to potential substrates. Receptor proteins have been observed to form clusters on membranes. To understand how receptor clusters might affect autophagy selectivity, we model cluster coarsening on a polydisperse collection of spherical drop-like substrates. Our model receptor corresponds to NBR1, which supports peroxisome autophagy. We recover dynamical scaling of cluster sizes, but find that changing the drop size distribution changes the cluster-size scaling distribution. The magnitude of this effect is similar to how changing the spatial-dimension affects scaling in bulk systems. We also observe a sudden onset of size-selection of the remaining drops with clusters, due to clusters evaporating from smaller drops and growing on larger drops. This coarsening-driven size selection provides a physical mechanism for autophagy selectivity, and may explain reports of size selection during peroxisome degradation.
1 Introduction
Domain coarsening describes multiple clusters growing in average size but decreasing in number, due to the conserved amount of constituents in the system.1 Biological coarsening has been considered in models of clustering on bacterial membranes2,3 and for membrane polarization.4 However, these models have focused only on a single membrane or membrane patch, whereas cells have multiple organelles and hence multiple disconnected surfaces.Autophagy is an important system for the degradation of large cellular substrates,5 including protein aggregates, organelles, and pathogenic bacteria. While autophagy was initially described as a non-selective “self-eating” degradation pathway,6 it is capable of selective substrate degradation. Autophagy substrates are directed to the lysosome for degradation in a multi-stage process that requires receptor protein attachment, and selectivity appears to be mediated by a growing list of autophagy receptor proteins.7 Although there is a developing understanding of how different receptor proteins select distinct organelles for autophagy,6,7e.g. peroxisomes vs. mitochondria, there has been little investigation of how individual organelles are selected from among a subcellular population. Specifically, what physical cues could lead to the selection of individual organelles?
Peroxisomes are drop-like organelles that range in size8 from ∼0.1–0.8 μm, and there can be hundreds in a single mammalian cell.9 The autophagy of peroxisomes, or pexophagy, can occur after peroxisome proliferation in order to reduce peroxisome numbers. Intriguingly, this autophagy response varies with peroxisome size.10,11 This suggests that organelle size might directly affect autophagy selectivity, i.e. size may be directly sensed by the autophagy machinery. We explore that possibility in this paper.
Self-interaction of receptor proteins is common. For the NBR1 receptor, which is necessary and sufficient for pexophagy, self-interaction is driven by coiled-coil domains that are essential for normal autophagy.12 Consistent with self-interaction, domains of receptor proteins have been observed on the surface of bacteria targeted for autophagy.13,14 NBR1 also has the distinctive “J” domain12 that allows it to anchor to membranes, and that is also essential for normal pexophagy. The combination of self-interaction, domains, and membrane anchoring suggests that NBR1 could exhibit biological coarsening dynamics. Since a threshold number of NBR1 appears to be required on a peroxisome to trigger pexophagy,12 coarsening could then be a mechanism to concentrate receptor proteins on particular organelles and so select them for degradation.
In order to understand how the physics of coarsening might influence biological processes such as autophagy substrate specificity, we model the coarsening of surface clusters on a polydisperse collection of spherical drops. There has been little study of coarsening on such a collection of disconnected objects, though coarsening is well understood in bulk systems. For well-separated bulk clusters, coarsening is driven by Ostwald ripening at late times – where material evaporates from clusters smaller than the critical radius rc and condenses onto clusters larger than rc.15,16 The key features are a growing critical cluster size,17,18 with rc(t) ∼ t1/3, and dynamic scaling1 of cluster size distributions with respect to rc(t). While scaling distributions vary with spatial dimension,1,15,17,19 the universal dynamical exponent 1/3 does not.1
We work in the dilute limit of Lifshitz–Slyozov–Wagner (LSW),1,17,18 with a uniform bulk concentration1,17 of molecules ρ(t) that couples clusters on different drops. A uniform bulk concentration is a good approximation when cluster separation is larger than cluster size.1,15,17 Our investigation considers three questions. First, in what way is canonical coarsening changed by having surface clusters on drops rather than bulk clusters in space? Second, how do the details of drop polydispersity, i.e. the drop size distribution, affect coarsening behaviour? Third, what aspects of this system could affect biological behaviour – in particular autophagy selectivity? We aim to understand the physical behaviour of idealized coarsening clusters on drops, and identify how the qualitative characteristics of this process could play a role in protein cluster selection of substrates for autophagy.
2 Model
The growth and evaporation of coarsening clusters on drops will be determined by the vapour phase surrounding the clusters on the drop surface. Accordingly, we first consider the dynamics of a dilute concentration field of molecules, f(θ,ϕ,t), on the surface of a single spherical drop of radius R, coupled to the bulk by association and dissociation from the drop surface: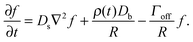 | (1) |
The molecule flux to the perimeter of a circular cluster of molecules on the sphere surface will be determined by the concentration field. There will not be a cluster on all spheres at all times since below a critical surface concentration clusters will be unstable to evaporation. Above this threshold concentration, clusters will nucleate and grow. Clusters in small biological systems, such as holin domains in bacteria3,21 and polarity clusters in yeast,22 often nucleate and coalesce rapidly. Similarly, we assume that nucleated clusters have resolved into (at most) a single circular cluster per drop.
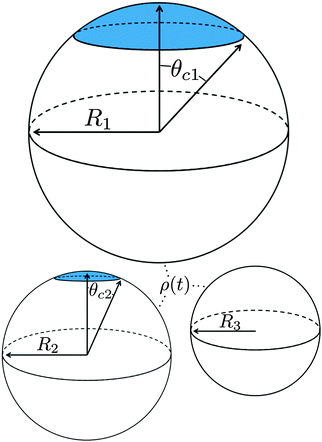
To determine the growth of a cluster of N particles subtending a polar angle θc on a spherical drop of radius R (see Fig. 1), the concentration field f must be found. In steady state, eqn (1) can be rewritten as a general Legendre equation and solved.23,24 (This solution, and subsequent development are shown in more detail in Appendix B.) We apply the Gibbs–Thomson boundary condition at the perimeter of the circular cluster, at θc, 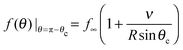 , with f∞ the concentration at a flat interface and ν the capillary length, which determines the decay length of the number density at the edge of the cluster and that we assume to be small.15,25–27 This gives us f(θ) = CPλ(cos
, with f∞ the concentration at a flat interface and ν the capillary length, which determines the decay length of the number density at the edge of the cluster and that we assume to be small.15,25–27 This gives us f(θ) = CPλ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) + Dbρ/Γoff, with the limiting form of the hypergeometric function of index λ
θ) + Dbρ/Γoff, with the limiting form of the hypergeometric function of index λ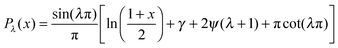 ,24γ the Euler–Mascheroni constant, ψ the digamma function,
,24γ the Euler–Mascheroni constant, ψ the digamma function, 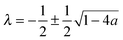 , and a ≡ ΓoffR/Ds. The coefficient C is given by
, and a ≡ ΓoffR/Ds. The coefficient C is given by
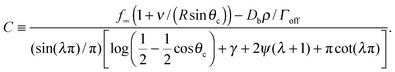 | (2) |
Mass balance with the diffusive flux of molecules to the cluster edge then determines the change in cluster size with time:
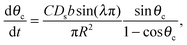 | (3) |
The denominator of C has a logarithmic term, as seen in two-dimensional coarsening.1,15,19 For fast diffusive equilibration compared to molecule number equilibration, a = ΓoffR/Ds ≪ 1, and a small cluster θc ≪ 1, the denominator of C is dominated by the cot(λπ) ≃ cot(−aπ) ≃ −1/a term. Using this approximation, dependence on the surface diffusivity Ds is cancelled, and we can express the result in terms of the number of molecules N in the cluster for small θc,
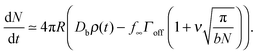 | (4) |
We investigate ensembles of many drops using two qualitatively-distinct radius distributions P0(R) with the same mean ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) : one with and the other without a continuous tail. A uniform distribution has no tail, with R ∈ [
: one with and the other without a continuous tail. A uniform distribution has no tail, with R ∈ [![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) − R0,
− R0, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) + R0], and P0(R) = 1/(2R0). The exponential distribution has a tail, with R ∈ [Rmin, ∞), P0(R) = R0−1
+ R0], and P0(R) = 1/(2R0). The exponential distribution has a tail, with R ∈ [Rmin, ∞), P0(R) = R0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−(R−Rmin)/R0, and Rmin =
e−(R−Rmin)/R0, and Rmin = ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) − R0. We choose
− R0. We choose ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) = 0.25 μm to be consistent with peroxisome sizes.28
= 0.25 μm to be consistent with peroxisome sizes.28
To obtain a simplified dynamical equation for number of particles Ni in the cluster on the ith drop, we define α ≡ 4πDb/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2, a corresponding dimensionless time t′ ≡ αt, the bulk density corresponding to surface saturation ρc ≡ f∞Γoff/Db, and the corresponding bulk supersaturation Δρ ≡ ρ(t) − ρc, so that
2, a corresponding dimensionless time t′ ≡ αt, the bulk density corresponding to surface saturation ρc ≡ f∞Γoff/Db, and the corresponding bulk supersaturation Δρ ≡ ρ(t) − ρc, so that
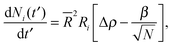 | (5) |
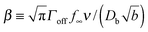 characterizes the effect of cluster curvature through the supersaturation necessary to avoid evaporation of finite-size surface clusters.
characterizes the effect of cluster curvature through the supersaturation necessary to avoid evaporation of finite-size surface clusters.
What is the expected scale of β? Capillary lengths of approximately one26 and several27 particle widths have been found for 2d and 3d systems, respectively. Assuming that the capillary length is approximately the size of a cluster molecule, 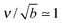 , then
, then 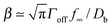 . A typical cytosolic protein diffusivity28 is Db ≃ 1 μm2 s−1, and an approximate lower-bound for f∞ is determined by a single molecule per sphere, i.e. f∞ ≳ 1/(4π
. A typical cytosolic protein diffusivity28 is Db ≃ 1 μm2 s−1, and an approximate lower-bound for f∞ is determined by a single molecule per sphere, i.e. f∞ ≳ 1/(4π![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2) ≃ 1 μm−2. The timescale for number equilibration on the drop surface is
2) ≃ 1 μm−2. The timescale for number equilibration on the drop surface is ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) /Γoff. We choose as our default value β = 0.01 μm−3, corresponding to equilibration in tens of seconds, and explore the effects of varying β below. We note that for a typical cellular volume V = 5000 μm3, this choice of β corresponds to supersaturation by only 50 cytosolic molecules. Larger capillary lengths,
/Γoff. We choose as our default value β = 0.01 μm−3, corresponding to equilibration in tens of seconds, and explore the effects of varying β below. We note that for a typical cellular volume V = 5000 μm3, this choice of β corresponds to supersaturation by only 50 cytosolic molecules. Larger capillary lengths, 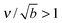 , require larger surface number equilibration times to achieve the same β.
, require larger surface number equilibration times to achieve the same β.
To get better statistics, 107 drops are used for each simulation, all of which initially have clusters, and results are also averaged over 100 sets of initial conditions, unless otherwise stated. The initial supersaturation Δρ(0) = Δρ0, and cluster sizes are initially proportional to their drop surface area, Ni(0) = N0(Ri/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) )2. Other initial conditions, such as equal cluster sizes or cluster sizes randomly drawn from a uniform distribution, give qualitatively similar results at late times. Unless otherwise stated, Δρ0 = 0.1 μm−3, and N0 = 50 – variation of these parameters is explored below. Our bulk volume is L3 = 100 μm3 per drop, so that the initial available bulk number of molecules is Δρ0L3 = 10 per drop. For stable numerical results at early times timesteps must be small, but can be larger at later times.29 We use a timestep Δt′ = 10(10t′)1/3 until Δt′ = 105, after which Δt′ is held constant.
)2. Other initial conditions, such as equal cluster sizes or cluster sizes randomly drawn from a uniform distribution, give qualitatively similar results at late times. Unless otherwise stated, Δρ0 = 0.1 μm−3, and N0 = 50 – variation of these parameters is explored below. Our bulk volume is L3 = 100 μm3 per drop, so that the initial available bulk number of molecules is Δρ0L3 = 10 per drop. For stable numerical results at early times timesteps must be small, but can be larger at later times.29 We use a timestep Δt′ = 10(10t′)1/3 until Δt′ = 105, after which Δt′ is held constant.
3 Results
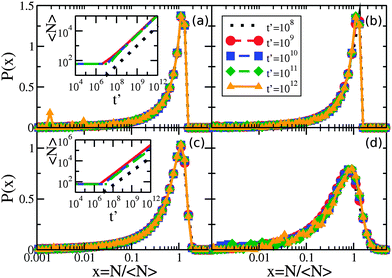
The critical cluster size rc(t) is an important quantity for LSW coarsening – we measure the average number of molecules in a cluster, 〈N〉, where 〈N〉 ∼ rc2. By numerically evolving eqn (5) we confirmed that the average cluster size follows the LSW1,17 power-law 〈N〉 ∼ t2/3 at later times, as shown in the insets of Fig. 2(a) and (c). Fig. 2 shows the cluster size distributions for uniform and exponential drop radius distributions. The cluster size distributions exhibit good dynamical scaling for at least three decades in time. The power-law growth and scaling was seen for all tested initial conditions, as well as for a range of two decades variation of β, the initial bulk supersaturation Δρ0, and the initial cluster size N0 values.However, Fig. 3 illustrates how the scaling function depends on the type of drop radius distribution. The scaled distribution is distinctly different for uniform vs. exponential drop radius distributions. For the uniform drop radius distribution, there is no dependence on the distribution width parameter, R0. For the exponential drop radius distribution, the scaled cluster size distributions depend on the width parameter R0, becoming sharper as R0 decreases. We also show two analytic solutions for scaling distributions of bulk clusters in 2d (dashed black line)19 and 3d (dotted black line).17 The scaling distributions for clusters on drops are qualitatively similar to the 2d distribution, rapidly approaching zero as the cluster size N → 0. Near the peak, the effect on the scaling function of changing the form of the drop size distribution is similar in magnitude to the effect of changing the spatial dimension between 2d and 3d for bulk coarsening.
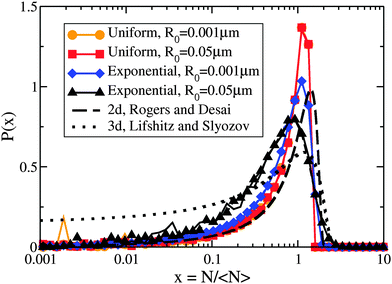 | ||
| Fig. 3 Non-universal cluster size distributions. Linear-log plot of cluster-size distributions P(N/〈N〉) vs. N/〈N〉 for several drop radius distributions as indicated in the legend. Two times, t′ = 1011 and 1012, are shown overlapping for each condition with dashed and solid coloured lines, respectively. Although each drop radius distribution exhibits scaling collapse, the different types of drop radius distributions do not collapse to the same scaling function. All uniform sphere radius distributions collapse to the same scaling function, while the exponential sphere radius distributions collapse to functions that vary with the drop distribution width. The black lines show analytic scaling distributions from the literature17,19 for d = 2 and d = 3, both in the dilute limit. | ||
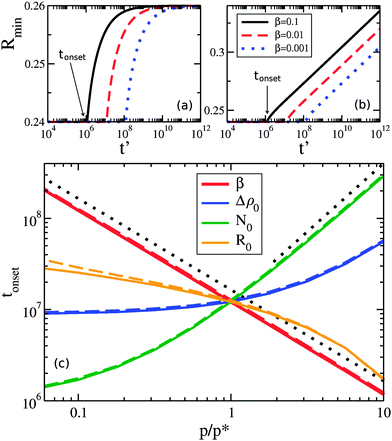
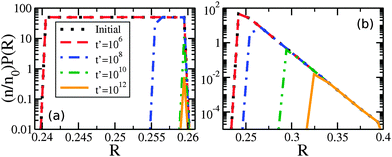
At later times only the larger drops retain clusters – a phenomenon we call size-mediated cluster selectivity. Fig. 4(a) and (b) show the radius of the smallest drop with a cluster, Rmin. With increasing times, Rmin suddenly increases at a characteristic onset time. This tonset coincides with the beginning of the power-law coarsening regime shown in the insets of Fig. 2, after which dynamical scaling collapse of cluster size distributions is observed. Further, by considering the size distribution of drops that retain clusters, as shown in Fig. 5, we see that the smallest of the drops still retaining clusters are always next to lose their clusters. The distribution of larger drops with clusters remains unchanged, indicating larger drops do not lose their clusters until all smaller drops have done so.
As seen in Fig. 4(c), the timing of tonset is controlled by β, Δρ0, N0, and R0. Both Δρ0 and N0 would be directly affected by protein expression rates: Δρ0 is related to the initial bulk concentration of proteins, and represents how much protein remains in the bulk once clusters have nucleated on drops, while N0 represents the number of proteins initially present in each cluster. While β, which is proportional to how quickly a protein dissociates from a membrane, may not be easily controlled, we do expect it to vary in vivo due to differences in membrane lipid composition,30,31 such as between organelles. The width of the drop size distribution, R0, is related to the amount and magnitude of organelle size variation, which could vary with conditions or cell type. We note that changing the initial cluster size distribution, so that instead of clusters proportional to drop area we used either equal or uniformly random cluster sizes, delayed tonset.
We can qualitatively understand some of the asymptotic behavior shown in Fig. 4(c). For example, tonset ∼ 1/β reflects the β dependence of the evaporative term in eqn (5) – indicating that cluster evaporation largely determines tonset. Consistent with this, at larger values of N0 we see that tonset ∼ N01.5. The cluster size-dependent term in eqn (5) is dN/dt ∼ −N−0.5, which gives an evaporation time ∼N01.5 for a cluster of initial size N0. The dependence on the initial bulk density Δρ0 is similar to N0. At smaller values of Δρ0 (at fixed N0) we see that tonset approaches a constant value. This occurs when the material in the initial clusters dominates the bulk density, and a similar cross-over is seen with smaller values of N0 at fixed Δρ0. Increasing R0 decreases tonset, as drop size differences drive the migration of material.
4 Discussion
Coarsening of clusters on drops exhibits LSW-like power law cluster growth1 and dynamic scaling, as shown in Fig. 2. Scaling distributions typically depend on both spatial dimension and volume fraction,1 but are also known to depend on some aspects of the evolution equations such as spatial anisotropy.32 In this paper we have shown that the scaling cluster-size distribution depends on the shape of the drop radius distribution, and can also depend on its width. Distinct distributions are seen with uniform vs. exponential drop-size distributions. We expect that drop-size distributions with compact support (e.g. the uniform distribution) will have the same cluster size scaling functions as the uniform distribution, while drop-size distributions with tails (e.g. power laws) may have scaling functions that vary with the drop-size distribution width. Power law growth, scaling collapse, and similar tonset behaviour are seen for both the uniform distribution, which has no tail at large drop sizes, and the exponential distribution, which does have a tail. At late times the remaining clusters are on large drops. Given the similarity of behaviour between uniform and exponential drop-size distributions, we expect similar behaviour independent of the details of the distribution. Both peroxisome33,34 and vesicle35 size distributions are qualitatively similar to our exponential distribution, with a continuously decreasing tail at large sizes.We have demonstrated that at later times larger drops are selected to retain clusters, while smaller drops have no clusters. The start of size-based selectivity is sudden, and described by the time tonset that approximately coincides with the onset of dynamical scaling in these systems. Once selectivity has begun, and as coarsening progresses, the clusters on the smallest occupied drops progressively evaporate while clusters on larger drops will grow.
The autophagy receptor protein NBR1 is able to both self-interact and bind to membranes, and is a receptor protein for peroxisome autophagy, i.e. pexophagy.12 In line with our results, we propose that NBR1 clusters on small peroxisomes will evaporate, while those on larger peroxisomes will grow. As NBR1 clusters on small peroxisomes shrink and evaporate, and those on larger peroxisomes grow, the NBR1 cluster growth on larger peroxisomes would push these peroxisomes over any threshold number of NBR1 for autophagy.12 This would be a physical mechanism leading to the selective degradation of larger organelles by autophagy, on the basis of size.
Our proposed mechanism of size-selection through receptor cluster coarsening is consistent with the observation of receptor protein clusters.13,14 It is also consistent with the observation by Deosaran et al.12 who show (see Fig. 5) significant colocalization of NBR1 and peroxisomes (indicated by catalase), but with an all-or-none character. Catalase spots either colocalize with significant amounts of NBR1 or background levels. Indeed, our model shows that significantly higher NBR1 levels on drops with clusters than without – and only some drops supporting clusters at later times. Finally, our mechanism could also explain the observation that, in situations inducing a reduction in peroxisome number, larger peroxisomes degrade earlier and preferentially relative to smaller peroxisomes.10 Degradation also depends upon peroxisome size in yeast.11
How does the timing of our cluster selectivity correspond to that of peroxisome autophagy? In Fig. 4, our default values of β, Δρ0, N0, and R0 result in tonset ∼ 107. Using t = t′/α, Db = 1 μm2 as a typical cytosolic diffusivity, so that α = 4πDb/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2 ≃ 200 s−1, the onset of cluster selectivity is as early as t ∼ 104–105 seconds. This timescale is consistent with mammalian autophagy, which occurs in days.36,37 Individual variation of β and N0, shown in Fig. 4(c), can push tonset down to 106, and combined variation (data not shown) can push tonset even earlier – these timescales are consistent with peroxisome autophagy in yeast, which occurs in hours.38,39 Therefore the segregation of clusters to larger organelles through coarsening, as proposed here, can be fast enough to play a significant role in the selective degradation of larger peroxisomes.
2 ≃ 200 s−1, the onset of cluster selectivity is as early as t ∼ 104–105 seconds. This timescale is consistent with mammalian autophagy, which occurs in days.36,37 Individual variation of β and N0, shown in Fig. 4(c), can push tonset down to 106, and combined variation (data not shown) can push tonset even earlier – these timescales are consistent with peroxisome autophagy in yeast, which occurs in hours.38,39 Therefore the segregation of clusters to larger organelles through coarsening, as proposed here, can be fast enough to play a significant role in the selective degradation of larger peroxisomes.
Fig. 4 shows how the parameters β, Δρ0, N0, and R0 can vary the timing of cluster selectivity, tonset. Increasing either the initial bulk supersaturation Δρ0 or the initial cluster size parameter N0, i.e. expressing more clustering proteins, has the counterintuitive effect of delaying size selectivity. This suggests that experimentally adjusting expression of receptor proteins such as NBR1 would have a significant effect on the speed of autophagy response, with moderately larger expression potentially delaying autophagy. A decreased off-rate of receptor (through Γoff and hence β) also leads to delayed size-selectivity. Larger numbers or more tightly bound receptors both lead to slower size-selectivity for our physical coarsening mechanism, since it depends upon the loss of receptors from smaller clusters. Conversely, increasing variation in drop size, represented by R0, leads to earlier size-selectivity.
We have explored a physical mechanism of size-selection exploiting cluster coarsening on drops. We were motivated by how this may provide a physical basis for autophagy substrate selectivity in pexophagy. A similar cluster-coarsening mechanism may allow PEX11, a protein important to the division of peroxisomes that self-interacts and sticks to membranes,40 to target larger peroxisomes. Similarly, SNARE proteins are required to facilitate vesicle fusion41 and are thought to form membrane clusters. A similar selective coarsening mechanism could thereby select larger vesicles for fusion. Nevertheless, we expect that in vivo other biological processes will also be involved and could modify cluster formation or selectivity. For example, ubiquitin is thought to play a role in recruiting NBR1 to peroxisome membranes,12 and a low peroxisome ubiquitin level28 or other signals or interactions may prevent NBR1 from forming clusters and selecting peroxisomes for autophagy. In addition, different types of autophagy receptors often interact.6,7 We have started with the properties of only one receptor, modelled after NBR1. Another receptor, p62, interacts with NBR142 and enhances pexophagy.12 It will be interesting to consider how interactions with p62 may modify the selectivity mechanism we have proposed here.
5 Conclusion
We model the coarsening behaviour of clusters of molecules on the surface of spherical drops. We determine the dynamical equation for cluster size and, using an ensemble of polydisperse drops, recover the Lifshitz–Slyozov–Wagner exponent for cluster growth and dynamical scaling. The cluster-size scaling function is found to depend on the drop-size distribution, which affects the scaling function to a similar degree as spatial dimension does in bulk systems. Among remaining clusters, evaporation occurs from smaller drops first, with clusters on larger drops growing. This selection of larger drops by clusters may be significant to the cell-biological process of autophagy. Autophagy receptor proteins are seen to cluster, and the receptor protein NBR1 is sufficient for peroxisome autophagy and has domains suggesting it clusters and associates with membranes. Our observation of the selection of larger drops by clusters suggests that clustering NBR1 proteins on peroxisome surfaces could similarly select larger peroxisomes for NBR1 clusters, thereby selecting these larger peroxisomes for degradation by autophagy. This presents a possible physical mechanism to explain reported size selection during peroxisome degradation by autophagy.Appendix A
Eqn (1) describes the change in molecule concentration f on the surface of a sphere of radius R due to diffusion-limited association of molecules from the bulk and dissociation of molecules from the sphere surface. The dissociation term is −Γofff/R, and is controlled by the Γoff parameter.Successful dissociation includes diffusive escape from the immediate surface. The probability of recapture20 by an absorbing sphere of radius R for a diffusive molecule initially at radial distance r is Pcapture = R/r. The probability of escape is then Pescape = 1 − R/r. A molecule initially immediately adjacent to the sphere surface will be at distance r = R + b for a molecule of radius b, and for b ≪ R,
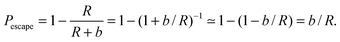 | (6) |
Appendix B
This appendix follows the development of a dynamical equation for cluster size on a sphere, eqn (5), starting with eqn (1)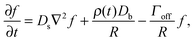 | (7) |
![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) = f − ρDb/Γoff, define ã = Γoff/R, go to steady state (∂f/∂t = 0), and only keep the θ dependence of the Laplacian due to assumed azimuthal symmetry for a polar cluster:
= f − ρDb/Γoff, define ã = Γoff/R, go to steady state (∂f/∂t = 0), and only keep the θ dependence of the Laplacian due to assumed azimuthal symmetry for a polar cluster: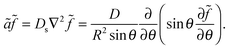 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and a = ãR2/Ds to give us
θ and a = ãR2/Ds to give us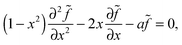 | (9) |
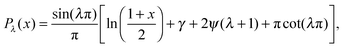 | (10) |
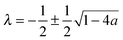 , γ is the Euler–Mascheroni constant, and ψ is the digamma function. So our solution for
, γ is the Euler–Mascheroni constant, and ψ is the digamma function. So our solution for ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) is then
is then ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) = CPλ(cos
= CPλ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), or
θ), orf = CPλ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) + ρDb/Γoff. θ) + ρDb/Γoff. | (11) |
The Gibbs–Thomson boundary condition15,25–27 determines the elevated vapour pressure in equilibrium with a curved interface. We apply this condition at the perimeter of our circular cluster on the pole of the sphere, which covers an angle θc from the pole:
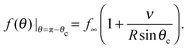 | (12) |
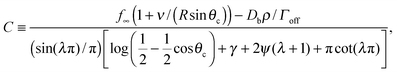 | (13) |
Now we apply mass balance, determining the change in cluster area by the diffusive flux of molecules to the cluster perimeter:
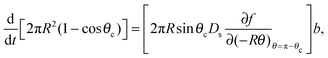 | (14) |
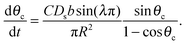 | (15) |
For θc ≪ 1 we have sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc ≃ θc, and cos
θc ≃ θc, and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θc ≃ 1 − θc2/2. Putting these into the expression for C gives us
θc ≃ 1 − θc2/2. Putting these into the expression for C gives us
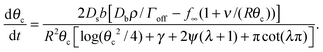 | (16) |
The denominator of the right side of this equation has four terms, with the relative size determined by θc ≪ 1, and a ≪ 1, which leads to λ ≃ −a. For the digamma function, ψ(λ + 1) ≃ ψ(−a + 1) ≃ ψ(1) = −γ, while cot(λπ) ≃ cot(−aπ) ≃ −1/(aπ). We assume that |ln(θc2/4)| ≪ 1/a, which is equivalent to θc2 ≫ e−1/a, which is expected to be the case for a ≪ 1. This implies that π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cot(λπ) ≃ −1/a is the dominant term of the denominator, and that
cot(λπ) ≃ −1/a is the dominant term of the denominator, and that
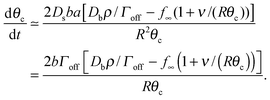 | (17) |
Assuming θc is small, bN = π(Rθc)2, we have 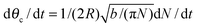 and so
and so
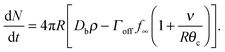 | (18) |
We define a mean sphere radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) , α = 4πDb/
, α = 4πDb/![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) 2, a dimensionless time t′ = αt, and bulk density corresponding to surface saturation ρc = f∞Γoff/Db, and a bulk supersaturation Δρ = ρ(t) − ρc. This then gives us
2, a dimensionless time t′ = αt, and bulk density corresponding to surface saturation ρc = f∞Γoff/Db, and a bulk supersaturation Δρ = ρ(t) − ρc. This then gives us
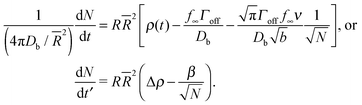 | (19) |
Acknowledgements
We thank the Natural Science and Engineering Research Council (NSERC) for operating grant support, and the Atlantic Computational Excellence Network (ACEnet) for computational resources. AIB thanks NSERC, the Sumner Foundation, and the Killam Trusts for fellowship support. We thank Peter K. Kim for useful discussions.References
- A. J. Bray, Adv. Phys., 2002, 51, 481–587 CrossRef.
- J. Derr and A. D. Rutenberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 011928 CrossRef.
- G. L. Ryan and A. D. Rutenberg, J. Bacteriol., 2007, 189, 4749–4755 CrossRef CAS PubMed.
- M. Semplice, A. Veglio, G. Naldi, G. Serini and A. Gamba, PLoS One, 2012, 7, e30977 CAS.
- A. Stolz, A. Ernst and I. Dikic, Nat. Cell Biol., 2014, 16, 495–501 CrossRef CAS PubMed.
- G. M. Fimia, G. Kroemer and M. Piacentini, Cell Death Differ., 2013, 20, 1–2 CrossRef CAS PubMed.
- V. Rogov, V. Dotsch, T. Johansen and V. Kirkin, Mol. Cell, 2014, 53, 167–178 CrossRef CAS PubMed.
- J. Ezaki, E. Kominami and T. Ueno, IUBMB Life, 2011, 63, 1001–1008 CrossRef CAS PubMed.
- S. J. Huybrechts, P. P. van Veldhoven, C. Brees, G. P. Mannaerts, G. V. Los and M. Fransen, Traffic, 2009, 10, 1722–1733 CrossRef CAS PubMed.
- M. Veenhuis, K. Zwart and W. Harder, FEMS Microbiol. Lett., 1978, 3, 21–28 CrossRef CAS PubMed.
- T. Y. Nazarko, J.-C. Farre and S. Subramani, Mol. Biol. Cell, 2009, 20, 3828–3839 CrossRef CAS PubMed.
- E. Deosaran, K. B. Larsen, R. Hua, G. Sargent, Y. Wang, S. Kim, T. Lamark, M. Jauregui, K. Law, J. Lippincott-Schwartz, A. Brech, T. Johansen and P. K. Kim, J. Cell Sci., 2013, 126, 939–952 CrossRef CAS PubMed.
- M. Cemma, P. K. Kim and J. H. Brumell, Autophagy, 2011, 7, 341–345 CrossRef CAS.
- P. Wild, H. Farhan, D. G. McEwan, S. Wagner, V. V. Rogov, N. R. Brady, B. Richter, J. Korac, O. Waidmann, C. Choudhary, V. Dotsch and D. Bumann and I. Dikic, Science, 2011, 333, 228–233 CrossRef CAS PubMed.
- J. H. Yao, K. R. Elder, H. Guo and M. Grant, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 110–125 Search PubMed.
- P. W. Voorhees, J. Stat. Phys., 1985, 38, 231–252 CrossRef.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- C. Wagner, Z. Elektrochem., 1961, 65, 581–591 CAS.
- T. M. Rogers and R. C. Desai, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 956–964 Search PubMed.
- H. C. Berg and E. M. Purcell, Biophys. J., 1977, 20, 193–219 CrossRef CAS.
- R. White, S. Chiba, T. Pang, J. S. Dewey, C. G. Savva, A. Holzenburg, K. Pogliano and R. Young, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 798–803 CrossRef CAS PubMed.
- A. S. Howell, M. Jin, C.-F. Wu, T. R. Zyla, T. C. Elston and D. J. Lew, Cell, 2012, 149, 322–333 CrossRef CAS PubMed.
- I. A. Stegun, Legendre functions, in Handbook of mathematical functions, ed. M. Abromowitz, I. A. Stegun, National Bureau of Standards, 1970 Search PubMed.
- A. Erdelyi, W. Magnus, F. Oberhettinger and F. G. Tricomi, Higher Transcendental Functions, McGraw-Hill, 1953, vol. 1 Search PubMed.
- D. O. Yi, M. H. Jhon, I. D. Sharp, Q. Xu, C. W. Yuan, C. Y. Liao, J. W. Ager III, E. E. Haller and D. C. Chrzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 245415 CrossRef.
- B. Krishnamachari, J. McLean, B. Cooper and J. Sethna, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 8899–8907 CrossRef CAS.
- M. Strobel, K.-H. Heinig and W. Moller, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 245422 CrossRef.
- A. I. Brown, P. K. Kim and A. D. Rutenberg, PLoS Comput. Biol., 2014, 10, e1003426 Search PubMed.
- B. P. Vollmayr-Lee and A. D. Rutenberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 066703 CrossRef.
- I. Ispolatov and A. Musch, PLoS Comput. Biol., 2013, 9, e1003125 CAS.
- C. C. Hayden, J. S. Hwang, E. A. Abate, M. S. Kent and D. Y. Sasaki, J. Am. Chem. Soc., 2009, 131, 8728–8729 CrossRef CAS PubMed.
- A. D. Rutenberg and B. P. Vollmayr-Lee, Phys. Rev. Lett., 1999, 83, 3772–3775 CrossRef CAS.
- F. Liu, Y. Lu, L. Pieuchot, T. Dhavale and G. Jedd, Dev. Cell, 2011, 21, 457–468 CrossRef CAS PubMed.
- F. J. Vizeacoumar, J. C. Torres-Guzman, D. Bouard, J. D. Aitchison and R. A. Rachubinski, Mol. Biol. Cell, 2004, 15, 665–677 CrossRef CAS PubMed.
- L. Golubovic and M. Golubovic, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 3219–3230 CrossRef CAS.
- D. E. Moody and J. K. Reddy, J. Cell Biol., 1976, 71, 768–780 CrossRef CAS.
- J. Iwata, J. Ezaki, M. Komatsu, S. Yokota, T. Ueno, I. Tanida, T. Chiba, K. Tanaka and E. Kominami, J. Biol. Chem., 2006, 281, 4035–4041 CrossRef CAS PubMed.
- H. W. Platta and R. Erdmann, Trends Cell Biol., 2007, 17, 474–484 CrossRef CAS PubMed.
- M. Veenhuis, A. Douma, W. Harder and M. Osumi, Arch. Microbiol., 1983, 134, 193–203 CrossRef CAS.
- N. A. Bonekamp, S. Grille, M. J. Cardoso, M. Almeida, M. Aroso, S. Gomes, A. C. Magalhaes, D. Ribeiro, M. Islinger and M. Schrader, PLoS One, 2013, 8, e53424 CAS.
- J. J. Sieber, K. I. Willig, R. Heintzmann, S. W. Hell and T. Lang, Biophys. J., 2006, 90, 2843–2951 CrossRef CAS PubMed.
- T. Lamark, M. Perander, H. Outzen, K. Kristiansen, A. Overvatn, E. Michaelsen, G. Bjorkoy and T. Johansen, J. Biol. Chem., 2003, 278, 34568–34581 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |