Formation of adhesion domains in stressed and confined membranes

Abstract

The adhesion bonds connecting a lipid bilayer to an underlying surface may undergo a condensation transition resulting from an interplay between a short range attractive potential between them, and a long range fluctuation-induced potential of mean force. Here, we use computer simulations of a coarse-grained molecular model of supported lipid bilayers to study this transition in confined membranes, and in membranes subjected to a non-vanishing surface tension. Our results show that confinement may alter significantly the condensation transition of the adhesion bonds, whereas the application of surface tension has a very minor effect on it. We also investigate domain formation in membranes under negative tension which, in free membranes, causes the enhancement of the amplitude of membrane thermal undulations. Our results indicate that in supported membranes, this effect of a negative surface tension on the fluctuation spectrum is largely eliminated by the pressure resulting from the mixing entropy of the adhesion bonds.

---

1 Introduction

Lipid bilayers serve as a physical barrier separating the content of the cell from its surroundings. They are embedded with different types of proteins responsible for numerous biological functions. An important class of membrane proteins are cell adhesion molecules that form specific (ligand-receptor) bonds with different biological elements, e.g., the extracellular matrix, the cytoskeleton, and neighboring cell membranes.¹ Cell adhesion plays a central role in many biological processes, such as T-cell activation as part of the immune response,² cell migration³ and tissue formation.⁴

When membranes adhere to another surface, the adhesion bonds may condense to form large adhesion domains,^5–7 which not only provide mechanical stability but also promote cellular signaling pathways necessary for many biological processes.^8,9 The aggregation of adhesion bonds is driven by attractive forces, including electrostatic and van der Waals forces,¹⁰ interactions resulting from cytoskeleton remodeling,¹¹ and membrane-mediated interactions.¹² The latter mechanism stems from the suppression of membrane thermal fluctuation caused by adhesion. The associated decrease in fluctuation entropy is minimized when the bonds cluster together into a single adhesion domain.

Over the past two decades, considerable efforts have been made to better understand the role of membrane mediated interactions in the formation of adhesion domains. To this end, a common theoretical approach is the use of discrete lattice models, where the occupied sites represent membrane adhesion bonds, while empty sites stand for freely fluctuating membrane segments.^13–19 Computer simulations of such models have shown that membrane fluctuations can facilitate conditions for condensation of adhesion bonds. Nevertheless, it has also been concluded that the fluctuation induced interactions alone are too weak to promote aggregation and, hence, other attractive interactions between the bonds must also exist. A similar conclusion was recently reached in simulation studies employing coarse-grained (CG) molecular models, which provide a more physical description of the system. In one such study, we simulated a bilayer membrane with a small fraction of lipids from the lower monolayer connected to an underlying surface, and additionally introduced a short range attractive potential of depth ε between the adhesive lipids.²⁰ Our simulations revealed that the adhesive lipids underwent a first order condensation transition when the strength of the short range potential between them exceeds a threshold value of ε_c > 0. The fact that adhesion domains do not form when ε = 0 implies that the fluctuation entropy gained by the aggregation of the adhesive lipids only partially compensates for their loss of mixing entropy. In another CG simulation study, Noguchi demonstrated that cell junctions connecting more than two membranes can aggregate without an additional attractive potential between them.²¹ This observation can be understood because the total entropy of thermal undulations increases linearly with the number of membranes, N_m, while the mixing entropy of the cell junctions is independent of N_m.

Previous simulation studies have focused on the aggregation behavior of adhesion bonds in tensionless membranes. Here, we wish to extend our investigations to lipid bilayers subjected to surface tension and confinement. Under such conditions, the membrane long wavelength thermal undulations are suppressed, which weakens the fluctuation induced attraction. Specifically, a harmonic confining potential of strength γ > 0 suppresses thermal fluctuations at length scales larger than ξ_γ ∼ (κ/γ)^1/4, where κ is the bending modulus of the membrane. Likewise, a surface tension of τ > 0 affects bending modes with wavelengths greater than ξ_τ ∼ (κ/τ)^1/2. The influence of tension and confinement on the fluctuation mediated potential of mean force (PMF) was analyzed for the case of two adhesion bonds.²² It was shown that the PMF depends logarithmically on the pair distance: ϕ(r) = Ck_BT ln(r), where C = 2 at short distances, C = 1 at long distances (r ≫ ξ_τ) for stressed membranes, and C = 0 for long distances (r ≫ ξ_γ) for confined membranes. These findings suggest that tension and confinement may hinder the formation of adhesion domains, and that the phase transition into the condensed state requires a stronger short range attraction between the bonds. Therefore, one should expect the transition threshold value ε_c to grow with τ and γ; however, the magnitude of the increase in ε_c remains hard to assess due to the many body nature of the PMF.¹⁹ One may also consider the case of a bilayer membrane under negative tension. Negative tensions amplify the amplitude of the long wavelength undulations (and, for very large negative values, even lead to instability), and this should cause a reduction in ε_c. It is especially interesting to examine whether ε_c can decrease to zero, in which case the adhesion domains will form without an additional short range potential, i.e., on purely entropic grounds. As will be shown further on, the results of the current study suggest that confinement might have a very strong impact on ε_c, while the application of a positive surface tension hardly influences the transition into an aggregated phase. In cases where the membrane is subjected to a negative surface tension, we observe the formation of elongated adhesion domains close to the transition point.

2 Monte Carlo simulations

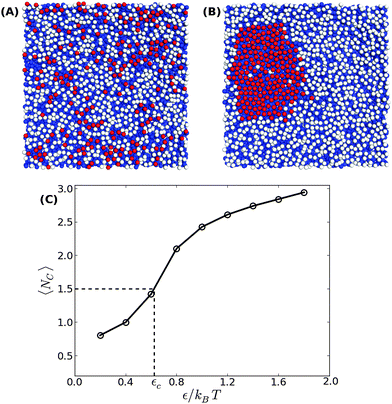
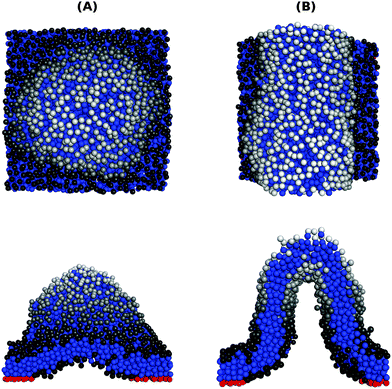
In order to address the above issues, we conducted Monte Carlo simulations of a lipid bilayer using the Cooke–Deserno implicit-solvent CG model.²³ The details of the simulations can be found in ref. 20. Briefly, we simulated bilayers of 2N = 2000 lipids (1000 lipids per monolayer), where each lipid consists of one hydrophilic (head) bead and two hydrophobic (tail) beads of size σ. A flat impenetrable surface was placed below the membrane at z = 0, and adhesion was established by connecting N_b head beads from the lower monolayer to it. A Lennard-Jones type potential with a tunable depth ε was introduced between the adhesive head beads. We simulated systems with various densities of adhesive lipids, ϕ = N_b/N, and for different values of the interaction potential depth ε. Our simulations for confined membranes included an additional impermeable surface placed above the upper monolayer at z = z_conf. Simulations of membranes under constant mechanical surface tension τ were carried out according to the method described in ref. 24.

Typical equilibrium configurations of tensionless membranes with ϕ = 0.2 are shown in Fig. 1 for ε = 0.2k_BT (A) and ε = 1.4k_BT (B). In the former, the adhesive lipids (whose head beads are shown in the figure in red) are scattered across the surface, while in the latter they condense into a large cluster. Fig. 1(C) shows the average energy E of pair interactions between adhesive beads, normalized per bond and expressed in dimensionless units by dividing by the potential strength ε. This quantity, which is a measure of the typical number of contacts between the adhesive beads 〈N_C〉, increases sharply when the condensation transition takes place. From the results in Fig. 1(C), we empirically determine the transition value as the one for which 〈N_C〉 ≃ 1.5.

Fig. 1 Bottom view of equilibrium snapshots of a tensionless bilayer with ϕ = 0.2 showing (A) a scattered distribution of adhesion bonds for ε = 0.2k_BT, and (B) a condensed phase for ε = 1.4k_BT. The head and tail beads are colored in white and blue, respectively, while the adhesive beads are colored in red. (C) The average number of contacts between the adhesion bonds as a function of ε. The condensation transition value ε_c is empirically defined via the equality 〈N_C〉 ≃ 1.5. The line serves as a guide to the reader's eye.

3 Results

3.1 Membranes under confinement

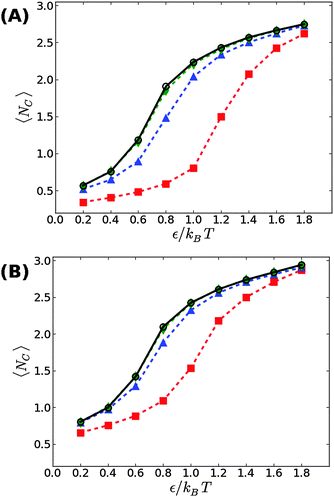
We first start with our simulation results for non-stressed membranes confined between the supporting underlying surface (on which the adhesive beads reside) and a second upper surface. The former is located at z = 0, just underneath the tips of the head beads of the lower leaflet, while the latter is placed at z = z_conf ≥ 6σ. The degree of confinement increases when z_conf decreases which, in turn, would lead to stronger suppression of the membrane thermal fluctuations and a shift in the transition threshold ε_c to larger values. This trend is demonstrated in Fig. 2, showing our simulation results for z_conf = 6σ, 7.5σ, and 9σ in supported membranes with ϕ = 0.1 (A) and ϕ = 0.2 (B). For z_conf = 9σ, our results (green diamonds) match perfectly with the results obtained for non-confined membranes (black circles). This means that the rate of collisions between the membrane and the upper surface is negligibly small and, therefore, it does not affect the fluctuation spectrum. Lowering the confining surface by a distance equal to the size of a bead and a half to z_conf = 7.5σ has a more noticeable effect on membrane thermal undulations, which leads to an increase in the condensation transition value from ε_c ≃ 0.65k_BT for non-confined membranes at ϕ = 0.1 to ε_c ≃ 0.8k_BT. For ϕ = 0.2, the shift is smaller, from ε_c ≃ 0.6k_BT to ε_c ≃ 0.7k_BT. When the upper surface is further lowered to z_conf = 6σ, it touches the tips of the head beads in the upper leaflet, as the thickness of the bilayer is equal to the size of six beads. A confining surface located at z_conf = 6σ completely suppresses thermal undulations, and eliminates the fluctuation mediated interactions between the adhesion bonds. Under these conditions, the threshold value for aggregation increases to ε_c ≃ 1.2k_BT at ϕ = 0.1, and ε_c ≃ 1k_BT for ϕ = 0.2. These values are approximately twice larger than the corresponding values found when no upper plate exists (ε_c ≃ 0.65k_BT and ε_c ≃ 0.6k_BT, respectively), which is in accord with the conclusions in ref. 19 and 21, that the entropic gain from the fluctuation spectrum compensates for, roughly, half of the loss in the mixing entropy of the adhesion bonds.

Fig. 2 The average number of contacts between the adhesion bonds in membranes confined by a surface located at z_conf = 9σ (green diamonds), z_conf = 7.5σ (blue triangles) and z_conf = 6σ (red squares), as a function of ε, for (A) ϕ = 0.1, and (B) ϕ = 0.2. Results for non-confined membranes are denoted by black circles. The lines serve as a guide to the reader's eye. The statistical errors are comparable to the size of the symbols.

3.2 Membranes under surface tension

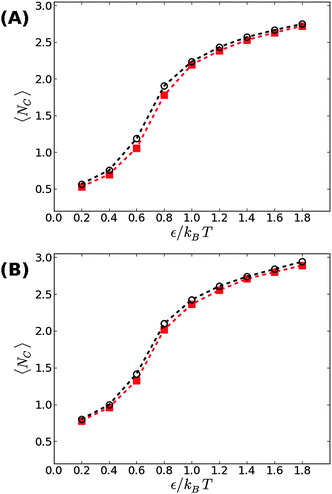
We now proceed to our simulation results for non-confined membranes subjected to a lateral surface tension τ > 0. Since, just like steric confinement, surface tension also suppresses the thermal undulations of the membrane, one may expect to also find an increase in the value of ε_c. However, our computational results that are depicted in Fig. 3 demonstrate that the 〈N_C〉 vs. ε curve remains almost unchanged when the tension increases from τ = 0 (black open circles) to τ = 0.48k_BT/σ² (red squares) for both ϕ = 0.1 (A) and ϕ = 0.2 (B). This observation suggests that the fluctuation spectrum of the simulated membranes is very little affected by the tension, which is expected, given that the bending modulus of the model membrane has been previously estimated to be κ ≃ 8k_BT.²⁵ For τ = 0.48k_BT/σ², the modes with wavelength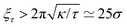 are suppressed, but this length scale is much larger than the typical distance 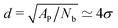between the adhesion bonds when the latter are uniformly distributed on the surface (where A_P is the projected area of the membrane). In order for the effect of the tension to be appreciable, one must apply stronger tensions; however, the application of a stronger tension would open pores in the membrane and tear it apart. In simulations with a surface tension of τ = 0.64k_BT/σ², we observed pores in most of the simulated membranes, and in the few that had managed to survive the tension, we still did not observe any considerable changes in the strength of membrane mediated interactions.

Fig. 3 The average number of contacts between the adhesion bonds in membranes under a mechanical surface tension of τ = 0.48k_BT/σ², as a function of ε for (A) ϕ = 0.1, and (B) ϕ = 0.2. The results are plotted in red squares, and are compared with the results for tensionless membranes (τ = 0) that are depicted by black open circles. The lines serve as guides to the eye. The statistical errors are comparable to the size of the symbols.

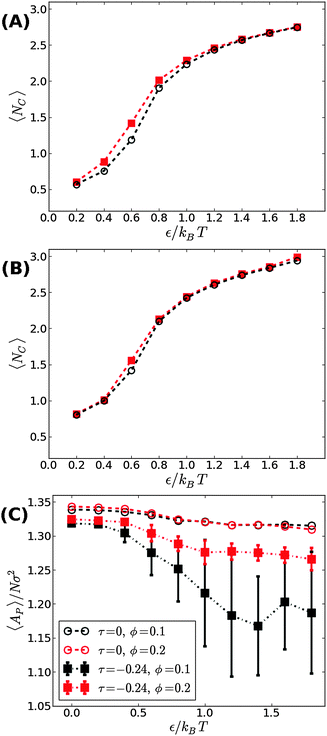
We next aimed to address the implications of applying a negative surface tension. In general, a negative tension imposed on the membrane leads to a reduction in its projected area, A_P, and amplifies the long wavelength bending modes. Hence, the fluctuation-induced attraction between the adhesion bonds is expected to be stronger which, in turn, implies that the threshold for condensation ε_c should become smaller than in tensionless membranes. To test this hypothesis, we simulated the membrane under a negative tension of τ = −0.24k_BT/σ². We performed two sets of independent MC simulations, one starting from a random distribution of adhesion bonds, and another where initially the adhesion bonds were organized in one large cluster. The system was equillibrated until configurations originating from these two distinct initial conditions achieved similar characteristics. Fig. 4 shows our results for 〈N_C〉 as a function of ε for ϕ = 0.1 (A) and ϕ = 0.2 (B). Contrary to our expectation to observe a reduction in ε_c, the data for τ = −0.24k_BT/σ² appear almost identical to the results of the tensionless case, with ε_c ≃ 0.6k_BT for both values of ϕ. Taken together with the data for τ = +0.48k_BT/σ² (see Fig. 3), we conclude that application of surface tension has a negligible effect on the condensation transition, within the range of tensions where the supported membrane is mechanically stable.

Fig. 4 The average number of contacts between the adhesion bonds in membranes under a surface tension of τ = −0.24k_BT/σ², as a function of ε for (A) ϕ = 0.1, and (B) ϕ = 0.2. The results are plotted in red squares, and are compared with the results for tensionless membranes (τ = 0) that are depicted by black open circles. (C) The mean projected area per lipid as a function of ε, for ϕ = 0.1 (black) and ϕ = 0.2 (red). Circles denote the results for tensionless membranes, while the results for τ = −0.24k_BT/σ² are shown in squares. The lines serve as guides to the eye.

The negative tension, however, does have an impact on the shape of membranes. Freely fluctuating bilayers assume buckled configurations at negative tensions larger (in absolute value) than τ_c ≃ −4π²κ/A_P.^26,27 In this study, A_P/N ≃ 1.33σ² [see Fig. 4(C)], which gives τ_c ≃ −0.24k_BT/σ². In ref. 28, a similar model membrane consisting of the same number of lipids was simulated and, indeed, for τ = τ_c the membrane appeared quite buckled. In supported membranes, however, the emergence of buckled configurations occurs only in membranes with large adhesion domains (i.e., for ε ≳ ε_c). Fig. 5 shows typical equilibrium configuration for ϕ = 0.1 with ε = 0 (A), 0.6k_BT (B), and 1.0k_BT (C). Each configuration is shown both in side and bottom views. When the attractive potential is set to ε = 0, the distribution of the adhesion bonds is scattered and the membrane remains fairly flat. This indicates that the mixing entropy of the bonds dominates the fluctuation entropy of the bilayer, despite the imposed negative tension [see Fig. 5(A)]. For ε = 1.0k_BT, the short range pair interactions between the bonds lead to their aggregation. Once the bonds condense, their influence on the thermal behavior of the membrane is greatly weakened, and strong bending undulations appear [see Fig. 5(C)]. Close to the condensation transition, at ε = 0.6k_BT, the system exhibits some interesting features: the amplitude of one of the two longest wavelength bending modes [with wavevect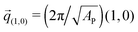or , or 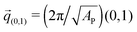] grows considerably, and the membrane assumes an anisotropic buckled configuration. The adhesion bonds are concentrated throughout the minimum of the dominating bending mode, forming an elongated domain (“stripe”) [see Fig. 5(B)]. These observed characteristics represent an intricate balance between the driving forces that govern the thermodynamic behavior of the system. Under negative tension, the system benefits from a reduction in the projected area, leading to a decrease in the Gibbs free energy. The membrane, however, is quite incompressible and, thus, the reduction in A_P must be accompanied by an increase in the area stored in thermal fluctuations whose amplitudes grow. The modes that experience the largest increase in amplitude are the softest ones, corresponding to q⃑_(1,0) and q⃑_(0,1)²⁶ (see footnote of ref. 29). In our simulations, we seldom observed situations where both these modes were simultaneously excited,³⁰ which can be linked to the mixing entropy of the adhesion bonds. When only one of the long modes is dominant, the contact area between the membrane and the surface, which is available for the presence of the adhesion bonds, is larger than in configurations where both modes are excited.

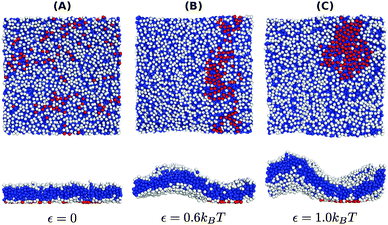Fig. 5 Typical equilibrium configurations of membranes under surface tension τ = −0.24k_BT/σ² with a density of adhesion bonds of ϕ = 0.1 for (A) ε = 0, (B) ε = 0.6k_BT and (C) ε = 1.0k_BT. The figures in the upper and lower rows display bottom and side views of the system, respectively. Color coding is the same as in Fig. 1.

The interplay between the mixing entropy of the adhesion bonds and the contribution of the negative tension to the free energy is further demonstrated in Fig. 4(C), depicting the mean projected area 〈A_P〉 (normalized by the number of lipids per monolayer N = 1000) as a function of ε for τ = −0.24k_BT/σ² (squares) and τ = 0 (circles). In the tensionless case, we observe a very mild decrease in 〈A_P〉 as ε increases, occurring mainly around ε_c. For τ = −0.24k_BT/σ², 〈A_P〉 maintains a value close to the tensionless case for ε < ε_c, and drops significantly for ε > ε_c. In the latter regime, we also observe an increase in the area fluctuations, resulting in larger uncertainties (error bars) in our estimates of 〈A_P〉. The sharp decrease in 〈A_P〉 and the concurrent increase in the area fluctuations are anticipated outcomes of a negative surface tension.²⁸ The fact that they are observed only above the condensation transition point is consistent with the picture discussed in the previous paragraph that, below ε_c, the effect of the negative tension is largely eliminated by the pressure resulting from the mixing entropy of the adhesion bonds. Notice that the sharp decrease in the mean projected area and the increase in the area fluctuations are much more noticeable for ϕ = 0.1 than for ϕ = 0.2. This is to be expected because the smaller the ϕ, the smaller the restrictions imposed by the adhesion bonds on large thermal undulations which are directly coupled to the projected area by the highly incompressible character of the membrane.

Applying an even stronger negative tension causes the membrane to lose its mechanical stability. This is demonstrated in Fig. 6, showing snapshots in top and side views of membranes with ϕ = 0.1 and ε = 1.0k_BT subjected to τ = −0.32k_BT/σ². In these snapshots, the head beads are colored in grayscale, with lighter colors indicating beads located higher above the underlying surface. The application of a strong negative tension causes the supported membrane to develop large protrusions with either spherical [Fig. 6(A)] or tubular [Fig. 6(B)] shapes. The adhesion bonds (which are colored in red, and are only partially visible) are concentrated in the periphery of the protrusion, where the membrane is in contact with the underlying surface. We note that the observed protrusions tend to evolve slowly and, therefore, the snapshots shown in Fig. 6 may not represent true equilibrium structures. On the other hand, we also note that very similar equilibrium structures, featuring spherical and tubular protrusions, have been recently observed in an experimental study where supported lipid bilayers were subjected to compression.³¹

Fig. 6 Configurations of membranes with ϕ = 0.1 and ε = 1.0k_BT under a strong negative tension τ = −0.32k_BT/σ², showing a spherical protrusion (A) and a tubular one (B). The upper and lower rows display top and side views of the membrane respectively. The tail and adhesive beads are colored in blue and red, respectively. The head beads are colored in grayscale to reflect their height above the surface, with lighter colors representing a higher bead.

4 Summary

The thermal fluctuations of a supported membrane induce an attractive PMF between the adhesion bonds, which promotes the formation of adhesion domains. In previous studies of systems where the adhesion bonds interact with each other via a pairwise short range attractive potential, it has been concluded that the fluctuation-induced PMF significantly decreases the condensation transition point, ε_c, of the adhesion bonds. In this work, we investigate adhesion domain formation in stressed and confined membranes by using MC simulations of a CG supported bilayer model. Our simulations reveal that placing a plate above the membrane (in addition to the surface supporting the membrane from below), significantly alters the condensation point. In the most extreme case, where the membrane is completely flattened between the two plates, the value of ε_c increases by almost a factor of two. In contrast to the impact of steric confinement, the application of a positive surface tension, which also acts to suppress membrane undulations, hardly affects the transition within the range of tensions where the supported membrane is mechanically stable. Similarly, we find that a negative tension also has a very minor effect on the condensation transition. Nevertheless, once the adhesion bonds are aggregated into a large domain (i.e., for ε > ε_c), the negative tension affects the shape of the membrane and causes it to buckle. Below ε_c the adhesion bonds are scattered across the membrane, which prevents the formation of buckled configurations. From the fact that ε_c is hardly affected by the application of a negative tension, we conclude that the mixing entropy of the adhesion bonds dominates the demixing entropy of the membrane thermal fluctuations. Close to ε_c, we observed the formation of elongated adhesion stripes. Such configurations emerge from an interplay between the mixing entropy of the adhesion bonds, the short range residual potential, and the applied negative tension. Finally, under a very strong negative tension, we observe tubular and spherical structures protruding out of the membrane's plane, which indicates that the system is at the onset of mechanical instability.

Acknowledgements

This work was supported by the Israel Science Foundation (ISF) through grant No. 1087/13.

References

1. B. Alberts, D. Bray, J. Lewis, M. Raff, K. Roberts and J. D. Watson, Molecular Biology of the Cell, Garland, New York, 1994.
2. T. A. Springer, Nature, 1990, 340, 425.
3. A. Huttenlocher, R. R. Sandborg and A. F. Horwitz, Curr. Opin. Cell Biol., 1995, 7, 697.
4. K. Vleminckx and R. Kemler, BioEssays, 1999, 21, 211.
5. Y. Wang and B. Rose, J. Cell Sci., 1995, 108, 3501.
6. C. R. F. Monks, et al. , Nature, 1998, 395, 82.
7. C. Selhuber-Unkel, M. López-García, H. Kessler and J. P. Spatz, Biophys. J., 2008, 95, 5424.
8. K. Burridge and M. Chrzanowska-Wodnicka, Annu. Rev. Cell Dev. Biol., 1996, 12, 463.
9. F. G. Giancotti and E. Ruoslahti, Science, 1999, 285, 1028.
10. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, San Diego, 1992.
11. C. Wulfing and M. M. Davis, Science, 1998, 282, 2266.
12. R. Bruinsma and P. Pincus, Curr. Opin. Solid State Mater. Sci., 1996, 1, 401.
13. R. Lipowsky, Phys. Rev. Lett., 1996, 77, 1652.
14. T. Weikl, et al. , Soft Matter, 2009, 5, 3213.
15. T. R. Weikl and R. Lipowsky, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 011903.
16. T. Speck and R. L. C. Vink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031923.
17. R. L. C. Vink and T. Speck, Soft Matter, 2013, 9, 11197.
18. T. Bihr, U. Seifert and A. S. Smith, Phys. Rev. Lett., 2012, 109, 258101.
19. N. Weil and O. Farago, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 81.
20. N. Dharan and O. Farago, J. Chem. Phys., 2014, 141, 024903.
21. H. Noguchi, Europhys. Lett., 2013, 102, 68001.
22. O. Farago, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 050902R.
23. I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506.
24. O. Farago and N. Grønbech-Jensen, Biophys. J., 2007, 92, 3228.
25. O. Farago, J. Chem. Phys., 2008, 128, 184105.
26. H. Noguchi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 061919.
27. W. K. den Otter, J. Chem. Phys., 2005, 123, 214906.
28. Y. Y. Avital and O. Farago, J. Chem. Phys., 2015, 142, 124902.
29. Notice that in ref. 26, the membrane is simulated in the fixed-area ensemble, A_P = L_xL_y, with L_x ≠ L_y, which generates buckled configurations with anistropic surface tension. In this study, we simulate the fixed (isotropic) tension ensemble, where the projected area A_P is allowed to fluctuate, but with L_x = L_y.
30. Out of 15 independent realizations of the system corresponding to ε = 0.6k_BT, in more than half we observed one dominant long Fourier mode. For larger values of ε, realizations where both modes were simultaneously excited occurred more frequently.
31. M. Staykova, M. Arroyo, M. Rahimi and H. A. Stone, Phys. Rev. Lett., 2013, 110, 028101.

---