An inventory for measuring student teachers' knowledge of chemical representations: design, validation, and psychometric analysis

Abstract

Chemical representations play an important role in helping learners to understand chemical contents. Thus, dealing with chemical representations is a necessity for learning chemistry, but at the same time, it presents a great challenge to learners. Due to this great challenge, it is not surprising that numerous national and international studies have shown that students have remarkable difficulties. Since most of the studies regarding chemical representations have focused on investigating high-school students' knowledge so far, little is known about university students' and especially student teachers' knowledge. The latter group is additionally challenged by the necessity of learning how to transform their own knowledge in order to teach chemical representations to their prospective students. Given this as a starting point, a paper-and-pencil test with 19 items in both semi-open and closed format was developed to investigate the extent of student teachers' knowledge of chemical representations. The present paper describes the design, validation, and psychometric analysis of this test instrument – the so-called Chemical Representations Inventory (CRI). The CRI includes a variety of chemical representations and chemical contents on both high-school and university level. Both classical test theory and Rasch modelling were used for the analysis. In addition, a qualitative analysis was performed, and factors which possibly influence the item difficulty were identified. Even though the CRI was originally developed for a sample of student teachers, it can also be used to measure chemistry students' knowledge on a basic level.

---

Introduction

As Kozma and Russell (1997) point out, “understanding chemistry relies on making sense of the invisible and untouchable” (p. 949). Since chemical representations serve as a tool to create a mental model of the unseen sub-microscopic level, they play an important role in helping learners to understand and learn chemistry. Thus, understanding chemical representations is a necessity for learning chemistry, but at the same time, it presents a great challenge to learners. This does not only apply to high-school students beginning to learn chemistry, but also to university students, since several chemical representations are first taught at university level. The challenge is even greater for student teachers, who additionally have to transform their knowledge of chemical representations in order to teach it to their prospective students.

Due to this great challenge, it is not surprising that numerous national and international studies have shown that students experience remarkable difficulties with chemical representations (Bucat and Mocerino, 2009; Taskin and Bernholt, 2014). However, most of the studies on chemical representations focused on the investigation of high-school students' knowledge of selected chemical representations. Little is known about university students' or student teachers' knowledge of chemical representations; this also includes those representations which are first taught at university level. One reason for that is the fact that adequate instruments for measuring these aspects have not been developed yet. Given this as a starting point, the aim of the project at hand was to develop a paper-and-pencil test which is supposed to investigate the extent of student teachers' knowledge of this very topic. Here, the knowledge of chemical representations includes the ability to apply conventional rules in order to interpret and draw chemical representations correctly (e.g. naming of compounds, balancing chemical equations, or translating equations to particle models). Additionally, it includes the awareness of certain inconsistencies and ambiguities with regard to these rules, mainly rooted in the historical development of the chemical symbolic system (e.g. NaOH instead of NaHO). Thus, this test instrument mainly focuses on the technical or language-based aspects of chemical representations, comparable to an understanding of grammar and syntax in reading ability (cf.Taskin and Bernholt, 2014). These aspects are seen as prerequisites for a comprehensive, expert-like understanding of representations. The test thus will lay the foundations for future research which can then investigate the knowledge of the conceptual meaning of chemical representations, i.e. their meaning on the sub-microscopic level. This kind of knowledge is necessary to both understand the meaning of chemical representations and chemistry. The present paper describes the design, validation, and psychometric analysis of this test instrument – the so-called Chemical Representations Inventory (CRI).

Theoretical background

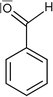
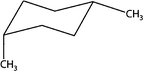
One of the basic – and at the same time one of the most important – features in chemistry is the naming of chemicals. For this purpose, a nomenclature system with its own rules and conventions was developed by practicing scientists in order to be able to communicate about chemical contents in a well-defined, but brief fashion. This system does not only involve systematic names in accordance with IUPAC, but also commonly used trivial names as well as names of classes of substances. Nomenclature is probably most important in the field of organic chemistry, where huge and branched compounds are considered on a regular basis. However, naming chemicals may present a great challenge to students. This is additionally complicated by the fact that chemical contents can be represented by different symbols. For example, a methyl group can be drawn as –CH₃, –H₃C or –Me (Bucat and Mocerino, 2009). In a similar fashion, different symbols can be used for ethyl, propyl, butyl, and even phenyl groups (Taber, 2009). In order to investigate students' conceptions with regard to nomenclature, Bernholt et al. (2012) presented the names and chemical formulae of several compounds to students. In some cases, however, the presented chemical formulae did not match the given compounds. The students were then asked to identify and correct these formulae. The authors concluded from their results that the percentage of adequate corrections increases with both the students' grade level and their familiarity with the given compounds. Schmidt (2000) observed that students name chemical compounds by following one single rule, i.e. naming oxo-salts as oxids, which corresponds to the nomenclature for binary compounds. Bodner and Domin (2000) asked students in the first semester of a non-major organic chemistry course to give the systematic names of the compounds whose molecules are shown in Fig. 1. To successfully solve this task, students had to understand the conventions concerning the intricacies of each representation and their meaning. The results showed that most students succeeded with the structure on the left, but many had trouble with naming the one on the right. In addition to the extra requirement of performing a mental operation during the analysis of the right structure, i.e. having to rotate the 3D representation and transform it into 2D, this type of chemical representation is probably less familiar to students than the left one.

Fig. 1 Compounds used in Bodner and Domin (2000).

Besides the nomenclature of chemical compounds, chemical equations are seen as indispensable for the communication about and learning of chemical contents. Hence, it is necessary for students to know the rules and conventions according to which such equations are set up. However, several studies have reported about students' difficulties with regard to chemical equations. This does not only apply to high-school students, but also to university students. With regard to the ability to balance chemical equations, Abraham et al. (1992) as well as Savoy and Steeples (1994) discovered that students tend to manipulate the formulae in a given equation by changing the subscripts, even though only coefficients had to be added. The reason for this problem is that students regard coefficients and subscripts as numbers which give the same information, but differ in their location in the equation (Schmidt, 1984; Yarroch, 1985; Savoy and Steeples, 1994). However, the ability to balance chemical equations does not necessarily involve knowledge of what the equations represent on a sub-microscopic level (Davidowitz et al., 2010). Nurrenbern and Pickering (1987) focused on students' conceptions of the sub-microscopic meaning of chemical equations. They provided a sub-microscopic picture of the reactant mixture and the product mixture for the imaginary reaction X + Y → XY₂ and asked students to decide which of the given equations matched the picture best. Only one-fifth of the students were successful. Several studies replicated this task, and all of them were able to show that the majority of students chose the equation 3X + 8Y → 3XY₂ + 2Y (e.g.Sawrey, 1990; Arasasingham et al., 2004). This took place under the assumption that a reaction arrow has the same meaning as a (mathematical) equal sign (Yarroch, 1985). When dealing with reaction mechanisms, additional symbols are involved in chemical equations. In particular, these are curly arrows which represent the movement of electron pairs. Taber (2009) stresses that it is important for students to grasp the meaning of these arrows, because an understanding of which electrons move from where to where is required in order to correctly interpret chemical equations.

In contrast to high school, where Lewis formulae are commonly used, learning chemistry at university level requires an understanding of skeleton formulae. Especially in organic chemistry courses, this type of chemical representation is permanently used. The ability to interpret it correctly is a prerequisite for predicting the products of chemical reactions. This could be shown by Bodner and Domin (2000). In their study, they asked students to “predict the major products of the reaction of bromine with methylcyclopentane [and] to estimate the ratio of the products that would be formed if bromine radicals were just as likely to attack one hydrogen atom as another” (p. 25). To be able to answer this question, an understanding of the inherent conventions with regard to the kind and number of atoms which are implied (rather than explicitly shown) in skeleton formulae is required. The results of the study showed that only a minority of the students were able to answer the question correctly and could predict four products with the relative abundance 3 : 4 : 4 : 1 (Fig. 2a). Most of the 200 students predicted that the reaction would result in products with the ratio 3 : 2 : 2 (Fig. 2b). In contrast to those who answered the question correctly, none of them translated the skeleton formula for the starting material into a drawing which showed the positions of all the hydrogen atoms in this compound, as shown in Fig. 2c.

Fig. 2 Students' answers to the task concerning the reaction of bromine with methylcyclopentane in Bodner and Domin (2000).

The challenge of dealing with skeleton formulae becomes even greater for students when dashed lines and wedges are additionally used in order to include information on the spatial arrangement of atoms. With regard to this type of representation, stereochemical considerations are typically in the focus of interest. A common task in university lectures is to decide whether given structures are mirror pictures or superimposable. Head and Bucat (2002) conducted interviews with students in order to investigate their strategies to solve tasks of this kind with the example of Alanine. They found out that most students tried to reduce the problem to 2D by rotating the given structures and aligning a corresponding bond in each of them. In a second step, the students analyzed the orientation (clockwise vs. counter-clockwise) of the other remaining functional groups, identified the configuration, and finally answered the questions. Ferk et al. (2003) analyzed students' appreciation of different three-dimensional structures. They were able to show that even at university level especially stereochemical formulae are not fully understood. The same could also be stated with regard to schematic representations which are usually known as ball-and-stick models. These models play an important role in illustrating the coordination of particles in ionic compounds as well as complex compounds and are therefore indispensable in university lectures.

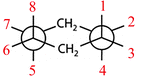
According to Gilbert (2008), being able to deal with chemical representations requires three capacities. These are: (a) understanding the conventions of representations, (b) constructing representations, and (c) translating between different representations. Kozma and Russell (1997) declare the last capacity to present a major contribution to the notion of expertise in chemistry. When investigating expert chemists' and novice students' understanding of different forms of representations, they found that the experts were much better than the novices in transforming one type of representation into another. Since individual types of representations illuminate only specific features of a chemical content and thus contribute only to a part of its entire meaning, working with several types of representations and being able to translate between them is a necessity to grasp chemical contents as a whole (Cheng and Gilbert, 2009). Bucat and Mocerino (2009) advanced this aspect by using the example of substituted cyclohexane, which can be “represented as a flat-looking hexagonal projection, or as a side-on view to show the ‘chair’ form, or as a Newman projection” (p. 24). The latter type of representation is useful in the field of stereochemistry. It helps to visualize different conformations of chemical compounds with carbon–carbon chemical bonds. Additionally, it helps to make predictions concerning their stability based on the orientation of side chains. However, reading and interpreting Newman projection formulae is not intuitive for students, as the shape of this representation and the geometrical structure of the underlying compound are quite unsimilar.

Aim of the study

As most of the studies on chemical representations have focused on the investigation of high-school students' knowledge of selected chemical representations so far, the present study aims at developing a valid and reliable test instrument to measure student teachers' knowledge of a variety of chemical representations. In this context, what is meant by knowledge is the ability to apply conventional rules in order to interpret and draw chemical representations correctly. Additionally, it includes the awareness of certain related inconsistencies and ambiguities that are not part of a coherent theory but are negotiated conventions, established over years by practicing chemists. However, the usage of chemical representations is not limited to algorithmic and conventional strategies, but also contains more complex approaches, as studies with experts illustrate (cf.Bodner and Domin, 2000; Stieff, 2007, 2010). For experts, chemical representations are both a tool to visualize and organize information and thoughts and a heuristic to re-think and explore new aspects (e.g. to propose a new compound or mechanism; Hoffmann and Laszlo, 1991). Although we agree in this fundamental value und function of chemical representations, we limited the focus of this test to the basic “grammar and syntax” of chemical representations, i.e. to the visualizations themselves (Talanquer, 2011) and their technical vocabulary (Taber, 2013). We think that knowing these aspects is a prerequisite for being able to use representations during conceptual, analytical or diagrammatic reasoning. In addition, numerous studies indicate that students' problems with chemical representations can often be attributed to shortcomings in students' knowledge about basic rules and conventions of chemical representations (Taskin and Bernholt, 2014). “Whereas instructors see chemistry in the representations that they draw, students may see only surface features – letters, numbers, and lines' (Wirtz et al., 2006, p. 965).

Design and validation

The development of the test instrument started with the review of chemistry textbooks, curricula of different German universities, and university exams in order to account for the validity of the test items. Additionally, existing literature about students' problems with chemical representations was reviewed. Five important topics were extracted. These are: (1) nomenclature, (2) chemical equations, (3) skeleton formulae, (4) ball-and-stick models, and, according to Gilbert (2008), the operation (5) “translation of chemical representations.” With regard to these five topics, items were developed. The chemical content and demands of these items will be described in the following subsections of the paper.

Nomenclature

Items regarding this topic require students either to name given chemical compounds or to draw chemical structures on the basis of given names. In one of these items, students have to check whether the given empirical or molecular formula matches the given compound name (item 1). If not, the formula has to be corrected. This item was originally developed and used by Bernholt et al. (2012) in an extended version. In other items of this group, an IUPAC-name, trivial name, or the name of a fundamental class of substances is presented, and the corresponding condensed Lewis formula or skeleton formula has to be drawn (items 9, 11, 15). In a further item, this sequence is reversed: The skeleton formula of a branched alkane is given, and the corresponding IUPAC-name has to be completed by adding the position numbers of the side chains (item 12). A similar item including a Lewis formula was used by Bodner and Domin (2000). Thus, items in this group require either students' memorization especially in the case of trivial names or the application of specific conventional rules concerning the naming of compounds in accordance to IUPAC.

Chemical equations

Items which refer to this topic ask students to work on chemical equations. In one of these items, students have to balance an incompletely given equation by adding coefficients (item 13). This kind of item was previously used in other studies (Abraham et al., 1992; Savoy and Steeples, 1994), but in the context of considerably easier equations. In another item, students are required to show their awareness of what a chemical equations means on the sub-microscopic level, i.e. they have to identify the corresponding chemical equations to a given particle model (item 6). This item is taken from the study by Nurrenbern and Pickering (1987). In a third item, the process character of chemical equations is in the focus. Students have to use arrows in order to represent the movement of lone pairs in a given reaction (item 10). In summary, items in this group require students to apply algorithmic rules (for balancing equations), to match symbolic equations with particle models, and to interpret chemical terms (“illustrate the displacement of electrons in the following reaction”) in form of the arrow pushing formalism.

Skeleton formulae

Items in this group require the knowledge of specific conventions with regard to skeleton formulae (also in combination with Natta projection) in order to be able to read these formulae correctly and draw correct conclusions from them. In one item, the number of hydrogen atoms (which are usually not shown in such formulae) has to be determined at marked positions (item 19). This item differs from that of Bodner and Domin (2000) with respect to the fact that it asks explicitly for the hydrogen atoms, whereas Bodner and Domin (2000) focused more on the content side, i.e. the prediction of major products of the given reaction. Here, the students' ability to determine the unseen hydrogen bonds was investigated indirectly. In another item of this group, the asymmetric carbon atoms – this term was concretized by saying “carbon atoms with four different neighboring groups” – have to be identified (item 16). In a similar fashion to Head and Bucat (2002), but on a quantitative level, the last item in this group requires knowledge of the meaning of dashed lines and wedges in order to identify the enantiomer – this term was clarified in the test item by using the words “mirror picture” – of a given compound (item 18). Accordingly, items in this group mainly require students to interpret explicit details (dashed lines) or implicit ones (“hidden” hydrogens) in skeleton formulae to infer structural or spatial information about the substance at hand.

Ball-and-stick models

Items which deal with this topic require students to work on ball-and-stick models, i.e. to interpret them correctly by using their spatial ability and to draw correct conclusions with regard to the underlying chemical content. In one item, students have to compare given ball-and-stick models and identify those which represent the same complex compound (item 5). In a further item which includes a larger and more demanding complex compound, students have to identify and mark the coordination positions (item 3). In yet another item, students have to determine the coordination number of the ions in a given elementary cell (item 2).

Translation

Items in the last group ask students to recognize the linkage between two types of representations. In one item, rather simple and short organic compounds given in condensed Lewis formulae have to be transformed into corresponding skeleton formulae which have to be explicitly drawn (item 8). With reference to Bucat and Mocerino (2009), one item asks for the translation of a flat-looking hexagonal projection into a side-on view showing the ‘chair’ form (item 7). In another item, students have to transform a side-on view into a Newman projection (item 17). In both items, the translation has to be made by adding structural units to one of the representations given incompletely in the items. With regard to glucose, these structural units are OH-groups in item 7. With regard to 1,4-dimethylcyclohexane, the units are CH₃-groups in item 17.

There are two more items which do not belong to any of the mentioned groups. They are included in the test instrument, because they refer to an important content in chemistry. In one of these items, students have to complete a particle model by drawing circles in order to visualize densest sphere packing with different layering (item 4). To correctly solve the second item, students have to recognize the equatorial and axial orientation of the side chains in a compound consisting of cyclohexane units (item 14).

Although the items of the test instrument focus on five topics described above, they include several types of chemical representations. These are simple particle models, ball-and-stick models, Lewis formulae, condensed Lewis formulae, skeleton formulae, Natta projection formulae, Sawhorse projection formulae (expressing a side-on view which shows the ‘chair’ form), Newman projection formulae, as well as empirical and molecular formulae and chemical equations. With regard to these representations, there is a fluent change from macroscopic to sub-microscopic level, and from there to symbolic level (Johnstone, 2000). Thus, unlike other studies which focused on a selection of chemical representations, the test instrument includes a variety of representations. In order to ensure that every student has the same understanding of the representations and their designation, the test instrument includes an introductory clarification of this issue.

Besides the types of chemical representations, variance can also be found regarding the chemical content of the items. These were chosen from the fields of general, inorganic, as well as organic chemistry. With regard to the latter field, the following chemical contents were chosen: branched alkanes, halogen alkanes, cyclic alkanes, nitrogenous compounds, hydroxycarboxylic acids, monosaccharide, aromatics, and heterocyclic aromatics. With regard to general and inorganic chemistry, the following chemical contents were included in the item development: acids and bases, salts and oxides, zinc blende structure, densest sphere packing, complex compounds, as well as redox reactions of specific and also more general compounds such as XY₂. Naturally, chemical representations are tightly linked to the related chemical contents. In other words, chemical representations are senseless without any content. Nevertheless, the intention behind the development of the test instrument was to focus on the chemical representations themselves. Thus, in order to reduce the influence of possibly missing content knowledge in connection to solving the items, compounds in general forms such as the ones mentioned above were preferred. In addition, instead of technical vocabulary, more descriptive phrases were used, e.g. “layering ABABA…“and “layering ABCABC…” instead of “hexagonal” and “cubic.”

Initially, 45 items were developed. Three chemistry professors reviewed them with regard to their comprehensibility, difficulty, and relevance for university studies. Additionally, think-aloud interviews with university students were conducted in order to again improve the comprehensibility of the items by excluding or changing misleading wordings. The items were then piloted with student teachers in order to detect and eliminate items with unsatisfactory statistical values, i.e. reliability and discrimination. Because the final test instrument should not take more than half an hour, an elimination of test items was also necessary. 19 items in both semi-open and closed format remained in the final version of the test instrument, including a variety of chemical representations and chemical contents on both high-school and university level. This test instrument is referred to as the Chemical Representations Inventory (CRI).

Data collection and sample

The CRI was administered in the summer semester 2013 as part of the KiL-project (Kleickmann et al., 2014). This project investigates the content knowledge, pedagogical content knowledge, and pedagogical knowledge of student teachers who study one of the science subjects (biology, chemistry, and physics) or math. The CRI was part of the test for measuring the chemical content knowledge of chemistry student teachers. The whole test procedure took four hours, including small breaks. For the inventory, a time slot of 30 minutes was given. This was sufficient for the students to solve the items. Altogether, 322 students from 12 German universities filled out the inventory. From each university, a minimum of seven, a maximum of 63, and an average of 27 students were involved in the administration. They averaged at an age of 23 years, and 62% of them were female. The students in the sample were in different stages of their university education. Throughout the whole research process, ethical guidelines for research within science education were followed. All participants have been involved after consent was given and after background information about the project was provided. Participation of the students was voluntarily, and all participants were informed that they, whenever, could decide to drop out from the study. The participating students are anonymous and the collected data has been treated confidentially.

Results

Quantitative analysis

All but two inventory items are to be solved in more than one step, require the identification of more than one correct answer, or consist of at least two subtasks. Accordingly, a partial credit coding system was generated for these items. The items were coded with 0 for any incorrect answer, with 1 for a partially correct or incomplete answer, and with 2 for the correct and complete answer. The identification of subtasks and the assignment of partial credits for incomplete answers are based on suggestions from experts. Before completing the test for this study, all items were presented to three chemistry experts (one professor for inorganic chemistry, two professors for organic chemistry) who were asked to evaluate the appropriateness of the items, their phrasing, and difficulty as well as to provide correct solutions for the items. The proposed solutions for each item were taken as a basis for formulating the scoring guide (cf. Appendix). As the scoring guide was formulated in a very explicit fashion, the assignment of partial and full credit was an immediate result of the students' answers, with almost no tolerance for interpretation. Hence, the coding process was completed nearly automatically, based on the scoring guide and by calculating the sum of all subtasks. In two items (item 17 and 18), no subtasks were included, so either an incorrect answer was coded with 0, or a correct answer was coded with 1. Missing values were coded with 0, because the students had enough time to fill out the inventory. Therefore, a missing value was likely to be caused by a lack of knowledge rather than a lack of time.

To evaluate the functionality of the developed inventory, several psychometric properties were analyzed using not only the classical test theory, but also Rasch modelling. The analysis in accordance with the classical test theory included the calculation of item difficulty, item discrimination, and internal consistency. The Rasch analysis covered the evaluation of the item fit to the Rasch model, the dimensionality of the whole inventory, local independence of the items, EAP-PV (expected a posteriori/plausible value) reliability, as well as the match between the difficulty of the items and the ability of the students. Thus, the use of Rasch modelling made it possible to assess further psychometric properties beyond the capability of classical test theory. Moreover, it provided additional useful information about the functionality of the inventory. The classical test theory analysis was conducted with the SPSS 19.0 software. For the Rasch analysis, ConQuest was used. The results will be presented separately according to the used method.

Classical test theory. With regard to the methods of classical test theory, the data was used to calculate the difficulty and discrimination of the items as well as the reliability of the whole inventory. The item difficulty represents the portion of students who answered the item correctly. The difficulty of the items with full credit coding equals their mean value. In order to calculate the difficulty of the items with partial credit coding, the corresponding mean values had to be divided by the maximum value achievable per item, i.e. divided in half in the current case. The difficulty values of the items in the inventory range from 0.19 to 0.88. A higher value indicates a higher number of students who answered the item correctly – and thus an easier item (Crocker and Algina, 2008). The item discrimination indicates whether an item is able to distinguish between different performance levels. The corresponding values of the items in the inventory range from 0.10 to 0.51. For concept inventories, the values of item difficulty should be in the range of 0.25–0.75 (Kline, 2005). With regard to discrimination, items with a value greater than or equal to 0.30 are considered as acceptable (Ebel and Frisbie, 2006). Fig. 3 shows the difficulty and discrimination values of each item. The square includes all items with values inside the suggested ranges. Items 1, 5, and 6 are the easiest ones; their difficulty values are greater than the suggested value of 0.75. Item 14 is the most difficult item; with a value of 0.19, it is also outside the suggested range. Since the discrimination of an item depends on its difficulty (i.e. items with a very low or high difficulty are not supposed to discriminate between low- and high-performing students (Barbera, 2013)), items 1, 5, 6, and 14 have a discrimination value smaller than the suggested value of 0.30. However, there is an even less discriminating item: With a value of 0.10, item 18 is the least discriminating item in the inventory. Hence, items 1, 5, 6, 14, and 18 (and strictly speaking also item 2) need further research to investigate their item functionality.

Fig. 3 Difficulty and discrimination values for all 19 items of the CRI. The square includes all items with values inside the suggested ranges.

The reliability of the CRI data was evaluated through the calculation of Cronbach's α. This value measures the internal consistency within a student's answers with the items of the inventory (Crocker and Algina, 2008). The data has an α value of 0.78. Since this value is in the acceptable range, the data is said to display acceptable internal consistency.

Rasch model. According to the assumptions of the Rasch model, students with higher ability are more probable to answer an item correctly than students of lower ability (Rasch, 1980). By using this probabilistic model, difficulties of items and abilities of persons are estimated. In addition, it is evaluated whether an item fits to this model. For this purpose, weighted mean squares (WMNSQ) which express the discrepancy between the observed data and the model are calculated. An acceptable fit is given when WMNSQ values are in the range between 0.70 and 1.30 (Wright and Linacre, 1994). More-over, t statistics were used to identify whether the deviation of the WMNSQ values from the expected value is significant. Acceptable t values range between −2 and 2. Table 1 shows the difficulty of each item in the inventory as well as the WMNSQ values and the t statistics. All items in the inventory have WMNSQ values inside the recommended range. The result remains the same when every single step of the items with partial credit coding are considered. With regard to the t values, only item 18 does not fit. However, when every step of the items with partial credit coding is considered, all t values are in the suggested ranges. This suggests that the items measure a unidimensional construct (cf.Bond and Fox, 2007, ch. 12).

Table 1 Item fit statistics for CRI data

Item	Difficulty value	WMNSQ	t
1	−1.49	0.99	−0.0
2	0.09	0.99	−0.1
3	0.02	0.94	−1.1
4	−0.37	1.07	1.0
5	−0.87	1.08	1.0
6	−1.41	1.01	0.2
7	−0.06	1.03	0.4
8	−0.35	0.96	−0.5
9	0.52	1.00	0.1
10	0.18	0.95	−0.9
11	−0.70	0.90	−1.4
12	1.01	1.02	0.4
13	−0.29	1.02	0.4
14	1.48	1.15	1.6
15	0.56	1.08	1.5
16	0.74	0.91	−1.6
17	0.91	0.97	−0.7
18	0.34	1.09	2.7
19	−0.29	0.97	−0.4

---

Beyond unidimensionality, local independence of all items is a central assumption when using the Rasch model. Students' responses on different items should be uncorrelated when students' ability (which is assumed to be measured by these items) is partialled out. Using the Standardized Root Mean Square Residual (SRMSR; Maydeu-Olivares, 2013), the obtained value of 0.069 indicates a slight amount of misfit.† However, it is still close to the suggested cut-off of 0.05, which would indicate a well-fitting IRT model for the ordinal data of this test. Based on Yen's (1993) Q3 statistic, the residual item scores under the CRI (i.e., observed – expected scores) are calculated and correlated with each other. A chi-squared test suggests that item 8 and 11 are responsible for this slight deviation (X² = 30.99, p_Holm = 0.0001). As both items require students to draw skeleton formulae, this interrelation seems plausible (This is also true for item 9, but here both paired chi-squared tests are non-significant, which suggests that no local dependence is induced at this point). Nevertheless, the global goodness-of-fit statistics indicates that local item independence can be assumed for the CRI.

In the Rasch model, both the difficulty of items and the ability of students are placed on the same scale. So, both variables can be compared directly with each other. For this purpose, Wright maps of the data were generated (see Fig. 4). These maps indicate that students have a 50% probability to solve the item which is located on the same height of the scale as their ability. The probability is higher for the items which are below their location and lower for the items which are higher up. Thus, individuals with the highest abilities as well as the most difficult items are presented on the upper part of the scale. Due to the use of the partial credit model, two maps of this kind are presented. In both maps, the distribution of personal abilities is the same. The only difference is that the left map in Fig. 4 shows the item difficulties, whereas the right map represents the so-called Thurstonian thresholds for every item with a partial credit coding. In the case of the items with a full credit coding (item 17 and 18), the thresholds equal their difficulties. The function of these thresholds is to indicate the location at which the probability of achieving at least the indicated level of performance on an item is 50% (Wu et al., 2007).

Fig. 4 Wright maps of the data. The left side of each map reflects the distribution of the students according to their ability measured by the inventory (from most able at the top to least able at the bottom). The right side of the first map shows the items distributed from the most difficult at the top to the least difficult at the bottom. The right side of the second map shows the Thurstonian thresholds for the items with a partial credit coding. The notation x·y is used to indicate the y-th threshold of the x-th item. For example, it was most difficult to achieve the second threshold, i.e. full credit, in item 14 and the easiest to get a partial credit in item 6. In both maps, M represents the mean and SD the standard deviation of personal abilities. The mean of the item difficulties is always centered automatically at zero. The difference of 0.33 logits between the students' and items' mean indicates that the CRI was slightly too easy for this sample of student teachers.

The Wright maps provide several pieces of information about the data. They show that the values of the personal abilities are distributed symmetrically. Since most of the values fall within ± one standard deviation (SD) from the mean (M), the data concerning the students' abilities is not skewed or bimodal. Additionally, the maps show the range of item difficulties. Even though the corresponding values are distributed along with nearly the same range as the personal abilities, there are gaps within the range, i.e. between the items 5 and 6 as well as between the items 12 and 14. Abilities of students that fall within these gaps cannot be evaluated accurately and have to be considered with caution. When regarding the levels of performance on each item with a partial coding, however, the gaps are redistributed; they are smaller as represented in the Wright map with the thresholds (Fig. 4, right side). Hence, the partial credit coding of the items in the inventory enlarges the amount of values, densifies the distribution, shrinks the gaps, and thus allows for a more accurate estimation of the students' abilities. The last information which can be gathered from Wright maps concerns the appropriateness of the inventory for the current sample. Since there is a high overlap between the distributions of the two variables and a small difference of only 0.33 log its between their means, it can be concluded that the difficulties of the items match the students' abilities. Thus, the inventory is seen as appropriate for the sample of student teachers.

In the Rasch model, the EAP-PV (expected a posteriori/plausible value) reliability is calculated. For the CRI data, it has a value of 0.78. The scale of this reliability measure is comparable to Cronbach's α, so that the value indicates an acceptable to good reliability of the CRI (Kline, 1999).

Qualitative analysis

The quantitative analysis was able to show that the items of the inventory were solved unequally well by the students. A qualitative analysis was performed in order to find possible explanations for these differences within each group. For this analysis, the item difficulties of the Rasch modelling shown in Table 1 were considered. Fig. 5 shows a Wright map of the data in which the item difficulties are shown separated according to the five topics used for item development: nomenclature, chemical equations, skeleton formulae, ball-and-stick-models, translations.

Fig. 5 Wright map of the data in which the item difficulties are shown separated according to the five topics used for item development: nomenclature, chemical equations, skeleton formulae, ball-and-stick-models, translations. Two items do not belong to any topic and are therefore assigned to the group “other”.

Nomenclature. Even though naming chemicals is a basic feature in chemistry, the items concerning this topic were not as easy as anticipated for the students. The easiest item (item 1) in this group had a difficulty value of −1.49, whereas the value of the most difficult item (item 12) was 1.01. It was expected that the easiest nomenclature items deal with IUPAC names, because knowledge of the corresponding conventions would be sufficient to solve such items independent of the size and complexity of the related chemical contents. In contrast, working with trivial names requires a specific degree of familiarity with the represented compounds due to the fact that trivial names do not provide any systematic information about the underlying structures. A comparison of all nomenclature items reveals that it does not make any difference whether IUPAC names, trivial names, or the name of a fundamental class of substances is considered. The most difficult item even included an IUPAC name. In that case, the students seemed to have problems with applying the conventions to the given complex structure with many branched side-chains correctly, even though they had less trouble with the item in which the IUPAC name of a considerably smaller and simpler compound was considered (item 11: −0.70). Thus, the results show that familiar trivial names and their linking to the requested chemical formulae are less demanding for students than knowledge of the conventions of IUPAC names and their application (item 1 vs. item 11; item 9 vs. item 12). In addition, the requested chemical formulae (i.e. empirical/molecular formulae, condensed Lewis formulae, and skeleton formulae) appear to have an influence on the difficulty of the items. It seems that the higher the familiarity with the type of formulae is the easier is an item (item 1 vs. item 15). However, all these results should merely be considered as first hints. The interplay between the type of naming and the type of formulae as well as their influence on the item difficulty need to be systematically analyzed in further studies.

Chemical equations. One of the items in this group had a difficulty value of −0.29, whereas the other two items were much more difficult, with nearly the same value of around 0.20. A comparison of item difficulties revealed that they required the students to employ different cognitive abilities. The easy one (item 13) asked to balance a chemical equation by adding coefficients. In order to find the correct coefficients, it is sufficient to make use of an algorithmic scheme. In contrast, one of the more difficult items asked to choose a chemical equation which best matched the given sub-microscopic diagram (item 6). Nakhleh and Mitchell (1993) state that tasks of this kind cannot be solved by algorithmic thinking. Instead, a deeper knowledge in the sense of a conceptual understanding is required. The reason why students lack such an understanding and therefore do not manage to solve this task may be the chemistry education itself: An algorithmic balancing of chemical equations is one of the best-practiced activities in both high school and university. In contrast, students are less-explicitly confronted with the conceptual meaning of chemical equations on the sub-microscopic level. Thus, the students seem to have approached this item more intuitively and therefore chose the equation 3X + 8Y → 3XY₂ + 2Y, simply translating the particle model into a chemical equation without excluding reactants and products in excess. This result is in line with other studies which also used the same task (Nurrenbern and Pickering, 1987; Sawrey, 1990; Arasasingham et al., 2004). A closer look at this equation reveals that it also includes correct parts: The coefficients and subscripts are used correctly. Moreover, the ratio is correct, too, which is not the case in the other chemical equations given in this item. So, a partial credit coding seems to be applicable. Under these circumstances, this item becomes even less difficult (−1.41) than the item requiring to balance the incomplete chemical equation (item 13: −0.29). Once more due to their chemistry education – especially at university – the students show remarkable difficulties in drawing curly arrows (item 10). These arrows are intensively used by chemistry lecturers, but they are usually treated as byproducts. Hence, students are not aware of the intricacies of these arrows and are likely to make mistakes when drawing them on their own. The results show that students mostly drew the arrows in the opposite directions, i.e. starting the arrows at the position where the lone pairs go to. So, students seem to think that the arrows show the movement of atoms rather than lone pairs.

Skeleton formulae. Determining the number of hydrogen atoms at marked positions in a given skeleton formulae (item 19) caused less trouble for students. The difficulty value of this item was −0.29. However, the students were more challenged when a given skeleton formulae additionally included wedges and dashes, which had to be interpreted correctly in order to be able to draw conclusions about the underlying chemical contents. In the case of item 18, students had to find the correct mirror picture of a given compound. Even though it was possible to choose the correct mirror picture by approaching this item more intuitively, i.e. looking for the mirror picture as it would be done in real life, only half of the students succeeded. This indicates that students lack familiarity with wedged and dashed lines. Here, confusion plays a role; the students supposedly tried to come up with the rules and conventions they had once learned but were not able to remember in detail anymore. The challenge gets even greater for the students when the number of steps for solving an item increases: The third item (item 16) – and, at the same time, the most difficult one in this group – asked to identify the asymmetric carbon atoms in a given structure which also included wedged and dashed lines as the one given in item 18. To solve this item, the students first had to identify the neighboring atoms of each carbon atom including the unseen hydrogen atoms. This was also required in item 19. Additionally, they had to decide whether these neighbors were all different. Actually, the appearance of wedged and dashed lines in the structure of this item is not relevant for its solution. In this case, they mainly function as a distractor, because students may assume that two neighbors are different only because they differ in the spatial orientation of their bonding represented by wedged and dashed lines. All in all, comparing all three items hinted at the assumption that additional and probably less familiar elements included in given chemical representations as well as the steps required in solving the items may have an influence on their difficulty.

Ball-and-stick models. The majority of the students were able to compare given ball-and-stick models and identify those which represent the same compound. Therefore, item 5 was the easiest one in this group, showing a difficulty value of −0.87. More demanding for students was item 3 (0.02), in which a larger and more complex chemical content was considered. In contrast to item 5, in which a complex compound with monodentate ligands was in the focus, item 3 referred to a complex compound with a chelate ligand coordinating all positions of the central ion. It has to be mentioned that item 3 also differs from item 5 with respect to the fact that two different types of chemical representations have to be compared. So, it remains open in the current study whether the size and complexity of the underlying chemical content or the challenge to compare two identical types of representations versus two different ones is the (more) influential aspect when it comes to item difficulty. Item 2 in this group presented a special challenge to the students. Working with the representation given in this item was not sufficient for its solution. It required the students to imagine a second elementary cell added to the given one in order to correctly identify the coordination number of its ions. Otherwise, the coordination number of one of the ions would be counted as two instead of four. This was also the common mistake the students made when trying to solve this item. Thus, comparing all three items in this group indicates that an increase of the size and complexity of the represented chemical contents as well as the necessity of imagining an additional structure seem to be influential factors for the item difficulty.

Translation of chemical representations. The students had the fewest problems with the translation of given condensed Lewis formulae into skeleton formula (item 8: −0.35). In this item, a direct transfer from one into another type of representation was possible. Nevertheless, the students had some trouble due to their incorrect assumption that the nitrogen atom appears as a side chain in the skeleton formula. The challenge of an item is greater when such a direct translation is not possible; this was the case in item 7 (−0.06). There is no simple rule which states that every OH-group with a dashed line in the Natta projection should be in equatorial position in the corresponding sawhorse formula. However, this item was not as difficult as expected for the students. One reason for that could be the students' familiarity with its chemical content, because glucose is a popular and well-practiced topic in German high schools. Another reason could be that in the text accompanying this item, students were given the hint that the OH-groups of glucose are all in equatorial position. So, students who know what the term “equatorial” means and also know which positions of the sawhorse formula these represent were probably able to solve this item easily without paying attention to the given Natta projection formula. The inclusion of item 17 (0.91) into the comparison indicates that the challenge which an item presents to students becomes even greater when in addition to the impossibility of direct translation, the chemical content and the type of representations are less familiar to them.

As mentioned above, there were also two further items which do not belong to any of the groups. Item 4, which asked to complete a particle model by drawing circles in order to visualize densest sphere packing with different layering, was solved by the majority of the students. The difficulty value of this item was −0.37. The item which required to recognize the equatorial and axial orientations of the side chains in a compound consisting of cyclohexane units was the most difficult one in the whole test (item 14: 1.48). These items will not be analyzed with regard to their difficulties, because there are no items presenting similar challenges with which they can be compared.

Summary of results

The aim of the present study was to develop a valid and reliable test instrument in order to measure student teachers' knowledge of chemical representations. Here, the focus was placed on both measuring the ability of student teachers to apply conventional rules in order to interpret and draw chemical representations correctly. Only two items (items 6 and 10) asked for the conceptual meaning of chemical representations. In order to account for the validity of the test items, chemistry textbooks, curricula of different German universities, and university exams were reviewed. Additionally, existing literature about students' problems with chemical representations was considered. As a result, a test instrument with 19 items in both semi-open and closed format was developed: the Chemical Representations Inventory (CRI). The CRI is characterized by the inclusion of a variety of chemical representations and chemical contents on both high-school and university level. It was administered to a sample of 322 student teachers from 12 German universities. The data was analyzed both quantitatively and qualitatively. The quantitative analysis included the analysis using classical test theory as well as Rasch modelling. With regard to the difficulty and discrimination which provide quantitative information about the item functioning, six items (i.e. 1, 5, 6, 14, 18, and strictly speaking also item 2) had values outside the recommended ranges. That is why these items do not provide useful data and need further research to investigate their item functioning. The results of the Rasch analysis showed that nearly all items fit the Rasch model. Only item 18, which was the least discriminating item according to the classical test theory results, did not fit the model based on its t value, although its weighted mean-square was in the suggested range. However, when every step of the partial credit coding of the items was considered, the fit values of all items were in the recommended ranges. Wright maps of the Rasch analysis showed that the difficulties of the CRI items are distributed along with nearly the same range as the abilities of the student teachers. Although a few small gaps appeared in the range of item difficulties, the small difference of 0.33 logits between the mean values of item difficulty and personal ability indicated that the CRI is appropriate for the sample of student teachers. Additionally, the reliability values of both methods, i.e. Cronbach's α in the classical test theory and EPA/PV (expected a posteriori/plausible value) in the Rasch analysis, were both 0.78 and thus in the acceptable range. Therefore, the CRI is said to have acceptable internal consistency.

The qualitative analysis of the data was performed separately for each topic which was used in the item development: nomenclature, chemical equation, skeleton formulae, ball-and-stick models, and translation. Within the topics, factors which possibly influence the item difficulty could be made out. One of these factors seems to be the type of chemical representation. Those types which show a higher resemblance to the shape of the underlying compounds seem to be less challenging for students than representations which require specific conventions for seeing the linkage, i.e. skeleton formulae (item 8) vs. Newman projections formulae (item 17). Another influencing factor seems to be the chemical content of an item, i.e. the size and complexity of the compounds. As expected, understanding larger and more complex compounds is likely to be more challenging for students compared to small and simple ones (item 3 vs. item 5). Moreover, the amount of steps which is required to solve an item seems to influence the difficulty of items, e.g. determining the unseen hydrogen atoms in a skeleton formulae (item 19) vs. identifying all neighboring atoms (including hydrogen atoms) and additionally deciding whether these are all different (item 16). Furthermore, it seems to make a difference whether students have to work only with the representations given in an item or are required to imagine additional structures (item 5 vs. item 2). Another influencing factor seems to be how demanding an item is, i.e. whether algorithmic thinking or conceptual understanding is required to solve it, as also Nakhleh and Mitchell (1993) found out previously. In every case, however, the degree of familiarity is considered to play an important role; an apparently challenging item may be easy to solve when it is frequently practiced in lectures and thus becomes more familiar for students. To conclude, chemistry education both at school and university determine students' degree of familiarity with chemical representations and thus is likely to influence indirectly whether an item is difficult or not. It needs to be mentioned that all these statements should be considered as hypotheses and should be researched systematically in further studies. As a first step, the items of the inventory were reorganized according to some of the factors which are supposed to influence the item difficulty: type of chemical representation (pictorial model representations vs. structural representations vs. symbolic representations), chemical content, i.e. the time of its introduction (high school vs. university) and the specific area of chemistry (general/inorganic chemistry vs. organic chemistry), and lastly the format of the items (closed vs. semi-open). However, variance analysis did not show any significant differences in any of the cases. Here, further research with a larger number of items is required.

Conclusions and outlook

Although a small number of items need further research, the results of applying both classical test theory and Rasch analysis to the CRI indicate that the test functions reasonably well as an instrument for large-scale assessments measuring student teachers' knowledge of chemical representations. In order to analyze the reproducibility of the students' answers, however, a test–retest calculation is still pending. This method compares students' answers on each of two administrations and draws conclusions about the match between their answers by calculating a correlation value (Barbera, 2013). In addition, for the purpose of validation it is required to compare students’ performance on the CRI with their performance on other inventories, e.g. inventories measuring the knowledge of chemical contents.

Since the CRI incorporates a variety of chemical representations, the qualitative analysis of the inventory merely provided hints with regard to possible factors which are supposed to have an influence on item difficulty and relate to students’ ability. Further qualitative research in the sense of interview settings is needed to systematically analyze students’ understanding of the chemical representations used in the CRI as well as the reasons for their failure. This will help to find out factors which make an item difficult or easy.

Besides the basic understanding of chemical representations as investigated by the CRI, the usage of chemical representations also contains more complex approaches (in particular by experts; Bodner and Domin, 2000; Stieff, 2007, 2010). Accordingly, students need to link their understanding of the representations themselves to the underlying chemical contents. As Ainsworth (2008) stated, “even if learners understand the form of the representation, they still need not to understand how this representation relates to the specific topic it is representing” (p. 201). For addressing these conceptual and explanatory levels of chemical representations (Taber, 2013), additional tests or at least extensions of the CRI need to be developed and analyzed. This could also shed more light on the question whether a basic understanding of representations themselves is a necessary (but not sufficient) prerequisite for a more complex, conceptual understanding or whether an understanding of both aspects develops in parallel. When thinking of extending the focus of the CRI, a particular attention should be also paid to students' ability to select among different representations according to the context or the goal of the task at hand.

In chemistry, molecules of chemical compounds can be represented in a large variety of ways (Hoffmann and Laszlo, 1991). Although all of them represent the same molecule, they differ in the point that they illustrate different features of it. Hence, each representation has its own scope as well as its own limitations. It would be interesting to see whether students recognize that the different representations do not stand for different structures, but point out different features of the same molecule. In this context, it is reasonable to investigate whether students manage to recognize the scope and limitations of each representation. Prior research suggests that students often have difficulties in recognizing these limitations, although they seem to have both a basic understanding of the representations and the conceptual knowledge (cf. the problem area “adequacy” in Taskin and Bernholt, 2014).

Both the ongoing revision and replication of the CRI as well as its systematic advancement to cover further aspects of using chemical representations will hopefully provide more systematic insights into students' use and difficulties with this chemical language.

Appendix: test instrument

Item 1

The chemical formulae for four different chemical compounds are given below. However, some of these formulae are incorrect or unusual with regard to the corresponding conventions. Mark those formulae which are incorrect or unusual and make a proposal for a correction.

Compound name	Formula	Formula is incorrect or unusual	Correction
Copper(II)oxide	CuO	□
Sodium hydroxide	NaHO	□
Magnesium chloride	MgCl2	□
Sulfuric acid	H3SO4	□

---

Coding of item 1
1 point	Correction of NaHO to NaOH
1 point	Correction of H3SO4 to H2SO4
−1 point	Any incorrect suggestion
Final score	Sum of all correct and incorrect suggestions, min. 0 points and max. 2 points

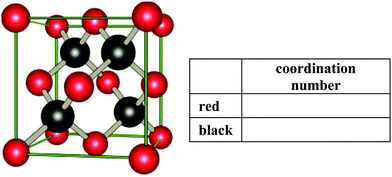
Item 2

So-called elementary cells include all necessary information which is needed to create a unique infinite lattice. The following picture represents such an elementary cell of a salt. Determine the coordination number of the given ions in this representation (i.e. the number of nearest neighbors).

Coding of item 2
1 point	Coordination number of red drawn ions: 4
1 point	Coordination number of black drawn ions: 4
Final score	Sum of all correct given coordination numbers, min. 0 points and max. 2 points

Item 3

By binding to a [EDTA]⁴⁻ ion, a copper(II) ion creates a copper(II)–EDTA complex which is represented as a ball-and-stick model in the left illustration below. The representation to the right visualizes the structure of the [EDTA]⁴⁻ ion. Mark those positions of the [EDTA]⁴⁻ ion in the representation to the right which coordinate to a copper(II) ion in the complex compound.

Coding of item 3
2 points	All 4 oxygen atoms with a negative charge and two nitrogen atoms are marked exclusively
1 point	All 4 oxygen atoms with a negative charge or two nitrogen atoms are marked exclusively
0 points	Any inadequate atoms are marked

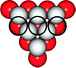
Item 4

In the following representations, an excerpt of two layers of the densest sphere packing is given. In each representation, draw the outline of three spheres which could be found in the third layer of a densest sphere packing with the layerings ABABA… and ABCABC… respectively.

Coding of item 4
1 point	ABABA…: the three drawn spheres are congruent with the red spheres
1 point	ABCABC…: the three spheres are placed on the gaps
Final score	Sum of all correct suggestions for the third layer, min. 0 points and max. 2 points

Item 5

In the following, octahedral complexes of type MA₃X₃ are given, where M is a metal and A and X are monodentate ligands. Check those of the given complexes which are identical to complex A (several answers possible).

Coding of item 5
1 point	The second drawing is checked
1 point	The third drawing is checked
−1 point	Any other drawing is checked
Final score	Sum of all correct and incorrect checks, min. 0 points and max. 2 points

Item 6

The reaction of the element X (black circles) with the element Y (white circles) is represented in the following diagram:

Check which of the given chemical equations a chemist would choose in order to represent the reaction between the elements X and Y.

□ 3X + 8Y → X₃Y₈

□ 3X + 6Y → X₃Y₆

□ X + 2Y → XY₂

□ 3X + 8Y → 3XY₂ + 2Y

□ X + 4Y → XY₂

Coding of item 6
2 points	The third equation is checked exclusively
1 points	The fourth equation is checked exclusively
0 points	Any other equation is checked

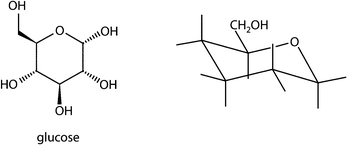
Item 7

The most stable form of glucose is a six-membered ring in chair form whose five substituents are all in equatorial position. Draw this conformation of the glucose molecule by adding OH-groups to the corresponding bondings of the chair conformer.

Coding of item 7
2 points	All four OH-groups are placed correctly
1 point	At least two OH-groups are placed correctly
0 points	Less than two OH-groups are placed correctly

Item 8

Draw the skeleton formula of the following condensed structural formulae.

Coding of item 8
1 point	The first skeleton formula is drawn as or
1 point	The second skeleton formula is drawn as
Final score	Sum of all correctly drawn skeleton formulae, min. 0 points and max. 2 points

Item 9

Draw the skeleton formula of benzaldehyde und benzoic acid.

Coding of item 9
1 point	The first skeleton formula is drawn as (1 point was also given when the lone pairs of the oxygen atom were missing)
1 point	The second skeleton formula is drawn as (1 point was also given when the lone pairs of the oxygen atom were missing)
Final score	Sum of all correctly drawn skeleton formulae, min. 0 points and max. 2 points

Item 10

Draw curly arrows () in order to represent the displacement of electrons in the following chemical reaction.

Coding of item 10
1 point	Arrow drawn correctly
−1 point	Arrow drawn incorrectly
Final score	Sum of all correctly and incorrectly drawn arrows: → Sum of 3 equals 2 points → Sum of 1 or 2 equals 1 point → Sum of 0 or less equals 0 points

Item 11

Draw the skeleton formula of 6-ethyl-4-methyltetradecane.

Coding of item 11
1 point	The structure is drawn as a skeleton formula (i.e. without explicitly drawing the methyl groups even the terminal ones)
1 point	Formula is drawn correctly (i.e. length of longest chain, length and position of side chains)
Final score	Sum of all correct steps, min. 0 points and max. 2 points

Item 12

Complete the systematic name of the compound seen below by adding adequate numbers in the corresponding fields.

Coding of item 12
2 points	All numbers are correct 2,11,11-Trimethyl-6-(1-methylethyl)-4-(2-methylpropyl)tridecan
1 point	All numbers except one are correct
0 point	More than one number is incorrect

Item 13

Potassium permanganate reacts with 3-methylpyridine to form pyrolusite and nicotinic acid. Complete the corresponding chemical equation by adding coefficients. Also put down “1” if it appears as coefficient.

Coding of item 13
2 points	Ratio of coefficients is correct and the smallest
1 point	Ratio of coefficients is correct, but not the smallest
0 point	Ratio of coefficients is incorrect

Item 14

By using technical terms, describe in which aspect the following three compounds structurally distinguish from each other.

Coding of item 14
2 points	Both terms equatorial and axial are mentioned
1 point	Only one of the terms equatorial and axial or the more general term conformation is mentioned
0 point	Other answers

Item 15

Draw the condensed structural formulae of any compound belonging to the fundamental class of hydroxycarboxylic acids.

Coding of item 15
1 point	A condensed structural formulae is drawn (such as CH3CH(OH)COOH or CH3–CH(OH)–COOH)
1 point	The formula represents a hydroxycarboxylic acid (including a COOH- and OH-group)
Final score	Sum of all correct steps, min. 0 points and max. 2 points

Item 16

Mark the asymmetrically-substituted carbon atoms (i.e. carbon atoms with four different neighboring groups) in the following molecule.

Coding of item 16
1 point	An asymmetrically-substituted carbon atom is marked
−1 point	A symmetrically-substituted carbon atom (or any other species) is marked
Final score	Sum of all correctly and incorrectly marked carbon atoms: → Sum of 5 equals 2 points → Sum of 3 or 4 equals 1 point → Sum of 2 or less equals 0 points

Item 17

The following representation is given:

This representation should be translated into the Newman formula. For this purpose, draw the two methyl groups of the representation shown above into the following Newman formula.

Coding of item 17
1 point	The methyl groups are placed at one of the following positions: • 1 and 7 • 2 and 8 • 3 and 5 • 4 and 6
0 point	Other combination of positions

Item 18

Check which of the following compounds is the enantiomer (i.e. mirror picture) of compound A.

Coding of item 18
1 point	The correct compound is chosen
0 point	One of the other incorrect compounds is chosen

Item 19

Determine the number of hydrogen atoms which are connected with each of the carbon atoms marked in the following compound.

Coding of item 19
2 points	All numbers are correct
1 point	All numbers except one are correct
0 point	More than one number is incorrect

---

Item	Reference
1	Item taken from:
	Bernholt S., Fischer I., Heuer S., Taskin V., Martens J. and Parchmann I., (2012), Die chemische Formelsprache – (un-)vermeidbare Hürden auf dem Weg zu einer Verständnisentwicklung? [The chemical formula language – pitfalls not only for students?], Chemkon, 19(4), 171–178.
5	Item adapted from:
	Brown T. L., LeMay H. E. and Bursten B. E., (2007), Chemie: Die zentrale Wissenschaft. 10., aktualisierte Auflage [Chemistry: The Central Science, 10th updated edition], München: Pearson Studium.
6	Item adapted from:
	Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: is there a difference? J. Chem. Ed., 64(6), 508–510.
7	Item adapted from:
	Bruice P. Y., (2007), Organische Chemie. 5., aktualisierte Auflage [Organic Chemistry, 5th updated edition], München: Pearson Studium.
8	Item adapted from:
	Bruice P. Y., (2007), Organische Chemie. 5., aktualisierte Auflage [Organic Chemistry, 5th updated edition], München: Pearson Studium.
10	Item adapted from:
	Bruice P. Y., (2007), Organische Chemie. 5., aktualisierte Auflage [Organic Chemistry, 5th updated edition], München: Pearson Studium.
16	Item adapted from:
	Bruice P. Y., (2007), Organische Chemie. 5., aktualisierte Auflage [Organic Chemistry, 5th updated edition], München: Pearson Studium.
19	Item adapted from:
	Bruice P. Y., (2007), Organische Chemie. 5., aktualisierte Auflage [Organic Chemistry, 5th updated edition], München: Pearson Studium.
2, 3, 4, 9, 11–15, 17–18	Own development

Acknowledgements

We thank Sabine Nick for her contribution to the item development as well as Jörg Großschedl for his support with statistical questions.

Notes and references

1. Abraham M. R., Grzybowski E. B., Renner J. W. and Marek E. A., (1992), Understanding and misunderstanding of eighth graders of five chemistry concepts found in textbooks, J. Res. Sci. Teach., 29(2), 105–120.
2. Ainsworth S., (2008), The educational value of multiple-representations when learning complex scientific concepts, in Gilbert J. K., Reiner M. and Nakhleh M. (ed.), Visualization: theory and practice in science education, Dordrecht: Springer, pp. 191–208.
3. Arasasingham R. D., Taagepera M., Potter F. and Lonjers S., (2004), Using knowledge space theory to assess student understanding of stoichiometry, J. Chem. Educ., 81(10), 1517–1523.
4. Barbera J., (2013), A psychometric analysis of the Chemical Concepts Inventory, J. Chem. Educ., 90(5), 546–553.
5. Bernholt S., Fischer I., Heuer S., Taskin V., Martens J. and Parchmann I., (2012), Die chemische Formelsprache – (un-)vermeidbare Hürden auf dem Weg zu einer Verständnisentwicklung? [The chemical formula language – pitfalls not only for students?], Chemkon, 19(4), 171–178.
6. Bodner G. M. and Domin D. S., (2000), Mental models: the role of representations in problem-solving in chemistry, Univ. Chem. Educ., 4(1), 24–30.
7. Bond T. G. and Fox, C. M., (2007), Applying the Rasch model. Fundamental measurement in the human sciences, 2nd edn, Mahwah, NJ: Lawrence Erlbaum Ass.
8. Bucat B. and Mocerino M., (2009), Learning at the sub-micro level: structural representations, in Gilbert J. K. and Treagust D. F. (ed.), Multiple representations in chemical education, Dordrecht: Springer, pp. 11–29.
9. Cheng M. and Gilbert J. G., (2009), Towards a better utilization of diagrams in research into the use of representative levels in chemical education, in Gilbert J. K. and Treagust D. F. (ed.), Multiple representations in chemical education, Dordrecht: Springer, pp. 55–73.
10. Crocker L. and Algina J., (2008), Introduction to classical and modern test theory, Mason: Cengage Learning.
11. Davidowitz B., Chittleborough G. and Murray E., (2010), Student-generated submicro diagrams: a useful tool for teaching and learning chemical equations and stoichiometry, Chem. Educ. Res. Pract., 11(3), 154–164.
12. Ebel R. L. and Frisbie D. A., (2006), Essentials of Educational Measurement, Englewood Cliffs: Prentice Hall.
13. Ferk V.,Vrtacnik M., Blejec A. and Gril A, (2003), Students' understanding of molecular structure representations, Int. J. Sci. Educ., 25(10), 1227–1245.
14. Gilbert J. K., (2008), Visualization: an emergent field of practice and enquiry in science education, in Gilbert J. K., Reiner M. and Nakhleh M. (ed.), Visualization: theory and practice in science education, Dordrecht: Springer, pp. 3–24.
15. Head J. and Bucat B., (2002), Visualisation and mental manipulation of molecular structures, Aust. J. Ed. Chem., 59, 25–29.
16. Hoffmann R. and Laszlo P., (1991), Representations in chemistry. Angew. Chem., Int. Ed. Engl., 30(1), 1–16.
17. Johnstone A. H., (2000), Teaching of chemistry – logical or psychological? Chem. Educ. Res. Pract., 1(1), 9–15.
18. Kleickmann T., Großschedl J., Harms U., Heinze A., Herzog S., Hohenstein F., Köller O., Kröger J., Lindmeier A., Loch C., Mahler D., Möller J., Neumann K., Parchmann I., Steffensky M., Taskin V. and Zimmermann F., (2014), Professionswissen von Lehramtsstudierenden der mathematisch-naturwissenschaftlichen Fächer – Testentwicklung im Rahmen des Projekts KiL [Professional knowledge of student teachers in mathematics and science subjects – test development in the context of the project KiL], Unterrichtswissenschaft, 42(3), 280–288.
19. Kline P., (1999), The handbook of psychological testing, 2nd edn, London: Routledge.
20. Kline T. J. B., (2005), Psychological Testing: A practical approach to design and evaluation, Thousand Oaks: Sage.
21. Kozma R. B. and Russell J., (1997), Multimedia and understanding: expert and novice responses to different representations of chemical phenomena, J. Res. Sci. Teach., 34(9), 949–968.
22. Maydeu-Olivares A., (2013), Goodness-of-fit assessment of item response theory models (with discussion), Measurement: Interdisciplinary Research and Perspectives, 11(3), 71–101.
23. Nakhleh M. B. and Mitchell R. C., (1993), Concept learning versus problem solving: there is a difference, J. Chem. Educ., 70(3), 190.
24. Nurrenbern S. C. and Pickering M., (1987), Concept learning versus problem solving: is there a difference? J. Chem. Educ., 64(6), 508–510.
25. Rasch G., (1980), Probabilistic models for some intelligence and attainment tests, Chicago: University of Chicago Press.
26. Savoy L. G. and Steeples B., (1994), Concept hierarchies in the balancing of chemical equations, Sch. Sci. Rev., 75(272), 97–103.
27. Sawrey B. A., (1990), Concept learning versus problem solving: revisited, J. Chem. Educ., 67(3), 253–254.
28. Schmidt H.-J., (1984), How pupils – empirical studies on pupil's understanding of simple quantitative relationships in chemistry, Sch. Sci. Rev., 66(234), 157–162.
29. Schmidt H.-J., (2000), In the maze of chemical nomenclature – how students name oxo salts, Int. J. Sci. Educ., 22(3), 253–264.
30. Stieff M., (2007), Mental rotation and diagrammatic reasoning in science, Learn. Inst., 17(2), 219–234.
31. Stieff M., (2010), When is a molecule three dimensional? A task-specific role for imagistic reasoning in advanced chemistry, Sci. Educ., 95(2), 310–336.
32. Taber K. S., (2009), Learning at the symbolic level, in Gilbert J. K. and Treagust D. F. (ed.), Multiple representations in chemical education, Dordrecht: Springer, pp. 169–191.
33. Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14(2), 156–168.
34. Talanquer V., (2011), Macro, submicro, and symbolic: the many faces of the chemistry “triplet”, Int. J. Sci. Ed., 33(2), 179–195.
35. Taskin V. and Bernholt S., (2014), Students' understanding of chemical formulae: a review of empirical research, Int. J. Sci. Educ., 36(1), 157–185.
36. Wirtz M. C., Kaufmann J. and Hawley G., (2006), Nomenclature made practical: student discovery of the nomenclature rules, J. Chem. Educ., 83(4), 595–598.
37. Wright B. D. and Linacre M. J., (1994), Reasonable mean-square fit values, Rasch Measurement Transactions, 8(3), 370.
38. Wu M. L., Adams R. J., Wilson M. R. and Haldane S. A., (2007), ACER ConQuest version 2.0: generalised item response modelling software, Camberwell: ACER Press.
39. Yarroch W. L., (1985), Student understanding of chemical equations balancing, J. Res. Sci. Teach., 22(5), 449–459.
40. Yen W. M., (1993), Scaling performance assessments: strategies for managing local item dependence, J. Educ. Meas., 30(3), 187–213.

---

Footnote

† For a pair of items, the standardized residual is defined as the sample (product-moment or Pearson) correlation minus the expected correlation. The SRMSR, then, is the square root of the average of these squared residual correlations (Maydeu-Olivares, 2013, p. 84f.)

---