Synthesis and characterisation of MOF/ionic liquid/chitosan mixed matrix membranes for CO2/N2 separation
Clara Casado-Coterillo*a,
Ana Fernández-Barquína,
Beatriz Zornozab,
Carlos Téllezb,
Joaquín Coronasb and
Ángel Irabiena
aDepartment of Chemical and Biomolecular Engineering, Universidad de Cantabria, Avda. Los Castros s/n, 39005 Santander, Spain. E-mail: casadoc@unican.es; Tel: +34 942 20 6777
bDepartment of Chemical and Environmental Engineering and Instituto de Nanociencia de Aragón, Universidad de Zaragoza, 50018 Zaragoza, Spain
First published on 23rd November 2015
Abstract
Mixed matrix membranes (MMMs) have been prepared by combining a small amount of highly absorbing non-toxic ionic liquid, [emim][Ac] (IL) (5 wt%), a biopolymer from renewable abundant natural resources, chitosan (CS), and nanometre-sized metal–organic framework (MOF) ZIF-8 or HKUST-1 particles to improve the selectivity of the IL–CS hybrid continuous polymer matrix. The TGA revealed that the thermal stability has been enhanced by the influence of both IL and ZIF-8 or HKUST-1 fillers, while keeping a water content of around 20 wt%, which suggests the potential of such materials for developing high temperature water resistant membranes for CO2 separation. The CO2 and N2 single gas permeation performance was tested at temperatures in the range of 25–50 °C, to compare with the previously reported IL–CS hybrid membranes. The best CO2 permeability and CO2/N2 selectivity performance is obtained for 10 wt% ZIF-8 and 5 wt% HKUST-1/IL–CS membranes, as high as 5413 ± 191 Barrer and 11.5, and 4754 ± 1388 Barrer and 19.3, respectively. This is attributed to a better adhesion and smaller particle size of ZIF-8 than HKUST-1 nanoparticles with respect to the IL–CS continuous matrix, as interpreted by Hansen solubility parameters and Maxwell-based models, modified to account for rigidification, pore blockage and crystallinity of the CS matrix, with very accurate predictions.
Introduction
Post-combustion capture to separate CO2 from flue gas in fossil-fuelled power plants is vital to tackle climate change issues. Although amine absorption is a mature technology widely available on the large scale, it presents several drawbacks in post-combustion, regarding steam regeneration, handling of corrosive liquids, amine losses, and a low temperature requirement for efficient separation. Its expensiveness leads to opportunities for new emerging processes for sustainable CO2 capture. Membrane separation is a promising alternative to conventional absorption processes because of the simplicity and durability of operation, low footprint and eco-friendliness and potential lower energy cost than amine absorption, all of which favour their use in small-scale applications. Although polymeric membranes have been commercialised because of their relatively easy processing at low costs, due to their limited resistance to high temperature and usual inadequacy to high flow rates or sensitiveness to clogging by dust, there is an absence of economy of scale and low CO2/N2 selectivity limitations.1 Inorganic membranes for CO2/N2 separation are inherently microporous and based on molecular sieving mechanisms, such as ceramic2 and zeolite membranes.3 Permeability and selectivity are the fundamental parameters that characterise the gas separation through membrane materials. There is usually a trade-off between both parameters that was well described by Robeson in his upper bound.4 At large scale post-combustion capture, however, we have to deal with low CO2 pressures of 0.15 bar, meaning low driving forces. High permeability becomes crucially important, while high selectivity would avoid pressure ratio dependence of membrane performance.5Mixed matrix membranes (MMMs), where the combination of organic and inorganic materials has been proved as a promising way of merging and enhancing the properties of both phases, have been attracting interest in the last decades.6–10 Recently the MMMs devoted as CO2 selective have been the object of an extended overview of CO2 selective membranes.11 New materials based on renewable resources are most recently sought for to avoid dependency on petroleum-based products. In order to overcome this trade off and obtain membranes with increased permeability and selectivity at the same time, the most important challenge on MMMs is the adhesion or compatibility between the components in order to form a homogeneous film with synergistic properties.
Room temperature ionic liquids (IL) combining good and tuneable solubility properties with negligible vapour pressure and good thermal stability have received much attention as an alternative to the existing CO2 absorption solvents in membrane contactors. Supported ionic liquid membranes (SILM) were thus proposed to take advantage of high CO2 absorption of non toxic ILs as a function of the type of anion was evaluated.12 The large number of publications dealing with ILs in membranes for CO2 separation has opened up the field for next generation membranes.8 In particular, the IL composed of the 1-ethyl-3-methylimidazolium cation and acetate anion, [emim][Ac], is the IL with the highest reported CO2 solubility even with increased temperature,13 as well as non-reported toxicity.14 MMMs consisting of polymerizable ionic liquids and free room temperature ILs have been proposed to improve the performance of SAPO-34-based membranes in CO2/CH4 separation,15,16 in the light of the outcome of PILs as promising materials for CO2 capture17 and polymerised ionic liquids filled with RTILs were also proposed for CO2/N2 separation,18 but the selectivity was still low.
Chitosan (CS), poly[β(1→4)-2-amino-2-deoxy-D-glucopyranose], is a linear polysaccharide obtained by deacetylation of chitin, abundant, cheap and acquired from renewable sources, i.e. the shell of crustaceans, as well as biodegradable, biocompatible, non-toxic and hydrophilic. The high hydrophilicity of CS makes it possible to hydrate and form water-swollen membranes with enhanced CO2/N2 permselectivity because of the high CO2 solubility in water.19 Swollen CS-based membranes have been studied for CO2/N2 separation in facilitated transport, by humidification of the feed gas prior to entering the membrane module.20 Its mechanical stability has nevertheless been tried to improve by coating on a porous polysulfone support,21 organic chemical crosslinking22 or physical mixing with zeolite particles.23 Because of the strong H-bonds forming with the OH groups in the polymer chain, ionic liquids are considered as good solvents for polysaccharides,24 and thus a good interaction with ILs was expected. With the aim of increasing mechanical and thermal stability of liquid membranes,25 hybrid solid IL–CS membranes were recently reported by introducing a small amount of [emim][Ac] IL into the CS matrix, leading to a good adhesion with improved flexibility, as well as a decrease of the influence of temperature on CO2/N2 separation.26 However, the selectivity was still below the Robeson's upper bound,4 by the increased amorphousness imparted by an IL into a semi-crystalline polymer matrix.27 The incorporation of microporous titanosilicate ETS-10 nanoparticles into CS and IL/CS hybrid matrices was observed to increase tensile strength, and simultaneously and monotonously increased the CO2/N2 separation performance by the addition of the same IL and microporous titanosilicate ETS-10 (ref. 28) as in other 3-phase MMMs based on PILs, RTILs and molecular sieves.16,17,29
Metal–organic frameworks (MOFs) have been proposed as promising fillers in MMMs for gas separation because their partly organic nature allows expectation of a higher compatibility with the polymer chains.30 Adams et al.31 studied a MOF based on copper and terephthalic acid (TPA) that improved the performance of the pure polymer. HKUST-1 or Cu3(BTC)2 (copper(II)-benzene-1,3,5-tricarboxylate) is a 3D porous metal organic framework (MOF) with high CO2 sorption ability and thermal stability32 that was introduced in MMM for gas separation by Car et al.33 ZIF-8 (Zn(2-methylimidazole)2) belongs to the zeolite imidazole framework subgroup of MOFs with exceptional chemical and thermal stability. ZIF-8 has cavities of 11.6 Å connected through small apertures of 3.4 Å, which makes this material highly studied in hybrid membranes to enhance their molecular sieving ability. Yilmaz and Keskin provided a computational approach that allows developing MOF- and ZIF-based MMMs for CO2/N2 separation.34 ZIF-8 nanoparticles may increase the free volume of low permeability Matrimid polyimide, at the expense of polymer plasticization and loss of selectivity.35 Both HKUST-1 (ref. 36) and ZIF-8 (ref. 29 and 37) have been used with the aim of improving the plasticization resistance in polyimide membranes for CO2 separation. The adsorption capacity of ZIF-8 increases in the presence of water.38 For CO2/N2 separation, there is an urge to match high permeable polymers with intimate mixing fillers that are water and thermally resistant; in this light, ZIF-7 was added to PEBAX and PTMSP permeable polymers to produce a composite membrane with a CO2 permeability of 145 Barrer and a CO2/N2 selectivity of 97.39 Recently, as high as 35% ZIF-8 was loaded into PEBAX forming a dual layer membrane with increased CO2 permeability and decreased selectivity, but long term stability under humid conditions.40 The major challenge in MMMs is the adhesion between the phases. Therefore, a ZIF-8 loading of 18.9 wt% in the ionic polymer p[vbim][NTf2] has been reported to increase the CO2 permeability of ionic polymer from 101 to 199 Barrer at a constant CO2/N2 selectivity of 20, at room temperature.29 Molecular simulations have also been realised using ionic liquids embedded in Cu–BTC to study CO2/N2 or CO2/CH4 mixtures,41 and the CO2 adsorption was recently analysed experimentally and validated by molecular simulation.42 Although small particle size ZIF-8 is better dispersed in the fabrication of MMMs for CO2/CH4, still particle modification protocols are needed to increase the selectivity from 19.4 to 28.5.43
Therefore, in this work ZIF-8 and HKUST-1 nanoparticles, without the need of particle surface modification, were added at different loadings (5–20 wt%) into the IL–CS hybrid matrix to try to improve the CO2/N2 selectivity of the IL–CS hybrid membranes.26 The 3-phase MMMs were characterised by single gas permeation of CO2 and N2 permeabilities as a function of temperature to study the thermal resistance of the membranes. Further characterisation was obtained from TGA, XRD and SEM analyses. The transport properties were fitted to Maxwell-based models as a function of temperature, type of filler and membrane morphology.
Materials and methods
Materials
Chitosan (CS, coarse ground flakes and powder, Sigma-Aldrich) with a deacetylation degree higher than 75 wt% and high viscosity was used as purchased. This CS product provides high density of amino groups for CO2 separation.20Zeolite imidazole framework (ZIF-8) nanocrystals were prepared in aqueous solution as reported elsewhere.44,45 HKUST-1 or Cu3(BTC)2 powder was also prepared by a procedure described elsewhere.46,47 The average particle size and morphology observed by SEM are shown in Fig. 1, giving average values of 0.16 ± 0.02 μm and 0.34 ± 0.20 μm for ZIF-8 and HKUST-1, respectively, from a total measured population of 45 particles.
 | ||
| Fig. 1 SEM images of the ZIF-8 (a) and HKUST-1 (b) particles used in the 3-phase IL–CS based membranes preparation. | ||
Methods
The procedure to prepare the MMM has been reported elsewhere.26,28 In a typical synthesis, CS 1.5 wt% was first dissolved in 2 wt% acetic acid (glacial, Panreac) aqueous solutions by stirring at 80 °C for 24 h under reflux. The CS solution obtained was filtered to remove insoluble impurities. At this point, the ionic liquid (IL, 97 wt%, Sigma Aldrich) was added in 5 wt% proportion with respect to the CS concentration in the solution, which was deemed the most thermally and mechanically stable in a previous work.26 The mixture was stirred for 2 h. In the case of the MMMs, the HKUST-1 or ZIF-8 nanoparticle filler was first stirred in a 2–3 mL DI water before addition to the IL–CS solution, in 5–20 wt% content with respect to the total IL–CS organic composition, to study the influence of filler loading on membrane performance. Then, the 8 mL hybrid solution was stirred for 24 h and degassed in an ultrasound bath, before casting on a polystyrene Petri dish and evaporated at room temperature for 2–3 days. The membranes were then removed from the Petri dish. A 14.45 cm2 membrane was cut from the film for gas permeation, neutralised in 1 M NaOH and rinsed with abundant distilled water. Excess water was carefully removed by blotting with a paper tissue before CO2 and N2 permeation tests. Once neutralised with NaOH solutions, there are OH and NH2 available groups in the chain structure for interaction with CO2 upon separation performance.Characterisation
Thicknesses were measured with a IP-65 Digital Micrometer (Mitutoyo Corp. with an accuracy of 0.001 mm). The thicknesses of the membranes were measured in five points over the whole membrane surface after gas permeation experiments are collected in Table 2, as a function of membrane material composition. The average thickness of all the MMMs prepared in this work range from 90 to 146 μm, although there seems to be a slightly increasing trend with increasing particle loading.The experimental density of the membrane films (ρm) was measured gravimetrically from the electronically measured weight of the circular film and the calculated volume of several membranes prepared under the same conditions at room temperature (20 °C).
Thermogravimetric analyses (TGA) were performed in a DTG 60H Shimadzu instrument in air from 25–700 °C at a heating rate of 10 °C min−1 to study the thermal stability of the resulting membranes. The decomposition temperature was calculated as the temperature at which 5 wt% loss occurs.
The X-ray diffractograms (XRD) of the materials and membranes were collected in the range of 2θ 2.5–40° with a step of 0.03° on a D/max 2500 diffractometer (Rigaku, Japan) operating at 40 kV and 80 mA, equipped with rotating Cu anode and a graphite monochromator to select the Cu Kα1 radiation.
The ZIF-8 and HKUST-1 particles and MMMs were characterised by SEM using an Inspect F scanning electron microscope (HITACHI S2300, Japan). In order to observe the cross section of the MMMs, the membranes were fractured by immersion in liquid nitrogen and then 15 nm thick gold sputtered at 10 kV. To evaluate the dispersion of the particles within the membrane matrix, the metal cations were analysed by EDX mapping.
The water uptake of the IL–CS based membranes was measured in membrane pieces of 2 × 2 cm2, after the neutralisation step in NaOH 1 M and thorough washing in DI water. The membrane pieces were immersed in DI water for 24 h. The wet weight was obtained by quickly blotting the piece of membrane onto a tissue paper to remove the excess of water. The total water uptake of the membrane material was calculated by the following equation,
 | (1) |
The porosity of the membrane can be calculated from the volume occupied by water and the volume of the membrane, by taking into account the water density at 25 °C (0.997 g cm−3) and the density of the membrane in the dry state,28 which was obtained gravimetrically from the circular membrane used in the permeation experiments. The void fraction, ϕv, can thus be calculated as
 | (2) |
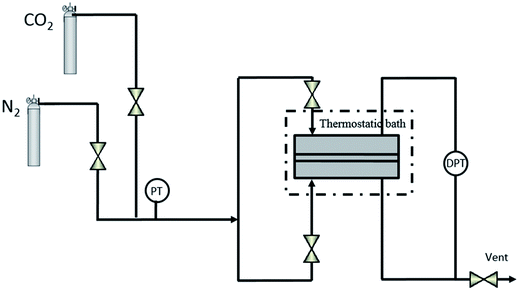
Pure N2 and CO2 gas permeation was carried out in the home-made constant volume system shown in Fig. 2, in the temperature interval of 25–50 °C. Membranes were placed in the permeation cell, and tested for N2 first and then for CO2. In a typical run, both retentate and permeate sides of the membrane module were filled in for a few minutes. Then, all valves were closed and the vent valve was opened to remove the gas in the permeate side and create the driving force across the membrane. The initial pressure was monitored by a pressure transducer, p0, and the pressure difference was monitored along the experimental run by differential pressure transducer (Omega, UK), Δp. In total, time an average single membrane spent in the permeation cell along all the experimental runs at least 12 h. An average of three single gas permeation experiments for each gas and membrane material were considered to account for reproducibility.
The permeability Pi of a pure gas component i through a polymer-based film is defined as follows
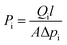 | (3) |
The transport mechanism across dense polymeric membranes follows the solution-diffusion model,
| Pi = Di × Si | (4) |
 | (5) |
 | (6) |
The solubility Si correlates with the Hansen solubility parameters (HSP), which are being recently presented as a practical tool to predict the material compatibility leading to a good adhesion among the components49 as well as preferential affinity for CO2 and N2.50 HSP are based on parameters from the dispersion, polar and hydrogen bonding cohesive energies, respectively, to identify the interaction between the components in a mixture and the gases and the blend, as
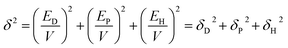 | (7) |
| Ra2 = 4(δD1 − δD2)2 + (δP1 − δP2)2 + (δH1 − δH2)2 | (8) |
The ideal selectivity is the intrinsic parameter describing the ability of a certain membrane material to separate an specific pair of gases and is usually calculated as the ratio of the single gas permeability of the high to low permeating gas, which for the CO2/N2 gas pair object of study, is
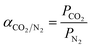 | (9) |
Results and discussion
Fig. 3 shows the XRD diffractograms of the materials and membranes studied in this work. The broad peaks around 12 and 20° are attributed to the form I and II of pristine CS polymer, accounting for the semicrystalline nature of CS,28 are discerned in the CS membranes, whereas for the IL–CS membrane these peaks almost disappear. This is attributed to disruption of the semi-crystalline nature upon addition of the IL.51 The characteristic peaks of ZIF-8 and HKUST-1 are not discerned, not even at the highest loading of 20 wt% studied. This can be related to the nanometre size of the filler particles and to the good interaction and mixing at molecular level between the fillers and the CS-based matrix.52 Hao et al.29 attributed the disappearance of ZIF-8 characteristic peaks at 7.2 and 10.4° to the destruction of the crystal structure at (001) and (002) by the acid environment induced by the IL, which in their case was [emim][BF4]. This phenomenon was probably enhanced by the use of diluted acetic acid solutions employed on the preparation of the IL–CS-based casting solutions in this work. The ZIF-8 and HKUST-1 loading in the hybrid IL–CS matrix is quite low compared with other MOF MMMs reported in literature, where only MOF and ZIF loadings of 43 and 60 wt%, respectively,53,54 could be observed by XRD, therefore the XRD are not conclusive.37The HSP of the materials proposed in this work as components for the hybrid and MMMs are displayed in Table 1. The values of solubility and interaction distance demonstrate the preferential affinity of the materials for CO2 vs. N2, as well as a relatively good interaction between CS and IL, CS and ZIF-8 and CS and HKUST-1, even though ZIF-8 is more compatible to CS and IL than HKUST-1. Using the additive method we can predict the interaction distance of IL–CS-based hybrid membranes, with CO2 and N2 gases in a mixture, as Ra = 20.1 and 30.0 MPa1/2, respectively, for IL–CS membranes. The conclusions of these calculations may be that the CO2/N2 separation performance of IL/CS hybrid membranes could be expected to improve by the addition of HKUST-1 or ZIF-8 particles, even without additional surface modifiers.
| δD (MPa1/2) | δP (MPa1/2) | δH (MPa1/2) | Ra (-CS) A | Ra (-IL) B | |
|---|---|---|---|---|---|
| a Because of lack of Hansen' solubility parameters available for ZIF-8, we take the parameters provided for the 2-methylimidazole (2MI) functional group as the one responsible in ZIF-8 for interactions with the other components.57 | |||||
| CS | 17.8 | 14.2 | 24.1 | 0 | 11.4 |
| IL | 14.2 | 8.8 | 17.0 | 11.4 | 0 |
| HKUST-1 | 17.9 | 9.9 | 10.7 | 14.1 | 9.7 |
| ZIF-8a | 20.8 | 8.6 | 16.4 | 11.2 | 11.8 |
| CO2 | 15.7 | 6.3 | 5.7 | 20.5 | 11.9 |
| N2 | 11.9 | 0 | 0 | 30.4 | 19.7 |
The smaller the solubility distance parameter Ra between two components, the better the compatibility. Therefore, since the Ra interaction distances between IL and ZIF-8 and HKUST-1 are 11.8 and 9.7 MPa1/2, respectively, a better ZIF-8/CS adhesion can be expected in the 3-component MMM. The thermal stability of IL–CS-based membranes in Fig. 4 correlates with the matrix interaction. According to HSP calculations, ZIF-8 is more compatible with CS and IL than HKUST-1, which agrees with the slightly higher thermal stability observed by TGA (Fig. 4) of ZIF-8/IL–CS MMM than HKUST-1/IL–CS MMM, and Zhu-Ryberg et al. observations for CS-based nanocomposites.49
The thermal degradation of the ZIF-8/IL–CS based membranes was measured by TGA in static air in the range 25 to 700 °C and represented in Fig. 4. The TGA curves follows the usual three steps of CS thermal degradation: a first step up to 119 °C corresponds to the removal of free water and is omitted from Fig. 4 to better observe the thermal changes on the new MMMs, taking into account the high water uptake of the CS-based membranes; a second step up to 427 °C for the removal of bound water and the start of deacetylation of the CS matrix; and a final decomposition step. The weight loss observed before 119 °C (not shown), as indicated, is attributed to the evaporation of adsorbed water, which increases from 0.22 wt% for the IL–CS membrane, in agreement with previous results,26,28 to 13.2, 25.4 and 46.1 wt% for the IL–CS-based membranes filled by 5, 10 and 20 wt% ZIF-8, respectively. The thermal decomposition temperature is included in Table 2. As the ZIF-8 content increased, the thermal decomposition temperature of the IL–CS-based membranes increased from 168 ± 32 °C to 186 ± 15 °C when increasing the ZIF-8 content from 5 to 20 wt%, probably because of the increasing interaction owed to increasing number of H-bonds and decreasing organic content in the membrane matrix.58 The thermal decomposition of the HKUST-1/IL–CS MMMs is lower than ZIF-8/IL–CS MMMs and decreases at the highest loading under study. Membranes with 20 wt% HKUST-1 were very fragile and full of defects, which made their characterisation more difficult than the others. The glass transition temperature falls within the experimental error given the difficult observation of the midpoint in the second run curve of DSC analyses CS-based membrane samples,28 thus these values are not reported here.
| Membrane materials | Thickness (μm) | ρm (g cm−3) | ϕv (%) | Td (°C) | Water uptake (%) |
|---|---|---|---|---|---|
| CS28 | 122 ± 4 | 0.73 ± 0.26 | 23 | 188 | 111 ± 29 |
| IL/CS28 | 128 ± 4 | 1.11 ± 0.20 | — | 195 | 93 ± 21 |
| 5 wt% ZIF-8/IL–CS | 90.4 ± 13 | 1.05 ± 0.08 | 37 ± 2.2 | 168 ± 32 | 58 ± 5 |
| 10 wt% ZIF-8/IL–CS | 115 ± 5.2 | 1.09 ± 0.27 | 36 ± 10 | 185 ± 1.8 | 48 ± 6 |
| 20 wt% ZIF-8/IL–CS | 125 ± 12 | 0.96 ± 0.26 | 24 ± 13 | 186 ± 15 | 26 ± 5 |
| 5 wt% HKUST-1/IL–CS | 91.8 ± 2.7 | 1.09 ± 0.19 | 49 ± 9 | 146 ± 1.8 | 79 ± 29 |
| 10 wt% HKUST-1/IL–CS | 120 ± 5.2 | 1.21 ± 0.46 | 42 ± 8 | 169 ± 27 | 69 ± 24 |
| 20 wt% HKUST-1/IL–CS | 146 ± 9.3 | 1.10 ± 0.26 | 33 ± 7 | 155 ± 6 | 57 ± 35 |
The dispersion and interaction between the components can also be observed after SEM in Fig. 5. Even at the low loading of 5 wt%, there is HKUST-1 particles sedimentation at the bottom during evaporation. However, the EDX mapping of 20 wt% MOF and ZIF/IL–CS MMMs (because of the difficulty of observing lower loadings) in Fig. 6(a) shows that the Cu presence is homogeneous all over the membrane matrix at a value of 19.6 ± 2.7 wt%, although not so uniformly as in ZIF-8-based membranes in Fig. 6(b). In the case of ZIF-8, EDX reveals a homogeneous dispersion of Zn all over the membrane matrix area and thickness, with an average value of 17.7 ± 0.1 wt% Zn. These values agree with the nominal loading of the MOF and ZIF in the MMMs. Since we cannot easily discern the nanometre size ZIF-8 particles by SEM, the image at 5 wt% ZIF-8 is omitted from Fig. 5.
The void volume fraction is a measure of the free volume that will be used to calculate the true volume fraction of the ZIF-8 or HKUST-1 filler particles dispersed in the MMM, to account for non-idealities in gas permeation performance, as will be shown below. As observed in Table 2, the void volume fraction decreased with both ZIF-8 and HKUST-1 content. The water uptake, which is a measure of hydrophilicity and swelling of the membrane calculated by eqn (1), followed the same trend as the void volume fraction and thermal decomposition, in agreement with Bushell et al. for ZIF-8/PIM-1 MMMs.53
The temperature does not affect the gas permeation through the IL–CS hybrid membranes used as base continuous membrane matrix in this work, in the range under study (25–50 °C).26 In Fig. 7, the permeability and selectivity of the membranes under study are plotted against the Robeson's upper bound and including values in the temperature range from 25 to 50 °C.
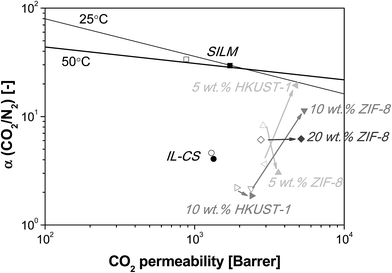 | ||
| Fig. 7 IL/CS-based membranes versus Robeson's upper bound for the CO2/N2 gas pair separation at 25 °C (ref. 4) and 50 °C (ref. 59) with different loadings of HKUST-1 (5, 10 wt%) and ZIF-8 (5, 10, 20 wt%). Supported Ionic Liquid Membrane (SILM) data are collected from Santos et al.,25 and RTIL/CS hybrid membranes from Santos et al.26 for comparison purposes. Temperature = 25 °C (void symbols) and 50 °C (full symbols). Arrows show the evolution of each membrane material with increasing temperature. | ||
The highest CO2 permeability and CO2/N2 ideal selectivity were obtained for 10 wt% ZIF-8 and 5 wt% HKUST-1/IL–CS membranes, as 5413 ± 191 Barrer and 11.5, and 4754 ± 1388 Barrer and 19.3, respectively, at 50 °C and 2 bar. ZIF-8/PEBAX MMMs of similar morphology gave a maximum 1300 Barrer CO2 and CO2/N2 selectivity of 32.3 at 25 °C and 2.6 bar, at the high ZIF-8 loading of 35%.40 Hao et al.29 reported, for the 3-phase ZIF-8/RTIL/PIL MMM, a CO2 permeability of 902.4 Barrer and a CO2/N2 selectivity of 21, at 35 °C and 3.5 bar, for the high loading of 25.8 wt%. The performance of HKUST-1 membranes is as expected given the fact that the small triangular windows connecting the main channels and the unsaturated Cu atom in tetrahedral pockets (0.35 nm) is very similar to the pore size of ZIF-8 (0.34 nm).60 The nominal loading at which defects appear differ for ZIF-8 or HKUST-1/IL–CS MMMs because of the poorer interfacial contact of HKUST-1 than ZIF-8. Although the CO2/N2 ideal selectivity obtained in this work is low, the separation performance of 10 wt% ZIF-8 and 5 wt% HKUST-1/IL–CS MMMs increases with filler and temperature, thus differing from the IL/CS membranes,26 where the CO2/N2 selectivity was 4.25 ± 0.5 and independent of temperature in the range under study.
The increase in permselectivity is attributed to the good adhesion and compatibility between the IL, the microporous particles and the polymer matrix,29 in agreement with the Ra interaction distances calculated from HSPs (see Table 1). The compatibility between MOF and polymer matrix is higher for the IL–CS hybrid matrix than the pristine CS polymer, and 2-component MOF/CS MMMs did not surpass an ideal CO2/N2 selectivity of around 2 (not shown). The best permselectivity is obtained at higher ZIF-8 (10 wt%) than HKUST-1 (5 wt%) loading, because the affinity of HKUST-1 with IL and CS is lower than that of ZIF-8, as discussed above.
The influence of temperature through novel MMMs at increasing filler loading is probably due to the creation of bypassing channels connecting the existing voids between the dispersed particles and the continuous matrix. The following study aims to observe how the temperature affects gas permeation from the point of view of the compatibility and adhesion of the components on membrane performance. In order to analyse the effect of temperature on membrane morphology and performance, several theoretical models are available to validate mathematically the gas transport properties of MMMs. Many researchers have tried to understand the influence of the morphology of MMMs on their separation performance, based only on the interaction between the phases, and several reviews have been published recently to compare the different models,61–63 with their advantages and limitations, especially using glassy polymers and zeolite filler particles.64
The most generalized models are those based on Maxwell equations, which have been recently extended to 3-phase MMM consisting of the dispersion of a small amount of solid dispersed fillers in a continuous polymer matrix and introducing an IL as liquid phase to improve the interaction among the other phases.15,29
Maxwell model is the most commonly used to predict the permeability through a dilute suspension of spherical fillers in a continuous polymer matrix, by the following equation,65
 | (10) |
The general assumption when the fillers can be estimated as ideal spherical-like inserts, as is the case of IL, ZIF-8 and HKUST-1 in the present work, is n = 1/3, which converts eqn (10) to the most popular expression of Maxwell model,
 | (11) |
When n = 1, eqn (10) corresponds to the mass transport takes place by a series mechanism through the phases,
 | (12) |
When n = 0, eqn (10) describes the effective permeability through the MMM usually takes into account a two-layer transport mechanism, that is, both phases are supposed to work in parallel to the flow direction, as
| Peff = Pcϕc + Pdϕd | (13) |
The density values of the single components in the MMMs is 1.43 g cm−3 for CS,6 1.03 g cm−3 (ref. 66) for the IL. The densities considered for the ZIF-8 and HKUST-1 dispersed particles are the calculated crystallographic values, 0.93 and 1.032 g cm−3, respectively. For the 3-phase MMM reported in this work, Pc is the permeability measured through the IL–CS based membranes as reported in a previous work26 and Pd is taken from the literature on pure ZIF-8 membrane layers, as 4390 and 180 Barrer for CO2 and N2, respectively.53 For HKUST-1-IL/CS MMM, the Pd values are taken from Varela-Guerrero et al.,67 as 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 313 and 2985 Barrer for CO2 and N2, respectively.
313 and 2985 Barrer for CO2 and N2, respectively.
ϕd is the true filler volume fraction calculated from the void fraction in Table 2 and the nominal filler volume fraction obtained from the densities of the components and the composition of the casting solution,
| ϕd = ϕdN(1 − ϕv) | (14) |
The accuracy of these model equations to adjust the experimental data are evaluated by the minimized average absolute error, AARE, between the calculated and experimental permeability for CO2 and N2, respectively, as
 | (15) |
We have observed that these simple Maxwell equations only provide an acceptable prediction in the case of N2 permeability, which may be due to the sensitivity of the permeation measurement, i.e. N2 permeability is much lower than CO2 permeability. In general, the AARE is an average of 20% for IL/CS hybrid membranes and 40% for ZIF-8 and HKUST-1-filled IL/CS MMMs, slightly reduced upon increasing temperature from 25 to 50 °C.
Therefore, we have applied the extended modified Maxwell equation to grasp the influence of the interparticle distance and compatibility of the materials, as well as other non-idealities such as gas molecular size, polymer chain rigidification,68 pore-blockage69 or the crystallinity65 of the polymer matrix when introducing porous inorganic particles into a semi-crystalline polymer as continuous matrix. The modified model considers a three pseudo-phase system accounting for the inorganic dispersed filler, the polymer continuous matrix and the interface voids. The permeability P3MM of this system is obtained by applying eqn (11) twice, first to predict the permeability through the “pseudo-insert” phase,
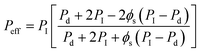 | (16) |
 | (17) |
 | (18) |
As ϕd + ϕI approaches unity, the interphases of neighbouring insert particles overlap and the whole matrix is rigidified, leading to effective properties differing from the pure polymer. This chain rigidification is represented by the phenomenological parameter β, which in single gas permeation depends upon the nature of the gas molecule.69
The semicrystalline nature of the base polymer is taken into account by a factor α, the volume fraction of the amorphous polymer responsible for gas transport,
| α = 1 − χ | (19) |
| P = S × D = S* × D* × α2 = P* × α2 | (20) |
The Pc in eqn (21) is replaced by the P* obtained in eqn (20). Likewise, the interphase permeability, PI, in eqn (16), accounting for the immobilization factor to represent the degree of rigidification in the inter-crystalline amorphous segments is now defined as,
| Pc = Pc*α2/β | (21) |
Fig. 8 compares the calculated and experimental permeabilities as a function of temperature using this extended Maxwell model with the effect of the ZIF-8 particle size and loading as dispersed phase and the crystallinity of the hybrid IL/CS matrix as continuous phase. In this case, the AARE is below 0.07% in all cases. The phenomenological parameters describing the interphase thickness, lI (μm), and immobilisation or rigidification factor, β, estimated from the minimisation of these AARE values, are collected in Table 3.
 | ||
| Fig. 8 Experimental CO2 (■) and N2 (●) permeability through ZIF-8/IL–CS MMMs at different loadings: 0 (black), 5 (light grey), 10 (grey), 20 (dark grey) wt%, respectively (a) and HKUST-1/IL–CS MMMs: 5 (light grey) and 10 (grey) (b). Lines correspond to extended modified model predictions after eqn (16)–(21): thick lines to CO2 and thin lines to N2 calculated permeabilities, respectively. Error bands are added to CO2 permeability only for clarification purposes. | ||
| T (°C) | lI (μm) | β(CO2) | β(N2) |
|---|---|---|---|
| 5 wt% ZIF-8/IL–CS MMMs | |||
| 25 | 0.20 | 1.095 | 0.77 |
| 40 | 0.20 | 0.80 | 0.06 |
| 50 | 0.20 | 0.88 | 0.27 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 10 wt% ZIF-8/IL–CS MMMs | |||
| 25 | 0.15 | 0.46 | 0.23 |
| 30 | 0.15 | 0.25 | 0.46 |
| 40 | 0.15 | 0.19 | 0.44 |
| 50 | 0.15 | 0.24 | 0.66 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 20 wt% ZIF-8/IL–CS MMMs | |||
| 25 | 0.10 | 0.51 | 0.58 |
| 30 | 0.10 | 0.16 | 0.52 |
| 40 | 0.10 | 0.24 | 0.37 |
| 50 | 0.10 | 0.28 | 0.38 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 5 wt% HKUST-1/IL–CS MMMs | |||
| 25 | 0.46 | 0.37 | 0.34 |
| 30 | 0.46 | 0.40 | 0.36 |
| 40 | 0.46 | 0.23 | 0.32 |
| 50 | 0.46 | 0.30 | 1.40 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| 10 wt% HKUST-1/IL–CS MMMs | |||
| 25 | 0.46 | 0.72 | 0.34 |
| 30 | 0.46 | 0.69 | 0.35 |
| 40 | 0.46 | 0.59 | 0.26 |
| 50 | 0.46 | 0.59 | 0.27 |
The interphase distances are independent of temperature and have values much lower than reported in the literature for zeolite–PES MMMs,69 ITQ-29–polysulfone MMMs70 or ZIF-20–polysulfone MMMs.71 This correlates with the relatively good compatibility of the chosen dispersed and continuous phases as hinted above by the Hansen' solubility theory. Although the Ra is somehow high compared to literature, the ZIF-8 is as soluble in IL as in CS, in a larger degree than HKUST-1, suggesting a better affinity between ZIF-8 than HKUST-1 and the IL–CS hybrid matrix contradicts the CO2 permeation performance of a membrane based in a semi-crystalline polymer.26 The interphase distance for HKUST-1/IL–CS MMM at only 5 wt% particle loading is higher than the value obtained for the organic hybrid IL–CS matrix and this explains why no good membranes with this MOF could be processed at higher loadings. The chain immobilisation factors are very low for the IL–CS hybrid membranes, due to the good compatibility between IL and CS components, and they generally increase upon ZIF-8 loading, thus accounting for the rigidification that the ordered porous structure imparts to the continuous matrix. The interphase distance between the porous fillers and the continuous ionic polymer matrix predicted by this model agrees with other three-phase MMMs reported in the literature. Although in those cases where the continuous phase was composed of an ionic polymer and a room temperature IL, and SAPO-34 zeolite15,16 or ZIF-8 (ref. 29) as dispersed phases, the lI and β(CO2) and β(N2) are larger than in the present work. We have also considered the crystallinity of the continuous matrix,65 which decreases with the addition of even a small amount of IL.28
As pointed out before, the IL may be acting as wetting medium between the ZIF-8 or HKUST-1 particles and the CS matrix, since the Ra distance between ZIF-8 or HKUST-1 with IL–CS material diminishes from the Ra distance with the pristine CS polymer, as calculated in Table 1. The good adhesion between the IL–CS continuous matrix and the ZIF-8 nanoparticles is slightly better than for the HKUST-1 nanoparticles, because of the similarity between ZIF-8 and the IL. This reason, together with the higher particle size of HKUST-1 causes that the best permselectivity of HKUST-1-based IL–CS MMMs is achieved at lower (5 wt%) loading than ZIF-8-based MMMs.
Conclusions
Three-component MMMs were prepared by adding a highly CO2 absorbing non-toxic ionic liquid, [emim][Ac] (IL), a biopolymer from abundant natural resources, chitosan (CS), and MOF ZIF-8 or HKUST-1 nanoparticles to improve the selectivity of the IL–CS hybrid continuous polymer matrix. The increasing amount of ZIF-8 and HKUST-1 does not deteriorate the thermal stability of the hybrid IL–CS membranes, which allows expecting the potential of such materials for developing high temperature resistant membrane materials for CO2 separation. This, together with the fact that the water content in the membrane is constant before and after the whole set of permeation runs allows expecting the potential of such materials for developing high temperature resistant membrane materials for CO2 separation. The influence of the temperature and MMMs morphology on CO2/N2 separation performance was analysed. The adhesion between the phases in terms of the gas transport properties was interpreted by Hansen solubility parameters (HSP) and Maxwell-based models, modified to account for chain rigidification, pore blockage and crystallinity of the IL–CS matrix, with very accurate predictions. In particular, HSP approach reveals better ZIF-8 compatibility with CS and IL than HKUST-1, and the preferential affinity of the chosen components towards CO2 vs. N2 is confirmed. The best permselectivity membranes are the 10 wt% ZIF-8/IL–CS and the 5 wt% HKUST-1/IL–CS MMMs, where the separation efficiency increases in the temperature range under study. This is due to the better affinity of ZIF-8, as predicted by HSP and confirmed by the extended modified Maxwell model with lower interphase thicknesses and chain rigidification factor for ZIF-8 than HKUST-1. To obtain performance enhancement and enable scale up of the separation process, scale down of the selective layer thickness is necessary and thus composite membranes composed of a thin hybrid selective layer coated on a robust porous supports are being studied in the laboratory and their performance will be reported in a future work.Acknowledgements
Financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) for the project CTQ2012-31229 at the University of Cantabria, and MAT2013-40556-R, at the University of Zaragoza, is gratefully acknowledged. C. C. C. and A. F. B. also thank the MINECO for the Ramón y Cajal contract (RYC-2011-08550) and the post-graduate research grant (BES2013-064266), respectively, at the Universidad de Cantabria. Dr Sara Sorribas is gratefully thanked for her technical assistance on the XRD, SEM and TEM analyses. The microscopy work was done at the Laboratorio de Microscopías Avanzadas of the Instituto de Nanociencia de Aragón (LMA-INA), and the XRD measurements were carried out at the Servicio General de Apoyo a la Investigación (SAI) of the Universidad de Zaragoza.References
- K. Ramasubramanian, Y. Zhao and W. S. W. Ho, AIChE J., 2013, 59, 1033–1045 CrossRef CAS.
- C. Casado-Coterillo, T. Yokoo, T. Yoshioka, T. Tsuru and M. Asaeda, Sep. Sci. Technol., 2011, 46, 1224–1230 CrossRef.
- J. Gascón, F. Kapteijn, B. Zornoza, V. Sebastián, C. Casado and J. Coronas, Chem. Mater., 2012, 24, 2829–2844 CrossRef.
- L. M. Robeson, J. Membr. Sci., 2008, 320, 390–400 CrossRef CAS.
- Y. Huang, T. C. Merkel and R. W. Baker, J. Membr. Sci., 2014, 463, 33 CrossRef CAS.
- J. K. Adewole, A. L. Ahmad, S. Ismail and C. P. Leo, Int. J. Greenhouse Gas Control, 2013, 17, 46–65 CrossRef CAS.
- Z. Dai, R. Noble, D. L. Gin, X. Zhang and L. Deng, J. Membr. Sci., 2016, 497, 1–20 CrossRef CAS.
- C. E. Powell and G. G. Qiao, J. Membr. Sci., 2006, 279, 1–49 CrossRef CAS.
- H. Mushardt, V. Kramer, D. Hülagü, T. Brinkmann and M. Kraume, Chem. Ing. Tech., 2013, 86, 83–91 CrossRef.
- J. Caro and M. Noack, Microporous Mesoporous Mater., 2008, 115, 215–233 CrossRef CAS.
- M. Rezakazemi, A. E. Amooghin, M. M. Montazer-Rahmati, A. F. Ismail and T. Matsuura, Prog. Polym. Sci., 2014, 39, 817–861 CrossRef CAS.
- L. C. Tomé, D. J. S. Patinha, R. Ferreira, H. García, C. S. Pereira, C. S. R. Freire, L. P. N. Rebelo and I. M. Marrucho, ChemSusChem, 2014, 7, 110–113 CrossRef PubMed.
- L. Gómez-Coma, A. Garea and A. Irabien, Sep. Purif. Technol., 2014, 132, 120–125 CrossRef.
- M. Alvarez-Guerra and A. Irabien, Green Chem., 2011, 13, 1507–1516 RSC.
- Y. C. Hudiono, T. K. Carlisle, A. L. LaFrate, D. L. Gin and R. D. Noble, J. Membr. Sci., 2011, 370, 141–148 CrossRef CAS.
- D. F. Mohshim, H. Mukhtar and Z. Man, Sep. Purif. Technol., 2014, 135, 252–258 CrossRef CAS.
- S. C. Kumbharkar, R. S. Bhavsar and U. K. Kharul, RSC Adv., 2014, 4, 4500 RSC.
- B. J. Adzima, S. R. Venna, S. S. Klara, H. He, M. Zhong, D. R. Luebke, M. S. Mauter, K. Matyjaszewski and H. B. Nulwala, J. Mater. Chem. A, 2014, 2, 7967 CAS.
- L. Liu, A. Chakma and X. Feng, J. Membr. Sci., 2008, 310, 66–75 CrossRef CAS.
- L. A. El-Azzami and E. A. Grulke, Ind. Eng. Chem. Res., 2009, 48, 894–902 CrossRef CAS.
- T. Kai, T. Kouketsu, S. Duan, S. Kazama and K. Yamada, Sep. Purif. Technol., 2008, 63, 524–530 CrossRef CAS.
- S. Xiao, X. Feng and R. Y. M. Huang, J. Membr. Sci., 2007, 306, 36–46 CrossRef CAS.
- M. B. Patil and T. M. Aminabhavi, Sep. Purif. Technol., 2008, 62, 128–136 CrossRef CAS.
- Z.-D. Ding, Z. Chi, W.-X. Gu, S.-M. Gu, J.-H. Liu and H.-J. Wang, Carbohydr. Polym., 2012, 89, 7 CrossRef CAS PubMed.
- E. Santos, J. Albo and A. Irabien, J. Membr. Sci., 2014, 452, 277–283 CrossRef CAS.
- E. Santos, E. Rodríguez-Fernández, C. Casado-Coterillo and A. Irabien, Int. J. Chem. React. Eng., 2015, 13 DOI:10.1515/ijcre-2014-0109.
- S.-C. Lu and I. F. J. Vankelecom, React. Funct. Polym., 2015, 86, 117–124 CrossRef CAS.
- C. Casado-Coterillo, M. d. M. López-Guerrero and A. Irabien, Membranes, 2014, 4, 287–301 CrossRef PubMed.
- L. Hao, P. Li, T. Yang and T.-S. Chung, J. Membr. Sci., 2013, 436, 221–231 CrossRef CAS.
- B. Zornoza, C. Tellez, J. Coronas, J. Gascon and F. Kapteijn, Microporous Mesoporous Mater., 2013, 166, 67–78 CrossRef CAS.
- R. Adams, C. Carson, J. Ward, R. Tannenbaum and W. Koros, Microporous Mesoporous Mater., 2010, 131, 13–20 CrossRef CAS.
- S. S.-Y. Chui, S. M.-F. Lo, J. P. H. Charmant, A. G. Orpen and I. D. Williams, Science, 1999, 283, 1148–1150 CrossRef CAS PubMed.
- A. Car, C. Stropnik and K.-V. Peinemann, Desalination, 2006, 200, 424–426 CrossRef CAS.
- G. Yilmaz and S. Keskin, J. Membr. Sci., 2014, 454, 407–417 CrossRef CAS.
- Q. Song, S. K. Nataraj, M. V. Roussenova, J. C. Tan, D. J. Hughes, W. Li, P. Bourgoin, M. A. Alam, A. K. Cheetham, S. A. Al-Muhtaseb and E. Sivaniah, Energy Environ. Sci., 2012, 5, 8359–8369 CAS.
- S. Shahid and K. Nijmeijer, J. Membr. Sci., 2014, 470, 166–177 CrossRef CAS.
- Y. Dai, J. R. Johnson, O. Karvan, D. S. Sholl and W. J. Koros, J. Membr. Sci., 2012, 401–402, 76–82 CrossRef CAS.
- Z. Zhang, S. Xian, Q. Xia, H. Wang, Z. Li and J. Li, AIChE J., 2013, 59, 2195–2206 CrossRef CAS.
- T. Li, Y. Pan, K.-V. Peinemann and Z. Lai, J. Membr. Sci., 2013, 425–426, 235–242 CrossRef CAS.
- V. Nafisi and M.-B. Hägg, J. Membr. Sci., 2014, 459, 244–255 CrossRef CAS.
- F. D. Silva, G. Magalhaes, E. Jardim, J. Silvestsre-Albero, A. Sepúlveda-Escribano, D. D. Azevedo and S. D. Lucena, Adsorpt. Sci. Technol., 2015, 33, 223–242 CrossRef.
- J. M. Vicent-Luna, J. J. Gutiérrez-Sevillano, J. A. Anta and S. Calero, J. Phys. Chem. C, 2013, 117, 20762 CAS.
- N. A. H. M. Nordin, A. F. Ismail, A. Mustafa, R. S. Murali and T. Matsuura, RSC Adv., 2014, 4, 52530–52541 RSC.
- Y. Pan, Y. Liu, G. Zeng, L. Z. Hao and Z. Lai, Chem. Commun., 2011, 47, 2071–2073 RSC.
- P. Burmann, B. Zornoza, C. Téllez and J. Coronas, Chem. Eng. Sci., 2014, 107, 66–75 CrossRef CAS.
- L. H. Wee, M. R. Lohe, N. Janssens, S. Kaskel and J. A. Martens, J. Mater. Chem., 2012, 22, 13742–13746 RSC.
- S. Sorribas, A. Kudasheva, E. Almendro, B. Zornoza, O. Iglesia, C. Téllez and J. Coronas, Chem. Eng. Sci., 2015, 124, 37–44 CrossRef CAS.
- E. L. Cussler, Diffusion. Mass transfer in fluid systems, Cambridge University Press, Cambridge, 3rd edn, 2007 Search PubMed.
- Y. Z. Zhu-Ryberg, U. Edlund and A.-C. Albertsson, Biomacromolecules, 2011, 12, 1355 CrossRef CAS PubMed.
- C. M. Hansen, Hansen solubility parameters. A user's handbook, CRC Press, Boca Raton, 2007, p. 546 Search PubMed.
- H. Xie, S. Zhang and S. Li, Green Chem., 2006, 8, 630 RSC.
- L. Casettari, D. Vllasaliu, E. Castagnino, S. Stolnik, S. Howdle and L. Illum, Prog. Polym. Sci., 2012, 37, 659 CrossRef CAS.
- A. F. Bushell, M. P. Attfield, C. R. Mason, P. M. Budd, Y. Yampolskii, L. Starannikova, A. Rebrov, F. Bazzarelli, P. Bernardo, J. C. Jansen, M. Lanc, K. Friess, V. Shantarovich, V. Gustov and V. Isaeva, J. Membr. Sci., 2013, 427, 48–62 CrossRef CAS.
- M. J. C. Ordoñez, K. J. Balkus Jr, J. P. Ferraris and I. H. Musselman, J. Membr. Sci., 2010, 361, 28–37 CrossRef.
- P. Weerachanchai, Y. Wong, K. H. Lim, T. T. Y. Tan and J.-M. Lee, ChemPhysChem, 2014, 15, 3580 CrossRef CAS PubMed.
- D. Elangovan, U. Nidoni, I. E. Yuzay, S. E. M. Selke and R. Auras, Ind. Eng. Chem. Res., 2011, 50, 11136 CrossRef CAS.
- L. Paseta, G. Potier, S. Abbott and J. Coronas, Org. Biomol. Chem., 2015, 13, 1724 CAS.
- J. Wang, X. Zheng, H. Wu, B. Zheng, Z. Jiang, X. Hao and B. Wang, J. Power Sources, 2008, 178, 9 CrossRef CAS.
- B. W. Rowe, L. M. Robeson, B. D. Freeman and D. R. Paul, J. Membr. Sci., 2010, 360, 58–69 CrossRef CAS.
- S. Basu, A. Cano-Odena and I. F. J. Vankelecom, Sep. Purif. Technol., 2011, 81, 31–40 CrossRef CAS.
- H. Vinh-Thang and S. Kaliaguine, Chem. Rev., 2013, 113, 4980 CrossRef CAS PubMed.
- Y. Shen and A. C. Lua, AIChE J., 2013, 59, 4715 CrossRef CAS.
- B. Shimekit, H. Mukhtar and T. Murugesan, J. Membr. Sci., 2011, 373, 152 CrossRef CAS.
- S. A. Hashemifard, A. F. Ismail and T. Matsuura, J. Membr. Sci., 2010, 347, 53 CrossRef CAS.
- M. Shen, Y. H. X. Lin, B. Ding, L. Zhang and X. Zhang, J. Appl. Polym. Sci., 2013, 127, 2938 CrossRef CAS.
- J. Blath, N. Deubler, T. Hirth and T. Schiestel, Chem. Eng. J., 2012, 181–182, 152 CrossRef CAS.
- V. Varela-Guerrero, Y. Yoo, M. C. McCarthy and H.-K. Jeong, J. Mater. Chem., 2010, 20, 3938 RSC.
- T. T. Moore, R. Mahajan, D. Q. Vu and W. J. Koros, AIChE J., 2004, 50, 311 CrossRef CAS.
- Y. Li, H.-M. Guan, T.-S. Chung and S. Kulprathipanja, J. Membr. Sci., 2006, 275, 17 CrossRef CAS.
- C. Casado-Coterillo, J. Soto, M. T. Jimaré, S. Valencia, A. Corma, C. Téllez and J. Coronas, Chem. Eng. Sci., 2012, 73, 116 CrossRef CAS.
- B. Seoane, J. M. Zamaro, C. Téllez and J. Coronas, RSC Adv., 2011, 1, 917 RSC.
| This journal is © The Royal Society of Chemistry 2015 |