Structural control over spin localization in triarylmethyls

Abstract

Triarylmethyls (TAMs) are a class of long-lived purely organic radicals discovered at the beginning of the twentieth century. The chemical versatility and high stability of TAMs have lead to their application in many fields of science and technology. All compounds of this class are composed of three aryl rings bonded to a central carbon atom, where their unpaired electron mainly resides. Due to the π-conjugated electronic nature of this molecular structure, the possibility arises of controlling the unpaired electron localization (i.e. spin localization) by the torsion angles of the three aryl rings. By using density functional theory calculations (DFT) we have carefully investigated this phenomenon for a wide range of TAMs and probed how it is influenced by other important parameters such as chemical functionalization and temperature. Our results demonstrate that a single general spin versus structure relation is followed for all of our studied TAMs confirming that having a predictable structure-dependent spin localisation is an intrinsic feature of these radicals. Considering that spin localisation in TAMs is linked to many other important properties (e.g. magnetic interactions, optical absorption bands, magnetoresistance phenomena), the fact that manipulation of aryl ring twist angles could lead to molecular level control over such features presents enormous potential for future scientific and technological applications.

---

Introduction

Over 100 years ago Moses Gomberg prepared the first persistent radical; the triphenylmethyl.¹ This discovery launched the field of radical chemistry at the beginning of the twentieth century and, since then, more than hundred triarylmethyl (TAM) derivatives have been synthesized.^2–20 All molecules in this class possess a main skeleton composed of three aryl rings bonded to a central carbon atom, where their unpaired electron mainly resides (Fig. 1). Such is the chemical versatility¹³ and high stability^21,22 of this class of aromatic organic radicals, they have been widely promoted for many applications such as Electron Spin Resonance (EPR) imaging,^23–29 oxygen detection and pH monitoring,^25,30–37 Dynamic Nuclear Polarization (DNP),^38–42 donor–acceptor systems,^12,43–46 spin labelling of biomolecules,^3,29 discotic liquid crystals,⁴⁷ organic light emitting diodes,^14,48 molecular magnetic materials^21,49–55 and molecular spintronics,^45,56–60 among others.^{12,14,61–63}

Fig. 1 Generic TAM structure. Their unpaired electron (green) mainly resides on the central methyl carbon atom (αC) but, due to the π-conjugated nature of these molecules, it partially delocalizes to the ortho- and para-positions of each aryl ring.

In TAMs, the most interesting physic-chemical properties such as magnetic interactions,⁵⁰ optical absorption bands,⁶⁴ electrical conductivities⁵⁹ or magnetoresistance phenomena⁶⁵ are closely linked to their unpaired electron. For this reason, it would be enormously useful for any TAM-based application to fully understand what factors mainly influence their unpaired electron distribution (i.e. spin distribution).

In 1944 Gilbert N. Lewis suggested that TAM radicals are not completely planar but, instead, their three aryl rings are twisted with respect to the sp² plane of the central methyl carbon atom (Fig. 1).⁶⁶ Later, this was confirmed by the measured magnetic properties of certain TAMs whereby it was found to be necessary to consider the non-planarity of the aryl rings in order to properly interpret the observations.^67–70 As suggested at the time, the link between non-planarity and magnetism is due to the influence of dihedral angles on the spin delocalization in magnetic aromatic systems.^67–71 With some simplifying assumptions (e.g. fixing all structural degrees of freedom apart from the torsion angle) one can employ π-orbital overlap arguments to estimate that the spin delocalization through a certain aryl ring is proportional to the cosine squared of its dihedral angle with respect to the sp² plane of the radical centre (i.e. cos² θ).^67,68,70,72 Later, experimental works on some specific TAMs also effectively showed that the spin distribution is influenced by the torsion angles of the aryl rings.^16,18,20,73 However, despite these important early studies, as far as we know, there exists no detailed systematic study of the spin-localization versus structure relation covering a wide range of TAMs. Moreover, the influence of chemical functionalisation and temperature on this relation is currently unclear. The existence of a general and robust spin versus structure relationship for all TAMs would be extremely useful for the tailored design of TAM-based applications, and could open the possibility of preparing molecular materials with controllable magnetic, optical and electrical properties.

Herein, we have used ab initio density functional theory (DFT) calculations to accurately study the dependence of spin localization in TAMs on their chemical and structural characteristics. We consider the first order assumption that the spin localisation should entirely depend on the average of the cosine squared of each dihedral angle of the three aryl rings (〈cos² φ_i〉). We test this proposal for a wide range of dihedral angle combinations and different chemical functionalisations. More generally, we also study whether this spin localisation versus structure relationship holds at finite temperatures. Our results also thus provide detailed insights into important and subtle dynamic factors that influence the degree of spin localization under more realistic conditions. We expect our results will be of interest and use for experimental chemists in order to optimize TAMs for future applications.

Methodology

The optimised structures of all TAM derivatives reported herein (see ESI† for chemical structures) were obtained using DFT calculations employing the PBE0 hybrid functional⁷⁴ and a 6-311++g(d,p) basis set as implemented in the GAUSSIAN-09 code.⁷⁵ The PBE0 functional has been demonstrated to provide a very good account of the geometry, electronic structure and spin polarisation in organic radicals.⁷⁴ Calculated spin densities were atomically partitioned using the Hirshfeld scheme.⁷⁶ For independently benchmarking our computational methodology we have also tested its capacity to reproduce reported EPR experimental data on a range of TAM derivatives.¹⁶ The good match between our calculated spin dipolar coupling constants and the experimental data further validates the level of theory utilised herein. A discussion of this comparison and the corresponding results can be found in the ESI.†

For assessing the validity of our proposal at higher temperatures, canonical ab initio molecular dynamics (AIMD) calculations of 10 picoseconds (5 ps of equilibration followed by 5 ps of production) at a temperature of 300 K were also performed employing a 0.5 femtosecond time step and the Bussi–Donadio–Parrinello thermostat.⁷⁷ The AIMD runs were calculated using the FHI-AIMS code⁷⁸ employing the PBE0 functional and a light basis set for all atoms.

Results and discussion

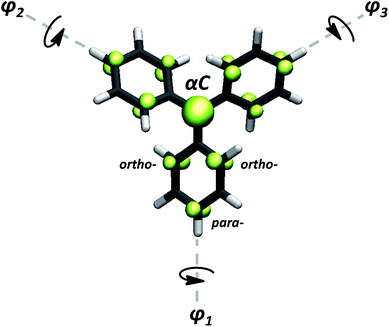
As suggested by Lewis⁶⁶ and later corroborated by experimental work,^16,20 the dihedral angle of each aryl ring in TAMs mainly depends on the particular chemical functionalization of the molecule. Thus, for assessing the spin localization dependence on the three aryl rings twists, we first studied the structural and electronic properties of a set of 27 previously reported TAMs with a wide range of chemical and structural properties. Besides studying some triphenylmethyl derivatives, we also included some perchloro- and perfluoro-TAMs with different functionalizations.^16,79 Among them, phenyl-,^69,80 terbutyl-,⁸¹ hydroxo-,⁸¹ methoxy-,^20,82 carboxyl-,^{31,41,54,83,84} amine-,⁸⁵ thioether^41,42,84 and nitro-functional⁸⁶ groups have been considered for our study. Some TAMs with direct aryl–aryl bonding that present constrained structures and more extreme angle values were also included.^17,20 Further, we also designed two TAMs (see ESI† for structural atomic coordinates) where the three aryl rings are forced by inter-ring linkages to be in perpendicular orientations with respect to the central sp² methyl plane, giving rise to configurations that have not yet been reported for any synthesized TAM. The chemical structures of TAMs 1–27 can be found in the ESI.†

Additionally, a series of constrained dihedral angle calculations were performed with the triphenylmethyl¹ (herein TAM4) and the perchloro-triarylmethyl^2,22,62 (TAM12). Here, the dihedral angles of the three aryl rings were constrained with equal (i.e. φ₁ = φ₂ = φ₃) or different (i.e. φ₁ ≠ φ₂ ≠ φ₃) values between 20–90°, while fully optimizing the rest of the molecular structure. In this way we could extract the intrinsic effect of aryl ring twisting on the spin distribution without the additional influence of chemical substitution (e.g. electro-withdrawing/donating nature of substituents). These calculations also mimic the hypothetical manipulation of the aryl ring twists by external stimulus, testing the spin-localization/structural relation for out-of-equilibrium configurations. For all cases the spin population on the central carbon atom (αC; see Fig. 1) was used as an indicator of the spin localization/delocalization, since this position is always that with the highest spin population in TAMs.

As a first order assumption, we consider that the spin delocalisation through a particular aryl ring only depends on the corresponding dihedral angle, regardless of its chemical functionalization. In this scenario, based on π-overlapping ideas,^67,68,70,72 the spin delocalization should be essentially captured by cos² φ_i, where φ_i is the dihedral angle of the considered aryl ring with the central sp² carbon atom plane. Secondly, we consider that the effect of twisting any one aryl ring on the spin localization to be independent of the other two rings torsions. This simplifies the complex TAM case to three independent methyl-aryl units and, as a consequence, the average of the three cos² φ_i (i.e. 〈cos² φ_i〉 = (cos² φ₁ + cos² φ₂ + cos² φ₃)/3) should become a first order spin localization descriptor for TAMs. In Fig. 2 we plot the αC spin population against 〈cos² φ_i〉 for our set of more than 40 TAM structures.

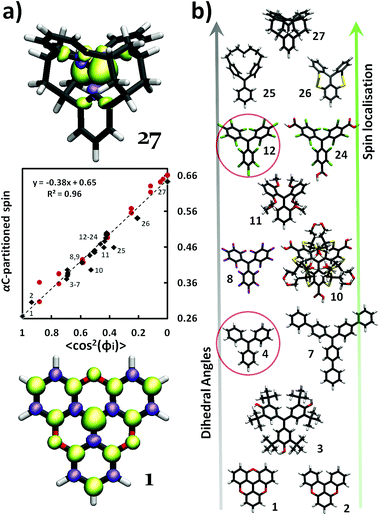Fig. 2 (a) Middle; partitioned spin population on αC against 〈cos² φ_i〉, where 〈cos² φ_i〉 = (cos² φ₁ + cos² φ₂ + cos² φ₃)/3, for each case. Black diamonds represent the fully optimized TAM1–27 (numbers, X, refer to the TAMX, see ESI†) and red spheres correspond to the constrained optimisations of TAM4 and TAM12. Values of φ lower than 20° were not possible in the constrained optimisations due to too large sterical hindrances between the three aryl rings. Upper/lower; spin population iso-surfaces (green = α; violet = β) for TAM27 (upper) and TAM1 (lower), exhibiting the most perpendicular and most planar aryl ring configurations, respectively. (b) Fully optimized structures of representative TAMs from our study, highlighting the broad range of studied structures. TAM4 (triphenylmethyl) and TAM12 (PTM), used for the constrained optimizations (red spheres in a), are circled. TAM26 and TAM27 have been specially designed for this study (see ESI† for atomic coordinates). Atom colour key: C – grey, H – white, O – red, S – yellow, Cl – green, F – violet.

As it can be seen in Fig. 2a, 〈cos² φ_i〉 is a good spin localization descriptor for the optimised TAM derivative structures (i.e. TAM1–27, Fig. 2b) where there is little scatter away from the ideal assumed behaviour (dashed line). The fact that the differently functionalized TAMs (black diamonds) nicely follow the main trend means that chemical functionalisation (see Fig. 2b) determines the spin localization by determining the three dihedral angles but other possible effects, such as the electro-donating/withdrawing nature of substituents, clearly play a secondary role. Therefore, for 0 K structures, the dihedral angles of the three aryl rings with αC almost entirely determine the spin localization in TAMs. As a consequence, by means of a proper chemical design, we can have a completely spin delocalized picture induced by a planar structure (TAM1, Fig. 2a-down) or, conversely, a configuration where most of the spin population resides on αC (TAM27) due to a perpendicular orientation of the three aryl rings (Fig. 2a-up).

The αC spin population for the structurally constrained versions of TAM4 and TAM12 structures (circled in Fig. 2b) also linearly varies with 〈cos² φ_i〉 (red spheres in Fig. 2a). This shows that the spin-localization structural relation is also maintained for out-of-equilibrium configurations. In effect, this set of calculations confirm the potential use of this relation for TAM-based materials and devices where the TAM structure could be externally controlled (e.g. by crystal packing, applied pressure) to affect physicochemical properties such as optical absorption bands, magnetic interactions, or electrical conductivities.

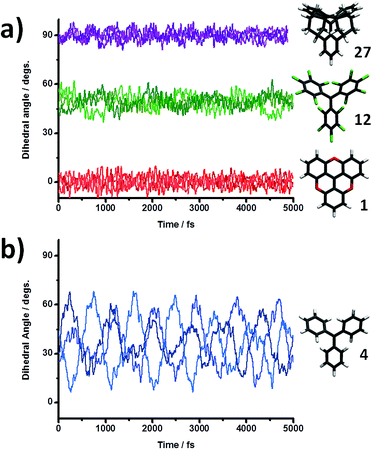
However, for real world applications temperature is a critical parameter that must also be taken into account. Thus, for testing the robustness of the spin-localization/structure relation at realistic conditions, we further performed AIMD simulations for radicals TAM1, TAM4, TAM12 and TAM27 at a temperature of 300 K (see computational details in the Methodology section). Fig. 3 shows the time evolution of the three dihedral angles (φ_1–3) for the four studied TAMs at 300 K. By comparing the structural oscillations of radicals TAM1, TAM12 and TAM27 (Fig. 3a) with that of radical TAM4 (Fig. 3b) we notice important differences due to the correspondingly different chemical functionalisations. Direct aryl–aryl bonding in TAM1 and TAM27 clearly prevents rotation of the three aryl rings and this is shown by the quite constant values of the corresponding dihedral angles over time (red and purple curves in Fig. 3a, respectively). In the case of the fully chlorinated TAM12 it is the strong sterical hindrance between chlorine atoms that inhibits free rotation of the aryl rings, giving rise to similarly dynamically restricted structural behaviour to that of radicals TAM1 and TAM27 (green curves in Fig. 3a). The triphenylmethyl (TAM4) though, presents a completely different scenario (Fig. 3b). Due to the lack of inter-ring bonding plus a low sterical hindrance between each phenyl ring, rotation is not prevented. This greater rotational freedom leads to the oscillations of each separate dihedral angle for TAM4 (blue curves in Fig. 3b) to be much higher than those in Fig. 3a. Therefore, chemical functionality does not only determine the most stable 0 K configuration of each aryl ring, but also their associated rotational freedom and thus their finite temperature dynamic structural behaviour. This also suggests that the ease with which dihedral angles could be manipulated by external means in TAM-based systems will depend on their individual chemical functionalization. Clearly, in addition to such molecular scale considerations, many other environmental factors can affect the degree to which the structure of a TAM can be tailored (e.g. type of solvent, crystal packing, applied external forces).

Fig. 3 Time dependence of φ_1–3 during the 5 ps AIMD calculations at 300 K for radicals TAM1, TAM12 and TAM27 (red, green and purple, respectively) in (a) and radical TAM4 in (b) (blue). The chemical structures of the radicals are provided to the right of the corresponding plots.

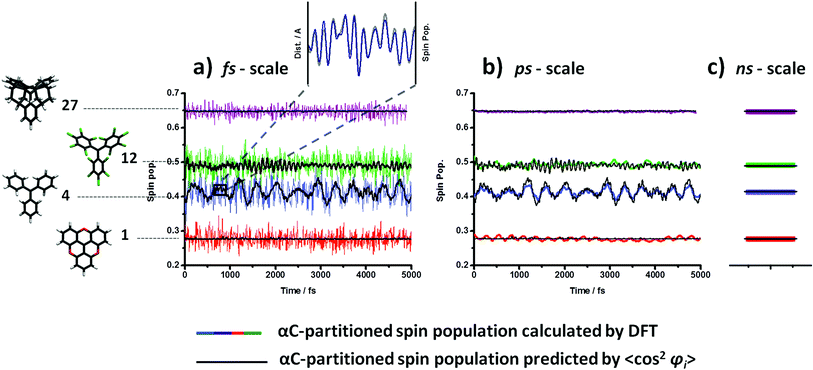
To test whether the structural dependence of the spin-localization is maintained at finite temperatures during these structural fluctuations, we compared the computed αC spin population over time with that predicted by the relation derived in Fig. 2a. Specifically, by using the fit equation in the plot of Fig. 2a, we extracted from the dihedral angle fluctuations (Fig. 3) a 〈cos² φ_i〉 – predicted αC spin population over time. In Fig. 4 we compare the actual calculated αC spin population (coloured lines), provided by DFT, with the 〈cos² φ_i〉 – predicted αC spin population (black line) for the four studied radicals.

Fig. 4 (a) Computed (coloured) and predicted (black) by 〈cos²φ_i〉 (where 〈cos² φ_i〉 = (cos² φ₁+ cos² φ₂+ cos² φ₃)/3) αC-partitioned spin population over 5 ps of the AIMD calculations at 300 K for radicals TAM1, TAM4, TAM12 and TAM27 (red, blue, green and purple, respectively). Inset: αC-partitioned spin population (blue) plotted together with the average distance of the three αC-aryl bonds (grey) over 0.2 ps for TAM4. (b) Smoothed αC-partitioned spin population (coloured; using the Savizky–Golay methodology) plotted together with the predicted one (black) over the same period of time. (c) Average of the computed αC-partitioned spin population (coloured) over the entire 5 ps AIMD simulation compared with the predicted one by using the average 〈cos² φ_i〉 value (black). The corresponding chemical structures of each TAM are also provided.

In Fig. 4a, the αC spin population is evaluated every 0.5 fs. Even for such a small sampling time the predictions by 〈cos² φ_i〉 (black lines) is approximately followed (with ∼10% variance) by the calculated spin localization (coloured lines) for each studied TAM over time. This consistent correlation confirms that the spin localization is also dynamically determined by the three aryl rings twists at finite temperatures and, thus, opens up the potential applicability of this dependence under realistic conditions. The computed αC spin populations (coloured curves in 4a) present a fast but fairly small oscillation over time that does not exist in the prediction (black curves in 4a). As already noted by M. Karplus in the 60 s',⁷² this faster oscillation is likely to be associated with bond vibrations which are not accounted for by 〈cos² φ_i〉. To verify this hypothesis the average distance of the three central αC-aryl bonds were monitored over time together with the spin population on αC. In the zoomed inset to Fig. 4a it can be seen that, at the femtosecond time scale the rapid αC spin population variation (blue) perfectly correlates with the average of the bond length oscillation of those three bonds (grey), corroborating Karplus' suggestion. Therefore, based on the same π–π overlap ideas, thermal vibrations influence the spin localization by stretching/shortening the C–C bonds of the three aryl rings with αC. However, by looking at the plots in Fig. 4a it seems that their effect on the αC spin population is to simply add small random deviations away from the ideal behaviour predicted by 〈cos² φ_i〉. To test this idea we use the Savitzky–Golay filtering procedure^87,88 for removing the high frequency oscillations due to bond vibrations. As it can be seen in Fig. 4b, we then recover a slower αC-spin population variation over time (coloured lines) that matches almost perfectly with the predicted one by 〈cos² φ_i〉 (black lines). This demonstrates that, at sufficiently long times (i.e. hundreds of femto-seconds or higher) the effect of bond vibrations is averaged out and the spin localization is essentially entirely determined by the three dihedral angle values (collected by 〈cos² φ_i〉).

Finally, since most of laboratory experiments do not measure the physic-chemical properties at the time-scales of femto- or pico-seconds, but from the nano-second time-scale upwards, we wanted to probe the applicability of 〈cos² φ_i〉 as a spin localization predictor at such typically measured time-scales. For this we calculated the average value of 〈cos² φ_i〉 from the dihedral angle oscillations shown in Fig. 3 over the entire AIMD simulation (5 picoseconds). Then, by using the fit equation of Fig. 2a, we extract the predicted αC spin population for each TAM radical. In Fig. 4c we compare this predicted value with the computed αC spin population mean value during the entire AIMD. As it can be seen, once again, the matches for all four radicals are excellent.

Overall, our AIMD results confirm the robustness of 〈cos² φ_i〉 as a spin localization descriptor for TAMs even at finite temperatures. Over short time scales bond vibrations also affect spin localization, but their effect simply adds a small random deviation over the value predicted by 〈cos² φ_i〉.⁷² For relatively long times (hundreds of femtoseconds or more) the effect of bond vibrations is averaged out and, then, the spin localization is essentially entirely determined by the dihedral angles of the three aryl rings. Therefore, at finite temperatures dihedral angles are shown to be effective spin localization descriptors in TAMs, opening the possibility of using them for tailoring this important electronic property and all related-characteristics under realistic conditions.

Conclusions

In summary, by using DFT calculations and by examining different TAMs with a range of chemical structures and at finite temperatures we have confirmed that, very generally, the average αC spin localization is well determined by 〈cos² φ_i〉 (where 〈cos² φ_i〉 = (cos² φ₁ + cos² φ₂ + cos² φ₃)/3 and φ_i are the dihedral angles of each aryl ring with respect to the central sp² carbon atom plane). Chemical functionality determines the spin distribution as long as it determines the three dihedral angles but other chemical effects such as the electro-donating/withdrawing nature of substituents play a secondary role. By performing AIMD simulations at 300 K, the predictive power of 〈cos² φ_i〉 at finite temperatures has been probed. Bond vibrations also affect the spin localization at the femto-second time scale but their effect simply adds a rapid and small random deviation over the predicted value by 〈cos² φ_i〉. Moreover, at relatively long time-scales (hundreds of femto-seconds or higher) their effect is averaged out and the spin localization is essentially entirely determined by the three dihedrals. In TAMs, the existence of the unpaired electron gives rise to their most interesting properties.^50,59,64,65 Therefore, this general and robust spin-localization/structure relationship also represents a powerful tool for controlling other important characteristics such as magnetic interactions, optical absorption bands, magnetoresistance phenomena or electrical conductivities. Besides the possibility of tunning dihedral angles by chemical design,^89–91 some theoretical studies have pointed out the possibility of manipulating this structural feature by external means such as electrical fields,⁹² mechanical strain⁹³ or optical excitations.^94,95 Hence, dihedral angles might be finely tuned by external stimulus in properly designed future materials and devices. In that scenario, we strongly believe that TAMs and their spin-localization versus structure dependence could become a key tool for the design and preparation of novel materials and devices with controllable magnetic, optical and electrical properties.

Acknowledgements

We acknowledge financial support from Spanish Government grant MAT2012-30924 and Generalitat de Catalunya grants (2014SGR97 and XRQTC). I. A. acknowledges the Generalitat de Catalunya for an FI-DGR PhD scholarship. We also acknowledge the Red Española de Supercomputacion (RES) for computing time. We also would like to thank Prof. Jaume Veciana and Prof. Juan-Carlos Paniagua for helpful discussions.

Notes and references

1. M. Gomberg, J. Am. Chem. Soc., 1900, 22, 757–771.
2. M. Ballester, J. Riera, J. Castañer, C. Badía and J. M. Monsó, J. Am. Chem. Soc., 1971, 93, 2215–2225.
3. M. Ballester, J. Riera, J. Castañer, C. Rovira, J. Veciana and C. Onrubia, J. Org. Chem., 1983, 48, 3716–3720.
4. L. Juliá, M. Ballester, J. Riera, J. Castañer, J. L. Ortin and C. Onrubia, J. Org. Chem., 1988, 53, 1267–1273.
5. M. K. Bowman, C. Mailer and H. J. Halpern, J. Magn. Reson., 2005, 172, 254–267.
6. S. López, J. Carilla, L. Fajarí, L. Juliá, E. Brillas and A. Labarta, Tetrahedron, 1995, 51, 7301–7312.
7. V. M. Domingo, J. Castañer, J. Riera and A. Labarta, J. Org. Chem., 1994, 59, 2604–2607.
8. O. Elsner, D. Ruiz-Molina, J. Vidal-Gancedo, C. Rovira and J. Veciana, Nano Lett., 2001, 1, 117–120.
9. J. Guasch, X. Fontrodona, I. Ratera, C. Rovira and J. Veciana, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2013, 69, 255–257.
10. Y. Hattori, T. Kusamoto and H. Nishihara, Angew. Chem., Int. Ed. Engl., 2014, 53, 11845–11848.
11. M. Ballester, J. Castañer, J. Riera and J. Pujadas, J. Org. Chem., 1984, 49, 2884–2887.
12. M. Souto, J. Guasch, V. Lloveras, P. Mayorga, J. T. López Navarrete, J. Casado, I. Ratera, C. Rovira, A. Painelli and J. Veciana, J. Phys. Chem. Lett., 2013, 4, 2721–2726.
13. T. T. Tidwell, in Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, ed. R. G. Hicks, John Wiley & Sons, Ltd, Chichester, UK., Ontario, 2010, pp. 1–31.
14. D. Velasco, S. Castellanos, M. López, F. López-Calahorra, E. Brillas and L. Juliá, J. Org. Chem., 2007, 72, 7523–7532.
15. O. Neunhoeffer and H. Haase, Chem. Ber., 1958, 91, 1801–1805.
16. O. Armet, J. Veciana, C. Rovira, J. Riera, J. Castañer, E. Molins, J. Rius, C. Miravitlles, S. Olivella and J. Brichfeus, J. Phys. Chem., 1987, 91, 5608–5616.
17. H. A. Staab, C. Kuo-chen and A. Ruland, Chem. Ber., 1982, 115, 1765–1774.
18. M. Stein and A. Rieker, Tetrahedron Lett., 1975, 25, 2123–2126.
19. Y. Tian, K. Uchida, H. Kurata, Y. Hirao, T. Nishiuchi and T. Kubo, J. Am. Chem. Soc., 2014, 136, 12784–12793.
20. M. J. Sabacky, C. S. Johnson, R. G. Smith, H. S. Gutowsky and J. C. Martin, J. Am. Chem. Soc., 1967, 89, 2054–2058.
21. N. M. Shishlov, Russ. Chem. Rev., 2006, 75, 863–884.
22. I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303–349.
23. N. Bézière, C. Decroos, K. Mkhitaryan, E. Kish, F. Richard, S. Bigot-Marchand, S. Durand, F. Cloppet, C. Chauvet, M.-T. Corvol, F. Rannou, Y. Xu-Li, D. Mansuy, F. Peyrot and Y.-M. Frapart, Mol. Imaging, 2012, 11, 220–228.
24. N. Chattergoon, F. Martínez-Santiesteban, W. B. Handler, J. H. Ardenkjaer-Larsen and T. J. Scholl, Contrast Media Mol. Imaging, 2013, 8, 57–62.
25. B. Driesschaert, V. Marchand, P. Levêque, B. Gallez and J. Marchand-Brynaert, Chem. Commun., 2012, 48, 4049–4051.
26. B. Driesschaert, P. Levêque, B. Gallez and J. Marchand-Brynaert, Tetrahedron Lett., 2013, 54, 5924–5926.
27. M. C. Krishna, S. Matsumoto, H. Yasui, K. Saito, N. Devasahayam, S. Subramanian and J. B. Mitchell, Radiat. Res., 2012, 177, 376–386.
28. T. J. Reddy, T. Iwama, H. J. Halpern and V. H. Rawal, J. Org. Chem., 2002, 67, 4635–4639.
29. G. Y. Shevelev, O. A. Krumkacheva, A. A. Lomzov, A. A. Kuzhelev, O. Y. Rogozhnikova, D. V. Trukhin, T. I. Troitskaya, V. M. Tormyshev, M. V. Fedin, D. V. Pyshnyi and E. G. Bagryanskaya, J. Am. Chem. Soc., 2014, 136, 9874–9877.
30. A. A. Bobko, I. Dhimitruka, D. A. Komarov and V. V. Khramtsov, Anal. Chem., 2012, 84, 6054–6060.
31. I. Dhimitruka, A. A. Bobko, T. D. Eubank, D. A. Komarov and V. V. Khramtsov, J. Am. Chem. Soc., 2013, 135, 5904–5910.
32. A. A. Bobko, I. Dhimitruka, T. D. Eubank, C. B. Marsh, J. L. Zweier and V. V. Khramtsov, Free Radicals Biol. Med., 2009, 47, 654–658.
33. V. K. Kutala, N. L. Parinandi, R. P. Pandian and P. Kuppusamy, Antioxid. Redox Signal., 2004, 6, 597–603.
34. Y. Liu, F. A. Villamena, J. Sun, T. Wang and J. L. Zweier, Free Radicals Biol. Med., 2009, 46, 876–883.
35. C. Rizzi, A. Samouilov, V. K. Kutala, N. L. Parinandi, J. L. Zweier and P. Kuppusamy, Free Radicals Biol. Med., 2003, 35, 1608–1618.
36. S. Xia, F. A. Villamena, C. M. Hadad, P. Kuppusamy, Y. Li, H. Zhu and J. L. Zweier, J. Org. Chem., 2006, 71, 7268–7279.
37. G. Meenakshisundaram, E. Eteshola, A. Blank, S. C. Lee and P. Kuppusamy, Biosens. Bioelectron., 2010, 25, 2283–2289.
38. K. Münnemann, C. Bauer, J. Schmiedeskamp, H. W. Spiess, W. G. Schreiber and D. Hinderberger, Appl. Magn. Reson., 2008, 34, 321–330.
39. R. A. Wind and J. H. Ardenkjaer-Larsen, J. Magn. Reson., 1999, 141, 347–354.
40. J.-L. Muñoz-Gómez, I. Marín-Montesinos, V. Lloveras, M. Pons, J. Vidal-Gancedo and J. Veciana, Org. Lett., 2014, 16, 5402–5405.
41. C. Gabellieri, V. Mugnaini, J. C. Paniagua, N. Roques, M. Oliveros, M. Feliz, J. Veciana and M. Pons, Angew. Chem., Int. Ed. Engl., 2010, 49, 3360–3362.
42. D. Banerjee, J. C. Paniagua, V. Mugnaini, J. Veciana, A. Feintuch, M. Pons and D. Goldfarb, Phys. Chem. Chem. Phys., 2011, 13, 18626–18637.
43. G. D'Avino, L. Grisanti, J. Guasch, I. Ratera, J. Veciana and A. Painelli, J. Am. Chem. Soc., 2008, 130, 12064–12072.
44. L. Grisanti, G. D'Avino, A. Painelli, J. Guasch, I. Ratera and J. Veciana, J. Phys. Chem. B, 2009, 113, 4718–4725.
45. J. Guasch, L. Grisanti, M. Souto, V. Lloveras, J. Vidal-Gancedo, I. Ratera, A. Painelli, C. Rovira and J. Veciana, J. Am. Chem. Soc., 2013, 135, 6958–6967.
46. V. Lloveras, J. Vidal-Gancedo, T. M. Figueira-Duarte, J. F. Nierengarten, J. J. Novoa, F. Mota, N. Ventosa, C. Rovira and J. Veciana, J. Am. Chem. Soc., 2011, 133, 5818–5833.
47. S. Castellanos, F. López-Calahorra, E. Brillas, L. Juliá and D. Velasco, Angew. Chem., 2009, 48, 6515–6519.
48. Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095.
49. A. Rajca, S. Rajca and J. Wongsriratanakul, J. Am. Chem. Soc., 1999, 121, 6308–6309.
50. A. Rajca, J. Wongsriratanakul and S. Rajca, Science, 2001, 294, 1503–1505.
51. S. Rajca, A. Rajca, J. Wongsriratanakul, P. Butler and S. M. Choi, J. Am. Chem. Soc., 2004, 126, 6972–6986.
52. A. Rajca, K. Lu and S. Rajca, J. Am. Chem. Soc., 1997, 119, 10335–10345.
53. D. Maspoch, D. Ruiz-Molina and J. Veciana, J. Mater. Chem., 2004, 14, 2713–2723.
54. D. Maspoch, D. Ruiz-Molina, K. Wurst, N. Domingo, M. Cavallini, F. Biscarini, J. Tejada, C. Rovira and J. Veciana, Nat. Mater., 2003, 2, 190–195.
55. N. Roques, D. Maspoch, A. Datcu, K. Wurst, D. Ruiz-Molina, C. Rovira and J. Veciana, Polyhedron, 2007, 26, 1934–1948.
56. N. Crivillers, M. Mas-Torrent, J. Vidal-Gancedo, J. Veciana and C. Rovira, J. Am. Chem. Soc., 2008, 130, 5499–5506.
57. N. Crivillers, M. Mas-Torrent, C. Rovira and J. Veciana, J. Mater. Chem., 2012, 22, 13883–13890.
58. N. Crivillers, M. Paradinas, M. Mas-Torrent, S. T. Bromley, C. Rovira, C. Ocal and J. Veciana, Chem. Commun., 2011, 47, 4664–4666.
59. N. Crivillers, C. Munuera, M. Mas-Torrent, C. Simão, S. T. Bromley, C. Ocal, C. Rovira and J. Veciana, Adv. Mater., 2009, 21, 1177–1181.
60. M. Mas-Torrent, N. Crivillers, C. Rovira and J. Veciana, Chem. Rev., 2012, 112, 2506–2527.
61. F. Vera, M. Mas-Torrent, J. Esquena, C. Rovira, Y. Shen, T. Nakanishi and J. Veciana, Chem. Sci., 2012, 3, 1958–1962.
62. J. Veciana and I. Ratera, in Stable Radicals: Fundamentals and Applied Aspects of Odd-Electron Compounds, ed. R. G. Hicks, John Wiley & Sons, Inc., 2010, pp. 33–80.
63. J. Guasch, L. Grisanti, S. Jung, D. Morales, G. D'Avino, M. Souto, X. Fontrodona, A. Painelli, F. Renz, I. Ratera and J. Veciana, Chem. Mater., 2013, 25, 808–814.
64. C. Simão, M. Mas-Torrent, N. Crivillers, V. Lloveras, J. M. Artés, P. Gorostiza, J. Veciana and C. Rovira, Nat. Chem., 2011, 3, 359–364.
65. R. Frisenda, R. Gaudenzi, C. Franco, M. Mas-Torrent, C. Rovira, J. Veciana, I. Alcon, S. T. Bromley, E. Burzurí and H. S. J. van der Zant, Nano Lett., 2015, 15, 3109–3114.
66. G. N. Lewis, D. Lipkin and T. T. Magel, J. Am. Chem. Soc., 1944, 66, 1579–1583.
67. M. J. S. Dewar, J. Am. Chem. Soc., 1952, 74, 3345–3350.
68. F. C. Adam and S. I. Weissman, J. Am. Chem. Soc., 1958, 80, 2057–2059.
69. A. H. Maki, R. D. Allendoerfer, J. C. Danner and R. T. Keys, J. Am. Chem. Soc., 1968, 90, 4225–4231.
70. M. Karplus and G. K. Fraenkel, J. Chem. Phys., 1961, 35, 1312–1323.
71. J. A. Pople and D. L. Beveridge, J. Chem. Phys., 1968, 49, 4725–4726.
72. M. Karplus, J. Am. Chem. Soc., 1963, 85, 2870–2871.
73. K. Schreiner, A. Berndt and F. Baer, Mol. Phys., 1973, 26, 929–939.
74. R. Improta and V. Barone, Chem. Rev., 2004, 104, 1231–1253.
75. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Had and D. J. Fox, Gaussian-09. Revision-D.01, 2009.
76. F. L. Hirshfeld, Theor. Chem. Acc., 1977, 44, 129–138.
77. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
78. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
79. C. Trapp, C. S. Wang and R. Filler, J. Chem. Phys., 1966, 45, 3472.
80. W. Schlenk, T. Weickel and A. Herzenstein, Justus Liebigs Ann. Chem., 1910, 372, 1–20.
81. B. Kirste, W. Harrer and H. Kurreck, J. Am. Chem. Soc., 1985, 107, 20–28.
82. S.-H. Jang, P. Gopalan, J. E. Jackson and B. Kahr, Angew. Chem., Int. Ed. Engl., 1994, 33, 775–777.
83. D. Maspoch, L. Catala, P. Gerbier, D. Ruiz-Molina, J. Vidal-Gancedo, K. Wurst, C. Rovira and J. Veciana, Chem.–A Eur. J., 2002, 8, 3635–3645.
84. A. A. Kuzhelev, D. V. Trukhin, O. A. Krumkacheva, R. K. Strizhakov, O. Y. Rogozhnikova, T. I. Troitskaya, M. V. Fedin, V. M. Tormyshev and E. G. Bagryanskaya, J. Phys. Chem. B, 2015, 119, 13630–13640.
85. L. Teruel, L. Viadel, J. Carilla, L. Fajarí, E. Brillas, J. Sañé, J. Rius and L. Juliá, J. Org. Chem., 1996, 61, 6063–6066.
86. R. Filler, A. E. Fiebig and B. K. Mandal, J. Fluorine Chem., 2000, 102, 185–188.
87. A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36, 1627–1639.
88. J. Steinier, Y. Termonia and J. Deltour, Anal. Chem., 1972, 44, 1906–1909.
89. L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907.
90. M.-H. Jung, K. H. Song, K. C. Ko, J. Y. Lee and H. Lee, J. Mater. Chem., 2010, 20, 8016–8020.
91. D. Vonlanthen, A. Rudnev, A. Mishchenko, A. Käslin, J. Rotzler, M. Neuburger, T. Wandlowski and M. Mayor, Chem.–Eur. J., 2011, 17, 7236–7250.
92. M. G. Vergniory, J. M. Granadino-Roldan, A. Garcia-Lekue and L.-W. Wang, Appl. Phys. Lett., 2010, 97, 262114.
93. T. B. Martins, A. Fazzio and A. J. R. da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115413.
94. K. M. Tibbetts, T. Bohinski, K. Munkerup, M. Tarazkar and R. Levis, J. Phys. Chem. A, 2014, 118, 8170–8176.
95. T. Bohinski, K. M. Tibbetts, K. Munkerup, M. Tarazkar, D. A. Romanov, S. Matsika and R. J. Levis, Chem. Phys., 2014, 442, 81–85.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra19008h

---