Superhigh-speed unidirectional rotation of a carbon nanotube in a sheared fluid and its decoupled dynamics†
Abstract
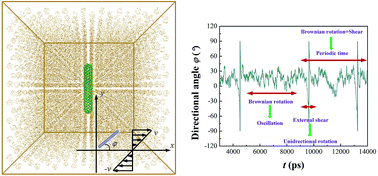
The superhigh-speed unidirectional rotation of a carbon nanotube (CNT) induced by a linear shear flow is investigated by molecular dynamics simulations. We have identified three rotational types: “continuous rotation”, “interrupted rotation” and “simple oscillation”, corresponding to a decreased number of unidirectional rotation circles over the same time duration. It was found that the unidirectional motion and oscillation respectively originate from the applied shear and rotary Brownian motion by a decoupled analysis of the rotational features. The angular velocity of the unidirectional motion is over one order of magnitude larger than the Jeffery's theory. To construct a CNT-based rotary motor with good performance, the high-speed unidirectional angular velocity can be achieved by carefully selecting the shear rate (e.g. ∼2 × 108 rad s−1 at 35 GHz) and the continuous rotating state can be approached by using a low aspect ratio carbon nanotube.

 Please wait while we load your content...
Please wait while we load your content...