Micron-scale rod-like scattering particles for light trapping in nanostructured thin film solar cells

Abstract

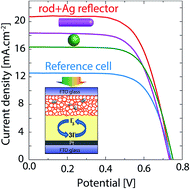
Spherical dielectric particles, nanofibers, and nanorods have been widely used as embedded scattering objects in nanostructured thin film solar cells. Here we propose micron-scale rod-like dielectric particles as a more effective alternative to the spherical ones for light trapping in thin film solar cells. The superior performance of these micro-rods is attributed to their larger scattering efficiency relative to the spherical particles as evidenced by full-wave optical calculations. Using a one-pot process, 1.7 μm-long bullet-shaped silica rods with 330 nm diameter are synthesized and their concentration in a N719-sensitized solar cell is optimized. A solar cell with an optimal concentration of rod-like particles delivers 8.74% power conversion efficiency (PCE), given the 6.33% PCE of the cell without any scattering particle. Moreover, a silver layer is deposited by chemical reduction of AgNO₃ (Tollens' process) on the rear-side of the counter electrode, and hence the PCE of the optimal cell reaches 9.94%, showing 14% extra improvement due to the presence of the silver back-reflector. The rod-like scattering particles introduced here can be applied to other sensitized solar cells such as quantum-dot and organometallic perovskite solar cells.

---

Introduction

Nanostructured thin film photovoltaic technologies,¹ such as dye,^2,3 quantum dot,⁴ and perovskite^5–10 sensitized solar cells have attracted significant interest due to their potentially lower production cost. These devices usually comprise a charge transfer sensitizer sandwiched between a mesoporous semiconductor, often a TiO₂, scaffold and a hole-transport layer. The sensitizers are dye molecules, quantum dots, or perovskite layers.

To improve the optical absorption efficiency in these devices a popular approach is to use a light scattering layer over the mesoporous sensitized film in order to prolong the light path length. This approach, however, is not appropriate for transparent solar cells applications. An alternative approach is to embed the scattering particles in the mesoporous scaffold to increase the optical path length.^11–18 This can be done by preparing a paste of semiconductor scaffold mixed with the scattering particles. This paste is then printed on a transparent conductive electrode followed by sensitization with the desired optical absorber material. The main advantage of this light trapping approach, in comparison to other techniques, is that it does not add any extra step to cell fabrication process.

In this context two class of scattering elements: (i) sub-micron particles and (ii) nanofibers (or nanowires)^19,20 have been largely used. Most of the sub-micron particles used so far have isotropic (nearly spherical) shape with dimensions chosen such that the particle supports optical resonance mode that enhance light scattering according to Mie theory.^21–24 Some examples of these scattering particles are voids,^16,25 TiO₂,²⁶ and SiO₂ (ref. 27) particles. Nanofibers and nanowires do not have light trapping effects as significant as sub-micrometre particles^19,20 due to their sub-wavelength cross sections. However their advantage is that they may facilitate charge transport through the dye sensitized layer.¹⁹

Here we propose and evaluate micron-scale rod-like silica particles as efficient embedded scattering elements for dye-sensitized solar cells (DSCs). Main advantage of these scattering particles, comparing to spherical ones, lies in their stronger light scattering efficiency. We synthesize 1.7 μm long silica rods of 330 nm diameter²⁸ and then mix them in the mesoporous layer of a N719-sensitized solar cell. The light scattering properties of these silica rods is studied using full-wave optical simulations. Then the concentration of these silica rods in a N719-sensitized solar cell is optimized using the results of a theoretical model²⁹ followed by experimental optimization. The device power conversion efficiency (PCE) is further improved by adding a silver layer on the rear-side of counter electrode (CE). This layer was deposited by chemical reduction of AgNO₃ using Sucrose (Tollens' process).

Experimental

Materials and reagents

Tetraethyl orthosilicate (TEOS, 98%; Merck), absolute ethanol (C₂H₆O, 99%; Merck), deionized water (DI water; >18.2 MΩ), ammonium hydroxide (NH₄OH, 25%; Merck), 1-pentanol (99%; Sigma-Aldrich), polyvinylpyrrolidone (PVP; average molecular weight Mn = 40.000; Sigma-Aldrich), silver nitrate (AgNO₃, 99%; Acros), sodium citrate dihydrate (HOC(COONa)(CH₂COONa)₂·2H₂O, 99%; Sigma-Aldrich), sucrose (C₁₂H₂₂O₁₁; Merck), potassium hydroxide (KOH, Merck), titanium(IV) chloride (TiCl₄, >99%; Merck), chloroplatinic acid (H₂PtCl₆, 99.95%; Merck), fluorine-doped tin oxide (FTO; Dyesol), cis-diisothiocyanato-bis(2,2′-bipyridyl-4,4′-dicarboxylato)ruthenium(II)bis(tetrabutylammonium) dye (N719; Dyesol), guanidinium thiocyanate (GSCN; Merck), guanidinium thiocyanate (GSCN; Merck), and a commercial TiO₂ paste (PST-20T, composed of 20 nm TiO₂ nanoparticles; Sharif Solar) were used without further purification.

Synthesis of silica particles

Monodisperse silica spheres were synthesized using the standard Stöber method³⁰ where 25 mL DI water, 62 mL ethanol, and 9 mL NH₄OH were mixed in a flask and stirred for 30 min until a homogeneous solution was formed. Then 4.5 mL TEOS was rapidly added and the solution was stirred for 3 h at 20 °C. The resulting white colloidal suspension was filtered, washed with DI water and absolute ethanol 5 times, and then dried at 60 °C for 24 h.

Rod-like silica particles were synthesized using a one-pot method.²⁸ In a closed 25 mL bottle, 1 g PVP was dissolved in 10 mL 1-pentanol by sonication for 2 h. When all PVP was dissolved, an aqueous solution of 1 mL absolute ethanol, 0.28 mL DI water, and 0.07 mL of 0.18 M sodium citrate dihydrate was added. The flask was shaken by hand to mix the content. Then 0.23 mL NH₄OH was added, flask was shaken again, then 0.1 mL TEOS was added to the solution. After shaking again, the bottle was left to rest at a 20 °C for 5 h. The resulting white colloidal solution was filtered, washed with DI water and absolute ethanol 5 times, and then dried at 60 °C for 24 h.

DSC device processing

Colloidal solution of silica particles in ethanol with different concentrations were mixed with standard TiO₂ paste (PST-20T) and were dispersed by sonication. The entire solution was stirred for 3 h after sonication. Then ethanol was removed by rotary evaporator to obtain a viscous paste of mesoporous TiO₂ nanoparticles with a defined concentration of silica particles.

FTO substrates were immersed in 40 mM TiCl₄ aqueous solution at 70 °C for 30 min and rinsed with DI water and ethanol. Nearly 11 μm-thick photoanode films were prepared by five-step screen-printing of the TiO₂ paste containing silica particles on these TiCl₄-treated FTO substrates. Then these films were annealed in air in 3 steps; 325 °C for 5 min, 375 °C for 5 min, and finally 450 °C for 45 min. Photoanode films were treated with 40 mM TiCl₄ aqueous solution once more followed by annealing at 500 °C for 30 min. After cooling down, the layers were immersed in N719 dye solution (0.2 mM) for 24 h, and then rinsed with acetonitrile. CE of 1 cm² surface area were fabricated by coating FTO substrates with one drop of 5 mM H₂PtCl₆ ethanolic solution followed by drying and then annealing at 450 °C for 15 min.

The dye-sensitized photoanodes were assembled with Pt CEs into sandwich-type cell by heating at 120 °C using a hot-melt film (Surlyn) as the spacer between the electrodes. The electrolyte solution was injected into the cell via vacuum backfilling through a hole created in CE. The electrolyte solution contains 1.0 M 1-butyl-3-methylimidazolium iodide, 0.03 M I₂, 0.05 M LiI, 0.1 M GSCN and 0.5 M TBP in acetonitrile and valeronitrile solvent mixture (85 : 15 volumetric ratio). Finally, the hole was sealed using additional Surlyn and a cover glass.

Deposition of silver layer

A silver reflective layer was applied on the rear-side of the CE using the Tollens' process.^31,32 The deposition process involves the following steps. Ammonium hydroxide was slowly dropped into 10 mL of a 0.6 M AgNO₃ solution. The solution initially turned turbid and then became transparent. A few drops of a 1.2 M KOH solution were added to this transparent solution till the solution turned dark brown. The solution was made transparent again by adding ammonium hydroxide. The Pt layer on FTO/glass substrate was masked by two layers of Scotch tape and then the FTO was immersed in this solution. 10 mL of 0.8 M sucrose aqueous solution was rapidly added to the solution to reduce AgNO₃ to Ag on the glass surface. The reaction was allowed to proceed for 1 h under slow stirring to obtain a uniform deposition of silver onto the glass. After Ag deposition, the Scotch tape was removed and then the electrode was thoroughly rinsed with ethanol to remove the tape residues from the CE surface.

Characterization

Scanning electron microscopy (SEM) was carried out using a Tescan (Czech Republic) Vega II XMU microscope. Diffuse reflection, transmittance, and absorptance measurements were carried out using an Avantes photo-spectrometer (Avaspec-2048TEC) equipped with an integrating sphere. Current–voltage plots were recorded using a Palmsens potentiostat under simulated AM1.5G light (Sharif Solar). Incident photon to current conversion efficiency (IPCE), measured using a setup consisting of a Jarrel-Ash monochromator, a 100 W halogen lamp and a calibrated photodiode (Thorlabs). Dye loading on mesoporous TiO₂ films was measured by desorption of dye through soaking dye-sensitized TiO₂ films in 0.1 M NaOH aqueous solution. Concentration of desorbed dyes was estimated from optical absorption of the 0.1 M NaOH aqueous solution containing the desorbed dye molecules.

Results and discussion

Fig. 1a shows the schematic of a DSC device with embedded silica rods in which the rods can have different orientation relative to the interfaces of the FTO and the electrolyte. The rods we study here are bullet-shaped meaning that they are flat at one end and round at the other end, which can be obtained by a one-pot quasi-vapour–liquid–solid (VLS) process.²⁸ The refractive index of silica rods is 1.44, embedded in a mesoporous TiO₂ medium with complex effective index of 1.966 + ik_x.³³ Therefore these particles function as void scattering elements, due to the lower refractive index of silica relative to the surrounding medium.³⁴

Fig. 1 (a) A schematic illustrating a DSC device with silica rods randomly distributed in the dye sensitized layer. ((b) and (c)) Schematic of a silica rod and its optical model. (d) Scattering cross section (C_sca) of rod-like (diameter of 330 nm and 1.7 μm long) and spherical (630 nm) silica particles as function of the wavelength. (e) Electric field amplitude of the scattered λ = 700 nm light from silica rods under TE-polarized light incidence.

In light trapping using scattering particles it is common to use the scattering cross-section (C_sca) of individual particles as a measure of the effectiveness of the light trapping process.²⁵ In dielectric particles the scattering is particularly strong due the optical resonances in these particles.³⁴ The scattering properties of individual rod-like and spherical particles can be described analytically with Mie theory. Although application of Mie theory to spheres is straightforward, the rod-like particles need to be treated as finite cylindrical resonators.^35–37 In radial direction, resonance modes of these particles can be expressed by Bessel functions from Mie theory. In axial direction, the rod can be viewed as a Gires–Tournois etalon^38,39 with partially reflecting mirrors at both ends of the rod formed by Fresnel reflectance of the silica/mesoporous TiO₂ interface. The resonance condition of the rods is therefore defined by the length of the rod at which the phase difference in a round-trip along the rod axis is a multiple of 2π (Fig. 1b).

The basic design rules of rod-like particles are as follows: (1) the rod diameter needs to be large enough to support Mie resonance modes in radial direction, and (2) the rod needs to be long enough to have resonance modes set by the Gires–Tournois etalon resonance condition. In fact number and density of the resonance modes of the rods can be increased by simply increasing the rod length.

In light trapping using embedded scattering particles the C_sca/V_sca where V_sca is the volume fraction of the scattering elements in the mesoporous layer, need to be maximized.²⁵ To increase the number of resonance modes of the sphere one needs to increase the sphere radius (a) leading the cubic increase the volume because V_sp ∝ a³. Conversely prolonging the rod leads to smaller increase in volume because V_rod ∝ L where L is the rod length. This feature constitutes the main advantage of rods over spheres.

To better illustrate the superior light scattering by silica rods relative to spheres we model light interaction with individual rod-like and spherical silica particles embedded in a N719-sensitized mesoporous TiO₂ medium. We basically calculate the scattered light from the particles under plane-wave incidence. We numerically solve the full-wave Maxwell equations over the entire geometry under the incidence of a plane wave of Ē(r̄) = r̂ exp(−jk̄.r̄). The simulation was carried out using Comsol Multiphysics, which uses a finite element method for solving Maxwell equations.^23,24

In the modelling process, the total electromagnetic field, Ē_t = Ē_i + Ē_s, is calculated which is the summation of the incident (Ē_i) and scattered fields (Ē_s). We calculate the scattering cross section, C_sca, of the particle at different angles of θ (only for rods) and at different wavelengths. C_sca is defined as C_sca = (1/P_inc) × ∫S⃑.da⃑, where P_inc is the power of the incident light and S⃑ = 1/2(E⃑ × H⃑*) is the Poynting vector describing the outgoing electromagnetic power per unit area.¹⁴ The integration is carried out over a closed surface surrounding the particle.

The polarization and angle of the incident wave are not important for spherical particles due to their geometrical symmetry. This is not the case for the rod-like particles. Therefore for rod-like particles we carried out the simulations once under transverse electric (TE) and once under transverse magnetic (TM) polarized light incidence at three different angles of θ = 0, 45, and 90° with respect to the rod axis. Then we took the average of all the C_sca values as the C_sca of rod-like particles.

We model a silica sphere with diameter of 630 nm and a silica rod with diameter of 330 nm and length of 1.7 μm. Such rod dimension is chosen because longer rods tend to bend and break during the particles centrifuging steps (Fig. S1 of the ESI†). The 630 nm sphere is chosen because it has the same volume as the silica rod does. In the sensitized layer, silica rods can have different orientations relative to incident light; hence they interact with incident light at different angles. Therefore in our simulations we consider light incidence on rods at different angles (θ) as defined in Fig. 1c. The C_sca spectra of the silica rod were calculated at θ = 0, 45, and 90° (Fig. S2 of the ESI†) and then the average of the three is reported in Fig. 1d. Over a large fraction of the wavelength range of study, C_sca of the rod is larger than that of the sphere showing stronger light scattering by the rods. The peaks observed in the C_sca spectra can be attributed to the optical resonances taking place inside the particles. Moreover, the C_sca spectra of rods with different length and diameter, shown in Fig. S3 of the ESI,† further confirm that the scattering cross-section of these rod-like particles is decreased if the length or diameter of the silica rod becomes smaller.

Fig. 1e show distribution of electric field amplitude of λ = 700 nm light scattered from a silica rod under TE-polarized light incidence. In these graphs the peaks of electric field amplitude within the rods illustrate the optical resonances taking place within these particles.

Fig. 2a shows the overall SEM image of the silica rods illustrating that rods of 1–2 μm length with several hundreds of nanometres diameter are formed. As shown in the higher magnification SEM image in Fig. 2b, typically, these rods are flat on one end and round at the other end, i.e. they are bullet-shape. The size distribution of the rods is rather narrow because the very small rods are removed from the solution though multiple centrifuge processes (Fig. S4 of the ESI†). Fig. 2c and d show the SEM images of the mesoporous TiO₂ electrodes containing 7 vol% silica rods illustrating the presence of well-dispersed silica rods within the layer. Thickness of the layers was estimated from the SEM image to be 11 ± 0.5 μm (Fig. S5 of the ESI†).

Fig. 2 ((a) and (b)) Overall and (b) high-magnification SEM images of silica micro-rod synthesized in this work. (c) Top-view and (d) cross-section images of mesoporous TiO₂ layers with 330 nm × 1.7 μm silica rods embedded.

Photovoltaic (PV) performance of the cells with different photoanode structures was measured on the masked area of 25 mm² under simulated AM1.5G illumination. Fig. 3a shows the current density versus voltage (J–V) curves of the reference cell and the DSCs with different concentrations of silica rods. Cells PV performance data along with the density of adsorbed dyes (N_dye) are summarized in Table 1. PV data and the J–V curve of a similar DSC with the optimal 6 vol% of 450 nm silica spheres²⁹ are also presented for comparison.

Fig. 3 Panel ((a), (b) and d)) show the current density versus voltage (J–V) curve, IPCE spectra, and optical absorbance spectra of DSCs with different concentrations of silica rods, the references DSC, and the DSC with optimized 6 vol% concentration of 450 nm silica spheres. Panel (c) shows the IPCE enhancement of the cells with optimized concentration of the scattering particles relative to the IPCE of the reference cell.

Table 1 Photovoltaic properties of the DSCs prepared with different concentration of silica rods, the references DSC cell (T), DSC with 7 vol% rodlike particles along with an Ag rear-reflector, and the DSC with optimized concentration of silica spheres

DSC composition	Number of dye molecule (cm^−2) × 10^15	JSC (mA cm^−2)	VOC (V)	FF (%)	PCE (%)
Ref. (no. particle)	16.53	12.52	0.744	0.68	6.33
5 vol% silica rods	15.37	16.00	0.740	0.66	7.81
6 vol% silica rods	15.17	17.28	0.735	0.64	8.12
7 vol% silica rods	14.73	18.29	0.735	0.65	8.74
8 vol% silica rods	14.21	15.63	0.735	0.65	7.47
10 vol% silica rods	13.54	14.89	0.735	0.65	7.11
6 vol% silica spheres	15.48	16.56	0.744	0.65	8.01
7 vol% silica rods/Ag layer on rear-side of CE	14.73	20.70	0.739	0.65	9.94

---

To find the optimal concentration of rod-like silica particles we explored the 5–10 vol% range for concentrations. We obtained this range from the design methods that has previously been proposed for embedded spherical dielectric scattering particles.²⁹ The PCE of the cell with 7 vol% silica rods reached 8.74% and it is the largest among all different silica rods concentrations. This shows 38% improvement relative to the 6.33% PCE of the reference cell and it is significantly larger than 8.01% PCE that is obtained using an optimum concentration of 450 nm silica spheres.²⁹ We should mention that the enhancement in PCE is obtained despite the relatively smaller dye adsorption in the cells with embedded scattering particles (Table 1). Fill-factor (FF) of the cells with scattering particles is slightly lower than the reference cell. However among different particle concentrations FF and V_OC are not significantly influenced. Therefore enhancement of the cells' PCE is due to the improvement in cells short-circuit current density (J_SC).

As shown in Table 1 and Fig. 3a, the cell containing 7 vol% of silica rods show J_SC of 18.29 mA cm⁻², compared to 16.56 and 12.52 mA cm⁻² obtained in the cell with 6 vol% of silica spheres and the reference cell, respectively. The amount of dye molecules adsorbed in the cell with 7 vol% of silica rods, in comparison to the one with 6 vol% of silica spheres, is slightly lower, whereas its J_SC is 10.44% larger. This is strong evidence demonstrating that the enhancement in J_SC, is mainly due to the more effective light scattering by silica rods relative to silica spheres.

Light trapping effects are better understood from incident photon-to-electron conversion efficiency (IPCE) spectra. IPCE is related to the J_SC through . Fig. 3b shows IPCE spectra of DSCs with different concentrations of silica particles together with IPCE of the reference cell. The impact of silica particles can be made better visible through the spectra of IPCE enhancement in DSCs containing either 7 vol% silica rods or 6 vol% silica spheres relative to the IPCE of the reference cell (Fig. 3c). The presence of the scattering particles improves the IPCE over the entire wavelength range confirming that the effect is a broadband effect. This enhancement is particularly strong at λ > 650 nm because in this wavelength range the optical absorption of the N719-sensitized layer is weak.

Absorbance spectra of the reference cell, the DSCs with either 7 vol% of silica rods or 6 vol% of silica spheres are illustrated in Fig. 3d. Absorbance is defined as −log(transmittance). In agreement with IPCE spectra, it shows that enhancements of optical absorption in the cells are broadband. Moreover it reconfirms that the cells performance enhancement and IPCE enhancement are solely due to improved light trapping in the cell. These conclusions are also supported by diffuse transmittance, diffuse reflectance and the absorbance measurements conducted on the layer before and after dye-loading. (Fig. S6 and S7 of the ESI†).

To further improve the PCE of the cell with 7 vol% of silica rods, a silver layer is applied on the rear-side of the CE as the back-reflector (the inset schematic of Fig. 4a). A nearly 40 nm-thick silver layer was deposited on the rear side of CE by Tollens' process. The presence of this layer improved the J_SC and PCE of the cell with 7 vol% silica rods to 20.70 mA cm⁻² and 9.94%, respectively (Fig. 4a and Table 1).

Fig. 4 (a) J–V data of DSC with 7 vol% silica rods before and after applying a silver layer to the rear-side of CE (the inset schematic). (b) IPCE and IPCE enhancement spectra of the cell with 7 vol% of silica rods and an Ag back-reflector. The enhancement is calculated relative to the IPCE of the reference cell.

Fig. 4b shows the IPCE and IPCE enhancement spectra of 7 vol% silica rods DSCs with silver back-reflector. The presence of this layer improves the IPCE over the entire wavelength range. The IPCE enhancement is stronger in the longer wavelength range (650–800 nm) where the optical absorption coefficient of the N719-sensitized layer is weak. This highlights an important feature of embedded scattering particles that the cell remains transparent and still other light trapping methods like back-reflector layer can be applied to further enhance the efficiency.

Conclusions

We showed that, due to their anisotropic shape, micron-scale silica rods (330 nm × 1.7 μm) embedded in dye-sensitized layer of a DSC device provide superior light trapping relative to silica spheres. This enhanced light trapping is related to larger scattering efficiency of rods relative to spheres. Full-wave simulation of light scattering with silica rods confirmed the stronger light scattering of silica rods relative to silica spheres. These silica rods can be viewed as optical resonators in which the wavelength and the density of resonance modes can be tuned by adjusting the rod dimension. This give a significant freedom in optimizing the scattering properties since the scattering is maximal at resonance. We optimized concentration of silica rods and achieved 8.74% PCE in an 11 μm-thick DSC with 7 vol% of silica rods. This showed 38% improvement relative to a similar cell without silica rods. We showed that application of a silver layer on the rear-side of the CE by Tollens' process further improves the cell PCE to 9.94%.

Notes and references

1. M. C. Beard, J. M. Luther and A. J. Nozik, Nat. Nanotechnol., 2014, 9, 951–954.
2. B. E. Hardin, H. J. Snaith and M. D. McGehee, Nat. Photonics, 2012, 6, 162–169.
3. B. O'Regan and M. Grätzel, Nature, 1991, 353, 737–740.
4. Y. L. Lee and Y. S. Lo, Adv. Funct. Mater., 2009, 19, 604–609.
5. G. E. Eperon, V. M. Burlakov, P. Docampo, A. Goriely and H. J. Snaith, Adv. Funct. Mater., 2014, 24, 151–157.
6. V. Gonzalez-Pedro, E. J. Juarez-Perez, W. S. Arsyad, E. M. Barea, F. Fabregat-Santiago, I. Mora-Sero and J. Bisquert, Nano Lett., 2014, 14, 888–893.
7. M. Grätzel, Nat. Mater., 2014, 13, 838–842.
8. N. J. Jeon, J. H. Noh, W. S. Yang, Y. C. Kim, S. Ryu, J. Seo and S. I. Seok, Nature, 2015, 517, 476–480.
9. M. A. Green, A. Ho-Baillie and H. J. Snaith, Nat. Photonics, 2014, 8, 506–514.
10. S. D. Stranks, P. K. Nayak, W. Zhang, T. Stergiopoulos and H. J. Snaith, Angew. Chem., Int. Ed., 2015, 54, 3240–3248.
11. A. Dabirian and N. Taghavinia, RSC Adv., 2013, 3, 25417–25422.
12. S. Dadgostar, F. Tajabadi and N. Taghavinia, ACS Appl. Mater. Interfaces, 2012, 4, 2964–2968.
13. T. G. Deepak, G. S. Anjusree, S. Thomas, T. A. Arun, S. V. Nair and A. Sreekumaran Nair, RSC Adv., 2014, 4, 17615–17638.
14. N. Ghazyani, M. H. Majles Ara, F. Tajabadi, A. Dabirian, R. Mohammadpour and N. Taghavinia, RSC Adv., 2014, 4, 3621–3626.
15. J. Kim, H. Lee, D. Y. Kim and Y. Seo, Adv. Mater., 2014, 26, 5192–5197.
16. T. T. Trang Pham, T. Bessho, N. Mathews, S. M. Zakeeruddin, Y. M. Lam, S. Mhaisalkar and M. Gratzel, J. Mater. Chem., 2012, 22, 16201–16204.
17. Q. Xu, F. Liu, Y. Liu, K. Cui, X. Feng, W. Zhang and Y. Huang, Sci. Rep., 2013, 3, 2112.
18. Q. Zhang, D. Myers, J. Lan, S. A. Jenekhe and G. Cao, Phys. Chem. Chem. Phys., 2012, 14, 14982–14998.
19. E. Ghadiri, N. Taghavinia, S. M. Zakeeruddin, M. Gratzel and J. E. Moser, Nano Lett., 2010, 10, 1632–1638.
20. M. Rahman, F. Tajabadi, L. Shooshtari and N. Taghavinia, ChemPhysChem, 2011, 12, 966–973.
21. M. L. Brongersma, Y. Cui and S. Fan, Nat. Mater., 2014, 13, 451–460.
22. Y. Yu, V. E. Ferry, A. P. Alivisatos and L. Cao, Nano Lett., 2012, 12, 3674–3681.
23. A. Dabirian, J. Opt., 2014, 16, 075001.
24. D. Danaei, R. Saeidi and A. Dabirian, RSC Adv., 2015, 5, 11946–11951.
25. S. Hore, P. Nitz, C. Vetter, C. Prahl, M. Niggemann and R. Kern, Chem. Commun., 2005, 2011–2013.
26. Y. Bai, Z. Xing, H. Yu, Z. Li, R. Amal and L. Wang, ACS Appl. Mater. Interfaces, 2013, 5, 12058–12065.
27. Y. Rho, M. Wanit, J. Yeo, S. Hong, S. Han, J. H. Choi, W. H. Hong, D. Lee and S. H. Ko, J. Phys. D: Appl. Phys., 2012, 46, 024006.
28. A. Kuijk, A. van Blaaderen and A. Imhof, J. Am. Chem. Soc., 2011, 133, 2346–2349.
29. M. M. Byranvand, A. Dabirian, A. N. Kharat and N. Taghavinia, RSC Adv., 2015, 5, 33098–33104.
30. W. Stöber, A. Fink and E. Bohn, J. Colloid Interface Sci., 1968, 26, 62–69.
31. Y. Yin, Z.-Y. Li, Z. Zhong, B. Gates, Y. Xia and S. Venkateswaran, J. Mater. Chem., 2002, 12, 522–527.
32. N. Sharifi and N. Taghavinia, Mater. Chem. Phys., 2009, 113, 63–66.
33. A. Dabirian and N. Taghavinia, ACS Appl. Mater. Interfaces, 2015, 7, 14926–14932.
34. S. A. Mann, R. R. Grote, R. M. Osgood and J. A. Schuller, Opt. Express, 2011, 19, 25729–25740.
35. H. Ditlbacher, A. Hohenau, D. Wagner, U. Kreibig, M. Rogers, F. Hofer, F. R. Aussenegg and J. R. Krenn, Phys. Rev. Lett., 2005, 95, 257403.
36. T. Nobis, E. M. Kaidashev, A. Rahm, M. Lorenz and M. Grundmann, Phys. Rev. Lett., 2004, 93, 103903.
37. M. E. Tobar and A. G. Mann, IEEE Trans. Microwave Theory Tech., 1991, 39, 2077–2082.
38. F. Gires and P. Tournois, C. R. Hebd. Seances Acad. Sci., 1964, 258, 6112–6615.
39. M. A. Kats, R. Blanchard, P. Genevet and F. Capasso, Nat. Mater., 2013, 12, 20–24.

---

Footnote

† Electronic supplementary information (ESI) available: C_sca of rods at different angles (average of TE- and TM-polarized light incidence), SEM images of silica rods, diffuse reflectance and diffuse transmittance spectra of the layers. See DOI: 10.1039/c5ra18349a

---