Structure–property relationships of aromatic polyamides and polythioamides: comparative consideration with those of analogous polyesters, polythioesters and polydithioesters†
Masayuki Nagasawa,
Tatsuya Ishii,
Daisuke Abe and
Yuji Sasanuma*
Department of Applied Chemistry and Biotechnology, Graduate School and Faculty of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan. E-mail: sasanuma@faculty.chiba-u.jp; Fax: +81-43-290-3394; Tel: +81-43-290-3394
First published on 22nd October 2015
Abstract
Conformational characteristics and configurational properties of aromatic polyamides and polythioamides, analogues of common aromatic polyesters such as poly(ethylene terephthalate) and poly(trimethylene terephthalate), have been investigated via NMR experiments and molecular orbital calculations on model compounds, and the refined rotational isomeric state calculations for the polymers. The polyamides and polythioamides were actually synthesized and characterized in terms of solubility, molecular weight, crystallinity, thermal transition, and thermal stability. Herein, the experimental results are discussed mainly from the viewpoint of the conformational characteristics and compared with those obtained from analogous aromatic polyesters, polythioesters, and polydithioesters to reveal the effects of the heteroatoms O, S, and NH included in the backbone on the polymer structures and properties.
1 Introduction
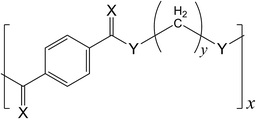
In previous studies, we investigated the conformational characteristics and configurational properties of aromatic polyesters1–3 and designed, synthesized, and characterized novel aromatic polythioesters and polydithioesters4,5 (Fig. 1). The polyesters have been produced on a large scale worldwide, whereas the polydithioesters have been quite recently introduced. Each polymer has its own conformational characteristics, higher-order structures, physical properties, and functions; therefore, one may clearly distinguish a polymer from others, search for the synthetic scheme and molding process suitable for the polymer itself, and explore its applications. On the other hand, molecular designers may consider, for example, the aromatic polymers shown in Fig. 1 as analogues. This is because the polymers have similar skeletal structures and differ from each other only in the combination of two heteroatoms, X and Y.This article deals mainly with four analogues, i.e., aromatic polyamides and polythioamides of y = 2 and 3 (Fig. 1 and 2): polyamides 2T (PA2T) and 3T (PA3T); polythioamides 2T (PTA2T) and 3T (PTA3T). In the present study, we have employed the following investigative approaches: (1) molecular orbital (MO) calculations and NMR and single crystal X-ray diffraction experiments on small model compounds to reveal conformational characteristics of the polymers through the models (Fig. 3); (2) the refined rotational isomeric state (RIS) calculations6–8 for the polymeric chains to quantify their configurational properties and thermodynamic functions; (3) synthesis and characterization of the polymers to investigate their physical properties. Herein, the structures and properties of the aromatic polyesters, polythioesters, polydithioesters, polyamides, and polythioamides are compared and discussed as functions of X, Y, and y.
2 Methods
In general, the following experimental setup was employed here: a three- or four-necked flask (under a stream of dry nitrogen) equipped with a mechanical or magnetic stirrer, a dropping funnel, and a Dimroth condenser connected to a calcium chloride drying tube.2.1 Synthesis of N,N′-ethylenedibenzamide (2DBA)9
Benzoyl chloride (5.6 g, 4.6 mL, 40 mmol), dissolved in dichloromethane (100 mL), was added dropwise to ethylenediamine (13 g, 14 mL, 220 mmol) and dichloromethane (300 mL) stirred in the flask dipped in ice water, and then the mixture was stirred at room temperature for 8 h. A white precipitate was collected using suction filtration, washed with distilled water, dried under a reduced pressure at 40 °C, recrystallized from methanol, and dried in vacuo at 40 °C to yield 2DBA (2.9 g).2.2 Synthesis of N,N′-trimethylenedibenzamide (3DBA)10
Benzoyl chloride (12.0 mL, 103 mmol) was added dropwise to 1,3-propane diamine (3.4 mL, 41 mmol) and aqueous sodium hydroxide (0.100 mol L−1, 61.5 mL), and then the mixture was stirred at 0 °C for 1 h. After distilled water (100 mL) was added, the solution was stirred at room temperature overnight. A white precipitate was collected using suction filtration, rinsed with distilled water, dried under reduced pressure at 40 °C, recrystallized from a mixed solvent of ethanol and toluene (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume), and dried in vacuo at 40 °C to yield 3DBA (3.1 g).
1 in volume), and dried in vacuo at 40 °C to yield 3DBA (3.1 g).
2.3 Synthesis of N,N′-ethylenedibenzothioamide (2DBTA)11
The 2DBA (1.0 g, 3.7 mmol) prepared as above and Lawesson’s reagent (1.8 g, 4.5 mmol) were dissolved in toluene (20 mL) and stirred at 110 °C for 8 h. A yellow precipitate was collected using suction filtration, washed with toluene, dried under a reduced pressure at 40 °C, recrystallized from ethanol, and dried in vacuo at 40 °C to yield 2DBTA (0.89 g).2.4 Synthesis of N,N′-trimethylenedibenzothioamide (3DBTA)
In place of 2DBA, 3DBA was used and treated as described above; however, the crude product was purified differently. The reaction mixture was concentrated and underwent column chromatography using chloroform as the eluent. Yellowish fractions (retardation factor Rf = 0.3) were collected, concentrated, dried under reduced pressure at 40 °C, recrystallized twice from a mixed solvent of ethyl acetate and diethyl ether (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume), and dried in vacuo to give 3DBTA (yield 48%).
1 in volume), and dried in vacuo to give 3DBTA (yield 48%).
2.5 Synthesis of polyamides 2T (PA2T) and 3T (PA3T)
These two polyamides were synthesized by interfacial polycondensation of terephthaloyl chloride with ethylenediamine (PA2T) or 1,3-propanediamine (PA3T) according to Shashoua and Eareckson.122.6 Synthesis of polythioamides 2T (PTA2T) and 3T (PTA3T)13
The synthetic procedure is common to PTA2T and PTA3T except for the starting material: PTA2T, ethylenediamine; PTA3T, 1,3-propanediamine. Sulfur powder (1.6 g, 50 mmol), N,N′-dimethylacetamide (70 mL, 0.76 mol), molecular sieve A4 (10 g), and ethylenediamine or 1,3-propanediamine (20 mmol) were mixed and stirred for 1 h, and then terephthalaldehyde (2.7 g, 20 mmol), dissolved in N,N′-dimethylacetamide (30 mL), was added dropwise. The solution was heated at 120 °C for 6 h. After being cooled down to room temperature, the reaction mixture was poured into methanol to yield a precipitate, which was collected by filtration, extracted with N,N′-dimethylformamide, and poured into methanol again. The precipitate was collected and rinsed with chloroform, carbon disulfide, and distilled water. The purification was performed once again and dried in vacuo at 40 °C to yield PTA2T (22%) or PTA3T (41%).According to the proposed reaction mechanism,13 water should preferably be eliminated as much as possible during the polymerization; therefore, we put the molecular sieve A4 in the flask so that it would adsorb water and promote the reaction.
2.7 Synthesis of N,N′-dibenzylideneethylenediamine (DB2A) and N,N′-dibenzylidene-1,3-propanediamine (DB3A)14
Ethylenediamine or 1,3-propanediamine (9.7 mmol) was added to distilled water (30 mL) including benzaldehyde (2.2 mL, 21 mmol), and the mixture was stirred for 2 h to separate into aqueous and oily organic layers. The latter phase was recrystallized from n-hexane to generate white crystals, which were collected using suction filtration and dried in vacuo to yield DB2A (29%) or DB3A (35%).2.8 Solution NMR
1H (13C) NMR spectra were recorded at 500 MHz (125.7 MHz) using a JEOL JNM-ECA500 spectrometer equipped with a variable temperature controller at the Center for Analytical Instrumentation of Chiba University. The sample temperatures were 25, 35, 45, and 55 °C and maintained within ±0.1 °C fluctuations. Free induction decays were accumulated 64 (256) times. The pulse duration, data acquisition time, and recycle delay were typically 5.7 (3.3) μs, 3.5 (0.8) s, and 5.0 (2.0) s, respectively. In the 13C NMR experiments, a gated decoupling technique was used under the conditions written in the above parentheses. Because of the poor solubilities of the model compounds, only dimethyl-d6 sulfoxide (DMSO-d6) was used as the NMR solvent. The NMR spectra were simulated with the gNMR program15 to determine the chemical shifts and coupling constants.2.9 Solid state NMR
High-resolution 13C cross polarization (CP) NMR experiments with magic angle spinning (MAS), abbreviated as CP/MAS, were carried out at a resonance frequency of 150.9 MHz using a JEOL JNM-ECA 600 spectrometer at the Center for Analytical Instrumentation of Chiba University. The sample was packed in a silicon nitride rotor of 4 mm in diameter and underwent a CP/MAS measurement under the following conditions: 1H decoupler pulse duration, 3.5 μs; contact time, 3.0 ms; relaxation delay, 20 s; accumulation, 300 times; spinning rate, 17.0 kHz.2.10 Solubility test
Solubilities of PA2T, PTA2T, PA3T, and PTA3T were examined for a number of solvents. The powdered polymer (2.0 mg) and a given solvent (1.0 mL) were mixed (solute concentration was 2.0 g L−1) and stirred at room temperature. When the powder did not completely dissolve in the solvent at room temperature, the mixture was heated up to a temperature close to the boiling point of the solvent with agitation. When the polymer still remained undissolved, the solubility was judged to be insoluble.2.11 Size exclusion chromatography (SEC)
Since PTA2T and PTA3T are soluble in some polar solvents, SEC measurements were conducted for these two polymers by Japan Analytical Industry Co., Ltd. (JAI) using a JAI LC9110 NEXT Recycling Preparative HPLC coupled with JAIGEL-3H-AF and 4H-AF columns. Each polythioamide (5.0 mg) was dissolved in N,N-dimethylformamide (DMF, 1.0 mL) containing LiBr (20 mM), purified with a 0.45 μm membrane filter, and injected into the HPLC. The LiBr additive prevents the polymer from aggregating, and the elute was fed at a rate of 1.0 mL min−1. The columns were calibrated with polystyrene standards of molecular weights (MPS) = 370, 2032, 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 100
000, 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and 600
000, and 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 according to a cubic polynomial: log
000 according to a cubic polynomial: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MPS = Aτ3 + Bτ2 + Cτ + D, where A, B, C, and D are empirical parameters and τ is the elution time. JAI RI-700 NEXT and JAL UV-370 (at 268 nm) detectors were used. The number-average (Mn) and weight-average (Mw) molecular weights were calculated using the built-in software JAI JDS-300.
MPS = Aτ3 + Bτ2 + Cτ + D, where A, B, C, and D are empirical parameters and τ is the elution time. JAI RI-700 NEXT and JAL UV-370 (at 268 nm) detectors were used. The number-average (Mn) and weight-average (Mw) molecular weights were calculated using the built-in software JAI JDS-300.
2.12 Wide-angle X-ray diffraction
X-ray diffraction measurements were carried out using θ–2θ scans on a Bruker D8 Advance powder diffractometer. The incident X-ray beam was a Cu Kα line generated at 40 kV and 40 mA. The powdered specimen was put on a glass sample holder. The diffracted X-rays were detected by a scintillation counter.2.13 Thermogravimetry (TG) and differential scanning calorimetry (DSC)
Thermogravimetric measurements were carried out using a Rigaku Thermo plus EVO II TG8120 under a nitrogen atmosphere at a heating rate of 10 °C min−1. Differential scanning calorimetric curves were recorded using a MAC DSC-3100 under nitrogen gas flow on first heating, first cooling, and second heating runs at a rate of 10 °C min−1.2.14 MO calculations
Density functional theory (DFT) and ab initio MO calculations were carried out with the Gaussian09 program16 installed on an HPC Silent-SCC T2 or a HITACHI SR16000 computer at the Institute of Management and Information Technologies of Chiba University. For each conformer of the model compounds surrounded by dimethyl sulfoxide (DMSO) molecules, the geometry was fully optimized at the B3LYP/6-311+G(2d,p) level17 with the self-consistent reaction field (SCRF) method using the conductor-like polarizable continuum model (CPCM),18 and the thermal-correction term to the Gibbs free energy (at 25 °C) was also calculated. All self-consistent field (SCF) calculations were conducted under tight convergence. With the optimized geometry, the electronic energy was computed at the MP2/6-311+G(2d,p)19 and M062X/6-311+G(2d,p)20 levels. The Gibbs free energy was evaluated from the electronic and thermal correction energies, being expressed by ΔGk (k: conformer) here as the difference from that of a given conformer. 1H–1H and 13C–1H coupling constants21 of the model compounds for the NMR analysis were calculated at the B3LYP/6-311++G(3df,3pd)//B3LYP/6-311+G(3df,2p) level.Herein, the dihedral angle is defined according to the tradition in polymer science:6 trans (t) ∼ 0°, gauche± (g±) ∼ ±120°, and cis (c) ∼ 180°. The dihedral angle (ϕ) can be converted to that (Φ) recommended by the International Union of Pure and Applied Chemistry22 according to Φ = −sign(ϕ)(180 − |ϕ|), where the function, sign(ϕ), returns the sign of ϕ, and vice versa: ϕ = −sign(Φ)(180 − |Φ|). Non-SI units are used: free energy in kcal mol−1 (1 kcal mol−1 = 4.184 kJ mol−1); bond length in Å (1 Å = 10−10 m).
3 Results and discussion
3.1 NMR of model compounds
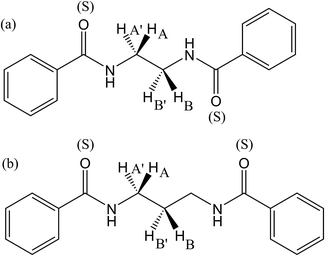
Conformation- and configuration-dependent properties of a polymer in the Θ state (without the excluded volume effect) depend only on short-range intramolecular interactions,6 which can be predicted both theoretically and experimentally from small model compounds with the same bond sequence as the polymer. In order to elucidate conformational characteristics of the polymers treated here, therefore, we carried out conformational analysis of their model compounds. The amide models are slightly soluble in methanol and well soluble in DMSO, trifluoroacetic acid (TFA) and 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP), and hence DMSO-d6 was used as the NMR solvent.Fig. 4 shows the 1H NMR spectra observed from 2DBA, 2DBTA, 3DBA, and 3DBTA dissolved in DMSO at 25 °C. The gNMR simulations reproduced the observed spectra well and yielded chemical shifts and spin–spin coupling constants. Only vicinal coupling constants (3JNC, 3JHH, and 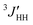 ) needed for the conformational analysis are listed in Table 1. The NH signals of 2DBTA at 35–55 °C and 3DBTA at 55 °C were observed to collapse into a single peak, from which the 3JNH value could not be derived; therefore, the corresponding lines of Tables 1 and 2 are blank.
) needed for the conformational analysis are listed in Table 1. The NH signals of 2DBTA at 35–55 °C and 3DBTA at 55 °C were observed to collapse into a single peak, from which the 3JNH value could not be derived; therefore, the corresponding lines of Tables 1 and 2 are blank.
 | ||
| Fig. 4 Observed (above) and calculated (below) 1H NMR spectra of (a) 2DBA, (b) 2DBTA, (c) 3DBA, and (d) 3DBTA: left, NH proton; center, HA and HA′; right, HB and HB′. | ||
| Compound | Temp, °C | 3JNC | 3JHH | |
|---|---|---|---|---|
| a In Hz.b The signal from the NH proton collapsed into a broad singlet, from which no 3JNC value can be derived. | ||||
| 2DBA | 25 | 5.69 | 6.61 | 6.01 |
| 35 | 5.70 | 6.62 | 6.02 | |
| 45 | 5.71 | 6.62 | 6.06 | |
| 55 | 5.72 | 6.62 | 6.14 | |
| 2DBTA | 25 | 5.40 | 6.10 | 5.79 |
| 35b | — | 6.03 | 5.81 | |
| 45b | — | 5.96 | 5.57 | |
| 55b | — | 5.68 | 5.34 | |
| 3DBA | 25 | 5.80 | 5.59 | 8.30 |
| 35 | 5.80 | 5.60 | 8.30 | |
| 45 | 5.79 | 5.60 | 8.30 | |
| 55 | 5.79 | 5.60 | 8.30 | |
| 3DBTA | 25 | 5.50 | 5.42 | 8.64 |
| 35 | 5.48 | 5.42 | 8.64 | |
| 45 | 5.47 | 5.42 | 8.64 | |
| 55b | — | 5.42 | 8.64 | |
| Compound | Temp, °C | pt | ||||
|---|---|---|---|---|---|---|
| N–CH2 | CH2–CH2 | |||||
| set Aa | set Bb | set Cc | set ad | set be | ||
a With the JG1, JG2, JE, and 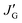 values derived from a Karplus equation of Pardi et al.23b With the JG1, JG2, JE, and values derived from a Karplus equation of Pardi et al.23b With the JG1, JG2, JE, and  values derived from a Karplus equation of Ludvigsen et al.24c With the JG1, JG2, JE, and values derived from a Karplus equation of Ludvigsen et al.24c With the JG1, JG2, JE, and 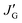 values derived from MO calculations for the model compounds.d With the JT and JG values obtained from NMR experiments on 2-methylpiperazine (for 2DBA and 2DBTA)25 and 2-methylpiperidine (for 3DBA and 3DBTA).26e With the JT and JG values obtained from MO calculations for the model compounds.f The 3JNC value was not obtained.g The B3LYP/6-311+G(2d,p) level using the geometry optimized at the B3LYP/6-311+G(2d,p) level with the solvent effect of DMSO.h The MP2/6-311+G(2d,p) level using the geometry and solvent effect.i The M062X/6-311+G(2d,p) level using the geometry and solvent effect. values derived from MO calculations for the model compounds.d With the JT and JG values obtained from NMR experiments on 2-methylpiperazine (for 2DBA and 2DBTA)25 and 2-methylpiperidine (for 3DBA and 3DBTA).26e With the JT and JG values obtained from MO calculations for the model compounds.f The 3JNC value was not obtained.g The B3LYP/6-311+G(2d,p) level using the geometry optimized at the B3LYP/6-311+G(2d,p) level with the solvent effect of DMSO.h The MP2/6-311+G(2d,p) level using the geometry and solvent effect.i The M062X/6-311+G(2d,p) level using the geometry and solvent effect. |
||||||
| NMR expt | ||||||
| 2DBA | 25 | 0.41 | 0.30 | 0.18 | 0.26 | 0.41 |
| 35 | 0.40 | 0.29 | 0.18 | 0.26 | 0.41 | |
| 45 | 0.40 | 0.29 | 0.18 | 0.26 | 0.41 | |
| 55 | 0.39 | 0.28 | 0.18 | 0.27 | 0.42 | |
| 2DBTA | 25 | 0.56 | 0.44 | 0.30 | 0.28 | 0.45 |
| 35f | — | — | — | 0.28 | 0.46 | |
| 45f | — | — | — | 0.27 | 0.45 | |
| 55f | — | — | — | 0.27 | 0.45 | |
| 3DBA | 25 | 0.45 | 0.31 | 0.14 | 0.49 | 0.63 |
| 35 | 0.45 | 0.31 | 0.14 | 0.49 | 0.63 | |
| 45 | 0.46 | 0.31 | 0.14 | 0.49 | 0.63 | |
| 55 | 0.46 | 0.31 | 0.14 | 0.49 | 0.63 | |
| 3DBTA | 25 | 0.52 | 0.40 | 0.32 | 0.53 | 0.69 |
| 35 | 0.53 | 0.40 | 0.32 | 0.53 | 0.69 | |
| 45 | 0.53 | 0.41 | 0.33 | 0.53 | 0.69 | |
| 55f | — | — | — | 0.53 | 0.69 | |
| B3LYPg | MP2h | M062Xi | B3LYPg | MP2h | M062Xi | ||
|---|---|---|---|---|---|---|---|
| MO calc | |||||||
| 2DBA | 25 | 0.29 | 0.15 | 0.44 | 0.19 | 0.01 | 0.03 |
| 35 | 0.29 | 0.15 | 0.44 | 0.19 | 0.01 | 0.04 | |
| 45 | 0.28 | 0.15 | 0.43 | 0.20 | 0.01 | 0.04 | |
| 55 | 0.28 | 0.16 | 0.43 | 0.20 | 0.01 | 0.04 | |
| 2DBTA | 25 | 0.32 | 0.42 | 0.40 | 0.31 | 0.02 | 0.08 |
| 35 | 0.32 | 0.42 | 0.39 | 0.31 | 0.02 | 0.09 | |
| 45 | 0.32 | 0.41 | 0.39 | 0.31 | 0.02 | 0.09 | |
| 55 | 0.32 | 0.41 | 0.39 | 0.31 | 0.03 | 0.10 | |
| 3DBA | 25 | 0.22 | 0.03 | 0.04 | 0.61 | 0.02 | 0.08 |
| 35 | 0.22 | 0.03 | 0.04 | 0.60 | 0.02 | 0.09 | |
| 45 | 0.22 | 0.03 | 0.05 | 0.60 | 0.03 | 0.10 | |
| 55 | 0.22 | 0.04 | 0.05 | 0.59 | 0.03 | 0.11 | |
| 3DBTA | 25 | 0.55 | 0.03 | 0.22 | 0.62 | 0.02 | 0.24 |
| 35 | 0.54 | 0.03 | 0.23 | 0.62 | 0.02 | 0.25 | |
| 45 | 0.54 | 0.04 | 0.24 | 0.61 | 0.03 | 0.25 | |
| 55 | 0.53 | 0.04 | 0.24 | 0.60 | 0.03 | 0.26 | |
From the Newman projections in Fig. 5, the observed vicinal coupling constants can be related to trans (pt) and gauche (pg) fractions of the individual bonds:
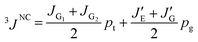 | (1) |
 | (2) |
 | (3) |
 , and
, and 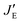 values are defined in Fig. 5. By definition, the following relation must be satisfied:
values are defined in Fig. 5. By definition, the following relation must be satisfied:| pt + pg = 1 | (4) |
 , and
, and  were derived from two Karplus equations optimized for peptides,23,24 DFT computations on the models, or experimental values of cyclic compounds, 2-methylpiperazine (2MPZ)25 and 2-methylpiperidine (2MPD)26 with –NH–CH2–CH2–NH– and –NH–CH2–CH2–CH2–NH– bond sequences, respectively.
were derived from two Karplus equations optimized for peptides,23,24 DFT computations on the models, or experimental values of cyclic compounds, 2-methylpiperazine (2MPZ)25 and 2-methylpiperidine (2MPD)26 with –NH–CH2–CH2–NH– and –NH–CH2–CH2–CH2–NH– bond sequences, respectively.
 | ||
| Fig. 5 Rotational isomeric states around the (a) N–CH2 and (b) CH2–CH2 bonds of the model compounds with definitions of vicinal trans (JT) and gauche (JG) coupling constants. | ||
From eqn (1) and (4), the pt and pg values of the N–CH2 bond were determined, while those of the CH2–CH2 bond, derived from eqn (2) and (3), were divided by the sum of pt and pg to satisfy eqn (4). The trans fractions (pt) of both N–CH2 and CH2–CH2 bonds, listed in Table 2, are seen to be sensitive to the JT, 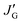 , and
, and  values employed in the analysis.
values employed in the analysis.
3.2 MO calculations on models
In the RIS approximation, the possible conformations of 2DBA and 2DBTA may be enumerated to be 33 (=27); however, the molecular symmetry leaves us with only 10 irreducible conformations, for which the MO calculations were carried out at different levels and yielded the Gibbs free energies as shown in Table 3. The numbers of allowed conformers of 2DBA and 2DBTA are 6 and 8, respectively. The conformer free energy can be seen to depend largely on the MO theory. The trans fractions were also calculated from the ΔGk values and compared with the NMR data (Table 2). Although the experimental pt values, depending on the JT, , and
, and  values, are somewhat scattered, the pt values calculated from the B3LYP energies are found to fall within the range of (or to be close to) the experimental observations, whereas those of the CH2–CH2 bond from the MP2 and M062X methods are far from the experimental values.
values, are somewhat scattered, the pt values calculated from the B3LYP energies are found to fall within the range of (or to be close to) the experimental observations, whereas those of the CH2–CH2 bond from the MP2 and M062X methods are far from the experimental values.
| k | Conformationc | Mkd | ΔGk, kcal mol−1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2DBAa | 2DBTAb | |||||||||
| B3LYPe | MP2f | M062Xg | B3LYPe | MP2f | M062Xg | |||||
a Relative to the tg+g− conformation.b Relative to the all-trans conformation.c In the HN–C–C–NH bond sequence. Both C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X (X = O or S) bonds were oriented to be trans–trans. The blank represents that the potential minimum was not found by the geometrical optimization at the B3LYP/6-311+G(2d,p) level.d Multiplicity.e At the B3LYP/6-311+G(2d,p) level.f At the MP2/6-311+G(2d,p) level.g At the M062X/6-311+G(2d,p) level. X (X = O or S) bonds were oriented to be trans–trans. The blank represents that the potential minimum was not found by the geometrical optimization at the B3LYP/6-311+G(2d,p) level.d Multiplicity.e At the B3LYP/6-311+G(2d,p) level.f At the MP2/6-311+G(2d,p) level.g At the M062X/6-311+G(2d,p) level. |
||||||||||
| 1 | t | t | t | 1 | — | — | — | 0.00 | 0.00 | 0.00 |
| 2 | t | t | g+ | 4 | — | — | — | −0.12 | −0.70 | −0.27 |
| 3 | t | g+ | t | 2 | — | — | — | −0.53 | −1.71 | −0.90 |
| 4 | t | g+ | g+ | 4 | — | — | — | — | — | — |
| 5 | t | g+ | g− | 4 | 0.00 | 0.00 | 0.00 | −0.70 | −3.88 | −2.38 |
| 6 | g+ | t | g+ | 2 | 0.49 | 2.21 | 1.79 | 0.11 | −0.96 | −0.48 |
| 7 | g+ | t | g− | 2 | 0.89 | 2.63 | 2.14 | −0.73 | −1.73 | −1.14 |
| 8 | g+ | g+ | g+ | 2 | 0.59 | 1.67 | 1.35 | −0.76 | −2.53 | −1.58 |
| 9 | g+ | g+ | g− | 4 | 1.03 | 1.67 | 1.93 | −0.39 | −2.72 | −1.17 |
| 10 | g+ | g− | g+ | 2 | 1.64 | −0.91 | 2.44 | — | — | — |
The number of irreducible conformers of 3DBA and 3DBTA is 25, and the Gibbs free energies are listed in Table 4. The MP2 and M062X methods, compared with B3LYP, yield small ΔGk values especially for tg+g−g−, g+g+g+g−, g+g+g−g+, and g+g+g−g−. These four conformers of 3DBA and 3DBTA are depicted in Fig. S1 and S2 (ESI†), respectively, in which the following intramolecular interactions can be found: π/π (in g+g+g−g− and g+g+g−g+); C–H⋯π (tg+g−g−); NH⋯X![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (X
C (X ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or S) (g+g+g+g−). The MP2 and M062X methods probably overestimate these attractions; the corresponding ΔGk energies were estimated to be so negative as to yield the extremely small pt values for both N–CH2 and CH2–CH2 bonds. It has often been pointed out that the MP2 theory tends to overestimate the stabilities of π/π and CH⋯π attractions.3,27–30 In contrast, the B3LYP energies showed that the pt values are consistent with the NMR experiments.
O or S) (g+g+g+g−). The MP2 and M062X methods probably overestimate these attractions; the corresponding ΔGk energies were estimated to be so negative as to yield the extremely small pt values for both N–CH2 and CH2–CH2 bonds. It has often been pointed out that the MP2 theory tends to overestimate the stabilities of π/π and CH⋯π attractions.3,27–30 In contrast, the B3LYP energies showed that the pt values are consistent with the NMR experiments.
| k | Conformationb | Mkc | ΔGka | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3DBA | 3DBTA | ||||||||||
| B3LYPd | MP2e | M062Xf | B3LYPd | MP2e | M062Xf | ||||||
a Relative to the all-trans conformation.b In the HN–C–C–C–NH bond sequence. Both C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X (X = O or S) bonds were oriented to be trans–trans. The blank represents that the potential minimum was not found by the geometrical optimization at the B3LYP/6-311+G(2d,p) level.c Multiplicity.d At the B3LYP/6-311+G(2d,p) level.e At the MP2/6-311+G(2d,p) level.f At the M062X/6-311+G(2d,p) level. X (X = O or S) bonds were oriented to be trans–trans. The blank represents that the potential minimum was not found by the geometrical optimization at the B3LYP/6-311+G(2d,p) level.c Multiplicity.d At the B3LYP/6-311+G(2d,p) level.e At the MP2/6-311+G(2d,p) level.f At the M062X/6-311+G(2d,p) level. |
|||||||||||
| 1 | t | t | t | t | 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 2 | t | t | t | g+ | 4 | −0.54 | −0.83 | −0.62 | 1.19 | 0.75 | 1.06 |
| 3 | t | t | g+ | t | 4 | — | — | — | 1.07 | 0.65 | 0.87 |
| 4 | t | t | g+ | g+ | 4 | 0.32 | −0.68 | −0.32 | 1.92 | 0.81 | 1.30 |
| 5 | t | t | g+ | g− | 4 | 0.57 | −0.57 | −0.17 | 1.37 | 0.31 | 1.03 |
| 6 | t | g+ | t | g+ | 4 | — | — | — | 1.28 | −0.86 | −0.29 |
| 7 | t | g+ | t | g− | 4 | — | — | — | 1.89 | 0.97 | 1.53 |
| 8 | t | g+ | g+ | t | 2 | — | — | — | 1.03 | −0.45 | 0.59 |
| 9 | t | g+ | g+ | g+ | 4 | — | — | — | 2.37 | 0.41 | 1.30 |
| 10 | t | g+ | g+ | g− | 4 | 0.68 | −1.62 | −0.29 | — | — | — |
| 11 | t | g+ | g− | t | 2 | — | — | — | 4.70 | 0.56 | 2.85 |
| 12 | t | g+ | g− | g+ | 4 | — | — | — | — | — | — |
| 13 | t | g+ | g− | g− | 4 | 1.11 | −2.09 | −0.27 | 2.89 | −0.98 | 1.40 |
| 14 | g+ | t | t | g+ | 2 | −0.32 | −0.91 | −0.60 | 1.45 | 0.52 | 1.22 |
| 15 | g+ | t | t | g− | 2 | −0.34 | −0.88 | −0.36 | 0.97 | −0.02 | 0.75 |
| 16 | g+ | t | g+ | g+ | 4 | 0.85 | −0.45 | 0.30 | 1.83 | −0.31 | 0.80 |
| 17 | g+ | t | g+ | g− | 4 | −0.11 | −1.46 | −0.71 | 1.84 | 0.07 | 1.21 |
| 18 | g+ | t | g− | g+ | 4 | 0.34 | −0.92 | −0.32 | — | — | — |
| 19 | g+ | t | g− | g− | 4 | 0.63 | −0.56 | −0.11 | 1.84 | 0.46 | 1.29 |
| 20 | g+ | g+ | g+ | g+ | 2 | 0.76 | −1.10 | −0.39 | 2.33 | 0.21 | 1.23 |
| 21 | g+ | g+ | g+ | g− | 4 | −0.29 | −4.03 | −2.74 | 1.57 | −2.63 | −0.82 |
| 22 | g+ | g+ | g− | g+ | 4 | 1.69 | −2.81 | −0.39 | 3.32 | −3.04 | 0.44 |
| 23 | g+ | g+ | g− | g− | 2 | 2.69 | −0.55 | 1.44 | 3.77 | −0.40 | 2.45 |
| 24 | g+ | g− | g+ | g− | 2 | — | — | — | — | — | — |
| 25 | g+ | g− | g− | g+ | 2 | — | — | — | — | — | — |
The two –Y–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) groups of aromatic polyesters (Y = O) and polythioesters (Y = S) are located on the benzene plane, and hence only two orientations, trans (dihedral angle ∼ 0°) and cis (∼180°), are allowed between the –Y–C(
O) groups of aromatic polyesters (Y = O) and polythioesters (Y = S) are located on the benzene plane, and hence only two orientations, trans (dihedral angle ∼ 0°) and cis (∼180°), are allowed between the –Y–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) groups connected to the same benzene ring.1,4 In contrast, the geometrical optimizations for model compounds of the aromatic polydithioester (X = Y = S),4,5 polyamides (X = O and Y = NH), and polythioamides (X = S and Y = NH) rendered the –Y–C(
O) groups connected to the same benzene ring.1,4 In contrast, the geometrical optimizations for model compounds of the aromatic polydithioester (X = Y = S),4,5 polyamides (X = O and Y = NH), and polythioamides (X = S and Y = NH) rendered the –Y–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X) groups out of the benzene plane. Therefore, the stereochemistry for the –Y–C(
X) groups out of the benzene plane. Therefore, the stereochemistry for the –Y–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X) groups must also be defined by another factor: the two C
X) groups must also be defined by another factor: the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X bonds are oriented in either the same (cis) direction or opposite (trans) directions with respect to the benzene plane. Four combinations of the former and latter factors are possible: trans–trans; trans–cis; cis–trans; cis–cis. However, the trans–cis and cis–trans combinations have two states with positive (+) and negative (−) dihedral angles: (trans–cis)± and (cis–trans)±. Consequently, there are six states in all: trans–trans, (trans–cis)±, (cis–trans)±, and cis–cis (see Fig. 6).
X bonds are oriented in either the same (cis) direction or opposite (trans) directions with respect to the benzene plane. Four combinations of the former and latter factors are possible: trans–trans; trans–cis; cis–trans; cis–cis. However, the trans–cis and cis–trans combinations have two states with positive (+) and negative (−) dihedral angles: (trans–cis)± and (cis–trans)±. Consequently, there are six states in all: trans–trans, (trans–cis)±, (cis–trans)±, and cis–cis (see Fig. 6).
The ΔGk energies of the six states were evaluated from the MO calculations at the B3LYP/6-311+G(2d,p) level for more simplified models, N,N′-dimethylterephthalamide and N,N′-dimethylterephthalthioamide, and the dihedral angles were obtained from the MO calculations at the same level for 2DBA, 2DBTA, 3DBA, and 3DBTA. In Table 5, the data are compared with those of the aromatic polyesters, polythioesters, and polydithioesters. Regardless of polymer type, the ΔGk differences between the six orientations are small, and hence the –Y–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X) group may be almost freely oriented in different directions, i.e., freely rotatable around the benzene ring.
X) group may be almost freely oriented in different directions, i.e., freely rotatable around the benzene ring.
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X (X = O or S) orientation: ξ X (X = O or S) orientation: ξ |
||||||
|---|---|---|---|---|---|---|
| trans–trans | (trans–cis)± | (cis–trans)± | cis–cis | |||
a In deg.b In kcal mol−1. Relative to the trans–trans orientation.c Because of the rounding error, the sum of the pξ values does not exactly agree with unity.d The –Y–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Y = O or S) groups are located on the benzene plane; thus, only two states, trans and cis orientations, are defined for the polyesters and polythioesters. O (Y = O or S) groups are located on the benzene plane; thus, only two states, trans and cis orientations, are defined for the polyesters and polythioesters. |
||||||
| Polyamide | ϕξa | PA2T | 0.00 | ±53.6 | ±123.0 | 180.0 |
| PA3T | 0.00 | ±46.9 | ±129.2 | 180.0 | ||
| ΔGξb | 0.00 | −0.10 | −0.38 | 0.08 | ||
| pξc | 0.12 | 0.15 | 0.24 | 0.11 | ||
| Polythioamide | ϕξa | PTA2T | 0.00 | ±79.6 | ±98.0 | 180.0 |
| PTA3T | 0.00 | ±75.8 | ±102.5 | 180.0 | ||
| ΔGξb | 0.00 | −0.19 | −0.32 | −0.14 | ||
| pξc | 0.12 | 0.16 | 0.20 | 0.15 | ||
| Polyesterd | ϕξa | PET | 0.00 | — | — | 180.0 |
| PTT | 0.00 | — | — | 180.0 | ||
| ΔGξb | 0.00 | — | — | 0.15 | ||
| pξ | 0.56 | — | — | 0.44 | ||
| Polythioesterd | ϕξa | P2TS2 | 0.00 | — | — | 180.0 |
| P3TS2 | 0.00 | — | — | 180.0 | ||
| ΔGξb | 0.00 | — | — | 0.15 | ||
| pξ | 0.56 | — | — | 0.44 | ||
| Polydithioester | ϕξa | P2TS4 | 0.00 | ±71.5 | ±106.3 | 180.0 |
| P3TS4 | 0.00 | ±70.8 | ±106.3 | 180.0 | ||
| ΔGξb | 0.00 | −0.10 | 0.15 | 0.05 | ||
| pξc | 0.17 | 0.20 | 0.13 | 0.16 | ||
3.3 Configurational properties and thermodynamic quantities derived from the RIS calculations
The refined RIS scheme8 that treats both the geometrical parameters and energies as functions of conformations of the current and neighboring bonds has been applied to the aromatic polyamides, polythioamides, polythioesters, and polydithioesters to evaluate the characteristic ratio, configurational entropy, bond conformations, and average geometrical parameters. The statistical weight matrices of the polymers are formulated in Appendices A and B (ESI†), and the geometrical parameters are tabulated in Tables S1–S6 (ESI†). Because the ΔGk energies at the B3LYP/6-311+G(2d,p) level (Tables 3 and 4) well reproduced the NMR experiments, the B3LYP free energies were employed in the RIS calculations for the polyamides and polythioamides, together with those of the six orientations (Table 5). For the energy parameters of the polythioesters and polydithioesters, see the original papers.4,5 The data on the polyesters are quoted from the literature.1,3The characteristic ratios (〈r2〉0/nl2) and configurational entropies (Sconf) are shown in Table 6, and the 〈r2〉0/nl2 ratios were calculated with the virtual bond connecting the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X (X = O or S) carbons (see Fig. 2); thus, the 〈r2〉0/nl2 values here can not be simply compared with those of nonaromatic polymers. Inasmuch as the statistical weight matrices were formulated with the ΔGk energies, the pt and pξ values given in Tables 2 and 5 are applicable as they are for the corresponding polymers. The geometrical parameters averaged over the existing conformations are listed in Tables S7 and S8 (ESI†). These theoretical data will be discussed later to interpret the characterization of the polymers.
X (X = O or S) carbons (see Fig. 2); thus, the 〈r2〉0/nl2 values here can not be simply compared with those of nonaromatic polymers. Inasmuch as the statistical weight matrices were formulated with the ΔGk energies, the pt and pξ values given in Tables 2 and 5 are applicable as they are for the corresponding polymers. The geometrical parameters averaged over the existing conformations are listed in Tables S7 and S8 (ESI†). These theoretical data will be discussed later to interpret the characterization of the polymers.
3.4 Synthesis and identification of PA2T and PA3T
The two polyamides were synthesized via interfacial polycondensation between terephthaloyl chloride and diamines according to Shashoua and Eareckson,12 who estimated the molecular weights of the polyamides by turbidimetry as 17.8 kDa (PA2T) and 23.7 kDa (PA3T). In Fig. S3 (ESI†), solid-state 13C NMR spectra of the two polyamides are compared with the solution spectra of the model compounds, and the observed signals, assigned as indicated there, clearly show the formation of the two polyamides. As will be stated below, PA2T and PA3T are only soluble in solvents that are irritants; thus, we avoided SEC measurements for these polyamides. However, both polymers are expected to have molecular weights comparable to those reported by Shashoua and Eareckson.3.5 Synthesis and identification of PTA2T and PTA3T
The two polythioamides were synthesized via the Willgerodt–Kinder type reaction according to Kanbara et al.13 In Fig. 7, solution 13C NMR spectra of PTA2T and PTA3T are compared with those of the model compounds, and the observed peaks are assigned as indicated. It is suggested that the Willgerodt–Kinder type reaction often yields Schiff base polymers with the CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond.13 Therefore, we also prepared DB2A and DB3A as models for the Schiff base polymers and measured their NMR (see Fig. 7). No signals related to the CH2
N bond.13 Therefore, we also prepared DB2A and DB3A as models for the Schiff base polymers and measured their NMR (see Fig. 7). No signals related to the CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond are found in the spectra of PTA2T and PTA3T; thus, the by-products were not generated.
N bond are found in the spectra of PTA2T and PTA3T; thus, the by-products were not generated.
3.6 Solubilities of PA2T, PA3T, PTA2T, and PTA3T
The solubilities of the four polymers were investigated for common and some special solvents. Both polyamides and polythioamides are insoluble in water, alcohols, chloroform, dichloromethane, and tetrahydrofuran but soluble in some acidic solvents used often for aromatic polyesters, e.g., TFA, HFIP, and sulfuric acid as shown in Table 7. The polythioamides are superior in solubility to the polyamides and soluble in pyridine, N,N-dimethylformamide (DMF), N,N-dimethylacetamide (DMAc), DMSO, and N-methylpyrrolidone (NMP) as well as the above acidic solvents.| Solventb | PA2T | PA3T | PTA2T | PTA3T |
|---|---|---|---|---|
| a Symbols: +, soluble at ambient temperature; ±, soluble at elevated temperatures; −, insoluble.b Abbreviations: NaOHaq, sodium hydroxide aqueous solution; DMF, N,N-dimethylformamide; DMAc, N,N-dimethylacetamide; DMSO, dimethyl sulfoxide; NMP, N-methylpyrrolidone; HFIP, 1,1,1,3,3,3-hexafluoro-2-propanol; TFA, trifluoroacetic acid. | ||||
| Water | − | − | − | − |
| Methanol | − | − | − | − |
| Ethanol | − | − | − | − |
| Chloroform | − | − | − | − |
| Dichloromethane | − | − | − | − |
| Tetrahydrofuran | − | − | − | − |
| NaOHaq | − | − | − | − |
| Triethylamine | − | − | − | − |
| Piperidine | − | − | − | − |
| Pyridine | − | − | + | + |
| DMF | − | − | + | + |
| DMAc | − | − | + | + |
| DMSO | − | − | + | + |
| NMP | − | − | + | + |
| HFIP | + | + | + | + |
| Phenol | − | ± | ± | ± |
| TFA | + | + | + | + |
| Sulfuric acid | + | + | + | + |
The polyamides are soluble only in the so-called helix-breaking solvents for polypeptides, such as TFA and HFIP, and their model compounds are soluble in not only the helix breakers but also DMSO. In our studies,1,4,5,31 the MP2 calculations have successfully yielded precise conformational energies of polyethers, polythioethers, polyamines, polyesters, polythioesters, and polydithioesters, except for aromatic polyesters with intramolecular π/π and CH⋯π attractions.2,3 In this study, however, the MP2 theory seems to overestimate the intramolecular N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and N–H⋯S
C and N–H⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds as well as π/π and C–H⋯π attractions (see Fig. S1 and S2†). In contrast, the B3LYP functional tends to underestimate attractive interactions such as dispersion forces,32 thus representing interactions of the amides and thioamides better than MP2 and giving results consistent with the NMR experiments.
C hydrogen bonds as well as π/π and C–H⋯π attractions (see Fig. S1 and S2†). In contrast, the B3LYP functional tends to underestimate attractive interactions such as dispersion forces,32 thus representing interactions of the amides and thioamides better than MP2 and giving results consistent with the NMR experiments.
3.7 Molecular weights of PTA2T and PTA3T
The novel polymers, PTA2T and PTA3T, are soluble in some polar organic solvents and hence underwent SEC measurements. The molecular weight distributions of PTA2T and PTA3T are shown in Fig. S4 (ESI†). The Mn and Mw values are, respectively, as follows: PTA2T, 10.7 kDa and 17.3 kDa; PTA3T, 13.9 kDa and 29.3 kDa. Accordingly, the polydispersity indexes can be estimated as 1.62 (PTA2T) and 2.11 (PTA3T).As shown in Fig. 8, films of PTA2T and PTA3T were cast on small Petri dishes from the DMF solutions; therefore, the polythioamides have molecular weights high enough to form the films, which are optically translucent and brown in color.
3.8 Crystal structures of the model compounds
The crystal structures of 2DBA and 3DBA were determined by Brisse et al.,33,34 and those of 2DBTA and 3DBTA by us35,36 (see Fig. 9). In the crystal, 2DBA, 2DBTA, 3DBA, and 3DBTA adopt g+tg−, g+g+g+, ttg+g+, and tttg+ conformations, respectively, which were not necessarily suggested by the DFT calculations to be the lowest in ΔGk but appear to be stabilized by intermolecular N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or N–H⋯S
C or N–H⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds. In the crystal, the C
C hydrogen bonds. In the crystal, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or C
O or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bonds make a dihedral angle with the adjacent phenyl ring: 2DBA, 19.4°; 3DBA, 27.6° and 33.5°; 2DBTA, 39.3° and 38.7°; 3DBTA, 43.0° and 33.3°.
S bonds make a dihedral angle with the adjacent phenyl ring: 2DBA, 19.4°; 3DBA, 27.6° and 33.5°; 2DBTA, 39.3° and 38.7°; 3DBTA, 43.0° and 33.3°.
 | ||
| Fig. 9 Crystal conformations of (a) 2DBA (in g+tg−), (b) 2DBTA (g+g+g+), (3) 3DBA (ttg+g+), and (d) 3DBTA (tttg+). | ||
Our studies31 have shown that polymeric chains without aromatic groups and strong intermolecular interactions as well as their model compounds tend to crystallize in the most stable conformation predicted from MO calculations for the models. This is not the case with the aromatic polyamides and polythioamides because of the strong intermolecular N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or N–H⋯S
C or N–H⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attractions.
C attractions.
3.9 X-ray diffraction
Fig. 10 shows the powder X-ray diffraction patterns observed from the annealed samples of the polyamides and polythioamides. The annealing was conducted for 2 h under reduced pressure at 150 °C, much higher than the Tg (see below). The polyamides exhibited broad peaks at around 2θ = 15–30° and 43°, which indicate the existence of distorted crystallites. On the other hand, the polythioamides yielded a broad amorphous halo at around 20°.3.10 Thermal analysis
Fig. 11 shows the TG curves of PA2T, PTA2T, PA3T, and PTA3T. The thermal decomposition temperatures (Td) were determined as follows: PA2T, 421 °C; PA3T, 391 °C; PTA2T, 261 °C; PTA3T, 250 °C. The polyamides are superior to the polythioamides in thermal resistance. The glass transition temperatures detected by DSC are 52 °C (PA2T), 30 °C (PA3T), 23 °C (PTA2T), and 10 °C (PTA3T). Shashoua and Eareckson12 determined the melting points of PA2T and PA3T to be 455 and 399 °C, respectively; however, these temperatures probably correspond to our Td.The equilibrium melting point T0m is related to the enthalpy (ΔHu) and entropy (ΔSu) of fusion by
 | (5) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds and π/π and C–H⋯π attractions, may be so large that the Tm would be higher than Td.
C hydrogen bonds and π/π and C–H⋯π attractions, may be so large that the Tm would be higher than Td.
The aromatic polydithioesters except P3TS4 and P4TS4 are amorphous,5 and so are the polythioamides treated here. This is partly due to the flexible rotation around the benzene ring. The six orientations with small energy differences (at most, 0.5 kcal mol−1) prevent the polymers from crystallizing into a single state. In addition, the large van der Waals radius of sulfur disturbs effective intermolecular π/π stackings. Because the electronegativities of carbon, sulfur, and oxygen are, respectively, 2.5, 2.5, and 3.5, the dipole moment of the amide group exceeds that of the thioamide part and, consequently, the dipole–dipole interactions of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S polymers are also weaker than those of the C
S polymers are also weaker than those of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ones.
O ones.
4 Concluding remarks
Conformational characteristics of the aromatic polyamides and polythioamides have been predicted from NMR experiments and MO calculations on the model compounds. The comparison between the NMR and MO data showed that the B3LYP functional yielded more reliable results than the MP2 theory. The MP2 calculations may overestimate the π/π and C–H⋯π attractions and unsatisfactorily reproduce the effects of the helix-breaking and polar solvents. The B3LYP energies and geometrical parameters were applied to the refined RIS scheme to evaluate the configurational properties and thermodynamic quantities of the polyamides and polythioamides.The polyamides were synthesized via interfacial polycondensation, and the polythioamides via the Willgerodt–Kindlet type reaction. The polymers were characterized in terms of solubility, molecular weight, crystallinity, thermal stability, and thermal transition. The experimental results were compared with those of the aromatic polyesters, polythioesters, and polydithioesters.
In general, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O polymers (polyesters, polythioesters, and polyamides) are superior in thermal stability but inferior in solubility to the C
O polymers (polyesters, polythioesters, and polyamides) are superior in thermal stability but inferior in solubility to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S ones (polydithioesters and polythioamides). This is probably due to the difference in thermal resistance between the functional groups and partly due to those between the former and latter polymers in the intermolecular hydrogen bonds and configurational entropy (Sconf). The magnitude of Sconf depends on not only the intramolecular interactions such as the hydrogen bonds, π/π and CH⋯π attractions, and dipole–dipole interactions but also the rotation of the C
S ones (polydithioesters and polythioamides). This is probably due to the difference in thermal resistance between the functional groups and partly due to those between the former and latter polymers in the intermolecular hydrogen bonds and configurational entropy (Sconf). The magnitude of Sconf depends on not only the intramolecular interactions such as the hydrogen bonds, π/π and CH⋯π attractions, and dipole–dipole interactions but also the rotation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O or C
O or C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond around the benzene ring. The polyesters and polythioesters have only two orientations (trans and cis) between the C
S bond around the benzene ring. The polyesters and polythioesters have only two orientations (trans and cis) between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups bonded to the same benzene ring, while the polydithioesters, polyamides, and polythioamides exhibit six orientations of trans–trans, (trans–cis)±, (cis–trans)±, and cis–cis. Hence, the C
O groups bonded to the same benzene ring, while the polydithioesters, polyamides, and polythioamides exhibit six orientations of trans–trans, (trans–cis)±, (cis–trans)±, and cis–cis. Hence, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O polymers are semicrystalline, and the C
O polymers are semicrystalline, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S ones are amorphous or of very low crystallinity and optically translucent.
S ones are amorphous or of very low crystallinity and optically translucent.
In a series of studies, we have investigated the aromatic polymers expressed as [–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X)C6H4C(
X)C6H4C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) X)–Y–(CH2)y–Y–]x (X = O or S and Y = O, S, or NH) and found that these polymers, depending on the combination of X and Y, show different conformational characteristics, which lead to various higher-order structures and physical properties.
X)–Y–(CH2)y–Y–]x (X = O or S and Y = O, S, or NH) and found that these polymers, depending on the combination of X and Y, show different conformational characteristics, which lead to various higher-order structures and physical properties.
Acknowledgements
We thank Mr Ezawa and Mr Kodaira of Japan Analytical Industry Co., Ltd. for the SEC measurements. This study was partly supported by a Grant-in-Aid for Scientific Research (C) (22550190) from the Japan Society for the Promotion of Science.References
- Y. Sasanuma, Macromolecules, 2009, 42, 2854–2862 CrossRef CAS.
- Y. Sasanuma and N. Suzuki, Macromolecules, 2009, 42, 7203–7212 CrossRef CAS.
- Y. Sasanuma, Y. Wagai, N. Suzuki and D. Abe, Polymer, 2013, 54, 3904–3913 CrossRef CAS.
- D. Abe and Y. Sasanuma, Polym. Chem., 2012, 3, 1576–1587 RSC.
- D. Abe, Y. Fukuda and Y. Sasanuma, Polym. Chem., 2015, 6, 3131–3142 RSC.
- P. J. Flory, Statistical Mechanics of Chain Molecules, Wiley & Sons, New York, 1969 Search PubMed.
- W. L. Mattice and U. W. Suter, Conformational Theory of Large Molecules: The Rotational Isomeric State Model in Macromolecular Systems, Wiley-Interscience, New York, 1994 Search PubMed.
- Y. Sasanuma, S. Asai and R. Kumagai, Macromolecules, 2007, 40, 3488–3497 CrossRef CAS.
- A. R. Jacobson, A. N. Makris and L. M. Sayre, J. Org. Chem., 1987, 52, 2592–2594 CrossRef CAS.
- H. Hart and J. L. Brewbaker, J. Am. Chem. Soc., 1969, 91, 706–711 CrossRef CAS.
- M. P. Cava and M. I. Levinson, Tetrahedron, 1985, 41, 5061–5087 CrossRef CAS.
- V. E. Shashoua and W. M. Eareckson, J. Polym. Sci., 1959, 40, 343–358 CrossRef CAS.
- T. Kanbara, Y. Kawai, K. Hasegawa, H. Morita and T. Yamamoto, J. Polym. Sci., Part A: Polym. Chem., 2001, 39, 3739–3750 CrossRef CAS.
- A. Simion, C. Simion, T. Kanda, S. Nagashima, Y. Mitoma, T. Yamada, K. Mimura and M. Tashiro, J. Chem. Soc., Perkin Trans. 1, 2001, 2071–2078 RSC.
- P. H. Budzelaar, gNMR, version 5.0, IvorySoft & Adept Scientific plc, Letchworth, U.K., 2004 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision B.01, Gaussian Inc., Wallingford CT 2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 CrossRef CAS.
- T. Helgaker, M. Watson and N. C. Handy, J. Chem. Phys., 2000, 113, 9402–9409 CrossRef CAS.
- IUPAC, Compendium of Chemical Terminology, (the “Gold Book”), ed. A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, UK, 2nd edn, 1997 Search PubMed.
- A. Pardi, M. Billeter and K. Wüthrich, J. Mol. Biol., 1984, 180, 741–751 CrossRef CAS PubMed.
- S. Ludvigsen, K. V. Andersen and F. M. Poulsen, J. Mol. Biol., 1991, 217, 731–736 CrossRef PubMed.
- Y. Sasanuma, S. Hattori, S. Imazu, S. Ikeda, T. Kaizuka, T. Iijima, M. Sawanobori, M. A. Azam, R. V. Law and J. H. G. Steinke, Macromolecules, 2004, 37, 9169–9183 CrossRef CAS.
- Y. Sasanuma, F. Teramae, H. Yamashita, I. Hamano and S. Hattori, Macromolecules, 2005, 38, 3519–3532 CrossRef CAS.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104–112 CrossRef CAS PubMed.
- E. C. Lee, D. Kim, P. Jurečka, P. Tarakeshwar, P. Hobza and K. S. Kim, J. Phys. Chem. A, 2007, 111, 3446–3457 CrossRef CAS PubMed.
- C. A. Morgado, P. Jurečka, D. Svozil, P. Hobza and J. Šponer, Phys. Chem. Chem. Phys., 2010, 12, 3522–3534 RSC.
- M. Pitoňák, P. Neogrády, J. Černý, S. Grimme and P. Hobza, ChemPhysChem, 2009, 10, 282–289 CrossRef PubMed.
- Y. Sasanuma, A. Watanabe and K. Tamura, J. Phys. Chem. B, 2008, 112, 9613–9624 CrossRef CAS PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CrossRef CAS.
- A. Palmer and F. Brisse, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 1447–1452 CrossRef.
- J. Brisson and F. Brisse, Macromolecules, 1986, 19, 2632–2639 CrossRef CAS.
- M. Nagasawa, Y. Sasanuma and H. Masu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, o586 CAS.
- M. Nagasawa, Y. Sasanuma and H. Masu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2014, 70, o639 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Statistical weight matrices of PA2T and PTA2T (Appendix A) and PA3T and PTA3T (Appendix B); intramolecular interactions of 3DBA (Fig. S1) and 3DBTA (Fig. S2); solid-state 13C NMR spectra observed from PA2T and PA3T (Fig. S3); molecular weight distributions of PTA2T and PTA3T (Fig. S4); geometrical parameters used in the refined RIS calculations for PA2T (Table S1), PTA2T (Table S2), PA3T (Table S3), PTA3T (Table S4), P3TS2 (Table S5), and P3TS4 (Table S6); averaged geometrical parameters of PA2T, PA3T, PTA2T, and PTA3T (Table S7) and P2TS2, P3TS2, P2TS4, and P3TS4 (Table S8). See DOI: 10.1039/c5ra17883e |
| This journal is © The Royal Society of Chemistry 2015 |