Charge density distribution and theoretical analysis of low and high energy phosphate esters†
Abstract
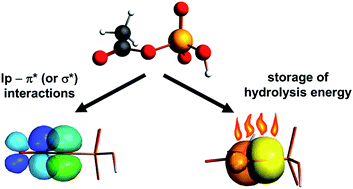
Charge density analysis has been performed for crystals of ammonium dihydrogen phosphoenolpyruvate (I) and diammonium hydrogen phosphoglycolate (II). The former compound is a high-energy phosphate ester that stores and provides energy for various biochemical processes, whereas the latter is a low energy one. The main difference between both molecules is mainly manifested by topological parameters of the P–O and C–O bonds within the ester C–O–P bridge. The charge density at the bond critical point in I is larger for C–O and smaller for P–O than in II. Theoretical DFT and NBO calculations show that the ester O atom has an approximate sp2 hybridization with two lone pairs: the spx (x = 1.2–1.6) and the p one. The latter, which is perpendicular to the C–O–P plane, interacts with the π*(C–C) orbital of the enolpyruvate fragment in I. Extended DFT calculations, performed for 15 model organic phosphates showed that the interaction of the p lone pair (called tlp hereinafter) with the organic part determines predominantly the geometry of the C–O–P fragment as well as the energy of hydrolysis. The interaction of tlp with a neighboring π* or a low-lying σ* orbital from the organic part creates an additional bonding effect along C–O, while the interaction of tlp with the σ* orbitals of the terminal P–O bonds strengthens the ester P–O bond. These two interactions are negatively correlated and the former is determinant. The P–O and C–O distances are additionally modified by interactions of the ester σ(P–O) and the sp2 pair with the organic part. On the other hand the hydrolysis energy is proportional to the interaction of tlp with the organic part. Regression analysis of the DFT results shows that the hydrolysis energy may be interpreted as being released mainly from the spx pair and the σ(P–O) orbital. It has been also shown that this energy may be in principle deduced from the topological parameters retrieved from the experimental charge density distribution.

 Please wait while we load your content...
Please wait while we load your content...