Ferromagnetism of three-dimensional graphene framework

Abstract

A three-dimensional graphene framework (3DGF) was synthesized via hydrothermal growth of graphene oxide (GO) suspension. The structure of 3DGF was characterized by scanning electron microscope, Raman spectroscopy and X-ray photoelectron spectroscopy. The reduction of GO with increased defect density has been confirmed, promoting the formation of 3D pore structure. The magnetic properties of 3DGF were investigated experimentally. Pure diamagnetism was observed in GO, while weak ferromagnetism was observed in 3DGF with saturated ferromagnetic magnetization of 0.005 emu g⁻¹ at 300 K. The observed ferromagnetism has been attributed to the presence of increased concentration of sp³-type hydroxyl groups attached on the basal plane at the interconnected 3D porous network structure of 3DGF.

---

1. Introduction

Graphene, a single layer of sp²-hybridized carbon atoms arranged in a two-dimensional hexagonal lattice, has attracted tremendous attention since its discovery in 2004.¹ Graphene has potential applications in various fields such as electronic devices,² composites,³ catalysis,⁴ bio-sensors,⁵ supercapacitors,⁶ Li ion batteries⁷ and hydrogen storage,⁸ mainly due to its superior electronic, thermal, mechanical properties, and excellent chemical stability. However, ideal graphene is nonmagnetic itself, and the localized magnetic moments are absent owing to a delocalized π bonding network, which limits its applications in spintronics devices.⁹

Traditional magnetic materials have been associated with the elements containing partially filled 3d or 4f subshells which possess the localized magnetic moments,¹⁰ magnetism appearing in graphene-based materials has attracted extensive attention because graphene contains only sp electrons. Theoretical studies confirmed that defects such as vacancies,¹¹ adatoms,¹² and zigzag edges¹³ can introduce localized magnetic moments. Experimentally, many approaches have been used to produce magnetism in graphene, including dopant atoms (H¹⁴, N¹⁵ and F¹⁶) and edge defects.¹⁷ Up to now, the reported magnetic researches on graphene-based materials still concentrated primarily on two-dimensional (2D) graphene. 2D graphene sheets could be self-assembled into complex three dimensional (3D) macrostructures. 3D graphene not only possesses intrinsic properties of 2D graphene sheets, but also provides advanced functions with improved performance in various applications, such as supercapacitors¹⁸ and energy storage,¹⁹ etc. However, the magnetic properties of 3D graphene have not yet been studied. In this paper, we report the magnetic properties of 3D graphene framework (3DGF), which was prepared by a facile one-step hydrothermal method, without any additives excepted for graphene oxide (GO) suspension.²⁰ Weak ferromagnetism with saturated magnetization of 0.005 emu g⁻¹ at 300 K has been observed. The reduction of GO with high concentration of sp³-type hydroxyl groups attached to the basal plane in the interconnected 3D porous network structure has been confirmed, which is believed to be the origin of magnetism.

2. Experimental details

GO was synthesized by the oxidation of natural graphite powder (325 mesh) according to a modified Hummers' method.²¹ The obtained GO was repeatedly washed by diluted hydrochloric acid several times to totally remove the possible remaining 3d transition metal contaminations. 3DGF was prepared based on the following procedure.²⁰ A 10 mL 2 mg mL⁻¹ GO aqueous dispersion was sealed in a 23 mL Teflon-lined autoclave without any additives and maintained at 180 °C for 6 h. Then the autoclave was naturally cooled to room temperature. Finally, 3DGF was obtained by freeze-drying.

The morphologies of the samples were observed by a scanning electron microscope (SEM, FEI Inspect F50). Raman measurements were performed on a Jobin Yvon LabRAM HR800 micro-Raman spectrometer using a laser excitation of 514 nm at room temperature. The electronic states were studied by X-ray photoelectron spectroscopy (XPS, ThermoFisher SCIENTIFIC) measurements using Al Kα X-ray source (hν = 1486.6 eV). The magnetic properties were measured by a vibrating sample magnetometer (VSM) integrated in a physical property measurement system (PPMS-9, Quantum Design).

3. Results and discussion

A homogeneous aqueous mixture of GO (2 mg mL⁻¹) allows the assembly of 3D porous graphene networks (Fig. 1a). The as-prepared 3DGF is so strong that it can be obtained as a free-standing cylinder. This has been attributed to the partial overlapping or coalescing of flexible graphene sheets via π–π stacking interactions during the hydrothermal reduction, which forms the strong cross-links of 3D graphene network.²⁰ SEM images reveal that the freeze-dried 3DGF has a well-defined and interconnected 3D porous network with pore sizes ranging from sub-micrometers to several micrometers and pore walls consisting of thin layers of stacked graphene sheets (Fig. 1b). During the reduction of GO, GO sheets changed from hydrophilic to hydrophobic. The combination of hydrophobic and π–π interactions caused a 3D random stacking between flexible graphene sheets.^20,22 Raman spectroscopy is an essential tool to characterize carbonaceous materials with ordered and disordered carbon structures. The Raman spectra of GO and 3DGF are shown in Fig. 1c. Two distinct peaks of 1350 and 1595 cm⁻¹ can be observed, which are assigned to the D and G band of graphene material, respectively. The G band corresponding to the first-order scattering of the E_2g mode symmetry is a characteristic feature of the graphitic layers,²³ while the D band due to the κ-point phonons of A_1g indicates the formation of defects and disorder such as the presence of in-plane hetero-atoms, grain boundaries, aliphatic chain, etc.²⁴ The relative intensity of D band compared to G band is often used to evaluate the defects density in graphene.²⁵ The higher D/G ratio in Raman spectra observed in 3DGF than GO can be attributed to additional defects, this agrees well with the previous report.²⁶ In addition, the intensity ratio of D and G bands (I_D/I_G) can also be utilized to evaluate the in-plane crystallite sizes (L_a) of graphene materials. The crystallite size can be determined based on the Tuinstra–Koenig relationship:

L_a (nm) = (2.4 × 10⁻¹⁰) × λ⁴ × (I_D/I_G)⁻¹ (1)

where λ is the Raman excitation wavelength (λ = 514 nm in our experiment).²⁷ The I_D/I_G values of GO and 3DGF were 0.92 and 1.02, and the crystallite size was calculated to be 18.2 and 16.4 nm, respectively. The crystallite size of 3DGF is smaller than GO, which indicates that the oxidized areas of GO sheets were partly restored upon hydrothermal reduction, forming small conjugated domains.

Fig. 1 (a) Photographs of 3DGF (b) SEM images of 3DGF interior microstructures. (c) Raman spectra of GO and 3DGF.

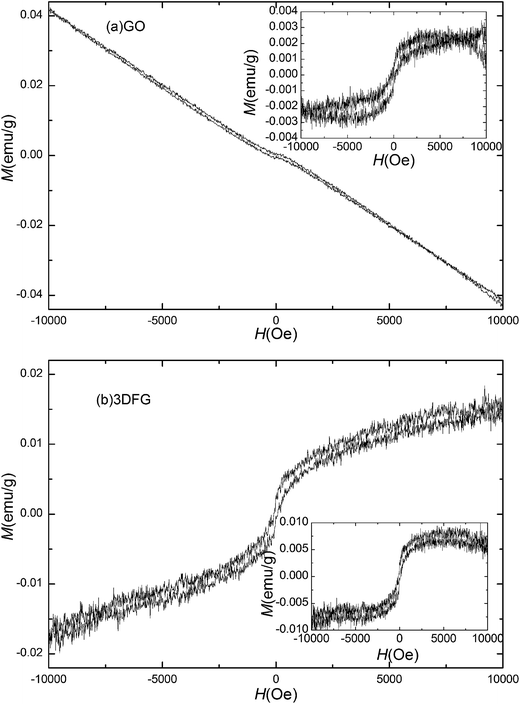
The field dependent magnetization (M–H) curves of GO and 3DGF were measured at room temperature in the field range of −10 kOe < H < 10 kOe, shown in Fig. 2a. The linear M–H curves with negative slope for the VSM rod and sample holder is shown in Fig. S1 (in the ESI†), demonstrating the pure diamagnetic background which has been subtracted in the magnetic data of the samples. Thus the possible ferromagnetic artifacts from the measuring system can be safely excluded. The linear M–H curve with negative slope suggests the diamagnetic properties of GO without any ferromagnetic signals. Besides the main diamagnetic background of 3DGF, a slightly S-shaped curve at low field can be observed in the M–H curve (Fig. 2b), suggesting the dominant diamagnetism with weak ferromagnetism. After subtracting the diamagnetic background, the ferromagnetic contribution can be obtained with saturated ferromagnetic magnetization (M_s) of 0.005 emu g⁻¹, as shown in the inset, which is comparable to the value of reduced GO (photo-irradiated GO for 6 h) reported by Taniguchi et al. (0.004 emu g⁻¹ at room temperature)²⁸ and hydrogenated graphene reported by Eng et al. (0.006 emu g⁻¹) previously.²⁹ It should be noted that the sensitivity of our VSM is in the order of 10⁻⁶ emu. The raw data of M–H curves for GO and 3DGF is shown in Fig. S2 (in the ESI†), and the ferromagnetic signal is one order larger than the sensitivity. To study the difference between the magnetic properties of 3DGF and 2D graphene, the rGO900 (2D graphene) was synthesized from GO by annealing at 900 °C in Ar atmosphere for 1 h. The M–H curve for rGO900 at 300 K is shown in Fig. S3 (in the ESI†). Ferromagnetism with a saturation magnetization of 0.0035 emu g⁻¹ at room temperature was found in the rGO900, a little lower than 3DGF (0.005 emu g⁻¹). We suggest that the stronger ferromagnetism in 3DGF might be due to 3D porous network structure, which needs further study. The observed ferromagnetism in graphene was generally very weak, which has been attributed to the large distance between the adjacent magnetic moments in graphene, leading to the too weak inter-cluster exchange interaction and hindering the formation of long-range magnetic ordering.³⁰ Fig. 3 shows M–H curves for GO and 3DGF at 5 K, with ferromagnetic magnetization shown in the insets. Interestingly, GO also exhibits weak ferromagnetism, which is generated by the interaction between separated magnetic regions and domains, this agrees with the previous report.²⁸ The negative slope at high field indicates the main diamagnetism in GO even at 5 K. Interestingly, the slope at high fields changes to positive for 3DGF. This suggests the high concentration of mainly isolated magnetic functional groups in 3DGF which suppress the diamagnetic contribution from GO matrix. The saturated ferromagnetic magnetization M_s of GO and 3DGF reaches 0.003 and 0.0085 emu g⁻¹, respectively. Compared with GO, the saturated ferromagnetic magnetization of 3DGF is significantly enhanced. The temperature-dependent magnetization (M–T) measurements for GO and 3DGF are shown in Fig. 4, which were measured in the presence of 1 kOe during the warming processes to 300 K after cooling down from 300 K under 1 kOe. For GO, the magnetization is negative above 13 K, which shows the diamagnetic properties of GO. The M–T curve of 3DGF shows two-step behavior, M starts to increase with decreasing T at around 100 K, and a drastic increase of M with decreasing T can be observed below 20 K. The transition at around 100 K is due to that a disordered magnetism exists where different magnetic correlations compete with each other.^31–33 The transition at 20 K indicates that paramagnetic behavior exists in 3DGF. The nearly constant magnetization up to 300 K further confirms the weak ferromagnetism in 3DGF and suggests that the Curie temperature of 3DGF is much higher than room temperature. GO contains many hydroxyl, carboxyl, epoxy, carbonyl groups on the main graphene skeleton.³⁴ Via one-step hydrothermal process, some of these groups were removed, and some of the damaged sp² carbon conjugations were restored. The restored conjugated structure generated partial overlapping or coalescing of flexible graphene sheets with greatly increased amount of π–π stacking sites, which resulted in the formation of physical cross-linking sites of the 3D framework of 3DGF.^20,35 The interconnected 3D porous network structure indicates the possible existence of high density of defects in the 3DGF.

Fig. 2 M–H curves for (a) GO and (b) 3DGF at 300 K. Insets show the ferromagnetic magnetization of 3DGF after subtracting the diamagnetic background.

Fig. 3 M–H curves for (a) GO and (b) 3DGF at 5 K. Insets show the ferromagnetic magnetization after subtracting the high field linear background.

Fig. 4 M–T curves for (a) GO and (b) 3DGF measured under 1 kOe.

To examine the composition of GO and 3DGF, XPS measurements were carried out. In the XPS spectra of GO (Fig. 5a) and 3DGF (Fig. 5b), the peaks appeared at about 284.6 and 532.3 eV corresponding to C 1s and O 1s. XPS studies show that the C/O atomic ratio is 2.3 for GO and 6.4 for 3DGF, respectively. Fig. 5c are the high-resolution C 1s peak of GO, which was deconvoluted into three types of carbon bonds at 284.6, 286.7, 287.7 eV, which correspond to C–C, C–O and C=O, respectively. The C 1s XPS spectrum of 3DGF (Fig. 5d) also exhibits the same peaks. Compared with the spectrum of GO, the peak intensities of the oxygen functional groups of 3DGF are much weaker. The decreasing concentration of oxygen functional groups reflects the reduction of GO to graphene by hydrothermal method. The ‘non-magnetic’ unstable oxygen groups in GO are removed and some ‘magnetic’ stable groups are left, resulting the existence of ferromagnetism in 3DGF.

Fig. 5 XPS survey spectra (a) GO and (b) 3DGF. C 1s spectra for (c) GO and (d) 3DGF.

To further understand which oxygen group plays the important role in the magnetic properties of graphene, the typical O 1s spectra of GO and 3DGF are shown in Fig. 6. Both spectra were decomposed into three main components; OH (hydroxyl C–O) near 531 eV, epoxy/ether (aliphatic C–O) around 523.3 eV, and carbonyl ([double bond splayed left]C=O) at 533.4 eV.^30,36 The peak intensity ratio of epoxy group in oxygen bondings in 3DGF is significantly less than that of GO, suggesting that epoxy group is not the origin of ferromagnetism in 3DGF. It is known that the carbonyl groups usually located at sheet edges, the contribution to magnetic moments by carbonyl groups is insignificant.³⁷ As for OH groups, they can covalently bond to the basal-plane carbon atoms to form sp³-type defects, not only limited to edge or vacancy sites.³⁰ In addition, XPS peak intensity of OH group in oxygen bondings in 3DGF is obviously larger than the other oxygen groups. The ratios of OH, epoxy/ether and carbonyl groups to carbon for GO and 3DGF are shown in Table 1. It can be clearly seen that the concentration of OH groups is significantly increased while the concentrations of the other two groups are obviously reduced. The results definitely suggest that the bonded OH groups in 3DGF contribute to the magnetic moments.

Fig. 6 XPS spectra of O 1s for (a) GO and (b) 3DGF.

Table 1 The ratios of OH, epoxy/ether and carbonyl to carbon for GO and 3DGF from XPS results

	OH/C	(Epoxy/ether)/C	Carbonyl/C
GO	2.15 at%	36.8 at%	4.53 at%
3DGF	7.42 at%	5.15 at%	3.05 at%

---

When ferromagnetism is observed in graphene-based materials, it is often questioned whether the ferromagnetic signals come from magnetic impurities. To check the possible contribution from magnetic impurities, XPS and inductively coupled plasma (ICP) spectrometry were performed. XPS is not a sensitive method for the trace element. The 3d impurity elements of all the samples are lower than the detection limit from the Fe 2p, Co 2p, Ni 2p XPS spectra (not shown here). The highly sensitive technique of ICP analysis was performed, the total amount of magnetic impurities (Fe, Co, Ni) in all the samples was determined to be below 2 ppm. An Fe impurity content of 1 μg g⁻¹ would give the magnetization of 2.2 × 10⁻⁴ emu g⁻¹,³⁸ the observed ferromagnetic magnetization for 3DGF (0.005 emu g⁻¹ at 300 K) should correspond to 23 ppm of Fe (or 167 ppm Ni and 63 ppm Co).²⁹ These results demonstrate the observed ferromagnetism in 3DGF originates from the possible existence of high density of sp³-type hydroxyl defects (OH group) at the interconnected 3D porous network structure instead of magnetic impurities.

4. Conclusions

In summary, we have observed the room temperature ferromagnetism of 3DGF obtained from 2D soluble graphene oxide sheets through one-step hydrothermal method. During the hydrothermal process, some of oxygen functional groups were removed, the restored conjugated structure of GO sheets forms the strong cross-links of the 3D graphene network, high concentration of sp³-type hydroxyl defects (OH group) are introduced in GO, which might be the source of the room temperature ferromagnetism observed in 3D porous graphene sheets network structure. Our results might stimulate more extensive studies on magnetism of three dimensional graphene-based materials and their related spintronics applications.

Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant number 51172044 and 51471085, the Natural Science Foundation of Jiangsu Province of China (BK20151400).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
3. S. Stankovich, D. A. Dikin, G. H. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286.
4. E. Yoo, T. Okata, T. Akita, M. Kohyama, J. Nakamura and I. Honma, Nano Lett., 2009, 9, 2255–2259.
5. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652–655.
6. Y. Zhu, S. Murali, M. D. Stoller, K. J. Ganesh, W. Cai, P. J. Ferreira, A. Pirkle, R. M. Wallace, K. A. Cychosz, M. Thommes, D. Su, E. A. Stach and R. S. Ruoff, Science, 2011, 332, 1537–1541.
7. H. F. Xiang, Z. D. Li, K. Xie, J. Z. Jiang, J. J. Chen, P. C. Lian, J. S. Wu, Y. Yu and H. H. Wang, RSC Adv., 2012, 2, 6792.
8. J. Zhang, X. Liu, H. Zhou, X. Yan, Y. Liu and A. Yuan, RSC Adv., 2014, 4, 28908.
9. L. Li, R. Qin, H. Li, L. Yu, Q. Liu, G. Luo, Z. Gao and J. Lu, ACS Nano, 2011, 5, 2601–2610.
10. D. C. Yan, S. Y. Chen, M. K. Wu, C. C. Chi, J. H. Chao and M. L. H. Green, Appl. Phys. Lett., 2010, 96, 242503.
11. O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408.
12. J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870.
13. S. Bhowmick and V. B. Shenoy, J. Chem. Phys., 2008, 128, 244717.
14. L. Xie, X. Wang, J. Lu, Z. Ni, Z. Luo, H. Mao, R. Wang, Y. Wang, H. Huang, D. Qi, R. Liu, T. Yu, Z. Shen, T. Wu, H. Peng, B. Özyilmaz, K. Loh, A. T. S. Wee, Ariando and W. Chen, Appl. Phys. Lett., 2011, 98, 193113.
15. Y. Liu, N. Tang, X. Wan, Q. Feng, M. Li, Q. Xu, F. Liu and Y. Du, Sci. Rep., 2013, 3, 2566.
16. Q. Feng, N. Tang, F. Liu, Q. Cao, W. Zheng, W. Ren, X. Wan and Y. Du, ACS Nano, 2013, 7, 6729–6734.
17. Z. J. Yue, D. H. Seo, K. Ostrikov and X. L. Wang, Appl. Phys. Lett., 2014, 104, 092417.
18. Z. S. Wu, A. Winter, L. Chen, Y. Sun, A. Turchanin, X. Feng and K. Mullen, Adv. Mater., 2012, 24, 5130–5135.
19. Z. S. Wu, Y. Sun, Y. Z. Tan, S. Yang, X. Feng and K. Mullen, J. Am. Chem. Soc., 2012, 134, 19532–19535.
20. Y. Xu, K. Sheng, C. Li and G. Shi, ACS Nano, 2010, 4, 4324–4330.
21. W. S. Hummers and R. E. Offeman, J. Am. Chem. Soc., 1958, 80, 1339.
22. L. Zhang and G. Shi, J. Phys. Chem. C, 2011, 115, 17206–17212.
23. H. Kim, J. Cho, S. Y. Jang and Y. W. Song, Appl. Phys. Lett., 2011, 98, 021104.
24. K. Krishnamoorthy, M. Veerapandian, K. Yun and S. J. Kim, Carbon, 2013, 53, 38–49.
25. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
26. Y. Xu, Z. Lin, X. Zhong, X. Huang, N. O. Weiss, Y. Huang and X. Duan, Nat. Commun., 2014, 5, 4554.
27. L. G. Cançado, K. Takai, T. Enoki, M. Endo, Y. A. Kim, H. Mizusaki, A. Jorio, L. N. Coelho, R. Magalhães-Paniago and M. A. Pimenta, Appl. Phys. Lett., 2006, 88, 163106.
28. T. Taniguchi, H. Yokoi, M. Nagamine, H. Tateishi, A. Funatsu, K. Hatakeyama, C. Ogata, M. Ichida, H. Ando, M. Koinuma and Y. Matsumoto, J. Phys. Chem. C, 2014, 118, 28258–28265.
29. A. Y. S. Eng, H. L. Poh, F. Sanek, M. Marysko, S. Matejkova, Z. Sofer and M. Pumera, ACS Nano, 2013, 7, 5930–5939.
30. T. Tang, N. Tang, Y. Zheng, X. Wan, Y. Liu, F. Liu, Q. Xu and Y. Du, Sci. Rep., 2015, 5, 8448.
31. P. Sun, K. Wang, J. Wei, M. Zhong, D. Wu and H. Zhu, Nano Res., 2014, 7, 1507–1518.
32. H. S. S. R. Matte, K. S. Subrahmanyam and C. N. R. Rao, J. Phys. Chem. C, 2009, 113, 9982–9985.
33. Y. Kopelevich, R. R. da Silva, J. H. S. Torres, A. Penicaud and T. Kyotani, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 092408.
34. S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217–224.
35. K. Sheng, Y. Xu, C. Li and G. Shi, New Carbon Mater., 2011, 26, 9–15.
36. A. Ganguly, S. Sharma, P. Papakonstantinou and J. Hamilton, J. Phys. Chem. C, 2011, 115, 17009–17019.
37. T. Tang, F. Liu, Y. Liu, X. Li, Q. Xu, Q. Feng, N. Tang and Y. Du, Appl. Phys. Lett., 2014, 104, 123104.
38. P. Esquinazi, A. Setzer, R. Höhne, C. Semmelhack, Y. Kopelevich, D. Spemann, T. Butz, B. Kohlstrunk and M. Lösche, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 024429.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra14377b

---