A theoretical study on borenium ion affinities toward ammonia, formaldehyde and chloride anions

Abstract

Various borenium ion affinities toward three ligands (L′ = NH₃, HCHO and Cl⁻) have been evaluated by DFT calculations in the gas-phase and in solvent (CH₂Cl₂). The gas-phase results have been rationalized on the basis of quantitative decomposition of the total binding energy into contributions from electrostatic, orbital, dispersion and Pauli interactions, and energy needed to deform the interacting fragments from their optimal geometry to that they adopt in an adduct. Twenty six borenium cations, differing in the type of the two R/R′ substituents covalently bound to the boron atom and the neutral stabilizing ligand L, have been examined. With a few exceptions, the most important stabilizing interaction is electrostatic, more pronounced in the case of the charged ligand Cl⁻. Next come orbital interactions, involving the coordinate covalent bond formation, other charge transfer interactions between the cation and ligand, and polarization. Dispersion forces provide the smallest attraction, except in four complexes with long B–L′ distances. We present how substituent (R/R′)/ligand (L) variations affect binding enthalpies (ΔH)/energies (ΔE). Our results also show that the observed trend in the magnitudes of ΔHs/ΔEs represents an interplay of the above mentioned (de)stabilizing energies, and can be explained by consideration of the boron–ligand distance and all charge/orbital interactions, rather than partial ones involving boron and ligand L′. Under solvent conditions, the Cl⁻ affinities are drastically reduced and made very similar to NH₃ affinities, but still larger than HCHO affinities.

---

Introduction

The chemistry of the three-coordinate boron cations, known as borenium ion 1,¹ is characterized by their exceptional Lewis acidity arising from the intrinsic electron deficiency of boron, enhanced by an overall positive charge (Fig. 1).² These species can be viewed as Lewis adducts of even more electrophilic di-coordinate borinium ion 2 with a Lewis base L. If another neutral ligand L′ binds to borenium ion 1, a four-coordinate boronium ion 3 is formed. While the majority of older reports were focused on the synthesis, characterization and gas-phase reactivity of boron cations,^1,2a their condensed-phase reactions have attracted considerable interest in recent years. Borenium ions 1 are increasingly exploited as (chiral) Lewis acid catalysts in organic synthesis^2b,3 and as electrophilic borylation agents.^2b,4

Fig. 1 Structures of borenium 1, borinium 2 and boronium 3 cations.

Although the borenium ion chemistry is based on their Lewis acidity, quantitative data that would allow one to rank a broader range of borenium species according to Lewis acidity are rather scarce. Prokofjevs^2b,5 calculated gas-phase ammonia affinities of a series of borenium ions, the majority of which comprised structures of synthetic interest. The results showed a wide range of ΔH values (>50 kcal mol⁻¹),^2b,5 compared to the narrower one for neutral borane derivatives (>30 kcal mol⁻¹).⁶ Solomon et al.^4c ranked [CatBNR₃]⁺[AlCl₄]⁻ and [(CatS₂)BNR₃]⁺[AlCl₄]⁻ with respect to their ability for electrophilic arene borylation and found the reactivity of [(CatS₂)BNR₃]⁺[AlCl₄]⁻ to lie between that of dichloro- and catecholato-boron electrophiles. The related N,N′-(2,6-diisopropylphenyl)-2-bromo-1,3,2-diazaborole was resistant to halide abstraction, obviously due to steric hindrance.^4c Clark et al.⁷ calculated hydride anion affinities (HIAs) and chloride anion affinities (CIAs) of [Cl₂BL]⁺, [PhClBL]⁺, [CatBL]⁺ and [(CatS₂)BL]⁺ species, where L = NR₃, PtBu₃, pyridine and 2,6-lutidine. Although, there was a general correlation between HIAs and CIAs, a number of deviations were explained by an enhancement of relative CIAs, compared to relative HIAs, due to the increased positive charge at boron and greater steric demand of chloride compared to hydride. Replacement of catechol with chlorides resulted in a significant increase of both HIAs and CIAs.⁷ In an earlier work, aimed at gaining insight into the structure and bonding in boron cations, the relative B–L bond dissociation energies in [R₂BL]⁺ species were calculated (R = H, NH₂; L = H₂O, pyridine, NH₂Me, HCN, CO, PH₃, H₂S). These actually correspond to the L affinities of borinium ions 2 and show the extent of borenium ion stabilization provided by ligand L.⁸ Borinium ion derived from CatBCl was estimated to be a powerful Lewis acid, having stronger affinity toward Et₃PO than Et₃Si⁺, BBr₃, AlCl₃ and B(C₆F₅)₃.⁹

Lewis acidity of an acid is dependant on the structure of a Lewis base. Hence, we will use the term binding affinity to refer to the strength of a coordinate covalent bonding (or dative bonding) between an ion of the type 1 and a new ligand L′, while an intrinsic Lewis acidity can be evaluated by determination of boron's valence deficiency and is not related to the covalent bond strength.⁶

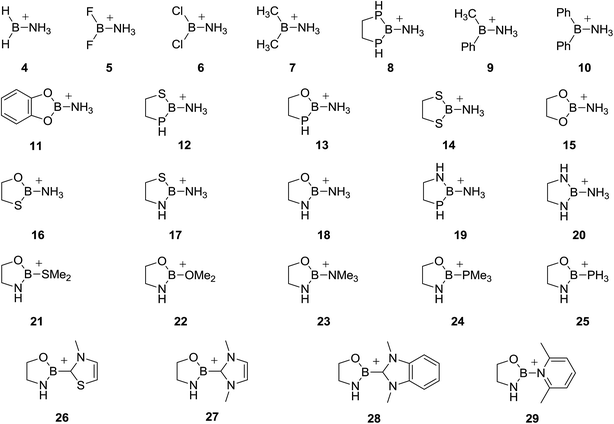
Due to the scarce literature data, we have performed a systematic computational study with an aim to obtain information about substituents (R/R′) and ligand (L) effects on binding affinities of a series of borenium ions 1 toward a new ligand L′. In the first part of the work, boron cations 4–20 differing in substituents R/R′ and having the same L = NH₃, were examined as model compounds (Fig. 2). Since many known and synthetically useful borenium ions are (poly)cylic systems, heteroatom substituents (N, O, P and S) were included in a five-membered ring (structures 8, 11–20). In the second part of the work, the R/R′ moiety, chosen to be 1,3,2-oxazaborolidine heterocycle, was kept constant, while L was varied to include model ligands of synthetic interest such as amines (Me₃N), phosphines (PH₃, Me₃P), ethers (Me₂O), thioethers (Me₂S), 2,6-lutidine (lut) and carbon-based ligands (carbenes), represented by structures 21–29. All cations were computationally tested for their binding affinities toward ammonia, formaldehyde and chloride anion, in the gas-phase and in the solvent, chosen to be CH₂Cl₂, often used in borenium-ion chemistry. Ammonia has been chosen because ammonia–borane complexes are considered as prototypes of the coordinate covalent bond.^6,10 Since an important synthetic application of borenium ions is their Lewis acid catalysis involving carbonyl compounds as substrates,^2b,3f formaldehyde was selected as a model ligand to represent this type of compounds. Finally, chloride anion is often the one that has to be removed from boron atom so that borenium ion can be generated. The accessibility of borenium species has thus been estimated by evaluation of chloride anion affinities.

Fig. 2 Structures of borenium cations examined in this work.

Computational details

All calculations have been done at the DFT level, by using the M06-2X functional¹¹ and 6-311++G(d,p) basis set.¹² The M06-2X functional has been shown to accurately model coordinate covalent bonding^6,13 and was chosen for this study (see ESI† for more details on comparison of the chosen theory level with experimental data and previous calculations, Table S1;† for additional calculations performed at the M06-2X/aug-cc-pVDZ¹⁴ and MP2/6-311++G(d,p)¹⁵ levels for NH₃-complexes of 4–8, see Table S2 in the ESI† and the associated discussion). All geometries were fully optimized using the Gaussian 09 program package,¹⁶ followed by frequency calculations to find whether they correspond to energy minima (no imaginary frequencies). The G09 default geometry convergence criteria were used, that is max force 4.5 × 10⁻⁴, RMS force 3 × 10⁻⁴, max disp 1.8 × 10⁻³ and RMS disp 1.2 × 10⁻³, and fine integration grid. At the theory level employed, structure 4, with shallow potential energy surface, could not be optimized as a true minima, that is, it contained an imaginary frequency: 140.23i cm⁻¹.

Binding enthalpies (ΔH) and binding energies (ΔE) were calculated as shown in eqn (1). Gas-phase values are corrected for the basis set superposition error (BSSE) by using the counterpoise (CP) method of Boys and Bernardi¹⁷ (for the effect of BSSE corrections on molecular geometries and thus obtained ΔHs/ΔEs, see Table S2 in the ESI† and the associated discussion).

ΔH/ΔE = ΔH/ΔE_{Lewis adduct} − [ΔH/ΔE_{borenium cation} + ΔH/ΔE_L′] (1)

The binding energy ΔE consists of two parts, deformation energy (ΔE_def) and interaction energy (ΔE_int), as shown in eqn (2):

ΔE = ΔE_def + ΔE_int (2)

When two species (cation and ligand L′) associate, their geometries change. An energy required for this change is described as deformation energy (ΔE_def), and represents energy of isolated cation and ligand L′ at adduct geometry minus energy of isolated cation and ligand L′ at their optimal geometry, eqn (3).

ΔE_def = (ΔE_{cation in adduct} + ΔE_{L′ in adduct}) − (ΔE_{cation optimal} + ΔE_{L′ optimal}) (3)

In the analysis, structural changes due to (partial) rehybridization of boron atom, following the complex formation, are involved in this energy term. The interaction energy (ΔE_int) reflects the energy of adduct formation from two deformed fragments, cation and L′.

To gain an insight into the nature of borenium cation–ligand interactions, the ΔE_int was partitioned into five energy terms (eqn (4)), by using the localized molecular orbital energy decomposition analysis (LMOEDA), developed by Su and Li¹⁸ and implemented into the Gamess programe package.¹⁹

ΔE_int = ΔE_elstat + ΔE_ex + ΔE_rep + ΔE_pol + ΔE_disp (4)

The electrostatic energy (ΔE_elstat) comprises attractive (nucleus–electron) and repulsive (nucleus–nucleus, electron–electron) forces between the two deformed fragments that adopt their position in the adduct. This energy is usually stabilizing, since attractive interactions outweigh the repulsive ones. The exchange energy (ΔE_ex) refers to the quantum mechanical exchange between the same-spin electrons and is simultaneously counteracted by the repulsion energy (ΔE_rep). Taken together, they form the exchange repulsion²⁰ or Pauli repulsion²¹ of other EDA schemes. Herein, we use the sum of ΔE_ex and ΔE_rep to represent the Pauli repulsion. The polarization energy (ΔE_pol) is an orbital relaxation energy accounting for charge transfer (donor–acceptor interactions between occupied orbitals on one fragment with empty orbitals on the other) and polarization (empty-occupied orbital mixing within one fragment due to the presence of another fragment). Although, this energy component is denoted as ΔE_pol in the original reference,¹⁸ herein we will label it as ΔE_oi, to account for all orbital interactions, and refer to it as the orbital interaction energy. The dispersion energy (ΔE_disp) comes from mutual correlation of electrons. All interaction energy terms are also counterpoise-corrected. The EDA was done for the gas-phase conditions, as was the natural bond orbital (NBO) analysis, performed at the same theory level by using the NBO version 6.0 (ref. 22) linked to Gaussian 09.

The gas-phase optimized geometries were used for the liquid-phase calculations of ΔEs. Solvent effects were taken into account by using the integral equation formalism polarizable continuum model (IEFPCM, solvent = CH₂Cl₂).²³

Results and discussion

Geometries of borenium ions 4–29

Optimized geometries of borenium ions 4–29 are presented in Fig. S1 in the ESI.† The [H₂BNH₃]⁺ cation 4 possesses a quite shallow potential energy surface (PES) with respect to the B–N bond rotation. The energy difference between the eclipsed (φ_HBNH = 0°) and orthogonal (φ_HBNH = 90°) structures, both of C_s symmetry, was less than 5 cal mol⁻¹. The lowest energy structure (by 0.9 cal mol⁻¹ more stable than the orthogonal one) had the HBNH torsional angle of 97° and it was taken as a reference for estimation of adduct formation energies. Halo-substituted borenium cations 5 and 6 feature the C_s symmetry structure with one of the N–H bonds lying perpendicularly to the Hal₂B plane. Dimethyl-substituted cation 7 has almost eclipsed N–H/B–C bonds with φ_HNBC = −1.5°. Two of the C–H bonds are also nearly eclipsed with the B–N and B–C bonds (φ_HCBN = 12.7° and φ_HCBC = −8.8°). All they point into the same direction. Optimization of Me,Ph-substituted cation 9 resulted in a structure in which one of the C–H bonds of Me part and one of the N–H bonds of NH₃ moiety are found almost in plane with the phenyl ring, and they point into the same direction, the C–H bond being oriented toward the Ph ring. In diphenyl-substituted borenium ion 10 one of N–H bonds forms a small diedral angle with one of the B–C bonds (φ_HNBC = 11.4°, while both phenyl rings are tilted from the CBN plane by ∼30° and ∼20°. Five-membered heterocyclic ring in borenium ions 8 (P,P), 14 (S,S), 16 (O,S), 17 (N,S) and 20 (N,N) adopts a half-chair conformation, which is significantly flattened in 20. One of the N–H bonds in the NH₃ moiety is nearly perpendicular to the RBR′ plane in 8 (φ = 89.4°), 14 (φ = 86.7°) and 20 (φ = 89.8°). When heteroatoms connected to boron atom differ, one of the N–H bonds in the NH₃ part is almost eclipsed with the B–O_ring bond in 16 (φ_HNBO = −4°) and B–N_ring bond in 17 (φ_HNBN = −5.1°). The N–H bond in the heterocycle is mostly in the NBN(S) plane in 17 (N,S) and 20 (N,N), which is not the case for the P–H bond. This is consistent with stronger electron-donating ability of N atom compared to P atom. The five-membered ring in cations 12, (P,S), 13 (P,O) and 19 (P,N) exists in envelope-like conformation with the C(4) atom, bound to phosphorus, being out of plane of the other four atoms. The conformation around the exocyclic B–N bond is such that one of the N–H bonds is found nearly eclipsed with the B–S_ring bond in 12, (φ_HNBS = −10.4°), B–O_ring bond in 13 (φ_HNBO = −6.4°) and B–N_ring bond in 19 (φ_HNBN = −5.4°). The heterocyclic part in cations 15 (O,O) and 18 (N,O) is nearly planar, while one of the N–H bonds in the NH₃ group is oriented almost perpendicularly with respect to the OBO(N) plane (φ = 83.9° in 15, φ = 86.2° in 18). The structure of [CatBNH₃]⁺11 possesses the C_s symmetry with one of the N–H bonds being perpendicular to the aromatic ring.

The B–R bond lengths in symmetrically substituted heterocyclic structures decrease in the following order: 1.865 Å in 8 (P,P) > 1.766 Å in 14 (S,S) > 1.389 Å in 20 (N,N) > 1.328 Å in 15 (O,O). If we order the heteroatoms as N, O, S, P it can be said that the replacement of any of these atoms in any of the heterocyclic structure (symmetrically or unsymmetrically substituted) by the one which is left to it will lengthen the remaining B–heteroatom bond, whereas substitution of any atom by the one which is right to it will shorten the remaining B–heteroatom bond.²⁴ The strength of the effect follows the above atomic order, that is nitrogen/phosphorus most increases/decreases the other B–heteroatom bond. For example, the B–P/B–N bond is the longest/shortest in 19, 1.913/1.369 Å. The B–L bond lengths range from 1.535 Å in 11 to 1.592 Å in 9. The B–R/R′ and B–L bond lengths for all studied borenium ions are given in Table S3 in the ESI.†

The 1,3,2-oxazaborolidine ring in all cations 21–29 adopts a significantly flattened half-chair conformation. One of the C–N, C–P and H–P bonds in L part of structures 23–25 is almost eclipsed with the B–N_ring bond (φ_CNBN = −3.5° in 23, φ_CPBN = −7.8° in 24 and φ_HPBN = −3° in 25). In 22, both C–O bonds form small diedral angles with the B–N_ring and B–O_ring bonds (φ_COBN = 5.8° and φ_COBO = −14.3°), which is the result of a strong O to B electron-donation making the oxygen atom mostly sp² hybridized. By contrast, ion 21, stabilized by Me₂S, is most stable in conformation in which the B–O_ring bond bisects the MeSMe angle. The two rings in carbene-stabilized structures 26 and 27 are just slightly twisted (by less than 11°). In the case of 26, the cis-ON conformation is by 1.5 kcal mol⁻¹ more stable than the cis-OS one, and it was used as a reference for the complex formation energies. The carbene part in 28 is tilted by 31° from the NBO plane of 1,3,2-oxazaborolidine moiety, while the two rings in 29 adopt a perpendicular conformation. Cartesian coordinates of all optimized structures are given in the ESI.†

Geometries of borenium ion complexes with NH₃, HCHO and Cl⁻

Optimized geometries of all complexes are presented in Fig. S2–S4 in the ESI.† In the case of NH₃-complexes with 4–9, 11–20 and 23–29, one binding geometry was obtained. For those formed from 10, 21 and 22, some conformational variations may be possible, particularly around the C_Ar–B bond in 10. In these cases one geometry was optimized. One binding geometry was obtained for HCHO-complexes derived from cations having the same R/R′. When R ≠ R′, two geometries, having HCHO oriented toward either substituent, were optimized. The more stable ones are discussed in this section and shown in the ESI.†

Upon complex formation, the trigonal planar geometry around boron atom changes to, more or less, tetrahedral. The hydrogen-, halo-, methyl- and Cat-substituted ammonia adducts formed from 4–7 and 11 feature the C_2v symmetry structures, while the adduct formed from Me,Ph-borenium ion 9 possesses the C_s symmetry with the B–Me bond lying in the plane of the phenyl ring. In ammonia adducts with ions having a heterocyclic ring, this ring adopts (flattened) half-chair conformation. Just one exception is complex formed from 12 (P,S), in which the heterocyclic part exists in the envelope conformation having the C(4) atom out of plane of the other four atoms. The structures with the same heteroatoms have the C₂ symmetry. While Me₂S-, Me₂O-, Me₃N- and Me₃P-stabilized borenium cations 21–24 form Lewis complexes with ammonia, reaction of phosphine-stabilized ion 25 ends up with PH₃ substitution. All carbene- and lut-stabilized ions 26–29 bind ammonia. Upon complex formation, the most drastic geometry change in a cation occurs in the case of 26 and 29. In the former, near-to-planar geometry changes to the orthogonal one having NH₃ at the sulfur side of thiazole ring. The opposite happens with 29, the structure of which changes from orthogonal to wing-shaped, in order to make a place for the NH₃ ligand. Otherwise, ligand approach to boron is blocked by the two ortho-methyl groups. These geometry changes are reflected in high ΔE_def values, as will be discussed. Geometries of 27 and 28 in an adduct are wing-shaped, due to the change in hybridization of the boron atom.

The lowest energy structures of Lewis adducts formed from hydrogen-, halo- and methyl-substituted cations 4–7 with formaldehyde (slightly) deviate from the fully symmetric ones (C_s). The COBN torsional angles amount: φ_COBN = −164.6° in [4-HCHO]⁺, φ_COBN = −155.8° in [5-HCHO]⁺, φ_COBN = −178.5° in [6-HCHO]⁺ and φ_COBN = ∼180° in [7-HCHO]⁺ complex. In the case of [9-HCHO]⁺ and [10-HCHO]⁺ adducts, the angles are φ_COBN = 155° and φ_COBN = 157.9°, respectively, with the H₂C-part of formaldehyde being oriented toward the phenyl ring in the former. In complex derived from [CatBNH₃]⁺ ion 11, one of formaldehyde hydrogen atoms is situated above an oxygen atom from the Cat-part, having φ_COBN = −149.3°. In complexes formed from cations 8 and 12–17, the heterocyclic ring exists in the half-chair conformation, which is flattened in the case of 15. The COBN diedral angles amount: φ_COBN = −164.9° in [8-HCHO]⁺ (P,P), φ_COBN = −155.5° in [12-HCHO]⁺ (P,S), φ_COBN = −139.2° in [13-HCHO]⁺ (P,O), φ_COBN = −168.6° in [14-HCHO]⁺ (S,S), φ_COBN = −141° in [15-HCHO]⁺ (O,O), φ_COBN = −142.4° in [16-HCHO]⁺ (O,S) and φ_COBN = −165° in [17-HCHO]⁺ (N,S). One of formaldehyde hydrogen atoms is always oriented toward or above a ring heteroatom. When they differ, it is the more electronegative one. Optimizations of [18-HCHO]⁺ (O,N) and [19-HCHO]⁺ (P,N) complexes starting from different geometries resulted in two structures: one in which HCHO is hydrogen-bonded to ring and ammonia NH bonds in [18-HCHO]⁺ and only ammonia NH bond in [19-HCHO]⁺, and other in which HCHO binds to boron atom. Hydrogen bonded complexes are by 4.8 kcal mol⁻¹ and 5.5 kcal mol⁻¹, respectively, lower in energy. In both boron-bound adducts, ring conformation is envelope with C(4) bound to N in [18-HCHO]⁺ and bound to P in [19-HCHO]⁺ pointing out of plane. In [18-HCHO]⁺, formaldehyde hydrogen atom lies above the ring oxygen atom (φ_COBN = 137°). The COBN diedral angle is larger in [19-HCHO]⁺ (φ_COBN = −172°), the HCHO just slightly pointing toward the ring nitrogen atom. Cation 20 (N,N) forms only hydrogen bonded complex in which carbonyl oxygen atom orients towards the two N–H bonds, one belonging to the heterocycle, the other to the NH₃ part. The heterocyclic ring in [21-HCHO]⁺ adduct adopts an envelope conformation with C(4) atom bound to N pointing out of plane of the other four atoms. One of the formaldehyde hydrogen atoms is placed above the ring oxygen and φ_COBS amounts 132.9°. In complexes formed from 22–25, the heterocyclic part is in the half-chair conformation, which is appreciably flattened in [24-HCHO]⁺. In [22-HCHO]⁺ and [23-HCHO]⁺ formaldehyde hydrogen atom is situated above the ring nitrogen, while in [24-HCHO]⁺ and [25-HCHO]⁺ it lies above the ring oxygen atom. Diedral angles are: φ_COBO = 150.4° in [22-HCHO]⁺, φ_COBN = 156.7° in [23-HCHO] ⁺, φ_COBP = −147.5° in [24-HCHO]⁺ and φ_COBP = −130° in [25-HCHO]⁺. Carbene-stabilized cations 26–28 bind HCHO in such a way that one of its hydrogen atoms orients toward the 1,3,2-oxazaborolidine ring nitrogen in 26, and 1,3,2-oxazaborolidine ring oxygen in 27 and 28, with φ_COBC = 141.8°, φ_COBC = −134.2° and φ_COBC = −117.8°, respectively. The 1,3,2-oxazaborolidine is in flat half-chair conformation. The OBN and carbene planes form angles of 18.5° in 26, 21.4° in 27, and 39.7° in 28. In the case of HCHO binding, the geometry of cation 26 does not change to the orthogonal one, as it does upon NH₃ binding. This could be ascribed to the long B–OCH₂ distances in adducts derived from 26–28 (together with [24-HCHO]⁺, they are the longest among all complexes studied), so that HCHO does not interfere much with the original cation structure. Borenium cation 29 does not bind HCHO at boron atom, but forms hydrogen-bonded complex involving carbonyl oxygen and NH_ring group.

Reactions of hydrogen-, fluoro-, methyl- and Cat-substituted borenium cations 4, 5, 7 and 11 with chloride anion result in structures with the C_s symmetry. The structure formed from chloro-substituted cation 6 has the C_3v symmetry. In the case of product obtained from Me,Ph-substituted ion 9, the Me–B bond forms small diedral angle with the phenyl ring, φ_CBCC = −15.5°. Products formed from 8 (P,P), 14 (S,S), 15 (O,O) and 17 (N,S) contain five-membered ring in half-chair conformation which is flattened in 15-Cl. The structure of the ring part in adducts obtained from 12 (P,S), 13 (P,O), 16 (O,S), 18 (O,N), 19 (P,N) and 20 (N,N) corresponds to envelope-like conformation with the C atom bound to P in 12, 13 and 19, and bound to O in 16 and 18 being out of plane. Reactions of Me₂S- and H₃P-stabilized cations 21 and 25 with chloride result in L substitution, while all other cations 22–24 and 26–29 form tetra-coordinated products. As in the case of the formation of ammonia-complexes, an analogous geometry change occurs in cations 26 and 29, while 27 and 28 adopt a wing-shaped structure due to the change in boron's hybridization. Cartesian coordinates of all optimized complexes are given in the ESI.†

Binding enthalpies and energy decomposition analysis

We first checked if there exists any correlation between the gas-phase binding enthalpies (ΔH)/energies (ΔE) and the following parameters: (1) B–L′ distance in a complex (given in Tables 1–4), (2) calculated NBO charge at boron atom of a borenium cation and (3) calculated electron occupancy of boron's p-orbital in a borenium cation. Values for the latter two are shown in Table S3 in the ESI.†

Table 1 Calculated B–NH₃ distances (d_BN, Å), NH₃ affinities (ΔH at 298.15 K and ΔE, values in italic are in CH₂Cl₂) and energy decomposition of binding interactions.^a,b,c,d All energy values are in kcal mol⁻¹

Ion	d BN	ΔH	ΔE	ΔEdef	ΔEint	ΔEelstat	ΔEex+rep	ΔEoi	ΔEdisp
a Calculated at the M06-2X/6-311++G(d,p)//M06-2X/6-311++G(d,p) level. b Gas-phase association enthalpies (ΔH), energies (ΔE) and all interaction energy terms are corrected for the BSSE by using the counterpoise method. c ΔE = total binding energy, ΔEdef = deformation energy, ΔEint = interaction energy, ΔEelstat = electrostatic energy, ΔEex+rep = exchange repulsion energy, ΔEoi = orbital interaction energy, ΔEdisp = dispersion energy. d Values in parentheses are percentage contribution to all attractive interactions.
4	1.613	−54.37	−58.88, −53.59	18.64	−77.63	−96.31 (45.4%)	134.37	−95.14 (44.9%)	−20.55 (9.7%)
5	1.618	−49.82	−52.40, −49.51	28.77	−81.17	−108.42 (46.8%)	150.33	−100.22 (43.3%)	−22.86 (9.9%)
6	1.608	−44.83	−48.23, −50.10	27.03	−75.26	−120.73 (45.5%)	190.32	−120.07 (45.2%)	−24.78 (9.3%)
7	1.640	−36.69	−40.47, −38.90	21.32	−61.79	−98.16 (46.3%)	150.44	−90.66 (42.7%)	−23.41 (11.0%)
8	1.621	−33.85	−37.07, −40.38	25.14	−62.21	−115.14 (46.1%)	187.82	−110.72 (44.3%)	−24.17 (9.6%)
9	1.638	−32.87	−36.32, −37.78	23.07	−59.39	−103.83 (46.2%)	164.84	−95.72 (42.6%)	−25.13 (11.2%)
10	1.630	−30.92	−33.70, −36.94	27.22	−60.92	−107.28 (46.1%)	172.03	−98.47 (42.3%)	−27.20 (11.6%)
11	1.628	−29.45	−31.72, −33.46	29.32	−61.04	−118.59 (47.6%)	187.89	−107.55 (43.2%)	−22.79 (9.2%)
12	1.627	−28.56	−31.52, −34.40	29.45	−60.97	−115.88 (46.1%)	190.23	−111.17 (44.3%)	−24.15 (9.6%)
13	1.643	−26.65	−29.20, −30.47	27.54	−56.74	−106.99 (46.8%)	171.88	−98.38 (43.0%)	−23.25 (10.2%)
14	1.625	−26.62	−29.42, −32.03	30.31	−59.73	−120.33 (46.2%)	200.47	−115.69 (44.5%)	−24.18 (9.3%)
15	1.639	−26.28	−28.30, −27.84	33.00	−61.30	−105.64 (47.5%)	161.24	−94.41 (42.4%)	−22.49 (10.1%)
16	1.638	−26.15	−28.69, −30.05	29.07	−57.76	−111.99 (47.0%)	180.72	−103.16 (43.3%)	−23.33 (9.7%)
17	1.653	−18.82	−20.86, −20.95	29.76	−50.62	−110.65 (47.2%)	183.86	−100.84 (43.0%)	−22.99 (9.8%)
18	1.653	−18.72	−20.56, −19.52	32.73	−53.29	−105.06 (47.7%)	166.92	−92.87 (42.2%)	−22.28 (10.1%)
19	1.655	−18.23	−20.32, −20.19	30.44	−50.76	−106.37 (47.1%)	175.16	−96.68 (42.8%)	−22.87 (10.1%)
20	1.667	−12.87	−14.74, −13.59	31.68	−46.42	−104.06 (47.9%)	170.87	−91.21 (42.0%)	−22.02 (10.1%)

---

The results show that ΔHs/ΔEs are moderately correlated with the B–L′ bond length having correlation coefficients of R² = 0.74/0.74 for NH₃ complexes with cations 4–20, R² = 0.88/0.88 for NH₃ complexes with cations 21–29, R² = 0.56/0.57 for HCHO complexes with 4–20, R² = 0.37/0.35 for Cl⁻ adducts with 4–20 and R² = 0.77/0.78 for Cl⁻ adducts with 21–29. As expected, better accommodation of a ligand (shorter B–L′ bond) leads to stronger attractive interactions (nucleus–electron electrostatic attraction, orbital and dispersion interactions), but also to larger repulsive interactions (nucleus–nucleus, electron–electron electrostatic repulsion and Pauli repulsion). It is their relative magnitude (substituent-dependent) that determines the strength of cation–ligand interaction, along with energy spent for fragment deformations. There was no correlation between ΔHs/ΔEs and B–O distance in the case of HCHO-complexes with cations 21–29.

The ΔHs/ΔEs did not show any correlation with the positive charge located at boron atom in borenium cations. Likewise, charges at boron do not correlate with the net electrostatic attractive energies between cation and ligand L′. This lack of correlation can be rationalized by taking into account the two effects: (1) distance-sensitivity of this type of interactions and (2) electrostatic forces could better be explained as an all-charge phenomenon, not as partial interactions between individual atoms or group of atoms. Therefore, these results show that electrostatic interactions between boron and ligand do not play an important role in overall binding affinity and are even not dominant electrostatic forces.

As the electron occupancy of boron's p-orbital increases, binding enthalpies/energies should decrease (become less negative), due to diminished availability of boron to accept electron density. This trend was found for complex formation between 4–20 and all examined ligands, though correlation coefficients were low: R² = 0.44/0.45 for NH₃ complexes, R² = 0.47/0.49 for HCHO complexes and R² = 0.27/0.29 for adducts with Cl⁻. Variations of boron's p-orbital electron occupancies due to change of L bound to boron in cations 21–29 did not show the correct correlation with ΔHs/ΔEs. The same stands for the orbital interaction energy ΔE_oi of complexes and boron's p-orbital occupancies. This can be explained by taking into account the following: (1) distance-dependence of orbital interactions and (2) in addition to coordinate covalent bonding, other cation–ligand charge transfer (hyperconjugative) interactions and polarization have important contribution to total orbital interactions.

Thus, the overall strength of cation–ligand interactions will be considered as an interplay of various interactions involving all atoms contained in cation and ligand L′, and a distance at which cation and L′ approach each other.

Ammonia affinity of cations 4–20

Calculated binding enthalpies (ΔH), energies (ΔE) and LMOEDA analysis of binding interactions between borenium ions 4–20 and NH₃ are presented in Table 1, along with the calculated B–NH₃ distances. The gas-phase results will be discussed first, followed by discussion of solvent effects on ΔEs, which are presented in the last paragraph of this section.

The ΔHs range from −54.4 kcal mol⁻¹ for the strongest acceptor 4 (H,H)²⁵ to −12.9 kcal mol⁻¹ for the weakest acceptor 20 (N,N). The ΔEs show almost the same trend as ΔHs (there are two exceptions, cations 13 and 14, and 15 and 16, for which the trend in ΔEs is the reverse to that in ΔHs, though energy differences are quite small and correlation between ΔHs and ΔEs is high, R² = 0.999). Calculated B–NH₃ distances range from 1.608 Å in 6 (Cl,Cl) to 1.667 Å in 20. As a comparison, the experimentally determined B–N bond length in BH₃–NH₃ complex amounts 1.6576(16) Å.²⁶ Deformation energy (ΔE_def) is the smallest for 4 (18.6 kcal mol⁻¹), which is expected due to the small steric hindrance from hydrogen atoms, and the largest for 15 (O,O) (33 kcal mol⁻¹). The net stabilizing energy of a complex is determined by the relative magnitudes of deformation and interaction energies, so that ΔE_int do not follow exactly the same trend as ΔHs/ΔEs.

The LMOEDA shows that the nature of binding interactions is pretty much the same in complexes formed from all cations 4–20: major contributions to complex stabilization come from ΔE_elstat (45.4% in 4 to 47.9% in 20) and ΔE_oi (42% in 20 to 45.2% in 6), while ΔE_disp range from 9.2% in 11 to 11.6% in 10. The contributions of ΔE_elstat and ΔE_oi are almost equal in 4 and 6, while in all other complexes the percentage contribution of electrostatic interactions slightly overcomes the percentage contribution of orbital interactions.

The strongest ammonia acceptor 4 (H,H), ΔH/ΔE = −54.4/−58.9 kcal mol⁻¹ owes its large binding affinity to the small deformation energy and large interaction energy (ΔE_int is larger only in adduct formed from 5). As a comparison, the counterpoise-corrected interaction energy in BH₃–NH₃ ranges from −39.8 kcal mol⁻¹ to −44.2 kcal mol⁻¹, at various theory levels employed.¹⁸ In the case of [4-NH₃]⁺, the magnitudes of electrostatic and dispersion energies are the smallest among all complexes studied, while orbital interactions exceed those in only four ammonia adducts (formed from 7, 15, 18 and 20). This means that the large ΔE_int originates from the small Pauli repulsion, not from strong attractive interactions, again related to the small steric hindrance in the case of hydrogen atoms as substituents.

The NH₃ affinity of 4 is followed by that of 5 (F,F), ΔH/ΔE = −49.8/−52.4 kcal mol⁻¹, and then by that of 6 (Cl,Cl), ΔH/ΔE = −44.8/−48.2 kcal mol⁻¹. Interestingly, whereas BCl₃ binds ammonia more strongly than BF₃ by ΔH/ΔE = 3.2/3.8 kcal mol⁻¹ at the employed theory level (see Tables S1 and S4 in the ESI† and ref. 6), the order of NH₃ affinities of 5 and 6 is reversed: cation 5 binds NH₃ more strongly than 6 by ΔH/ΔE = 5/4.2 kcal mol⁻¹. The reason for this opposite trend lies in the interaction energy term, since deformation energies are almost the same in the case of the two neutral boranes (Table S4†), and slightly larger for the adduct formation from 5. As LMOEDA reveals, in both borane and borenium ion adducts with NH₃ the Pauli repulsion is larger in the case of chloro derivatives and more so for neutral boranes. Thus, the reversed order of interaction energy (ΔE_int = −48.3/−52.1 kcal mol⁻¹ for BF₃–NH₃/BCl₃–NH₃, ΔE_int = −81.2/−75.3 kcal mol⁻¹ for [5-NH₃]⁺/[6-NH₃]⁺) stems from a significant increase in ΔE_elstat (by 13.1 kcal mol⁻¹) and ΔE_oi (by 25.2 kcal mol⁻¹) when one fluorine in BF₃ is replaced with NH₃. In the case of chloro-compounds, the increase in electrostatic and orbital stabilization in complexes upon one chlorine substitution in BCl₃ with NH₃ is much smaller, by 0.9 kcal mol⁻¹ and 7 kcal mol⁻¹, respectively. Dispersion interactions practically do not change in the case of fluoro derivatives, but decrease by 1.2 kcal mol⁻¹ when more polarizable chlorine is exchanged with the ammonia. It should also be noted that 5 deserves its higher affinity toward ammonia than 6 to smaller Pauli repulsion, while all attractive energy components are larger in [6-NH₃]⁺. Thus, in the case of complex formation with borenium cations, larger atoms, from the second octal row of periodic table, provide more electrostatic, orbital and dispersion stabilization and larger Pauli destabilization. This holds for other heteroatoms, too, as will be seen in further discussion.

When halogen substituents in borenium ion are substituted with two methyl groups to form 7, the affinity toward NH₃ drops by ΔH/ΔE = 8.1/7.8 kcal mol⁻¹, compared to 6, and by ΔH/ΔE = 13.1/11.9 kcal mol⁻¹, compared to 5. This drop is related exclusively to less favourable ΔE_int, because ΔE_def decreases, too. The Pauli repulsion in [7-NH₃]⁺ is almost the same as in [5-NH₃]⁺ and smaller than in [6-NH₃]⁺ (Table 1). Thus, the decrease in the interaction energy by 13.5 kcal mol⁻¹ compared to [6-NH₃]⁺ and by 19.4 kcal mol⁻¹ compared to [5-NH₃]⁺ is connected with a decrease in electrostatic and orbital interactions. As mentioned before, electrostatic stabilization is not simply related to the charge at boron atom, which amounts 1.412, 0.566 and 1.087 for 5, 6 and 7, respectively, but to all charge interactions (attractive and repulsive) and B–NH₃ distance, which is longer in [7-NH₃]⁺, 1.640 Å, compared to 1.618 Å and 1.608 Å in [5-NH₃]⁺ and [6-NH₃]⁺, respectively, and diminishes ΔE_elsatat. The NBO analysis shows that the electron occupancy of boron's p-orbital decreases in the order: 6 (0.460e) > 5 (0.289e) > 7 (0.167e). Thus, the drop in the orbital interactions should be related to a decrease in covalency due to the larger B–NH₃ bond, smaller polarization and other cation–ligand hyperconjugative interactions.

Replacement of one or both methyl groups in 7 with phenyl ring to form 9 and 10 further decreases affinity of borenium cations toward ammonia by ΔH/ΔE = 3.8/4.2 kcal mol⁻¹ and ΔH/ΔE = 5.8/6.8 kcal mol⁻¹, respectively. In the case of [9-NH₃]⁺, this is related both to the increase in deformation energy (by 1.8 kcal mol⁻¹ with respect to [7-NH₃]⁺) and decrease in the interaction energy (by 2.4 kcal mol⁻¹ compared to [7-NH₃]⁺). Major factor responsible for smaller binding affinity of 10 is increase in deformation energy (5.9 kcal mol⁻¹ with respect to [7-NH₃]⁺ and 4.2 kcal mol⁻¹ with respect to [9-NH₃]⁺), while interaction energy drops by only 0.9 kcal mol⁻¹ compared to [7-NH₃]⁺, and is by 1.5 kcal mol⁻¹ more stabilizing compared to [9-NH₃]⁺. For both [9-NH₃]⁺ and [10-NH₃]⁺, ΔE_int reduces solely due to the increased Pauli repulsion, while all attractive energy components become more favourable than in [7-NH₃]⁺. The increase in ΔE_oi and ΔE_disp partly relates to the presence of more polarizable π-electrons enhancing dispersion interactions and affecting polarization part of ΔE_oi more than the charge transfer interactions associated with the B–N bond formation. For the latter, presence of one or two phenyl rings is not favourable because it decreases availability of boron's p-orbital to accept nitrogen lone pair, due to the π_Ph → p_B electron donation (calculated boron's p-orbital occupancies are 0.249e in 9 and 0.285e in 10 compared to 0.167e in 7). The B–N bond lengths in [9-NH₃]⁺ and [10-NH₃]⁺ are almost equal/slightly smaller than in [7-NH₃]⁺, suggesting the presence of strong attractive forces.

In the rest of borenium cations to be discussed, boron atom is included in a heterocycle, structures 8 and 12–20, or is connected to catechol, structure 11. The strongest affinity toward NH₃ is found for 8 (P,P), ΔH/ΔE = −33.8/−37.1 kcal mol⁻¹, and it is even higher than that observed for Me,Ph- and Ph,Ph-substituted cations 9 and 10. Binding affinity of 11, ΔH/ΔE = −29.4/−31.7 kcal mol⁻¹, is somewhat weaker than that of 10. Among the complexes formed from 8 and 11–20, the [8-NH₃]⁺ possesses the shortest B–NH₃ bond length, d_BN = 1.621 Å, and its formation is accompanied by the smallest deformation energy, ΔE_def = 25.1 kcal mol⁻¹, and the largest interaction energy, ΔE_int = −62.2 kcal mol⁻¹. These observations could be ascribed to the long B–P bonds in 8, which sterically least impedes with the NH₃ approach. Once the complex is formed, the Pauli repulsion becomes strong, ΔE_ex+rep = 187.8 kcal mol⁻¹, but is significantly exceeded by very favourable ΔE_elstat = −115.1 kcal mol⁻¹, ΔE_oi = −110.7 kcal mol⁻¹ and ΔE_disp = −24.2 kcal mol⁻¹. All interaction energy components are similar or larger only in adducts derived from 6 (Cl,Cl), 12 (P,S) and 14 (S,S), which have similar or shorter B–NH₃ bonds and both heteroatoms come from the second octal row of the periodic table. Dispersion interactions are also more prominent in [9-NH₃]⁺ (Me,Ph) and [10-NH₃]⁺ (Ph,Ph), having polarizable π-electrons, than in [8-NH₃]⁺. In addition, [11-NH₃]⁺ shows similar Pauli repulsion as [8-NH₃]⁺, slightly stronger electrostatic stabilization, but somewhat weaker orbital and dispersion interactions. This results in 1.2 kcal mol⁻¹ smaller ΔE_int compared to that in [8-NH₃]⁺. Deformation energy accompanying the formation of [11-NH₃]⁺ is by 4.2 kcal mol⁻¹ higher than that needed for the formation of [8-NH₃]⁺, so that both energy terms lead to lower association energy in the case of [CatBNH₃]⁺. As the major part of deformation energy relates to geometry change of a cation, bending of the exocyclic B–N bond in the aromatic 11 is energetically more costly than the same change in 8, which is the main structural change in these two cations. Even more energy is spent to deform cation 15, having two oxygen atoms connected to boron, like 11. In fact, ΔE_def = 33 kcal mol⁻¹ needed for the formation of [15-NH₃]⁺ is the highest one in Table 1 and has to be ascribed to a significant ring puckering occurring during the cation–NH₃ association, along with the B–N bond bending. The reason why 15 is weaker NH₃ acceptor than 11 is solely its high ΔE_def, while ΔE_int are almost equal in the formation of both complexes. This somewhat contrasts with our intuitive prediction that 11 would be a weaker lone pair acceptor, because boron's p-orbital in it is part of the aromatic 10π-electron system. Even so, orbital interaction energy is more stabilizing in [11-NH₃]⁺ than in [15-NH₃]⁺, resulting from slightly shorter B–N distance and polarization part of orbital interactions. In addition, electrostatic energy is by the similar magnitude more stabilizing in [11-NH₃]⁺, but Pauli repulsion is smaller in [11-NH₃]⁺.

In fact, cations 13–16 have very similar NH₃ affinities, ΔH = −26.4 ± 0.2 kcal mol⁻¹, and are followed by the group of three cations, 17–19, the affinities of which amount ΔH = −18.5 ± 0.3 kcal mol⁻¹. The weakest ammonia acceptor is 20 (N,N), ΔH = −12.9 kcal mol⁻¹. All these enthalpies are exceeded by that of 12 (P,S), ΔH = −28.6 kcal mol⁻¹. The strongest affinity of 12, among 12–20, owes to the relatively low ΔE_def and high ΔE_int, the latter exceeded by only [15-NH₃]⁺ just because of smaller Pauli repulsion. Therefore, the P,S heteroatom combination in 12 lowers association enthalpy compared to the P,P heteroatom combination in 8, but leads to somewhat larger ammonia affinity with respect to all other combinations involving P, S and O. This is the result of relative magnitudes of ΔE_def and ΔE_int, and could not be ascribed to any particular interaction. Weak ammonia affinities of nitrogen-containing heterocyclic cations 17–20 certainly come from a decrease in the interaction energy, which does not exceed −54 kcal mol⁻¹, while deformation energy values compare with those of other heterocycle-containing cations. Small magnitudes of ΔE_int are a consequence of long B–NH₃ distances (the longest among all NH₃-complexes studied) and a change in individual energy components affected by the type of atoms involved in a heterocycle. The reason why 17–20 keep the NH₃ ligand at the longest distance could be a combination of good electron-donating ability of nitrogen which increases boron's p-orbital electron occupancy and steric hindrance due to the short B–N_ring bonds. Although, it should be noted that electrostatic and orbital interaction energies in some of adducts formed from 17–20 are larger than in those obtained from nitrogen-lacking heterocyclic structures and boron's p-orbital occupancy is not the highest. Here, again, elements from the second octal row (S and P) provide more electrostatic and orbital stabilization, and larger Pauli repulsion, more pronounced for S than for P. This is evident when comparing interaction energy components in adducts derived from 17–19, which all have (almost) the same B–N distances.

When comparison between related heterocycles is made, the following can be said. The replacement of oxygen by nitrogen, that is 13 (P,O) → 19 (P,N), 15 (O,O) → 18 (O,N) and 16 (S,O) → 17 (S,N), affects mainly the Pauli repulsion upon complex formation which increases by 3.1–5.7 kcal mol⁻¹ and orbital interaction energy which decreases by 1.5–2.3 kcal mol⁻¹. In addition to a slight increase in the B–NH₃ distance by 0.012–0.015 Å, which inherently decreases interaction energy components, the drop in ΔE_oi is consistent with nitrogen's better electron-donating ability with respect to oxygen (also see electron occupancy values in Table S3†). The ΔE_elstat and ΔE_disp are less affected by O to N replacement, and both decrease by 0.6–1.3 kcal mol⁻¹ and 0.2–0.4 kcal mol⁻¹, respectively. Due to increase in repulsive energy and decrease in attractive energy, interaction energy becomes weaker, while binding enthalpies drop by 7.3–8.4 kcal mol⁻¹ (also modulated by ΔE_def). More drastic changes in various interaction energy components occur when sulfur is substituted with nitrogen, that is 12 (P,S) → 19 (P,N), 14 (S,S) → 17 (N,S) and 16 (O,S) → 18 (O,N). All interaction energy components decrease: ΔE_elstat by 6.9–9.7 kcal mol⁻¹, ΔE_oi by 10.3–14.8 kcal mol⁻¹, ΔE_disp by 1.1–1.3 kcal mol⁻¹ and ΔE_ex+rep by 13.8–16.6. Since decrease in attractive energy exceeds decrease in repulsive energy, overall interaction energy decreases. More importantly from experimental point of view, S to N substitution weakens binding enthalpies by 7.4–10.3 kcal mol⁻¹. In fact, both O → N and S → N substitutions lead to a similar decrease in binding enthalpies. Sulfur to oxygen exchange has much smaller effect on binding enthalpies, which decrease by 0.1–1.9 kcal mol⁻¹ for the changes 12 (P,S) → 13 (P,O), 14 (S,S) → 16 (S,O) and 17 (N,S) → 18 (N,O), or increase by 0.1 kcal mol⁻¹ for 16 (O,S) → 15 (O,O). Apart from any change in 8 (P,P), phosphorus exchange with oxygen or sulfur has a smaller effect on binding enthalpies (not exceeding 2.4 kcal mol⁻¹), while its substitution with nitrogen, that is 12 (P,S) → 17 (N,S) and 13 (P,O) → 18 (N,O), diminishes enthalpy values by 8.4–9.7 kcal mol⁻¹. Introduction of nitrogen instead of S, O and P in 17–19 to form 20, decreases NH₃ association enthalpies by 5.4–6 kcal mol⁻¹. The weakest affinity of 20 (N,N) mainly originates from relatively low electrostatic stabilization and the weakest orbital interaction energy, making ΔE_int the least favourable.

Inclusion of solvent into calculations either decrease or increase binding energies. For majority of cations, the effect does not exceed 3.3 kcal mol⁻¹. The largest decrease in ΔE is observed for 4, 5.3 kcal mol⁻¹. The above mentioned three cationic groups with similar ΔEs can still be discerned: 20 as the poorest NH₃ acceptor (ΔE = 13.6 kcal mol⁻¹), 17–19 having larger acceptor abilities (ΔE ∼20 kcal mol⁻¹) and the third group now involves cations 11–16, the ΔEs of which are around 30 kcal mol⁻¹. In solvent conditions, 8 (P,P) binds NH₃ somewhat stronger than 7 (Me,Me) by 1.5 kcal mol⁻¹, and 5 (F,F) appears to be a poorer acceptor than 6 (Cl,Cl), though the difference in binding energies is small (0.6 kcal mol⁻¹).

Formaldehyde affinity of cations 4–20

Calculated binding enthalpies (ΔH), energies (ΔE) and LMOEDA analysis of binding interactions between borenium ions 4–20 and HCHO are given in Table 2, along with the calculated B–OCH₂ distances. Discussion of the gas-phase results is followed by discussion of solvent effects, which is given in the last paragraph of this section.

Table 2 Calculated B–OCH₂ distances (d_BO, Å), HCHO affinities (ΔH at 298.15 K and ΔE, values in italic are in CH₂Cl₂) and energy decomposition of binding interactions.^a,b,c,d All energy values are in kcal mol⁻¹

Ion	d BO	ΔH	ΔE	ΔEdef	ΔEint	ΔEelstat	ΔEex+rep	ΔEoi	ΔEdisp
a Calculated at the M06-2X/6-311++G(d,p)//M06-2X/6-311++G(d,p) level. b Gas-phase association enthalpies (ΔH), energies (ΔE) and all interaction energy terms are corrected for the BSSE by using the counterpoise method. c Labeling of all energy terms is the same as in Table 1. d Values in parentheses are percentage contribution to all attractive interactions.
4	1.576	−40.53	−44.59, −33.60	15.14	−59.73	−73.14 (42.5%)	112.51	−79.22 (46.0%)	−19.88 (11.5%)
5	1.593	−37.25	−39.40, −30.08	22.70	−62.10	−80.58 (43.3%)	124.04	−82.98 (44.6%)	−22.58 (12.1%)
6	1.585	−30.88	−33.32, −28.32	22.85	−56.17	−92.05 (43.0%)	157.68	−97.32 (45.5%)	−24.48 (11.5%)
7	1.633	−25.26	−28.06, −21.04	16.26	−44.32	−71.24 (43.5%)	119.43	−69.45 (42.4%)	−23.00 (14.1%)
8	1.563	−22.79	−25.05, −21.37	23.05	−48.10	−97.23 (43.8%)	173.73	−99.38 (44.8%)	−25.22 (11.4%)
9	1.636	−22.14	−25.07, −20.56	17.96	−43.03	−77.33 (44.2%)	131.89	−72.26 (41.3%)	−25.33 (14.5)
10	1.623	−19.44	−21.63, −19.36	22.83	−44.46	−80.93 (44.0%)	139.36	−75.63 (41.1%)	−27.26 (14.9%)
11	1.658	−18.95	−20.77, −15.80	17.66	−38.43	−82.63 (45.5%)	143.22	−75.71 (41.7%)	−23.31 (12.8%)
12	1.601	−18.47	−20.66, −17.34	23.66	−44.32	−91.54 (44.2%)	162.58	−90.67 (43.8%)	−24.69 (12.0%)
13	1.626	−17.94	−19.81, −15.94	21.92	−41.73	−81.57 (44.5%)	141.69	−78.01 (42.5%)	−23.84 (13.0%)
15	1.682	−15.94	−17.53, −11.83	20.91	−38.44	−70.87 (45.3%)	117.98	−63.59 (40.7%)	−21.96 (14.0%)
16	1.632	−15.03	−16.85, −12.75	24.07	−40.92	−83.44 (44.8%)	145.46	−79.56 (42.7%)	−23.38 (12.5%)
14	1.628	−14.54	−16.67, −12.68	23.98	−40.65	−90.34 (44.7%)	161.45	−87.54 (43.3%)	−24.22 (12.0%)
18	1.754	−10.95	−12.28, −5.62	17.07	−29.35	−64.18 (46.5%)	108.64	−52.84 (38.3%)	−20.97 (15.2%)
19	1.728	−9.21	−10.79, −4.35	18.75	−29.54	−69.60 (45.9%)	122.22	−59.77 (39.4%)	−22.39 (14.7%)
17	1.704	−9.16	−10.73, −5.17	21.35	−32.08	−75.57 (45.9%)	132.47	−66.30 (40.3%)	−22.68 (13.8%)

---

In this case, ΔHs/ΔEs span a somewhat narrower range from −40.5/−44.6 kcal mol⁻¹ for 4 (H,H) to −9.2/−10.7 kcal mol⁻¹ for 17 (N,S). Magnitudes of all HCHO association enthalpies are smaller than the corresponding NH₃ binding enthalpies by 7.8–14 kcal mol⁻¹, which should be ascribed to the sp²-hybridized oxygen lone pair being poorer electron donor than ammonia lone pair. ΔHs and ΔEs follow the same trend (R² = 0.998) which, with few exceptions, match that for NH₃ affinity. Differences in affinities toward NH₃ and HCHO are the following: (1) cation 14 is slightly weaker HCHO acceptor than cations 15 and 16 by 1.4 and 0.5 kcal mol⁻¹, respectively; (2) cation 17 is slightly weaker HCHO acceptor compared to 18 and 19 by 1.8 and 0.05 kcal mol⁻¹, respectively. Calculated distances between boron and carbonyl oxygen atom of HCHO range from 1.563 Å in 8 (P,P) to 1.754 Å in 18 (N,O). Deformation energy (ΔE_def) is the smallest for complex formation from 4 (15.1 kcal mol⁻¹) and the largest for complex formation from 16 (24.1 kcal mol⁻¹). All ΔE_def and ΔE_int values are smaller than those in the corresponding ammonia complexes. Like in NH₃-adducts, ΔE_int do not follow the same trend as ΔHs and ΔEs, since the latter two are influenced by deformation energies, as well.

The LMOEDA shows that in the case of adducts formed from 4–6 and 8 the percentage contribution of the orbital interaction energy (ΔE_oi: 44.6–46%) slightly prevails over the electrostatic interaction energy (ΔE_elstat: 42.5–43.8%), while for all other complexes contribution of electrostatic stabilization (ΔE_elstat: 43.5–46.5%) is slightly more pronounced than that of orbital interaction energy (ΔE_oi: 38.3–43.8%). The role of dispersion interactions in complex stabilization is slightly increased (11.4–15.2%) compared to cation–NH₃ complexes (9.2–11.6%), which is possibly due to the presence of more polarizable π-electrons in the ligand (HCHO).

Cation 4, again, exhibits the strongest tendency to bind the ligand (HCHO), ΔH/ΔE = −40.5/−44.6 kcal mol⁻¹, which stems from small ΔE_def = 15.1 kcal mol⁻¹ and large ΔE_int = −59.7 kcal mol⁻¹ (ΔE_int is larger only in adduct formed from 5, which is similar to NH₃-complexes). The ΔE_int owes to the small Pauli repulsion, but also to the ΔE_oi component, while ΔE_elstat exceeds values in just four other complexes formed from 7 (Me,Me), 15 (O,O), 18 (N,O) and 19 (P,N). This differs from ammonia-adducts where electrostatic stabilization was the smallest in the case of [4-NH₃]⁺ and can be partly rationalized by the long B–O bonds in the HCHO-adducts derived from 7, 15, 18 and 19, d_BO = 1.633–1.754 Å compared to 1.576 Å in [4-HCHO]⁺, which diminishes charge interactions. In the case of NH₃-adducts, orbital interaction energy in [4-NH₃]⁺ was among the weakest ones. However, in [4-HCHO]⁺, ΔE_oi = −79.2 kcal mol⁻¹ exceeds values in many other HCHO-complexes and is approximately in the middle between the highest and the lowest values, ΔE_pol = −99.4 in [8-HCHO]⁺ and −52.8 kcal mol⁻¹ in [18-HCHO]⁺, respectively. This, again, could be ascribed to B–O distances which are more lengthened in HCHO-complexes than in NH₃-complexes with respect to B–O and B–N bonds in [4-HCHO]⁺ and [4-NH₃]⁺.

The HCHO affinity of 5 (F,F), ΔH/ΔE = −37.2/−39.4 kcal mol⁻¹, is larger than that of 6 (Cl,Cl), ΔH/ΔE = −30.9/−33.3 kcal mol⁻¹, because of the more favourable ΔE_int (by 5.9 kcal mol⁻¹), while ΔE_def is smaller by only 0.2 kcal mol⁻¹. Like in NH₃-complexes, it is the lower Pauli repulsion which is responsible for the larger ΔE_int in [5-HCHO]⁺ compared to [6-HCHO]⁺, while all attractive energy terms are more stabilizing in the latter.

The effect of methyl and phenyl substituents on HCHO affinity of cations 7 (Me,Me), 9 (Me,Ph) and 10 (Ph,Ph) is the same as their influence on NH₃ affinity and can be rationalized in a similar way as already discussed in the preceding section, where it was compared to halo-substituted cations. If compared with 4 (H,H), the replacement of hydrogen atoms by two methyl groups decreases affinity toward HCHO mainly due to the interaction energy, which decreases by 15.4 kcal mol⁻¹ (ΔE_def rises by only 1.1 kcal mol⁻¹). The drop in the ΔE_int has to be attributed to the increased Pauli repulsion and much more to the decreased orbital interactions, which together reduce ΔE_int by 16.7 kcal mol⁻¹ (the net effect of ΔE_elstat and ΔE_disp is stabilization by 1.2 kcal mol⁻¹, the former/latter becoming less/more stabilizing). A decrease in ΔE_oi can be ascribed to σ_CH → p_B hyperconjugation which enhances boron's p-orbital occupancy to 0.167e compared to only 0.023e in 4, resulting in smaller coordinate covalent bond strength and longer boron–ligand distance (also affected by steric hindrance from methyl groups). The latter, in turn, reduces polarization, which should actually increase upon hydrogens substitution with methyl groups. Further substitution of one methyl group in 7 with phenyl group to form 9 decreases binding affinity by ΔH/ΔE = 3.1/3 kcal mol⁻¹ due to somewhat larger deformation of interacting fragments and less stabilizing ΔE_int. The latter is made less favourable solely due to the increase in the Pauli repulsion. Replacement of another methyl by phenyl group to give 10 decreases HCHO affinity exclusively due to increase in the ΔE_def, while enhancement of all attractive energy components makes the ΔE_int slightly more favourable with respect to that in [7-HCHO]⁺ and [9-HCHO]⁺.

Among the heterocycle-containing cations 8 and 11–19, high binding affinity of 8 (P,P), ΔH/ΔE = −22.8/−25.1 kcal mol⁻¹, owes to the favourable interaction energy which partly results from the very short B–O bond. This is the shortest B–O bond among all HCHO-complexes studied and can be explained in the same way as for NH₃-complexes. Thus, due to the long B–P bonds in 8, ligand approach is sterically least impeded. In the complex, all interaction energy terms, attractive (ΔE_elstat, ΔE_oi and ΔE_disp) and repulsive (ΔE_ex+rep), are the strongest, compared to all other complexes. Their net result is very favourable ΔE_int, being stronger in just three other complexes obtained from 4–6.

While [CatBNH₃]⁺11 showed the highest affinity toward NH₃ among heterocyclic cations 11–20 mostly due to the favourable interaction energy (Table 1), its high affinity for HCHO comes from small deformation energy which is amongst the smallest ones of all cations 4–19 (ΔE_def in [11-HCHO]⁺ exceeds ΔE_def in just three other adducts formed from 4 (H,H), 7 (Me,Me) and 18 (N,O)). Thus, binding of HCHO to 11 is accompanied by the smaller B–N bond bending than binding of the more nucleophilic NH₃ (see previous section). The ΔE_int in [11-HCHO]⁺ is not large and exceeds ΔE_int only in adducts obtained from nitrogen-containing heterocyclic cations 17–19. Magnitudes of ΔE_int and ΔE_def are obviously a consequence of the relatively long B–OCH₂ distance. As in the case of NH₃-complexes, smaller affinity of 15 (O,O) toward HCHO compared to 11 comes from an increase in the 1,3,2-dioxaborolidine ring puckering and B–N bond bending in the former, leading to higher deformation energy. Interaction energies in the two adducts are the same, despite the longer B–O bond in [15-HCHO]⁺ by 0.024 Å (in the case of NH₃-complexes, the B–N bond in [15-NH₃]⁺ is also longer than in [11-NH₃]⁺, but the difference is smaller, 0.011 Å). The reason why interaction energies are almost the same in adducts formed from 11 and 15 is not larger attraction in the case of 15, but smaller Pauli repulsion.

Unlike the case of NH₃ as ligand, cations 12–16, containing P, O and S as heteroatoms, are poorer HCHO acceptors than 11 due to the larger geometry changes associated with the complex formation, while the interaction energy is similar or higher than that in [11-HCHO]⁺.

The trend in HCHO affinities of 12–19 differs somewhat from that found for NH₃ affinities. Whereas in the case of the latter, two cation groups, having very similar affinities within each, could be identified, the HCHO accepting ability continually decreases in the order: 12 (P,S) > 13 (P,O) > 15 (O,O) > 16 (S,O) > 14 (S,S) > 18 (O,N) > 19 (P,N) > 17 (N,S) and represents a balance between ΔE_def and ΔE_int. Compared to 8 (P,P), cation 12 (P,S) shows weaker HCHO affinity by 4.3 kcal mol⁻¹ mostly because of smaller attractive energy components making ΔE_int less favourable. This is mainly related to the longer B–O bond in [12-HCHO]⁺ compared to that in [8-HCHO]⁺, by 0.038 Å. The B–N distances in the corresponding NH₃-complexes vary by less than 0.01 Å resulting in quite similar attractive interaction energy components, but larger Pauli repulsion in [12-NH₃]⁺ (Table 1).

Sulfur substitution in 12 with oxygen to give 13 (P,O) decreases all interaction energy components and net ΔE_int, but also ΔE_def. The resulting HCHO affinity drops slightly by ΔH/ΔE = 0.5/0.8 kcal mol⁻¹. A change in ΔE_int partially comes from the change in the type of atoms, as already discussed, and partially from the increase in the B–OCH₂ distance by 0.025 Å. When two oxygen atoms are connected to boron, such as in 15, formaldehyde approach is even more impeded leading to the long boron–ligand distance of 1.682 Å (by 0.056 Å longer than in [13-HCHO]⁺ and by 0.081 Å longer than in [12-HCHO]⁺). This further decreases all interaction energy components. As decrease in attractive part is larger than decrease in the repulsive part, overall interaction energy becomes less favourable, which is the cause for the drop in HCHO affinities along the series: 12 > 13 > 15 (ΔE_def decreases, as well). This contrasts with the behaviour of NH₃-complexes in which the B–N distance in [15-NH₃]⁺ is comparable to that in [13-NH₃]⁺ and attractive interactions are just slightly reduced due to P → O exchange. In that case, the overall ΔE_int is increased in [15-NH₃]⁺, compared to [13-NH₃]⁺ (Table 1) because of the weaker Pauli repulsion associated with the P → O substitution. Since the calculated boron's p-orbital availability to accept electron density decreases in the order 13 (P,O; p-orbital occupancy 0.378e) > 15 (O,O; p-orbital occupancy 0.411e) > 12 (P,S; p-orbital occupancy 0.542e), it appears that the B–OCH₂ distance in the three HCHO-complexes is mainly affected by steric effects and it increases with increasing number of oxygen atoms: 1.601 Å in 12 (P,S), 1.626 in 13 (P,O) and 1.682 Å in 15 (O,O). The larger steric effect coming from oxygen atom should be ascribed to the short B–O_ring bond lengths, making the HCHO approach more difficult. These effects are not pronounced in the case of more nucleophilic NH₃.

In HCHO-adduct obtained from 16 (S,O), the B–OCH₂ distance is marginally increased relative to that obtained from 13 (P,O) and its lower HCHO affinity by ΔH/ΔE = 2.9/3 kcal mol⁻¹ mainly stems from the large ΔE_def = 24.1 kcal mol⁻¹, which is the largest value among all studied HCHO-adducts (ΔE_int decreases by only 0.8 kcal mol⁻¹). While all 13–16 have very similar affinities toward NH₃ (Table 1), 14 (S,S) shows the weakest affinity for HCHO. This is the result of high ΔE_def = 24 kcal mol⁻¹ and high Pauli repulsion, whereas two sulfur atoms provide favourable electrostatic, orbital and dispersion interactions.

The remaining three cations 17–19, possessing one N_ring atom, form complexes with the longest B–OCH₂ distances (1.704–1.754 Å). Cation 20 forms only hydrogen-bonded complex with HCHO. The long B–ligand bond should be ascribed to a combination of electronic (increase of boron's p-orbital occupancy) and steric effects, both more pronounced in complexes with the less nucleophilic formaldehyde. Although [18-HCHO]⁺ features the longest B–ligand distance amongst the 17–19, binding affinity of 18 (N,O) is slightly greater than that of 19 (P,N) and 17 (N,S), of the latter two being almost the same. This trend is determined by ΔE_def, which increase in the order: 18 < 19 < 17, while ΔE_int become more stabilizing in the same order. The changes in both energies are consistent with the decrease in the B–OCH₂ distances along the series 18 > 19 > 17. These three cations show the smallest interaction energy upon complex formation, which concurs with results for NH₃-adducts, and is partly affected by long boron–ligand distances. For example, in the case of 18 (O,N) steric hindrance to HCHO approach due to the short B–O_ring/N_ring bonds (1.340/1.376 Å) combined with high boron's p-orbital occupancy (0.457e) keep formaldehyde relatively distant from boron atom. In fact, formation of hydrogen-bonded adducts of 18 and 19 with HCHO is energetically more favoured (see section describing Geometries of borenium ion complexes).

Under solvent conditions, all binding energies are lowered by up to 11 kcal mol⁻¹. The gas-phase obtained trend in ΔEs is retained, with small variations (12 (P,S) > 11 (Cat), 14 (S,S) and 16 (O,S) > 15 (O,O) and 17 (N,S) > 19 (P,N)).

Chloride affinity of cations 4–20

The chloride anion binding enthalpies (ΔH), energies (ΔE), LMOEDA results and boron–chlorine bond lengths are listed in Table 3. Gas-phase results are analyzed first and solvent effects are included in the last paragraph of this section.

Table 3 Calculated B–Cl distances (d_BCl, Å), Cl⁻ affinities (ΔH at 298.15 K and ΔE, values in italic are in CH₂Cl₂) and energy decomposition of binding interactions.^a,b,c,d,e All energy values are in kcal mol⁻¹

Ion	dBCl	ΔH	ΔE	ΔEdef	ΔEint	ΔEelstat	ΔEex+rep	ΔEoi	ΔEdisp
a Calculated at the M06-2X/6-311++G(d,p)//M06-2X/6-311++G(d,p) level. b Gas-phase association enthalpies (ΔH), energies (ΔE) and all interaction energy terms are corrected for the BSSE by using the counterpoise method. c Labeling of all energy terms is the same as in Table 1. d Values in parentheses are percentage contribution to all attractive interactions. e These values were not available.
5	1.850	−165.27	−165.30, −52.10	40.14	−205.44	−210.12 (58.2%)	155.61	−125.47 (34.8%)	−25.46 (7.0%)
4	1.875	−162.42	−164.11, −52.39	22.25	−186.36	−186.59 (57.6%)	137.62	−114.85 (35.4%)	−22.54 (7.0%)
6	1.833	−161.97	−162.46, −54.62	39.12	−201.58	−218.18 (54.9%)	195.51	−152.08 (38.3%)	−26.83 (6.8%)
8	1.862	−144.43	−144.79, −42.03	36.20	−180.99	−198.96 (55.0%)	180.57	−136.65 (37.8%)	−25.95 (7.2%)
7	1.906	−143.33	−144.30, −37.97	26.19	−170.49	−187.46 (58.3%)	150.83	−108.56 (33.8%)	−25.30 (7.9%)
11	1.852	−139.83	−139.47, −36.27	40.84	−180.31	—^e	203.99	—^e	−25.25
9	1.898	−138.28	−139.31, −38.00	31.68	−170.99	−187.43 (56.5%)	160.96	−116.93 (35.2%)	−27.59 (8.3%)
12	1.862	−137.38	−137.48, −35.39	41.48	−178.96	−200.92 (54.8%)	187.88	−140.05 (38.2%)	−25.87 (7.0%)
10	1.892	−136.17	−136.15, −38.78	34.56	−170.71	−188.85 (55.1%)	171.85	−124.18 (36.3%)	−29.53 (8.6%)
14	1.857	−135.98	−135.98, −33.66	41.95	−177.93	−207.11 (54.7%)	200.99	−145.75 (38.5%)	−26.06 (6.8%)
13	1.890	−134.60	−134.48, −30.99	29.02	−163.50	−200.73 (57.0%)	188.59	−126.13 (35.8%)	−25.23 (7.2%)
16	1.877	−134.39	−134.23, −31.38	36.61	−170.84	−201.92 (56.6%)	186.20	−129.77 (36.3%)	−25.35 (7.1%)
15	1.894	−131.89	−131.36, −27.74	38.42	−169.78	−194.81 (58.3%)	164.37	−114.83 (34.4%)	−24.51 (7.3%)
17	1.869	−126.79	−126.32, −21.90	50.15	−176.47	−203.68 (56.4%)	184.55	−131.82 (36.5%)	−25.52 (7.1%)
19	1.879	−126.49	−126.14, −20.42	46.80	−172.94	−202.07 (57.0%)	181.32	−126.58 (35.7%)	−25.61 (7.3%)
18	1.905	−124.91	−124.33, −19.91	41.16	−165.49	−197.09 (59.0%)	168.40	−112.25 (33.6%)	−24.55 (7.4%)
20	1.913	−119.40	−118.97, −13.89	43.01	−161.98	−197.65 (59.5%)	170.41	−110.31 (33.2%)	−24.43 (7.3%)

---

Since the formation of chloride-adducts involve oppositely charged species, all binding energies are significantly larger than the previous ones. Binding enthalpies/energies span a range from ΔH/ΔE = −119.4/119 kcal mol⁻¹ for the weakest acceptor 20 (N,N) to ΔH/ΔE = −165.3/165.3 kcal mol⁻¹ for the strongest acceptor 5 (F,F). ΔHs and ΔEs are more similar in this case (R² = 0.999) and do not differ by more than 1.7 kcal mol⁻¹ (the majority of values differ by less than 1 kcal mol⁻¹). Deformation energies are larger with respect to the corresponding values calculated for NH₃- and HCHO-complexes, which could be ascribed to larger nucleophilicity of Cl⁻. They range from 22.2 kcal mol⁻¹ for 4 (H,H) to 50.2 kcal mol⁻¹ for 17 (N,S). In this case, these energies correspond solely to deformation of borenium ion upon its reaction with Cl⁻. Boron–chlorine bond lengths vary from 1.833 Å in 6-Cl to 1.913 Å in 20-Cl. The LMOEDA shows that the nature of chloride–borenium cation interactions is primarily electrostatic. Percentage contribution of ΔE_elstat to all attractive interactions amounts 54.7–59.5%. Next come orbital interactions, contribution of which ranges from 33.2–38.5%, and the smallest stabilization is provided by dispersion forces, 6.8–8.6%. Contribution of the latter is also smaller than in NH₃- and HCHO-complexes, which is expected for charged species.

The order of Cl⁻ affinities differ from the order of NH₃ and HCHO affinities. This could be related to Cl⁻ increased nucleophilicity and stronger attractive forces with a cation, while Pauli repulsive energies compare with those observed for NH₃-adducts. Thus, cation 5 (F,F) binds chloride more strongly than cation 4 (H,H) (by ΔH = 2.8 kcal mol⁻¹), which originates from somewhat altered balance between interaction and deformation energies: ΔE_int overcomes ΔE_def to the extent that the total binding energy in 5-Cl exceeds the value in 4-Cl. Next comes the affinity of cation 6 (Cl,Cl), which is quite similar to that of 4. In the case of NH₃ and HCHO as ligands, the binding enthalpies of 4 and 6 differ by ∼9.5 kcal mol⁻¹. This can also be explained by the altered balance between ΔE_int and ΔE_def. In the adduct 6-Cl, ΔE_elstat and ΔE_oi are very favourable, and are the strongest compared to all other chloride-adducts. Dispersion interactions in 6-Cl are exceeded only by those in 9-Cl and 10-Cl, obviously due to the presence of polarizable π-electrons in the latter two. These strong attractive forces in 6-Cl are also attenuated by the large Pauli repulsion and deformation energy, which are both higher than those in 4-Cl. In fact, the two chlorine substituents in 6 also provide the strongest ΔE_elstat and ΔE_oi in [6-NH₃]⁺ compared to all other ammonia-complexes, and very strong electrostatic and orbital interactions in [6-HCHO]⁺, exceeded by only those in [8-HCHO]⁺. The existence of strong attractive interactions in the case of 6 is also evident in very short B–L′ bonds.

The chloride affinity of 8 (P,P) (ΔH/ΔE = −144.4/−144.8 kcal mol⁻¹) is slightly stronger than that of 7 (Me,Me) (ΔH/ΔE = −143.3/−144.3 kcal mol⁻¹) which differs from the order of NH₃ and HCHO affinities. This again comes from a somewhat altered balance between ΔE_int and ΔE_def, because all interaction energy components, as well as ΔE_def, are larger in the case of 8 and this concurs with NH₃- and HCHO-adducts. [CatBNH₃]⁺11 binds Cl⁻ slightly stronger (ΔH/ΔE = −139.8/−139.5 kcal mol⁻¹) than 9 (Me,Ph) (ΔH/ΔE = −138.3/−139.3 kcal mol⁻¹) and stronger than 10 (Ph,Ph) (ΔH/ΔE = −136.2/−136.2 kcal mol⁻¹). Since ΔE_int in 9-Cl and 10-Cl is very similar to ΔE_int in 7-Cl, weaker Cl⁻ affinity of 9 and 10 compared to 7 is associated with larger deformation energies. The reversed order of Cl⁻ affinities, 11 being stronger acceptor than 9 and 10, comes from the short B–Cl bond in 11-Cl, which is by ∼0.05 Å shorter than in 9-Cl and 10-Cl. This leads to favourable ΔE_int, which now overcomes ΔE_def to the larger extent.

Among the heterocycle-containing borenium cations 8 and 12–20, the affinity of 8 (P,P) toward Cl⁻ is the largest (ΔH/ΔE = −144.4/−144.8 kcal mol⁻¹), next coming that of 12 (P,S) (ΔH/ΔE = −137.4/−137.5 kcal mol⁻¹). This concurs with NH₃ and HCHO affinities. Chloride affinities then follow the trend: 14 (S,S) > 13 (P,O) ≈ 16 (S,O) > 15 (O,O) > 17 (N,S) ≈ 19 (N,P) > 18 (N,O) > 20 (N,N), which partly reflects chloride steric demand. Thus, in the case of 8 and 12–16, the affinity drops as the sum of the two B–R/R′ bonds become smaller, though it is clear that ΔHs/ΔEs are determined by the final B–Cl distances, which do not follow the same trend. In fact, the worst correlation between ΔHs/ΔEs and B–L′ distances was found for Cl⁻ as a ligand, suggesting that Cl⁻ interactions with other atoms are least dependent on its proximity to boron. The regularity between Cl⁻ affinity and the sum of the two B–R/R′ bonds does not hold for nitrogen-containing heterocyclic ions 17–20. Here, a decrease in interaction energy fully follows the trend in binding enthalpies/energies (not found for NH₃ and HCHO ligands). This trend of decreasing ΔE_int is mostly determined by the magnitudes of orbital interactions, the drop of which is the most prominent. However, this should not be attributed only to electron-donating properties of heteroatoms connected to boron, since boron's p-orbital electron occupancy does not follow the same trend: it is the highest for 17 (N,S) having the largest Cl⁻ affinity and highest ΔE_oi among the four cations, 17–20, and the shortest B–Cl bond in the adduct. Obviously, other charge transfer interactions, polarization and electrostatic stabilization play an important role in determining the magnitude of total binding interactions.

Inclusion of solvent drastically reduces binding energies, by 97.4–113.2 kcal mol⁻¹. In solvent conditions, affinities toward Cl⁻ are still stronger than affinities toward HCHO for all cations, but very similar with NH₃ affinities. The trend in ΔE values is somewhat changed, that is 6 (Cl,Cl) > 4 (H,H) and 5 (F,F), 9 (Me, Ph) and 10 (Ph, Ph) > 7 (Me,Me) and 16 (O,S) > 13 (P,O).

Effect of ligand (L) on NH₃, HCHO and Cl⁻ affinities of cations 21–29

Calculated binding enthalpies (ΔH), energies (ΔE) and LMOEDA analysis of binding interactions between borenium ions 21–29 and NH₃, HCHO and Cl⁻ are presented in Table 4, along with the calculated B–L′ (L′ = NH₃, HCHO, Cl) distances. All structures 21–29 contain 1,3,2-oxazaborolidine ring, also present in 18, and differ in ligand L positioned at the third coordination place of boron. The following three subsections contain analysis of the gas-phase results. Solvent effects analysis is included in a separate subsection.

Table 4 Calculated B–L′ distances (d_BL′, Å), L′ affinities (ΔH at 298.15 K and ΔE, values in italic are in CH₂Cl₂) and energy decomposition of binding interactions.^a,b,c,d,e All energy values are in kcal mol⁻¹

Ion	L′	d BL′	ΔH	ΔE	ΔEdef	ΔEint	ΔEelstat	ΔEex+rep	ΔEoi	ΔEdisp
a Calculated at the M06-2X/6-311++G(d,p)//M06-2X/6-311++G(d,p) level. b Gas-phase association enthalpies (ΔH), energies (ΔE) and all interaction energy terms are corrected for the BSSE by using the counterpoise method. c Labeling of all energy terms is the same as in Table 1. d Values in parentheses are percentage contribution to all attractive interactions. e These values were not available.
21	NH3	1.626	−20.99	−23.80, −25.74	30.31	−54.11	−113.20 (46.8%)	187.75	−104.55 (43.2%)	−24.11 (10.0%)
22	NH3	1.624	−20.27	−22.43, −23.25	39.58	−62.01	−109.22 (47.0%)	170.17	−98.69 (42.5%)	−24.27 (10.5%)
23	NH3	1.669	−14.57	−16.67, −18.74	30.91	−47.58	−103.01 (47.4%)	169.68	−88.28 (40.6%)	−25.97 (12.0%)
24	NH3	1.651	−13.35	−15.02, −17.04	28.00	−43.02	−107.17 (47.3%)	183.70	−96.05 (42.4%)	−23.50 (10.3%)
26	NH3	1.694	−8.76	−10.76, −12.21	27.89	−38.65	−97.85 (47.8%)	166.21	−82.97 (40.5%)	−24.04 (11.7%)
27	NH3	1.711	−6.26	−8.20, −9.55	26.10	−34.30	−93.43 (47.7%)	161.51	−78.25 (40.0%)	−24.13 (12.3%)
28	NH3	1.715	−4.82	−6.30, −8.85	26.41	−32.71	−93.52 (47.7%)	163.22	−78.14 (39.9%)	−24.27 (12.4%)
29	NH3	1.687	−4.20	−6.57, −8.72	36.09	−42.66	−99.65 (47.5%)	167.21	−84.49 (40.3%)	−25.73 (12.2%)
24	HCHO	2.650	−10.25	−11.51, −7.01	0.89	−12.40	−14.78 (45.4%)	21.31	−5.39 (16.5%)	−12.40 (38.1%)
21	HCHO	1.668	−9.16	−11.27, −8.64	20.02	−31.29	−76.78 (45.1%)	138.99	−70.18 (41.2%)	−23.32 (13.7%)
25	HCHO	1.640	−8.66	−10.18, −4.26	23.96	−34.14	−82.23 (45.2%)	147.81	−77.46 (42.6%)	−22.26 (12.2%)
22	HCHO	1.669	−8.36	−10.06, −6.49	27.81	−37.87	−74.46 (45.3%)	126.56	−66.03 (40.2%)	−23.94 (14.5%)
26	HCHO	2.678	−8.32	−9.88, −5.85	0.50	−10.38	−12.37 (44.4%)	17.47	−4.34 (15.6%)	−11.14 (40.0%)
28	HCHO	2.700	−8.25	−9.66, −5.96	0.45	−10.11	−11.87 (42.5%)	17.82	−3.91 (14.0%)	−12.15 (43.5%)
27	HCHO	2.778	−7.70	−8.87, −4.36	0.36	−9.23	−10.21 (46.7%)	12.65	−3.32 (15.2%)	−8.35 (38.1%)
23	HCHO	1.824	−6.46	−8.18, −5.15	16.50	−24.68	−55.94 (45.9%)	97.18	−42.25 (34.7%)	−23.67 (19.4%)
22	Cl^−	1.849	−119.76	−120.65, −22.87	57.30	−177.95	−195.31 (55.0%)	177.09	−132.92 (37.4%)	−26.81 (7.6%)
23	Cl^−	1.914	−114.30	−115.43, −19.96	40.89	−156.32	−191.81 (57.5%)	177.46	−113.40 (34.0%)	−28.57 (8.5%)
24	Cl^−	1.913	−111.32	−111.84, −17.29	35.03	−146.87	−188.77 (56.8%)	185.70	−117.12 (35.2%)	−26.68 (8.0%)
26	Cl^−	1.939	−100.69	−101.57, −11.41	39.14	−141.94	—^e	172.34	—^e	−27.19
29	Cl^−	1.925	−99.71	−100.82, −8.72	46.76	−147.58	−182.01 (56.5%)	174.30	−111.72 (34.7%)	−28.15 (8.8%)
28	Cl^−	1.968	−99.22	−100.01, −10.75	34.53	−134.54	−172.88 (57.2%)	167.75	−102.25 (33.8%)	−27.16 (9.0%)
27	Cl^−	1.976	−99.20	−99.44, −8.67	33.75	−133.19	−172.52 (58.0%)	164.09	−98.33 (33.1%)	−26.43 (8.9%)

---

Ammonia affinities of cations 21–29

Ammonia affinities of cations 21–24 and 26–29 range from ΔH/ΔE = −21/−23.8 kcal mol⁻¹ for 21 (L = Me₂S) to ΔH/ΔE = −4.2/−6.6 kcal mol⁻¹ for 29 (L = 2,6-lutidine). As mentioned before, interaction of 25 (L = PH₃) with NH₃ results in PH₃ substitution. Except for 29, ΔHs and ΔEs show the same trend, with R² = 0.997. Deformation energies range from 26.1 kcal mol⁻¹ for the complex formation from 27 (L = 1,3-dimethylimidazol-2-ylidene) to 39.6 kcal mol⁻¹ for the association of ammonia with 22 (L = Me₂O). Apart from [21-NH₃]⁺ and [29-NH₃]⁺, interaction energies show the same trend as ΔHs/ΔEs (R² = 0.96 for the correlation between ΔE and ΔE_int in the case of NH₃-complexes with 22–28). The ΔE_int are thus important for the relative NH₃ affinity order. Deformation energies decrease in the same order, that is from [22-NH₃]⁺ to [28-NH₃]⁺ (for the latter, ΔE_def just slightly exceeds that for the [27-NH₃]⁺). The B–NH₃ bond lengths vary from 1.624 Å in [22-NH₃]⁺ to 1.715 Å in [28-NH₃]⁺. As a comparison, the calculated B–NH₃ bond length in [18-NH₃]⁺ amounts 1.653 Å.

The LMOEDA shows that the nature of the cation–NH₃ interactions is not much dependent on the structure of L: major percentage contribution to all attractive forces still comes from ΔE_elstat (46.8% in [21-NH₃]⁺ to 47.8% in [26-NH₃]⁺), followed by that of ΔE_oi (39.9% in [28-NH₃]⁺ to 43.2% in [21-NH₃]⁺), though dispersion interactions are now slightly more pronounced ranging from 10% in [21-NH₃]⁺ to 12.4% in [28-NH₃]⁺.

Replacement of ammonia ligand L in 18 with weaker nucleophiles (better leaving groups) such as Me₂S in 21 and Me₂O in 22 increases NH₃ affinity by 2.3 kcal mol⁻¹ and 1.6 kcal mol⁻¹, respectively. The B–NH₃ distance in a complex reduces by ∼0.028 Å. In fact, nitrogen from the incoming NH₃ ligand forms stronger bond with boron than sulfur and oxygen from dimethyl(thio)ether, resulting in a significant increase in the B–SMe₂ and B–OMe₂ bond lengths by 0.201 Å and 0.214 Å, respectively.

The corresponding B–L bond lengthening upon complex formation with 18 (L = NH₃), 23 (L = NMe₃) and 24 (L = PMe₃) is smaller: 0.104 Å for the B–NH₃, 0.103 Å for the B–NMe₃ and 0.083 Å for the B–PMe₃ bond. The shorter B–N bond in [21-NH₃]⁺ and [22-NH₃]⁺ relative to [18-NH₃]⁺ and adducts obtained from 23, 24 and 26–29, leads to quite favourable interaction energy. It is more stabilizing in [22-NH₃]⁺ than in [21-NH₃]⁺ just because of the smaller Pauli repulsion. These favourable ΔE_int are attenuated by ΔE_def, which is larger for 22.

The presence of L = NMe₃ in 23 and L = PMe₃ in 24 decrease complex formation enthalpies by 4.2 kcal mol⁻¹ and 5.4 kcal mol⁻¹, respectively, compared to 18. Since ΔE_def are smaller than in the case of 18, weaker NH₃ affinity of 23 and 24 is associated with a decrease in the ΔE_int. Thus, substitution of L = NH₃ in 18 with the larger ligand NMe₃ increases the B–NH₃ distance by 0.016 Å. This, in turn, weakens orbital and electrostatic stabilization by 4.6 kcal mol⁻¹ and 2 kcal mol⁻¹, respectively. Otherwise, charge transfer interactions corresponding to the B–NH₃ bond formation should be increased due to the somewhat lower boron's p-orbital occupancy in 23 (0.438e) than in 18 (0.457e). The NMe₃ stabilizing ligand brings about larger Pauli repulsion in the complex, though larger by only 2.8 kcal mol⁻¹ with respect to that in [18-NH₃]⁺. The complex geometry is obviously adjusted to escape strong repulsive interactions, for example by somewhat increased cation–ligand distance. As data in Table 4 show, even in this case the dispersion interactions are larger in [23-NH₃]⁺ than in [18-NH₃]⁺. The presence of phosphorus in 24 instead of nitrogen in 23 leads to the shorter B–NH₃ bond, quite similar to that in [18-NH₃]⁺, and larger electrostatic and orbital stabilization. The ammonia approach is here less hindered due to the longer B–PMe₃ bond (1.939 Å) with respect to B–NMe₃ bond (1.535 Å). What makes 24 to be weaker NH₃ acceptor than both 18 and 23 is complex destabilization by larger Pauli repulsion.

All carbene-stabilized cations 26–28 form more labile adducts with ammonia than all the previously discussed ones. The ΔHs/ΔEs decrease in the order: 26 (ΔH/ΔE = −8.8/−10.8 kcal mol⁻¹) > 27 (ΔH/ΔE = −6.3/−8.2 kcal mol⁻¹) > 28 (ΔH/ΔE = −4.8/−6.3 kcal mol⁻¹). These cations keep ammonia at relatively long distance, 1.694–1.715 Å, resulting in smaller Pauli repulsion, but also in weaker attractive energies (ΔE_elstat and ΔE_oi). Calculated boron's p-orbital occupancy amounts 0.441e in 26, 0.436e in 27 and 0.430e in 28, which are all smaller than in 18 (0.457e) and majority of cations 21–24 (Table S3†). This means that the lower NH₃ affinities of 26–28 do not originate from smaller capability of boron's p-orbital to accept an electron pair. Rather, it seems as if steric factors interfere with ligand approach, keeping it somewhat farther from boron and thus decreasing the cation–L′ interaction energy. This is the cause of smaller binding energy of these cations, since ΔE_def is also smaller than in the case of 18 and 21–24. Among the three carbene-stabilized cations, 26 (L = 3-methylthiazole-2-ylidene) shows the highest affinity and 28 (L = 1,3-dimethybenzimidazole-2-ylidene) is the weakest NH₃ acceptor. Higher affinity of 26 comes from more favourable ΔE_int, related to the smaller steric hindrance to ligand approach and shorter B–N bond. Only in [26-NH₃]⁺ the 1,3,2-oxazaborolidine and thiazole rings are quasiorthogonal, with NH₃ situated at the sulfur side of thiazole. In the other two adducts, the two rings adopt a wing-shaped conformation. The B–N bond lengths in [27-NH₃]⁺ and [28-NH₃]⁺ are almost the same, and the lower affinity of 28 mainly comes from a decrease in ΔE_int (by 1.6 kcal mol⁻¹ relative to [27-NH₃]⁺), less from increase in ΔE_def, by only 0.3 kcal mol⁻¹. The amount of electrostatic, orbital and dispersion interactions in [28-NH₃]⁺ compares with those in [27-NH₃]⁺, so the smaller ΔE_int of [28-NH₃]⁺ originates from an increased Pauli repulsion.

The weaker NH₃ affinity of 29 relative to affinities of 26–28 stems from an increased deformation energy needed to accommodate NH₃. The most favourable geometry of cation 29, having the two rings in an orthogonal position, must change to a wing-shaped one to allow NH₃ to approach boron atom. When the complex is formed, the interaction energy becomes more stabilizing than in adducts formed from 26–28.

Formaldehyde affinities of cations 21–29

Formaldehyde affinities of cations 21–28 span a narrow range from ΔH/ΔE = −10.2/−11.5 kcal mol⁻¹ for 24 (L = PMe₃) to ΔH/ΔE = −6.5/−8.2 kcal mol⁻¹ for 23 (L = NMe₃), and are all smaller than the affinity of 18 (L = NH₃). As mentioned before, 29 (L = lut) forms only hydrogen-bonded complex with HCHO. The trend in ΔHs and ΔEs is the same, having R² = 0.929. Interaction and deformation energies vary greatly (Table 4) due to large variations in the B–OCH₂ distances. They are pretty long (2.650–2.778 Å) in HCHO-complexes with cations 24 (L = PMe₃) and 26–28 (carbene-stabilized) resulting in small deformation (0.4–0.9 kcal mol⁻¹) and small interaction energies (−9.2 to −12.4 kcal mol⁻¹). In other HCHO-adducts, boron–ligand distances are shorter and range from 1.640 Å in [25-HCHO]⁺ (L = PH₃) to 1.824 Å in [23-HCHO]⁺ (L = NMe₃).

The LMOEDA shows that in all adducts having long boron–ligand distances the percentage contributions of electrostatic and dispersion forces (42.5–46.7% and 38.1–43.5%, respectively) to all attractive interactions is much greater than the contribution of orbital interactions (3.3–16.5%). Therefore, they should be considered as electrostatic-dispersion adducts rather than coordinate covalent ones. In other complexes, the percentage contributions of the three attractive interactions are more similar to those found for adducts derived from 4–20.

It is not clear why 24 forms an adduct with such a long B–OCH₂. Steric factors may be involved, and they are more prominent in the case of the less nucleophilic HCHO than for NH₃ and Cl⁻. Nevertheless, the weak ΔE_int in [24-HCHO]⁺ is counteracted by the very small energy required to deform fragments at such large distances, and is strong enough to place 24 at the beginning of the affinity scale of 21–28. By contrast, its nitrogen counterpart 23 binds HCHO at shorter distance increasing both ΔE_int and ΔE_def, though they are still smaller than in the case of 18, due to longer B–OCH₂ distance. The latter could be induced by steric repulsion with NMe₃ in 23. The relative magnitudes of ΔE_int and ΔE_def determined the lowest HCHO affinity of 23 amongst 18, 21, 22 and 24–28. Due to longer B–ligand distance, the role of dispersion attraction in complex stabilization is increased in [23-HCHO]⁺, at the expense of ΔE_oi, compared to adducts derived from 4–20 and 21, 22, 24 and 25.

Cations 21, 22 and 25, containing better leaving groups L = SMe₂, OMe₂ and PH₃, respectively, form complexes with short B–OCH₂ bonds which inherently increases interaction and deformation energies, compared to those corresponding for the complex formation from 18, 23 and 24. The 21, 22 and 25 are weaker HCHO acceptors than 18 and 24 just because of larger deformations, but stronger acceptors than 23 due to the increased interaction energy. The trend of decreasing HCHO affinities along the series 21 > 25 > 22 is determined by their ΔE_def which increase in the same order, while ΔE_int become more stabilizing. As in the case of NH₃-complexes, the B–ligand distances in [21-HCHO]⁺ and [22-HCHO]⁺ are almost the same and the more favourable ΔE_int for the latter results from smaller Pauli repulsion, whereas sulfur in 21 provides more electrostatic and orbital stabilization. The latter possibly comes from polarization part, since boron's p-orbital occupancy in 21 (0.474e) is higher than in 22 (0.447e).

The three carbene-stabilized cations 26–28 show quite similar affinities toward formaldehyde, which also compare with that of 22. The highest and the lowest enthalpy differ by only 0.6 kcal mol⁻¹, while ammonia affinities of cations 26 and 28 differ by ∼4 kcal mol⁻¹, which should be related to NH₃ closer approach to boron thus more influencing interaction and deformation energy parts. In fact, 27 and 28 show smaller tendency to bind ammonia than to bind formaldehyde, while NH₃ and HCHO affinities of 26 are comparable.

Chloride affinities of cations 21–29

The enthalpies/energies for the formation of adducts between cations 22–24, 26–29 and chloride anion are all lower than ΔH/ΔE for the corresponding Cl⁻ association with 18. They range from ΔH/ΔE = −119.8/−120.6 kcal mol⁻¹ for 22 (L = OMe₂) to ΔH/ΔE = −99.2/−99.4 kcal mol⁻¹ for 27 (L = 1,3-dimethylimidazole-2-ylidene). As already mentioned, Cl⁻ substitutes ligand L in cations 21 (L = SMe₂) and 25 (L = PH₃). ΔHs and ΔEs are strongly correlated (R² = 0.999). With just one exception (cation 29), interaction energies follow the same trend as ΔHs/ΔEs and are thus important for the relative Cl⁻ affinity order. Deformation energies, reflecting solely geometry changes of borenium ions, vary from 33.8 kcal mol⁻¹ for association of Cl⁻ with 27 (L = 1,3-dimethylimidazol-2-ylidene) to 57.3 kcal mol⁻¹ for the adduct formation between Cl⁻ and 22 (L = OMe₂). The B–Cl bond lengths range from 1.849 Å in 22-Cl to 1.976 Å in 27-Cl. The B–Cl bond length in 18-Cl is intermediate and amounts 1.905 Å.

The LMOEDA results show that the nature of the cation–chloride interactions in adducts derived from 22–24 and 26–29 is the same as in adducts formed from 4–20: the main percentage contribution to all attractive interactions comes from ΔE_elstat (55–58%), next come orbital interactions (33.1–37.4%), and dispersion forces provide the smallest contribution (7.6–9%).

As in the case of L′ = NH₃ and HCHO, substitution of L = NH₃ in 18 for better leaving group OMe₂ in 22, decreases the B–L′ distance. In the case of Cl⁻, the exocyclic B–O bond in 22 is significantly elongated upon adduct formation, by 0.294 Å, while the newly formed B–Cl bond is by 0.086 Å longer than it would be if a full OMe₂ substitution occurred. Large geometry changes in the cation leading to high ΔE_def are responsible for weaker Cl⁻ affinity of 22 compared to 18, even though interaction energy increases by as much as 12.5 kcal mol⁻¹. When better nucleophiles than NH₃ are bound to boron, such as NMe₃ and PMe₃ in cations 23 and 24, respectively, the Cl⁻ affinity drops by more than 10 kcal mol⁻¹. The presence of NMe₃ in 23 instead of NH₃ in 18 results in just a slight B–Cl bond elongation (<0.01 Å), which is smaller than in the case of L′ = NH₃ and HCHO and can be attributed to the larger nucleophilicity of Cl⁻. The reason why 23 behaves as weaker Cl⁻ acceptor than 18 lies in the smaller interaction energy, made such mostly by increase/decrease in the Pauli/electrostatic interactions, while orbital and dispersion interactions are more favourable in the case of 23. The B–Cl bond in 24-Cl is the same as in 23-Cl and smaller Cl⁻ affinity of 24 relates to larger repulsive energy (by 8.2 kcal mol⁻¹), but curiously to a drop in ΔE_elstat by ∼3 kcal mol⁻¹ and ΔE_disp by 1.9 kcal mol⁻¹. This could be explained by the longer distances between Cl and atoms contained in the ligand L, due to longer B–P bond relative to B–N bond. The reason why 23 and 24 are weaker Cl⁻ acceptors than 22 is a drop in ΔE_int, related to longer B–Cl bonds, which outweighs the drop in ΔE_def.

The Cl⁻ affinities of carbene-stabilized cations 26–28 and lut-stabilized cation 29 are all within 1.5 kcal mol⁻¹, the highest affinity found for 26 (L = 3-methylthiazole-2-ylidene) and the lowest for 27 (L = 1,3-dimethylimidazole-2-ylidene). Cation 26 binds Cl⁻ at shorter distance than the related cations 27 and 28, resulting in significantly higher interaction energy, but also more energy costly geometry changes (near-to-planar geometry in 26 becomes orthogonal in the adduct, with Cl being positioned at the sulfur side of thiazole ring). Their relative magnitudes are such that 26 shows slightly higher affinity toward Cl⁻ than 27 and 28, whose affinities are the same. Although, 29-Cl formation results in a (significantly) more favourable interaction energy than the adduct formation from the carbene-stablized ions 26–28, the high deformation energy places the Cl⁻ affinity of 29 close to those of 26–28. In this case, too, high ΔE_def mostly originates from cation geometry change from orthogonal to the wing-shaped, which is necessary in order to make a space for the incoming ligand.

Generally, borenium cations 21–25 having L with sp³-hybridized heteroatom possess higher affinities toward a new ligand L′ than carbene-stabilized cations 26–28 and lut-stabilized cation 29. In the case of 29, its weak affinity is determined by high ΔE_def and smaller ΔE_int, the latter partly related to the longer B–L′ distance compared to that in adducts derived from 21–25. The smaller binding energies of 26–28 have to be attributed to lower interaction energies, which is primarily due to the long B–L′ distances, particularly in the case of HCHO-adducts. The relative order of L′ affinities compares when L′ = NH₃ and Cl⁻, but differs significantly when L′ = HCHO.

Solvent effects on L′ affinity of cations 21–29

Solvent affects binding energies in the same way as discussed before: chloride affinities are significantly reduced and are still larger than HCHO affinities, which are decreased by up to 6 kcal mol⁻¹. Affinities toward Cl⁻ and NH₃ become similar. The trend in ΔEs when L′ = NH₃ is the same as in the gas-phase, almost the same when L′ = Cl⁻ (one exception: 28 > 29) and somewhat changed when L′ = HCHO (21 (L = SMe₂) > 24 (L = PMe₃), 25 (PH₃) < 27 (L = 1,3-dimethylimidazol-2-ylidene) and 23 (NMe₃) > 27).

Conclusions

In this paper, we have theoretically studied borenium ion affinities toward the three ligands: L′ = NH₃, HCHO and Cl⁻. General trend in both gas- and liquid-phase is such that R/R′ = H, F, Cl provide the strongest L′ binding. Then come cations with R/R′ = Me and P, the latter contained in the five-membered heterocycle. Substitution of Me groups with one or two Ph decreases affinity toward the L′ (in solvent conditions the influence on Cl⁻ affinity is opposite). Cat-containing cation shows higher affinity than other studied heterocycle-containing cations, in which R/R′ = O, S, N and P, except the cation 8 (P,P) in the gas-phase, and 8 and 12 (P,S) in the solvent, when L′ = NH₃ and HCHO. The high calculated affinity of 8 has been attributed to the long B–P bonds, which sterically least impedes with ligand approach. Among the heterocyclic cations, those that possess O, S and P as heteroatoms show stronger tendency to bind new ligand than nitrogen-containing ones. The variations of L showed that, with two exceptions, Me₂S-, Me₂O-, H₃N-, Me₃N- and Me₃P-stabilized borenium cations bind L′ more strongly than carbene- and 2,6-lutidine-stabilized cations.

When L = constant, the observed trend is determined by the cation–ligand distances and type of substituents R/R′. It was found that heteroatoms from the second octal row of the periodic table (P, S, Cl) provide larger electrostatic and orbital stabilization than heteroatoms from the first row (N, O, F) and it appears that the stabilizing effect increases when going from left to the right in the period. However, the repulsive Pauli energy is also stronger for larger heteroatoms. Phenyl substituents show larger electrostatic, orbital and dispersion stabilization than methyl groups, but also larger repulsion. It is the relative magnitude of attractive and repulsive interactions, along with the B–L′ distance that determines the overall interaction energy. When L′ = NH₃ and HCHO, the B–L′ distance is determined by the three factors: (1) steric effects, in the case of 4–20 mostly related to the B–R/R′ bond lengths (as they are longer, approach to the boron atom is easier), (2) substituent electronic effects influencing boron's p-orbital occupancy and (3) net attractive forces. Thus, the B–L′ distance is longer when one or both heteroatoms are nitrogen, and shorter for R/R′ = H, F, Cl and P. No such regularity was found for the more nucleophilic Cl⁻. When R/R′ = constant, the B–L′ distances are generally longer when L = carbene and shorter when L = S(O)Me₂.

We have to keep in mind that the total binding enthalpies/energies are not determined only by the magnitude of cation–ligand interaction energy. There is another factor that influences ΔHs/ΔEs: the energy that has to be spent to deform the two interacting molecules from their equilibrium geometry to that they have in a complex. Therefore, predictions and rationalizations of ΔHs/ΔEs must consider both ΔE_int and ΔE_def. For example, 29 (L = 2,6-lutidine) interacts more strongly with NH₃ than any of the carbene-stabilized cations 26–28, but its NH₃ affinity is the weakest because this cation has to undergo a significant conformational change in order to bind the L′.

With a few exceptions, major contribution to complex stabilization comes from electrostatic interactions (43–48% when L = NH₃ and HCHO; 55–60% when L = Cl⁻), next come orbital interactions (35–45% when L = NH₃ and HCHO; 33–39% when L = Cl⁻), while dispersion forces provide the smallest attraction (9–15% when L = NH₃ and HCHO; 7–9% when L = Cl⁻). Four HCHO-complexes, derived from 24 and 26–28, in which HCHO is found at a large distance from boron atom, should be considered as being of electrostatic-dispersion type.

Acknowledgements

This work was supported by the Ministry of Education, Science and Technological Development of the Republic of Serbia (Grant No. 172020).

References

1. P. Kölle and H. Nöth, Chem. Rev., 1985, 85, 399–418.
2. (a) W. E. Piers, S. C. Bourke and K. D. Conroy, Angew. Chem., Int. Ed., 2005, 44, 5016–5036; (b) T. S. de Vries, A. Prokofjevs and E. Vedejs, Chem. Rev., 2012, 112, 4246–4282.
3. (a) S. E. Denmark and Y. Ueki, Organometallics, 2013, 32, 6631–6634; (b) J. Chen, R. A. Lalancette and F. Jäkle, Chem. Commun., 2013, 49, 4893–4895; (c) P. Eisenberger, A. M. Bailey and C. M. Crudden, J. Am. Chem. Soc., 2012, 134, 17384–17387; (d) A. Prokofjevs, A. Boussonnière, L. Li, H. Bonin, E. Lacôte, D. P. Curran and E. Vedejs, J. Am. Chem. Soc., 2012, 134, 12281–12288; (e) J. M. Farrell, J. A. Hatnean and D. W. Stephan, J. Am. Chem. Soc., 2012, 134, 15728–15731; (f) E. J. Corey, Angew. Chem., Int. Ed., 2009, 48, 2100–2117.
4. (a) J. R. Lawson, E. R. Clark, I. A. Cade, S. A. Solomon and M. J. Ingleson, Angew. Chem., Int. Ed., 2013, 52, 7518–7522; (b) V. Bagutski, A. Del Grosso, J. A. Carrillo, I. A. Cade, M. D. Helm, J. R. Lawson, P. J. Singleton, S. A. Solomon, T. Marcelli and M. J. Ingleson, J. Am. Chem. Soc., 2013, 135, 474–487; (c) S. A. Solomon, A. Del Grosso, E. R. Clark, V. Bagutski, J. J. W. McDouall and M. J. Ingleson, Organometallics, 2012, 31, 1908–1916.
5. A. Prokofjevs, PhD Dissertation, University of Michigan, 2013.
6. J. A. Plumley and J. D. Evanseck, J. Phys. Chem. A, 2009, 113, 5985–5992.
7. E. R. Clark, A. Del Grosso and M. J. Ingleson, Chem.–Eur. J., 2013, 19, 2462–2466.
8. W. F. Schneider, C. K. Narula, H. Nöth and B. E. Bursten, Inorg. Chem., 1991, 30, 3919–3927.
9. A. Del Grosso, R. G. Pitchard, C. A. Muryn and M. J. Ingleson, Organometallics, 2010, 29, 241–249.
10. J. A. Plumley and J. D. Evanseck, J. Phys. Chem. A, 2007, 111, 13472–13483.
11. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
12. J. B. Foresman and A. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian, Inc., 1996.
13. J. A. Plumley and J. D. Evanseck, J. Chem. Theory Comput., 2008, 4, 1249–1253.
14. T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1024.
15. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
16. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2013.
17. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
18. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
19. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, J. Comput. Chem., 1993, 14, 1347–1363.
20. (a) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340; (b) K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300.
21. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fronseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
22. (a) E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2013; (b) E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42; (c) F. Weinhold and C. R. Landis, in Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, Inc., 2012.
23. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
24. In few cases only, lengths of B–heteroatom bonds remain the same.
25. This binding enthalpy was estimated as −55.6 kcal mol⁻¹ in ref. 2b and 5, at the M06-2X/6-311++G(3df,2p)//M06-2X/6-31+G(d,p) level.
26. L. R. Thorne, R. D. Suenram and F. J. Lovas, J. Chem. Phys., 1983, 78, 167–171.

---

Footnote

† Electronic supplementary information (ESI) available: Validity of theory level employed in the study, additional calculations done at the M06-2X/aug-cc-pVDZ and MP2/6-311++G(d,p) levels, influence of BSSE corrections on geometries, calculated B–R/R′ and B–L bond lengths, NBO charges at boron atom and electron occupancies of boron's p-orbital of borenium cations 4–29, energy decomposition analysis of binding interactions in BF₃–NH₃ and BCl₃–NH₃, optimized structures of borenium cations and their adducts with NH₃, HCHO and Cl⁻, absolute energies and x, y, z coordinates of the optimized structures. See DOI: 10.1039/c5ra13825f

---