Vapour pressure and mixing thermodynamic properties of the KNbO3–NaNbO3 system†
A. Popovič*a,
L. Benczeb,
J. Koruza‡
 a and
B. Maliča
a and
B. Maliča
aJožef Stefan Institute, Jamova cesta 39, SI-1000 Ljubljana, Slovenia. E-mail: arkadij.popovic@ijs.si
bEötvös Loránd University, Dept. of Physical Chemistry, Pázmány Péter sétány 1/A, H-1117 Budapest, Hungary
First published on 1st September 2015
Abstract
Equilibrium vapour pressures of sodium and potassium over a KxNa1−xNbO3 solid solution within its whole compositional range at temperatures between 1173 K and 1303 K were determined by Knudsen Effusion Mass Spectrometry. It should be noted that the thermodynamic equilibrium between the condensed and the vapour phase could be established only after prolonged annealing (more than 10 h at 1263 K). The equilibrium vapour pressure of potassium over K0.5Na0.5NbO3 (KNN) is a few times larger than that of sodium, i.e., 8 × 10−3 Pa as compared to 3 × 10−3 Pa at 1263 K. From the obtained results, the excess thermodynamic functions for the pseudo-binary KNbO3–NaNbO3 system were evaluated. The excess Gibbs energy was found to be positive, the excess enthalpy is close to zero, while the negative excess entropy indicates a partial ordering of alkaline ions in the solid solution. The comparison of the obtained results to the well-established lead-based piezoelectric systems revealed, that the vapour pressure of alkalis over the respective niobates at 1200 K is almost three orders of magnitude lower as compared to the values reported for lead oxide over Pb(Zr,Ti)O3.
1. Introduction
Piezoelectrics are technologically important materials, which enable coupling between mechanical and electrical signals and are therefore widely used in various electronic applications.1 Lead-based perovskite materials, such as, Pb(Zr1−x,Tix)O3 (PZT) or Pb(Mg1/3Nb2/3)O3–PbTiO3 (PMN–PT) are most widely used; however, these materials contain up to 70 wt% lead, which represents a possible health and ecological hazard. The increased environmental awareness, supported by the restriction of the use of hazardous substances,2 drives the search for new lead-free piezoelectric materials, that would replace the widely used lead-based piezoelectrics. Good ferroelectric and piezoelectric properties were observed in alkali-niobate based ceramics, including the K0.5Na0.5NbO3 solid solution (KNN).3 Moreover, these materials enable the use of nickel electrodes – a large advantage over PZT, due to the significant reduction in processing cost.4Despite the large potential of KNN-based lead-free piezoelectric materials, the poor reproducibility of the functional properties still prevents their wide use in commercial applications.3,5,6 The reasons for the observed variation of the properties are mostly related to difficult and poorly understood processing, originating from hygroscopicity of the starting compounds,7 different phase composition of the precursors,8 different diffusion rates of constituent ions resulting in local compositional inhomogeneities,9 and specific sintering mechanism.10 Furthermore, presence of secondary alkali-poor phases and consequent degradation of functional properties has been attributed to loss of alkaline species upon sintering. In different studies loss of either sodium or potassium from the ceramic matrix was determined or assumed,11,12 and according to our opinion such discrepancies could be due to different solid-state synthesis or sintering conditions, different stoichiometries of the studied materials, or even difficulties related to exact determination of the local chemical composition.13,14 According to our knowledge no data on vapour pressures of alkali species in the KNbO3–NaNbO3 system have been reported. It should be recalled at this point that a few decades ago, a similar situation was encountered in the case of PZT ceramics. Seminal works of Holman and Fulrath,15 Härdtl and Rau,16 and Kingon17 contributed to our present understanding and ability to control the vapour pressure of lead oxide during sintering of PZT within its whole compositional range.
Thus the aim of this work has been to measure the vapour pressure of both alkali metals over the whole compositional range from which the excess thermodynamic functions of mixing could be evaluated for the KNbO3–NaNbO3 pseudo-binary system. As in our previous study of the Na2O–Nb2O5 system,18 Knudsen Effusion Mass Spectrometry (KEMS) was used. Finally, the obtained vapour pressures of alkalis over respective niobates are compared to the vapour pressures of bismuth and potassium over Bi0.5K0.5TiO3,19 and PbO over Pb(Zr,Ti)O3 solid solution.16,20
Thermodynamic background
In a typical KEMS experiment, the sample is heated within an almost closed container (Knudsen cell) so that the thermodynamic equilibrium is established between gaseous and condensed phases. Molecules and/or atoms of the gas phase are let to effuse through the orifice into the evacuated surrounding, entering the ion source of the mass spectrometer. The as-formed ions are analyzed by their m/z (mass to charge) ratio and their abundance is measured by an appropriate detector.The vapour pressure (pj) of any species (j) within the Knudsen cell is proportional to the measured ion intensity (Iij) of the ion i (counts per second in our case) originating from species j and the absolute temperature of the cell (T) according to eqn (1),21 where K is the instrumental sensitivity constant and σj is the ionisation cross section of species j. K can be determined e.g. by evaporation of a material with known vapour pressure (e.g. Ag) in a separate experiment.
 | (1) |
In studies of binary systems Belton and Fruehan22 as well as Neckel and Wagner23 independently showed that it is possible to obtain the thermodynamic activities of both components without determining the absolute vapour pressures of the components just by measuring the ion intensity ratio of ions originating from the components over the complete compositional range. This in the present case means that one should measure the ion intensity ratio of ions originating from NaNbO3 and KNbO3. However, in recent KEMS study of NaNbO3 (ref. 18) it was found that at elevated temperatures, the main gaseous species in equilibrium over the condensed phase were sodium atoms and oxygen molecules, as the result of the equilibrium decomposition reaction (2), as follows:
| 4NaNbO3(s) ⇔ Na2Nb4O11(s) + 2Na(g) + 1/2O2(g) | (2) |
Similarly, potassium atoms and oxygen molecules could be anticipated to be the main gaseous components in the case of KNbO3. It will be shown below, that it is possible to obtain the activities of both components, i.e., KNbO3 and NaNbO3, also by measuring the K+/Na+ ion intensity ratio over the complete composition interval. In the case of KxNa1−xNbO3 solid solution (ss) within the pseudo-binary NaNbO3–KNbO3 system, both sodium and potassium take part in the following equilibrium exchange evaporation reaction:
| NaNbO3(ss) + K(g) ⇔ KNbO3(ss) + Na(g) | (3) |
The equilibrium constant (Keq) of reaction (3) is defined as
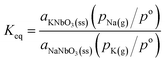 | (4) |
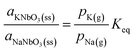 | (5) |
Applying the relationship between the vapour pressure and ion intensity presented in eqn (1) and (5) turns to:
 | (6) |
The corresponding equation for the ratio of the activity coefficients is as follows:
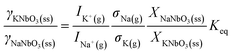 | (7) |
The activity of NaNbO3 using the well-known Gibbs–Duhem relationship can be obtained as follows:24
 | (8) |
The corresponding equation for the activity coefficients is as follows:
 | (9) |
The change of the logarithm of the ratio of the activity coefficients by changing the composition can be obtained from eqn (7) as:
 | (10) |
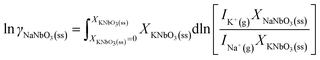 | (11) |
Analogous formulas hold for KNbO3.
It should be notified at this point, that the ion intensities of Na+ and K+ linearly correlate with the partial pressures of Na(g) and K(g) (see eqn (1)) which, in turn, correlate with the activities of Na2O and K2O in a multi-oxide (in our case ternary oxide) system as follows:18
 | (12) |
2. Materials and methods
Materials and sample preparation
The starting powder mixtures with different K/Na molar ratios (10/90, 20/80, 30/70, 40/60, 50/50, 60/40, 70/30, 80/20 and 90/10) were prepared according to the stoichiometric formula KxNa1−xNbO3 from high purity Nb2O5 (99.9%, Sigma-Aldrich, Taufkirchen, Germany), K2CO3 (anhydrous 99.9%, Chempur, Karlsruhe, Germany) and Na2CO3 (anhydrous 99.9%, Chempur, Karlsruhe, Germany). Hereafter the samples will be further referred to by their K/Na molar ratio, e.g., “KNN50/50”. Both carbonates were high-energy milled prior to mixing in a planetary ball mill for 4 h (Pulverisette 4 Vario-Mill, Fritsch, Idar-Oberstein, Germany) using a tungsten carbide vial and balls. The starting compounds were weighted under dry atmosphere and homogenized in a planetary ball mill for 4 h using zirconia vial and balls and acetone as a liquid medium. Finally the powder mixtures were dried and kept in closed vials for further use.The X-ray diffractograms (XRD) were recorded using the PANalytical X'Pert PRO diffractometer with CuKα1 radiation and a graphite monochromator (PANalytical B.V., Almelo, the Netherlands). The data were collected in the 2θ range from 10° to 60° with a step of 0.034°/100 s.
KEMS experiments
A 60-degree magnetic low-resolution mass spectrometer with a modified Nier-type ion source was used. A detailed description of the apparatus can be found elsewhere.18 In preliminary experiments, 330 mg of alkali carbonates and niobium oxide mixture with 50/50 Na-to-K molar ratio (KNN50/50) was loaded into the platinum Knudsen cell with an orifice diameter of 0.05 mm. The sample was then calcined for 12 h at 950 °C in open air. The purpose of such small orifice was to minimize any possible loss of alkali elements from the powder, still letting the carbon dioxide to escape. As a result of such arrangement, K0.5Na0.5NbO3 (KNN) was formed under predominant CO2 atmosphere. After fast cooling, a portion (204 mg) of such KNN sample was loaded in the Pt Knudsen cell with the orifice diameter of 1 mm, placed into the evaporator of the mass spectrometer and evacuated. When the vacuum reached 10−6 Torr, the sample was heated at a rate of 10 K min−1 until the Na+ and K+ ions could be detected at about 800 °C. The temperature was then rapidly increased to 890 °C and kept constant for 21 h. The temperature was subsequently increased again to 990 °C and kept constant for additional 24 h.In the second series of KEMS experiments, the activities of the KNN samples with different KN/NN molar ratios were determined in the Knudsen cell with the 1 mm orifice. About 200 mg of carbonate–oxide mixture in the required stoichiometric ratio were loosely pressed into an alumina cell and annealed at 950 °C for 10 h in open air. The Knudsen cell with the sample was immediately transferred into the evaporator, evacuated, and heated to 990 °C at the rate of 10 K min−1. When the final temperature was reached, the ion intensities IK+ and INa+ were monitored until their values became constant. This usually took about 10 h, much faster than in the preliminary experiment. During this equilibration time some alkalis were also lost, slightly altering the stoichiometry; however, it was assessed to have no significant effect on final results. The temperature was then increased to 1030 °C at which the measurement was started. The data were collected at each 10 °C down to 900 °C. Each experimental point was collected for 10 s or 60 s when the counting rate became less than 100 s−1.
3. Results and discussion
In the preliminary KEMS experiment the KNN50/50 specimen was loaded in a Pt Knudsen cell with the orifice diameter of 0.09 mm, and heated at 890 °C and 990 °C. The measured intensities of K+ and Na+ ions are presented in Fig. 1, while the full set of data is given in the ESI (Table S-I†). The time dependencies of the pressures of both alkalis clearly indicate that the thermodynamic equilibrium of the system was not reached during the solid state synthesis at 950 °C for 12 h in the CO2-enriched atmosphere, related to the extremely fine orifice of the cell. | ||
| Fig. 1 Time–temperature dependence of sodium and potassium vapour pressures over K0.5Na0.5NbO3, previously prepared by calcination of the oxide–carbonate mixture at 950 °C, 12 h. The values of vapour pressures were calculated from the measured intensities according to eqn (1). | ||
Evidently, the activity of Na2O attains, or is close to the equilibrium upon heating for 21 h at 890 °C, while the activity of K2O keeps decreasing upon additional heating step for 23 h at 990 °C (see Fig. 1), until the thermodynamic equilibrium is finally reached.
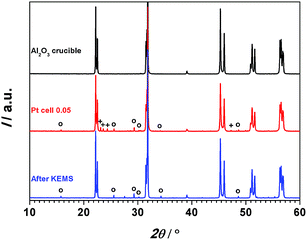
The XRD patterns of the KNN50/50 samples before (in a Pt-cell) and after the KEMS experiment are depicted in Fig. 2, together with the pattern of a KNN50/50 sample, conventionally calcined at 950 °C in an Al2O3 crucible, which is added for comparison. The latter crystallizes in the perovskite phase, in agreement with ref. 25. In the sample calcined in the Pt-cell the perovskite phase coexists with traces of Nb2O5 and traces of (K,Na)6Nb10.88O30. This niobium-rich phase can be formed either at too low thermal budget,26 or as a result of excessive alkali-loss during prolonged heating at high temperatures.9 In the present case its presence could be related to the CO2-enriched atmosphere during heating, which presumably shifts the equilibrium of the KNN synthesis reaction towards the reagents side. The pattern of the sample after KEMS analysis, revealed the presence of the perovskite and (K,Na)6Nb10.88O30 phases, while reflections of Nb2O5 were not detected. This result underlines the importance of the careful control of the calcination conditions, which should enable removal of the gaseous reaction product (in this case CO2). This can be achieved by selecting a low-enough powder/container volume ratio thus allowing the gas exchange between the container and surrounding atmosphere.
During this experiment, which lasted 45 h, a certain amount of alkalis evaporated from the sample. The loss of sodium and potassium from the Knudsen cell was assessed using the Hertz–Knudsen–Langmuir equation (eqn (13)).21
 | (13) |
 is the mass flux of the effusing species i in mg s−1, A is orifice area in cm2, pi is the pressure of species i in Pa, Mi is the molecular mass of species i and T is the absolute temperature. The total mass losses of sodium and potassium were obtained by integration of the pressure–time data depicted in Table S-I.† The conversion of ion intensity (in s−1) to pressure (columns 5 and 6) was performed using eqn (1).
is the mass flux of the effusing species i in mg s−1, A is orifice area in cm2, pi is the pressure of species i in Pa, Mi is the molecular mass of species i and T is the absolute temperature. The total mass losses of sodium and potassium were obtained by integration of the pressure–time data depicted in Table S-I.† The conversion of ion intensity (in s−1) to pressure (columns 5 and 6) was performed using eqn (1).
As a result it was obtained that 1.16 mg of potassium and 0.14 mg of sodium evaporated from the initial 204 mg of KNN50/50 sample during the KEMS experiment – this represents almost 5 mol% of the total potassium, while the loss of sodium was about 10 times lower. Quite surprisingly, in spite of such massive loss of potassium, neither additional secondary phases were detected in the residual material nor a change in the relative amount of the (K,Na)6Nb10.88O30 phase could be observed (see Fig. 2). Certainly, the above assessment should not be correlated with the loss of alkalis during conventional solid-state synthesis of KNN, which is conducted in air atmosphere where the rate of alkali evaporation is hindered both kinetically and thermodynamically. In several auxiliary experiments it was observed that the evaporation rate in air is about fifty times lower than in vacuum.
Measurements of activity of KNbO3 and NaNbO3 in KNN solid solutions
In the second series of KEMS experiments, the larger orifice of the Knudsen cell allowed better interchange of CO2 with air and in this case the as-synthesized KNN solid solutions consisted of pure perovskite phase only (XRD patterns not shown).The data for a selected analysis of the KNN20/80 sample are shown in Fig. 3, while the raw data can be found in the ESI (Table S-II†).
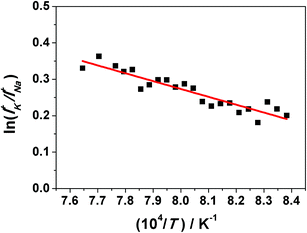 | ||
| Fig. 3 ln(IK+/INa+) vs. (104/(T/K)) for a selected analysis of the KNN20/80 sample. The line represents the linear fit. | ||
The resulting slope and the intercept for this particular measurement are −2157 ± 200 and 1.999 ± 0.7, respectively. Several similar runs were performed for each composition starting from KNN10/90 to KNN90/10. The complete results for the nine studied compositions are collected in Table 1, where the necessary data to evaluate the excess thermodynamic functions/properties of mixing of the studied binary system are included. The parameters A and B determine the IK+/INa+ ion intensity ratio at the temperature T according to eqn (14) as follows:
| ln(IK+/INa+) = A/T + B | (14) |
| Comp. | No. of runs | −A | B |
|---|---|---|---|
| 10/90 | 5 | 2098(±148) | 1.66(±0.20) |
| 20/80 | 5 | 2167(±409) | 2.19(±0.43) |
| 30/70 | 6 | 2134(±566) | 2.60(±0.46) |
| 40/60 | 6 | 1998(±200) | 2.87(±0.23) |
| 50/50 | 3 | 1968(±275) | 3.13(±0.30) |
| 60/40 | 4 | 1994(±235) | 3.52(±0.30) |
| 70/30 | 4 | 2067(±300) | 3.79(±0.25) |
| 80/20 | 3 | 2182(±453) | 4.16(±0.28) |
| 90/10 | 5 | 1953(±492) | 4.38(±0.49) |
In order to calculate the activity coefficients as described by eqn (11), it should be rewritten in the trapezian summation form as:
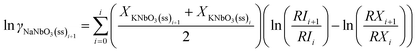 | (15) |
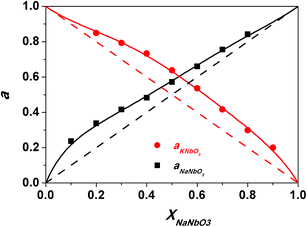
The activities of both KNbO3 and NaNbO3, were extracted from both activity coefficients, as shown in Fig. 4. Evidently, the system exhibits a positive deviation from Raoult's law.
Furthermore, the excess integral molar thermodynamic functions (GE, HE and SE) can generally be fitted to the Redlich–Kister (R–K) sub-regular mixture model.27 Accordingly, the excess integral molar Gibbs energy, for the KNbO3–NaNbO3 system, can be expressed as:
| GE = XNaNbO3(ss)XKNbO3(ss)[C0 + C1(XNaNbO3(ss) − XKNbO3(ss)) + C2(XNaNbO3(ss) − XKNbO3(ss))2] | (16) |
 | (17) |
In eqn (17) Gex denotes the seven experimental values of the excess Gibbs energy obtained from activity coefficients and, XNa as well as XK in matrix M denote the mole fractions of NaNbO3 and KNbO3, respectively.
The resulting parameters (C0, C1 and C2) are temperature-dependent and can be expressed as: C0 = 6.65T − 450, C1 = −1.07T − 527 and C2 = 2.53T − 219. Thus inserting the temperature dependence into eqn (16) it follows:
| GE = XNaNbO3XKNbO3[(6.65T − 450) + (−1.07T − 527)(XNaNbO3 − XKNbO3)+ + (2.53T − 219)(XNaNbO3 − XKNbO3)2] | (18) |
Furthermore, the derivative of  with respect to temperature provides the excess enthalpy according to eqn (19) as follows
with respect to temperature provides the excess enthalpy according to eqn (19) as follows
 | (19) |
Finally, the excess entropy is obtained as:
 | (20) |
The obtained integral excess thermodynamic properties as a function of the composition at 950 °C are presented in Fig. 5.
 | ||
| Fig. 5 Excess integral functions in (K,Na)NbO3 solid solution system at 950 °C. Square points represent the experimental data obtained by Gibbs–Duhem integration. Also shown are uncertainties calculated from uncertainties of parameters A and B, also depicted in Table 1. | ||
It is interesting to note that the system exhibits a positive deviation from Raoult's law with the negative excess entropy while the excess enthalpy is very low (close to zero). This could be also predicted directly from observing the values of parameters “A” depicted in Table 1. A great effort was undertaken in order to detect the heat effect directly, using the high temperature differential scanning calorimetry (DSC) in order to compare the heat values obtained by KEMS. Nevertheless, no heat effect was detected by DSC. This could be due to a rather low heat effect as obtained by KEMS on one hand and to a relatively low rate of mixing reaction on the other. Namely, previous studies have shown that the synthesis of KNN50/50 from the binaries required a larger thermal budget (higher temperatures and extended heating times) in order to obtain a homogeneous solid solution7,25,28 as compared to the synthesis from the carbonate–oxide mixture.
Since the excess enthalpy is negligible as compared to excess Gibbs energy, the latter arises mainly from the excess entropy as GE ≈ −TSE. A relatively large negative value suggests that a partial ordering may occur during mixing. In other words, during mixing of NaNbO3(s) and KNbO3(s) the Na+ and K+ ions are not distributed randomly but should be partly occupying certain lattice sites. Other systems having negative excess entropies exhibit also some kind of ordering, e.g., formation of associates in a melt, see Fraser et al.29 The paper is one of the numerous investigations of molten mixed alkali feldspars, where KEMS measurement of K+/Na+ provided information on thermodynamics of mixing. However, for solid solution systems such information is sparse. To our knowledge, no work regarding mixing thermodynamics of KNN has been published yet, despite of its potential to replace PZT. For the latter the GE of mixing at 1373 K was determined by Jacob and Rannesh as +2 kJ mol−1 with maximum at the PbZrO3 rich side.30 It seems that both systems reveal similar behaviour from the GE point of view. Mixing enthalpy of PZT was previously reported to be about +10 kJ mol−1, as measured by Rane et al. using drop solution calorimetry.31 In this case a large difference between GE and HE of mixing seems to be unrealistic from the SE point of view. This therefore raises the question whether or not the drop solution method would be appropriate to confirm small heat effect of mixing found in the present work.
Comparison of vapour pressures of volatile species over selected perovskites
The obtained vapour pressures of potassium and sodium18 over respective oxides and niobates were compared to the vapour pressure of PbO over pure PbO and Pb(Zr,Ti)O3 solid solution, using the data reported in the literature.16,20 It should be noted that in contrast to alkalis, which exist in the vapour phase in atomic form, cf. eqn (2), in the case of lead oxide and PZT, the vapour phase consists predominantly of monomeric lead oxide (PbO) and to a much lesser amount of lead (Pb) and dimeric lead oxide (Pb2O2). For sake of simplicity, this total vapour phase is in further text described as ‘lead oxide’. Thus in the calculation an average molar mass of the vapour phase was implemented, cf. ref. 20 and 32. The results for the temperature range 900–1200 K are presented in Fig. 6. As described earlier in the paper, the vapour pressure of potassium over K2O in the temperature range 900–1200 K is more than an order of magnitude higher than that of sodium over Na2O, reaching the value of about 1 × 102 Pa for potassium at 1200 K. The vapour pressures of potassium and sodium over respective niobates are more than five orders of magnitude lower, ∼2 × 10−3 Pa and ∼6 × 10−4 Pa at 1200 K, respectively. Interestingly, the vapour pressure of lead oxide over condensed lead oxide is only slightly below the sodium over Na2O curve, ∼10 Pa at 1200 K, while the vapour pressure of lead oxide over the PZT solid solution is one order of magnitude lower, ∼1 Pa at 1200 K. | ||
| Fig. 6 Vapour pressures of potassium (this work) and sodium18 over respective oxides and niobates, of lead oxide over PbTiO3 + TiO2 (PT + T), PbZrO3 + ZrO2 (PZ + Z), Pb(Zr0.5Ti0.5)O3 + ZrO2 (PZTss + Z),16,20 and of bismuth and potassium over Bi0.5K0.5TiO3 (BKT).19 | ||
In addition, the results are compared to the vapour pressures of bismuth and potassium over Bi0.5K0.5TiO3 (BKT) reported in ref. 19. BKT was selected as a representative of the second largest group of lead-free piezoelectrics, i.e. the Bi-based materials.3 The vapour pressure of bismuth over BKT at 1200 K is ∼1 Pa and is very close to the pressure of lead-oxide vapour over PZT, while the vapour pressure of potassium over BKT is almost two orders of magnitude lower.
Based on the comparison presented above it can be concluded, that the vapour pressures of the volatile species during the high-temperature processing (calcination, sintering) of the PZT- and Bi-based piezoelectrics are orders of magnitude higher than the vapour pressures of alkalis in KNN-based systems.
4. Conclusions
Equilibrium vapour pressures of sodium and potassium over KxNa1−xNbO3 solid solution within its whole compositional range at temperatures between 1173 K and 1303 K were determined by Knudsen Effusion Mass Spectrometry. The main gaseous species are alkaline atoms and oxygen molecules. The vapour pressure of potassium over (K0.5Na0.5NbO3)ss is a few times higher as the vapour pressure of sodium. The thermodynamic equilibrium between the gaseous and condensed phase could be attained only after prolonged annealing (at least 10 h at 1263 K).The ratio of the alkali ion intensities proved to be suitable for the determination of the activities of NaNbO3 and KNbO3 in solid solution using Gibbs–Duhem integration. The system exhibits a positive deviation from Raoult's law. The obtained negative excess entropy indicates that the alkalis are partially ordered in ((KxNa1−x)NbO3)ss.
The vapour pressures of alkalis over potassium and sodium niobate are almost three orders of magnitude lower than the vapour pressure of lead oxide over PZT or bismuth over BKT at 1200 K. Under the investigated experimental conditions there is no significant interaction between NaNbO3 and KNbO3.
Acknowledgements
The authors would like to thank Jena Cilenšek and Katarina Korenčan for their help with the experimental work and Edi Kranjc for performing the X-ray diffraction measurements. This work was financially supported by the Slovenian Research Agency (1000-08-310121; P2-0105; J2-1227).References
- K. Uchino, Ferroelectric Devices, Marcel Dekker, Inc, New York, Basel, 2000, p. 308 Search PubMed.
- Council, E. P. a.t.E., Directive 2011/65/EU on the restriction of the use of certain hazardous substances in electrical and electronic equipment, in Directive 2011/65/EU, E. Union, Editor, 2011, Official Journal of the European Union, Strasbourg, p. 23.
- J. Rödel, W. Jo, K. T. P. Seifert, E. M. Anton, T. Granzow and D. Damjanovic, Perspective on the Development of Lead-free Piezoceramics, J. Am. Ceram. Soc., 2009, 92(6), 1153–1177 CrossRef PubMed.
- S. Kawada, M. Kimura, Y. Higuchi and H. Takagi, (K,Na)NbO3-Based Multilayer Piezoelectric Ceramics with Nickel Inner Electrodes, Appl. Phys. Express, 2009, 2(11), 111401 CrossRef.
- B. Malic, A. Bencan, T. Rojac and M. Kosec, Lead-free Piezoelectrics Based on Alkaline Niobates: Synthesis, Sintering and Microstructure, Acta Chim. Slov., 2008, 55(4), 719–726 CAS.
- Lead-Free Piezoelectrics, ed. S. Priya and S. Nahm, Springer, New York, 2012 Search PubMed.
- N. M. Hagh, B. Jadidian and A. Safari, Property-processing relationship in lead-free (K,Na,Li)NbO(3)-solid solution system, J. Electroceram., 2007, 18(3–4), 339–346 CrossRef.
- J. Hrescak, A. Bencan, T. Rojac and B. Malic, The influence of different niobium pentoxide precursors on the solid-state synthesis of potassium sodium niobate, J. Eur. Ceram. Soc., 2013, 33(15–16), 3065–3075 CrossRef CAS PubMed.
- B. Malic, D. Jenko, J. Holc, M. Hrovat and M. Kosec, Synthesis of sodium potassium niobate: A diffusion couples study, J. Am. Ceram. Soc., 2008, 91(6), 1916–1922 CrossRef CAS PubMed.
- J. Koruza and B. Malic, Initial stage sintering mechanism of NaNbO3 and implications regarding the densification of alkaline niobates, J. Eur. Ceram. Soc., 2014, 34(8), 1971–1979 CrossRef CAS PubMed.
- D. Jenko, A. Bencan, B. Malic, J. Holc and M. Kosec, Electron microscopy studies of potassium sodium niobate ceramics, Microsc. Microanal., 2005, 11(6), 572–580 CrossRef CAS PubMed.
- A. Kupec, B. Malic, J. Tellier, E. Tchernychova, S. Glinsek and M. Kosec, Lead-Free Ferroelectric Potassium Sodium Niobate Thin Films from Solution: Composition and Structure, J. Am. Ceram. Soc., 2012, 95(2), 515–523 CrossRef CAS PubMed.
- Z. Samardzija, S. Bernik, R. B. Marinenko, B. Malic and M. Ceh, An EPMA study on KNbO3 and NaNbO3 single crystals – Potential reference materials for quantitative microanalysis, Microchim. Acta, 2004, 145(1–4), 203–208 CrossRef.
- S. Sturm, A. Bencan, M. A. Gulgun, B. Malic and M. Kosec, Determining the Stoichiometry of (K,Na)NbO3 Using Optimized Energy-Dispersive X-Ray Spectroscopy and Electron Energy-Loss Spectroscopy Analyses in a Transmission Electron Microscope, J. Am. Ceram. Soc., 2011, 94(8), 2633–2639 CrossRef CAS PubMed.
- R. L. Holman and R. M. Fulrath, Intrinsic Nonstoichiometry in Lead Zirconate Lead Titanate System Determined by Knudsen Effusion, J. Appl. Phys., 1973, 44(12), 5227–5236 CrossRef CAS PubMed.
- K. H. Härdtl and H. Rau, PbO Vapour Pressure in Pb(Ti1−xZrx)O3 System, Solid State Commun., 1969, 7(1), 41–45 CrossRef.
- A. I. Kingon and J. B. Clark, Sintering of PZT Ceramics .1. Atmosphere Control, J. Am. Ceram. Soc., 1983, 66(4), 253–256 CrossRef CAS PubMed.
- A. Popovič, L. Bencze, J. Koruza, B. Malič and M. Kosec, Knudsen effusion mass spectrometric approach to the thermodynamics of Na2O-Nb2O5 system, Int. J. Mass Spectrom., 2012, 309, 70–78 CrossRef PubMed.
- J. König, M. Spreitzer, B. Jancar, D. Suvorov, Z. Samardzija and A. Popovic, The thermal decomposition of K0.5Bi0.5TiO3 ceramics, J. Eur. Ceram. Soc., 2009, 29(9), 1695–1701 CrossRef PubMed.
- A. Popovic, B. Malic and L. Bencze, Knudsen cell mass spectrometric investigation of the PbO-ZrO2-TiO2 system, Rapid Commun. Mass Spectrom., 1999, 13(12), 1129–1137 CrossRef CAS.
- Mass Spestrometry, in The Caracterisation of High Temperature Vapours, ed. J. L. Margrave, John Wiley&Sons, New York, London, Sidney, 1967, p. 225 Search PubMed.
- G. R. Belton and R. J. Fruehan, Determination of Activities by Mass Spectrometry.I. Liquid Metallic Systems Iron-Nickel and Iron-Cobalt, J. Phys. Chem., 1967, 71(5), 1403 CrossRef CAS.
- A. Neckel and S. Wagner, Mass Spectrometry of Thermodynamic Activities.1. Gold-Copper Systems, Bunsen-Ges. Phys. Chem., Ber., 1969, 73(2), 210 CAS.
- Vaporization of oxide glasses and glass forming melts, in Mass spectrometric study of the vaporization of oxide systems, ed. V. L. Stolyarova, G. A. Semenov and J. H. Beynon, Wiley&Sons, New York, 1994, p. 237 Search PubMed.
- J. Tellier, B. Malic, B. Dkhil, D. Jenko, J. Cilensek and M. Kosec, Crystal structure and phase transitions of sodium potassium niobate perovskites, Solid State Sci., 2009, 11(2), 320–324 CrossRef CAS PubMed.
- B. Y. Kim, T. G. Seong, I. T. Seo, M. S. Jang, S. Nahm, J. Y. Kang and S. J. Yoon, Effects of annealing atmosphere on the structural and electrical properties of (Na0.5K0.5)NbO3 thin films grown by RF magnetron sputtering, Acta Mater., 2012, 60(6–7), 3107–3112 CrossRef CAS PubMed.
- O. Redlich and A. T. Kister, Algebraic Representation of Thermodynamic Properties and the Classification of Solutions, Ind. Eng. Chem., 1948, 40(2), 345–348 CrossRef.
- B. Malic, J. Bernard, A. Bencan and M. Kosec, Influence of zirconia addition on the microstructure of K0.5Na0.5NbO3 ceramics, J. Eur. Ceram. Soc., 2008, 28(6), 1191–1196 CrossRef CAS PubMed.
- D. G. Fraser, W. Rammensee and A. Hardwick, Determination of the Mixing Properties of Molten Silicates by Knudsen Cell Mass-Spectrometry .2. The Systems (Na-K)AlSi4O10 and (Na-K)AlSi5O12, Geochim. Cosmochim. Acta, 1985, 49(2), 349–359 CrossRef CAS.
- K. T. Jacob and L. Rannesh, Thermodynamic activities in the Pb(Zr1−xTix)O3 solid solution at 1373 K, Mater. Sci. Eng., B, 2007, 140(1–2), 53–58 CrossRef CAS PubMed.
- M. V. Rane, A. Navrotsky and G. A. Rossetti, Enthalpies of formation of lead zirconate titanate (PZT) solid solutions, J. Solid State Chem., 2001, 161(2), 402–409 CrossRef CAS.
- J. Drowart, R. Colin and G. Exsteen, Mass-Spectrometric Study of Vaporization of Lead Monoxide – Dissociation Energy of PbO, Trans. Faraday Soc., 1965, 61(511P), 1376–1383 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra11874c |
| ‡ Present address: Institute of Materials Science, Technische Universität Darmstadt, 64287 Darmstadt, Germany. |
| This journal is © The Royal Society of Chemistry 2015 |