First principles study of the electronic properties of a Ni3(2,3,6,7,10,11-hexaaminotriphenylene)2 monolayer under biaxial strain
Abstract
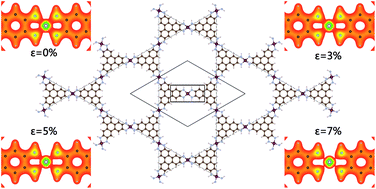
Applying first principles calculations, the electronic structure of a Ni3(HITP)2 (HITP = 2,3,6,7,10,11-hexaaminotriphenylene) monolayer have been investigated with both GGA and GGA + U methods. The Ni3(HITP)2 monolayer is semi-conductive with a narrow indirect band in an unstrained system. Under biaxial strain, our computation results reveal that the monolayer becomes metallic after the band gap gradually decreases to zero with increased strain. The 2D sheet is verified to have typical π-conjugated characteristics with each Ni atom adopting the dsp2 hybridization at zero strain. We demonstrate the variation of the charge density of the monolayer to show the gradual weakening of the Ni–N bond as the strain increases. Our band structure and charge density analysis indicate the variation of the band gap can be the result of charge redistribution between the Ni and N atoms due to the biaxial strain applied.

 Please wait while we load your content...
Please wait while we load your content...