Luminescence properties and crystal structure of α′-Sr₂Si_3x/4O₂N_x:Eu²⁺ phosphors with different concentrations of N³⁻ ions

Abstract

A series of disordered α′-Sr₂Si_3x/4O₂N_x:Eu²⁺ (1.333 ≤ x ≤ 2.4) phosphors were synthesized by the conventional solid state reaction method. The disordered α′-Sr₂Si_3x/4O₂N_x:Eu²⁺ (α′-SSON:Eu²⁺) phosphors have two distinct activation centers: Eu(I) and Eu(II). With the increase of N concentration, both the luminescence intensity and the dominant peak wavelength (DPWs, which is about 490 nm) of the Eu(I) site were extraordinarily unchanged. In comparison with the yellow emissions (∼580 nm) of the Eu(II) site of the disordered α′-Sr₂SiO₄:Eu²⁺, the DPWs of Eu(II) emissions were at red spectral regions (609–618 nm), which depends on the amount of N³⁻. The PL intensity of the Eu(II) emission band increased first and then decreased, and reached a maximum at x = 2. The disordered α′-SSON is a substitutional solid solution. Compared with the disordered α′-Sr₂SiO₄, all the lattice constants of disordered α′-SSON became smaller which led to the decrease of the cell volume. The peaks of the Si–N and Sr–N bond could be observed in FT-IR spectra. The Si–(N/O)₄ tetrahedrons transformed from Si–O₄, Si–NO₃, and Si–N₂O₂ into Si–N₃O with the increase of N content. The bond lengths of Si–N and Sr–(N/O) were within the normal ranges compared with other silicon-based oxynitrides. The Si–O bond lengths became shorter due to the extrusion effects of longer Si–N bonds. Both of the average bond lengths of Sr₁–(N/O) and Sr₂–(N/O) in disordered α′-SSON became longer than that of disordered α′-Sr₂SiO₄. Due to the red emission and high photoluminescence intensity of the disordered α′-Sr₂Si_3x/4O₂N_x:Eu²⁺ (1.333 ≤ x ≤ 2.4), we anticipate that these materials can be used as red phosphors in white light emitting diodes.

---

1 Introduction

The most widely used commercial white LEDs are made of blue GaInN chips and a yellow phosphor (Y_1−xGd_x)₃(Al_1−yGa_y)₅O₁₂:Ce³⁺ (YAG:Ce³⁺).¹ However, they have drawbacks such as low color-rendering index (CRI) and high color temperature because of the deficiency of the green and red compounds. As promising fluorescent materials for white LEDs, rare earth doped nitride and oxynitride phosphors have excellent luminous performances, such as high thermal and chemical stability, a wide effective excitation spectral region, rich luminous color which covers the whole visible region, structural diversity, high quantum efficiency, etc.^2–5 A series of these compounds have been synthesized and investigated, such as CaAlSiN₃:Eu²⁺,^6–8 M₂Si₅N₈:Eu²⁺/Ce³⁺,^2,3,9–12 α/β-SiAlONs:Eu²⁺,^13–15 and MSi₂O₂N₂:Eu²⁺/Ce³⁺ (M = Ca, Ba, Sr).^16–20 The production costs of commercial red phosphors, such as CaAlSiN₃:Eu²⁺ and Sr₂Si₅N₈:Eu²⁺, are too expensive due to their severe preparation conditions. The preparation of such red phosphors requires not only high temperature and high pressure conditions but also an oxygen-free atmosphere. Therefore, it is urgent to develop a novel high efficient, cost-effective and red emitting phosphor that can be used for white pc-LEDs.

As a traditional phosphor, Sr₂SiO₄:Eu²⁺ has been extensively studied because of its special structure and tunable light-emitting properties.^21–32 Sr₂SiO₄ has two crystallographic phases: orthorhombic (α′-Sr₂SiO₄) and monoclinic (β-Sr₂SiO₄).^21–26 Both of them have two luminescence centers: Eu(I) and Eu(II). Eu(I) is ten-coordinated and Eu(II) is nine-coordinated by oxygen atoms within a limited range.^27–32 Recently, due to the intense emission in the red spectral range, Sr₂SiO₄:Eu²⁺ with N³⁻ substitution has been extensively studied.^33–37 Sohn et al. prepared Sr₂SiO_4−xN_2x/3:Eu²⁺ phosphors through spark plasma sintering (SPS) method and their luminescent properties were investigated.³³ Zhao et al. reported the detailed crystal structure of Sr₂SiN_zO_4−1.5z:Eu²⁺ (0.7 < z < 1.2) by Rietveld refinement and the red emission of this phosphor was attributed to the overlapped two bands due to two distinct Eu(I) and Eu(II) sites.³⁴ (Sr, M)₂Si(O_1−xN_x)₄:Eu²⁺ (M = Ca, Ba, Mg) reported by Kim et al. was considered as a non-stoichiometric solid-solution with the substitution of N³⁻ for O²⁻ and the red emission was assigned to the Eu(II) site.^35,36 Kim et al. proposed that the nitridation effect led to a dramatic change in the crystal field surrounding the Eu(II) site but rarely affected the Eu(I) site.³⁶ Ju et al. obtained a strong red-emission in Sr₂SiO₄:Eu²⁺ phosphors through the incorporation of a very small amount of nitrogen. They studied the coordination environment of Eu²⁺ and the interaction mechanism of nitrogen on red-shift emission.³⁷ All the studies focused on the photoluminescence properties and crystal structure. They either simply attributed the red emission to the strong crystal field splitting and the nephelauxetic effect of N³⁻ or used the interaction mechanism of nitrogen and the coordination environment of Eu²⁺ to explain the red-shift emission.^33–37

However, there is no such study that has been done about the influence of N content on the luminescence properties and crystal structure in Sr₂SiO₄:Eu²⁺. Unlike previous studies,^33–37 in this work, we successfully synthesized the disordered α′-Sr₂Si_3x/4O₂N_x:Eu²⁺ (1.333 ≤ x ≤ 2.4) phosphors through the conventional solid-state reaction method. We investigated the N³⁻ ions effects on the crystal structural and luminescent properties of α′-SSON:Eu²⁺ by varying N content, and also interpreted the intensity change and red-shift phenomenon of the disordered α′-SSON:Eu²⁺.

2 Experimental sections

2.1 Sample preparation

For comparison, the disordered α′-Sr₂SiN_zO_4−1.5z:Eu²⁺ (0 ≤ z ≤ 1.333) and disordered α′-Sr₂Si_3x/4O₂N_x:Eu²⁺ (1.333 ≤ x ≤ 2.4) phosphors were synthesized by the conventional solid-state reaction method in a horizontal tube furnace using starting materials of SrCO₃ (AR), α-Si₃N₄ (Alfa 99.9%), and SiO₂ (AR). Eu₂O₃ (99.9%) was added as activator.

Raw materials were mixed in an agate mortar and then filled into BN crucibles. The powder mixtures were preheated at 1100 °C for 2 h, and then fired at 1500 °C (with a heating rate of 5 °C min⁻¹) for 6 h, followed by cooling down to 300 °C at a rate of 5 °C min⁻¹ and down to the room temperature in the furnace with the power switched off. In order to prevent samples from being oxidized, all heating and cooling processes were conducted under flowing reduction atmosphere of 95% N₂/5% H₂.

2.2 Characterization

The phase composition and crystallinity of the synthesized compositions were investigated by the powder X-ray diffraction (Bruker Axs D2 PHASER diffractometer) with Cu Kα radiation (λ = 1.5405 Å) over the angular range of 10° ≤ 2θ ≤ 80°, operating at 30 kV and 10 mA (scanning rate of 1° min⁻¹). The excitation and emission spectra of the phosphors were measured at room temperature on a PL3-211-P spectrometer (HORIBA JOBIN YVON, America) and a 450 W xenon lamp was used as the excitation source. Rietveld refinements on the X-ray diffraction data were performed using the software TOPAS, using the Sr₂SiO₄ structure as a starting model. The detail atom arrays in the crystal structure of the samples were determined by the software of Diamond basis on the refined data. The nitrogen and oxygen contents (atomic ratios) were measured by energy dispersive spectrometry system (TEAM Apollo XL EDS, EDAX, America). Fourier-transform infrared spectra (FT-IR) were measured on a BRUKER TENSOR 27 spectrophotometer in the range of 400–4000 cm⁻¹ using the KBr pellet (∼2 wt%) method. The morphology of the synthesized phosphors was observed by scanning electron microscopy (FE-SEM, SU8010, HITACHI, Japan). The absorbance spectra of the samples were measured by an ultraviolet-visible-near infrared spectrophotometer (Uv3600) using BaSO₄ as a reference in the range of 200–800 nm. All the above measurements were performed at room temperature.

3 Results and discussion

3.1 Crystal structure

The XRD patterns of Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ powders prepared with various N content (x = 1.333–2.4) are shown in Fig. 1. When sintered at 1500 °C, it shows that almost all of diffraction peaks matched well with the α′-Sr₂SiO₄ (JCPDS no. 39-1256) except for a few impurity associated with β-Sr₂SiO₄ (JCPDS no. 38-0271) phase. In this paper, we abbreviated the α′-Sr_1.98Si_3x/4O₂N_x to α′-SSON. The impurity peak (2θ = 27.85°) of β-Sr₂SiO₄ phase was marked as β symbol in Fig. 1. With the N content increased from 1.333 to 2.4, the diffraction peak of β phase gradually increased and the degree of crystallinity became worse. These results indicate that a predominant pure α′-SSON phase have been formed accompanied by a small portion of β-SSON phase.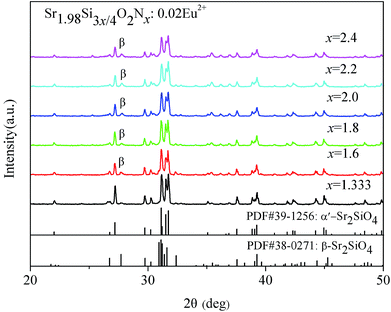

Fig. 1 XRD patterns of α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) powders with different N content.

In order to compare the disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) phosphors, we also successfully synthesized the disordered α′-Sr_1.98SiN_zO_4−1.5z:0.02Eu²⁺ (0 ≤ z ≤ 1.333) phosphors through the conventional solid-state reaction method. Fig. 2 shows the XRD patterns of disordered α′-Sr_1.98SiN_zO_4−1.5z:0.02Eu²⁺ (0 ≤ z ≤ 1.333). These patterns show that almost all of diffraction peaks matched well with the α′-Sr₂SiO₄ (JCPDS no. 39-1256). These results indicate that a predominant pure α′-Sr_1.98SiN_zO_4−1.5z:0.02Eu²⁺ (0 ≤ z ≤ 1.333) phase was obtained.

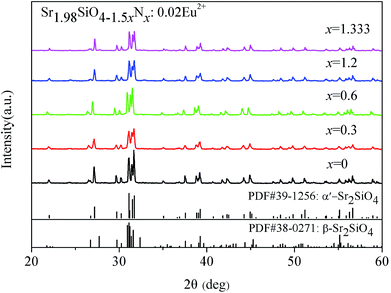Fig. 2 XRD patterns of α′-Sr_1.98SiN_zO_4−1.5z:0.02Eu²⁺ (0 ≤ z ≤ 1.333) powders with different N content.

Fig. 3 shows the observed (black line), calculated (red line) and difference (green line) XRD profiles for the Rietveld refinement of α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (x = 2). The peaks (2θ = 27.85°, 32.68°, 36.03°) of β-SSON phase was marked as β symbol in Fig. 2. The actual crystal structure of α′-Sr_1.98Si_3x/4O₂N_x (1.333 ≤ x ≤ 2.4) was analyzed by the software of TOPAS on the basis of the XRD data, using α′-Sr₂SiO₄ (ICSD: 35666), β-Sr₂SiO₄ (ICSD: 36041) structure as a starting model. These results indicate that the α′-Sr_1.98Si_3/2O₂N₂:0.02Eu²⁺ host is composed of 92.62% α′-SSON and 7.38% β-SSON phase structures.

Fig. 3 Rietveld refinement XRD patterns of α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (x = 2) by TOPAS package. (Observed – black line, calculated – red line and difference – green line).

Table 1 only gives the XRD refinement data of the α′-Sr_1.98Si_3/2O₂N₂:0.02Eu²⁺ phase because α′-SSON phase is the main phase of all the samples. These refinement data include cell parameters, wyckoff site, atomic coordinates, occupancy, b_eq and phase ratios. The α′-Sr₂Si_3/2O₂N₂ crystallizes in an orthorhombic unit cell belonging to a space group of Pmnb:bac̄ (no. 62). The refinement finally converged to R_exp = 4.64, R_wp = 6.57, R_p = 5.08 and GOF = 1.42, as shown in Table 1. There are obvious differences of the atomic positions and cell volume between the α′-SSO:Eu²⁺ and α′-SSON:Eu²⁺ according to ref. 22 and 23.

Table 1 Rietveld refinement and crystal data for α′-Sr_1.98Si_3/2O₂N₂:0.02Eu²⁺ (α′-phase: 92.62%, β-phase: 7.38%)

Space group: Pmnb:bac̄ (orthorhombic)
Cell parameter	Reliability factors
a = 5.6663566 Å	Rexp (%) = 4.64
b = 7.0713812 Å	Rwp (%) = 6.57
c = 9.7319768 Å	Rp (%) = 5.08
Cell volume = 389.95026 Å^3	GOF = 1.42
z = 4

---

Site	Np	x	y	z	Atom	Occ	Beq
Sr1	8d	0.23429	0.34045	0.57915	Sr^2+	0.5	0.5578
Sr2	8d	0.26898	0.99850	0.30157	Sr^2+	0.5	1.07
Si1	4c	0.25000	0.77880	0.58320	Si^4+	1	3.645
O1	8d	0.29751	0.98876	0.57106	O^2−	0.5	5.02
O2	8d	0.18151	0.66957	0.42333	O^2−	0.5	−3.579
O3	8d	0.50569	0.70488	0.67266	O^2−	0.5	−3.5
O4	8d	0.07687	0.73160	0.64576	O^2−	0.5	6.309

---

Fig. 4 shows the coordination spheres of the two different Sr²⁺ sites of the ordered α′-SSO, disordered α′-SSO and disordered α′-SSON (x = 2). Due to the change of O atoms positions and occupation, the α′-SSO phase has two structure model: disordered (isotropic) and ordered (anisotropic) model.²³ The O1 and O2 lain on the mirror plane (x = 0.25, occupation = 0.5), but the occupation of O3 and O4 were constrained to be 1 − p and p (p is occupation factor), respectively. In the order α′-SSO model, p = 0, the O1 and O2 lain on the mirror plane (x = 0.25, occupation = 0.5), it has only O3 (occupation = 0.5) but not O4, as shown in Fig. 4(a). In the disordered α′-SSO model, p = 0.5, each atom lying on the mirror plane (x = 0.25) was split into two, in very close positions equivalent by symmetry, and it has O3 (occupation = 0.5) and O4 (occupation = 0.5), as shown in Fig. 4(b). Si had not shifted significantly from the mirror plane, it was constrained at x = 0.25.²³

Fig. 4 (a) Coordination spheres of the two different Sr²⁺ sites of the ordered α′-SSO; (b) coordination spheres of the two different Sr²⁺ sites of the disordered α′-SSO; (c) coordination spheres of the two different Sr²⁺ sites of the disordered α′-SSON (x = 2).

In our experiments, the results of refinement indicate that α′-SSON:Eu²⁺ presents disordered feature. Fig. 4(c) shows coordination spheres of the two different Sr²⁺ sites of disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (x = 2) which is obtained by Rietveld refinement data in Table 1. Zhao et al. had studied detailed crystal structure of Sr₂SiN_zO_4−1.5z:Eu²⁺ (z ∈ 0.7–1.2) by Rietveld refinement.³⁴ But the distinction of ordered α′-SSON, disordered α′-SSON and β-SSON structures hadn't been effectively distinguished. Owing to the significant difference between the coordination bond length of oxygen and nitrogen, it is feasible to distinguish O and N by XRD refinement data. Fig. 4(b) shows the bond lengths of Sr–O of disordered α′-SSO are evaluated to be in the range of 2.384–3.077 Å. Fig. 4(c) shows the bond lengths of Sr–(N/O) of disordered α′-SSON are evaluated to be in the ranges of 2.357–3.053 Å. The average bond lengths of Sr₁–O and Sr₂–O in disordered α′-SSO are 2.753 Å and 2.634 Å, respectively. The average bond lengths of Sr₁–(N/O) and Sr₂–(N/O) in disordered α′-SSON (x = 2) are 2.820 Å and 2.644 Å, respectively.

Apparently, both of the average bond length of Sr₁–(N/O) and Sr₂–(N/O) in disordered α′-SSON got longer than disordered α′-SSO. The disordered α′-SSON is a substitutional solid solution because the N³⁻ ions substituted for O²⁻ ions. The ionic bond length is the sum of anion and cation radius, so the larger ionic radius will lead to longer ionic bond length. In addition, the ionic radius of N³⁻ (1.32 Å) is larger than O²⁻ (1.24 Å). It can be ascribed to the smaller atomic number, the smaller atomic nuclear mass, and the smaller electronic attraction of N³⁻. So theoretically, the N³⁻ substitution for O²⁻ could make the average bond length of Sr–O getting longer. Therefore, the results of our experiment are consistent with the theoretical analysis. The Sr–(N/O) bonds in disordered α′-SSON:Eu²⁺ are between the normal range observed for Sr–O, Sr–N in other oxonitridosilicates or nitrides, such as Sr₃Si₂O₄N₂:Sr–O = 2.388–3.157 Å, Sr–N = 2.611–3.096 Å;³⁸ SrSi₂O₂N₂:Sr–O = 1.942–3.029 Å, Sr–N = 2.738–3.064 Å;³⁹ Sr₂Si₅N₈:Sr–N = 2.542–3.231 Å;⁴⁰ and SrSi₇N₁₀:Sr–N = 2.706–3.497 Å.⁴¹ However, these results only roughly demonstrate that nitrogen ions have partially been incorporated into the disordered α′-SSO lattice, forming a solid-solution of disordered α′-SSON. In order to further check that the N³⁻ ions have substituted for O²⁻ sites successfully, the formation of disordered α′-SSON will be verified in details by the interpretation of the PL spectra, the analysis of N/O element content, the comparison of FT-IR spectra and the interpretation of Si–(N/O)₄ tetrahedrons.

Fig. 5 shows the bond length change of different Sr1/Sr2–O bonds between the disordered α′-Sr₂Si_1.5O₂N₂ and disordered α′-Sr₂SiO₄. As shown in Fig. 5, the bond length of Sr1–O3 and Sr2–O4 of disordered α′-SSON got longer than that of disordered α′-SSO; the bond length of Sr2–O3 of disordered α′-SSON got shorter than that of disordered α′-SSO. Compared with the change of Sr1/Sr2–O1 and Sr1/Sr2–O2, the Sr1/Sr2–O3 and Sr1/Sr2–O4 bond length was changed more obviously due to the substitution of N³⁻. The bond changes of Sr2–O were more significant than that of Sr1–O. Therefore, we can speculate that N³⁻ was easier to substitute for the site of O3 and O4 atoms. And the Sr2 site was easier to be affected by nitridation, which could be demonstrated in the sections of PL spectra of disordered α′-SSON:0.02Eu²⁺. But the specific substitution site couldn't be effectively ensured in this article.

Fig. 5 The bond length contrast patterns of Sr1/Sr2–O between the disordered α′-Sr₂Si_1.5O₂N₂ and disordered α′-Sr₂SiO₄.

Table 2 shows the XRD Rietveld refinement of disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ with different N content. Compared with the disordered α′-SSO, all the lattice constants of disordered α′-SSON got smaller which resulted in the decrease of the cell volume. With the increase of N content from 1.333 to 2, the lattice constants and cell volume of disordered α′-SSON decreased first and then increased. It demonstrated that the N³⁻ ions have successfully been introduced into the crystal lattice. The proportion of β-phase is gradually increased from 5.25% to 9.72% with the increase of N content. The specific reasons of the changes of lattice constants and cell volume will be further discussed in the section of Si–(N/O)₄ tetrahedrons.

Table 2 Lattice parameters of disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) (unit: Å, degree)

N(x)	a (Å)	b (Å)	c (Å)	Cell volume (Å^3)	Rwp (%)	β-SSO proportion
1.333	5.6722	7.0789	9.7422	391.17	6.39	5.25%
1.6	5.6680	7.0738	9.7352	390.32	6.77	6.89%
1.8	5.6678	7.0726	9.7340	390.20	6.49	7.27%
2.0	5.6664	7.0714	9.7320	389.95	6.57	7.38%
2.2	5.6678	7.0740	9.7351	390.32	6.65	9.44%
2.4	5.6681	7.0742	9.7357	390.38	7.71	9.72%
Disorder α′-SSO	5.682	7.090	9.773	393.71

---

3.2 Comparison of FT-IR spectra for disordered α′-SSO:Eu²⁺ and disordered α′-SSON:Eu²⁺

Fig. 6 presents the FT-IR spectra of disordered α′-SSO:0.02Eu²⁺, disordered α′-SSON:0.02Eu²⁺ and Sr₂Si₅N₈:Eu²⁺ phosphors. Apparently, these FT-IR spectra show remarkable differences between the disordered α′-SSO and disordered α′-SSON. The disordered α′-SSON contained a peak of Sr/Eu–N bond (1363 cm⁻¹),³⁷ while the disordered α′-SSO didn't show such peaks. Besides, the Sr/Eu–N bond (1363 cm⁻¹) in disordered α′-SSON was different from the Sr/Eu–N bond (1209 cm⁻¹) in Sr₂Si₅N₈. With the increase of N content from 1.333 to 2.4, the peak positions of Sr/Eu–N bond (1363 cm⁻¹) had not noticeably altered. While the absorption bands of Si–(N/O)₄ tetrahedrons with symmetric and antisymmetric stretching vibration in the range of vibration energy (700 cm⁻¹ to 1100 cm⁻¹) were gradually broadened.^42–44 This can be ascribed to the different absorption energy between Si–N and Si–O bond because the longer the bond length, the weaker the bond energy. Then the bond energy of Si–N was less than Si–O due to the longer bond length of Si–N than that of Si–O. With the increase of N content, the quantity of Si–N bond increased simultaneously. Then the left absorption bands of Si–(N/O)₄ tetrahedrons were extended toward lower energy. On the other hand, the bond length of Si–O was shortened due to the extrusion effect of the longer Si–N bonds. This led to the results that the right absorption bands of Si–(N/O)₄ tetrahedrons were extended toward higher energy position. These results could confirm that nitrogen had entered the crystal lattice and formed chemical bonds with surrounding Sr²⁺/Eu²⁺ ions and Si atoms in the disordered α′-SSON:Eu²⁺ phosphor.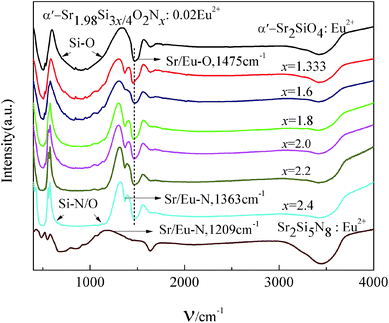

Fig. 6 FT-IR spectra of disordered α′-SSO:0.02Eu²⁺, disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ and Sr₂Si₅N₈:Eu²⁺ phosphors.

3.3 N/O contents for disordered α′-Sr₂Si_3x/4O₂N_x as a function of x

The N/O contents were measured by energy dispersive spectrometry system (EDS). The measurements and theoretical calculation values of N/O contents are shown in Table 3. With the x values increased from 1.333 to 2.4, the molar ratio of N gradually increased, which is consistent with the theoretical value of the N content. The difference between the experimental and theoretical values is within the limit of error because of the surface oxidation and the measuring error.

Table 3 Measured oxygen and nitrogen contents in disordered Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4)

Sample	Nitrogen (atomic%)	Oxygen (atomic%)	Theoretical value of the N content (atomic%)
SSON(x = 1.333)	17.50	33.90	21.05
SSON(x = 1.6)	19.93	31.46	23.53
SSON(x = 1.8)	21.72	27.80	25.17
SSON(x = 2.0)	26.41	26.98	26.67
SSON(x = 2.2)	28.57	22.26	28.02
SSON(x = 2.4)	30.44	20.02	29.27

---

3.4 The analysis of SEM images

Fig. 7 shows the SEM images of disordered α′-SSO:Eu²⁺ and disordered α′-Sr₂Si_3/2O₂N₂:Eu²⁺ phosphors. The powders of disordered α′-SSO and disordered α′-SSON consist of irregular polyhedrons. When sintered at 1500 °C, the particle size of disordered α′-SSO was ∼40 μm due to severe sintering, the particle size of disordered α′-SSON was 15–20 μm. The nitrogen incorporation caused little influence on the morphology of the disordered α′-SSO:Eu²⁺ phosphors. Obviously, compared with disordered α′-SSO, appropriate particle size of disordered α′-SSON powder could be obtained easily under the high temperature (1500 °C) sintering condition. This is because the optimum synthesis temperature of α′-SSO was ∼1200 °C.^26,27 For the disordered α′-SSO, the higher temperature could result in severe sintering. So 1500 °C is too high to get an appropriate particle size in disordered α′-SSO. However, the introduction of N³⁻ would need higher temperature because the break of Si–N bond and the formation of Sr–N bond required higher energy. Therefore, the disordered α′-SSON could get smaller particle size than disordered α′-SSO in the same sintering temperature.

Fig. 7 SEM images of (a) disordered α′-SSO:Eu²⁺, (b) disordered α′-Sr₂Si_3/2O₂N₂:Eu²⁺ phosphors.

3.5 Photoluminescence properties of disordered α′-Sr_2−ySi_3x/4O₂N_x:yEu²⁺

Fig. 8 shows the PL spectra of disordered α′-SSO:Eu²⁺ and disordered α′-SSON:Eu²⁺ (x = 2) phosphors under 300, 360 and 460 nm excitation. The Sr²⁺ ions in α′-SSO have two sites: Sr1 and Sr2. Sr1 is 10-fold coordiated (CN = 10) whereas Sr2 is 9-fold coordinated (CN = 9) by oxygen atoms within a limited range.^23,30–32 Because of the small difference of the ionic radii between Sr²⁺ (1.31 Å, 9CN; 1.36 Å, 10CN) and Eu²⁺ (1.30 Å, 9CN; 1.35 Å, 10CN), the Eu²⁺ will occupy Sr1 and Sr2 sites and form two luminescence center Eu(I) and Eu(II), respectively.⁴⁵ As shown in Fig. 8, under the 300 nm and 360 nm excitation, the emission peak of Eu(I) position (∼495 nm) had almost no change, whereas the emission peak of Eu(II) position appeared an obvious red-shift which shifted from yellow (∼570 nm) to red spectral ranges (∼612 nm). However, under the 460 nm excitation, the emission peak of Eu(I) site almost disappeared and only Eu(II) site emission could be observed significantly. The emission peak of the Eu(II) position was changed from 578 nm to 616 nm and PL intensity was quite close to the disordered α′-SSO:Eu²⁺. The specific rules and the reasons for this phenomenon will be discussed in details while studying the effect of N content change in the remainder of this article.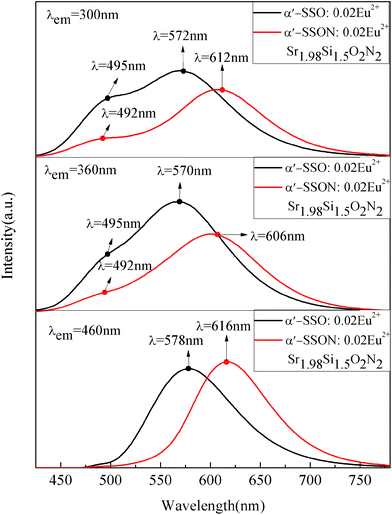

Fig. 8 PL spectra comparison of disordered α′-Sr_1.98Si₂O₄:0.02Eu²⁺ and disordered α′-Sr_1.98Si_3/2O₂N₂:0.02Eu²⁺ under 300, 360 and 460 nm excitation.

According to the emission dominant peak wavelengths (DPWs) of the disordered α′-SSO and α′-SSON, the 490 nm, 580 nm and 616 nm were chosen as the emission wavelengths to test the excitation spectrum of disordered α′-Sr_1.98Si_3/2O₂N₂:0.02Eu²⁺. The corresponding PL excitation (PLE) spectra are shown in Fig. 9. As can be seen from the Fig. 9, compared with blue light excitation (λ_ex = 460 nm), the UV-light excitation (λ_ex = 360 nm) produced more efficient the cyan emission (490 nm) of Eu(I) site.

Fig. 9 Excitation spectra of disordered α′-Sr_1.98Si_3/2O₂N₂:0.02Eu²⁺ corresponded to 490 nm, 580 nm, 616 nm emission, respectively.

The blue light (λ_em = 460 nm) excitation led to efficient red light emission (615 nm) of Eu(II) site than UV-light excitation. The disordered α′-SSON:0.02Eu²⁺ (x = 2) could realize an intense red emission at ∼615 nm under 360–500 nm excitation.

Fig. 10 shows the absorption spectra of disordered α′-Sr₂Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) and disordered α′-Sr₂SiO₄:0.02Eu²⁺ phosphors. The strong absorption band was located in 250–550 nm in the disordered α′-SSON:Eu²⁺ and disordered α′-SSO:Eu²⁺. The disordered α′-SSON:Eu²⁺ (1.333 ≤ x ≤ 2.4) have stronger absorption than disordered α′-SSO:Eu²⁺. With the increase of N content, the absorption band was appeared an obvious red-shift, as showed in the shaded area of Fig. 10. This was because the disordered α′-SSON:Eu²⁺ of longer wavelength emission was easier to be excitated by longer wavelength compared with disordered α′-SSO:Eu²⁺ of shorter emission, as shown in Fig. 8 and 9.

Fig. 10 Absorption spectra of disordered α′-Sr₂Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4), disordered α′-Sr₂SiO₄:0.02Eu²⁺ and Sr₂Si₅N₈:Eu²⁺.

Fig. 11 shows the PL spectra of disordered α′-Sr_1.98SiN_zO_4−1.5z:0.02Eu²⁺ (0 ≤ z ≤ 1.333). The DPWs of Eu(II) site presented a red-shift and the PL intensity of Eu(II) site of α′-SSON:Eu²⁺ gradually decreased with the increase of N content from 0 to 1.333.

Fig. 11 PL spectra of disordered α′-Sr_1.98SiN_zO_4−1.5z:0.02Eu²⁺ (0 ≤ z ≤ 1.333) with varying N content under 460 nm excitation.

Fig. 12 shows the PL spectra of disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) phosphors. The emission peaks of β phase were not expected to be observed due to its tiny content. The emission peak of Eu(I) site of disordered α′-SSON:Eu²⁺ was around 490 nm, which was close to the α′-SSO:Eu²⁺ emission peak of Eu(I) site. It gradually disappeared with the excitation wavelength increased from 300 nm to 460 nm. The emission intensity and position of Eu(I) site was not changed obviously with the increase of N content. However, with the increase of N content from 1.333 to 2.4, the emission peaks corresponding to Eu(II) site in disordered α′-SSON:Eu²⁺ appeared a significant red-shift. And the emission intensity increased first and then decreased, reaching the maximum at x = 2. These results indicate that Eu(I) positions was not significantly affected by nitridation, whereas Eu(II) positions changed dramatically.

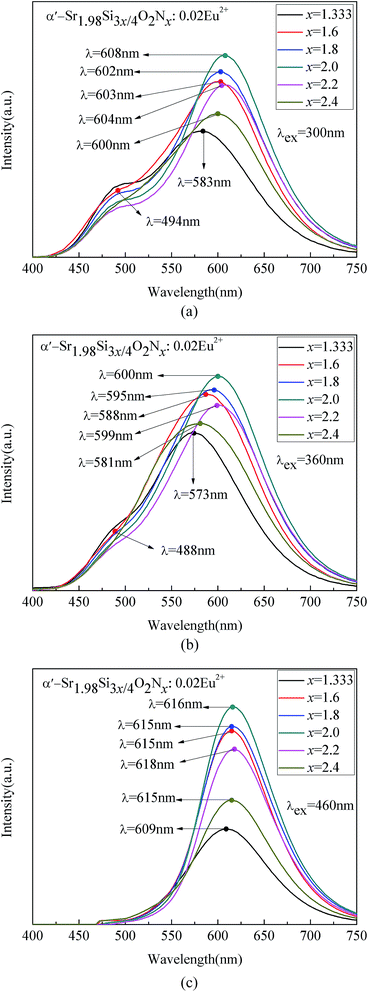Fig. 12 PL spectra of disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) with varying N content under (a) 300, (b) 360, and (c) 460 nm excitation.

As shown in Fig. 12(c), the emission peak of Eu(I) site almost disappeared whereas Eu(II) site showed significant red light emitting under λ_ex = 460 nm excitation. Compared with the disordered α′-SSO:Eu²⁺ (λ_Eu(II) = 580 nm), the 580 nm emission bands of disordered α′-SSO:Eu²⁺ are completely diminished, and a red emission band around 616 nm appeared instead.

Similar to the α′-SSO:Eu²⁺,⁴⁶ the PLE spectrum of α′-SSON:Eu²⁺ consists of two emission bands at ∼490 and ∼616 nm which originate from two luminescence centers: Eu(I) and Eu(II). The ten-coordinated Eu(I) (10-coordiation O atoms, CN = 10) has a loose site and correspond with a higher energy (shorter-wavelength) emission peak at 490 nm. The 9-coordinated Eu(II) (9-coordiation O atoms, CN = 9) has a tight site and correspond with a lower-energy (longer-wavelength) emission peak at 616 nm.^29,34,47

The reasons for obvious red shift of Eu(II) site emission can be explained as follows. The partial incorporation of nitrogen ions caused a larger crystal field splitting and gave rise to the nephelauxetic effect due to the covalent bond. It induced a shift of the lowest 5d excitation level toward the ground level of the Eu²⁺ ions at the Eu(II) site and broadened the PLE spectra, which is a typical 4f⁷–4f⁶5d¹ transition.^36,48

The nitridation caused two different spectral variations: the emission peak of Eu(I) site was unchanged while intensity changed slowly and the emission peak of Eu(II) site showed a remarkable red-shift. Kim et al. proposed two possible explanations:^35,36 (1) the odds of the N³⁻ ions substitution for O²⁻ ions on Eu(II) position was more than that of Eu(I) position. (2) Two Eu sites have the same N substitution rate. Because of the smaller coordination number (CN) of Eu(II)(CN = 9), the length of Eu(II)–N bond was shorter than Eu(I)–N, which led to the results that Eu(I)(CN = 10) sites of α′-SSON:Eu²⁺ was not significantly affected by nitridation, whereas the Eu(II) sites was changed dramatically. The dramatic change was because Eu(II) sites was strongly affected by the crystal field that originated from the substituted nitrogen ions.

As shown in Fig. 11, when the substituted nitrogen ions content gradually increased from 0 to 1.333, the luminescence intensity of Eu(II) site gradually reduced, the dominant peak wavelengths (DPWs) emission of Eu(II) showed apparent red-shift because of a stronger crystal field splitting and the nephelauxetic effect. However, as shown in Fig. 12, starting with x = 1.333, when the substituted nitrogen ions content increased from 1.333 to 2.4 continually, the PL intensity of Eu(II) positions raised firstly and then decreased, rather than a continued decrease as it was expected.

3.6 The intensity change of Eu(II) site emission in disordered α′-SSON:Eu²⁺

Fig. 13 exhibits the transformation of Si-(N/O)₄ tetrahedrons in disordered α′-SSON:Eu²⁺. The bond lengths of Si–(N/O) are in the range of 1.202–1.780 Å. As shown in Fig. 13, during the process of formation of disordered α′-SSON solid-solution, part of the original Si–O₄ tetrahedrons gradually transformed into Si–NO₃, Si–N₂O₂ and Si–N₃O tetrahedrons with the increase of N-introduction content.

Fig. 13 Si–(N/O)₄ tetrahedrons of the disordered α′-SSON:0.02Eu²⁺ at (a) disordered α′-SSO (z = 0), (b) x = 1.333, (c) x = 2, (d) x = 2.4.

Table 4 shows the Si–O or Si–N bond lengths with different tetrahedron types in various silicon-based oxynitrides and they were compared with those of disordered α′-SSO and disordered α′-SSON. Obviously, the Si–N bond lengths in disordered α′-SSON are within the normal ranges observed for Si–N bond in other silicon-based oxynitrides.^{38–41,49,50} However, paradoxically, the Si–O bond lengths in disordered α′-SSON deviated from the normal ranges observed in other silicon-based oxynitrides and got shorter than disordered α′-SSO. Through the introduction of N³⁻ ions, the partial Sr–N and Si–N bonds substituted for Sr–O and Si–O bonds (bond length: Sr–N > Sr–O, Si–N > Si–O). The Si–O bonds were extruded by the longer Si–N bonds and got shorter obviously in the process of forming Si–(N/O)₄ tetrahedrons in substitutional solid solution disordered α′-SSON. The Si–O bond lengths of the other silicon-based oxynitrides in Table 4 are within the normal ranges because they are not solid-solutions.

Table 4 The Si–(N/O) bond lengths with different tetrahedron types

Silicon-based oxynitrides	Tetrahedron types	Si–O bond lengths (Å)	Si–N bond lengths (Å)
Y4Si2O7N2 (ref. 49)	Si–NO3	1.595–1.706	1.708, 1.731
Sr3Si2O4N2 (ref. 38)	Si–N2O2	1.619–1.657	1.660–1.732
SrSi2O2N2 (ref. 39)	Si–N3O	1.603–1.608	1.740–1.746
Si2N2O (ref. 50)	Si–N3O	1.623	1.691–1.750
Disordered α′-SSO	Si–O4	1.621–1.655
Disordered α′-SSON	Si–(N/O)4	1.202–1.567	1.692–1.780

---

Fig. 14 compares the unit cell volume of disordered α′-SSO:0.02Eu²⁺ and disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺. As shown in Table 2 and Fig. 14, all the lattice constants and cell volume of disordered α′-SSON got smaller than that of disordered α′-SSO, rather than being larger as expected. This is because Si–O bonds were extruded by the longer Si–N bonds and got shorter obviously, as shown in Fig. 13. Due to the mutual extruding effect of the Si–N bonds, with the increase of N content, the Si–O bonds were extruded easily at first and then that would become difficult. Compared with a large amount N³⁻ substituting for O²⁻, the Si–O bonds was extruded more obviously with a small amount N³⁻ substituting for O²⁻ due to without appearing mutual extruding effect, as show in Fig. 13(a). Therefore, the unit cell volume of disordered α′-SSON:Eu²⁺ decreased first and then increased with the N-introduction content increased from 1.333 to 2.4.

Fig. 14 Unit cell volume of disordered α′-SSO:0.02Eu²⁺ and disordered α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4).

As shown in Fig. 13(a) and (b), when the content of nitrogen substitution was less than or equal to 1.333, an asymmetric Si–NO₃ tetrahedron was observed in local scale, which undermined the crystal symmetry. At the same time, the degree of crystallinity for disordered α′-SSON:Eu²⁺ became worse due to the increased proportion of Si–N and (Sr/Eu)–N bonds. Hence, the PL intensity of disordered α′-SSON:Eu²⁺ gradually declined with the N content increased from 0 to 1.333, as shown in Fig. 11.

As shown in Fig. 13(b) and (c), as the content of nitrogen substitution increased from 1.333 to 2, the Si–(N/O)₄ tetrahedrons gradually transformed from asymmetric Si–NO₃ tetrahedrons to symmetric Si–N₂O₂ tetrahedrons and the quantity of (Sr/Eu)–N bonds increased continually. Hence, the proportion of symmetric Si–N₂O₂ tetrahedrons in the whole crystal increased gradually, and the symmetry degree around Sr²⁺/Eu²⁺ sites got better. These results led to an improvement of PL intensity. Furthermore, the optimum crystal symmetry of disordered α′-SSON:Eu²⁺ was observed when the N/O ratio was 1 : 1, which corresponded to the highest PL intensity of disordered α′-SSON:Eu²⁺, as shown in Fig. 12. Therefore, the optimal content of N³⁻ ions introduction is x = 2.

However, Fig. 12 shows that the PL intensity of disordered α′-SSON decrease again when the substituted nitrogen ions content further increased from 2 to 2.4. As shown in Fig. 13(c) and (d), the Si–(N/O)₄ tetrahedrons began to transform from symmetric Si–N₂O₂ tetrahedrons to asymmetric Si–N₃O tetrahedrons when the N/O ratio was more than 1 : 1. Meanwhile, the Sr²⁺/Eu²⁺ coordinated with more N³⁻ than O²⁻ ions. These facts resulted in a decline of the PL intensity and low crystal symmetry of the entitled phosphors.

3.7 The optimum Eu²⁺ ions concentration of disordered α′-SSON:yEu²⁺

Fig. 15 shows the PL spectra of disordered α′-SSON:Eu²⁺ phosphors with the increase of Eu²⁺ ions concentration. As can be seen from Fig. 15, with the increase of Eu²⁺ ions concentration from 0.01 to 0.05, the PL intensity of disordered α′-SSON:yEu²⁺ raised first and then reduced, reached the maximum at y = 0.02. Therefore, the optimal Eu²⁺ ions concentration is 2 mol%.

Fig. 15 PL spectra of disordered α′-Sr_2−ySi_3/2O₂N₂:yEu²⁺ with varying Eu²⁺ content under 460 nm excitation.

4 Conclusions

We have obtained the disordered α′-SSON:Eu²⁺ phosphors successfully through the solid state reaction method. Along with the increase of the content of nitrogen introduction from 0 to 2.4 continually, the effects of N³⁻ ions substitution for O²⁻ in α′-SSO:Eu²⁺ on the structural and luminescent properties was investigated. The disorder of α′-Sr_1.98Si_3x/4O₂N_x:0.02Eu²⁺ (1.333 ≤ x ≤ 2.4) has been identified to have an orthorhombic structure in the Pmnb:bac̄ (no. 62) space group. And it is a substitutional solid solution. Consistent with the theoretical analysis, both of the average bond length of Sr₁–(N/O) and Sr₂–(N/O) in disordered α′-SSON:Eu²⁺ became longer than that of disordered α′-SSO:Eu²⁺. The Si–N and Sr–(N/O) bond lengths in disordered α′-SSON are within the normal ranges observed for Si–N and Sr–(N/O) bond in other silicon-based oxynitrides. The Si–O bond lengths became shorter obviously due to the extrusion effects of longer Si–N bonds. With the increase of N content, the quantity of Sr/Eu–N bonds increased continually and the Si–(N/O)₄ tetrahedrons transformed from Si–O₄, Si–NO₃, and Si–N₂O₂ into Si–N₃O. It led to the result that the PL intensity of Eu(II) sites emission declined in the range of 0–1.333, raised first and then decreased in the range of 1.333–2.4, reaching the maximum at x = 2. The peaks of Si–N and Sr–N bond in disordered α′-SSON:Eu²⁺ could be observed in FT-IR spectra. The absorption band was appeared an obvious red-shift with the increase of N content. Compared with disordered α′-SSO:Eu²⁺, with the increase of N content, the Eu(I) site emission peak and intensity of disordered α′-SSON:Eu²⁺ had hardly change. Whereas the Eu(II) site emission peak of disordered α′-SSON:Eu²⁺ appeared a obvious red-shift which changed from yellow (∼578 nm) to red (∼618 nm). It can be ascribed to a large crystal field splitting and the increase of nephelauxetic effect. These results indicate that the Eu(I) sites is not significantly affected by nitridation, whereas both of the dominant peak wavelengths (DPWs) and the PL intensity of the Eu(II) emissions changed dramatically due to the effect of N³⁻ introduction. The disordered α′-SSON:Eu²⁺ can achieve red emission under excitation in the range of 300–500 nm. The optimal PL intensity (x = 2) of the Eu(II) position of disordered α′-SSON:Eu²⁺ is quite close to disordered α′-SSO:Eu²⁺. The excellent properties demonstrate that the disordered α′-SSON:Eu²⁺ phosphors can be applied as red phosphors for white LEDs.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (Grant no. 51272243 and 61405185), the Zhejiang Provincial Natural Science Foundation of China (LY14E020008 and LZ14F050001).

Notes and references

1. S. Nakamura and G. Fasol, The Blue Laser Diode: GaN-Based Light Emitting Diode and Lasers, Springer, Berlin, 1997.
2. X. Piao, T. Horikawa, H. Hanzawa and K. Machidaa, Appl. Phys. Lett., 2006, 88, 1619.
3. Y. Q. Li, J. E. J. van Steen, J. W. H. van Krevel, G. Botty, A. C. A. Delsing, F. J. DiSalvo, G. de With and H. T. Hintzen, J. Alloys Compd., 2006, 417, 273.
4. Y. Kim, J. Kim and S. Kang, J. Mater. Chem. C, 2013, 1, 69.
5. C. Y. Wang, R. J. Xie, F. Li and X. Xu, J. Mater. Chem. C, 2014, 2, 2735.
6. J. W. Li, T. Watanabe, N. Sakamoto, H. S. Wada, T. Setoyama and M. Yoshimura, Chem. Mater., 2008, 20, 2095.
7. Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takeda and M. Mitomo, Chem. Mater., 2008, 20, 6704.
8. J. Zhu, L. Wang, T. Zhou, Y. Cho, T. Suehiro, T. Takeda, M. Lu, T. Sekiguchi, N. Hirosaki and R. J. Xie, J. Mater. Chem. C, 2015, 3, 3181.
9. X. Piao, T. Horikawa, H. Hanzawa and K. J. Machida, J. Electrochem. Soc., 2006, 153, H232.
10. Y. Q. Li, G. de With and H. T. J. Hintzen, J. Solid State Chem., 2008, 181, 515.
11. S. E. Brinkley, N. Pfaff, K. A. Denault, Z. Zhang, H. T. (Bert) Hintzen, R. Seshadri, S. Nakamura and S. P. DenBaars, Appl. Phys. Lett., 2011, 99, 241106.
12. L. Chen, S. Xue, X. Chen, E. Zhao, J. Deng, X. Deng, S. Chen, Y. Liu, Y. Jiang and H. Li, RSC Adv., 2014, 4, 44317.
13. T. Suehiro, N. Hirosaki, R. J. Xie, K. Sakuma, M. Mitomo, M. Ibukiyama and S. Yamada, Appl. Phys. Lett., 2008, 92, 191904.
14. R. J. Xie, N. Hirosaki, M. Mitomo, T. Suehiro, X. Xu and H. J. Tanaka, J. Am. Ceram. Soc., 2005, 88, 2883.
15. R. J. Xie, N. Hirosaki, K. Sakuma, Y. Yamamoto and M. Mitomo, Appl. Phys. Lett., 2004, 84, 5404.
16. B. Lei, K. Machida, T. Horikawa and H. Hanzawa, Chem. Lett., 2011, 40, 140141.
17. Y. Q. Li, G. de With and H. T. J. Hintzen, Chem. Mater., 2005, 15, 4492.
18. J. A. Kechele, O. Oeckler, F. Stadler and W. Schnick, Solid State Sci., 2009, 11, 537.
19. V. Bachmann, C. Ronda, O. Oeckler, W. Schnick and A. Meijerink, Chem. Mater., 2009, 21, 316.
20. C. H. Hsu and C. H. Lu, J. Mater. Chem., 2011, 21, 2932.
21. B. G. Hyde, J. R. Sellar and L. Stenberg, Acta Crystallogr., Sect. B: Struct. Sci., 1986, 42, 423.
22. M. Catti, G. Gazzoni and G. Ivaldi, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 29.
23. M. Catti, G. Gazzoni and G. Ivaldi, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 674.
24. M. Catti, G. Gazzoni and G. Ivaldi, Acta Crystallogr., Sect. B: Struct. Commun., 1983, 39, 679.
25. L. C. Ju, C. Cai, Q. Q. Zhu, J. Y. Tang, L. Y. Hao and X. Xu, J. Mater. Sci.: Mater. Electron., 2013, 24, 4516.
26. A. Nag and T. R. N. Kutty, J. Mater. Chem., 2004, 14, 1598.
27. J. H. Lee and Y. J. Kim, Mater. Sci. Eng., B, 2008, 146, 99.
28. A. Docheon, S. Namsso and D. P. Ki, J. Electrochem. Soc., 2009, 156, 242.
29. Y. S. Won and S. S. Park, J. Phys. Chem. Solids, 2010, 71, 1742.
30. J. K. Han, M. E. Hannah and A. Piquette, J. Lumin., 2012, 132, 106–109.
31. J. S. Kim, P. E. Jeon, J. C. Choi and H. L. Park, Solid State Commun., 2005, 133, 187.
32. H. D. Nguyen, I. H. Yeo and S. Mho, J. Electrochem. Soc., 2010, 28, 167.
33. K. S. Sohn, J. H. Kwak, Y. S. Jung, H. Yan and M. J. Reece, J. Electrochem. Soc., 2008, 155, J58.
34. Z. Zhao, Z. Yang, Y. Shi, C. Wang, B. Liu, G. Zhu and Y. Wang, J. Mater. Chem. C, 2013, 1, 1407.
35. S. J. Lee, S. H. Hong and Y. J. Kim, J. Electrochem. Soc., 2012, 159, J163.
36. J. Park, S. J. Lee and Y. J. Kim, Cryst. Growth Des., 2013, 13, 5204.
37. L. C. Ju, X. Xu, L. Y. Hao, Y. Lin and M. H. Lee, J. Mater. Chem. C, 2015, 3, 1567.
38. X. M. Wang, C. H. Wang, X. J. Kuang, R. Q. Zou, Y. X. Wang and X. P. Jing, Inorg. Chem., 2012, 51, 3540–3547.
39. O. Oeckler, F. Stadler, T. Rosenthal and W. Schnick, Solid State Sci., 2007, 9, 205.
40. T. Schlieper, W. Milius and W. Schnick, Z. Anorg. Allg. Chem., 1995, 621, 1380.
41. G. Pilet, H. A. Höppe, W. Schnick and S. Esmaeilzadeh, Solid State Sci., 2005, 7, 391.
42. R. W. G. Syme, D. J. Lockwood and H. J. J. Kerr, J. Phys. C: Solid State Phys., 1977, 10, 335.
43. J. Etchepare, Spectrochim. Acta, Part A, 1970, 26, 2147.
44. P. McMillan, Am. Mineral., 1984, 69, 622.
45. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751.
46. N. Lakshminarasimhan and U. V. Varadaraju, J. Electrochem. Soc., 2005, 152, H152.
47. K. S. Sohn, B. Lee, R. J. Xie and N. Hirosaki, Opt. Lett., 2009, 34, 3427.
48. P. Dorenbos, J. Lumin., 2000, 91, 155.
49. K. J. D. MacKenzie, G. J. Gainsford and M. J. Ryan, J. Eur. Ceram. Soc., 1996, 16, 553.
50. C. Brosset and I. Idrestedt, Crystal structure of silicon oxynitride, Si₂N₂O, Nature Publishing Group, 1964, vol. 4925, p. 1211.

---