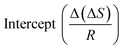Selectivity-column temperature relationship as a new strategy in predicting separation of structural analogues in HPLC by using different stationary phases
Shu-ying Han*,
Hui-min Yu,
Yu-qiong Pei and
Yu-mei Chi*
College of Pharmacy, Nanjing University of Chinese Medicine, 138 Xianlin Avenue, Nanjing 210023, China. E-mail: njutcmhsy@163.com; ymchii@njutcm.edu.cn; Tel: +86-25-85811053
First published on 16th July 2015
Abstract
The effect of changes in column temperature on the van't Hoff equation, as well as the relationship between separation efficiency and column temperature in high performance liquid chromatography (HPLC) by using different stationary phases, have been discussed and compared in this paper. For this purpose, six flavonoid glycosides were selected to establish van't Hoff equations on C18, cholesterol, C8 and porous polymer octadecyl bonded (ODP) stationary phases. The results indicated that, for all the columns, the changes in phase ratio arising from the varying column temperatures had no significant impact on the linearity of the van't Hoff equation, however, it indeed led to certain errors in the intercept (change in entropy, ΔS0) and slope (change in enthalpy, ΔH0) of the equation, which are considered to be important parameters in illuminating the chromatographic mechanism in HPLC. Thereby, a new protocol has been proposed in this paper to correct these errors, with the aim of offering solid data for ΔS0 and ΔH0. Furthermore, a relationship relating selectivity and column temperature was deduced in theory, and then validated by using the six flavonoid glycosides in this work. This relationship has been applied to predict the separation of six steroid hormones in HPLC with high consistency between experimental and predicted selectivity factors (average relative errors less than 2.2%, 1.0%, 6.1% and 5.1% for C18, cholesterol, C8 and ODP columns, respectively). The proposed new strategy in predicting selectivity greatly facilitates optimization processes for HPLC by avoiding tedious condition experiments, and furthermore, column temperature is proposed to be involved in the optimization processes as an important parameter, making separation of structural analogues effective. In this temperature-involved optimization method, a stationary phase sensitive to temperature change, i.e. cholesterol, is recommended.
1. Introduction
Good separation has been always a prerequisite for high performance liquid chromatography (HPLC),1 especially in recent years since the ion-suppression or ion-enhancement effect resulting from the co-eluted analytes in mass spectrometry (MS) has been recognized, which recalls the requirement for good separation in LC-MS. However, separation of structural analogues, such as isomers and stereoisomers, is always a thorny problem for chromatographic analysis to date. In developing and validating an HPLC method, the most common approach is to optimize the mobile phase composition after an appropriate column has been selected.2,3 It is worth noting that column temperature is also a potential variable with many virtues.4–9 First, a change in temperature can have a pronounce effect on analysis speed and separation efficiency because the mass transfer rate relating with mobile phase viscosity and solute diffusion is affected largely by temperature. Second, temperature can have a marked effect on the selectivity of chromatographic separation as the change in retention with temperature is often different for various analytes. More importantly, the regulation of temperature is very convenient and simple, as it requires only a column thermostat allowing fast enough equilibration over the working temperature range. In spite of the strong role of temperature in HPLC, the correlational studies have been rarely reported, which may be mainly due to the fact that the temperature generally has only a narrow regulating range in the practical work because the thermal stability of traditionally used silica-based stationary phase has rigorous conditions (often less than 60 °C), which limits the application of temperature for optimization.10This situation, however, is changing gradually because novel stationary phases have been emerging in recent years. Some thermally stable phase materials, such as graphitized carbon types, zirconium oxide based phases and polystyrene/divinylbenzene copolymers have been used in HPLC,11,12 which can greatly expand the available temperature range even up to over 100 °C. But these stationary phases usually show lower separation efficiency than the silica-based column materials.11 In consequence, column materials sensitive to the temperature changes, for instance, recently developed cholesterol bonded-silica stationary phase, is another promising alternative, as tiny temperature changes may have appreciable impact on retention, efficiency, and selectivity on HPLC.13,14
In an HPLC separation, the mechanism can be described as the increasing temperature alters analyte retention by changing the free energy between the analyte and the stationary phase, which can be depicted using van't Hoff equation, commonly presented as the dependence of retention factor (k) on temperature (T). In van't Hoff equation, the phase ratio (β) is always regarded as a constant over the experimental temperature range.15,16 In fact, the influence of change in temperature on the mobile phase volume is obviously greater than that on the stationary phase volume, which may give rise to variation in β under different temperatures. Nevertheless, no researches involved in van't Hoff equation took this change into careful consideration as far as our knowledge goes. Moreover, almost all the published studies only focused on using van't Hoff equation to interpret retention behavior and mechanism of small molecules on various columns at different temperatures,17–23 but few report was aimed to improve selectivity of temperature-programmed HPLC method, let alone making reliable prediction for separation tendency on the basis of van't Hoff equation.
Accordingly, it is the purpose of this paper to evaluate the effect of phase ratio differing in various temperatures on van't Hoff equation, and proposed a new protocol to correct the errors in enthalpy and entropy resulting from this effected van't Hoff equation. Furthermore, a novel relationship based on the selectivity and column temperature was deduced theoretically and validated by using homologous flavonoid glycosides. This relationship was then applied to predict the selectivity of C18, cholesterol, C8 and porous polymer octadecyl bonded (ODP) stationary phases for structurally analogous estrogens under different temperatures.
2. Theoretical section
In HPLC, the thermodynamic partition coefficient (K) between the stationary and the mobile phases is proportional to the free energy of transfer (ΔG0) involving the change in enthalpy (ΔH0) and entropy (ΔS0)24
ΔG0 = ΔH0 − TΔS0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K
| (1) |
 | (2) |
Since K equals k × β, eqn (2) becomes
 | (3) |
 is known as the phase ratio of a column (VS is the volume of the stationary phase, and VM is the volume of the mobile phase, respectively). VS can be understood as a part of the total column volume, VC, into which non-retained compounds cannot penetrate.25,26 With this simplified convention, β can be expressed as
is known as the phase ratio of a column (VS is the volume of the stationary phase, and VM is the volume of the mobile phase, respectively). VS can be understood as a part of the total column volume, VC, into which non-retained compounds cannot penetrate.25,26 With this simplified convention, β can be expressed as
 | (4) |
Therefore, the dependence of k on column temperature called van't Hoff equation is given
 | (5) |
In general, if a single mechanism controls the retention over the experimental temperature range, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus 1/T plots should be linear.27 By plotting ln
k versus 1/T plots should be linear.27 By plotting ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k with 1/T, the enthalpic and entropic contributions to the chromatographic retention can be calculated: −ΔH0 from the slope, and ΔS0 from the intercept of the plot. However, as mentioned above, the intercept of eqn (5), Ai, is not a definite constant due to the uncertainty of β invariable over the experimental temperature range, which may exert an influence on the ln
k with 1/T, the enthalpic and entropic contributions to the chromatographic retention can be calculated: −ΔH0 from the slope, and ΔS0 from the intercept of the plot. However, as mentioned above, the intercept of eqn (5), Ai, is not a definite constant due to the uncertainty of β invariable over the experimental temperature range, which may exert an influence on the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus 1/T plot. On the contrary, it is observed that ln
k versus 1/T plot. On the contrary, it is observed that ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K is explicitly linear with 1/T as described in eqn (2), and K can be calculated through eqn (3) by k and β measured at different temperatures, which means establishment of ln
K is explicitly linear with 1/T as described in eqn (2), and K can be calculated through eqn (3) by k and β measured at different temperatures, which means establishment of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K versus 1/T linear plot is more rational because it can effectively avoid the possible errors arising from changed β existing in ln
K versus 1/T linear plot is more rational because it can effectively avoid the possible errors arising from changed β existing in ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k versus 1/T plot.
k versus 1/T plot.
In HPLC, the selectivity factor (α) is usually represented as
 | (6) |
The change in α between two adjacent solutes with temperature can be derived by substituting eqn (2) into (6)
 | (7) |
Based on eqn (7), the selectivity of column at arbitrary temperature can be predicted by the fitted parameters, ΔH0 and ΔS0 obtained from the linear ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K versus 1/T plot of eqn (2).
K versus 1/T plot of eqn (2).
3. Experimental
3.1 Materials and reagents
Methanol and acetonitrile of HPLC grade were obtained from Merck (Darmstadt, Germany). Acetic acid of analytical grade (36%) was provided by Sinopharm Chemical Reagent Beijing Co., Ltd (Beijing, China). Distilled water was purified using a Milli-Q water purification equipment (Millipore Intertech., MA, USA).Flavonoid glycosides such as flavonoid glycosides I, II, III, IV, V and VI used as the training set were all laboratory-made. Estrogens, i.e. estriol (E3), 17β-estradiol (17β-E2), 17α-estradiol (17α-E2), ethinyl estradiol (EE), estrone (E1) and progesterone (P4) used as the test set were purchased from the National Institute for the Control of Pharmaceutical and Biological Products (Beijing, China).
3.2 Apparatus
All chromatographic experiments were carried out on a fully automated ThermoFisher LC-U3000 liquid chromatography (ThermoFisher Scientific, Massachusetts, USA) equipped with a double gradient pump, an auto-sampler with a 20 μL loop and a diode array detector. All the data were collected and processed by Chromeleon 7.20 work station (TheromFisher Scientific, California, USA). The chromatographic columns used were Sepax GP-C18, 150 mm × 4.6 mm i.d., 5 μm (Sepax Technologies Inc., SuZhou, China), Cosmosil cholesterol column, 5 μm, 150 mm × 4.6 mm i.d. (Nacalai Tesque Inc., Kyoto, Japan), Sepax GP-C8, 150 mm × 4.6 mm i.d., 5 μm (Sepax), and Shodex Asahipak ODP-50 4D, 150 mm × 4.6 mm i.d., 5 μm (Showa Denko K. K., Tokyo, Japan).3.3 Methods
For C18 column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70, v/v) with the flow rate at 1.0 mL min−1. For cholesterol column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (25
70, v/v) with the flow rate at 1.0 mL min−1. For cholesterol column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, v/v) with the flow rate at 0.4 mL min−1. For C8 column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (30
75, v/v) with the flow rate at 0.4 mL min−1. For C8 column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, v/v) with the flow rate at 1.0 mL min−1. For ODP column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (30
75, v/v) with the flow rate at 1.0 mL min−1. For ODP column: solutes were eluted by the mobile phase consisting of methanol and 0.1% acetic acid (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75, v/v) with the flow rate at 0.8 mL min−1. The type and composition of mobile phases were individually the optimized conditions for each stationary phase. For all the stationary phases, temperatures were ranged from 25 °C to 55 °C. The wavelength was set at 277 nm for flavonoid glycosides and 220 nm for estrogens, respectively. The solutes were dissolved in the mobile phase used for the cholesterol column and the injected volume was 10 μL in each experiment. All the experimental retention times (tR) were obtained by averaging the results of at least three independent injections. The retention factors k was calculated according to the equation k = (tR − tM)/tM, where tM was the column hold-up time, determined by using sulfourea as the non-retained marker.14 The column hold-up volume, VM, was calculated by tM and Fc (VM = Fc × tM, where Fc is the volumetric flow rate), and then corrected by subtracting extra-column volume (V0), which was determined through substituting the column with a zero-volume union.28,29 The volume of the stationary phase (VS) was calculated as a difference between VC and the corrected VM.
75, v/v) with the flow rate at 0.8 mL min−1. The type and composition of mobile phases were individually the optimized conditions for each stationary phase. For all the stationary phases, temperatures were ranged from 25 °C to 55 °C. The wavelength was set at 277 nm for flavonoid glycosides and 220 nm for estrogens, respectively. The solutes were dissolved in the mobile phase used for the cholesterol column and the injected volume was 10 μL in each experiment. All the experimental retention times (tR) were obtained by averaging the results of at least three independent injections. The retention factors k was calculated according to the equation k = (tR − tM)/tM, where tM was the column hold-up time, determined by using sulfourea as the non-retained marker.14 The column hold-up volume, VM, was calculated by tM and Fc (VM = Fc × tM, where Fc is the volumetric flow rate), and then corrected by subtracting extra-column volume (V0), which was determined through substituting the column with a zero-volume union.28,29 The volume of the stationary phase (VS) was calculated as a difference between VC and the corrected VM.
4. Results and discussion
4.1 Effect of temperature on the phase ratio
To investigate the effect of temperature on phase ratio, values of β were experimentally measured by VC and VM via eqn (4) with temperatures ranged from 25 °C to 55 °C with 10 °C increments on C18, cholesterol, C8, and ODP columns, respectively. Fig. 1 shows the regression of the experimental phase ratios and column temperatures on four columns. It was obvious that, β increased as temperature increased, which confirmed the suspicion we proposed that β varies during temperature changes. However, the good linear relationship of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = a + b/T−1 can be obtained with the correlation coefficients R2 better than 0.99. By substituting this linear fitting into eqn (5), van't Hoff equation can be re-written as:
β = a + b/T−1 can be obtained with the correlation coefficients R2 better than 0.99. By substituting this linear fitting into eqn (5), van't Hoff equation can be re-written as:
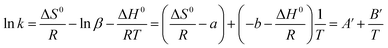 | (8) |
Although the form of eqn (8) is just the same as van't Hoff equation, the physical significance of the slope and intercept are both totally different, that is, the intercept and slope of the classical van't Hoff equation cannot truly express ΔH0 and ΔS0 in a chromatographic process. On the contrary, since it makes no assumptions about the fixed quantity of β at different temperatures, the slope and intercept of eqn (2) truly reflect ΔH0 and ΔS0 values in the chromatographic process because ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K was calculated by k and β measured at each temperature through eqn (3). The experimental ln
K was calculated by k and β measured at each temperature through eqn (3). The experimental ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k, as well as ln
k, as well as ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K of six flavonoid glycosides, were respectively plotted against 1/T on C18, cholesterol, C8 and ODP columns, and the fitting parameters are shown in Table 1. It can be seen from Table 1 that, although the straight line seemed to fit the data well when ln
K of six flavonoid glycosides, were respectively plotted against 1/T on C18, cholesterol, C8 and ODP columns, and the fitting parameters are shown in Table 1. It can be seen from Table 1 that, although the straight line seemed to fit the data well when ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k was plotted against 1/T, the slope and intercept were markedly different from those of ln
k was plotted against 1/T, the slope and intercept were markedly different from those of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–1/T plot due to the additional items a and b respectively involved in intercept and slope in eqn (8). The relative errors of k-related and K-related ΔH0 (2.8–3.3% for C18, about 0.9% for cholesterol, 4.4–5.5% for C8 and 11.5–17.4% for ODP, respectively), as well as the errors of ΔS0 (2.8–3.4% for C18, 3.6–4.1% for cholesterol, 2.7–3.6% for C8 and 21.5%–28.3% for ODP, respectively) are listed in Table 1, revealing the inaccuracy of conventional van't Hoff equation in acquiring ΔH0 and ΔS0, while it is suggested that the solid and accurate ΔH0 and ΔS0 data should be obtained through eqn (2) and (3). For ODP column, the errors of ΔH0 and ΔS0 were more significant than others, which may be attributed to the large values of intercept and slope of the ln
K–1/T plot due to the additional items a and b respectively involved in intercept and slope in eqn (8). The relative errors of k-related and K-related ΔH0 (2.8–3.3% for C18, about 0.9% for cholesterol, 4.4–5.5% for C8 and 11.5–17.4% for ODP, respectively), as well as the errors of ΔS0 (2.8–3.4% for C18, 3.6–4.1% for cholesterol, 2.7–3.6% for C8 and 21.5%–28.3% for ODP, respectively) are listed in Table 1, revealing the inaccuracy of conventional van't Hoff equation in acquiring ΔH0 and ΔS0, while it is suggested that the solid and accurate ΔH0 and ΔS0 data should be obtained through eqn (2) and (3). For ODP column, the errors of ΔH0 and ΔS0 were more significant than others, which may be attributed to the large values of intercept and slope of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β–1/T plot shown in Fig. 1(d), which means temperature has much more influence on β for ODP stationary phase.
β–1/T plot shown in Fig. 1(d), which means temperature has much more influence on β for ODP stationary phase.
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–1/T K–1/T |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k–1/T k–1/T |
RE (ΔS) (%) | RE (ΔH) (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intercept | Slope | R2 | ΔS0 (J) | −ΔH0 (KJ) | Intercept | Slope | R2 | ΔS0 (J) | −ΔH0 (KJ) | |||
a 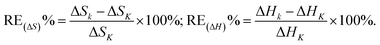 |
||||||||||||
| C18 | ||||||||||||
| I | −11.21 ± 0.22 | 4340.4 ± 70.0 | 0.9992 | −93.22 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 086.5 086.5 |
−11.39 ± 0.22 | 4204.5 ± 67.5 | 0.9992 | −95.97 | 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 956.0 956.0 |
3.0 | 3.1 |
| II | −10.00 ± 0.18 | 4026.1 ± 55.4 | 0.9994 | −83.18 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 472.7 472.7 |
−10.18 ± 0.15 | 3890.9 ± 47.9 | 0.9996 | −85.96 | 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 348.8 348.8 |
3.3 | 3.4 |
| III | −11.36 ± 0.18 | 4495.3 ± 55.2 | 0.9996 | −94.48 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 374.1 374.1 |
−11.54 ± 0.15 | 4360.1 ± 47.6 | 0.9996 | −97.26 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250.2 250.2 |
2.9 | 3.0 |
| IV | −11.12 ± 0.30 | 4420.7 ± 93.1 | 0.9987 | −92.45 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 754.0 754.0 |
−11.29 ± 0.28 | 4282.7 ± 88.1 | 0.9987 | −95.15 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 606.3 606.3 |
2.9 | 3.1 |
| V | −10.75 ± 0.25 | 4416.1 ± 78.5 | 0.9991 | −89.34 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715.5 715.5 |
−10.91 ± 0.23 | 4278.1 ± 72.3 | 0.9991 | −92.04 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567.7 567.7 |
3.0 | 3.1 |
| VI | −12.00 ± 0.26 | 4768.1 ± 80.5 | 0.9992 | −99.73 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642.3 642.3 |
−12.18 ± 0.24 | 4634.9 ± 73.8 | 0.9992 | −102.55 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534.7 534.7 |
2.8 | 2.8 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| Cholesterol | ||||||||||||
| I | −12.90 ± 0.04 | 4824.6 ± 12.7 | 0.9999 | −107.25 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 111.9 111.9 |
−12.93 ± 0.07 | 4638.8 ± 21.5 | 0.9999 | −108.23 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567.3 567.3 |
0.9 | 3.9 |
| II | −11.81 ± 0.02 | 4512.7 ± 6.2 | 0.9999 | −98.19 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 518.3 518.3 |
−11.84 ± 0.05 | 4326.7 ± 15.2 | 0.9999 | −99.16 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 972.3 972.3 |
0.9 | 4.1 |
| III | −12.98 ± 0.04 | 4920.9 ± 13.0 | 0.9999 | −107.91 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912.1 912.1 |
−13.01 ± 0.07 | 4734.7 ± 21.9 | 0.9999 | −108.87 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364.0 364.0 |
0.9 | 3.8 |
| IV | −12.49 ± 0.01 | 4793.1 ± 1.9 | 1.0000 | −103.87 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.9 849.9 |
−12.52 ± 0.04 | 4607.0 ± 11.2 | 0.9999 | −104.83 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 302.4 302.4 |
0.9 | 3.9 |
| V | −12.15 ± 0.03 | 4743.4 ± 7.9 | 0.9999 | −101.03 | 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436.7 436.7 |
−12.18 ± 0.05 | 4557.3 ± 16.6 | 0.9999 | −102.00 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889.5 889.5 |
0.9 | 3.9 |
| VI | −13.51 ± 0.01 | 5213.2 ± 2.8 | 1.0000 | −112.33 | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342.8 342.8 |
−13.54 ± 0.04 | 5027.0 ± 11.5 | 0.9999 | −113.29 | 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794.6 794.6 |
0.9 | 3.6 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| C8 | ||||||||||||
| I | −9.43 ± 0.03 | 3208.2 ± 9.3 | 0.9999 | −78.40 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673.0 673.0 |
−9.79 ± 0.06 | 3317.3 ± 18.3 | 0.9999 | −74.93 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 580.0 580.0 |
4.4 | 3.4 |
| II | −8.58 ± 0.03 | 2993.3 ± 9.7 | 0.9999 | −71.33 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 886.3 886.3 |
−8.91 ± 0.05 | 3093.5 ± 14.4 | 0.9999 | −67.62 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 719.4 719.4 |
5.2 | 3.3 |
| III | −8.99 ± 0.13 | 3148.6 ± 40.4 | 0.9995 | −74.74 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 177.5 177.5 |
−9.32 ± 0.10 | 3247.3 ± 32.4 | 0.9997 | −71.03 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 998.1 998.1 |
5.0 | 3.1 |
| IV | −9.56 ± 0.05 | 3333.4 ± 16.4 | 0.9999 | −79.48 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713.9 713.9 |
−9.89 ± 0.03 | 3429.7 ± 8.1 | 0.9999 | −75.77 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 514.5 514.5 |
4.7 | 3.0 |
| V | −9.76 ± 0.17 | 3450.2 ± 53.2 | 0.9992 | −81.14 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685.0 685.0 |
−10.07 ± 0.15 | 3542.4 ± 46.3 | 0.9995 | −77.26 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451.5 451.5 |
4.8 | 2.7 |
| VI | −8.70 ± 0.39 | 3131.1 ± 121.3 | 0.9955 | −72.33 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 032.0 032.0 |
−9.00 ± 0.37 | 3220.6 ± 114.9 | 0.9962 | −68.37 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776.1 776.1 |
5.5 | 2.9 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| ODP | ||||||||||||
| I | −10.65 ± 0.32 | 3609.1 ± 101.1 | 0.9977 | −88.54 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 006.1 006.1 |
−14.07 ± 0.12 | 4632.3 ± 36.3 | 0.9998 | −103.98 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512.9 512.9 |
17.4 | 28.3 |
| II | −9.84 ± 0.29 | 3389.5 ± 89.9 | 0.9979 | −81.81 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180.3 180.3 |
−13.04 ± 0.10 | 4348.8 ± 30.5 | 0.9999 | −95.42 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 155.9 155.9 |
16.6 | 28.3 |
| III | −10.18 ± 0.32 | 3521.8 ± 100.1 | 0.9976 | −84.64 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 280.2 280.2 |
−13.29 ± 0.05 | 4454.1 ± 14.7 | 0.9999 | −97.50 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031.4 031.4 |
15.2 | 26.5 |
| IV | −10.81 ± 0.36 | 3735.1 ± 113.3 | 0.9973 | −89.87 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 053.6 053.6 |
−13.90 ± 0.02 | 4660.0 ± 7.7 | 0.9999 | −102.57 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743.2 743.2 |
14.1 | 24.8 |
| V | −9.88 ± 0.42 | 3485.1 ± 132.5 | 0.9957 | −82.14 | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 975.1 975.1 |
−12.77 ± 0.13 | 4350.6 ± 39.1 | 0.9998 | −93.17 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170.9 170.9 |
13.4 | 24.8 |
| VI | −11.50 ± 0.16 | 4024.1 ± 51.0 | 0.9995 | −95.61 | 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 456.4 456.4 |
−14.39 ± 0.19 | 4887.6 ± 60.5 | 0.9995 | −106.64 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 635.5 635.5 |
11.5 | 21.5 |
The retention mechanisms of flavonoid glycosides on C18, cholesterol, C8 and ODP stationary phases also had been compared. The results showed that all the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–1/T had good linear relationships (R2 > 0.99), as well as the similar fitting parameters (ΔH0 < 0, ΔS0 < 0), which implied that the retention mechanisms of these analytes on four kinds of stationary phases were all dominated by hydrophobic interaction, and all belonged to enthalpy-driving process.1,15 On the other hand, the calculated values of a and b for each flavonoid glycoside respectively obtained from the differences between k-related and K-related ΔS0 and ΔH0 via eqn (8) were evaluated. Since ln
K–1/T had good linear relationships (R2 > 0.99), as well as the similar fitting parameters (ΔH0 < 0, ΔS0 < 0), which implied that the retention mechanisms of these analytes on four kinds of stationary phases were all dominated by hydrophobic interaction, and all belonged to enthalpy-driving process.1,15 On the other hand, the calculated values of a and b for each flavonoid glycoside respectively obtained from the differences between k-related and K-related ΔS0 and ΔH0 via eqn (8) were evaluated. Since ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = a + b/T, the parameters a and b should be always constants under the same chromatographic conditions regardless of the analytes investigated. However, it was observed that a and b values calculated by using various flavonoid glycosides had more or less differences with each other. The cholesterol-bonded stationary phase exhibited only slight discrepancy in obtaining a and b for the six flavonoid glycosides with RSDs at 2.0% and 0.1%, respectively, while the RSDs of a and b obtained from the six solutes on C18, C8 and ODP stationary phase were higher with values at 3.4% and 1.4%, 7.0% and 7.0%, and 6.4% and 6.5% for a and b, respectively. These results indicated that the property of the solutes might have influence on the mobile and stationary phases. The high consistency on the cholesterol-bonded stationary phase is probably attributed to the decline in numbers of residual silanols on stationary phase surface which are apt to cause secondary interactions such as hydrogen-bonding and so on in comparison with C18, C8, and ODP stationary phases, and in consequence, the minor structural differences among various solutes can be ignored. Moreover, as shown in Table 1, the slopes of ln
β = a + b/T, the parameters a and b should be always constants under the same chromatographic conditions regardless of the analytes investigated. However, it was observed that a and b values calculated by using various flavonoid glycosides had more or less differences with each other. The cholesterol-bonded stationary phase exhibited only slight discrepancy in obtaining a and b for the six flavonoid glycosides with RSDs at 2.0% and 0.1%, respectively, while the RSDs of a and b obtained from the six solutes on C18, C8 and ODP stationary phase were higher with values at 3.4% and 1.4%, 7.0% and 7.0%, and 6.4% and 6.5% for a and b, respectively. These results indicated that the property of the solutes might have influence on the mobile and stationary phases. The high consistency on the cholesterol-bonded stationary phase is probably attributed to the decline in numbers of residual silanols on stationary phase surface which are apt to cause secondary interactions such as hydrogen-bonding and so on in comparison with C18, C8, and ODP stationary phases, and in consequence, the minor structural differences among various solutes can be ignored. Moreover, as shown in Table 1, the slopes of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k–1/T and ln
k–1/T and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–1/T plots obtained on the cholesterol column were both obviously larger than those obtained on other columns, which confirmed the fact that the cholesterol bonded stationary phase was indeed more sensitive to temperature changes.
K–1/T plots obtained on the cholesterol column were both obviously larger than those obtained on other columns, which confirmed the fact that the cholesterol bonded stationary phase was indeed more sensitive to temperature changes.
4.2 Relationship between selectivity and column temperature on RPLC
To evaluate the effect of column temperature on chromatographic selectivity based on eqn (7), as well as to compare the thermodynamic chromatographic properties of four types of stationary phases for the separation of structural analogues, experiments were conducted by separating a mix of six flavonoid glycosides with temperatures ranged from 25 °C to 55 °C with 10 °C increments on C18, cholesterol, C8 and ODP columns, respectively. The chromatograms of the six flavonoid glycosides on C18 and cholesterol columns at different temperatures are shown in Fig. 2. It can be observed that, elevated temperature reduced the analysis times of analytes on both of the two columns (the same tendency could be also seen on C8 and ODP columns, which were not shown in Fig. 2), which might due to the exothermic enthalpy change associated with transfer of solutes from the mobile to stationary phases dominated the retention process in all the four chromatographic systems.16,17 The shorter retention times and smaller relative retention values resulting from rising temperature would go against good separation from the perspective of chromatographic thermodynamics. However, it is obvious from Fig. 2 that the increasing temperature played a beneficial impact on separation efficiency, especially for cholesterol-bonded stationary phase. Thus, it is assumed that on the cholesterol column the improved and narrower peak shapes caused by elevated temperatures according to chromatographic kinetics may dominate the separation process, that is, the half peak width rapidly decreases on the cholesterol column as column temperature rising, which compensates the negative influence on the separation effect brought by the shortened retention factors. | ||
| Fig. 2 Chromatograms of the six flavonoid glycosides on C18 column (a–e) and cholesterol column (f–j) under different temperatures. See Fig. 1 for chromatographic conditions. Peaks: (1) flavonoid glycoside I (schaftoside); (2) flavonoid glycoside II; (3) flavonoid glycoside III (isoschaftoside); (4) flavonoid glycoside IV; (5) flavonoid glycoside V; (6) flavonoid glycoside VI. | ||
Fig. 3 illustrated the change in selectivity factor α, which was obtained by the experimental tR values of two adjacent solutes via eqn (6), against the temperature. As shown in Fig. 3 that, α varied at different temperatures for all the investigated compounds. For C18 column, as can be seen from Fig. 3(a), α2 and α4 decreased as temperature increased, while α1 and α5 increased with the temperature increased. However, these α values were all larger than 1.12 over the investigated temperature interval, which means all the flavonoid glycosides exhibited acceptable separation from 25 °C to 55 °C, except for compounds III and IV, the peaks of which were completely overlapped (α3 ≈ 1) on the C18 column within the experimental temperature range (see Fig. 2(a)–(e)). For cholesterol column, as shown in Fig. 3(b), the changes in selectivity with temperatures led to differences in resolution: the positive slope indicated that α2 and α5 rapidly decreased as temperature increased, while α1, α3 and α4 increased gradually with the temperature increased. In consequence, these tendency resulted in the optimal separation for the six flavonoid glycosides at 50 °C with all the α values larger than 1.2. As the temperature further increased (up to 55 °C), the separation between compounds II and III (α2 = 1.08 in Fig. 3(b)), as well as V and VI (α5 = 1.08 in Fig. 3(b)) were not complete on the cholesterol column. For C8 column, as it can be seen in Fig. 3(c), α2, α3 and α4 decreased as temperature increased, while α1 increased with the temperature increased. For compounds V and VI, the peaks of which were completely overlapped on C8 column at the low temperature range (α5 ≈ 1, 25 °C and 35 °C). Additionally, as shown in Fig. 3(c), the smaller slope of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α–1/T plot suggested that the chromatographic behaviors of the flavonoid glycosides were not sensitive to changes in temperature on C8 stationary phase. For ODP stationary phase, α2, α3 and α5 gradually decreased as temperature increased, while α1 and α4 increased with the temperature increased. According to the tendency of selectivity with temperature changes, it can be speculated that the appropriate column temperature for separating all the analytes is ranged between 25 °C and 35 °C on ODP column.
α–1/T plot suggested that the chromatographic behaviors of the flavonoid glycosides were not sensitive to changes in temperature on C8 stationary phase. For ODP stationary phase, α2, α3 and α5 gradually decreased as temperature increased, while α1 and α4 increased with the temperature increased. According to the tendency of selectivity with temperature changes, it can be speculated that the appropriate column temperature for separating all the analytes is ranged between 25 °C and 35 °C on ODP column.
 | ||
Fig. 3 Effect of temperature on the selectivity factor on C18 column (a), cholesterol column (b), C8 column (c) and ODP column (d). See Fig. 1 for chromatographic conditions.  α1 (selectivity factor of I and II); α1 (selectivity factor of I and II);  α2 (selectivity factor of II and III); α2 (selectivity factor of II and III);  α3 (selectivity factor of III and IV); α3 (selectivity factor of III and IV);  α4 (selectivity factor of IV and V; α4 (selectivity factor of IV and V;  α5 (selectivity factor of V and VI). α5 (selectivity factor of V and VI). | ||
On the other hand, the slope and intercept of each ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α–1/T plot in Fig. 3 respectively implied the differences in the enthalpy and entropy change of two adjacent solutes based on eqn (7). Table 2 lists the best-fit values of the intercept, the slope, as well as the correlation coefficient of each plot on C18, cholesterol, C8 and ODP columns. It can be observed from Table 2 that, all the fittings had satisfactory linearity with R2 larger than 0.94, except for the ln
α–1/T plot in Fig. 3 respectively implied the differences in the enthalpy and entropy change of two adjacent solutes based on eqn (7). Table 2 lists the best-fit values of the intercept, the slope, as well as the correlation coefficient of each plot on C18, cholesterol, C8 and ODP columns. It can be observed from Table 2 that, all the fittings had satisfactory linearity with R2 larger than 0.94, except for the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T plot (R2 = 0.3617) on C18 column, ln
α3–1/T plot (R2 = 0.3617) on C18 column, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T plot on C8 (R2 = 0.8299) and ODP (R2 = 0.9260) columns, respectively, which due to the inevitable error arising from the completely overlapped peaks of III and IV on C18 column, as well as V and VI on C8 and ODP columns. The fitted Δ(ΔS) and Δ(ΔH) were compared with the calculated ones obtained from relevant data from Table 1, and the results were presented in Table 3. The high agreement of fitted and calculated data (with the RE values of Δ(ΔS) 0.1–2.5% for C18, 0.0–0.1% for cholesterol, 0.2–4.0% for C8 and 0.3–0.7% for ODP, and the RE values of Δ(ΔH) 0.1–2.1% for C18, 0.0% for cholesterol, 0.0–1.6% for C8 and 0.0% for ODP, respectively) confirmed that availability of the deduced eqn (7). With the new strategy of prediction in resolution by eqn (7) proposed in this study, one can conveniently evaluate the separation tendency of the tested compounds on a column with the change in temperature, thereby cleverly avoiding those time-consuming and laborious condition experiments.
α5–1/T plot on C8 (R2 = 0.8299) and ODP (R2 = 0.9260) columns, respectively, which due to the inevitable error arising from the completely overlapped peaks of III and IV on C18 column, as well as V and VI on C8 and ODP columns. The fitted Δ(ΔS) and Δ(ΔH) were compared with the calculated ones obtained from relevant data from Table 1, and the results were presented in Table 3. The high agreement of fitted and calculated data (with the RE values of Δ(ΔS) 0.1–2.5% for C18, 0.0–0.1% for cholesterol, 0.2–4.0% for C8 and 0.3–0.7% for ODP, and the RE values of Δ(ΔH) 0.1–2.1% for C18, 0.0% for cholesterol, 0.0–1.6% for C8 and 0.0% for ODP, respectively) confirmed that availability of the deduced eqn (7). With the new strategy of prediction in resolution by eqn (7) proposed in this study, one can conveniently evaluate the separation tendency of the tested compounds on a column with the change in temperature, thereby cleverly avoiding those time-consuming and laborious condition experiments.
| R2 | |||
|---|---|---|---|
| C18 | |||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
1.208 ± 0.054 | −314.7 ± 16.9 | 0.9914 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−1.362 ± 0.006 | 470.2 ± 1.7 | 1.0000 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
0.250 ± 0.148 | −76.1 ± 46.4 | 0.3617 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
−0.884 ± 0.095 | 349.9 ± 29.6 | 0.9788 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
1.253 ± 0.012 | −353.0 ± 3.8 | 0.9997 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Cholesterol | |||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
1.090 ± 0.021 | −312.0 ± 6.6 | 0.9987 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−1.169 ± 0.022 | 408.2 ± 6.9 | 0.9992 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
0.486 ± 0.035 | −127.8 ± 11.1 | 0.9778 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
0.341 ± 0.020 | −49.7 ± 6.1 | 0.9560 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
−1.359 ± 0.024 | 469.8 ± 7.3 | 0.9993 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| C8 | |||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
0.854 ± 0.026 | −214.9 ± 8.2 | 0.9956 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−0.420 ± 0.148 | 156.2 ± 46.3 | 0.9400 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
−0.561 ± 0.087 | 181.9 ± 27.1 | 0.9714 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
−0.192 ± 0.125 | 115.8 ± 39.1 | 0.9573 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
1.058 ± 0.258 | −319.1 ± 80.7 | 0.8299 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| ODP | |||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
0.814 ± 0.039 | −219.6 ± 12.2 | 0.9907 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−0.338 ± 0.037 | 132.2 ± 11.5 | 0.9777 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
−0.634 ± 0.043 | 213.3 ± 13.5 | 0.9880 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
0.933 ± 0.072 | −250.0 ± 22.5 | 0.9760 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
−1.628 ± 0.278 | 539.0 ± 86.8 | 0.9260 |
| Δ(ΔS)a | Δ(ΔS)b | REΔ(ΔS) (%) | −Δ(ΔH)a | −Δ(ΔH)b | REΔ(ΔH) (%) | |
|---|---|---|---|---|---|---|
a Best-fit parameters via eqn 7.b Calculated values obtained by relating data from ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K–1/T plots in Table 1.c K–1/T plots in Table 1.c  |
||||||
| C18 | ||||||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
10.047 | 10.039 | 0.1 | −2616.7 | −2613.8 | 0.1 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−11.328 | −11.304 | 0.2 | 3909.0 | 3901.4 | 0.2 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
2.081 | 2.038 | 2.1 | −633.2 | −620.1 | 2.1 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
−7.349 | −7.282 | 0.9 | 2909.1 | 2888.3 | 0.7 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
10.416 | 10.390 | 2.5 | −2935.1 | −2926.8 | 0.3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Cholesterol | ||||||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
9.064 | 9.063 | 0.01 | −2593.9 | −2593.0 | 0.03 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−9.719 | −9.712 | 0.07 | 3393.8 | 3393.8 | 0.00 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
4.045 | 4.044 | 0.02 | −1062.4 | −1062.2 | 0.02 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
2.832 | 2.832 | 0.00 | −413.1 | −413.1 | 0.00 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
−11.295 | −11.295 | 0.00 | 3906.0 | 3906.0 | 0.00 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| C8 | ||||||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
7.100 | 7.067 | 0.46 | −1786.7 | 1786.7 | 0.00 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−3.489 | −3.409 | 2.29 | 1298.6 | 1291.2 | 0.57 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
−4.660 | −4.739 | 1.70 | 1512.1 | 1536.4 | 1.61 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
−1.599 | −1.663 | 4.00 | 963.1 | 971.1 | 0.83 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
8.794 | 8.813 | 0.22 | −2653.4 | 2653.0 | 0.02 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| ODP | ||||||
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1–1/T α1–1/T |
6.765 | 6.73 | 0.52 | −1825.6 | 1826.2 | 0.03 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α2–1/T α2–1/T |
−2.814 | 2.83 | 0.57 | 1099.5 | 1099.9 | 0.04 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α3–1/T α3–1/T |
−5.268 | 5.23 | 0.72 | 1773.7 | 1773.4 | 0.02 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α4–1/T α4–1/T |
7.755 | 7.73 | 0.32 | −2078.6 | 2078.5 | 0.00 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α5–1/T α5–1/T |
−13.533 | 13.47 | 0.47 | 4481.6 | 4481.3 | 0.00 |
4.3 Prediction of selectivity for estrogens
As shown in Fig. 2, all the flavonoid glycosides tested cannot reach to acceptable separations at commonly used temperatures (25–35°C) on the four columns even with the optimized type and proportion of the mobile phase. However, after column temperature was introduced into the optimization process as the third parameter, the satisfactory separation on cholesterol column would be realized by regulating temperatures. However, this regulating measure would not be helpful in separating the investigated compounds on C18 and C8 columns. Therefore, setting up a simple model incorporating retention with temperatures such as Fig. 3 may allow chromatographers to conveniently predict separation trend of structural analogues on various chromatographic columns at different temperatures. To further demonstrate the applicability of this selectivity prediction protocol at different temperatures, six estrogens used as the test set were analyzed on C18, cholesterol, C8 and ODP columns, respectively. For this purpose, the type and proportion of the mobile phase were simply optimized at first. Acetonitrile (B)–water (A) with the gradient program (30–40% solvent B from 0 to 5 min; 40% solvent B at 15 min; 40–55% solvent B from 15 to 22 min; 55% solvent B at 35 min; 55–30% solvent B from 35 to 36 min; 50% solvent B at 38 min) were selected for C18 column, and acetonitrile–water (40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, v/v) were selected for cholesterol, C8, and ODP columns, respectively. On C18, cholesterol and C8 columns, the flow rate was 1.0 mL min−1, while on ODP the flow rate was 0.8 mL min−1. The injection volume was 10 μL, and the wavelength was set at 220 nm. Every single sample of the six estrogens was injected and tR was recorded individually. Since the rigorous linearity of eqn (7) has been deduced in theory and further confirmed in Section 4.2, in this section two temperature points (30 °C and 55 °C) were chosen as the reference temperatures to build the model of ln
60, v/v) were selected for cholesterol, C8, and ODP columns, respectively. On C18, cholesterol and C8 columns, the flow rate was 1.0 mL min−1, while on ODP the flow rate was 0.8 mL min−1. The injection volume was 10 μL, and the wavelength was set at 220 nm. Every single sample of the six estrogens was injected and tR was recorded individually. Since the rigorous linearity of eqn (7) has been deduced in theory and further confirmed in Section 4.2, in this section two temperature points (30 °C and 55 °C) were chosen as the reference temperatures to build the model of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α–1/T, by using which the selectivity between two adjacent solutes under other temperatures can be predicted directly. The predicted and experimental values for α at 40 °C and 50 °C are summarized in Table 4. As shown in Table 4, the predicted α values were extremely close to the calculated ones with the relative errors of 0.0–2.2% for C18 column, 0.0–1.0% for cholesterol column, 0.0–6.1% for C8 column and 0.0–5.1% for ODP column, respectively, which demonstrated that the proposed method can effectively predict the resolution of estrogens over the experimental temperature range. By comparing the predicted α values obtained on four columns, it can be observed that these four stationary phases showed little difference in separating the investigated steroid hormones, indicating that all of the four columns can be used in analysis of the six hormones. As shown in Table 4, α5 increased as temperature increased, while α1, α2, α3 and α4 decreased with the temperature increased on all the columns, which suggested that the investigated steroid hormones should be separated at lower temperature on the four stationary phases. Since the cholesterol bonded stationary phase is more sensitive to temperature changes, a greater improvement in separation should be observed on the cholesterol column at lower column temperature. The chromatograms for a mix of the six steroid hormones on cholesterol column at different column temperatures are shown in Fig. 4, which confirmed our speculation.
α–1/T, by using which the selectivity between two adjacent solutes under other temperatures can be predicted directly. The predicted and experimental values for α at 40 °C and 50 °C are summarized in Table 4. As shown in Table 4, the predicted α values were extremely close to the calculated ones with the relative errors of 0.0–2.2% for C18 column, 0.0–1.0% for cholesterol column, 0.0–6.1% for C8 column and 0.0–5.1% for ODP column, respectively, which demonstrated that the proposed method can effectively predict the resolution of estrogens over the experimental temperature range. By comparing the predicted α values obtained on four columns, it can be observed that these four stationary phases showed little difference in separating the investigated steroid hormones, indicating that all of the four columns can be used in analysis of the six hormones. As shown in Table 4, α5 increased as temperature increased, while α1, α2, α3 and α4 decreased with the temperature increased on all the columns, which suggested that the investigated steroid hormones should be separated at lower temperature on the four stationary phases. Since the cholesterol bonded stationary phase is more sensitive to temperature changes, a greater improvement in separation should be observed on the cholesterol column at lower column temperature. The chromatograms for a mix of the six steroid hormones on cholesterol column at different column temperatures are shown in Fig. 4, which confirmed our speculation.
| α1 | α2 | α3 | α4 | α5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Predicted | Experimental | Predicted | Experimental | Predicted | Experimental | Predicted | Experimental | Predicted | Experimental | |
| C18 | ||||||||||
| 40 °C | 3.812 | 3.798 | 1.145 | 1.145 | 1.137 | 1.134 | 1.085 | 1.093 | 1.770 | 1.750 |
| RE% | 0.4 | 0.0 | 0.3 | 0.7 | 1.1 | |||||
| 50 °C | 3.755 | 3.728 | 1.143 | 1.142 | 1.113 | 1.102 | 1.077 | 1.073 | 1.853 | 1.894 |
| RE% | 0.7 | 0.1 | 1.0 | 0.4 | 2.2 | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| Cholesterol | ||||||||||
| 40 °C | 6.713 | 6.702 | 1.142 | 1.141 | 1.194 | 1.194 | 1.083 | 1.084 | 2.399 | 2.389 |
| RE% | 0.2 | 0.1 | 0.0 | 0.1 | 0.4 | |||||
| 50 °C | 6.245 | 6.261 | 1.136 | 1.136 | 1.144 | 1.144 | 1.070 | 1.081 | 2.507 | 2.492 |
| RE% | 0.3 | 0.0 | 0.0 | 1.0 | 0.6 | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| C8 | ||||||||||
| 40 °C | 8.509 | 8.489 | 1.186 | 1.187 | 1.169 | 1.167 | 1.112 | 1.111 | 3.002 | 3.196 |
| RE% | 0.2 | 0.01 | 0.2 | 0.1 | 6.1 | |||||
| 50 °C | 7.869 | 8.070 | 1.184 | 1.185 | 1.127 | 1.140 | 1.095 | 1.101 | 3.185 | 3.125 |
| RE% | 2.5 | 0.1 | 1.1 | 0.5 | 0.0 | |||||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||
| ODP | ||||||||||
| 40 °C | 8.662 | 9.131 | 1.186 | 1.189 | 1.099 | 1.100 | 1.155 | 1.159 | 1.528 | 1.530 |
| RE% | 5.1 | 0.2 | 0.1 | 0.4 | 0.1 | |||||
| 50 °C | 7.646 | 7.389 | 1.178 | 1.178 | 1.073 | 1.073 | 1.152 | 1.153 | 1.581 | 1.581 |
| RE% | 3.5 | 0.0 | 0.0 | 0.1 | 0.0 | |||||
5. Conclusions
The use of temperature programming in HPLC is gaining momentum in recent years, and the explanation of separation mechanism from the view of chromatographic thermodynamics by using van't Hoff equation is commonly available in the literatures. However, it is clear that changes in phase ratio at various temperatures would result in certain errors of enthalpy and entropy obtained from classical van't Hoff equation. In this paper, a new strategy for gaining accurate values of enthalpy and entropy was proposed, providing solid data support for theoretical research in separation mechanism. More importantly, by examining the role temperature played in the selectivity of compounds, a new model relating the separation tendency of analytes and column temperature on HPLC was deduced and validated in this work. According to this promising method, the change in resolution between homologous analytes with column temperature can be predicted conveniently, making HPLC optimization process greatly simplified, and furthermore, in this way adjustable parameters that can be optimized in HPLC are expanded since temperature can be considered as the third dimension besides mobile phase type and composition. In addition, by comparing the separation characteristics of C18, cholesterol, C8 and ODP bonded stationary phases on HPLC, it is suggested that stationary phase sensitive to temperature, e.g. cholesterol is particularly suitable to this temperature-involved optimization method, which points out a new direction for developing column materials.Acknowledgements
This work was supported by National Natural Science Foundation of China (81303311), Natural Science Foundation of Jiangsu (BK20130958), Natural Science Foundation for Colleges of Jiangsu (13KJB150030), Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), Natural Science Foundation of Nanjing University of Chinese Medicine (12XZR27).References
- L. R. Snyder, J. L. Glajch and J. J. Kirkland, Practical HPLC Method Development, Wiley-Interscience, New York, 1988 Search PubMed.
- G. Vanhoenacker and P. Sandra, J. Chromatogr. A, 2005, 1082, 193–202 CrossRef CAS PubMed.
- J. Soukup and P. Jandera, J. Chromatogr. A, 2012, 1245, 98–108 CrossRef CAS PubMed.
- H. Chen and C. Horváth, J. Chromatogr., 1995, 705, 3–20 CrossRef CAS.
- H. Colin, J. C. Diez-masa, G. Guiochon, T. Czajkowska and I. Miedziak, J. Chromatogr., 1978, 167, 41–65 CrossRef CAS.
- W. S. Hancock, R. C. Chloupek, J. J. Kirkland and L. R. Snyder, J. Chromatogr., 1994, 686, 31–43 CrossRef CAS.
- R. C. Chloupek, W. S. Hancock, B. A. Marchylo, J. J. Kirkland, B. E. Boyes and L. R. Snyder, J. Chromatogr., 1994, 686, 45–59 CrossRef CAS.
- W. H. Pirkle and J. A. Burke, J. Chromatogr., 1991, 557, 173–185 CrossRef CAS.
- T. Takagi and T. Suzuki, J. Chromatogr., 1992, 625, 163–168 CrossRef CAS.
- K. D. Nugent, W. G. Burton, T. K. Slattery and B. F. Johnson, J. Chromatogr. A, 1988, 443, 381–397 CrossRef CAS.
- T. Greibrokk and T. Andersen, J. Chromatogr. A, 2003, 1000, 743–755 CrossRef CAS.
- J. W. Li and P. W. Carr, Anal. Chem., 1997, 69, 2202–2206 CrossRef CAS.
- J. W. Li and P. W. Carr, Anal. Chem., 1997, 69, 837–843 CrossRef CAS.
- J. Soukup, S. Bocian, P. Jandera and B. Buszewsk, J. Sep. Sci., 2014, 37, 345–351 CrossRef CAS PubMed.
- G. Vanhoenacker and P. Sandra, J. Chromatogr. A, 2005, 1082, 193–202 CrossRef CAS PubMed.
- S. Bocian, J. Soukup, P. Jandera and B. Buszewski, Chromatographia, 2015, 78, 21–30 CAS.
- W. Melander, D. E. Campbell and C. Horváth, J. Chromatogr. A, 1978, 158, 215–225 CrossRef CAS.
- W. Kiridena, C. F. Poole and W. W. Koziol, Chromatographia, 2003, 57, 703–707 CAS.
- K. Jinno and A. Ishigaki, J. High Resolut. Chromatogr., 1982, 5, 668–673 CAS.
- T. L. Chester and J. W. Coym, J. Chromatogr. A, 2003, 1003, 101–111 CrossRef CAS.
- C. F. Poole, W. Kiridena and W. W. Koziol, Chromatographia, 2003, 57, 703–708 Search PubMed.
- D. Cho, S. Park, J. Hong and T. Chang, J. Chromatogr. A, 2003, 986, 191–198 CrossRef CAS.
- D. Cho, S. Park, J. Hong and T. Chang, J. Chromatogr. A, 2003, 986, 199–206 CrossRef CAS.
- E. Ferrannini, Metabolism, 1988, 37, 287–301 CrossRef CAS.
- P. Jandera, H. Colin and G. Guiochon, Anal. Chem., 1982, 54, 435–441 CrossRef CAS.
- T. L. Chester and J. W. Coym, J. Chromatogr. A, 2003, 1003, 101–111 CrossRef CAS.
- P. Jandera, K. Krupczyńsk, K. Vyňuchalová and B. Buszewski, J. Chromatogr. A, 2010, 1217, 6052–6060 CrossRef CAS PubMed.
- D. V. Mccalley, J. Chromatogr. A, 2000, 902, 311–321 CrossRef CAS.
- P. Molander, S. J. Thommesen, I. A. Bruheim, R. Trones, T. Greibrokk, E. Lundanes and T. E. Gundersen, J. High Resolut. Chromatogr., 1999, 22, 490–494 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |