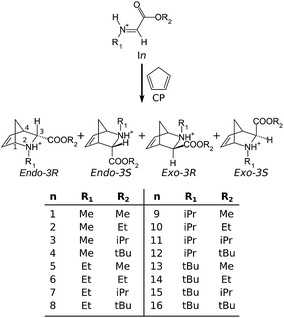
Simple descriptors for assessing the outcome of aza-Diels–Alder reactions

Abstract

The iminium aza-Diels–Alder (iADA) reaction of cyclopentadiene with 16 protonated alkyl alkylimineglyoxilates was studied using density functional theory (DFT) in order to elucidate how different substitution patterns in the dienophile may affect the reaction’s outcome. Additionally, the application of the polarisable continuum model (PCM) together with the evaluation of the thermodynamic properties at different temperatures further allowed the surveying of the importance of such factors. These effects were combined into linear models which use the temperature, Taft’s constants and characteristics of the solvent as descriptors for modelling and predicting the activation enthalpy and enthalpic balance of the iADA reactions under study. This model performs in a satisfactory manner, providing a cross-validation of the DFT framework traditionally used for predicting the outcome of these reactions and also uncovering novel insights into how the substitution patterns in the dienophile, the solvent and the temperature interact in order to give the characteristic regio- and stereoselectivity of the iADA reaction. Moreover, the results show that Taft’s polar and steric substituent constants are important descriptors for assessing the outcome of iADA reactions.

---

1 Introduction

The aza-Diels–Alder (ADA) reaction, a subclass of the hetero-Diels–Alder additions, is a universal method for the preparation of many heterocyclic compounds.¹ These products may bear interesting biological properties, or find usefulness as intermediates in the synthesis of catalysts,² herbicides, antibiotics or anti-viral agents.^1,3 Moreover, high chemo-, regio- and stereoselectivity are usually achieved with high atom economy, making the ADA reaction an important tool for fulfilling the principles of Green Chemistry.^4,5 This is particularly evident in the case of the ADA reaction between iminium cations and a dienophile, such as cyclopentadiene. Indeed, the introduction of iminium ions as dienophiles in ADA reactions was first developed in the 1980’s and has seen wide acceptance due to the high yields it usually provides under mild conditions.³ Mechanistic insights into ADA reactions involving iminium ions (iADA) may therefore be relevant in the development of novel applications in organic synthesis, specially when considering that some Lewis acid catalysts used in ADA reactions form adducts which mimic the behaviour of iminium ions.³

Experimental studies on the kinetics of iADA reactions involving cyclopentadiene strongly suggest that these cycloadditions occur in a concerted rather than stepwise manner.³ Nevertheless, both experimental evidence and current computational studies have shown this mechanism to be highly asymmetric.^3,6–12 More recently, attempts at characterising possible stepwise pathways for this reaction revealed that such intermediate structures (zwitterions) would exist in an “open” conformation, within which direct cyclisation would be impossible.¹³

Theoretical studies of iADA reactions involving cyclopentadiene are usually performed using Density Functional Theory (DFT) with a hybrid Generalised Gradient Approximation (hybrid-GGA) functional such as B3LYP or X3LYP in conjunction with a polarised split-valence basis set.^6,9,10,14,15 The energies for the free reactants, molecular complexes, transition states and final products may be refined using larger basis sets, and the effect of the solvent on the energetic balance of the different reaction pathways is usually determined by applying continuum solvent models without further relaxation of the molecular geometries.^6,9,10 Despite its relative simplicity, this theoretical framework achieved good accord between theoretical predictions and experimental observations.^{6,9,10,16–18} The soundness of this framework was partially evaluated by Szefczyk et al., who observed good agreement between a similar DFT-based framework and high level Complete Active-Space Self-Consistent Field (CASSCF) calculations for the reaction between butadiene and several alkylglyoxylates.⁸ Previously, in 2002, Domingo had already shown that the geometries obtained in the gas-phase approximation are excellent approximations to those obtained in dichloromethane under the Polarisable Continuum Model (PCM),¹⁹ thus justifying the use of the former when considering solvent effects.

Beside their relative energies and geometries, more information on the reactivity of the species involved in iADA reactions may be gathered from theoretical calculations. This includes the quantitative characterisation of the global electrophilicity power of the iminium species, ω = μ²/2η, where μ is the electronic chemical potential (given by (ε_H + ε_L)/2) and η represents Pearson’s chemical hardness (defined as ε_L − ε_H).^20,21 In both cases, ε_H and ε_L represent the energies of the HOMO and LUMO molecular orbitals, respectively. Moreover, the effective atomic charges of the relevant species also provide valuable insight into the electronic structure of the reactants, products and intermediates. These have been traditionally obtained using the Natural Bond Orbital (NBO) formalism,^9,10,22 although recent studies by Domingo and co-workers,^11,12 and Li and Fang²³ using the Quantum Theory of Atoms In Molecules (QTAIM) and/or the Electron Localisation Function (ELF) frameworks have yielded novel insights into similar cycloadditions.¹²

The successful modelling of several iADA reactions encourages the quest to find general tendencies within the accepted theoretical model. For this purpose, the addition of cyclopentadiene to 16 protonated alkyl alkylimineglyoxylates (Fig. 1) was studied using the theoretical framework described above. This included the determination of the exo/endo selectivity for each case, taking into account the four possible reaction pathways shown in Fig. 1. The results given by the DFT calculations were interpreted using NBO, in conjunction with empirical group additivity constants such as Taft’s polar and steric substituent constants, σ* and E_S, respectively.^24,25 The model reported in this work also incorporates the combined effects of both the temperature and the solvent medium. These results are given in the hope of shedding some light on the effect of the substituents at the imine (R₁) and at the ester (R₂) on the exo/endo selectivity. Furthermore, it provides an interpretation of such effects under well known parameters such as Taft’s constants, which may be useful for the interested synthetic chemist.

Fig. 1 Generic depiction of the aza-Diels–Alder addition of cyclopentadiene (CP) to a protonated imine carboxylate, and the four possible cycloadducts. In the absence of stereocentres in either R₁ or R₂, the two endo products form an enantiomeric pair, as do the two exo products. The substitution patterns of the iminium cations studied in this work are also depicted.

2 Computational methods

Initial guess geometries for all plausible stationary points were found by extensive computational experimentation. In this procedure, special care was taken in order to assure that the orientation of the R₁ and R₂ groups corresponds to the absolute minimum along their respective torsional modes. The stationary points on the Potential Energy Surface (PES) were optimised without any geometrical or symmetry constrains at the X3LYP/6-31G(d)^26,27 level of theory using the Rational Function Optimisation (RFO) method, as implemented in the GAMESS program.²⁸ Harmonic vibrational frequencies were then calculated at the same level of theory. Transition state structures were characterised by the presence of one imaginary harmonic frequency, whereas the absence of imaginary frequencies characterised the minima in the PES (i.e. reactants, intermediates and products). The harmonic frequencies were also used to estimate zero-point energies (ZPEs), as well as vibrational corrections to the enthalpy at 0, 193.0, 233.0, 273.15 and 298.15 K. Rotational and translational thermal energies were also calculated, using the classical equipartition energy theorem.

In order to assure that each saddle point connects two putative minima, Intrinsic Reaction Coordinate (IRC) calculations were performed using the quadratic approximation step in both forward and backward directions,²⁹ also at the X3LYP/6-31G(d) level of theory.

The electronic energy of each stationary point in the PES was refined using X3LYP and the 6-311G(2df,2p) basis set. These energies were used in conjunction with the translational, rotational and vibrational corrections calculated previously for the calculation of the relevant relative energies, enthalpies and Gibbs energies. This hybrid approach may be referred to as X3LYP/6-31G(d)//X3LYP/6-311G(2df,2p). The electronic properties of the relevant intervening species were further analysed using NBO as implemented in the NBO 5.9 plug-in for GAMESS.³⁰ The output from the X3LYP/6-311G(2df,2p) calculations was used in these analyses.

The effect of different solvents on the electronic energy of the stationary points was determined through single point calculations using the Polarisable Continuum Model (PCM) of Tomasi and co-workers,³¹ with parameters for chloroform, dichloromethane, tetrachloromethane, chlorobenzene, and 1,2-dichloroethane. In these calculations, the cavitation contribution to the total energy in solution was obtained for the range of temperatures mentioned above. All calculations accounting for solvent effects were performed at fixed geometry using X3LYP/6-311G(2df,2p).

Statistical analysis was performed using the R language,³² taking the energetic balances and structural data obtained from the DFT and NBO calculations, with the primary aim of studying their relationship with Taft’s polar and steric substituent constants, σ* and E_S, respectively.^24,25 Except where stated otherwise, the general procedure for deriving these models was a stepwise backwards linear regression in which the dependent variable was first expressed as a combination of σ* and E_S for both R₁ and R₂. At each iteration the least significant factor was excluded until all predictor variables had a significance of 99%, or higher, using t-Student statistics as described by Teixeira et al.³³ For each linear model, the relative importance of the predictor variables was further asserted using Johnson’s relative weights method.³⁴

3 Results and discussion

In this section, the structure and gas-phase properties at 0 K of the relevant species (reactants, molecular complexes, transition states and products) are presented and discussed. Then, the effect of increasing temperature will be briefly described. Finally, the results from incorporating solvent effects under the PCM formalism will be presented and discussed.

Since the reactions under scrutiny form two pairs of enantiomers (the two endo and the two exo paths being energetically equivalent) the results will be presented for the endo-3R and exo-3R pathways, for the sake of simplicity. The interested reader may find more information on the endo-3S and exo-3S pathways in the ESI.†

Throughout this work, the following nomenclature will be used: each reaction will be identified by its parent protonated imine or iminium cation (In, following the numbering in Fig. 1), and each of the four possible reaction pathways will be named by appending the configuration (endo-3R, endo-3S, exo-3R, or exo-3S) of its final product to the parent imine. Moreover, an additional suffix to the name of any given reaction pathway will denote a particular stationary point: Im, MC, TS or Prod, denoting the protonated imine, the molecular complex between cyclopentadiene and the imine, the transition state, or the product, respectively. An exception to this rule is made when referring to the protonated imines (or iminium cations), in which the reaction pathway is omitted. In order to make the discussion of the geometrical features of each species as straightforward as possible, the atom numbering in CP and In-IMGLX will be based on the numbering of their respective residues in the products, as shown in Fig. 1.

3.1 Free reactants

At their equilibrium geometry, all 16 iminium species exhibit a planar conformation around their C=N bond, for which an average bond length of 1.277 Å is observed. The C_1′–N₂–C₃–C_4′ dihedral average is 179.6°, with an associated standard deviation of 0.3°. As an example, the equilibrium geometry of I1-Im is given in Fig. 2a, together with the numbering scheme used in this work. As expected, the equilibrium geometry of CP (shown in Fig. 2b) is planar with bond lengths of 1.506 Å for the C₍₁₎–C₍₇₎ and C₍₄₎–C₍₇₎ bonds, 1.348 Å for the C₍₁₎–C₍₆₎ and C₍₄₎–C₍₅₎ bonds and 1.469 Å for the C₍₅₎–C₍₆₎ bond.

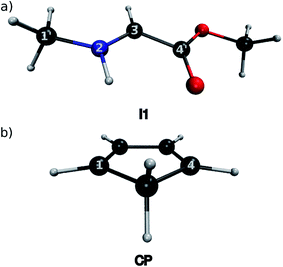Fig. 2 Structures of (a) I1-IM and (b) CP at their equilibrium geometries, optimised at the X3LYP/6-31G(d) level of theory.

The variation of R₁ and R₂ has a limited effect on the electronic chemical potential, μ, of these 16 species, which averages at about −10.1 ± 0.3 eV, and on the chemical hardness, η, which attains an average value of 5.03 ± 0.18 eV. On the other hand, the global electrophilicity index, ω, shows a distinct trend, decreasing steadily with increasing n (see Fig. 1). This behaviour raised the hypothesis that ω may be modelled exclusively from the electronic group contributions of R₁ and R₂. Indeed, a linear model for ω was devised using Taft’s polar substituent constants, σ*, for R₁ and R₂ as the independent variables. A good fitting was obtained between our calculations and the values derived from the Taft’s constants (r_adj² = 0.9964), as shown in Fig. 3. The equation behind the model depicted in Fig. 3 shows that the contribution of R₁ is about four times as intense as that of the group at the ester moiety of the imine. On the other hand, ω appears to be fairly independent from Taft’s steric substituent constants, E_S, since similar linear models score only a meagre r_adj² of 0.8012.

Fig. 3 Linear model for the global electrophilicity index, ω, as a function of Taft’s polar substituent constant, σ*, for R₁ and R₂.

Fig. 3 also shows that ω ranges from 9.529 eV (I16-Im) to 11.030 eV (I1-Im). Taking into account the global electrophilicity index of cyclopentadiene (0.956 eV, at the level of theory in use), the reactions in this study present an estimated Δω that ranges from 8.573 eV to 10.074 eV. These values of Δω are comparable to those published for the reaction of methyl and tert-butyl propynyliminoglyoxylates as well as that of methyl glyoxylate oxime with the same diene, with Δω values of 11.72 eV, 10.49 eV and 10.63 eV, respectively.^10,35 At the same time, they are also considerably smaller than that published for the reaction between methyl benzylimineglyoxylate and cyclopentadiene (13 eV),⁶ and much larger than that determined for the reaction between cyclopentadiene and methyl phenylethylimineglyoxylate (4.18 eV).⁹ Thus, the range of Δω used in this study is representative of the middle to high range of the reactions previously published. The amplitude of Δω is also satisfactory, as it allows the distinction between electronic and steric effects in the reactions under scrutiny, as it will be shown later.

Natural bond orbital analysis of the protonated imines shows that the natural charge of N₍₂₎ varies from −0.399e to −0.379e. These bounding values are found in I16-Im and I1-Im, respectively. Likewise, the natural charge of C₍₃₎ ranges from +0.189e (I13-Im) to +0.216e (I4-Im). In summary, the effective atomic charges of N₍₂₎ and C₍₃₎ vary along a narrow range of about 0.03e, and, although being apparently sensitive to Taft’s constants σ* and E_S, their small variation hinders the development of a linear model similar to the one established for ω.

3.2 Molecular complexes

For each reactant pair (CP + In-Im), careful exploration of the PES yielded the discovery of four molecular complexes, corresponding to the four endo-3R, endo-3S, exo-3R and exo-3S approaches. When evaluating their energy at 0 K, these molecular complexes lie −42.2 kJ mol⁻¹ to −23.3 kJ mol⁻¹ below CP and their parent iminium cation at infinite distance. Moreover, the two endo molecular complexes available for each reaction are degenerated to within 1 kJ mol⁻¹, as are the two concurrent exo molecular complexes. As a general trend, more sterically hindered alkylimines yield the less stable molecular complexes, as shown in Fig. 4. Despite these findings, the theoretical linear model for ΔE_MC shows that the variations in the relative energies of the molecular complexes are best explained by expressions involving σ* and not E_S, as given by

ΔE^Endo_MC = −40.1 − 40.6σ^*_R1 − 22.0σ^*_R2, r_adj² = 0.9235 (1)

and

ΔE^Exo_MC = −43.2 − 44.3σ^*_R1 − 22.2σ^*_R2, r_adj² = 0.9771 (2)

for the endo-3R and exo-3R approaches, respectively. Both models suggest that the electronic effect of R₁ dominates over that of R₂ and also over the steric effect of either group. This may indicate that the polar attraction between the two reactants is the driving force behind the stability of these molecular complexes. As can be observed in Fig. 4, both models appear to fail the most for R₁ = iPr. This deviation may be due to a marginal influence of Taft’s steric constants in the particular case of R₁ = iPr (although not significant enough to be accepted in the overall model), or to the fact that energetic evaluation of long range interactions always raises reasonable uncertainties when using DFT,³⁶ or because modelling these initial stages of the reaction may be outside the application scope of Taft’s substituent constants.³⁷

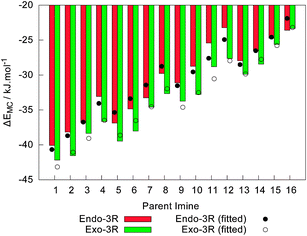Fig. 4 Variation of the relative energy at 0 K of the endo-3R and exo-3R molecular complexes, Δ_fE_MC, involving cyclopentadiene and the 16 iminium cations under scrutiny, together with the values obtained from the linear models depicted in eqn (1) and (2). All values are given in kJ mol⁻¹, using the energy of the free reactants as the reference, and include zero-point vibrational corrections.

The gas-phase geometry of these molecular complexes is characterised by the approach of C₍₁₎ and C₍₄₎ to N₍₂₎ and C₍₃₎, respectively, as shown in Fig. 5. An evaluation of the distances between C₍₁₎ and N₍₂₎, d_CN, and between C₍₃₎ and C₍₄₎, d_CC, may provide some insight into how the asynchronicity of iADA reactions arises, and how it is affected by sterically hindering either side of the imine reactant. Indeed, the four reaction pathways derived for each reactant pair behave in a manner that mirrors the degeneracies exposed previously. Taking I1-endo-3R-MC (Fig. 5a) as a comparative standard, d_CN and d_CC are 3.19 Å and 2.72 Å, respectively. When considering the other molecular complexes in the endo-3R approach, both distances increase with the sterical hindrance around the imine moiety according to

d^Endo_CC = 2.71 − 0.39σ^*_R1 − 0.16σ^*_R2 − 0.10E_S,R1, r_adj² = 0.9654 (3)

Fig. 5 Equilibrium geometries of the molecular complexes I1-endo-3R-MC (a), I1-exo-3R-MC (b), I16-endo-3R-MC (c), and I16-exo-3R-MC (d) at the X3LYP/6-31G(d) level of theory. Distances d_CN and d_CC are given in Angstrom.

This expression may lead to an erroneous assertion of dominance of the electronic over the steric parameters. However, the relative weights of σ^*_R1, σ^*_R2 and E_S,R1 in eqn (3) are 47.1%, 2.9% and 50.0%, respectively. Thus, this reveals an overall dominance of the steric factors in governing the geometry of these complexes. On the other hand, d_CN apparently follows the expression

d^Endo_CN = 3.14 − 0.75E_S,R1, r² = 0.9424 (4)

The relatively low r² obtained in this latter case is mostly due to the catastrophic behaviour of d_CC with respect to R₁. Indeed, d_CN appears be constant at around 3.27 ± 0.14 Å for R₁ = Me, Et and iPr, and 4.32 ± 0.05 Å for R₁ = tBu, as exemplified in Fig. 5a and c.

On the other hand, the molecular complexes that imply an exo approach show a gradual increase in both d_CC and d_CN with increasing sterical hindrance of the dienophile, giving rise to

d^Exo_CC = 2.71 − 0.14E_S,R1, r² = 0.9536 (5)

and

d^Exo_CN = 3.27 − 0.11σ^*_R2 − 0.40E_S,R1, r_adj² = 0.9965 (6)

The lower sensitivity of d_CC towards E_S,R1 is also illustrated in Fig. 5, which shows the d_CC and d_CN for the endo-3R and exo-3R molecular complexes involving the least and most sterically hindered iminium cations.

The charge transferred between CP and the imine in these molecular complexes (q_T = 1 − q_CP, where q_CP is the sum of effective atomic charges of the atoms belonging to CP) follows the same pattern of less intense interaction between the two reactants in the molecular complexes with increasing sterical hindrance in the dienophile. However, the charge transfer between the two reactants remains relatively constant across the different reaction pathways available for any given reactant pair. Under the NBO formalism, q_T varies from 0.218 ± 0.005e for the four molecular complexes involving I1-Im, to 0.112 ± 0.011e when considering the case of I16-Im. For the particular case of the endo-3R molecular complexes, this variation may be expressed as

q_T = 0.215 + 0.158σ^*_R1 + 0.081σ^*_R2 + 0.029E_S,R1, r_adj² = 0.9822 (7)

which again shows a dominance of R₁ over R₂. This conclusion is reinforced by the relative weights of σ^*_R1 (46.7%), σ^*_R2 (6.5%) and E_S,R1 (46.8%) in this model. Similar results were obtained using the other three reaction pathways.

3.3 Transition states

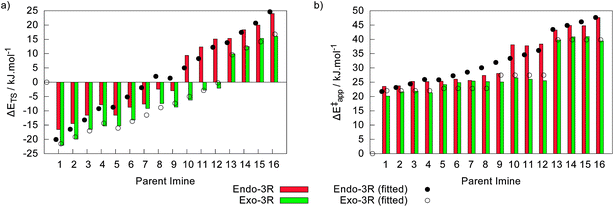
Starting from the geometry of the molecular complexes, a total of 64 transition states were found. Again, the two endo and the two exo pathways are degenerated within 2 kJ mol⁻¹, as was observed for their parent molecular complexes. Relative to the energy of their corresponding free reactants, ΔE_TS, these transition states spread over a large range from −22.0 kJ mol⁻¹ to +24.0 kJ mol⁻¹, as depicted in Fig. 6a. Taking the energy of their corresponding initial molecular complexes as the reference leads to the apparent activation energies (ΔE^‡_app) shown in Fig. 6b, which range from 20.1 kJ mol⁻¹ to 47.6 kJ mol⁻¹.

Fig. 6 Variation of the relative energies of the transition states for the endo-3R and exo-3R reaction paths involving cyclopentadiene and 16 protonated imines, taking the free reactants as reference (a); with their parent molecular complexes as reference (b), yielding apparent activation energies for both pathways.

Fig. 6a shows that the linear models devised for ΔE_TS behave slightly better than those developed for the formation of their respective molecular complexes. For the endo-3R transition states, this model takes the form

ΔE^Endo_TS = −20.05 − 112.90σ^*_R1 − 36.01σ^*_R2, r_adj² = 0.9359 (8)

with relative weights of 90.8%, and 9.2% for σ^*_R1, and σ^*_R2, respectively. At the same time, a similar model for the formation of the exo-3R transition states takes the form

ΔE^Exo_TS = −21.55 − 47.15σ^*_R1 − 23.94σ^*_R2 − 11.06E_S,R1, r_adj² = 0.9898 (9)

which translates into relative weights of 46.6%, 4.8% and 48.6% for σ^*_R1, σ^*_R2 and E_S,R1, respectively. Both Fig. 6 and the models described by eqn (8) and (9) suggest a strong preference for the exo, which apparently becomes more intense with increasing electron donating power of the group connected to the nitrogen atom of the protonated imine.

On the other hand, the step-like shape of the data in Fig. 6b yielded linear models with poor performances. Indeed, the linear model apparent energy barrier of the endo-3R pathway, ΔE^‡_app,endo = 21.742 − 36.12σ^*_R1 − 13.99σ^*_R2 − 7.01E_S,R1, only accomplishes a modest r_adj² = 0.9193 with a 95% significance level for σ^*_R1, σ^*_R2 and E_S,R1 (instead of the 99% criteria followed in the other models). The poor performance of this model is well illustrated in Fig. 6b. The linear model for ΔE^‡_app,exo was somewhat more successful (r_adj² = 0.9529), yielding the expression ΔE^‡_app = 22.03 − 11.56E_S,R1, which only depends on E_S,R1 at a 99% significance level. By comparing these two models to those described by eqn (8) and (9), we may postulate that the poor performance of the former may be due to inaccuracies when evaluating the energy of the molecular complexes.

Fig. 7 depicts the transition states of the endo-3R and exo-3R pathways for the cycloadditions involving I1 and I16. Following the trend observed in their parent molecular complexes (cf. Fig. 5), these structures are characterised by a strong approach between C₍₃₎ and C₍₄₎, with d_CC showing an average value of 2.01 ± 0.03 Å, while d_CN averages at around 2.87 ± 0.05 Å. At this stage, the asynchronicity of the reaction may be defined as the difference between d_CC and d_CN. This difference is depicted in Fig. 8, which shows a tendency for the exo pathways to be more asynchronous than their respective endo analogues. However, an important exception to this observation happens for R₁ = tBu, in which case the endo pathways become slightly more asynchronous than their exo counterparts.

Fig. 7 Equilibrium geometries of the transition states I1-endo-3R-TS (a), I1-exo-3R-TS (b), I16-endo-3R-TS (c), and I16-exo-3R-TS (d) and their respective imaginary (negative) frequencies, in cm⁻¹, at the X3LYP/6-31G(d) level of theory. Distances d_CN and d_CC are given in Angstrom.

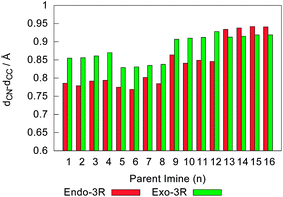Fig. 8 Asynchronicity, defined as d_CN − d_CC, in Angstrom, of the endo-3R and exo-3R pathways for the reaction between cyclopentadiene and each of the 16 iminium cations under study.

Starting from each transition state, all Intrinsic Reaction Coordinate (IRC) calculations converged to the expected minima in the PES, linking each transition state to both their respective final cycloadducts and parent molecular complexes, as exemplified in Fig. 9 for the endo-3R and exo-3R paths of the reactions involving I1-Im and I16-Im. The results show that the reaction involving I1-Im takes place along a shallower path than that involving I16-Im, and should therefore require milder conditions. Fig. 9 also presents the evolution of d_CC and d_CN along the reaction coordinate, thus revealing the asynchronicity of the bond formation process. Indeed, the C₍₃₎–C₍₄₎ bond achieves its final length within ζ = 2.5 a.u. of the transition state, in all cases considered (ζ representing the reaction coordinate). At this point, d_CN is between 1 Å and 1.5 Å larger than the final C₍₁₎–N₍₂₎ bond length. Moreover, d_CN increases its variation with respect to the reaction coordinate at about the same point where d_CC reaches its final values, thus suggesting that the C₍₁₎–N₍₂₎ bond formation process only takes place after formation of the C₍₃₎–C₍₄₎ bond. In the case of I1 (Fig. 9a and b), this point in the reaction coordinate presents a shoulder in the accompanying energy profile, which has been identified by Domingo and Szefczyk as a consequence of the asynchronous bond formation process.^38–40

Fig. 9 Energy profile and evolution of the d_CC and d_CN lengths along the Intrinsic Reaction Coordinate (IRC) for the CP + I1 system along the endo-3R (a) and exo-3R (b) reaction paths, as well as for CP + I16 along the endo-3R (c) and exo-3R (d) pathways. Graphics in the same row share the same scale for the right and left vertical axis, the inner scales being omitted for visual simplicity. The reaction coordinate, ζ, is presented in atomic units, the positive direction of ζ implying movement towards the formation of the products, and the transition state lying at ζ = 0 a.u.

The charge transferred between CP and the protonated imine moiety in these transition states appears to be relatively constant, with an average value of 0.480 ± 0.009e. These results may imply that the position of the transition state along the reaction coordinate, ζ, for iADA reactions may be dictated (or at least strongly influenced) by the amount of charge transferred from CP to the iminium cation. These results are in agreement with those collected from previous studies.^{6,9,10,41–43}

3.4 Final products

The equilibrium geometries of the final cycloadducts were found at the end of the IRC. The typical geometry of these compounds is illustrated by I1-endo-3R-Prod and I1-exo-3R-Prod (Fig. 10a and b, respectively). In all cases, d_CC and d_CN are almost invariant with respect to R₁ and R₂, both measurements averaging at about 1.57 Å.

Fig. 10 Equilibrium geometries of the products I1-endo-3R-PROD (a) and I1-exo-3R-PROD (b) at the X3LYP/6-31G(d) level of theory. In both pictures, the distances d_CC and d_CN are given in Angstrom.

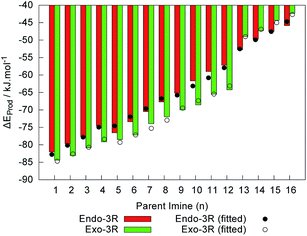
Previous studies have systematically reported the exo cycloadducts to be sterically less hindered, and thus thermodynamically more stable than their endo counterparts.^6,9,10,17,41 In this study, however, we noticed the endo products with R₁ = tBu to be slightly more stable than their exo analogues when considering their energy at 0 K relative to the free reactants, ΔE_Prod. These results are depicted in Fig. 11, and may be interpreted as a consequence of the preferred trans configuration of the parent iminium cations. Interestingly, this coincides with the greater asynchronicity found for the transition states leading to the endo adducts with R₁ = tBu (cf. Fig. 8). Moreover, the two linear models for ΔE^Endo_Prod and ΔE^Exo_Prod using Taft’s substituent constants fit well with the data obtained from the DFT calculations. These models are described by

ΔE^Endo_Prod = −82.76 − 79.01σ^*_R1 − 26.10σ^*_R2 − 4.25E_S,R1, r_adj² = 0.9907 (10)

and

ΔE^Exo_Prod = −84.70 − 44.09σ^*_R1 − 21.10σ^*_R2 − 14.59E_S,R1, r_adj² = 0.9968 (11)

Fig. 11 Relative energies, ΔE_Prod, of the 16 endo-3R and 16 exo-3R cycloadducts at 0 K relative to those of cyclopentadiene and their parent protonated alkyl alkylimineglyoxilate. All values are given in kJ mol⁻¹ and include zero-point vibrational corrections.

The quality of both models is patent in the values of r_adj², and can also be visually inferred from Fig. 11. Taking into consideration the variation of σ* and E_S, the relative weights for σ^*_R1, σ^*_R2 and E_S,R1 are respectively 50.8%, 6.2% and 43.0% for the model described by eqn (10), and 46.3%, 2.9% and 50.8% for the model in eqn (11). These results suggest that while the stability of the endo species is dominated by the polar effect of R₁, that of the exo species is more sensitive towards the steric effect of that same group. In Fig. 11 the crossover between the exo- and endo-preference of these reactions is shown. Such crossover suggests a conflict between the kinetic control of the reaction, which always prefers the exo paths (Fig. 6), and the thermodynamic control, which prefers the formation of endo cycloadducts given a strong enough electron donating or voluminous group, such as tBu. This prompts further exploration of the energies involved in the formation of the transition states and of their respective products by considering non-zero temperature and also possible effects of the solvent.

3.5 Temperature

The discussion of the effect of temperature in the iADA reactions under scrutiny will take place by analysing the variations in the relative enthalpies of the transition states (ΔH_TS) and of the final products (ΔH_Prod) relative to the enthalpy of the free reactants (CP + In-Im) at a given temperature. This is done mainly because the relatively high weight of the temperature in the Gibbs function may muffle the possibly more subtle effects of R₁ and R₂. Indeed, the entropic term, −TΔS, for these reactions raises linearly with T, reaching up to about 180 kJ mol⁻¹ at 298.15 K. Despite this, the differences in −TΔS between the endo-3R and exo-3R pathways are smaller than 6 kJ mol⁻¹ for the transition states, and smaller than 10 kJ mol⁻¹ for the final products. This accounts for a minute relative difference between pathways which may be discarded, especially when considering the plausible sources of error in the determination of the entropic terms.^44–47 Moreover, the use of relative enthalpies eases the comparison between the results presented in this work and the data published previously.^6,9,10

Fig. 12 shows the results from the four linear models which relate ΔH^Endo_TS, ΔH^Exo_TS, ΔH^Endo_Prod, and ΔH^Exo_Prod to Taft’s polar and polar substituent constants for R₁ and R₂ and also to the temperature. The equations behind these models involve only the temperature (T), σ^*_R1, σ^*_R2 and eventually E_S,R1. The coefficients of each descriptor variable, together with information on their respective weights and the final r_adj², are given in Table 1. Despite the excellent accord between the DTF model and the one derived from Taft’s parameters, shown in Fig. 12, the relative weight of the temperature in these models is small, and the four models may be considered as refined versions of those described by eqn (8)–(11).

Fig. 12 Plots of ΔH^Endo_TS (a), ΔH^Exo_TS (b), ΔH^Endo_Prod (c), and ΔH^Exo_Prod (d), calculated using DFT (at the X3LYP/6-31G(d)//X3LYP/6-311G(2df,2p) level of theory) and with the values fitted using the temperature and Taft’s substituent constants for R₁ and R₂ as descriptor variables.

Table 1 Coefficients and relative weights of T, σ^*_R1, σ^*_R2 and E_S,R1 as well as the final adjusted-r² for the linear models devised for ΔH^Endo_TS, ΔH^Exo_TS, ΔH^Endo_Prod, and ΔH^Exo_Prod, accounting for variations in R₁, R₂ and temperature

Variable	Coefficients				Rel. weights (%)
	ΔH^EndoTS	ΔH^ExoTS	ΔH^EndoProd	ΔH^ExoProd	ΔH^EndoTS	ΔH^ExoTS	ΔH^EndoProd	ΔH^ExoProd
Intercept	−19.4	−21.8	−82.9	−85.0
σ^*R1	−104.0	−44.9	−78.4	−42.1	89.1	45.6	49.1	44.8
σ^*R2	−35.4	−26.0	−25.6	−22.4	10.3	6.1	5.8	3.1
ES,R1	—	−10.5	−4.5	−14.9	—	47.5	41.9	49.6
T	−8.73 × 10^−3	−9.14 × 10^−3	−2.01 × 10^−2	−2.09 × 10^−2	0.6	0.7	3.2	2.5
radj^2	0.9484	0.9924	0.9915	0.9966

---

The results shown in Fig. 12 and Table 1 suggest that ΔH^Exo_Prod is slightly more sensitive towards T than ΔH^Endo_Prod. Because of this, it may be postulated that at high enough temperatures ΔH^Exo_Prod will eventually become smaller than ΔH^Endo_Prod, and both kinetic and thermodynamic controls will push the reaction towards the formation of the exo cycloadducts. However, for the reactions in this study for which R₁ = tBu, this crossover temperature is above T = 2500 K, which is beyond the limit of applicability of the model. Nevertheless, the model predicts some variation in the endo/exo selectivity with respect to the temperature, as observed by Kobuke et al.⁴⁸

3.6 Solvent effects

The energetic balance for the relative enthalpies of transition states and final products was evaluated at different temperatures, accounting for the effect of the solvent at fixed geometry. The selected solvents were chosen with the criteria of their relative permittivity being equal to or smaller than that of dichloromethane (ε = 8.93), as this is the largest value for which previous studies assure the validity of the gas-phase geometries.¹⁹ Alongside with Taft’s parameters for R₁ and R₂ and temperature, the variables used in the parameterisation of Tomasi’s PCM were used as descriptors for ΔH^Endo_TS, ΔH^Exo_TS, ΔH^Endo_Prod, and ΔH^Exo_Prod. These variables are: the solvent radius (r_solv), the relative permittivity (dielectric constant, ε), the thermal expansion coefficient (α), and the molar volume (V_M). Moreover, the gas-phase relative enthalpies were excluded from the model. Following the same stepwise backwards regression procedure outlined earlier, we arrived at four expressions for the relative enthalpies of the endo-3R and exo-3R transition states and products, which are summarised in Table 2.

Table 2 Coefficients, relative weights and final adjusted-r² for the linear models devised for ΔH^Endo_TS, ΔH^Exo_TS, ΔH^Endo_Prod, and ΔH^Exo_Prod, accounting for variations in R₁, R₂, temperature and solvent

Variable	Coefficients				Rel. weights (%)
	ΔH^EndoTS	ΔH^ExoTS	ΔH^EndoProd	ΔH^ExoProd	ΔH^EndoTS	ΔH^ExoTS	ΔH^EndoProd	ΔH^ExoProd
Intercept	157.9	136.7	147.6	142.6	—	—	—	—
σ^*R1	−37.0	−50.0	−28.3	−6.4	17.2	3.6	12.7	19.1
σ^*R2	−18.4	−58.9	−13.4	—	3.4	2.5	1.2	—
ES,R1	−38.3	−9.2	−6.3	−14.8	15.8	3.6	13.1	24.7
ES,R2	—	—	—	−21.1	—	—	—	0.8
T	−7.31 × 10^−2	0.366	−0.102	−0.0963	49.4	89.3	64.1	47.7
rsolv	−36.9	−36.9	−71.7	−68.6	10.1	0.7	3.4	2.9
α	−3.93 × 10^4	−3.92 × 10^4	−4.36 × 10^4	−4.45 × 10^4	4.1	0.3	1.9	1.8
VM	—	—	0.443	0.393	—	—	3.5	3.1
radj^2	0.9393	0.9707	0.9818	0.9890

---

Although not achieving an r_adj² as high as those shown in Table 1, the linear models described by the coefficients shown in Table 2 do present valuable information on how the polar and steric effects of R₁ and R₂, the temperature and the properties of the solvent interact. As shown in Fig. 13, the inclusion of solvent effects destabilises both transition states and products (cf. Fig. 12), effectively raising the energetic barrier posed by the transition states above the energy of the reactants, and giving positive effective activation enthalpies, which are expected from the experimental data.^{6,17,42,43,49} This effect becomes more evident with increasing temperature, and is particularly dramatic for the case of ΔH^Exo_TS, for which energetic barriers as high as 169.7 kJ mol⁻¹ are observed for the reaction between CP and I16-Im in CH₂Cl₂ at 298.15 K, thus effectively blocking this reaction pathway. On the other hand, the concurrent endo-3R pathway (for the same reaction) presents an activation enthalpy of only 18.5 kJ mol⁻¹ that decreases with increasing temperature, as demonstrated in the DFT calculations and determined by inspecting Table 2. As discussed previously, I16-Im forms endo cycloadducts that are energetically more stable than their exo analogues. This effect is further enhanced by increasing the temperature, as shown by the DFT calculations and mirrored by the corresponding models for ΔH^Endo_Prod and ΔH^Exo_Prod in Table 2. The use of a low polarity solvent such as CC1₄ may help in reducing the activation enthalpies and also making the overall reaction more exothermic; however, this effect affects both the endo and exo pathways in the same way and by approximately the same amount. Therefore, in solvent medium at non-zero temperature, a strong selectivity towards the formation of the endo isomers is expected for the CP + I16-Im system.

Fig. 13 Plots of ΔH^Endo_TS (a), ΔH^Exo_TS (b), ΔH^Endo_Prod (c), and ΔH^Exo_Prod (d), calculated using DFT (at the X3LYP/6-31G(d)//X3LYP/6-311G(2df,2p) level of theory) and with the values fitted using the temperature, Taft’s substituent constants for R₁ and R₂ and solvent descriptors as independent variables.

In summary, the characteristics of the solvent media will affect the energetics of both endo and exo pathways in the same manner, as can be inferred from Table 2. Thus, the effect of the solvent may be considered as an enhancement to that of the temperature, as seen by comparing the relative weights for the models delineated in Table 1 and 2 Moreover, the relative weights portrayed in Table 2 show that the combined effect of the solvent and temperature overcomes the polar and steric effects of R₁ and R₂, giving an overall kinetic preference for the formation of endo cycloadducts, despite the general thermodynamic preference towards the formation of their exo counterparts (within the range of electron donating power and steric hinderance explored in this work and with the already mentioned exception of R₁ = tBu). This balance between the kinetic control and thermodynamic preference of the diene/dienophile system is at the heart of the selectivity of the iADA reaction^3,50 and can be modelled using DFT^9,10,17,23 or, as proven in this work, with a combination of Taft’s substituent parameters and some characteristics of the solvent, in particular r_solv and α.

4 Conclusions

This work offers a cross-validation of the already known DFT model for iADA reactions in solvent media at different temperatures using a combination of Taft’s polar and steric substituent constants, as well as easily available data describing the intended solvent. The results show that the outcomes from the DFT calculations are acceptably described as a linear combination of such empirical constants. The relevance of these findings is two-fold: from the computational point of view, the results offer some insight into the possible weaknesses of the current model, mainly the possible poor description of the initial molecular complexes. The results should also entice the exploration of the relaxed geometries of the relevant stationary points of the PES when accounting for different solvents (both implicitly and explicitly). At the same time, these results open the possibility of screening a large range of iADA reactions with different combinations of R₁, R₁ and solvent at different temperatures. This may prove to be a valuable tool when optimising the synthesis procedure for a particular compound.

Acknowledgements

This work has been supported by the Fundação para a Ciência e Tecnologia (FCT) through Grant UID/QUI/50006/2013 (LAQV-REQUIMTE). FT also benefited from a Post Doctoral Grant with reference INCENTIVO-LA6-2014/ASM/2 (FCT).

References

1. G. Masson, C. Lalli, M. Benohoud and G. Dagousset, Chem. Soc. Rev., 2013, 42, 902–923.
2. D. C. Limburg, B. E. Thomas IV, J. Li, M. Fuller, D. Spicer, Y. Chen, H. Guo, J. P. Steiner, G. S. Hamilton and Y. Wu, Bioorg. Med. Chem. Lett., 2003, 13, 3867–3870.
3. M. G. Memeo and P. Quadrelli, Chem.–Eur. J., 2012, 18, 12554–12582.
4. I. T. Horváth and P. T. Anastas, Chem. Rev., 2007, 107, 2169–2173.
5. D. Bhuyan, R. Sarma, Y. Dommaraju and D. Prajapati, Green Chem., 2014, 16, 1158–1162.
6. J. E. Rodríguez-Borges, X. García-Mera, F. Fernandez, V. H. C. Lopes, A. L. Magalhães and M. N. D. S. Cordeiro, Tetrahedron, 2005, 61, 10951–10957.
7. L. R. Domingo, E. Chamorro and P. Pérez, J. Phys. Chem. A, 2008, 112, 4046–4053.
8. B. Szefczyk, T. Andrunów and W. A. Sokalski, J. Mol. Model., 2008, 14, 727–733.
9. F. Teixeira, J. E. Rodríguez-Borges, A. Melo and M. N. D. S. Cordeiro, Chem. Phys. Lett., 2009, 447, 60–64.
10. F. Teixeira, A. Melo and M. N. D. S. Cordeiro, Comput. Theor. Chem., 2013, 1012, 54–59.
11. L. R. Domingo and P. Perez, Phys. Chem. Chem. Phys., 2014, 16, 14108–14115.
12. L. R. Domingo, J. Chil. Chem. Soc., 2014, 59, 2615–2618.
13. R. Jasinski, Comput. Theor. Chem., 2014, 1046, 93–98.
14. L. R. Domingo, M. Ríos-Gutiérrez and P. Pérez, Tetrahedron, 2015, 71, 2421–2427.
15. A. Zeroual, A. Benharref and A. El Hajbi, J. Mol. Model., 2015, 21, 1610–2940.
16. C. D. D. Rosa, P. M. Mancini, M. N. Kneeteman, A. F. L. Baena, M. A. Suligoy and L. R. Domingo, J. Mol. Struct., 2015, 1079, 47–53.
17. J. E. Rodríguez-Borges, S. Gonçalves, M. L. do Vale, X. García-Mera, A. Coelho and E. Sotelo, J. Comb. Chem., 2008, 10, 372–375.
18. L. Stella, H. Abraham, J. Feneau-Dupont, B. Tinant and J. P. Declerq, Tetrahedron Lett., 1990, 31, 2603–2606.
19. L. R. Domingo, Tetrahedron, 2002, 58, 3765–3774.
20. R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516.
21. L. R. Domingo, M. J. Aurell, P. Pérez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423.
22. J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218.
23. Y. Li and D.-C. Fang, Phys. Chem. Chem. Phys., 2014, 16, 15224–15230.
24. D. Datta, J. Phys. Org. Chem., 1991, 4, 96–100.
25. P. N. Craig, J. Med. Chem., 1971, 14, 680–684.
26. X. Xu and W. A. Goddard III, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677.
27. A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5649.
28. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
29. P. Culot, G. Dive, V. H. Nguyen and J. M. Ghuysen, Theor. Chim. Acta, 1992, 82, 189–205.
30. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.9, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2009, http://www.chem.wisc.edu/nbo5.
31. B. Mennucci, J. Tomasi, R. Cammi, J. R. Cheeseman, M. J. Frisch, F. J. Devlin, S. Gabriel and P. J. Stephens, J. Phys. Chem. A, 2002, 106, 6102–6113.
32. R. Core Team, R.: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2013.
33. F. Teixeira, R. A. Mosquera, A. Melo, C. Freire and M. N. D. S. Cordeiro, Phys. Chem. Chem. Phys., 2014, 16, 25364–25376.
34. J. W. Johnson, Multivariate Behav. Res., 2000, 35, 1–19.
35. C. A. Sousa, M. L. C. do Vale, J. E. Rodríguez-Borges, X. García-Mera and J. Rodríguez-Otero, Tetrahedron Lett., 2008, 49, 5777–5781.
36. F. Jensen, Introduction to Computational Chemistry, John Wiley & Sons Ltd, Chichester, England, 2nd edn, 2007.
37. E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, 1st edn, 2006.
38. B. Szefczyk, W. A. Sokalski and J. Leszczynski, J. Chem. Phys., 2002, 117, 6952–6958.
39. L. R. Domingo, M. Arnó and J. Andrés, J. Org. Chem., 1999, 64, 5867–5875.
40. L. R. Domingo, J. Org. Chem., 1999, 64, 3922–3929.
41. Y. B. Ruiz-Blanco, M. J. Alves, J. E. Rodriguez-Borges and R. Molina, J. Chil. Chem. Soc., 2013, 58, 2243–2247.
42. X. García-Mera, M. J. Alves, A. Goth, M. L. do Vale and J. E. Rodríguez-Borges, Tetrahedron, 2013, 69, 2909–2919.
43. X. García-Mera, J. E. Rodríguez-Borges, M. L. C. Vale and M. J. Alves, Tetrahedron, 2011, 67, 7162–7172.
44. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
45. F. Teixeira, A. Melo and M. N. D. S. Cordeiro, J. Chem. Phys., 2010, 133, 114109.
46. R. L. Jacobsen, R. D. Johnson III, K. K. Irikura and R. N. Kacker, J. Chem. Theory Comput., 2013, 9, 951–954.
47. K. K. Irikura, R. D. Johnson III and R. N. Kacker, J. Phys. Chem. A, 2005, 109, 8430–8437.
48. J. Furukawa, Y. Kobuke and T. Fueno, J. Am. Chem. Soc., 1970, 92, 6548–6553.
49. M. J. Alves, X. García-Mera, M. L. C. do Vale, T. P. Santos, F. R. Aguiar and J. E. Rodríguez-Borges, Tetrahedron Lett., 2006, 47, 4594–4597.
50. E. Caballero, J. Figueroa, P. Puebla, R. Peláez, F. Tomé and M. Medarde, Eur. J. Org. Chem., 2008, 2008, 4004–4014.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra08307a

---