Prediction of novel crystal structures and superconductivity of compressed HBr

Abstract

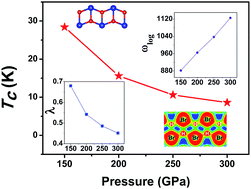
The crystal structures of HBr under high pressure have been explored systematically using the particle swarm optimization method. Two new stable structures (I4̄2d and C2/m) were predicted above 100 GPa which have lower energies than the previously suggested P1̄ structure. A sequence of phase transitions from molecular to cluster, to chain, and then to the atomic phase was revealed. Enthalpy and phonon calculations affirm the thermodynamic stability of the high-pressure polymorphs. Significantly, both high pressure phases (C2/m and Pmmn) were found to be superconducting with a maximum critical temperature close to 30 K at 150 GPa. The present results provide a clear high-pressure transformation pathway that helps to understand the structural evolution and superconductivity of highly compressed HBr.

---

Introduction

It has been suggested that solid hydrogen (H₂) will transform to a metallic state and possess a very high superconducting critical temperature at very high pressure.¹ So far, this suggestion has not been realized and the most recent experiment shows solid hydrogen is not metallized up to a pressure of 342 GPa.² The very high pressure expected for the metallization of hydrogen has led to an alternate suggestion. It was proposed, if the hydrogen atoms can be pre-compressed in a hydrogen-rich molecular solid to the desirable density, high temperature superconductivity will also be possible. This proposal has led to recent focus on compressed hydrides as the metallization pressure of these hydrogen-rich compounds are expected to occur at much lower pressures.³ In fact, superconductivity has reported on compressed silane⁴ and hydrogen sulphide.^5–7 However, the origin and structure of the superconducting phase has not been fully characterized. At ambient pressure, HBr is a molecular crystal solid with strong hydrogen bonds. An experiment study has established a sequence of phase transitions under pressure.⁸ At low pressure, the hydrogen bonds between HBr molecules are very weak and resulted in the orientationally disordered molecular phases phase I and phase II at high temperatures.⁹ At low temperature phase III was stable and found to transform into phase IV at 26 GPa with symmetric hydrogen bonds. The experimental sequence was examined by theoretical calculations by Zhang et al.¹⁰ It was predicted that phase IV should transform to a P1̄ structure at 58 GPa. Eventual dissociation of HBr into solid H₂ and Br₂ was suggested at about 150 GPa. Later, another first-principle calculation predicted yet a new high-pressure structure with P2₁/m symmetry is stable from 134 GPa to 196 GPa and the structure will become unstable and decompose into the molecular fragments at higher pressure.¹¹

The conflicting theoretical results are puzzling. Compound with a lack of experimental information at high pressure the structural stability and whether HBr will dissociate into the molecular components are still not clear. Stimulated by a recent experiment report that a very high superconducting critical temperature T_c of about 190 K was found in hydrogen sulphide (H₂S) at ∼200 GPa (ref. 5) has motivated us to search for the structures and potential superconductivity property of HBr. In this paper, using the particle swarm optimization (PSO)^12,13 method, two previously unknown stable forms (I4̄2d and C2/m) are found above 100 GPa. These two new phases have different structures and electronic properties. The results also show that molecular HBr is stable with respect to dissociation into molecular fragments at least up to 300 GPa. Most significantly, the predicted structures (C2/m and Pmmn) are found to be superconductors with critical temperature range from 10–30 K at and above 150 GPa. The new information helps to revise the zero-temperature diagram of HBr.

Results

The PSO method implemented in the CALYPSO code was used in this study. This technique has been demonstrated to be successful for the prediction global minimum energy structures on variety systems at ambient and high pressure.^14–18 The structure models employed here consist of up to eight HBr and a population of 50 trial structures. Structure search were performed at 20, 50, 100, 200 and 300 GPa. The convergence criterion is that once a lowest enthalpy structure was found and no new structures emerge after 30 successive generations then the calculation is terminated. We started the structure search at 20 GPa. The experimental phase IV Cmcm structure was reproduced readily. At 100 GPa, a new stable structure with I4̄2d symmetry and 8 f.u. per unit cell was found. At lower pressure, the energy of this structure is competitive with the P1̄ structure proposed by Zhang et al.¹⁰ but became the most stable phase above 100 GPa. This structure is consisted of 2D layers and in each layer, the H and Br atoms formed rectangular chains built from [Br–H–Br] units. H atoms are found to situate at the middle of two Br atoms leading to symmetric hydrogen bonds. Another new structure with C2/m symmetry was discovered upon further compression to 125 GPa. In this structure, each H atom is bonded to three Br atoms, showing a denser packing in the I4̄2d structure. There is a large volume reduction associated with the phase transition that helps to increase the stability owing to the favourable PV (P-pressure and V-volume) work. We have also found a structure with Pmmn symmetry and 4 atoms per unit cell. At 300 GPa, the enthalpy of this structure is only 9 meV f.u.⁻¹ higher than the C2/m structure. Since this is a metastable structure we will not discuss the structure and the properties in detail. However, it is noteworthy that this again has layer structure of puckered 2D-square nets formed from edge-shard H–Br units [Fig. S1†]. The theoretical results reported here disagree with a previous theoretical calculation suggesting HBr will become unstable and dissociate into solid H₂ and Br₂ above 150 GPa. To quantify the condition for the dissociation into solid H₂ and Br₂, we calculated and compare enthalpy of the various predicted structures relative to H₂ and Br₂ in Fig. 1. It is shown that molecular HBr is stable and will not dissociate at least up to a pressure of 300 GPa. This observation brings a new perspective to the stability of molecular HBr and the structural evolution at high pressure. In addition, as will be shown below the implication to superconductivity behaviours.

Fig. 1 The enthalpy curves of candidate structures relative to Cmcm phase of HBr as a function of pressure.

Discussion

To gain insight into the hydrogen-bond symmetrisation and chemical bonding in the new high-pressure HBr structures, we have computed the electron localization function (ELF). The topological analysis of ELF is commonly used to determine the degree of electron localization and, therefore, the tendency to form two electron covalent bonds in molecules and solids. Represented in a convenient scale, ELF = 1 corresponds to perfect localization and at the low limit ELF = 0.5 reflects the behaviour of a homogeneous electron gas. The contour plots of the ELF for P1̄, I42d̄ and C2/m structures are shown in Fig. 2a–c. At 100 GPa, the relatively high ELF value of a 0.8 indicates strong covalent bonds between H and Br atoms showing HBr is still a molecular phase. The P1̄ structure formed from perfect squares of (HBr)₄ with symmetric H-bond and linear H–Br–H bonds. In comparison, the energetically competitive I4̄d structure, HBr molecules form a 1D zigzag chain, again with the H atoms situated symmetrically between two Br atoms. A usual feature of this structure is the H–Br–H angle less than 90° (86°) and that the Br atoms are pushed closer to each other. At 300 GPa, the symmetric hydrogen bond structure in no longer favourable and it transformed to a new C2/m structure (Fig. 2c) consisted of 1D-ribbons formed by corner sharing H–Br units. The H–Br–H angles of 71° deviated significantly from 90°. The ELF plot (Fig. 2c) shows the H–Br bond has weaken significantly and the H and Br are close to an atomic solid.

Fig. 2 P1̄ phase and ELF at 100 GPa (a), I4̄d phase and ELF at 100 GPa (b), C2/m phase and ELF at 200 GPa (c).

To investigate the electronic states, band structures for the P1̄, I4d̄, C2/m and Pmmn structures were calculated and compared in Fig. 3 and S3† (Pmmn). The results show I4d̄, C2/m and Pmmn (Fig. S3†) are metallic phases. The projected density of states shown in Fig. 3 show the P1̄ structure at 100 GPa is a semi-metal with an indirect band closure at Γ and K. In contrast, the I4̄d structure is a genuine metal with parabolic dispersive bands crossing the Fermi surface. The layer structure is clearly highlighted by the flat bands along the X → P direction. The band structure of the C2/m structure is quite different from the other two structures. Two bands cross the Fermi level. The band dispersions along the A–P–Z symmetry axis and close to the zone center (Γ) are relativity flat. This resulted in a high electronic density states at the Fermi energy (Fig. 3c). In comparison, the band dispersion along Z–M–A and P–Z–V directions are parabolic-like and cross the Fermi level with steep slopes indicating mobile electrons along these symmetry directions. The co-existence of electrons with large effect masses (flat band) and itinerant electrons with high mobility (steep bands) is suggested of superconducting behaviour.

Fig. 3 The calculated electronic band structure and partial density of states of P1̄ (a), I4̄d (b), and C2/m (c).

Phonon calculations reveal no imaginary frequency in all the predicted phases (I4̄d, C2/m and Pmmn), indicating they are dynamically stable. Phonon band structures and projected density of vibration states (PVDOS) within the stable pressure range of these structures are shown in Fig. 4 and S4† To examine possible superconductivity, the Eliashberg spectral functions α²F(ω) of the I4̄2d, C2/m and Pmmn structures at 100 GPa, 200 GPa and 300 GPa were calculated and the results are depicted in Fig. 4b and S4† (Pmmn). At 150 GPa (Fig. 4b), the electron–phonon coupling parameter (λ) for the C2/m structure is 0.67 with an average phonon frequency ln(ω) of 960 K. Using the Allen Dynes equation,¹⁹ which is an extension of the McMillan theory,²⁰ with a nominal Coulomb pseudopotential parameter (μ*) of 0.12 the estimated superconducting critical temperature T_c is 24.8 K. We have performed addition calculations to investigate the pressure dependence of the superconductivity of the C2/m structure.

Fig. 4 The phonon spectrum, phonon density of states and Eliashberg phonon spectral function for phase I4̄d (top) and C2/m (bottom). Red solid circles in (bottom) show the electron–phonon coupling with the radius proportional to their respective strength.

As shown in Fig. 5, the calculated λ decreases with increasing pressure but the average frequency increases, as expected. However, the predicted T_c dropped from 28.4 K at 150 GPa to 15.7 K at 200 GPa. This is mainly due to the fact that λ has decreased from 0.67 at 150 GPa to 0.54 at 200 GPa and then to 9.8 K at 300 GPa. The origin of the superconductivity can be traced back by a comparison of the calculated Eliashberg spectral function (α²F(ω)) and the PVDOS. As shown in Fig. 4b, 39% of the electron–phonon coupling is contributed by low-frequency vibrations in the region 100 to 400 cm⁻¹, which are mostly the vibrations of the Br atoms. The remained 61% derived from high-frequency vibrations from 900 to 1600 cm⁻¹ which are predominately H–Br stretch and H–Br–H bend modes. The superconducting critical temperature of 28.4 K at 150 GPa can be compare to 39 K in MgB₂.²¹ We further analyse the coupling parameters at each q-point in the Brillouin zone (Fig. 4b). It is clear that the dominant electron–phonon couplings are along the Z–Γ direction. We have also examined possible superconducting in the I4̄d phase. The results show the I4̄d phase is indeed superconducting but the T_c is close to zero at 100 GPa as the electron–phonon coupling parameter (λ < 0.4) is very small. Our calculation also suggested the superconductivity in Pmmn phase with a T_c of 24 K at 300 GPa.

Fig. 5 Superconducting temperature (T_c) vs. pressure. The coupling parameters, the average phonon frequencies ω_ln and superconducting temperatures of C2/m phase for HBr as a function of pressure.

Computational details

The structural searches were performed using the particle swarm optimization method implemented in the CALYPSO program. Structural optimizations, enthalpies, and electronic structures calculations were carried out with the Vienna ab initio simulation (VASP)^22–24 program and projector-augmented planewave (PAW)^25,26 potentials employing the Perdew–Burke–Ernzerhof (PBE)²⁷ functional. The valence configurations for the H and Br potentials are 1s¹ and 4s²4p⁷, respectively. A planewave basis set with an energy cutoff of 1000 eV was used. Dense k-point meshes were employed to sample the first Brillouin zone (BZ) to ensure the energies are converged to within 5 meV per atom. The elements of the interatomic force constant (IFC) and electron–phonon coupling (EPC) matrices were computed using the linear response method with a 5 × 5 × 3 q-point mesh and 20 × 20 × 12 k-point mesh for the first Brillouin zone integrations.²⁸

Conclusions

In summary, we have investigated systematically the phase transitions of solid HBr under high pressure using the PSO technique in combination with first-principle electronic structure calculations. Several interesting structures were uncovered above 100 GPa. Contrary to previous studies, we predicted that HBr did not dissociate into molecular H₂ and Br₂ at 150 GPa. Instead, the theoretical results indicated solid HBr is thermodynamics stable up to 300 GPa. The calculations also show the new phases are metallic and superconductive. Electron–phonon coupling calculations show C2/m and Pmmn structures are good superconductors. The results presented established a progressively dense pack HBr structure with increase pressure: starting from the low pressure molecular phase I and II, to isolated and centrosymmetric H-bond (HBr)₄ squares in the P1̄ structure, then progress to 1D zigzag chains followed by 1D ribbons and eventually at the highest pressure studied, a 2D puckered square-net. In all the structures, there is no segregation of H and Br. However, hints on the formation of the atomic phases are found in the C2/m and Pmmn structures. The results presented here had provided a new perspective on stability and superconducting behaviour of compressed solid HBr.

Acknowledgements

This work was supported by the National Science Foundation of China (51373065, 91123031 and 21221063), the National Basic Research Program of China (2012CB933800), and Specialized Research Fund for the Doctoral Program of Higher Education (20130061130010). Part of the calculations has been performed by the use of computing resources provided by WestGrid and Compute Canada. Hanyu Liu and John S. Tse acknowledge the National Science Foundation of CHINA (11474126) and support from the University of Saskatchewan research computing group and the use of the HPC resources (Plato machine).

References

1. N. W. Ashcroft, Phys. Rev. Lett., 1968, 21, 1748.
2. C. Narayana, H. Luo, J. Orloff and A. L. Ruoff, Nature, 1998, 393, 46.
3. N. Ashcroft, Phys. Rev. Lett., 2004, 92, 187002.
4. M. Eremets, I. Trojan, S. Medvedev, J. Tse and Y. Yao, Science, 2008, 319, 1506.
5. A. Drozdov, M. Eremets and I. Troyan, arXiv preprint arXiv:1412.0460, 2014.
6. Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, J. Chem. Phys., 2014, 140, 174712.
7. D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968.
8. K. Aoki, E. Katoh, H. Yamawaki, M. Sakashita and H. Fujihisa, Phys. B, 1999, 265, 83.
9. M. Ito, M. Suzuki and T. Yokoyama, J. Chem. Phys., 1969, 50, 2949.
10. L. Zhang, Y. Wang, X. Zhang and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014108.
11. D. Duan, F. Tian, Z. He, X. Meng, L. Wang, C. Chen, X. Zhao, B. Liu and T. Cui, J. Chem. Phys., 2010, 133, 074509.
12. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
13. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063.
14. X. Wang, Y. Wang, M. Miao, X. Zhong, J. Lv, T. Cui, J. Li, L. Chen, C. J. Pickard and Y. Ma, Phys. Rev. Lett., 2012, 109, 175502.
15. L. Zhu, Z. Wang, Y. Wang, G. Zou, H.-k. Mao and Y. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 751.
16. J. Lv, Y. Wang, L. Zhu and Y. Ma, Phys. Rev. Lett., 2011, 106, 015503.
17. L. Zhu, H. wang, Y. Wang, J. Lv, Y. Ma, Q. Cui, Y. Ma and G. Zou, Phys. Rev. Lett., 2011, 106, 145501.
18. H. Liu, H. Wang and Y. Ma, J. Phys. Chem. C, 2012, 116, 9221.
19. R. D. P. B. Allen, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 905.
20. R. Dynes, Solid State Commun., 1972, 10, 615.
21. J. Nagamatsu, N. Nakagawa, T. Muranaka and Y. Zenitani, Nature, 2001, 410, 63.
22. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
23. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
24. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
25. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
26. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
28. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni and D. Ceresoli, J. Phys.: Condens. Matter, 2009, 21, 395502.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra06998j

---