Influence of lamellar structure on the stress–strain behavior of β nucleated polypropylene under tensile loading at elevated temperatures
Tong Wu,
Ming Xiang,
Ya Cao,
Jian Kang and
Feng Yang*
State Key Laboratory of Polymer Materials Engineering, Polymer Research Institute of Sichuan University, Chengdu 610065, People's Republic of China. E-mail: yangfengscu@126.com
First published on 8th May 2015
Abstract
In this article, five β nucleated polypropylene (β-iPP) cast films were prepared through crystallizing from 110 °C to 135 °C. The differential scanning calorimetry (DSC), wide-angle X-ray diffraction (WAXD) and scanning electron microscopy (SEM) results show that all the five β-iPP samples had similar crystallinity, a high content of β-crystals but different β-lamellae distribution. Then the stress–strain behaviors of β-iPP at elevated temperatures were investigated in detail. We found that the slight difference in the β-lamellae distribution in β-iPP would affect the stress–strain behavior of β-iPP significantly. Based on the characterization of the morphological evolutions during stretching by 2D-WAXD and SEM, it is concluded that the β-iPP sample whose β-lamellae content along the flow direction was higher than that of the transverse direction would form a coarse fibrillar structure after longitudinal stretching and thus result in a low strain-hardening modulus. However, the β-iPP precursor film crystallizing at 126 °C, whose β-lamellae distribution with different angles to the tensile axis is most uniform, produced highly oriented fibrils and a homogeneous distribution of cavities, leading to the highest strain-hardening modulus and the narrowest pore size distribution after biaxial stretching.
1. Introduction
The stress–strain behaviors of semi-crystalline polymers under tensile loading have been extensively studied in the past. From the conventional viewpoint, the tensile behavior of semi-crystalline polymers could be regarded as stretching of the interpenetrated network of crystalline blocks. At sufficiently low stress and strain, the polymeric material behaves as a linear elastic solid. The Young's modulus and the elastic limit are intimately related to the initial morphology such as the degree of crystallinity and the lamellar alternating structure within spherulites. Further extension above the elastic limit causes the destruction of spherulites or stacked lamellae and indicates the onset of permanent plastic deformation, resulting in a local maximum in the conventional stress–strain curve which is called the yield point. Beyond the yield point, large scale plastic deformation occurs and a concave contraction then catastrophically initiates on the specimen and coalesces into a well-defined neck; meanwhile, a plateau origins in the nominal stress–strain curves. During necking processes, which is also called ‘cold drawing’, isotropic spherulitic structure transforms into anisotropic fibrillar one, accompanied by the fragmentation and/or rearrangement of the stacked lamellae. With further deformation, after the necking region has propagated throughout the whole length of the specimen, an abrupt increase in nominal stress appears up until break. This phenomenon is called “strain-hardening”. The stress–strain behavior of a semi-crystalline polymer depends on the crystalline morphology such as degree of crystallinity, stacked lamellar cluster, and spherulitic superstructure.1–20Isotactic polypropylene (iPP) is a typical polymorphic material with several crystal modifications, i.e. the monoclinic α form, hexagonal β form and the triclinic γ form.14,21,22 It has been widely reported that stretching β nucleated polypropylene (β-iPP) at low temperature results in a β to smectic transformation, while at higher drawn temperature (>55 °C), β to α transformation occurs.5,6,10,22–28 In our previous paper,29 we studied the influence of lamellar structure on stress–strain of β-iPP under tensile loading at room temperature. We first discovered a peculiar double yield phenomenon in stretching β-iPP and declaimed that a narrower β-lamellar thickness distribution would result in a delayed occurrence of second yield point under tensile loading and a more uniform pore size distribution in the microporous membranes made from β-iPP. Shi et al.27 studied the stress–strain curves of β-iPP and α-iPP at elevated temperatures and found that the β-iPP has a lower strength and a lower yield drop than α-iPP; moreover, the strain-hardening of β-iPP occurred much earlier than that of α-iPP. All these finding could be related to the observation of a more homogeneous deformation of β-iPP sample. Cai2 investigated the uniaxial drawing-induced deformation β-iPP at varying temperatures and discovered the lateral expansion of the β-iPP samples with tension in the elastic deformation stage before the yield point. They ascribed this phenomenon to the rotation of parent and daughter lamellae from initial 40° or 140° to close to 90°. However, they only focused on the stress–strain behaviors of β-iPP at small strains. Up to now, the stress–strain behaviors of β-iPP at elevated temperature under tensile loading have not been investigated systematically.
In this present study, five β-iPP samples consisting almost pure β-crystals were prepared through crystallizing at a wide temperature range (Tc) from 110 °C to 135 °C, since studies on crystallization of β-iPP have compared the growth rates of α and β crystals as a function of temperature within a temperature window of 105–140 °C, where the growth rate of β crystals is faster than that of α crystals.30,31 Then the uniaxial tensile testing at different temperatures was performed to investigate the stress–strain curves of β-iPP comprehensively.
2. Experimental
2.1. Materials and sample preparation
A commercially available iPP, T38F, with a melt flow rate (MFR) of 2.9 g/10 min (230 °C, 2.16 kg), Mw = 3.8 × 105 g mol−1 and Mw/Mn = 4.7, was purchased from Petroleum Chemical Incorporation (Lanzhou, China). A highly active β-nucleating agent, NAB-83, was supplied by GCH Technology Co., Ltd (Guangzhou, China).A master batch containing 5 wt% NAB-83 in iPP was prepared by melt blending; then the master batch and pure iPP were extruded to produce β-iPP specimens containing 0.3 wt% NAB-83 on a twin crew extruder. The pelletized granules were subsequently extruded into β-iPP cast films through a Hapro single screw extruder (Rheometer 200C) fitted with a slit die of 0.5 mm × 100 mm (thickness × width) and a three-roll calender. The extrusion was carried out at 220 °C and five cast films were prepared by getting into contact with the surface of rolls maintained at 110 °C (PP-110), 120 °C (PP-120), 126 °C (PP-126), 130 °C (PP-130), and 135 °C (PP-135).
2.2. Measurements
A sequential biaxial stretching was performed in the tensile testing machine to obtain porous membranes, comprising the longitudinally stretching to 200% at 90 °C and then transversely stretching to 200% at 115 °C.28,32–34
 | (1) |
The overall crystallinity, Xc,XRD, was calculated according to the following equation:35,36
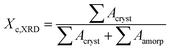 | (2) |
3. Results and discussion
3.1. Characterization of precursor films
Thermal and X-ray techniques were employed to provide insight about the populations of crystals in the five β-iPP precursors, and several key properties arising from the crystallinity are presented in Table 1. Owing to the melt-recrystallization that occurs in β-iPP during the heating DSC scan, the calculated crystallinity (XDSC) and content of β-crystals (Kβ,DSC) may not be reliable. Thus, it is more practical to use WAXD measurement to track these properties individually. The WAXD spectra in Fig. 1a disclose that all the five samples exhibited two characteristic diffraction peaks at 2θ = 16.1° and 21.2° which correspond to the respective (300) and (301) crystal plane of β-form, and the diffraction peaks at 14.1°, 16.9°, and 18.6° which correspond to the α (110), α (040), and α (130) were undetectable, indicating that all the five samples were composed of almost pure β-crystals.31,35,36 Additionally, the crystallinity (XDSC and XWAXD) of these precursors with different Tc were nearly the same. However, their thermodynamic behaviors (shown in Fig. 1b) differed considerably. The first heat flows of these precursor films showed distinct melting peaks for β and α endotherms. Since the WAXD results have proven that the contents of β-crystals in these five samples were higher than 99.0%, the melting peaks of α-crystals were originated from the melting-recrystallization of unstable β-crystals.31,38,39 The Kβ,DSC, obtained from DSC, increased dramatically from 69.2% (PP-110) to 91.0% (PP-135), which implies that the stability of β-crystals improves with increasing Tc. Furthermore, the sample PP-110 exhibited double β peaks, seen in the form of β1 and β2, which are typical of polymorphic β-iPP and result from the instability of the β1 crystals formed at high cooling rates and propensity to recrystallize to β2, providing additional evidence that the β-crystal formed at Tc = 110 °C was least stable. Moreover, the melting temperature of β-crystals (Tmβ) ascended monotonously from 143.6 °C (PP-110) to 153.1 °C (PP-135), indicating that the β-lamellar thickness increases with elevating Tc. More interestingly, the full width of β melting peak at half maximum (FWHM), which is related to β-lamellar thickness distribution, decreased markedly from 11.2 °C (PP-110), through the minimum 3.9 °C (PP-126), finally reaching 5.2 °C (PP-135), implying that the precursor crystallizing at 126 °C has the narrowest lamellar thickness distribution.| Samples | Tmβb (°C) | FWHMb (°C) | XDSCb (%) | XXRDa (%) | Kβ,DSCb (%) | Kβ,XRDa (%) |
|---|---|---|---|---|---|---|
| a Crystallinity and the relative amount of the β phase were calculated by WAXD.b Crystallinity and melting temperature were measured by DSC. | ||||||
| Tc = 110 °C | 143.6 | 11.2 | 44.8 | 54.2 | 69.2 | >99.0 |
| Tc = 120 °C | 146.7 | 4.6 | 46.4 | 54.9 | 80.0 | >99.0 |
| Tc = 126 °C | 149.0 | 3.9 | 46.7 | 55.3 | 88.9 | >99.0 |
| Tc = 130 °C | 150.7 | 5.0 | 46.0 | 55.7 | 90.2 | >99.0 |
| Tc = 135 °C | 153.1 | 5.2 | 48.6 | 57.1 | 91.0 | >99.0 |
In order to gain the direct evidence of the crystalline structures, the micrographs of five etched β-iPP samples were examined by SEM (shown in Fig. 2). Apparently, all these β-iPP were composed of “bundle-like” lamellae without fully developed spherulite which distributed randomly in the cast films. Since the tie chains are less abundant in β-iPP than in α-iPP, the etching acid is much easier to permeate into the amorphous region of β-iPP than that of α-crystals with interlocked structure.31 Furthermore, it is clear to see that the β-lamellae thickened gradually with increasing Tc, which was consistent with the trend of Tmβ in Table 1.
 | ||
| Fig. 2 SEM images of β-iPP samples after etched: (a) PP-110; (b) PP-120; (c) PP-126; (d) PP-130; (e) PP-135. | ||
Furthermore, the 2D-WAXD technique was performed to detect the β-lamellar orientation of five β-iPP precursor films. Taking PP-126 for example, it is clear to see in Fig. 3a that the intensity of β (300) diffraction peak was almost constant in every direction, implying that the β-iPP cast film was isotropy. Since the draw rate of β-iPP melt after extrusion was very low to avoid the β–α transformation, the orientation of β-lamellae was almost undetectable. However, the azimuthal intensity distribution of β (300) of these five β-iPP cast films (shown in Fig. 3b) differs considerably. The PP-110 exhibited a strong diffraction peak at the transverse direction (TD), indicating that substantial β-lamellae were parallel to the extrusion direction.5,6,40 The PP-120 and PP-135 samples showed the similar trend with PP-110 that the content of β-lamellae along the flow direction was higher than that of TD direction. On the other hand, the β (300) diffraction intensity of PP-126 and PP-130 was almost constant at any azimuth, especially the cast film with Tc = 126 °C that disclosed the most smooth curve of β (300) diffraction intensity, which implies that β-lamellae distribute uniformly in the β-iPP cast films with Tc = 126 °C and Tc = 130 °C. Moreover, it should be noted that the relative intensity of β (300) diffraction of these five β-iPP cast films were extremely low, thus the orientation degree of β-lamellae was almost undetectable. Nevertheless, the slight difference of β-lamellae distribution among these β-iPP cast films would bring about a significant effect on the stress–strain behaviors of β-iPP during stretching at elevated temperature.
 | ||
| Fig. 3 (a) 2D-WAXD patterns of Tc = 126 °C and (b) azimuthal intensity distributions of β (300) of five β-iPP cast films. | ||
3.2. Stress–strain behaviors
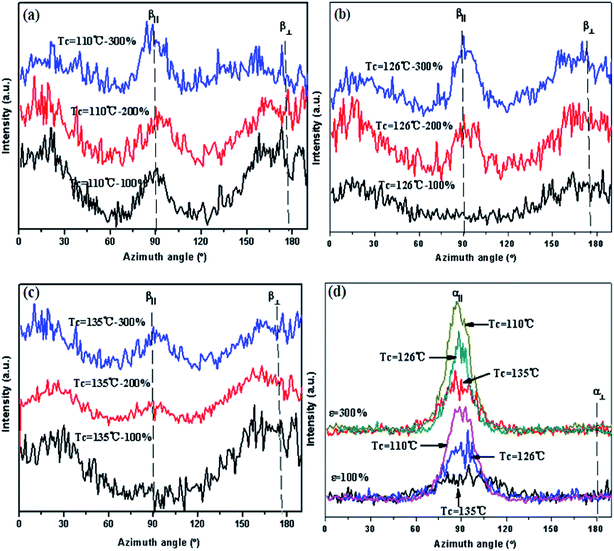
Fig. 4a–d show the nominal stress–strain curves of five β-iPP samples under tensile loading at Td = 50 °C, 70 °C, 90 °C and 110 °C. All the average mechanical properties were obtained from five specimens for each condition. Firstly, it should be pointed that in our previous study on the stress–strain behavior of β-iPP under tensile loading at Td = 25 °C,29 we first discovered a peculiar second yield point, where the fragmented crystals begin to disintegrate and transform into amorphous phase. However, when Td was higher than 50 °C, the double yield phenomenon of β-iPP disappeared even at extremely high strain rate (for example 500 mm min−1 which was not shown in this article), indicating that slight thermal effect would change the deformation behavior of β-iPP substantially. In the case of stretching at 50 °C (shown in Fig. 4a), the β-iPP samples exhibited the typical stress–strain of semi-crystalline polymer. After the short linear elastic region, a local maximum which is called yield point occurred in the stress–strain curves, and all the β-iPP films whitened immediately and a homogeneous deformation developed in the whole sample, indicating that numerous cavities have formed during yield. With further extension, a plateau which is called “cold drawing” originated in the stress–strain curves and a slight neck appeared in the deformed sample. When the strain was higher than 300%, the β-iPP sample exhibited a typical strain-hardening phenomenon. Nevertheless, when Td was elevated to 70 °C, it is very interesting to see from Fig. 4b that the stress of all the five β-iPP samples increased instantly with the strain just after the yield point and the “cold drawing” region disappeared, which was analogous to the stress–strain behaviors of β-iPP at Td = 90 °C (shown in Fig. 4c) and Td = 110 °C (shown in Fig. 4d). Although the five β-iPP films exhibited the similar stress–strain curves at high temperature, they had different deformation characteristics at a certain Td. Taking Td = 90 °C for example, the stress of PP-110 dropped rapidly after yield, resulting in the formation of a broad and sharp peak in the stress–strain curve; while the strain softening phenomenon retarded with elevating Tc of β-iPP. More interestingly, the cast film with Tc = 126 °C had the narrowest necking width during yield and its strain-hardening modulus was the highest among the five β-iPP samples. Furthermore, in order to examine the effect of Td on the tensile behavior of β-iPP, the stress–strain curves of PP-126 with various Td were shown in Fig. 4e. It is clear to see that the yield peak weakened and the strain-hardening modulus increased gradually with elevating Td; however, an opposite trend occurred when Td was higher than 90 °C, namely the strain-hardening modulus declined rapidly with increasing Td. In order to further differentiate the stress–strain behaviors of β-iPP at elevated temperature, the characteristic parameters of the five precursors during stretching will be discussed in detail in the following section.First of all, the WAXD measurement was employed to detect the phase transformation during stretching at different Td (shown in Fig. 5a). Obviously, when Td increased to 50 °C, the β-iPP sample of PP-126 that was stretched to 100% exhibited three characteristic diffraction peaks at 14.1°, 16.9°, and 18.6° which correspond to the α (110), α (040), and α (130), indicating that β–α transformation could be activated markedly by even slight heat, which is different with the conventional view point that the β phase begins to transform into α phase when Td is higher than 80 °C.23–25,38,39,41 Moreover, the β–α transformation rate accelerated with the elevating Td. It has been widely accepted that the molecular chains of α-crystal arrange in alternating right-handed and left-handed chain layers, while the β-crystal has the same directional helical chains, thus the change of packing pattern from hexagonal to monoclinic cannot be achieved by simple adjustment of the relative positions of the neighbouring chains through slipping at low temperature but involves the destruction (melting) of the original β-crystal and rearrangement (recrystallization) of the chains to form new α-crystal at high temperature.5,6,23–26,31 Since substantial β-crystal transformed into α-crystal at elevated temperature which is denser and more stable, the double yield phenomenon was prevented and the stress ascended instantly with strain after yield point. Moreover, the necking ratio of the deformed β-iPP sample when stretched to different strains at Td = 90 °C was calculated according to the equation: r = l/l0, where l0 is the original width of the undeformed specimen and l is the neck width of the stretched sample during deformation (shown in Fig. 5b). It is interesting to see that the yield process of PP-110 was the slowest among the five β-iPP samples, while that of PP-126 sample was the fastest (about 65%). Meanwhile, the deformed PP-126 sample exhibited a dramatic necking during yield process and its neck width was even narrower than that of PP-110 at 20% which had the thinnest β-lamellae. However, when the strain was higher than 100%, the neck width of PP-126 was broader than PP-135 whose β-lamellae was the thickest and the most stable among the five β-iPP samples. In our previous study,42 we found that the β-iPP with higher β-lamellar thickness and stability would undergo the β–α transformation more slowly and thus hindered the shrinkage efficiently during stretching at 90 °C. Obviously, this trend is not suitable in the present research, implying that the orientation of β-lamellae is critical to the tensile behavior of β-iPP.
On the other hand, the characteristic parameters of stress–strain curves of β-iPP samples during stretching at 90 °C were listed in Table 2. Firstly, one should notice that the yield stress (σy) elevated with increasing Tc, which is consistent with the conventional idea that σy is directly proportional to the lamellae thickness.43,44 Secondly, the stress drop (σ△) during yield which is related to the neck width of deformed sample shows that the PP-110 had the most notable strain-softening phenomenon (σ△ = 2.4 MPa), and the σ△ finally declined to 1.3 MPa with elevating Tc. Furthermore, the neck width of the yield peak in the stress–strain curve (ε) decreased from 93.2% (PP-110), through 64.6% (PP-126), finally reaching 88.0% (PP-135). It is widely established that the yield process is determined by the defect in the semi-crystalline polymer and the irreversible plastic deformation is always triggered by the weakest part in the sample.1–20 In our prior research,42 we have discovered that yield was initiated from the substantial weak interfaces between lamellae of β-iPP without fully developed spherulite, leading to the homogeneous deformation in the whole sample during stretching. Therefore, it is concluded that the defects distributed most uniformly in β-iPP with Tc = 126 °C, resulting in its fastest yield process. More importantly, the strain-hardening modulus of PP-126 (E = 1.3 × 10−2 MPa) was much higher than that of the other four β-iPP samples, indicating that PP-126 had formed the finest oriented microfibrils in the strain-hardening region. Furthermore, it is worth mentioning that the trend of ε and E, obtained from tensile testing at high temperature, directly accorded with the difference of β-lamellae distribution in the five β-iPP cast films. In order to explore the key structural factors that determine the stress–strain behavior of β-iPP at elevated temperature, the morphological evolution at every deformation stage will be discussed in detail below.
| Samples | σy (MPa) | σ△ (MPa) | ε (%) | E (MPa) |
|---|---|---|---|---|
| Tc = 110 °C | 8.2 | 2.4 | 93.2 | 7.0 × 10−3 |
| Tc = 120 °C | 8.4 | 1.8 | 90.5 | 7.4 × 10−3 |
| Tc = 126 °C | 8.5 | 1.3 | 64.6 | 1.3 × 10−2 |
| Tc = 130 °C | 8.5 | 1.3 | 87.5 | 8.1 × 10−3 |
| Tc = 135 °C | 8.7 | 1.3 | 88.0 | 7.5 × 10−3 |
3.3. Characterization of morphological evolution
2D-WAXD experiments were performed to detect the phase transitions and orientation of β-iPP during stretching at 90 °C. Taking PP-110, PP-126 and PP-135 for example, when the strain was higher than 100%, where the yield process had finished, three arcs corresponding to α (1 1 0), α (0 4 0) and α (1 3 0) reflections appeared in equator for the three β-iPP samples, implying that the β–α transformation entered into action at Td = 90 °C.23–27 Furthermore, β–α transformation of the sample with Tc = 110 °C propagated most rapidly, owing to its lowest stability of β-crystal. It is also worth mentioning that a nearly intact β (300) ring was observed during the whole stages of deformation, which indicates that the chains orientation of β-lamellae was almost unchanged during stretching. However, the intensity of β (300) at varying angles was different. For all the three β-iPP samples, the diffraction intensity exhibited a maximum at meridian and then declined gradually towards the equator, which implies that the β-lamellae perpendicular to the loading direction deformed at early stage and those parallel to the drawing axis separate and slip at higher strain (Fig. 6).Furthermore, the azimuthal intensity of β (300) and α (110) reflection peaks, which could characterize the β and α crystal phase orientation during stretching at Td = 90 °C, are presented in Fig. 7a–d. The corresponding diffraction maxima are indicated as β∥ and β⊥. It is clear to see that the azimuthal intensity of β (300) at equator (β∥) was low while the intensity at meridian (β⊥) was very high for both PP-126 and PP-135 at 100%, which indicates that substantial β-lamellae perpendicular to the drawing direction had deformed and transformed into α phase, while there were still large amount of vertical β-lamellae in β-iPP. Nevertheless, PP-110 exhibited the maximum at β∥ when stretched to 100%. This is because abundant β-lamellae of PP-110 had fragmented and flowed towards the loading direction, owing to its lowest β-lamellar thickness and stability at Tc = 110 °C. With further deformation, the intensity at β∥ increased gradually and even exceeded that at β⊥ when stretched to 300% for the β-iPP samples, resulting from the substantial fragmentation and orientation of β-crystal along the loading direction at high strain. On the other hand, the α (110) intensity of all the three β-iPP samples shows one strong reflection peak along the drawing axis (α∥) during the whole deformation stage, indicating that the fragmented β-crystal transformed into oriented α-fibril. Moreover, the α∥ intensity declined gradually with elevating Tc of β-iPP, which further corroborates that β–α transformation retarded with increasing β-lamellae thickness. More interestingly, among the three β-iPP samples, the reflection peaks of PP-126 along α∥ at 100% and 300% were the narrowest, implying that the α-fibril of PP-126 which formed during longitudinal stretching at elevated temperature distributed most uniformly.
Fig. 8 shows the SEM micrographs of β-iPP at various strains when stretched at 90 °C. Firstly, it should be pointed out that the deformation and pore formation mechanism of β-iPP at high temperature have been studied systematically in our previous article.42 We found that when stretched at 90 °C, where β–α transformation entered into action, the lamellae at different angles to the tensile axis would result in different deformational modes and lead to the formation of randomly distributed defects during stretching. At the early stage of deformation (as shown in Fig. 8a), the horizontal lamellae and those at a tilt angle to the loading direction separated and formed slender crazes which could be enlarged or even collapsed with excessive deformation. On the other hand, sporadic intra-lamellar slip which leads to the formation of small crazes was also observed for vertical lamellae. As for the lamellae with c axis perpendicular to the drawing direction, lamellar rotation may be retarded because the stretching stresses exerted on are from the four directions and counteract each other, consequently, these lamellae would become thinner and pack more densely, and the newly born α-crystal would create rigid areas at higher strain. As the strain increased to 300% (shown in Fig. 8b–d), the lamellar structure converted into an oriented fibrillar structure, where abundant cavities were formed and distributed unevenly in the membrane. Nevertheless, only sporadic small crazes existed in PP-110 membranes and the oriented fibrillar structure was inconspicuous (shown in Fig. 8c), resulting from the continuous deformation of unstable β-lamellae and rapid β–α transformation which would cause a serious volume contraction and hinder the microvoid formation. That is why PP-110 sample had the lowest strain-hardening modulus when stretched at elevated temperature. As for PP-135 stretched to 300% (shown in Fig. 8d), there were numerous large size cavities and oriented microfibrils which distributed heterogeneously in the membrane. More importantly, fine oriented fibrillar structure, where the fibrils were slender and the defects distribution was most uniform, were formed in the specimen with Tc = 126 °C after longitudinal stretching (shown in Fig. 8b), resulting in its highest strain-hardening modulus among these five β-iPP samples.
On the other hand, the stress–strain curves of transverse stretching of five β-iPP films after stretched to 300% at Td = 90 °C were presented in Fig. 9. It is very interesting to see that the five β-iPP samples behaved diversely during transverse stretching. Both of PP-110 and PP-120 exhibited a marked yield peak; in addition, the yield stress and elongation at break were the highest. Because there were still numerous rigid areas in PP-110 and PP-120 after longitudinal drawing and their oriented fibrillar structures were inconspicuous, resulting in the highest yield stress. Furthermore, the content of defects formed during longitudinal stretching was low for PP-110 and PP-120, leading to their extremely high elongation at break. However, as for the samples of PP-126, PP-130 and PP-135, the yield peaks were invisible, and their yield stress and elongation at break were very low, especially the β-iPP sample with Tc = 126 °C. Since SEM micrograph had shown (seen in Fig. 8b) that highly oriented fibrils, among which large amount of defects distributed uniformly, were formed in PP-126 after longitudinal stretching, thus its fibrillar structure is much easier to separate and deform during transverse drawing, consequently, resulting in its lowest yield stress and elongation at break. More importantly, the trend of stress–strain behaviors during transverse stretching directly accorded with the differences of β-lamellae distribution in the five β-iPP cast films.
 | ||
| Fig. 9 The stress–strain curves of five β-iPP films in transverse drawing after longitudinal stretching to 300% at Td = 90 °C. | ||
3.4. Discussion of influence of β-lamellae distribution on the stress–strain behavior of β-iPP at elevated temperature
Based on the prior studies,29,42 we found that when stretched at room temperature, where β-smectic transformation is predominant, the amorphous chains of β-iPP have comparable modulus to the β-lamellae, thus the rotation of β-lamellae towards the loading direction is retarded, leading to the continuous fragmentation of β-lamellae. With elevating Td, β–α transformation gradually enters into action (Td ≥ 50 °C) and β-crystal transforms into α-crystal which is denser and more stable. In addition, owing to the promotion of the mobility of amorphous chains and lamellar movement, partial rotation of β-lamellae along the tensile axis is allowed and fine oriented fibrillar structure is formed. Thus, the stress ascends rapidly with strain after yield point and the strain-hardening modulus of β-iPP increases progressively with Td (≤90 °C). However, at high Td (>90 °C), β–α transformation accelerates and substantial β-lamellae fragment and transform into α phase, which could cause a marked volume shrinkage and formation of coarse oriented fibrillar structure after longitudinal stretching, thus resulting in the monotonous decrease of strain-hardening modulus with elevating Td (>90 °C). Therefore, Td = 90 °C is the optimum temperature to produce membrane with finest oriented fibrillar structure and most uniform cavities distribution during longitudinal stretching.On the other hand, we also discovered that the horizontal lamellae produce cavities and slender fibrils, while the vertical lamellae would form rigid areas or coarse fibrils during stretching at high temperature.42 Since the β-lamellae at different angles to the tensile axis could result in different deformational modes, the β-lamellae distribution would have great effects on the stress–strain behavior of β-iPP. We postulate two typical models detailing the lamellar deformation process to explain the various stress–strain curves of β-iPP when stretched at 90 °C (shown in Fig. 10d). If the β-lamellae distribution is heterogeneous (as marked with B in Fig. 10d), such as the samples of PP-110, PP-120 and PP-135 whose β-lamellae content along the flow direction is higher than that of TD direction, substantial β-lamellae parallel to the loading direction would pack together to produce rigid areas and coarse fibrillar structure, thus resulting in the low strain-hardening modulus. Moreover, in the case of PP-126 whose orientation degree is extremely low (as marked with A in Fig. 10d), the distribution of β-lamellae with different angles to the tensile axis is most uniform; consequently, the cavities produced by horizontal lamellar slip can separate those rigid areas created by vertical lamellar deformation efficiently, leading to the formation of highly oriented fibrils and uniform distribution of cavities in the β-iPP membrane during longitudinal stretching. Therefore, PP-126 has the fastest yield process and highest strain-hardening modulus among the five β-iPP samples.
Furthermore, a sequential biaxial stretching was performed to fabricate microporous membranes (shown in Fig. 10a–c). It is clear to see from the SEM images that there were abundant coarse fibrils in PP-110 and PP-135 which were too rigid to separate and the pore size distribution was very poor, while PP-126 (shown in Fig. 10b) had the most uniform pore size distribution, which further confirms the deformation mechanism of β-iPP during longitudinal drawing. In addition, the stress–strain curve of β-iPP under tensile loading at elevated temperature provides a simple and efficient tool to discriminate β-lamellae orientation in the precursor β-iPP films and to evaluate the cavities distribution during longitudinal stretching.
4. Conclusions
In this work, five β-iPP samples were prepared through crystallizing from 110 °C to 135 °C. The WAXD, DSC and SEM results illustrate that all the five β-iPP samples had similar crystallinity, high contents of β-crystals but different β-lamellae distribution. Furthermore, they behaved diversely in tensile testing at elevated temperatures: PP-110 and PP-120 exhibited the notable yield peaks and low strain-hardening modulus, while PP-126 had the fastest yield process and highest strain-hardening modulus. Based on the detailed characterization of morphological evolutions during stretching by 2D-WAXD and SEM measurements, we postulate two typical models to explain the peculiar stress–strain curves of β-iPP. The samples of PP-110, PP-120 and PP-135 whose β-lamellae content along the flow direction was higher than that of TD direction formed coarse fibrillar structure during longitudinal stretching at elevated temperature, resulting in the low strain-hardening modulus in the stress–strain curves. On the contrary, as for the sample of PP-126, whose orientation degree was extremely low and the distribution of β-lamellae with different angles to the tensile axis was most uniform, produced highly oriented fibrils and homogeneous distribution of cavities after longitudinal drawing, thus leading to its highest strain-hardening modulus and the narrowest pore size distribution after biaxial stretching.References
- P. B. Bowden and R. J. Young, J. Mater. Sci., 1974, 9, 2034–2051 CrossRef CAS.
- Z. Cai, Y. Zhang, J. Li, F. Xue, Y. Shang, X. He, J. Feng, Z. Wu and S. Jiang, Polymer, 2012, 53, 1593–1601 CrossRef CAS PubMed.
- H. Chen, J. Karger-Kocsis, J. Wu and J. Varga, Polymer, 2002, 43, 6505–6514 CrossRef CAS.
- O. Darras and R. Seguela, J. Polym. Sci., Part B: Polym. Phys., 1993, 31, 759–766 CrossRef CAS PubMed.
- E. Lezak and Z. Bartczak, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 92–108 CrossRef CAS PubMed.
- E. Lezak, Z. Bartczak and A. Galeski, Polymer, 2006, 47, 8562–8574 CrossRef CAS PubMed.
- V. Gaucher-Miri and R. Seguela, Macromolecules, 1997, 30, 1158–1167 CrossRef CAS.
- S. Humbert, O. Lame and G. Vigier, Polymer, 2009, 50, 3755–3761 CrossRef CAS PubMed.
- T. Juska and I. R. Harrison, Polym. Eng. Sci., 1982, 2, 13–28 CAS.
- X. Li, H. Wu, T. Huang, Y. Shi, Y. Wang, F. Xiang and Z. Zhou, Colloid Polym. Sci., 2010, 288, 1539–1549 CAS.
- L. Lin and A. S. Argon, J. Mater. Sci., 1994, 29, 294–323 CrossRef CAS.
- G. Meinel, N. Morosoff and A. Pete, J. Polym. Sci., Part A-2, 1970, 8, 1723–1740 CrossRef CAS PubMed.
- G. Meinel and A. Peterlin, J. Polym. Sci., Part A-2, 1971, 9, 67–83 CrossRef CAS PubMed.
- G. Natta and P. Corradini, La Rivista del Nuovo Cimento, 1960, 15, 40–51 CrossRef CAS.
- Y. Nozue, Y. Shinohara, Y. Ogawa and T. Sakurai, Macromolecules, 2007, 40, 2036–2045 CrossRef CAS.
- A. Peterlin, J. Polym. Sci., Part C: Polym. Symp., 1966, 15, 427–443 CrossRef PubMed.
- A. Peterlin, J. Polym. Sci., Part C: Polym. Symp., 1967, 18, 123–132 CrossRef CAS PubMed.
- R. Seguela, Macromol. Mater. Eng., 2007, 292, 235–244 CrossRef CAS PubMed.
- T. Wu, Y. Cao, F. Yang and M. Xiang, Mater. Des., 2014, 60, 153–163 CrossRef CAS PubMed.
- F. Zuo, J. K. Keum, X. Chen, B. S. Hsiao, H. Chen, S.-Y. Lai, R. Wevers and J. Li, Polymer, 2007, 48, 6867–6880 CrossRef CAS PubMed.
- A. T. Jones, J. M. Aizlewood and D. R. Beckett, Makromol. Chem., 1964, 75, 134–158 CrossRef PubMed.
- J. Kang, G. S. Weng, Z. F. Chen, J. Y. Chen, Y. Cao, F. Yang and M. Xiang, RSC Adv., 2014, 4, 29514–29526 RSC.
- F. Chu, Polymer, 1996, 37, 573–579 CrossRef CAS.
- F. Chu, T. Yamaoka, H. Ide and Y. Kimura, Polymer, 1994, 35, 3442–3448 CrossRef CAS.
- F. Chu, T. Yamaoka and Y. Kimura, Polymer, 1995, 36, 2523–2530 CrossRef CAS.
- S. Ran and M. Xu, Chin. J. Polym. Sci., 2004, 22, 123–130 CAS.
- G. Shi, F. Chu, G. Zhou and Z. Hang, Makromol. Chem., 1989, 190, 907–913 CrossRef CAS PubMed.
- W. Zhu and M. Xu, Polym. Adv. Technol., 1996, 7, 743–748 CrossRef CAS.
- T. Wu, M. Xiang, Y. Cao, J. Kang and F. Yang, RSC Adv., 2014, 4, 43012–43023 RSC.
- R. A. Phillips and M. D. Wolkowicz, Polypropylene Handbook, Hanser Gardner Publications, Inc., OH, USA, 2005 Search PubMed.
- J. Varga, J. Macromol. Sci., Part B: Phys., 2002, 41, 1121–1171 CrossRef.
- H. M. Fisher and G. C. Wensley, Polypropylene microporous membrane for battery separator, U.S. Pat., 6,368,742, 2002.
- K. Hiroshi, A. Tetuo and K. Akira, Porous multi-layer film, U.S. Pat., 5,691,047, 1997.
- M. Xu, S. Hu, J. Guan, X. Sun, W. Wu and W. Zhu, Polypropylene microporous film, U.S. Pat., 5,134,174, 1992.
- H. Bai, Y. Wang, Z. Zhang, L. Han, Y. Li, L. Liu, Z. Zhou and Y. Men, Macromolecules, 2009, 42, 6647–6655 CrossRef CAS.
- H. W. Bai, F. Luo, T. N. Zhou, H. Deng, K. Wang and Q. Fu, Polymer, 2011, 52, 2351–2360 CrossRef CAS PubMed.
- R. H. Olley and D. C. Bassett, Polymer, 1982, 23, 1707–1710 CrossRef CAS.
- G. Offord, S. Armstrong, B. Freeman, E. Baer, A. Hiltner and D. Paul, Polymer, 2013, 54, 2796–2807 CrossRef CAS PubMed.
- G. Offord, S. Armstrong, B. Freeman, E. Baer, A. Hiltner, J. Swinnea and D. Paul, Polymer, 2013, 54, 2577–2589 CrossRef CAS PubMed.
- J. Ščudla, M. Raab, K.-J. Eichhorn and A. Strachota, Polymer, 2003, 44, 4655–4664 CrossRef.
- S. Armstrong, G. Offord, D. Paul, B. Freeman, A. Hiltner and E. Baer, J. Appl. Polym. Sci., 2014 DOI:10.1002/app.39765.
- T. Wu, M. Xiang, Y. Cao, J. Kang and F. Yang, RSC Adv., 2014, 4, 36689–36701 RSC.
- R. Seguela and O. Darras, J. Mater. Sci., 1994, 29, 5342–5352 CrossRef CAS.
- R. Seguela and F. Rietsch, J. Mater. Sci. Lett., 1990, 9, 46–47 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |