Density functional theory study on organically surface-modified silicene†
Abstract
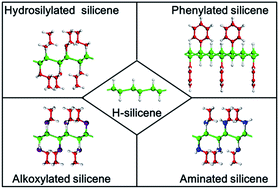
Organic surface modification may be critical to the practical use of silicene, which is a novel two-dimensional layered material. It is intriguing to know if organic surface modification seriously impacts the structural, electronic and optical properties of silicene. In this work, we focus on four hydrogenation-based organic surface modification schemes (hydrosilylation, alkoxylation, aminization and phenylation) with the experimentally demonstrated surface coverage of ∼33%. The geometrical structures, band structures and optical absorption of organically surface-modified silicene have been compared with those of silicene and hydrogenated silicene (H-silicene) in the framework of density functional theory. It is found that organic surface modification leads to the increase of the buckling distance of silicene, while causing the angles of bonds in the honeycomb structure of silicene to decrease. Although the initial hydrogenation makes silicene become an indirect-bandgap semiconductor, the subsequent organic surface modification schemes further change the band structure of silicene. Hydrosilylation, phenylation, alkoxylation and amination all give rise to the reduction of the bandgap of H-silicene. Hydrosilylated and phenylated silicene are indirect-bandgap semiconductors, while alkoxylated and aminated silicene are direct-bandgap semiconductors. Changes of the optical absorption induced by organic surface modification are well correlated to the corresponding changes of the band structure.

 Please wait while we load your content...
Please wait while we load your content...