Open Access Article
Open Access ArticleEngineering thermal rectification in MoS2 nanoribbons: a non-equilibrium molecular dynamics study†
Leonardo
Medrano Sandonas
abc,
Rafael
Gutierrez
*ac,
Arezoo
Dianat
ac and
Giovanni
Cuniberti
acd
aInstitute for Materials Science and Max Bergmann Center of Biomaterials, TU Dresden, 01062 Dresden, Germany. E-mail: rafael.gutierrez@nano.tu-dresden.de; Fax: +49 (0)351 4633 1422; Tel: +49 (0)351 4633 1419
bMax Planck Institute for the Physics of Complex Systems, 01187 Dresden, Germany
cDresden Center for Computational Materials Science (DCCMS), TU Dresden, 01062 Dresden, Germany
dCenter for Advancing Electronics Dresden, TU Dresden, 01062 Dresden, Germany
First published on 3rd June 2015
Abstract
Phononics in two-dimensional (2D) materials is an emergent field with a high potential impact from the basic as well as applied research points of view. Thus it is crucial to provide strategies to control heat flow via atomic-scale engineering of the materials. In this study, thermal diodes made of single layer MoS2 nanoribbons are investigated using non-equilibrium classical molecular dynamics. Specifically, we focus on the influence of shape asymmetries of the nanoribbons on the thermal current, and obtain thermal rectification ratios up to 30% for the T-shaped nanoribbons. This behavior is then rationalized through a detailed analysis of the vibrational spectrum of the ribbons. In particular, it turns out that thermal rectification is mostly related to (i) the transversal finite size of the ribbon and (ii) to the different localization behavior of high-frequency modes for forward and backward heat flow directions. We expect our results to shed light on the potential of 2D materials for the engineering of highly efficient nanoscale thermal devices.
1 Introduction
Over the last years, the field of phononics, aiming at controlling heat flow in tailored structures as well as developing thermal devices such as diodes, transistors, and thermal logic gates, has experienced an accelerated progress.1–4 As a result, novel applications in the fields of nanomachines, electronics, refrigeration, energy harvesting, and energy generation have been suggested.5,6 In order to carry these ideas into thermal device design, several theoretical and experimental studies have been performed over different length scales, e.g. the first solid-state active three-terminal thermal device based on VO2 with large rectification of the heat current has recently been demonstrated.7 Other successful experimental findings are thermal rectifiers based on carbon or boron-nitride nanotubes, with asymmetric mass loading,8 and reduced graphene oxide.9 A thermal rectifier should provide a large heat flow for a certain temperature gradient, but ideally be insulating when the direction of the gradient, and thus that of the heat flow, is reversed. From a theoretical point of view, it has been found that thermal rectification in nanostructured systems sensitively depends on several parameters such as heat bath features,10,11 the device geometry,12,13 and on the interface properties between different materials inside the device.14–17 A common conclusion from these studies is that the simplest mechanism to induce thermal rectification in confined nanoscale systems is to introduce structural asymmetries.Most of these investigations have focused on carbon-based nanomaterials like carbon nanotubes and graphene nanoribbons.4,12,13,18–20 In particular, graphene has drawn much attention due to its extremely high thermal conductivity.21 Besides graphene, however, there are meanwhile a variety of novel two-dimensional (2D) materials like transition metal dichalcogenides, boron nitride (BN), phosphorene, and silicine, which are expected to display different electrical and thermal properties due to the differences in their chemical composition, and thus offer a new broad playground to explore and develop nanoscale devices with tailored electrical, optical, and thermal properties. In particular, molybdenum disulphide (MoS2) has recently attracted considerable interest in the construction of field effect transistors (FET) and optical devices due to its sizable electronic band gap;22,23 also its potential thermoelectric performance has been highlighted.24 Although a variety of theoretical studies have been published, addressing the phonon dispersion and thermal conductivity of MoS2 layers and ribbons,25–38 less attention has so far been devoted to the possibility of engineering the thermal response of MoS2 nanostructures via structural asymmetries.
Here, we study MoS2 nanoribbons with strong structural asymmetries by using non-equilibrium molecular dynamics simulations of the thermal transport. We show that thermal rectification ratios of up to 30% can be achieved depending on the degree of asymmetry of the ribbons and rationalize our findings by analyzing in detail the vibrational structure of the systems. This includes an analysis of the mode localization in the nanoribbon, an issue which has been indicated to strongly influence thermal rectification in asymmetric or defective nanostructures made of a single material.12,39 We find out that different degrees of spatial localization of high-frequency modes for forward and backward heat flow directions are an important factor in determining thermal rectification. We remark that nanostructures such as those investigated here may be already accessible to state-of-the-art experimental approaches. Here, quasi one-dimensional MoS2 nanoribbons have been successfully synthesized40 as well as triangular and hexagonal MoS2 nanoplatelets.41,42
2 System and methodology
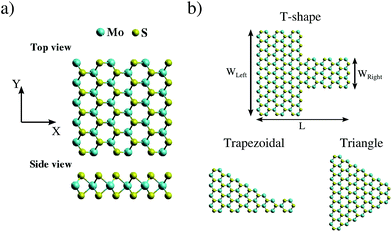
The atomic structure of a symmetric MoS2 nanoribbon is shown in Fig. 1a, while Fig. 1b displays three different geometrical shapes for MoS2 nanoribbons, which we will consider to study possible thermal rectification effects: T-shaped, trapezoidal, and triangular nanoribbons. To quantify the degree of structural asymmetry of these nanostructures, the dimensionless quantity WLR = WLeft/WRight is introduced. Here, WLeft and WRight are the widths of the left and right ends of the nanoribbon, respectively, and the case of WLR = 1.0 corresponds to a fully symmetric rectangular structure.Non-equilibrium molecular dynamics (NEMD) simulations were carried out by using the LAMMPS code.43 One crucial issue is the choice of the appropriate force field, since parametrizations developed for bulk systems may in general not be transferable to nanoribbons. In the case of MoS2, several force fields have recently been developed.32,33,44 However, they turned out to have different problems when applied to the simulation of systems with open boundary conditions, such as nanoribbons, at room temperature. Therefore, after careful checks, we have used in our investigation a force field developed on the basis of tight-binding quantum chemistry calculations by Onodera et al.,45 which includes ionic, covalent, and van der Waals interactions among Mo and S atoms. This interatomic potential has already been successfully applied to study mechanical45,46 and thermal35 properties of monolayer MoS2.
In our simulations, we have considered asymmetric MoS2 nanoribbons with free boundary conditions in all directions. We have fixed the ends in the X-direction (one layer) to avoid global rotations of the system during the simulation. The standard velocity Verlet algorithm was used to integrate Newton’s equations of motion, and the MD time step was set to 0.5 fs. All investigated nanostructures were initially relaxed using a quickstep method. The lattice constant for MoS2 obtained after relaxation is a = 3.38 Å. Equilibration runs for 2 ns and at T0 = 300 K were first performed in the NVT ensemble with a Nosé–Hoover thermostat using a relaxation time equal to 0.1 ps. The choice of a thermostat is a sensitive issue in NEMD simulations, but as discussed in ref. 10, different algorithms in NEMD simulations only led to negligible differences in the computed heat flows (see the ESI† for a discussion of the thermostat parameters used in our simulations). Once the temperature reached the required value, the thermostat was removed, and the NEMD simulations were carried out for 20 ns. The temperatures for left and right heat baths were defined as TL = (1 + α)T0 and TR = (1 − α)T0 for the forward direction of the heat flux (heat flows left-to-right or wider-to-narrower) and the opposite case for the backward direction (heat flows right-to-left or narrower-to-wider). We consider as temperature bias ΔT = |TL − TR| = 2αT0 (α > 0). Each heat bath extended over four atomic layers corresponding to a length of roughly 2.3 nm. Time averages of the temperature and the heat current were carried out over the last 10 ns of the simulation. The temperature profile was then computed by dividing the system into a certain number of slabs and using the relation: 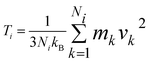 , where Ni is the number of atoms in the ith slab, and mk and vk correspond to the atomic mass and velocity of atom number k, respectively. Furthermore, the calculated temperature for each slab, Ti, was averaged over a predefined time interval to obtain a smooth temperature profile. To avoid spurious effects related to the specific choice of initial velocities, an average over five random choices of the initial velocity distribution was additionally performed. To quantify the efficiency of thermal transport in both temperature bias directions, a thermal rectification (TR) ratio η can be defined as:
, where Ni is the number of atoms in the ith slab, and mk and vk correspond to the atomic mass and velocity of atom number k, respectively. Furthermore, the calculated temperature for each slab, Ti, was averaged over a predefined time interval to obtain a smooth temperature profile. To avoid spurious effects related to the specific choice of initial velocities, an average over five random choices of the initial velocity distribution was additionally performed. To quantify the efficiency of thermal transport in both temperature bias directions, a thermal rectification (TR) ratio η can be defined as:
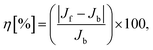 | (1) |
3 Results and discussion
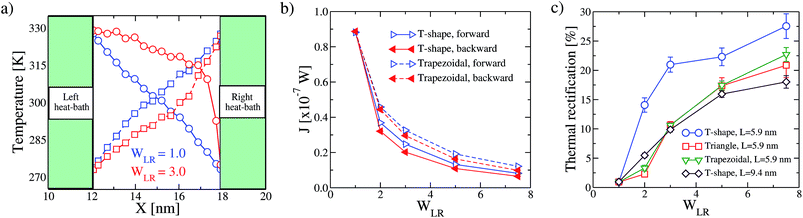
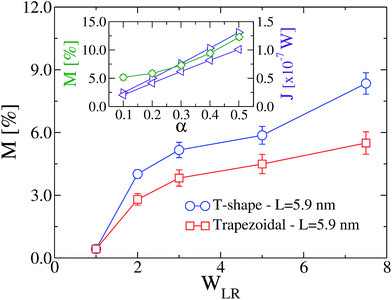
In Fig. 2a we show the temperature profile for α = 0.1, for trapezoidal MoS2 nanoribbons of length L = 5.9 nm (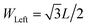 ) with WLR = 1.0 (symmetric) and WLR = 3.0 (asymmetric). For symmetric nanoribbons, the temperature profile has a symmetric and nearly linear behavior for both directions, forward and backward, of the applied temperature bias, so that no rectification of the thermal current can take place, as expected. On the contrary, for WLR = 3.0, the temperature gradient along the nanoribbon becomes non-linear and displays a different dependence on the spatial distance from the heat baths for forward and backward heat flows. Notice also that the mean temperature is mainly controlled by the wider heat bath (left bath), and this shows up in the strong non-linear evolution of the temperature profile with increasing distance from the wider bath. As a result of the asymmetric temperature profiles for both temperature bias directions, the corresponding thermal currents are also different and heat rectification can take place, see Fig. 2b. In other words, the heat flux runs preferentially from the wider to the narrower region, so that the device behaves as a “good” thermal conductor in that direction. This behavior is improved when the temperature bias is increased, as shown in the inset of Fig. 5. In Fig. 2c, the TR ratio η is displayed as a function of the geometrical asymmetry parameter WLR. For the different nanoribbon shapes, the qualitative trends are rather similar: with increasing structural asymmetry, the degree of rectification increases and can achieve rather high values of roughly 30%, values which are comparable with those found in more complex engineered graphene nanoribbons.12,20 This behavior is related to the increasing difference in the number of atoms involved in the nanoribbon–heat bath interaction at both ends with increasing WLR, which increasingly breaks the heat flux symmetry as the temperature bias is reversed. Similar effects have been reported for graphene ribbons.12,13,18 There is however a clear quantitative difference in the heat rectification efficiency of the T-shaped ribbons when compared to the triangular and trapezoidal ones, namely, the former has a larger TR ratio for the same length L. This is largely related to how the transition from the wider to the narrower region is built in: in the triangular and trapezoidal nanoribbons, the transition is smooth (we may call it adiabatic as done with quantum point contacts47), while for the T-shaped ribbon there is a narrow interface region where an abrupt transition from wider to narrower sections takes place. Thus, heat flow differences resulting from the global asymmetry of the nanoribbon will be enhanced due to this sharp interface. We also notice that upon increasing the system size, the effect of the structural asymmetry in thermal rectification weakens and eventually disappears, i.e. η → 0 for L(or W) → ∞. This tendency is illustrated for the T-shaped ribbons with two different lengths: L = 5.9 nm and L = 9.4 nm (see Fig. 2c) and highlights the fact that, besides structural asymmetry, another major factor influencing thermal rectification is the transversal finite size of the nanostructures. This has been previously discussed in carbon-based nanostructures.1,12,13
) with WLR = 1.0 (symmetric) and WLR = 3.0 (asymmetric). For symmetric nanoribbons, the temperature profile has a symmetric and nearly linear behavior for both directions, forward and backward, of the applied temperature bias, so that no rectification of the thermal current can take place, as expected. On the contrary, for WLR = 3.0, the temperature gradient along the nanoribbon becomes non-linear and displays a different dependence on the spatial distance from the heat baths for forward and backward heat flows. Notice also that the mean temperature is mainly controlled by the wider heat bath (left bath), and this shows up in the strong non-linear evolution of the temperature profile with increasing distance from the wider bath. As a result of the asymmetric temperature profiles for both temperature bias directions, the corresponding thermal currents are also different and heat rectification can take place, see Fig. 2b. In other words, the heat flux runs preferentially from the wider to the narrower region, so that the device behaves as a “good” thermal conductor in that direction. This behavior is improved when the temperature bias is increased, as shown in the inset of Fig. 5. In Fig. 2c, the TR ratio η is displayed as a function of the geometrical asymmetry parameter WLR. For the different nanoribbon shapes, the qualitative trends are rather similar: with increasing structural asymmetry, the degree of rectification increases and can achieve rather high values of roughly 30%, values which are comparable with those found in more complex engineered graphene nanoribbons.12,20 This behavior is related to the increasing difference in the number of atoms involved in the nanoribbon–heat bath interaction at both ends with increasing WLR, which increasingly breaks the heat flux symmetry as the temperature bias is reversed. Similar effects have been reported for graphene ribbons.12,13,18 There is however a clear quantitative difference in the heat rectification efficiency of the T-shaped ribbons when compared to the triangular and trapezoidal ones, namely, the former has a larger TR ratio for the same length L. This is largely related to how the transition from the wider to the narrower region is built in: in the triangular and trapezoidal nanoribbons, the transition is smooth (we may call it adiabatic as done with quantum point contacts47), while for the T-shaped ribbon there is a narrow interface region where an abrupt transition from wider to narrower sections takes place. Thus, heat flow differences resulting from the global asymmetry of the nanoribbon will be enhanced due to this sharp interface. We also notice that upon increasing the system size, the effect of the structural asymmetry in thermal rectification weakens and eventually disappears, i.e. η → 0 for L(or W) → ∞. This tendency is illustrated for the T-shaped ribbons with two different lengths: L = 5.9 nm and L = 9.4 nm (see Fig. 2c) and highlights the fact that, besides structural asymmetry, another major factor influencing thermal rectification is the transversal finite size of the nanostructures. This has been previously discussed in carbon-based nanostructures.1,12,13
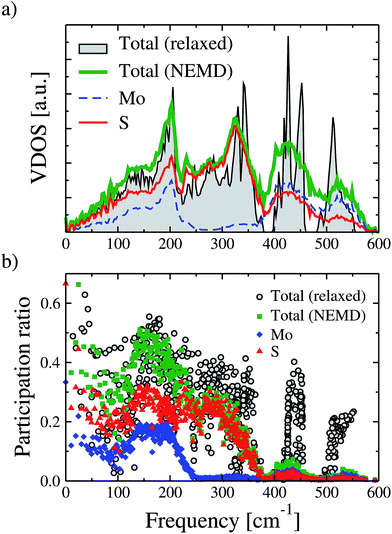
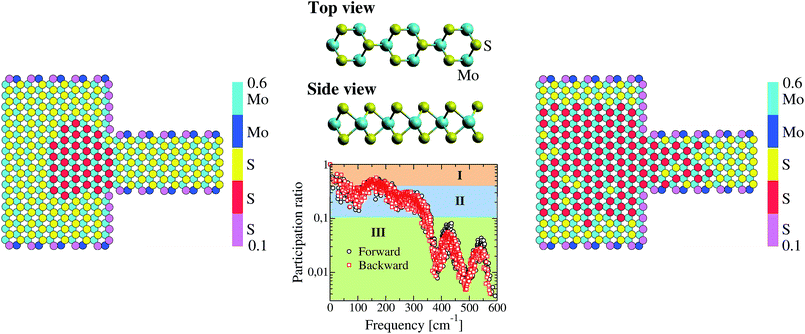
To rationalize the process of thermal rectification in asymmetrically structured MoS2 nanoribbons, we have performed a real-space mode analysis.48 For the sake of clarity, we focus on the T-shaped nanoribbon with L = 5.9 nm and WLR = 3.0, since the results for the other geometries are qualitatively similar. Fig. 3a shows the total and partial vibrational density of states (PVDOS) of the T-shaped ribbon. The PVDOS is defined as:49
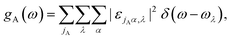 | (2) |
In Fig. 3a, we also show as reference the VDOS of the structurally relaxed T-shaped nanoribbon before running the NEMD simulation (black solid line). The major difference to the VDOS obtained from the NEMD simulation (green solid line) is the spectral broadening, which manifests more clearly for the high-frequency vibrational modes above 400 cm−1. Looking now at the PVDOS for the two atom types in the nanoribbon, Mo and S, we can roughly identify three different spectral regions:32 a low frequency range (up to 200 cm−1) where both S and Mo atoms carry similar spectral weights, although the contributions of the S atoms are slightly larger; an intermediate range (∼200–380 cm−1), where the spectral weight is carried almost exclusively by S atoms; a high frequency range (>380 cm−1) where again both atom types contribute similarly to the total VDOS, although here Mo atoms have a slightly larger spectral weight. For the backward heat flow direction a similar qualitative behavior was obtained (not shown). The information provided by the VDOS analysis does not reveal the degree of localization or delocalization of the vibrational modes in different spectral ranges. Hence, to characterize each mode λ with respect to these features, the participation ratio (PR) has been calculated, which is defined according to:
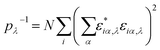 | (3) |
Here, εiα,λ is the vibrational eigenvector component of atom i and N is the number of atoms in the system. The PR measures the fraction of atoms participating in a mode and hence varies between 1.0 for delocalized modes to O(1/N) for localized modes. The PR is displayed in the lower panel of Fig. 3. We also show as a reference, similar to the VDOS plot in Fig. 3a, the PR for the T-shaped relaxed nanoribbon previous to starting the NEMD simulation. Additionally, partial PRs separately associated to the sulfur and molybdenum atoms are shown. Partial PRs are obtained by restricting the summation over the atom index i in eqn (3) to only atoms of a given type.50
The first point to notice is that the non-equilibrium vibrational spectrum is mostly modified in the higher frequency part with modes lying roughly above 400 cm−1. While for the relaxed nanoribbon two clear groups of modes in this spectral range with PR ∼ 0.4 and 0.25 can be identified, the non-equilibrium modes show a considerably larger degree of localization with PR below 0.1. For lower frequencies the differences between these two cases are much weaker, though. The partial PRs show that modes with a higher degree of delocalization (larger PR) involve in general a larger contribution from sulfur atoms. In general terms, apart from the very low frequency vibrations below 100 cm−1 and a narrow region between 150 cm−1 and 220 cm−1, almost all modes in the nanoribbon display a stronger tendency to localization with PRs smaller than 0.4, which is a signature of the strong impact of the structural asymmetries, finite cross-section of the nanoribbons, and temperature. It is worth mentioning that, based on their polarization vector, the atoms are essentially vibrating in-plane during the NEMD simulation, but this behavior depends on the specific frequency of the vibrational mode (see the ESI† for additional details).
To complement the previous analysis, the spatial distribution of the vibrational modes located within a specific spectral range (Λ) was analyzed by defining the quantity ϕiα,Λ, which is computed as:39
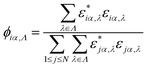 | (4) |
A large value of ϕiα,Λ indicates a strong contribution of the ith atom to vibrational modes belonging to the spectral region defined by Λ. To define the set Λ, three possible PR regions were selected, as shown in the central panel of Fig. 4: (I) p > 0.4, (II) 0.1 < p < 0.4, and (III) p < 0.1. The behavior of ϕiα,Λ for domains I and II turned out to be almost the same for forward and backward heat flows and we show these results in the ESI.† Hence, the modes in those spectral ranges do not seem to strongly determine the rectification of the heat current. Major differences were however found for region III as displayed in the left and right panels of Fig. 4. At this point, we need to make a remark concerning the graphical representation of the spatial distribution of the vibrational modes. In contrast to other 2D materials, which consist of a single atomic layer like graphene or BN, the MoS2 nanoribbon is made of three atomic layers. This makes the visualization of the quantity ϕiα,Λ more involved. We have however found, by analyzing the contribution of each atomic layer separately, that the two sulfur planes contribute in similar ways to the spatial distribution of the modes, something to be expected for symmetry reasons. Hence, we only show in Fig. 4 the contributions arising from the top S-layer as well as from the Mo-layer. The left and right panels of Fig. 4 illustrate the spatial distribution for the modes in region III for the forward (left panel) and backward (right panel) directions. The main observed feature is the strong increase, in the backward flow direction, in the number of atoms giving a low contribution (0.2–0.3) to the modes in spectral region III, i.e. for frequencies above 350 cm−1. This behavior mainly affects a set of atoms in the bulk of the nanoribbon, while atoms along the edges do not appreciably change the degree of their contribution to the selected spectral range. Moreover, we find that sulfur atoms are those mostly influenced upon reversal of the heat flow, while the contribution from Mo atoms is considerably less modified and remains relatively high (ϕiα,Λ > 0.5). A simple mathematical relationship between the degree of spatial localization of the vibrational modes and the heat current as computed in a NEMD run is difficult to establish. In this sense, our results only hint at the fact that the strong modification in the spatial distribution of certain groups of modes upon reversal of the direction of heat current flow in asymmetric nanostructures is a major factor determining the size of the thermal rectification effect found in the structurally asymmetric MoS2 nanoribbons. This conclusion is however further supported by a corresponding analysis carried out for the trapezoidal shaped nanoribbons, which show a very similar behavior (see the ESI†): a strong modification in the mode spatial distribution over the inversion of the heat current flow. To this effect, which has also been highlighted in earlier works on graphene nanoribbons,11,12 one also needs to add, as mentioned previously, the finite transversal size of the ribbons, which modifies the boundary conditions for the vibrational spectrum as well as its localization properties, and thus also strongly determines the heat transport features of the system. Clearly, these factors – asymmetry, finite size, mode localization – are not independent from each other and their interplay induces the observed rectification features in the MoS2 nanoribbons.
Lastly, to round off our discussion and to provide a better illustration of the influence of the lateral confinement on the thermal rectification, we have introduced the parameter:
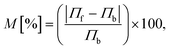 | (5) |
4 Conclusions
We have performed classical non-equilibrium molecular dynamics simulations to address thermal rectification effects in structurally asymmetric MoS2 nanoribbons. As a result of our study, the T-shaped nanoribbons displayed the largest rectification ratio (up to 30%), when compared with the trapezoidal and triangular structures, thus illustrating the strong sensitivity of thermal transport to the specific design of the lateral confinement. Our results clearly indicate that the thermal rectification effect is related to (i) shape asymmetries and (ii) changes in the degree of spatial localization of high-frequency modes (frequencies larger than 350 cm−1) under non-equilibrium heat transport conditions. Due to the more complex atomic structure of the MoS2 nanoribbons, we may expect that atomic-scale engineering, e.g. of the nanoribbon edges, will open broad possibilities for tailoring the thermal response of the systems. This goes, however, beyond the scope of the current study.Acknowledgements
L.M.S. thanks the International Max Planck Research School “Dynamical processes in atoms, molecules and solids” for the financial support. This work has also been partly supported by the German Research Foundation (DFG) within the Cluster of Excellence “Center for Advancing Electronics Dresden”. Computational resources were provided by the ZIH at the Dresden University of Technology and the Condensed Matter Group at National University of San Marcos (Peru).References
- N. Li, J. Ren, L. Wang, G. Zhang, P. Hänggi and B. Li, Rev. Mod. Phys., 2012, 84, 1045–1066 CrossRef.
- M. Maldovan, Nature, 2013, 503, 209–217 CrossRef CAS PubMed.
- H. Han, L. G. Potyomina, A. A. Darinskii, S. Volz and Y. A. Kosevich, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 180301 CrossRef.
- W.-R. Zhong, D.-Q. Zheng and B. Hu, Nanoscale, 2012, 4, 5217–5220 RSC.
- A. A. Balandin and D. L. Nika, Mater. Today, 2012, 15, 266–275 CrossRef CAS.
- J. Gomis-Bresco, D. Navarro-Urrios, M. Oudich, S. El-Jallal, A. Griol, D. Puerto, E. Chavez, Y. Pennec, B. Djafari-Rouhani, F. Alzina, A. Martnez and C. S. Torres, Nat. Commun., 2014, 5, 1–6 Search PubMed.
- J. Zhu, K. Hippalgaonkar, S. Shen, K. Wang, Y. Abate, S. Lee, J. Wu, X. Yin, A. Majumdar and X. Zhang, Nano Lett., 2014, 14, 4867–4872 CrossRef CAS PubMed.
- C. W. Chang, D. Okawa, A. Majumdar and A. Zettl, Science, 2006, 314, 1121–1124 CrossRef CAS PubMed.
- H. Tian, D. Xie, Y. Yang, T.-L. Ren, G. Zhang, Y.-F. Wang, C.-J. Zhou, P.-G. Peng, L.-G. Wang and L.-T. Liu, Sci. Rep., 2012, 2, 523 Search PubMed.
- J. Lee, V. Varshney, A. K. Roy, J. B. Ferguson and B. L. Farmer, Nano Lett., 2012, 12, 3491–3496 CrossRef CAS PubMed.
- T. S. Komatsu and N. Ito, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 010103 CrossRef PubMed.
- Y. Wang, A. Vallabhaneni, J. Hu, B. Qiu, Y. P. Chen and X. Ruan, Nano Lett., 2014, 14, 592–596 CrossRef CAS PubMed.
- N. Yang, G. Zhang and B. Li, Appl. Phys. Lett., 2009, 95, 033107 CrossRef.
- W. Kobayashi, Y. Teraoka and I. Terasaki, Appl. Phys. Lett., 2009, 95, 171905 CrossRef.
- A. K. Vallabhaneni, B. Qiu, J. Hu, Y. P. Chen, A. K. Roy and X. Ruan, J. Appl. Phys., 2013, 113, 064311 CrossRef.
- J. Lan and B. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 214305 CrossRef.
- Y. Chalopin and S. Volz, Appl. Phys. Lett., 2013, 103, 051602 CrossRef.
- J. Hu, X. Ruan and Y. P. Chen, Nano Lett., 2009, 9, 2730–2735 CrossRef CAS PubMed.
- Q.-X. Pei, Y.-W. Zhang, Z.-D. Sha and V. B. Shenoy, Appl. Phys. Lett., 2012, 100, 101901 CrossRef.
- G. Zhang and H. Zhang, Nanoscale, 2011, 3, 4604–4607 RSC.
- X. Xu, L. F. C. Pereira, Y. Wan, J. Wu, K. Zhang, X. Zhao, S. Bae, C. T. Bui, R. Xie, J. T. L. Thong, B. H. Hong, K. P. Loh, D. Donadio, B. Li and B. Özyilmaz, Nat. Commun., 2014, 5, 3689 CAS.
- R. Kappera, D. Voiry, S. E. Yalcin, B. Branch, G. Gupta, A. D. Mohite and M. Chhowalla, Nat. Mater., 2014, 1128–1134 CrossRef CAS PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- J. Wu, H. Schmidt, K. K. Amara, X. Xu, G. Eda and B. Özyilmaz, Nano Lett., 2014, 14, 2730–2734 CrossRef CAS PubMed.
- H. Babaei, J. M. Khodadadi and S. Sinha, Appl. Phys. Lett., 2014, 105, 193901 CrossRef.
- D. D. Fan, H. J. Liu, L. Cheng, P. H. Jiang, J. Shi and X. F. Tang, Appl. Phys. Lett., 2014, 105, 133113 CrossRef.
- T.-H. Liu, Y.-C. Chen, C.-W. Pao and C.-C. Chang, Appl. Phys. Lett., 2014, 104, 201909 CrossRef.
- D. Wickramaratne, F. Zahid and R. K. Lake, J. Chem. Phys., 2014, 140, 124710 CrossRef PubMed.
- J.-W. Jiang, X. Zhuang and T. Rabczuk, Sci. Rep., 2013, 3, 2209 Search PubMed.
- Y. Cai, J. Lan, G. Zhang and Y.-W. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035438 CrossRef.
- W. Li, J. Carrete and N. Mingo, Appl. Phys. Lett., 2013, 103, 253103 CrossRef.
- V. Varshney, S. S. Patnaik, C. Muratore, A. K. Roy, A. A. Voevodin and B. L. Farmer, Comput. Mater. Sci., 2010, 48, 101–108 CrossRef CAS.
- J.-W. Jiang, H. S. Park and T. Rabczuk, J. Appl. Phys., 2013, 114, 064307 CrossRef.
- J.-W. Jiang, Nanoscale, 2014, 6, 8326–8333 RSC.
- X. Liu, G. Zhang, Q.-X. Pei and Y.-W. Zhang, Appl. Phys. Lett., 2013, 103, 133113 CrossRef.
- M. Buscema, M. Barkelid, V. Zwiller, H. S. J. van der Zant, G. A. Steele and A. Castellanos-Gomez, Nano Lett., 2013, 13, 358–363 CrossRef CAS PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS PubMed.
- R. Yan, J. R. Simpson, S. Bertolazzi, J. Brivio, M. Watson, X. Wu, A. Kis, T. Luo, A. R. Hight Walker and H. G. Xing, ACS Nano, 2014, 8, 986–993 CrossRef CAS PubMed.
- J. Chen, G. Zhang and B. Li, Nano Lett., 2010, 10, 3978–3983 CrossRef CAS PubMed.
- Z. Wang, H. Li, Z. Liu, Z. Shi, J. Lu, K. Suenaga, S.-K. Joung, T. Okazaki, Z. Gu, J. Zhou, Z. Gao, G. Li, S. Sanvito, E. Wang and S. Iijima, J. Am. Chem. Soc., 2010, 132, 13840–13847 CrossRef CAS PubMed.
- J. V. Lauritsen, J. Kibsgaard, S. Helveg, H. Topsoe, B. S. Clausen, E. Laegsgaard and F. Besenbacher, Nat. Nanotechnol., 2007, 2, 53–58 CrossRef CAS PubMed.
- J. Kibsgaard, J. V. Lauritsen, E. Lgsgaard, B. S. Clausen, H. Topse and F. Besenbacher, J. Am. Chem. Soc., 2006, 128, 13950–13958 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- J. A. Stewart and D. E. Spearot, Modell. Simul. Mater. Sci. Eng., 2013, 21, 045003 CrossRef.
- T. Onodera, Y. Morita, A. Suzuki, M. Koyama, H. Tsuboi, N. Hatakeyama, A. Endou, H. Takaba, M. Kubo, F. Dassenoy, C. Minfray, L. Joly-Pottuz, J.-M. Martin and A. Miyamoto, J. Phys. Chem. B, 2009, 113, 16526–16536 CrossRef CAS PubMed.
- T. Onodera, Y. Morita, R. Nagumo, R. Miura, A. Suzuki, H. Tsuboi, N. Hatakeyama, A. Endou, H. Takaba, F. Dassenoy, C. Minfray, L. Joly-Pottuz, M. Kubo, J.-M. Martin and A. Miyamoto, J. Phys. Chem. B, 2010, 114, 15832–15838 CrossRef CAS PubMed.
- B. J. van Wees, H. van Houten, C. W. J. Beenakker, J. G. Williamson, L. P. Kouwenhoven, D. van der Marel and C. T. Foxon, Phys. Rev. Lett., 1988, 60, 848–850 CrossRef CAS PubMed.
- L. Zhu and B. Li, Sci. Rep., 2014, 4, 4917 CAS.
- A. Bodapati, P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 245207 CrossRef.
- P. K. Schelling and S. R. Phillpot, J. Am. Chem. Soc., 2001, 84, 2997–3007 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra05733g |
| This journal is © The Royal Society of Chemistry 2015 |