A reversible turn-off fluorescence probe (HNAPP) for Zn(ii) ion and inorganic phosphate ions (H2P and HP) at physiological pH

Abstract

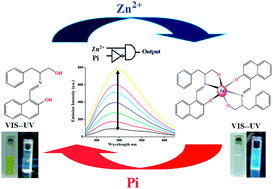
A simple and low-cost new Schiff base compound (HNAPP) of 2-hydroxynaphthaldehyde and 2-amino-3-phenyl-1-propanol was synthesized and characterized by ¹H NMR and mass spectroscopic technique. The optimized structure of the probe in different polarity solvents and the potential energy scan reveal that the probe is stable as an enol tautomer in polar solvent, while in less polar solvent the keto tautomer is more prominent. In dichloromethane, the keto tautomeric form of the probe undergoes an excited state intramolecular proton transfer, ESIPT, into a stable enol structure that reveals unusual relaxation routes after electronic excitation. The results, accompanied by TDDFT calculations, are used to diagram the relaxation routes of an excited HNAPP molecule. The probe exhibited highly selective and sensitive turn-on fluorescence emission towards Zn²⁺ over other common metal ions in a physiological pH window with a 2 : 1 binding mode. The association constant, K_assoc, was observed at 5.2 × 10⁴ M⁻¹. The fluorescence decay constant (s) values were determined from time-resolved fluorescence study. The addition of inorganic phosphate ions quenched the fluorescence intensity of the complex at different pH values, enabling the receptor HNAPP to act as a reversible chemosensor and a pH modulator. On the basis of these observations, I developed a unique molecular system capable of performing logic functions such as INHIBIT by simply varying the level of various ionic inputs in a systematic manner.