Vibrational spectra of solid cis- and trans-2-thioxohexahydroquinazolin-4(1H)-one and theoretical calculations towards the interpretation of its thermal reactivity

Abstract

FT-Raman and FT-IR spectra of solid cis- and trans-2-thioxohexahydroquinazolin-4(1H)-one are reported from 4000 to 200 cm⁻¹. The molecular geometry, Wiberg Index, NBO analysis and vibrational wavenumbers in the ground state have been calculated using a density functional method (B3LYP) with 6-31+G** and 6-311+G** basis set. Both compounds are stable as dimers in the solid phase, possessing C2 symmetry. The scaled theoretical wavenumbers showed very good agreement with the experimental values. This work contributes to the knowledge of important data which are rather scarce for quinazolinones.

---

Introduction

Despite the wide range of biological activity that compounds containing the RNH–C(X)–NR–C(O)R (X = S, O) moiety possess,^1–3 many molecules with fused quinazoline or isoquinazoline rings have not been studied thoroughly.⁴ Beyond their attractiveness as biological and pharmacological active agents, their use as models to understand important organic chemical processes is another relevant topic. For that reason, in the last years many efforts were focused on studying the structural characteristics. Thus, two interesting compounds have been recently reported:⁵ 5-benzyl-2-thiohydantoin (5-BTH) and 1-acetyl-5-benzyl-2-thiohydantoin (1-Ac-5-BTH), which possess the thiohydantoine nucleus. The structural study of these molecules evidenced the near planarity of the thiohydantoine ring, showing a slight deviation from the plane of 0.036 and 0.052 Å for 5-BTH and 1-Ac-5-BTH, respectively. Besides, the X-ray diffraction analysis indicates that both compounds are present as dimers in the solid, linked by O⋯H and S⋯H interactions (with bond distances of 2.07(2) Å and 2.58(2) Å, respectively).

Recently, we have synthesized and analyzed 5-benzyl-3-phenyl-2-thioxoimidazolidin-4-one (BPT) and its dehydrogenated derivative compounds, phenylmethylene-3-phenyl-2-thioxoimidazolidin-4-one (PPT) in both solid and gas phases.⁶ These species possess the 5-arylmethylene-2-thioxoimidazolidin-4-one nucleus, which has demonstrated to be important as antimycobacterials,⁷ immunomodulators,⁸ anticonvulsivants⁹ and antifungals.¹⁰ Particularly, PPT was obtained in crystal form, thus X-ray diffraction analysis could be done to conclude that a substantial part of the molecule is planar, excluding the aromatic ring attached to the N3 atom. This planar conformation was attributed to the conjugation of the heterocycle with the aromatic ring at the position of the methylene moiety. The intramolecular distance N–H⋯S indicates hydrogen bonding, linking the molecules into dimers [N–H⋯S = 2.583(18)Å].⁶

In recent times, we have also studied the thermal dissociation of a series of hexahydroquinazoline-4(1H)-one compounds using flash vacuum pyrolysis (FVP) techniques,³ where the thermal reaction occurs through a four-center transition state yielding isothiocyanates as products. In a latter study,¹¹ we have also dealt with the analysis of the specific forms that the cis and trans 2-thioxo-hexahydroquinazolin-4(1H)-one molecules adopt in the gas phase, in order to have a deeper insight into this process. Two tautomers were found in the gas (NH and SH forms), with the equilibrium shifted to the NH one. Since the energy difference between them is around 12 kcal mol⁻¹ – in the solid at room temperature – only the NH form should be expected. Nevertheless, the reaction in gas phase takes place from the SH tautomer.

As we have already analyzed the entire energetic of the mechanism of thermal decomposition,¹¹ we are now interested in describing ways to correlate the reactivity of the compounds in the gas phase with variables experimentally observed (such as the vibrational spectra of the solid), mainly considering that the acquisition of the infrared or Raman spectra of the SH conformers in the gas phase could be a very difficult task.

Thus, we report here a comprehensive analysis of the Raman and IR spectra of 2-thioxohexahydroquinazolin-4(1H)-one, complemented with structural parameters and calculus of electronic delocalizations.

Result and discussion

Vibrational analysis

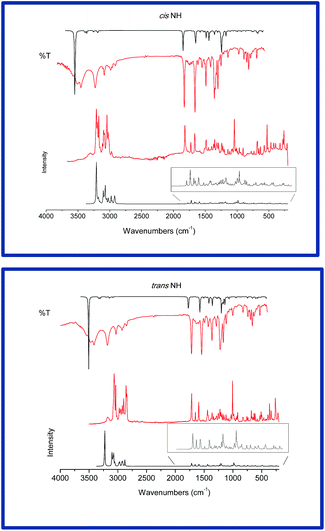
Quantum chemical calculations have demonstrated to be a powerful tool to simulate both IR and Raman spectra. Particularly, DFT functional theory calculations provide excellent vibrational frequencies of organic compounds if these frequencies are scaled to compensate for the approximate treatment of electron correlation, the basis set deficiencies and the anharmonicity.^12–14 Although it is possible to calculate the anharmonicities through second-order perturbation theory with commercial programs such as GAUSSIAN 09,¹⁵ this is still prohibitive for larger molecules. Nevertheless, by scaling the calculated harmonic frequencies, the accuracy is similar to that achieved through the direct calculus because the overestimation of the vibrational frequencies is fairly uniform.¹⁶ For the thioxo-hexahydroquinazolin-4(1H)-ones we used the uniform scale factor of 0.9679, since it proved to be the more appropriate (rms error < 37%) for the 6-311+G(d,p) basis set.¹⁶ Fig. 1 shows graphic representations of experimental vs. scaled frequencies for the cis and trans NH dimers. In both cases, the slopes are close to one, indicating the appropriateness of the chosen parameter for all the vibrational modes.

Fig. 1 Experimental vs. calculated wavenumbers for cis (upper) and trans (bottom) NH tautomers. The curves corresponding to the IR experimental data are displaced 300 cm⁻¹ from the real values, in order to show more clearly the observed trend.

Both dimers belong to the C₂ symmetry group, thus their normal modes can be split up in two blocks (A and B). 186 normal modes of vibration are expected, 91 as A while 89 modes belong to the B block (all of them active in both infrared and Raman).

The observed bands with their relative intensities, scaled wavenumbers and assignments are given in Table S1 (ESI†). For a visual comparison, the experimental and simulated FT-IR and FT-Raman spectra are presented in Fig. 2.

Fig. 2 Experimental and calculated vibrational spectra of cis and trans NH molecules. Black traces, calculated infrared (upper) and Raman (bottom) spectra. Red traces, experimental infrared (upper) and Raman (bottom) spectra.

N–H vibrations

It is reported that the calculated wavenumber (DFT method) of the N–H stretching vibration in molecules where the bond is participating in H-bridges, falls ±200 cm⁻¹ from the pure N–H experimentally observed.^17–20

For both cis and trans NH tautomers, the calculus predicts for the Raman spectra: 3245 cm⁻¹ (block B) and 3220 cm⁻¹ (A block) (attributed to the signals located at 3165 cm⁻¹), for the cis NH; and 3257 cm⁻¹ (B block) and 3235 cm⁻¹ (A block), assigned to the band at 3178 cm⁻¹ for trans NH.

The number of infrared signals in this region is higher than the expected. This fact can be explained through the Fermi resonance, which appears when fundamental vibrational levels lie close in energy to an overtone or a combination level of the same symmetry giving new signals. These new peaks are observed with their spectral intensities as a combination of the corresponding fundamentals.²¹ In several cases,^{19,20,22–24} this effect is enough to explain the experimental/calculated spectral differences, but when the molecule shares both N–H and C–H groups, the bands attributed to the Fermi effect appear in the 3650–3300 cm⁻¹ region while in the Raman spectra, they are observable as broad low intensity signals (centered at 3161 and 3184 cm⁻¹, for cis and trans NH tautomers, respectively).^25,26

C–H vibrations

The 3100–3000 cm⁻¹ region is characteristic for the ready identification of C–H stretching vibrations. Again here, a higher number of signals due to the Fermi resonance clearly appear in the spectra of both compounds, causing a noticeable modification of the appearance of the experimental vs. calculated spectra, specifically in the higher wavenumber's region.

C=O vibrations

The location of the carbonyl group signals has a strong dependence on both the functional groups attached and the crystal form in the solid, being commonly observed in the 1850–1550 cm⁻¹ region. Taking into account the vibrational analysis performed for the molecules used as reference (ref. 5 and 27), a large spread in the assigned values is observed, depending on the spatial configurations that the thiohydantoines adopt in the solid, i.e. whether the oxygen atom participates in intermolecular bridges. For example, 5-BTH⁵ is a cyclic dimer, possessing two H-bridges from the thioamide and amide moieties, respectively. For that compound, the carbonyl vibrational mode was assigned to the signals at 1740 cm⁻¹ (IR) and 1724 cm⁻¹ (Raman). Besides, the C=O stretching of 1-Ac-5-BTH (which forms an infinite chain in the crystal), was attributed to the band at 1747 and 1756 cm⁻¹ in the infrared and Raman spectra, respectively. In this case, it was proved that the oxygen atom participates actively determining the intermolecular bonds.

On the other hand, 1-acetyl-2-thiohydantoine,²⁷ can be either found as a trimer (called T_A) or tetramer (called T_B) in the solid. For T_A, the carbonyl stretching appears at 1740 and 1747 cm⁻¹ (IR and Raman, respectively), while for T_B, this mode is assigned to the band at 1666 and 1674 cm⁻¹ (Raman and infrared, respectively). For this species, the oxygen also participates in an H-bridge.

In the case of PPT,⁶ it was determined that the molecule is a dimer in the solid, linked only by N–S⋯H interactions, which means that there are not O⋯H bridges present in the crystal. For this compound, the signal at 1743 cm⁻¹ in the infrared spectra is assigned to the C=O stretching vibration.

With this in mind, the carbonyl stretching for the cis NH tautomer was assigned to the sharp signal in the infrared at 1742 cm⁻¹ and at 1732 cm⁻¹ in the Raman; and at 1719 cm⁻¹ (IR) and 1723 cm⁻¹ (Ra) for the trans one. At this point, it should be important to recall our assumption about the hexahydroquinazolinones as dimer in the solid, with both monomers connected to form cyclic dimers via the hydrogen bonds of the thioamide moiety solely.⁶ In order to rule out any other spatial arrangement, i.e. structures with the oxygen atom forming hydrogen bonds, DFT calculations were performed proposing a dimer with both S⋯H/O⋯H bonds. The results show that the carbonyl stretching band is shifted down for about 40 cm⁻¹ approximately. These results are in disagreement with the experimental evidence, thus confirming our assumption of the dimers linked by S⋯H interactions only.

C=S vibrations

The position of the C=S band also depends on the different forms in which the thiohydantoines crystallize, because there could exist a variable number of H-bridges in which the sulfur atom participates, causing that the frequency of vibration falls into a wide range of wavenumbers. For example, 1-acetyl-2-thiohydantoine²⁷ is a polymorph, and the stretching band is located at 1039 and 1037 cm⁻¹ (IR and Ra, respectively) for T_A, and at 1040 and 1033 cm⁻¹ (IR and Ra, respectively) for T_B. In the case of 2-thiohydantoine, it is observed at 1156 and 1158 cm⁻¹ (IR and Ra, respectively) for the trimer and at 1165 cm⁻¹ for the tetramer (Raman only).²⁸ The PPT molecule is the one with both C=S⋯H interactions, analogous to the hexahydroquinazolinones under study. The stretching mode of vibration was assigned at 1251 cm⁻¹ in the IR spectrum, and it is predicted at 1247 (B block) and 1243 cm⁻¹ (A block), according to the B3LYP/6-31+(d,p) method. In all the cited cases, it was observed a very strong coupling with those movements involving C and N atoms. In our case, this normal mode is attributed to the bands located at 1237 and 1242 cm⁻¹ (for cis NH, infrared and Raman, respectively) and 1225 cm⁻¹ (both, infrared and Raman) for trans NH. It is worth to mention that the coupling with C–N stretching is also observed.

C2–N3 vibrations

On the basis of the equation taken from the simple harmonic oscillator model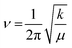 , (with k = force constant; μ = reduced mass), it is possible to obtain valuable information about bond strengths by comparing the frequencies of the modes of vibration. For the title compounds, the C2–N3 bond in both cis and trans conformers are determinant in the thermal reaction; hence, the analysis of this mode is the key to understand the whole process to obtain the corresponding isothiocyanates.^3,11 Considering that he reduced mass of the C2–N3 stretching vibration is the same in both cases, the strength of the bond only depends on the force constant (k), thus it is strongly affected by electronic interactions.

The clue in the thermal reaction (FVP) is the rupture of the C2–N3 bond to produce isothiocyanates, which takes place at different temperatures depending on the conformation (cis or trans) of the starting reagent (Fig. S1, ESI†). For that reason, our efforts are focused upon elucidating the relationship between geometric parameters/electronic distributions and the lability of the mentioned bond. The analysis of the normal mode of vibration is an effective means to carry out this task. According to the calculus, the C2–N3 stretching is strongly coupled with the N1–C2 stretching, determining two (symmetric and antisymmetric) vibrations for both cis and trans NH tautomers (both symmetric and antisymmetric modes of vibration are highlighted in Table S1, in the ESI†). The N1–C2–N3 antisymmetric stretching appears at higher wavenumbers (200 cm⁻¹ approximately) than the symmetric one in both cis and trans tautomers. In the cases of the cis NH, the antisymmetric stretching (ν_a) was experimentally observed at 1392 cm⁻¹ in both infrared and Raman spectra; while the symmetric (ν_s) was assigned to the bands at 1237 (IR) and 1242 (Raman) cm⁻¹. The calculus predict the location of ν_a at 1415 cm⁻¹ (A block) and 1398 cm⁻¹ (B block), and at 1235 cm⁻¹ (A and B) for the ν_s. For the trans tautomer, the corresponding values for the ν_a was attributed to the 1421 cm⁻¹ (only observed in the infrared spectra); while the ν_s was observed in both infrared and Raman spectra, and it was assigned to the bands at 1225 cm⁻¹. It should be noted that theoretical C–N antisymmetric stretching values (of both cis and trans NH tautomers) fall into the 1415–1410 cm⁻¹ range, while in the experimental spectra there exist a difference of 30 cm⁻¹. The same occur with the symmetric mode, presenting a difference about 15 cm⁻¹ in the infrared and Raman spectra. The analysis of the vibrations effectively observed in the solid opens the way to saying that the trans molecule has the C–N bond stronger than the cis one, thus being more difficult to be broken.

In the gas phase, the SH tautomers gain importance and participate in the thermal reaction through the breaking of the C2–N3 bond, as was mentioned previously. For them, theoretical results indicate a bigger difference between the stretching wavenumbers of cis (1263 cm⁻¹) and trans (1282 cm⁻¹), which is in accordance with the experimentally observed for the NH species, i.e. the trans compounds (NH and SH) have the C2–N3 bonds vibrating at higher wavenumbers, thus needing higher energy to break them down.

For comparison, this stretching is assigned at 1353 cm⁻¹ (IR) and 1350 cm⁻¹ (Raman) for 1-acetyl-2-thiohydantoine (T_A) and at 1329 and 1336 cm⁻¹ (infrared and Raman, respectively) for the tetramer.²⁷ For 5-BTH, this mode is assigned to the bands located at 1549 and 1522 cm⁻¹ (IR and Raman, respectively); and for 1-Ac-5-BTH, to the signals 1464 cm⁻¹ (infrared) and 1432 cm⁻¹ (Raman).

Structural analysis

As was mentioned elsewhere,¹¹ the predominant tautomer in the solid is the NH, with a substantial increase in the concentration of the SH form at temperatures reaching the dissociation. In Fig. 3 it is shown the atom numbering of the conformations (for both monomer and dimer forms), while in Fig. S2 (ESI†) it is depicted the tridimensional representation of the dimers.

Fig. 3 (Top) tautomers and conformers of 2-thioxo-hexahydroquinazolin-4(1H)-ones. In the solid phase, the equilibrium is displaced toward the NH form. (Bottom) atom numbering of cis/trans NH dimer, defined as two block I and II.

Table 1 presents the optimized geometric parameters (bond lengths and torsion angles) of cis and trans NH tautomer in comparison with structural data of 5-BTH, 1-Ac-5-BTH and PPT taken as references. In the table it is also presented the parameters of the SH forms, because the infrared spectra are registered in the solid phase – where the species are present as NH tautomers – while the FVP reaction takes place from the SH species,³ as was mentioned previously. Thus, it is important to establish a valid correlation between parameters calculated for the solid, to their direct application into the gas phase.

Table 1 Geometrical parameters (bond length and torsional angles) calculated and compared with experimental results

Parameters^c	Calculated (B3LYP/6-31+G**)				X-ray diffraction data
	cis NH	trans NH	cis SH	trans SH	5-BTH^a	1-Ac-5-BTH^a	PPT^b
a Ref. (5).b Ref. (6).c Mean value for calculated H-bond lengths.
Bond lengths
C5–C10	1.533	1.529	1.537	1.536
C10–N1	1.460	1.461	1.470	1.462	1.462(2)	1.477(2)	1.388(2)
N1–C2	1.340	1.341	1.273	1.273	—	—	1.347(2)
C2–N3	1.406	1.405	1.417	1.416	—	—	1.385(2)
N3–C4	1.415	1.414	1.410	1.408	—	—	1.397(2)
C4=O13	1.216	1.217	1.218	1.218	1.214(2)	1.217(2)	1.205(2)
C2=S12	1.689	1.688	—	—	1.666(1)	1.645(2)	1.651(2)
C4–C5	1.526	1.518	1.518	1.519	—	—	—
N3–C14	1.451	1.451	1.444	1.445	—	—	1.431(2)
C2–S12	—	—	1.794	1.798	—	—	—
S12–H11	—	—	1.347	1.347	—	—	—
S12⋯H	2.39	2.43	—	—	2.58(2)	2.00(2)	2.58(2)
Torsion angles (°)
C10–N1–C2–N3	6.6	−8.0	−3.7	−2.4	—	—	—
C4–N3–C2–S12	−165.4	166.2	160.3	163.1	178.5(1)	−178.0(1)	178.3(2)
N1–C2–N3–C4	14.5	−13.5	−18.7	−16.4	—	—	0.7(2)
C2–N3–C4–C5	2.8	−1.5	−0.3	−1.9	—	—	−0.7(2)
N3–C4–C5–C13	−37.2	34.1	35.5	33.4	—	—	—
C4–C5–C10–N1	53.0	−50.3	−55.7	−50.4	—	—	—
O13–C4–N3–C14	3.5	−3.3	−1.7	−2.7	—	—	3.6(2)
O13–C4–N3–C2	179.7	−179.8	−178.7	−179.7	−178.7(2)	−178.6(1)	179.0(2)
N1–C2–S12–H11	—	—	0.6	0.3	—	—	—

---

NBO analysis

The electronic interactions were studied by NBO (natural bond order) analysis, which transforms the canonical delocalized Hartree–Fock molecular orbital into localized orbital that are closely tied to chemical bonding concepts.²⁹ Filled NBOs describe the hypothetical, strictly localized Lewis structure.

The interactions between filled and antibonding orbitals represent the deviation of the molecule from the Lewis structure and can be used as a measure of delocalization.³⁰

As was specified in the Introduction section, all the equilibria between different isomers as well as the structural analysis of the molecules have been already studied,¹¹ thus we will start analyzing the most relevant electronic characteristics.

Taking into account the unit O13–C4–N3–C2–S12 (red sequence in Fig. 3), it is possible to differentiate two representative dihedral angles: O13–C4–N3–C2 and C4–N3–C2–S12, both highlighted in the table. The corresponding experimental values of these angles in 5-BTH, 1-Ac-5-BTH and PPT are close to 180°, corroborating the planar structure of thiohydantoines. For our both tautomers (NH and SH), only the O13–C4–N3–C2 angle presents a value close to 180°. The C4–N3–C2–S12 dihedral has a difference of ≈20°, implying that the hexahydroquinazoline moiety is slightly deviated from planarity. Nevertheless, the NBO results show strong delocalizations in the ring, suggesting that the orbitals present an adequate overlapping to favor electronic interactions. In Table 2 are presented the most relevant NBO donor–acceptor interactions for all the tautomers, together with their corresponding values.

Table 2 Donor acceptor interactions and NBO delocalization energies

Orbitals		Deloc. energy (kcal mol^−1)
Donor	Acceptor A–B bond	cis NH	cis SH	trans NH	trans SH
LP N3	σ*C2–S12	7.29	1.12	3.15	0.86
	π*C2–S12	21.84	—	34.18	—
	π*C4=O13	48.15	48.94	48.47	49.26
	π*C2–N1	—	39.51	—	40.33
LP N1	σ*C2–S12	15.80	2.38	8.73	2.59
	π*C2–S12	19.51	—	30.82	—
	σ*C2–N3	—	17.88	—	18.01
LP O13	σ*C4–N3	30.43	31.22	30.35	31.72
	σ*C4–C5	19.87	18.30	19.51	21.59

---

The most stabilizing interaction in molecules containing the N–C=O moiety is the delocalization from the lone pair of the nitrogen atom toward the pi antibonding orbital of the carbonyl group (LP N → π*C=O) that contributes largely to the resonance effect,^{19,20,31–34} and it was also observed in hexahydroquinazolines. From the point of view of the delocalization, it is reasonable to think that this moiety will remain bonded after the thermic rupture independently of the tautomer considered. Following in importance, we find the LP N3 → π*C2–N1 that reinforces the electronic density of the C2–N3 bond through the passage of the electrons toward the antibonding C2–N1 orbital. The value is higher (40.33 as opposed to 39.51 kcal mol⁻¹) for the trans thiol tautomer suggesting an increased stability for it. Another analysis that shows why the trans thiol tautomer should be more stable, has to do with the delocalization afforded by the LP N1 → σ*C2–N3 that leads to an increased electronic density directly over the antibonding C2–N3 orbital (thus weakening the C2–N3 bond), and which is more pronounced for the cis tautomer. Fig. 4 depicts the mentioned interactions for a more clear understanding.

Fig. 4 Representation of the most representative electronic delocalizations in (a) cis SH and (b) trans SH; LP N3 → π*C2–N1 (right) and LP N1 → σ*C2–N3 (left), in each figure respectively.

For the cis and trans NH conformers, the delocalization from the LP N3 to π*C2=S12 orbitals (with an energy of 21.84 kcal mol⁻¹ (for the cis) and 34.18 kcal mol⁻¹ (for the trans)), indicates that the C2–N3 bond is stronger in the trans NH than in the cis one, thus following the same trend than the thiol tautomers.

Other useful tool to this kind of studies is the bond order analysis from the natural atomic orbitals (NAO formalism, included in the NBO package). These parameters, called Wiberg bond indexes, consist on the sum of the squares of off-diagonal density matrix elements between atoms, and it is a positive quantity giving idea of the corresponding bond order in the molecule. Thus, values close to 1 suggest a single bond, while those closer to 2 indicate bonds with double bond character. The magnitude of the values is related to the electronic population that results of electronic delocalizations to bonding or antibonding orbitals. Table 3 shows the Wiberg indexes obtained for both dimer and monomer cis/trans NH and SH species. The calculus was carried out for all of the possible forms present in the solid and for the monomeric SH species present in the gas.

Table 3 Wiberg indexes calculated for the most important bonds

	Bond	Molecules
		Monomers				Dimers
		cis NH	trans NH	cis SH	trans SH	cis NH	trans NH
Wiberg index	C2–N3	1.0496	1.0534	1.0160	1.0185	1.0584	1.0621
	C4=O13	1.7423	1.7418	1.7377	1.7364	1.7470	1.7460
	C2–S12	1.5730	1.5743	1.0744	1.0746	1.4721	1.4745
	C4–N3	1.0473	1.0476	1.0477	1.0495	1.0391	1.0411
	C2–N1	1.2200	1.2171	1.7654	1.7641	1.2944	1.2904

---

The first row shows the indexes corresponding to the C2–N3 bond. It can be seen that for the cis thiol tautomer, the value is the lowest, which implies that this bond is the weakest of the molecule. This fact together with the electronic contributions calculated through the NBO subroutine, would justify the weakness of the bond, hence its reactivity. Even though the row corresponding to the C4–N3 bond has values somewhat lower than those corresponding to the C2–N3 bond (excepting for the cis and trans thiol tautomers), this factor is not enough to overcome the strong effect caused by the resonance over the N–C=O moiety (discussed in the NBO section), in both dimer and monomer NH species. Thus, this C2–N2 bond will remain unbroken. Other remarkable feature is the low double bond character of both C4=O13 and C2–N1 bonds, suggesting strong electronic delocalizations, i.e. the presence of resonant structures. These results are in accordance with the interactions calculated by NBO.

A comparison of the last two columns (cis and trans tautomers) reveals a comparable trend, that is, the same bonds are expected to be broken under thermal excitation. Nevertheless, the trans SH presents a higher value that could be associated to the lower reactivity of the bond, ergo to the temperature of reaction, i.e. the trans species reacts at higher temperature than its cis counterpart.

We also compared the indexes for both cis and trans NH monomers in solid state. In general, it was observed that the C2–N3 bond index is slightly higher for the trans NH, suggesting that this bond is stronger also in the solid phase.

Conclusions

The assignment of the experimentally observed vibrational spectra of NH tautomers was performed for the first time. Both structure and electronic delocalizations were analyzed and it was possible to show a rather clear dependence between the C2–N3 bond strength and the thermal behavior under FVP conditions.

Experimental section

The title compounds were synthesized following reported procedures.³ Raman spectra between 3600–200 cm⁻¹ were registered using a FTIR-Raman Spectrum GX from Perkin Elmer, (spectral resolution 4 cm⁻¹). The 9395 cm⁻¹ radiation line of a Nd/YAG laser was used for excitation and the detector was InGaAs. Infrared spectra were recorded at room temperature with a Bruker IFS-28 FT IR spectrometer, in the range 4000–400 cm⁻¹. The spectra were recorded from solid samples in KBr pellets, (spectral resolution 2 cm⁻¹). The solid samples were handled at room temperature.

Computational details

Full geometry optimization was performed by using the GAUSSIAN 09 (ref. 15) program. Optimized structural parameters of the molecules (both monomers and dimers) were used in the calculus of the harmonic vibrational frequencies, infrared intensities and Raman scattering activities.

We have utilized the gradient corrected density functional theory,³⁵ with the three-parameter hybrid functional (B3) for the exchange part³⁶ and the Lee–Yang–Parr (LYP) correlation function,³⁷ accepted as a cost-effective approach for the computation of the molecular structure, vibrational frequencies and energies of optimized structures. The PED analysis was carried out with the aid of the VEDA program.³⁸ By combining the results of the VEDA and GAUSSVIEW program³⁹ with symmetry considerations, and by comparison with related molecules, vibrational frequency assignments were made with a high degree of confidence.

A powerful tool used to study the electronic interactions is the NBO subroutine, which allows to analyze many-electron wavefunctions in terms of localized electron-pair bonding units,²⁹ i.e. interactions between the filled (donor) Lewis-type NBO and empty (acceptor) non-Lewis NBO.⁴⁰ Thus, delocalization energy values obtained from the calculus are the measure of the importance of each interaction. Electronic delocalizations, orbital populations and Wiberg bond orders⁴¹ were analyzed using NBO 5.0 program⁴⁰ implemented in Gaussian 09. All the calculations were performed in vacuum without considering the environment of the molecule.

Acknowledgements

Authors thank Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) and Secretaría de Ciencia y Tecnología–Universidad Nacional de Córdoba (SECyT-UNC) for financial support.

Notes and references

1. V. Alagarsamy, D. Shankar, V. R. Solomon, R. V. Sheorey and P. Parthiban, Acta Pharm., 2009, 59, 75–88.
2. C. A. Mosley, T. M. Acker, K. B. Hansen, P. Mullasseril, K. T. Andersen, P. Le, K. M. Vellano, H. Bräuner-Osborne, D. C. Liotta and S. F. Traynelis, J. Med. Chem., 2010, 53, 5476–5490.
3. W. J. Peláez, Z. Szakonyi, F. Fülöp and G. I. Yranzo, Tetrahedron, 2008, 64, 1049–1057.
4. C. Y. Panicker, H. T. Varghese, K. R. Ambujakshan, S. Mathew, S. Ganguli, A. K. Nanda and C. Van Alsenoy, J. Raman Spectrosc., 2009, 40, 1262–1273.
5. K.-K. Kunimoto, M. Ichitani, T. Ogawa, S. Kitoh, A. Kuwae and K. Hanai, Spectrosc. Lett., 2009, 42, 73–80.
6. A. J. Pepino, W. J. Peláez, E. L. Moyano and G. A. Argüello, Eur. J. Org. Chem., 2012, 2012, 3424–3430.
7. E. Szyman, Farm., 2002, 57, 909–916.
8. V. Chazeau, M. Cussac and A. Boucherle, Eurasian J. Med., 1992, 27, 615–625.
9. W. Chui, T. Wong and J. Thenomozhiyal, J. Med. Chem., 2004, 47, 1527–1535.
10. J. Marton and J. Enisz, J. Agric. Food Chem., 1993, 41, 148–152.
11. W. J. Peláez, A. G. Iriarte, Z. Szakonyi, F. Fülöp and G. A. Argüello, J. Anal. Appl. Pyrolysis, 2012, 96, 181–187.
12. N. C. Handy and C. W. Murray, J. Phys. Chem., 1993, 97, 4392–4396.
13. P. Stephens, F. Devlin, C. Chabalowski and M. J. Frisch, J. Phys. Chem. Lett., 1994, 98, 11623–11627.
14. F. J. Devlin, J. W. Finley, P. J. Stephens and M. J. Frisch, J. Phys. Chem., 1995, 99, 16883–16902.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2010.
16. M. P. Andersson and P. Uvdal, J. Phys. Chem. A, 2005, 109, 2937–2941.
17. M.-A. Mroginski, K. Németh, T. Bauschlicher, W. Klotzbücher, R. Goddard, O. Heinemann, P. Hildebrandt and F. Mark, J. Phys. Chem. A, 2005, 109, 2139–2150.
18. C. Y. Panicker, H. T. Varghese, K. R. Ambujakshan, S. Mathew, S. Ganguli, A. K. Nanda, C. Van Alsenoy and Y. S. Mary, J. Mol. Struct., 2010, 963, 137–144.
19. A. G. Iriarte, M. F. Erben, K. Gholivand, J. L. Jios, S. E. Ulic and C. O. Della Védova, J. Mol. Struct., 2008, 886, 66–71.
20. A. G. Iriarte, E. H. Cutin, M. F. Erben, S. E. Ulic, J. L. Jios and C. O. Della Védova, Vib. Spectrosc., 2008, 46, 107–114.
21. P. Kondratyuk, Spectrochim. Acta, Part A, 2005, 61, 589–593.
22. R. Ryason and M. K. Wilson, J. Chem. Phys., 1954, 22, 2000–2003.
23. M. P. Freitas, C. F. Tormena, R. Rittner and R. J. Abraham, Spectrochim. Acta, Part A, 2003, 59, 1783–1789.
24. R. M. S. Alvarez, R. N. Farías and P. Hildebrandt, J. Raman Spectrosc., 2004, 35, 947–955.
25. O. Hritzová and D. Koscik, Collect. Czech. Chem. Commun., 1994, 59, 951–956.
26. V. Krishnakumar and S. Muthunatesan, Spectrochim. Acta, Part A, 2007, 66, 1082–1090.
27. A. Sharma, V. Gupta, P. Tandon, P. Rawat, S. Maeda and K.-K. Kunimoto, Spectrochim. Acta, Part A, 2012, 90, 141–151.
28. A. Sharma, V. Gupta, R. Mishra, P. Tandon, S. Maeda and K.-K. Kunimoto, J. Mol. Struct., 2011, 1004, 237–247.
29. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
30. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
31. A. G. Iriarte, E. H. Cutin and G. A. Argüello, Aust. J. Chem., 2011, 64, 1366–1372.
32. A. G. Iriarte, E. H. Cutin and G. A. Argüello, Spectrochim. Acta, Part A, 2014, 120, 137–143.
33. A. G. Iriarte, E. H. Cutin and C. O. Della Védova, J. Mol. Struct., 2006, 800, 154–157.
34. A. G. Iriarte, E. H. Cutin, S. E. Ulic, J. L. Jios and C. O. Della Védova, Vib. Spectrosc., 2007, 43, 290–296.
35. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
36. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
37. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
38. M. H. Jamróz, Vib. Energy Distrib. Anal. VEDA 4, 2010.
39. A. Frisch, A. B. Nielson and A. J. Holder, Gaussview Users Manual, Gaussian Inc., Pittsburg, 2000.
40. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO 3.1.
41. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1092.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra05645d

---