Highly stable ionic liquid-in-water emulsions as a new class of fluorescent sensors for metal ions: the case study of Fe³⁺ sensing

Abstract

The first example of a fluorescent highly stable pure binary ionic liquid (IL)-in-water emulsion is here described. The system is inexpensive, easy to synthesize and can be used as a selective fluorescent probe for metal ions. In particular, the system is able to recognize Fe³⁺ ions in pure water by a fluorescence “turn-off” mechanism.

---

Introduction

Ionic liquids (ILs) are a class of electrolytic solvents endowed with appealing characteristics, including non-flammability, negligible vapor pressure, and high chemical and thermal stability. They have been widely investigated in recent years since they can find application in various fields.^1–3 Remarkably, they have been used as water or oil substitutes, as well as additives or surfactants in the formulation of a huge number of soft matter based colloidal systems, such as micelles, microemulsions, liquid crystals, and emulsions.^4–7 Similarly to traditional oil-in-water emulsions,^8,9 IL-in-water emulsions are thermodynamically unstable dispersions, whose kinetic stability is generally increased by adding to the binary system a number of different stabilizers, including surfactants,¹⁰ liquid crystals, fine particles (Pickering emulsions),¹¹ carbon nanotubes,¹² or microgels.¹³

However, practical applications would plainly benefit from the formulation of stable binary IL-in-water emulsions, not to mention the central importance the study of the pristine IL-water interface may have from a theoretical point of view.

Although a very limited number of examples of oil-in-water,^14,15 truly binary, stable, and surfactant-free emulsions has been described so far, IL-in-water analogues have not been reported yet. In the following, we will discuss about the first case of such systems originated by simply dispersing in water via sonication at room temperature a newly synthesized fluorescent IL.

Taking into account the fluorescent characteristics of this IL and given the extreme relevance the research of highly selective and sensitive fluorescent probes for metal ions recognition has gained in the last decades for environmental and biological applications,^16–24 the emulsion was checked for its ability to recognize metal ions in water.

Experimental methods

All reactions were performed in oven-dried glassware. ¹H-NMR (500 MHz) and ¹³C NMR (125 MHz) spectra were determined on a Varian INOVA-500 spectrometer. Chemical shifts for ¹H NMR are reported in parts per million (ppm), calibrated to the residual solvent peak set, with coupling constants reported in Hertz (Hz). The following abbreviations are used for spin multiplicity: d = doublet, t = triplet, q = quadruplet, m = multiplet. Chemical shifts for ¹³C NMR are reported in ppm, relative to the central line of a triplet at δ = 77.16 ppm for deuterated chloroform. Infrared (IR) spectra were recorded on a NICOLET 5700 FT-IR spectrophotometer and reported in wavenumbers (cm⁻¹). UV-vis spectra were recorded on a Thermo Nicolet Evolution 300 spectrophotometer. Fluorescence spectra were recorded on a Cary Eclypse spectrofluorimeter. To allow comparison among emission intensities we performed corrections for instrumental response, inner filter effect, and phototube sensitivity.²⁵ All solvents and starting materials were purchased from commercial sources where available. Fluorescence titrations were performed by adding aliquots of the putative metallic guest (as the nitrate or perchlorate salt) in a solution of NEAH⁺/OAc⁻ (8.82 × 10⁻⁵ M) in 100% water. Quantum yield was determined using 2-aminopyridine (Φ = 0.60 in 0.1 M H₂SO₄).

Caution: perchlorate salts can be explosive.

Synthesis and characterization of naphtylethylammonium oleate (NEAH)⁺/(OAc)⁻

A solution of oleic acid (0.158 g, 0.56 mmol) in DCM (3 mL) was added under stirring to a solution of R-(+)-1-(1-naphtyl)ethylamine (0.096 g, 0.56 mmol) dissolve in DCM (5 mL). The mixture was left under stirring at room temperature for 48 hours and evaporate under reduce pressure to yield (NEAH)⁺/(OAc)⁻ (0.250 g, 0.55 mmol, 98%) as an orange oil. ¹H NMR (500 MHz, CDCl₃) δ (ppm): 0.88 (t, J = 7 Hz, 3H, CH₃), 1.25–1.36 (m, 20H, 10 × CH₂), 1.60 (m, 5H, CH₃, CH₂), 2.02 (q, J = 5.5 Hz, 2H, 2 × CH₂–CH), 2.28 (t, J = 7.5 Hz, 2H, CH₂–COO⁻), 4.21 (s, br, 3H, NH₃⁺), 5.02 (q, J = 6.5 Hz, 1H, CH–CH₃), 5.35 (m, 2H, 2 × CH=CH), 7.47–7.56 (m, 3H, H_Arom), 7.63 (d, J = 7.0 Hz, 1H, H_Arom), 7.77 (d, J = 8.0 Hz, 1H, H_Arom), 7.88 (d, J = 8.0 Hz, 1H, H_Arom), 8.11 (d, J = 8.5 Hz, 1H, H_Arom). ¹³C NMR (125 MHz, CDCl₃) δ (ppm): 14.21, 22.46, 22.78, 25.99, 27.34, 29.36, 29.41, 29.42, 29.44, 29.52, 29.64, 29.89, 32.01, 37.12, 46.48, 122.43, 125.69, 125.88, 126.65, 128.41, 129.13, 129.92, 129.98, 130.20, 133.90, 137.47, 180.88. IR (KBr) ν (cm⁻¹): 3387 (N–H), 3004 (C=H), 2925, 2853 (C–H), 1561 (C=O)asym, 1400 (C=O)sym.

Emulsion preparation

Aqueous emulsions of (NEAH)⁺/(OAc)⁻ were prepared by dispersing 4 mg of (NEAH)⁺/(OAc)⁻ in 4 mL of Milli-Q water using an ultrasonic bath for 4 h to obtain a concentration of (NEAH)⁺/(OAc)⁻ 2.2 × 10⁻³ M (0.1% wt).

Dynamic light scattering experiments

The size and the ζ-potential of the nanoparticles were measured, respectively, by means of dynamic light scattering (DLS) and electrophoretic mobility measurements. DLS experiments were carried out using either of two instruments: (i) a ZetaSizer Nano ZSP (Malvern Instruments Ltd., Worshestershire, UK), equipped with a 10 mW helium–neon laser (633 nm), operating in backscattering mode (θ = 173°); (ii) a 90Plus Particle Size Analyzer (Brookhaven Instruments, New York, USA), with a 35 mW red diode laser (659 nm), in which the scattered intensity is collected at 90°. Electrophoretic mobility measurements were performed either at θ = 17° (Malvern instrument) or at θ = 15° (Brookhaven instrument) using a PALS (Phase Analysis Light Scattering) technique to detect the particle motion, used to determine its electrophoretic mobility and the ζ-potential through the Helmholtz–Smoluchowski equation. The samples were put in disposable polystyrene cuvettes of 1 cm optical path length, and the two types of measurements were thereafter conducted one after another (DLS first). Emulsions of (NEAH)⁺/(OAc)⁻ were diluted 1 : 25 times (with respect to 2.2 × 10⁻³ M, 0.1% wt) with Milli-Q water prior to the measurements. The measured time autocorrelation functions of the scattered intensity were analysed to obtain the intensity-weighted size distributions of the apparent hydrodynamic diameters, d_H, which are calculated from the Stokes–Einstein relation d_H = kT/3πη₀D; here, D is the translational collective diffusion coefficient, obtained from the decay time of the correlation function, and η₀ is the viscosity of water. The reported d_H values correspond to an average of between three to five measurements. DLS data were analyzed using the cumulant method where the Z-average (intensity-weighted) d_H is calculated from the first cumulant of the second order analysis, while the polydispersity index (PDI) is defined as the second cumulant, i.e. the width of the size distribution, divided by the first cumulant squared. For all systems and both techniques, at least two independently prepared samples were investigated. All experiments were performed at 25 (±0.1) °C.

Negative stain electron microscopy

A 5 μL drop of sample solution was adsorbed to a glow-discharged carbon-coated copper grid (Canemco & Marivac, Canada), washed with deionized water, and stained with 5 μL of uranyl acetate 2%. The samples were imaged at room temperature using a Tecnai F20 electron microscope (FEI, The Netherlands) operating at an acceleration voltage of 200 kV. Images were taken at a magnification of 5000× and recorded with an Eagle camera 4098 × 4098 pixels (FEI, The Netherlands).

Small-angle neutron scattering (SANS) experiments

Small-Angle Neutron Scattering (SANS) experiments were performed on the PACE line at the LLB facility (CEA Saclay, France). The available Q-range (2.0 × 10⁻³ Å⁻¹ < Q < 0.37 Å⁻¹) was obtained by using three different combinations of neutron wavelength (λ) and sample-to-detector distance (d) (in detail, low Q range: λ = 17 Å, d = 4.7 m; medium Q range: λ = 6 Å, d = 4.7 m; high Q range: λ = 6 Å, d = 1 m). The sample was prepared in deuterated water in order to enhance the IL/solvent scattering contrast (Δρ)², obtaining 3.32 × 10²¹ cm⁻⁴, and to minimize the incoherent background from H₂O. All scattering length densities of the chemical species used were calculated from their formulas and densities. The IL/D₂O suspension was introduced in a quartz sample holder having 1 mm inner thickness, and SANS acquisitions were performed at room temperature and atmospheric pressure. Scattering from a cadmium sample was used to correct the experimental intensity for the detector background noise. This was followed by standard correction procedures (sample volume, neutron beam transmission, empty cell signal, detector efficiency),²⁶ carried out using the Pasinet software.²⁷ The scattered intensity I(Q) is expressed in absolute scale (cm⁻¹).

Potentiometric measurements

Equilibrium constants for protonation and complexation reactions were determined by means of potentiometric measurements (pH = −log[H⁺]), carried out in 0.1 M NaCl at 298 ± 0.1 K, by using the equipment that has been already described.²⁸ Protonation and Fe³⁺ complexation with NEA were studied in H₂O/EtOH 50 : 50 (vol : vol) solution, due to the poor solubility of not protonated NEA in water, while protonation of (NEAH)⁺/(OAc)⁻ and Fe³⁺ coordination were analysed in aqueous solution. Protonation of NEA, OAcH and (NEAH)⁺/(OAc)⁻ and Fe³⁺ complexation by NEA were investigated in the pH range 2–11, while in the case of Fe³⁺ complexation by (NEAH)⁺/(OAc)⁻ the pH range was 2–6, due to precipitation of Fe³⁺ complexes at pH values higher than 6. Fe³⁺ forms insoluble complexes with OAc⁻ or OAcH at any pH values, preventing the analysis of Fe³⁺ binding by oleic acid. The reference electrode was an Ag/AgCl electrode in saturated KCl solution. The glass electrode was calibrated as a hydrogen concentration probe by titrating known amounts of HCl with CO₂-free NaOH solutions and determining the equivalent point by the Gran's method.^29,30 This allows one to determine the standard potential E^o, and the ionic product of water (pK_w = 13.83 ± 0.01 in 0.1 NaCl aqueous solution, while pK_w = 14.27 ± 0.01 in 0.1 NaCl H₂O/EtOH 50 : 50 (v/v) solution). Ligands were generally employed at a concentration of 5 × 10⁻⁴ M in the potentiometric measurements. In the study on metal complexation, the metal to ligand molar ratio was varied from 0.5 : 1 to 3 : 1. The concentration of (NEAH)⁺/(OAc)⁻ was estimated by measuring the quantum yield of NEA (Φ_NEA) and (NEAH)⁺/(OAc)⁻ (Φ_NEAH⁺/_OAc⁻). The molar concentration obtained by simple dissolution of weighed (NEAH)⁺/(OAc)⁻ compound was then multiplied by the Φ_NEAH⁺/_OAc⁻/Φ_NEA ratio to finally obtain the (NEAH)⁺/(OAc)⁻ concentration to be used in data treatment. The software HYPERQUAD³¹ was used to calculate the stability constants of the complexes from e.m.f. data. At least three measurements (consisting of about 100 experimental points each one) were performed for each system. The titration curves for each system were treated either as a single set or as separated entities without significant variations in the values of the protonation or complexation constants.

Results and discussions

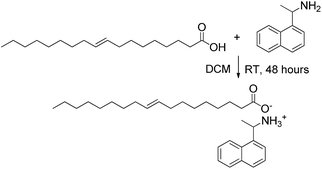
The molten (at room temperature) organic salt naphtylethylammonium oleate (NEAH)⁺/(OAc)⁻ was obtained in 98% yield by mixing, R(+)-1-(1-naphtyl)ethylamine (NEA) and oleic acid (OAcH) in 1 : 1 ratio in dichloromethane (DCM) at room temperature for 48 h. After evaporation of the solvent, an orange oil was obtained (Scheme 1).

Scheme 1 Synthetic strategy used for the preparation of (NEAH)⁺/(OAc)⁻.

The formation of the salt was demonstrated by means of infrared spectroscopy by comparing the spectrum of the oleic acid with that of the (NEAH)⁺/(OAc)⁻ salt (see ESI, Fig. S1†). The disappearance of the carboxylic acid absorption band at 1712 cm⁻¹ and the appearance of the carboxylate stretching symmetric and asymmetric bands at 1400 cm⁻¹ and 1561 cm⁻¹, respectively, confirmed the formation of the salt.³²

To test its behaviour in aqueous solution, 0.1 wt% of this newly engineered IL was dispersed in water using an ultrasonic bath. Remarkably, from a macroscopic point of view, this system appeared as a liquid-like, low viscous, bluish dispersion with a pH = 8.2, strongly suggesting that the IL, rather than being molecularly dispersed, tends to aggregate forming particles with size in the nanometer range. Morphology and size of such particles were investigated via negative stain electron microscopy (EM) and dynamic light scattering (DLS) analysis. The latter evidenced the presence of colloidal aggregates with an average hydrodynamic diameter of 200 nm endowed with a low polydispersity (0.2) and a high, negative ζ-potential (−53 ± 1 mV) (see ESI Fig. S2 and S3,† respectively). EM performed on 0.1 wt% of the IL in water (Fig. 1) clearly shows that the assemblies are spherical aggregates, with size consistent with the DLS results.

Fig. 1 Negative stain TEM image of a 0.1 wt% dispersion of (NEAH)⁺/(OAc)⁻ in water.

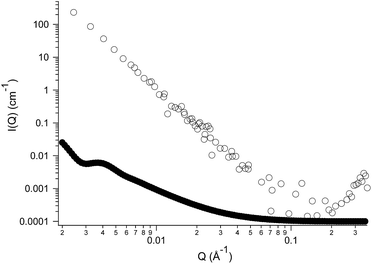
However, both techniques do not provide conclusive information about the inner structure of the nanoparticles. Given the size and the shape of the aggregates observed, two types of very different colloidal dispersions can be envisaged to explain their nature: spherical hollow vesicles, whose shell is constituted by a double layer of self-assembled IL surrounding an aqueous core or, alternatively, emulsion droplets originated by the segregation of the IL itself. In order to address this issue, we turned to Small-Angle Neutron Scattering (SANS), a powerful tool for the determination of the structure at the nanoscale in colloidal systems. Fig. 2 is a plot of the SANS scattered intensity (I(Q), in cm⁻¹) as a function of the scattering vector Q (in Å⁻¹) for a sample of (NEAH)⁺/(OAc)⁻ dispersed in D₂O (IL concentration 0.05 wt%; pH = 8.2). The scattering curve (Fig. 2, empty circles) presents a clear trend following a Q⁻⁴ power law spanning the entire Q range. Such behaviour corresponds to the typical form factor P(Q) of spherical objects whose size is larger than the experimental window in the direct space, 2π/Q_min (260 nm), with a sharp interface between the dispersed phase and the bulk medium.³³ Interestingly, the typical signature of a bilayer is here absent. Indeed, if the dispersed phase were represented by vesicles, we would have observed a Q⁻² trend in the medium-Q regime, as shown in the calculated curve (full circles) reported in Fig. 2. Such curve was obtained using a standard form factor of core–shell spheres, setting the same scattering length density (SLD, that of D₂O) for the core and the solvent, while the shell's SLD was set equal to that of the ionic liquid. The core's diameter was set to 200 nm with 0.2 polydispersity index (in agreement with DLS results), while the shell thickness was set to 2 nm according to the IL's molecular dimensions. The present comparison between form factors clearly states that the dispersed objects formed by (NEAH)⁺/(OAc)⁻ in water are not hollow vesicles but rather solid spheres. Following these results, the most plausible hypothesis is the formation of a highly stable IL-in-water emulsion stabilized by a huge surface charge.

Fig. 2 SANS experimental scattered intensity (empty circles) for a sample of (NEAH)⁺/(OAc)⁻ dispersed in deuterated water (0.05 wt%, pH = 8.2), and the calculated form factor (full circles) for vesicles having a core diameter of 200 nm (polydispersity index 0.2).

The colloidal stability of the system was investigated by DLS measurements repeated over time, to check for changes in size of the IL droplets, and we noticed that the average diameter remains unaltered even after 2 months of storage time. After two more months, although no macroscopic phase separation could be seen, we observed a 60% increase of the droplets size.

Potentiometric measurements in aqueous medium showed that the (NEAH)⁺/(OAc)⁻ assembly presents two protonation steps (ESI, Table S1†). While the first protonation step occurs at acidic pH values, (Fig. 3 and ESI Fig. S4†) in agreement with protonation of the OAc⁻ carboxylate groups (ESI Table S1, Fig. S5†), the second one takes place in the alkaline pH region. As shown in Fig. 3, deprotonation of (NEAH)⁺/(OAc)⁻ starts occurring above pH 9, as expected for deprotonation of naphtylethylammonium cation alone (ESI Table S1, Fig. S6†).

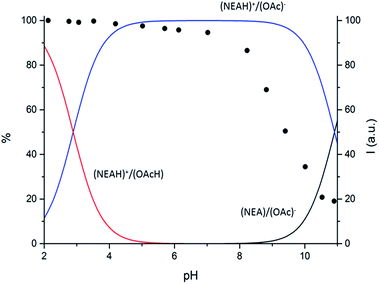Fig. 3 Distribution diagram vs. pH for (NEAH)⁺/(OAc)⁻ ((NEAH)⁺/(OAc)⁻ = 8.82 × 10⁻⁵ M) I = 0.1 M water solution, 298 K. and (•) spectrofluorimetric emission intensities at 333 nm.

The photophysical properties of the (NEAH)⁺/(OAc)⁻ emulsion in water were tested by UV-vis and fluorescence spectroscopy. The UV-vis spectrum ((NEAH)⁺/(OAc)⁻ = 8.82 × 10⁻⁵ M) showed a structured band centred at 281 nm (ε = 8010 M⁻¹ cm⁻¹), attributed to the presence of the naphtyl moiety (Fig. 4, black curve). Upon excitation at 281 nm, an emission band centred at 333 nm (Φ = 0.041) was observed (Fig. 4, red curve).

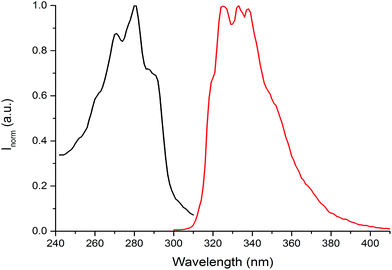Fig. 4 Absorption (black curve) and emission (red curve) spectra of (NEAH)⁺/(OAc)⁻ emulsion in water ((NEAH)⁺/(OAc)⁻ = 8.82 × 10⁻⁵ M), λ_exc = 281 nm.

The effect of the concentration of the IL on the emulsion fluorescence was evaluated. As shown in Fig. S7,† an increase of the fluorescence emission was observed up to a concentration of 1.0 × 10⁻⁴ M, followed by an almost complete switching off at a concentration of 2.0 × 10⁻³ M probably due to a self-quenching effect. For this reason the concentration at which all the fluorescence measurements were performed was fixed at 8.82 × 10⁻⁵ M that corresponds to the maximum of the emission intensity.

Variable pH fluorescence measurements on the (NEAH)⁺/(OAc)⁻ emulsion in water were compared to the data obtained by potentiometric measurements. Both the diprotonated (NEAH)⁺/(OAcH) and the mono-protonated (NEAH)⁺/(OAc)⁻ forms are fluorescent (Fig. 3), while the negative form (NEA)/(OAc)⁻ is not emissive, probably because of a Photoinduced Electron Transfer (PET) process from the amine group to the excited fluorophore.

The presence of the emulsion in the pH range explored (2.0–11.0) was demonstrated by DLS measurements at variable pH (Fig. S8†). The average hydrodynamic diameters of the IL droplets, as well as the variation of ζ-potential for the same samples, were investigated at different pH values. Concentrated aqueous solutions of NaOH and HCl were used to adjust pH between the values 2.7 and 11.0 without significantly diluting the samples. Particle sizes vary with a sharp increase from 278 nm (pH 2.7) to 549 nm (pH 4.0), to begin decreasing again as the medium becomes more alkaline. At the same time, the ζ-potential decreases with increasing pH, going from +36.4 mV at pH = 2.7, down to −73.4 mV at pH 11.0. The point of zero charge is found approximately at pH 4.0. Accordingly, at around this pH value the hydrodynamic diameters are larger due to coalescence of IL droplets in the absence of electrostatic repulsions. This suggests that the sign of the particles' surface charge switches from negative to positive in correspondence of the pK_a of oleic acid. Indeed, at pH < 4 oleic acid is protonated (and electrically neutral), while the NH₂ function of naphtylethylamine is protonated and positively charged. The stability of the emulsion was also assessed in NaCl 0.1 M (see ESI Table S3† for details). At pH 7.0 no influence of the NaCl on the stability of the emulsion was observed and, in agreement with expectations, there is only an increase of hydrodynamic sizes (diameters around 300 nm) of the droplets, but noticeably, no significant change of ζ-potential is observed with respect to neat water as medium. Interestingly, at pH 10.7 a double distribution in the dimensions of the aggregates is observed. This can be explained by considering that at this pH value oleate is in its deprotonated form and can interact both with the neutral NEA to form (NEA)/(OAc⁻) droplets and with Na⁺ to form worm-like micelles of sodium oleate in accordance with the data previously reported in the literature.³⁴

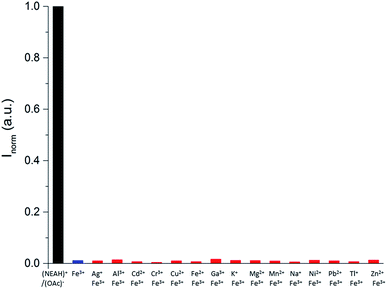
Following our interest in the development of fluorescent sensors for metal ions recognition in water,^35–41 we investigated the behaviour of this unique IL-in-water fluorescent emulsion in the presence of different metal ions. Interestingly, although some metal ions (Al³⁺, Ga³⁺, Ni²⁺, Pb²⁺, Zn²⁺) caused an enhancement in the intensity of the emission of the emulsion, only upon addition of Fe³⁺ we observed a dramatic quenching of the fluorescence (Fig. S8†). Indeed, as shown in Fig. 5 addition of increasing amounts of Fe³⁺ to the (NEAH)⁺/(OAc)⁻ emulsion in water leads to the decrease of the emission band at 333 nm.

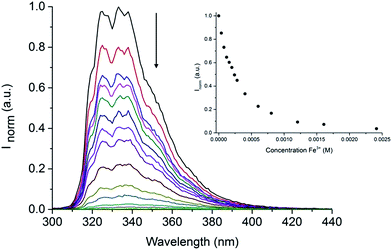Fig. 5 Fluorescence of (NEAH)⁺/(OAc)⁻ [8.82 × 10⁻⁵ M] in water upon addition of Fe³⁺ (λ_em = 333 nm, λ_exc = 281 nm). Inset: plot of I_normvs. [Fe³⁺] at 333 nm.

At a concentration of Fe³⁺ of 5.0 × 10⁻⁴ M the residual emission is 26% of the original (Fig. 5 inset).

Competition studies (Fig. 6) confirmed the selective quenching of the fluorescence of the (NEAH)⁺/(OAc)⁻ emulsion caused by Fe³⁺ even in the presence of a 2.5 fold excess of other metal ions.

Fig. 6 Ion competition study for (NEAH)⁺/(OAc)⁻ [8.82 × 10⁻⁵ M] in the presence of 20 equivalents of Fe³⁺ and 50 equivalents of the other metal ions in pure water at 298 K (λ_em = 333 nm, λ_exc = 281 nm); (NEAH)⁺/(OAc)⁻ (black); (NEAH)⁺/(OAc)⁻ + Fe³⁺ (blue); (NEAH)⁺/(OAc)⁻ + metal cations + Fe³⁺ (red). Emulsions of (NEAH)⁺/(OAc)⁻ were diluted 1 : 25 times prior to the measurements.

The effect of the presence of anions (added as tetrabutylammonium salts) on the fluorescence of the (NEAH)⁺/(OAc)⁻ emulsion in water was also investigated. Interestingly, negligible changes were observed (ESI Fig. S9†). Moreover, almost no effects on the fluorescence of the emulsion were observed when using different Fe³⁺ salts, suggesting that anions should not interfere with the spectrofluorimetric response of the system.

Potentiometric titrations (Table S2; Fig. S10†) pointed out that Fe³⁺ is strongly bound by the (NEAH)⁺/(OAc)⁻ emulsion to form the [((NEA)/(OAc))₂Fe]⁺ complex at acidic pH values. Precipitation of iron complexes prevents the investigation of the system above pH 6. The stoichiometry of the Fe³⁺ assembly strongly resembles that of the complexes formed by naphtylethylamine (Table S2, Fig. S11†), as expected considering that two not protonated naphtylethylamine molecules are involved in Fe³⁺ coordination even in the emulsion system.

However, the constant for the formation of the [((NEA)/(OAc))₂Fe]⁺ complex is by far higher than that of the corresponding complex with naphtylethylamine, [Fe(NEA)₂]³⁺ (22.95 vs. 17.85 log units). In principle, the higher binding ability of (NEAH)⁺/(OAc)⁻ system could be due to both the proximity of the NEA units in the droplet and the involvement of the carboxylate groups in iron binding. The superimposition of the fluorescence emission intensity of the ((NEAH)⁺/(OAc)⁻)/Fe³⁺ system at different pH with the distribution diagrams obtained by the potentiometric experiments (Fig. 7) suggested that the species [((NEA)/(OAc))₂Fe]⁺ is responsible for the quenching of the fluorescence. The existence of the emulsion at pH 4 in the presence of Fe³⁺ was demonstrated by DLS measurements.

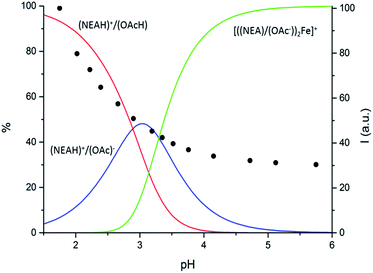Fig. 7 Distribution diagram vs. pH for (NEAH)⁺/(OAc)⁻. ((NEAH)⁺/(OAc)⁻ = 8.82 × 10⁻⁵ M; [Fe³⁺] = 0.1 M) in NaCl 0.1 M water solution, 298 K and (•) spectrofluorimetric emission intensities at 333 nm.

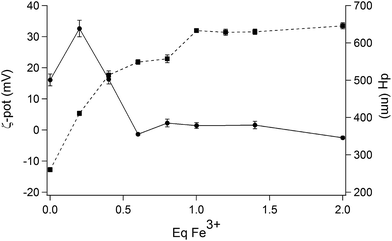
At this pH value, DLS and ζ-potential measurements were employed to obtain further information on the interaction between the IL and increasing amounts of Fe³⁺. A preliminary screening involved the addition of different amounts of Fe³⁺ (from zero to ten equivalents of Fe³⁺; see ESI Fig. S13†). This study showed that the ζ-potential of the droplets increases with increasing Fe³⁺ concentrations to finally achieve an almost constant value after the addition of 1 eq. of the metal. An opposite behaviour was found for the hydrodynamic diameter of the droplets, which decreases upon addition of Fe³⁺. The region between 0 and 2 eq. of Fe³⁺ was more closely investigated (Fig. 8), evidencing that the value of the surface charge is slightly negative in the absence of iron ions, and increases up to +30 mV upon complexation with 1 equivalent of Fe³⁺. The average diameter measured by DLS reaches its maximum value in correspondence with the neutral surface charge, the ζ-potential being close to 0 after the addition of 0.2 equivalents of Fe³⁺; in consequence of the increase of the superficial charge, the diameters are reduced at almost half their original value, confirming a stabilization of the droplets by electrostatic repulsion.

Fig. 8 Variation of ζ-potential values (in mV; square symbols) and average hydrodynamic diameters (d_H in nm; round symbols) of (NEAH)⁺/(OAc)⁻ emulsion droplets in water as a function of increasing amounts of Fe³⁺.

This system represents, to the best of our knowledge, the first example of a stable pure binary IL-in water emulsion whose fluorescence can be tuned by the presence of metal ions.

Conclusions

In conclusion, we report here on the emulsion system easily obtained by dispersing in water a new, fluorescent ionic liquid, namely naphtylethylammonium oleate. To the best of our knowledge, this system represents the first example of an extremely stable, truly binary, surfactant-free fluorescent IL-in-water emulsion. Furthermore, we demonstrated here that the fluorescence of this system can be selectively switched off by the presence of Fe³⁺ in 100% aqueous solution.

This new class of ILs is quite promising for the development of new fluorescent soft nanosized sensors able to work in pure water. In principle, suitable combinations of the cationic and anionic components could easily lead to stable fluorescent IL emulsions able to sense selectively different metal cations.

Acknowledgements

We would like to thank Regione Autonoma della Sardegna (CRP-59699) and Fondazione Banco di Sardegna for financial support. We would also like to thank Laboratoire Léon Brillouin (LLB, CEA Saclay, France) for granting access to small-angle neutron scattering facilities, Giulia Fadda (CEA Saclay, France) for technical support to SANS experiments, and Véronique Peyre (Université Pierre et Marie Curie, Paris, France).

Notes and references

1. J. Hao and T. Zemb, Curr. Opin. Colloid Interface Sci., 2007, 12, 129–137.
2. S. Murgia, M. Monduzzi, F. Lopez and G. Palazzo, J. Solution Chem., 2013, 42, 1111–1122.
3. T. Welton, Chem. Rev., 2005, 9, 2071–2084.
4. T. L. Greaves and C. J. Drummond, Chem. Soc. Rev., 2013, 42, 1096–1120.
5. S. Murgia, G. Palazzo, M. Mamusa, S. Lampis and M. Monduzzi, J. Phys. Chem. B, 2009, 113, 9216–9225.
6. Z. Qiu and J. Texter, Curr. Opin. Colloid Interface Sci., 2008, 13, 252–262.
7. S. Murgia, G. Palazzo, M. Mamusa, S. Lampis and M. Monduzzi, Phys. Chem. Chem. Phys., 2011, 13, 9238–9245.
8. D. J. McClements, Crit. Rev. Food Sci. Nutr., 2007, 47, 611–649.
9. M. Mosca, S. Murgia, A. Ceglie, M. Monduzzi and L. Ambrosone, J. Phys. Chem. B, 2006, 110, 25994–26000.
10. J. Li, J. Zhang, Y. Zhao, B. Han and G. Yang, Chem. Commun., 2012, 48, 994–996.
11. H. Ma and L. L. Dai, Langmuir, 2011, 27, 508–512.
12. L. Gao, H. Yin and D. Wang, Phys. Chem. Chem. Phys., 2010, 12, 2535–2540.
13. H. Monteillet, M. Workamp, X. Li, B. Schuur, J. M. Kleijn, F. A. M. Frans, A. M. Leermakersa and J. Sprakel, Chem. Commun., 2014, 50, 12197–12200.
14. K. Kamogawa, G. Okudaira, M. Matsumoto, T. Sakai, H. Sakai and M. Abe, Langmuir, 2004, 20, 2043–2047.
15. N. Maeda, K. J. Rosenberg, J. N. Israelachvili and R. M. Pashley, Langmuir, 2004, 20, 3129–3137.
16. V. Amendola, L. Fabbrizzi, F. Foti, M. Licchelli, C. Mangano, P. Pallavicini, A. Poggi, D. Sacchi and A. Taglietti, Coord. Chem. Rev., 2006, 250, 273–299.
17. C. Bargossi, M. C. Fiorini, M. Montalti, L. Prodi and N. Zaccheroni, Coord. Chem. Rev., 2000, 208, 17–32.
18. A. P. De Silva, H. Q. N. Gunaratne, T. Gunnlaugsson, A. J. M. Huxley, C. P. McCoy, J. T. Rademacher and T. E. Rice, Chem. Rev., 1997, 97, 1515–1566.
19. M. Formica, V. Fusi, L. Giorgi and M. Micheloni, Coord. Chem. Rev., 2012, 256, 170–192.
20. Y. Jeong and J. Yoon, Inorg. Chim. Acta, 2012, 381, 2–14.
21. K. Kikuchi, Chem. Soc. Rev., 2010, 39, 2048–2053.
22. E. M. Nolan and S. J. Lippard, Chem. Rev., 2008, 108, 3443–3480.
23. B. Valeur and I. Leray, Coord. Chem. Rev., 2000, 205, 3–40.
24. X. Zhang, J. Yin and J. Yoon, Chem. Rev., 2014, 114, 4918–4959.
25. A. Credi and L. Prodi, Spectrochim. Acta, Part A, 1998, 54, 159–170.
26. A. Brûlet, D. Lairez, A. Lapp and J. P. Cotton, J. Appl. Crystallogr., 2007, 40, 165–177.
27. D. Lairez, P. Pasinet software http://didier.lairez.fr/.
28. S. Bartoli, C. Bazzicalupi, S. Biagini, L. Borsari, A. Bencini, E. Faggi, C. Giorgi, C. Sangregorio and B. Valtancoli, Dalton Trans., 2009, 1223–1230.
29. G. Gran, Analyst, 1952, 77, 661–670.
30. F. J. C. Rossotti and H. Rossotti, J. Chem. Educ., 1965, 42, 375–378.
31. P. Gans, A. Sabatini and A. Vacca, J. Chem. Soc., Dalton Trans., 1985, 1195–1200.
32. C. Bize, J. C. Garrigues, M. Blanzat, I. Rico-Lattes, O. Bistri, B. Colasson and O. Reinaud, Chem. Commun., 2010, 46, 586–588.
33. G. Porte, Neutrons, X-rays and Light – Scattering Methods Applied to Soft Condensed Matter, North Holland, 2002.
34. K. Edwards, M. Silvander and G. Karlsson, Langmuir, 1995, 11, 2429–2434.
35. M. C. Aragoni, M. Arca, A. Bencini, C. Caltagirone, A. Garau, F. Isaia, M. E. Light, V. Lippolis, C. Lodeiro, M. Mameli, R. Montis, M. C. Mostallino, A. Pintus and S. Puccioni, Dalton Trans., 2013, 14516–14530.
36. M. Arca, C. Caltagirone, G. De Filippo, M. Formica, V. Fusi, L. Giorgi, V. Lippolis, L. Prodi, E. Rampazzo, M. A. Scorciapino, M. Sgarzi and N. Zaccheroni, Chem. Commun., 2014, 50, 15259–15262.
37. C. Bazzicalupi, C. Caltagirone, Z. Cao, Q. Chen, C. Dinatale, A. Garau, V. Lippolis, L. Lvova, H. Liu, I. Lundström, M. C. Mostallino, M. Nieddu, R. Paolesse, L. Prodi, M. Sgarzi and N. Zaccheroni, Chem.–Eur. J., 2013, 19, 14639–14653.
38. A. Bencini, F. Caddeo, C. Caltagirone, A. Garau, M. B. Hurstouse, F. Isaia, S. Lampis, V. Lippolis, F. Lopez, V. Meli, M. Monduzzi, M. C. Mostallino, S. Murgia, S. Puccioni, J. Schmidt, P. P. Secci and Y. Talmon, Org. Biomol. Chem., 2013, 11, 7751–7759.
39. A. Garau, P. Caboni, C. Caltagirone, F. Demartin, F. Isaia and V. Lippolis, RSC Adv., 2013, 3, 12149–12154.
40. E. Arturoni, C. Bazzicalupi, A. Bencini, C. Caltagirone, A. Danesi, A. Garau, C. Giorgi, V. Lippolis and B. Valtancoli, Inorg. Chem., 2008, 47, 6551–6563.
41. M. Mameli, V. Lippolis, C. Caltagirone, J. L. Capelo, O. N. Faza and C. Lodeiro, Inorg. Chem., 2010, 49, 8276–8286.

---

Footnote

† Electronic supplementary information (ESI) available: Protonation constants of NEA and OAcH, and (NEAH)⁺/(OAc)⁻, formation constants of the Fe³⁺ complexes with NEA and with (NEAH)⁺/(OAc)⁻, distribution diagrams, FT-IR spectra of OAcH and (NEAH)⁺/(OAc)⁻, changes of the fluorescence intensity of (NEAH)⁺/(OAc)⁻vs. concentration and in the presence of metal cations and anions, variation of ζ-potential values and average hydrodynamic diameters of (NEAH)⁺/(OAc)⁻vs. Fe³⁺ equivalents. See DOI: 10.1039/c5ra05055c

---