A quest for stable 2,5-bis(halobora)cyclopentenylidene and its Si, Ge, Sn and Pb analogs at theoretical levels

Abstract

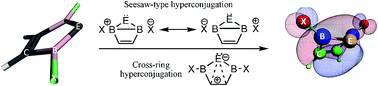
Replacing the two nitrogen atoms of Arduengo's N-heterocyclic carbenes (NHCs) with electron deficient boron atoms forms B-heterocyclic carbenes (BHCs) which may appear destabilizing at first glance. Yet, among the 40 optimized singlet (s) and triplet (t) BHCs and their Si, Ge, Sn and Pb homologues (BHËs), eight species are found that show higher stability than their corresponding NHËs for exhibiting wider singlet–triplet energy gaps (ΔE_st), at B3LYP/TZ2P, as well as CBS-QB3 and G4MP2 ab initio levels. Moreover, triplet BHËs assume a planar geometry with a dihedral angle (D1) of about zero degrees. In contrast, their corresponding singlets show a high tendency for puckering with D1 ≅ 66°. The preference of the latter for puckered nonplanar geometries is evidenced by NBO calculations and visually through their frontier molecular orbitals. The main stabilizing interactions appear to be π- and σ-bond hyperconjugation across the ring. The resulting eight species that demonstrate higher stability are: 2,5-bis(iodobora)cyclopentensilylene, 2,5-bis(Z-bora)cyclopenten-germylene and -stannylene, for Z = Br and I; as well as 2,5-bis(Z₂-bora)cyclopentenplumbylene, for Z₂ = Cl, Br and I.

---

1 Introduction

Now as ever before, researchers are fascinated with group 14 divalents including carbenes,^1–5 silylenes,^4–6 germylenes,^2,4,5,7,8 stannylenes,^4,5,7,9,10 and plumbylenes.^5,10,11

-As for carbenes, immense interest was regenerated upon the isolation and characterization of the first stable one, called N-heterocyclic carbene (NHC), by Arduengo in 1991.^12–15 This appeared in a clear contrast to “the parent” highly reactive methylene (:CH₂), once labelled as “the most indiscriminate reagent in organic chemistry”.¹⁶ Nevertheless, most acyclic and/or alkyl carbenes tend to be intrinsically triplet with rather high reactivity.

The scenario totally changes on going from carbene to its homologues metallylenes (silylene, germylene, stannylene and plumbylene). In so doing, multiplicity may alter from triplet to singlet, while the stability increases (on descending group 14). This phenomenon is attributed to the “inert pair effect”, where s electrons become progressively lower in energy upon descending the group.¹⁷

-Arduengo type N-heterocyclic silylenes (NHSis) constitute the vast majority of such species with different stability and diverse structure and reactivity. Among them is that reported by Denk et al. in 1994.¹⁶ These practically started after the seminal work of Atwell and Wyenberg on the matrix isolation of transient Me₂Si: in 1960s.¹⁸

-As for germylenes, they have been the center of attention due to their importance in chemical vapour deposition, semiconductor manufacturing, photonics, and aerospace industries.^19–21 Long before their carbene homologues, N-heterocyclic germylenes were developed by Veith and Meller.^22,23

-Considerable progress has been made in the chemistry of stable derivatives of divalent tin.^24,25 Specifically, N-heterocyclic stannylenes (NHSns) have received their share of great attention.^26–29

-Finally, dialkyl and diarylplumbylenes have been isolated and characterized by Lappert et al.^30–32 Despite the toxicity of lead which has somewhat hampered its scrutiny, several examples of N-heterocyclic plumbylenes (NHPbs) have surfaced.^23,33,34

Moreover, there are some carbenes which contain one or more boron atoms in their cyclic structures,³⁵ or appear as the boryl anion.^36–41 Synthesis of phosphino(boryl)methanes⁴² is recently been followed by theoretical investigations on the reactivity of acyclic boryl(phosphino)-based B–Ë–P species which suggests that the relative divalent reactivity decreases in the order C > Si > Ge > Sn > Pb.⁴³ In other words, the heavier is a group 14 atom (E), the more is its stability.

Unstable four-membered species containing B–C̈–B carbene moieties were characterised long ago.^44,45 Recently, by making use of the strong σ-donor properties and high steric loadings, monomeric species, Sn{B(NDippCH)₂}{N-(SiMe3)Dipp} and Sn{B(NDippCH)₂}₂ were synthesized in solid state.⁴⁶

Here, we have set up to study boron-heterocyclic carbenes (BHCs) where the nitrogen atoms of an Arduengo cyclic carbene are replaced with electron deficient boron atoms. In fact, the substitution of nitrogens with borons in NHCs means a change from p⁶ electron-rich system (of the two nitrogens) to a p² electron deficient system (of the two borons). In particular, following up on our quest for more stable halogenated group 14 divalent species,^47–51 in this manuscript we have carried out comparative theoretical studies on possible configurations of singlet and triplet⁵² of C₂H₂B₂EX₂ (Ë = C; X = F, Cl, Br and I) as well as their group 14 divalent homologues (Ë = Si, Ge, Sn, and Pb). In addition, to give a more clear physical picture about the thermodynamic stabilities of BHËs, some isodesmic reactions are employed which show the tendency of carbene dimerization, hydrogenation, coupling, as well as carbenoid formation with Cu, Ag and Au.

2 Computational details

Divalent species and their corresponding metal complexes (Fig. 1 and 2, respectively) are optimized at UB3LYP,⁵³ and second-order Møller–Plesset perturbation, UMP2, using 6-311++G** basis set⁵⁴ of the GAUSSIAN 98 (ref. 55) and an analogous basis set (TZ2P; triple zeta double polarized) in the ADF system of programs.^56–58 Moreover, optimizations are carried out on all BHËs, other than those containing heavy atoms (1_I, 2_I, 3_I, 4_X and 5_X), using the high accuracy CBS-QB3 and G4MP2 methods.

Fig. 1 A general structure for 40 structures optimized in this work including: carbenes (Ë = C: 1_s-X, 1_t-X); silylenes (Ë = Si: 2_s-X, 2_t-X), germylenes (Ë = Ge: 3_s-X, 3_t-X), stannylenes (Ë = Sn: 4_s-X, 4_t-X), and plumbylenes (Ë = Pb: 5_s-X, 5_t-X).

Fig. 2 Schematic representation for 1_X–, 2_X–, and 3_X–MCl (X = F, Cl; M = Cu, Ag, Au).

Global minima are specified on the corresponding energy surfaces through relax scan using keyword “FOPT (Z-matrix)” at UB3LYP/6-311++G** level of theory. Obtained minimum via scanning, the latter are used as inputs for the UB3LYP/6-311++G** (basis set of McGrath,⁵⁹ Curtiss⁶⁰ included the diffuse functions) calculations. This is for obtaining more accurate values of optimized geometries, energetic parameters, orbital interactions and electronic configurations. Single-point calculations on the “second order perturbation theory analysis of fock matrix in natural bonding orbitals (NBO) basis” which summarizes the second order perturbative estimates of donor–acceptor (bond–antibond) interactions in the NBO basis are also performed.

All divalent species with heavy or transition atoms (I, Sn, Pb, Cu, Ag, and Au) acquire spin–orbit interactions, calculated using “Extrabasis” keyword (LANL2DZ, McGrath–Curtiss basis set, in the GAUSSIAN 98 (ref. 61)), and zeroth order relativistic approach (ZORA,^62–66 in the ADF program). To confirm the nature of the stationary species, frequency calculations are carried out. For minimum state structures, only real and positive frequency values are accepted.

3 Results and discussion

We begin discussing our calculated data on novel BHËs (Fig. 1), by estimating their stability through singlet–triplet energy gaps (ΔE_st) and energetic advantages of puckering for singlet states. Then we take up the effects of geometrical parameters and orbital interactions on the stability of the divalents. The discussion is continued by characterization of the scrutinized species through their electronic configurations, electrophilicity, nucleophilicity, isodesmic reactions and the study of their metal complexes (Fig. 2).

3.1 Singlet–triplet energy gap (ΔE_st)

Singlet states of all BHËs appear puckered with more stability than their corresponding planar triplets for showing relatively higher values of ΔE_st (Tables 1, 1S–4S, Fig. 1 and 1S (ESI†)).

Table 1 Comparison between singlet–triplet energy gaps, ΔE_st, (in kcal mol⁻¹) of carbenes (1_X) with heavier group 14 divalents including silylenes (2_X), germylenes (3_X), stannylenes (4_X) and plumbylenes (5_X), with X = F, Cl, Br and I, at UB3LYP/TZ2P

X	1X	2X	3X	4X	5X
F	0.51	22.78	23.86	21.99	27.40
Cl	4.29	27.18	28.12	26.79	34.79
Br	4.85	27.80	28.70	27.47	33.96
I	5.58	29.14	30.06	28.85	39.98

---

On the basis of ΔE_st, carbenes (1_X) emerge considerably less stable than their corresponding silylenes (2_X), germylenes (3_X), stannylenes (4_X) and plumbylenes (5_X). In other words, the stability order of our sextet divalent species generally increases on descending group 14 (to be discussed in more details in sections 3.3 and 3.4.2). This convenes a small drop from 3_X to 4_X in UB3LYP/TZ2P level which is not encountered when MP2, G4MP2 and CBS-QB3 are employed (ESI Tables 2S–4S,† respectively).

As to ΔE_st of 1_X–3_X (X = F, Cl, Br), the performance of the B3LYP functional relative to those at the CBS-QB3 and G4MP2 levels is determined^67,68 (Table 2). This assessment is demonstrated via absolute (column (a) and (b) in Table 2) and mean absolute errors (MAE). As the latter indicates, deviation of B3LYP with G4MP2 level is smaller than that with CBS-QB3.

Table 2 Absolute and mean absolute errors on ΔE_st calculated with B3LYP functional relative to CBS-QB3 and G4MP2

Species	(a) CBS-QB3 ΔE^B3LYP − ΔE^CBS-QB3	(b) G4MP2 ΔE^B3LYP − ΔE^G4MP2
1F	−0.91	−2.01
1Cl	−0.03	−0.73
1Br	−0.08	−0.86
2F	3.97	2.79
2Cl	5.57	4.69
2Br	5.59	4.55
3F	2.18	1.74
3Cl	3.39	3.03
3Br	3.32	2.77
Mean absolute errors	2.56	1.77

---

In addition to the above comparison between the stability of our boron substituted BHËs, it is interesting to compare and contrast the stability of our divalent species with their corresponding Arduengo's. At the first glance, such replacement of the two nitrogen atoms of Arduengo's N-heterocyclic carbenes, NHCs, with electron deficient boron atoms, BHCs, appears highly destabilizing. Yet, among 40 optimized singlet and triplet BHCs and their Si, Ge, Sn and Pb homologues (BHËs), eight (2_I, 3_Br, 3_I, 4_Br, 4_I, 5_Cl, 5_Br, and 5_I) are found which show higher stability than their corresponding NHËs for exhibiting wider singlet–triplet energy gaps (ΔE_st) and hence a greater δ(ΔE_st) = (ΔE^NHEs_st − ΔE^BHEs_st) at UB3LYP/TZ2P (Table 3). Besides, 2_Br, 4_Cl, and 5_F emerge energetically comparable with their NHË analogues. This is somewhat similar to the results obtained with other methods such as G4MP2 (Table 5S†). In fact, calculations show a decrease of ΔE_st for NHËs from lighter to heavier atoms of Ë and/or X. This means that from X = F to X = I and also descending group 14, the NHË species exhibits narrower singlet–triplet energy gaps (ΔE_st) which is in reverse to the analogues BHËs. The G4MP2 results show larger ΔE_st for 2_Br, 3_Cl in addition to B3LYP results. Expanding the G4MP2 results demonstrates that they may acceptably cover B3LYP results, hence comparable ΔE_st between BHËs and their NHË counterparts are obtained.

Table 3 Comparison between the stability of our divalent species (BHËs: 1_X–5_X) with their corresponding Arduengo's (NHËs) by considering their energy differences, δ(ΔE_st) = (ΔE^NHEs_st − ΔE^BHEs_st), (in kcal mol⁻¹) at UB3LYP/TZ2P^a

X	1X	2X	3X	4X	5X
a A negative sign indicates higher stability of BHËs while positive numbers signify higher relative stability of NHËs.
F	58.24	34.08	19.97	10.34	2.03
Cl	35.68	12.56	8.02	4.30	−6.72
Br	23.11	2.67	−2.03	−4.25	−11.44
I	15.77	−1.37	−6.22	−11.49	−20.30

---

3.2 Puckering energy (PE)

Singlet state structures demonstrate energetic advantages through “puckering” (Scheme 1).

Scheme 1

A clear contrast between energies of singlet and triplet BHËs as a function of their divalent dihedral angle D1(∠C–B–Ë–B) is observed at UB3LYP/TZ2P (Fig. 3). For example an energy difference of 18 kcal mol⁻¹ is encountered between the planar and fully puckered (D1 ≅ 60°) singlet chlorinated germylene 3_s-Cl which decreases to 12 kcal mol⁻¹ for the corresponding carbene 1_s-Cl (Fig. 3, left). This is in contrast to the corresponding triplet state structures which prefer planarity and display an aversion to puckering (Fig. 3, right). Also an energy difference of 12.6 kcal mol⁻¹ is encountered in favour of the planar structure vs. the puckered (D1 ≅ 45°) of triplet chlorinated germylene 3_t-Cl.

Fig. 3 Conspicuous contrast between energies of bis(boryl)-based divalents as a function of their dihedral angle D1(∠C–B–Ë–B) for puckered singlets (left, with the minimum at ∼60°) and planar triplets (right, with the minimum at 0°), at UB3LYP/TZ2P.

The same results are found when PE surfaces are sketched for the selected germylenes 3_s-X vs. 3_t-X as a function of D1 (Fig. 1S†).

It seems that the empty valence shell p orbital of Ë has no tendency to overlap with the empty p orbitals of the boron atoms. This is anticipated, because of the instability of vinylic cation that may be the result of such an overlap. This argument is to be continued and established with more details in proceeding section.

3.3 Geometric parameters and orbital interactions

Even though there is no experimental geometrical data for 1–5, but a comparison of the theoretical structures with experimental geometries of related noncyclic B–Ë–B and B–Ë–N systems^44–46 indicates that the calculated values may be accurate and reliable. The theoretically predicted Ë–B distances for Ë = C, Si, Ge and Sn with averages of 1.503, 2.039, 2.124 and 2.334 Å are in good agreement with the experimental values 1.515, 2.036, 2.141 and 2.334 Å, respectively.

Geometrical parameters of carbenes appear to be somewhat different and often in contrast to those of the rest of the group 14 divalents (Tables 4 and 6S†).

Table 4 Selected bond length (R1 and R3) in Å, bond angle (A1) and dihedral angle (D1) in degrees, for the singlet BHËs (1_X–5_X with X = F, Cl, Br and I) at UB3LYP/TZ2P

Species	R1	R3	R4	B–B	A1	*D1
1s-F	1.512	1.578	1.391	2.363(2.510)	102.8	58.3
1s-Cl	1.503	1.577	1.390	2.343(2.521)	102.4	61.0
1s-Br	1.500	1.575	1.391	2.348(2.513)	102.5	60.2
1s-I	1.495	1.571	1.390	2.286(2.500)	99.7	61.4
2s-F	2.051	1.545	1.399	2.449(2.868)	73.3	66.8
2s-Cl	2.041	1.533	1.406	2.395(2.899)	71.9	72.1
2s-Br	2.037	1.530	1.407	2.387(2.876)	71.1	71.1
2s-I	2.027	1.526	1.409	2.313(2.882)	69.6	71.3
3s-F	2.135	1.541	1.400	2.489(2.918)	71.3	66.8
3s-Cl	2.128	1.529	1.407	2.451(2.952)	70.3	71.5
3s-Br	2.122	1.526	1.406	2.451(2.948)	70.5	71.1
3s-I	2.112	1.523	1.410	2.363(2.934)	68.0	71.2
4s-F	2.356	1.543	1.395	2.624(3.041)	67.7	61.0
4s-Cl	2.345	1.527	1.406	2.565(3.077)	66.3	68.0
4s-Br	2.343	1.524	1.409	2.581(3.079)	66.8	67.8
4s-I	2.332	1.518	1.412	2.452(3.049)	63.3	68.9
5s-F	2.491	1.542	1.393	2.643(3.101)	64.1	59.8
5s-Cl	2.477	1.527	1.402	2.586(3.283)	62.9	66.2
5s-Br	2.473	1.525	1.404	2.585(3.279)	63.0	64.9
5s-I	2.461	1.518	1.408	2.482(3.260)	60.6	65.8

---

Divalent angle (A1) appears indirectly proportional to the Ë atomic size. So the largest A1 is found for carbenes while the smallest is that of plumbylenes (Tables 3, 6S and Fig. 2S†).

An interesting interaction is hyperconjugation which we believe is the pretext for the puckerings of BHËs discussed earlier in this study (Scheme 1). As a matter of fact, most geometrical parameters including bond lengths, bond angle, dihedral angle etc. appear consistent with our suggested hyperconjugation types of resonance (Scheme 2, Tables 4 and 6S†).

Scheme 2

For instance, there are evidences for an unprecedented seesaw-type hyperconjugation interaction for singlet species and not their corresponding triplets (Scheme 2a). In order to focus on the B–B interaction we have simplified Scheme 2a and written in the form of eqn (1):

[X–B B–X] ↔ [X⁻ B–B X⁺] ↔ [X⁺ B–B X⁻] (1)

Interestingly, B–B distance appears shorter for every singlet state divalent compared to its corresponding triplet state (Table 4). For instance, B–B bond length for singlet species 1_s-I–5_s-I are 2.29, 2.31, 2.36, 2.45 and 2.48 which are clearly shorter than those for their corresponding triplet states: 2.50, 2.88, 2.94, 3.05 and 3.26. This is consistent with significant Wiberg Bond Indices (WBI) for B–B interaction which decreases from iodine to fluorine in singlet BHËs (eqn (1) and Table 5).

Table 5 Calculated “Wiberg bond indices” (WBI) for the singlet BHËs (1_s-X, 2_s-X, 3_s-X, 4_s-X and 5_s-X with X = H, F, Cl, Br and I) at B3LYP/TZ2P and donor–acceptor energies (in kcal mol⁻¹) for most important interactions at B3LYP/6-311++g**

Species	WBI		Donor–acceptor energies^a
	B–B	Ë–∥^b	π(C=C) → p(Ë)	σ(B–Ë) → p(B)	σ(B–C) → p(Ë)
a The conventional statement for donor and acceptor orbitals.b ∥ is a symbol for C=C bond. The values of the Ë–∥ column are the products of the first column multiplied by 2 (WBI(Ë–∥) = WBI(Ë–CDB) × 2).
1F	0.105	0.498	23.00	94.41	18.27
1Cl	0.114	0.496	23.08	100.25	17.64
1Br	0.113	0.494	21.87	101.81	17.1
1I	0.123	0.472	—	—	—
2F	0.235	0.394	13.62	15.63	4.68
2Cl	0.278	0.400	15.27	17.58	4.36
2Br	0.285	0.390	14.11	18.27	3.99
2I	0.322	0.376	—	—	—
3F	0.225	0.308	10.90	13.95	3.41
3Cl	0.269	0.298	11.74	15.70	3.02
3Br	0.279	0.294	11.65	16.26	2.78
3I	0.323	0.284	—	—	—
4F	0.214	0.246
4Cl	0.269	0.254
4Br	0.279	0.250
4I	0.343	0.250
5F	—	—
5Cl	0.281	0.182
5Br	0.294	0.178
5I	0.362	0.180

---

Generally, the more polarizable a halogen (X), the more significant is the above hyperconjugation interaction (eqn (1)). Accordingly, divalents with iodine show the highest differences between their singlet–triplet B–B distances. Hence, the following general trend for the significance of eqn (1) is observed: 1_s-I–5_s-I > 1_s-Br–5_s-Br > 1_s-Cl–5_s-Cl > 1_s-F–5_s-F.

Generally, the more polarizable a halogen (X), the more significant is the above hyperconjugation interaction (eqn (1)). Accordingly, divalents with iodine show the highest differences between their singlet–triplet B–B distances. Hence, the following general trend for the significance of eqn (1) is observed: 1_s-I–5_s-I > 1_s-Br–5_s-Br > 1_s-Cl–5_s-Cl > 1_s-F–5_s-F.

Now, let's summarize Scheme 2b in eqn (2) where author pretext for puckering is illustrated through hyperconjugation.

[Ë⁻–C–C⁺] ↔ [Ë C=C] ↔ [C⁺–C–Ë⁻] (2)

For singlet divalents 1_X–5_X, rather significant Ë–∥ are found (Table 5).

Cross-ring hyperconjugation in our bis(boryl)-based heterocyclic divalents appear to be facilitated by the donor–acceptor interaction energies (Scheme 2b).^69,70

Here the BD(C=C) → LP*(Ë) overlap (i.e. commonly written as π → p_(Ë)) decreases from 1_s-X through 3_s-X which is consistent with the calculated WBI values. Fig. 4 demonstrates cross-ring hyperconjugation in 1_s-F, 2_s-F, and 3_s-F.

Fig. 4 Schematic depiction of the σ → p[B–B in Scheme 2a] and π → p_(E) [Scheme 2b] cross-ring hyperconjugative interactions as possible pretexts for puckerings in 1_s-F and 3_s-F. The orange and blue arrows show the orbitals incorporated in these overlaps.

Scheme 2c and d are inspired from σ → p_(B) and σ → p_(Ë) overlaps respectively (Tables 5, 7S and 8S†). The latter, in fact, is only significant in carbenes and decreases notably in its heavier homologues.

3.4 Electronic configurations

3.4.1 Frontier orbitals (FOs). In all carbenes, as well as 2_F, 2_Cl, 3_F and 4_F, the nonbonding σ (conventionally acknowledged as sp²) orbital is the highest occupied molecular orbital (HOMO) and in 2_Br, 2_I, 3_Cl, 3_Br, 3_I, 4_Cl, 4_Br, 4_I, and all plumbylenes, this σ orbital is HOMO-1.⁷¹ The energy of this orbital with σ-symmetry increases with increasing the divalent atomic radius. Table 9S,† represents the percentage for the contribution of the most populated atomic orbitals in the HOMO (and HOMO−1 anywhere needed) and lowest unoccupied molecular orbital (LUMO) of divalent atom in all BHËs. The energy of each orbital is included in Table 9S.†

Furthermore, the gap between HOMO and LUMO (ΔE_LUMO–HOMO) decreases from silylenes to plumbylenes. Schematic view of FOs for 3_s-Br (employed as an example) along with the relative MO level energies of a series of bis(boryl)-based brominated BHËs are calculated at B3LYP/TZ2P (Fig. 5). Interestingly, the p_y character of HOMO in heavier BHËs appears orthogonal to the σ (HOMO−1) orbital (Fig. 5 and Table 9S†).

Fig. 5 Calculated frontier molecular orbital energies for carbene1_s-Br, silylene 2_s-Br, germylene 3_s-Br, stannylene 4_s-Br, and plumbylene 5_s-Br along with HOMO−1, HOMO and LUMO images for 3_s-Br.

The occupied σ orbital along with the unoccupied orthogonal p orbital in heavy divalent species of group 14 have attracted attention.^43,72 Quests continue to recognize their potential reaction molds and mechanistic studies in depth. The contribution of p in the hybrid orbital of divalent atom (E) in its Ë–B bond increases significantly while in contrast the s orbital in the hybrid orbital of Ë including the LP incorporates to a great extent (Tables 6 and 10S†). This is an evidence for the stabilization of the singlet states with larger valance orbitals also known as the “inert s-pair effect”, as mentioned previously.^43,72

Table 6 Average contributions (%) of s and p atomic orbitals in the hybrid orbitals of divalent atom (E)

	σB–Ë bonds	LP orbital
1X	sp^0.99	—
2X	sp^7.27	sp^0.32
3X	sp^10.42	sp^0.21
4X	sp^10.99	sp^0.19
5X	sp^12.16	sp^0.16

---

3.4.2 Linear relationships. Calculated energy differences between HOMO and LUMO of singlet states, ΔE_{(LUMO–HOMO)}, for the halogenated BHËs appear to have linear relationships with the corresponding ΔE_st values. They show correlation coefficients (R²) of 0.949, 0.914, 0.872 and 0.949 for 2_X, 3_X, 4_X, and 5_X respectively (Fig. 6 and 3S†).

Fig. 6 Linear relationships between singlet LUMO–HOMO energy gaps ΔE_{(LUMO–HOMO)}, and their corresponding singlet–triplet energy separations (ΔE_st), for the two series of halogenated five-membered-rings: 3_s-X and 5_s-X; with correlation factors: 0.914 and 0.949, respectively.

As mentioned above, substitution of heavier group 14 atoms at the divalent centre increases the energy gap between HOMO-1 and HOMO with an increasing trend in going from carbon to lead. Such a substitution slightly decreases the energy of LUMO (known as p–π orbital), after sharing a sharp increase in carbenes (Fig. 5). Intriguingly, a reverse linear trend is observed for ΔE_st of BHËs vs. their corresponding band gap (ΔE_{(LUMO–HOMO)}) values (Fig. 6 and 3S†). Evidently, the latter is concerned only with the singlet state while ΔE_st is associated with both singlet and triplet states. One may attribute this observation to the possibility of puckering in singlet species vs. its absence in the corresponding triplet states.

In accordance to discussion made on eqn (1), linear relationships are found between the B–Ë–B angles and their corresponding halogen atom radius, for the five-membered-rings: 2_s-X, 3_s-X, 4_s-X and 5_s-X with correlation factors of 0.844, 0.703, 0.970 and 0.990, respectively (Fig. 4S†). This angle reduces with increasing the halogen atomic radius.⁷³

3.5 Electrophilicity and nucleophilicity

Bis(boryl)-based heterocyclic carbenes (1_s-X) show considerably stronger electrophilicity than their corresponding heavier group 14 homologues (2_s-X–5_s-X) (Table 11S†). In Arduengo's divalents (NHËs), this is reversed. Electrophilicity of 1_s-X–5_s-X (X = F, Cl and Br, except for 1_s-Br) appear more than their corresponding halogenated NHËs. This may be due to the electron-deficiency of boron atoms. All iodinated BHËs show less electrophilic properties than their NHË homologues (Table 11S†). This may partly be due to the higher significance of seesaw-type hyperconjugation interaction discussed above (Scheme 2a) where filling the vacant orbitals of boron atoms reduces the electrophilicity, specially for 5_s-X (X = F, Cl, Br and I) species.

The nucleophilicity index for BHËs and equivalent NHËs increases from 1_s-X through 5_s-X (except for 5_s-I in BHËs). The values of nucleophilicity for all NHËs (except 1_s-F) are greater than the homologues BHËs (Table 11S†) which is expected.

The singlet and triplet species have a σ² and σ¹p¹ configuration respectively which is obtained through a sequence of calculations documenting the interaction of the singlet and triplet species with Lewis acids and bases. The paths for approaching of the Lewis species to the singlet and triplet BHËs are shown in Scheme 3a and b, respectively. For example, in the interaction of 2_s-Cl and 2_t-Cl with AlH₃, approaching the Lewis acid from the aligned direction is more favourable and consumes less energy (Fig. 7).

Scheme 3

Fig. 7 Relative energies for the interactions of Lewis acid (AlH₃) with (a) 2_s-Cl and (b) 2_t-Cl.

As Al gets closer to the Si atom, the energy increases, particularly for Si–Al distances lower than 250 pm (Fig. 7). Furthermore, while the singlet species (2_s-Cl) shows sensitivity toward the direction of AlH₃ approach, the triplet one (2_t-Cl) appears much less sensitive (Fig. 5S†).

3.6 Isodesmic reactions

Isodesmic reactions suggest a high degree of correlation between ΔE_st and the relative energies of reaction with methane, coupling with hydroxymethylcarbene, and dimerization (Scheme 4). Firstly, reaction with methane (Scheme 4c) produces hydrogenated BHË and is defined as a measure for hydrogenation (ΔE_{hydrogenation}).^74,75 Secondly, coupling with hydroxymethylcarbene (Scheme 4b) leads to the important Breslow-type intermediate.^75,76 Finally, dimerization (Scheme 4a) is an intrinsic reaction of divalents whose prevention increases the “Divalent Species Stabilization Energy; DSSE”.^72,77,78

Scheme 4

Stannylenes (4_s-X) show the greatest values of ΔE_{hydrogenation} and hence are the most stable (Table 7). The general order for relative ΔE_{hydrogenation} is: 4_s-X > 3_s-X > 2_s-X > 5_s-X > 1_s-X (X = F, Cl, Br, I). This is except for 4_s-I which falls below the values for plumbylenes. Partially in each series, the BHË with X = I shows the highest ΔE_{hydrogenation} (Scheme 4a). The order for the stability of the Breslow-type intermediates is: 5_s-X > 4_s-X > 3_s-X > 2_s-X > 1_s-X for X = F, Cl, Br, and I (Scheme 4b). The third reaction (with ΔE_dimerization) shows an order of decreasing relative energy similar to the coupling reaction.

Table 7 Relative energies of hydrogenation (ΔE_(a)), hydroxymethylcarbene coupling (ΔE_(b)) and dimerization (ΔE_(c)) in kcal mol at B3LYP/TZ2P^a

BHË	ΔE(a)	ΔE(b)	ΔE(c)
a The smaller values imply less stable BHËs (easier reactivity).
1F	21	0	0
1Cl	26	5	13
1Br	26	5	15
1I	28	9	20
2F	78	82	100
2Cl	81	84	107
2Br	81	84	108
2I	82	85	111
3F	98	106	114
3Cl	101	108	120
3Br	102	108	121
3I	103	109	123
4F	109	116	121
4Cl	112	118	126
4Br	113	118	127
4I	64	118	134
5F	—	—	—
5Cl	72	128	135
5Br	72	126	—
5I	73	125	136

---

As a result, the BHË gains more stability and shows less reactivity as the size of the divalent atom increases.

Correlation of the three reactions of our halogenated bis(boryl)-divalents (Fig. 8 and 6S†) appear consistent with the reactivity of divalent species previously concluded according to the effects of ΔE_st (ref. 5, 43, 55, 72 and 77) and divalent angle (∠BËB).^72,77

Fig. 8 Linear relationships between singlet–triplet energy separations (ΔE_st) of X₂-BHËs (Ë = Si; X = F, Cl, Br, I) and their relative energies of isodesmic reactions (a) with methane (b) coupling with hydroxylmethylcarbene and (c) dimerization, as shown in Scheme 4, respectively.

3.7 Complexation of BHË with group 11 metals

Possibility of interaction between BHËs and group 11 chlorides (CuCl, AgCl, and AuCl) are assessed (Table 12S†). Each complexation energy is predicted through an isodesmic reaction ΔE_complexation = E_complex − (E_BHË + E_MCl). The Au complexes appear the most exothermic, after which come the complexes of copper, followed by that of silver. On the other hand, the trend of ΔE for divalents complies with the following order:

1_X–MCl > 2_X–MCl > 3_X–MCl

Simultaneously, puckering angle (D1) of 1_X, 2_X, and 3_X (X = F, Cl) decreases significantly in the corresponding complex structures with the following trend:

Cu > Ag > Au

The decrease in WBI and donor–acceptor energies for Ë–∥ proves this observation. WBI for B–B is considerably reduced, as well.

Calculations also reveal that the geometries around the metal atoms (∠Ë–M–Cl), are not essentially linear, the most bent of which is for carbenes (1_X: X = F, Cl) with an average angle of 170.90°. Silylenes, 2, and germylenes, 3, make more straight angles (an average of 178.58° and 177.8° for 2_X- and 3_X–MCl, respectively). In view of the metal atoms, the ∠Ë–M–Cl in Cu complexes is smaller than the related angle in Ag and Au complexes.

The bond lengths Ë–B in 1_X–MCl (X = F, Cl; M = Cu, Ag, and Au) are longer than in the free divalents (ligands). The trend is reversed in all complexes of 2_X and 3_X.

Every Au–Ë bond is apparently shorter than the corresponding Ag–Ë which is verified with WBI. The Cu–Ë is shorter than both of them.

In view of the metal atom, π-back bonding energies (Ë ← MCl) obey the order of Au > Cu > Ag, which is in accordance with the above order of ΔE_complexation (Table 12S†). Considering the divalent atom and consistent with the complexation energy order, the back donation descends from 1_X to 2_X and to 3_X. Therefore, 1_X–AuCl bears the most back-bonding energy and 3_X–AgCl is at the lowest end.

4 Conclusions

The challenging introduction of electron-withdrawing groups such as boryl substituents flanking the carbenic center (Ë) produces a good model of pull–pull carbene story profiting from the ability of boron to stabilize a LP in an adjacent position. Every bent singlet structure for all studied species is more stable than its corresponding planar triplet. Carbenes have the least stability among their corresponding heavier group 14 homologues. The stability of the singlets with a puckered geometry (D1 ≅ 66°) is achieved via cross-ring hyperconjugative interactions, the most important of which we believe is a seesaw-type with a significant amount of bond index between the cross boron atoms (Scheme 2a and eqn (1)) and a kind of π → p overlap between the divalent atom and the C=C bond (Scheme 2b and eqn (2)), again with a notable amount of WBI (Table 5). These interactions make BHËs (Ë = Si, Ge, Sn, Pb) considerably stable; the stability of which is demonstrated with singlet–triplet energy gaps (ΔE_st) and also proved by isodesmic reactions (Scheme 4). Moreover, eight species (2_I, 3_Br, 3_I, 4_Br, 4_I, 5_Cl, 5_Br, and 5_I) are found enjoying more stability than their corresponding NHË homologues and three species (2_Br, 4_Cl, and 5_F) with comparable energies.

The σ² (sp²) orbital in singlet species is HOMO in BHCs and HOMO−1 in heavier BHËs with Ë = Si, Ge, Sn and Pb, while the electronic configuration for the triplets is σ¹p¹.

There are linear relations between ΔE_st and ΔE_{(LUMO–HOMO)} and also between ΔE_st and the atomic size of the divalent atom for each species.

The trend of the adduct formation energies of BHË–MCl illustrate that for the ligands, the order for ΔE_complexation is carbene > silylene > germylene and for the metals Au > Cu > Ag. The most important change for the ligand geometries is the lengthening of the B–Ë bond for Ë = C and its shortening for Ë = Si and Ge. The puckering of the BHËs decreases in the structure of all surveyed complexes which is a consequence of decline in cross-hyperconjugations noticed in BHË cycles. Obviously, such metal π-back-donation recompense the electron deficiency while increases the stability of the complex.

Acknowledgements

The authors are indebted to Prof. Hassan Sabzyan for his kind help and useful technical discussions.

Notes and references

1. A. K. Guha, C. Das and A. K. Phukan, J. Organomet. Chem., 2011, 696, 586–593.
2. M. Z. Kassaee, M. R. Momeni, F. A. Shakib, Z. Najafi and H. Zandi, J. Phys. Org. Chem., 2011, 24, 1022–1029.
3. W. Kirmse, Angew. Chem., Int. Ed., 2010, 49, 8798–8801.
4. V. C. Rojisha, S. De and P. Parameswaran, Inorg. Chem., 2012, 51, 8265–8274.
5. C.-S. Wu and M.-D. Su, J. Comput. Chem., 2011, 32, 1896–1906.
6. M. Z. Kassaee, H. Zandi, B. N. Haerizade and M. Ghambarian, Comput. Theor. Chem., 2012, 1001, 39–43.
7. L. Broeckaert, P. Geerlings, A. Ruzicka, R. Willem and F. D. Proft, Organometallics, 2012, 31, 1605–1617.
8. A. Chrostowska, V. Lemierre, A. Dargelos, P. Baylère, W. J. Leigh, G. Rima, L. Weber and M. Schimmel, J. Organomet. Chem., 2009, 694, 43–51.
9. A. Bundhun, P. Ramasami, P. P. Gaspar and H. F. Schaefer, Inorg. Chem., 2012, 51, 851–863.
10. K. Izod, C. Wills, W. Clegg and R. W. Harrington, Organometallics, 2009, 28, 5661–5668.
11. D. Heitmann, T. Pape, A. Hepp, C. Mück-Lichtenfeld, S. Grimme and F. E. Hahn, J. Am. Chem. Soc., 2011, 133, 11118–11120.
12. A. J. Arduengo, Acc. Chem. Res., 1999, 32, 913–921.
13. A. J. Arduengo, R. L. Harlow and M. Kline, J. Am. Chem. Soc., 1991, 113, 361–363.
14. D. Bourissou, O. Guerret, F. o. P. Gabbaï and G. Bertrand, Chem. Rev., 1999, 100, 39–92.
15. W. A. Herrmann and C. Köcher, Angew. Chem., Int. Ed. Engl., 1997, 36, 2162–2187.
16. M. Denk, R. Lennon, R. Hayashi, R. West, A. V. Belyakov, H. P. Verne, A. Haaland, M. Wagner and N. Metzler, J. Am. Chem. Soc., 1994, 116, 2691–2692.
17. W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272–295.
18. V. Y. Lee and A. Sekiguchi, in Organometallic Compounds of Low-Coordinate Si, Ge, Sn and Pb, John Wiley & Sons, Ltd, 2010, pp. 139–197.
19. P. Boudjouk, E. Black and R. Kumarathasan, Organometallics, 1991, 10, 2095–2096.
20. D. J. Lucas, L. A. Curtiss and J. A. Pople, J. Chem. Phys., 1993, 99, 6697–6703.
21. M. R. Zachariah and W. Tsang, J. Phys. Chem., 1995, 99, 5308–5318.
22. A. Meller and C.-P. Gräbe, Chem. Ber., 1985, 118, 2020–2029.
23. M. Veith and M. Grosser, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1982, 37, 1375–1381.
24. J. Barrau and G. Rima, Coord. Chem. Rev., 1998, 1, 593–622.
25. N. Tokitoh and R. Okazaki, Coord. Chem. Rev., 2000, 210, 251–277.
26. A. E. Ayers, D. S. Marynick and H. V. R. Dias, Inorg. Chem., 2000, 39, 4147–4151.
27. J. R. Babcock, C. Incarvito, A. L. Rheingold, J. C. Fettinger and L. R. Sita, Organometallics, 1999, 18, 5729–5732.
28. H. V. R. Dias and W. Jin, J. Am. Chem. Soc., 1996, 118, 9123–9126.
29. T. Gans-Eichler, D. Gudat and M. Nieger, Angew. Chem., Int. Ed., 2002, 41, 1888–1891.
30. P. J. Davidson, D. H. Harris and M. F. Lappert, J. Chem. Soc., Dalton Trans., 1976, 2268–2274.
31. P. J. Davidson and M. F. Lappert, J. Chem. Soc., Chem. Commun., 1973, 317a.
32. M. Weidenbruch, J. Organomet. Chem., 2002, 646, 39–52.
33. J. P. H. Charmant, M. F. Haddow, F. E. Hahn, D. Heitmann, R. Frohlich, S. M. Mansell, C. A. Russell and D. F. Wass, Dalton Trans., 2008, 6055–6059.
34. B. Gehrhus, P. B. Hitchcock and M. F. Lappert, J. Chem. Soc., Dalton Trans., 2000, 3094–3099.
35. Y. Ishida, B. Donnadieu and G. Bertrand, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13585–13588.
36. M. M. Brahmi, J. Monot, M. Desage-El Murr, D. P. Curran, L. Fensterbank, E. Lacôte and M. Malacria, J. Org. Chem., 2010, 75, 6983–6985.
37. J. Monot, A. Solovyev, H. Bonin-Dubarle, É. Derat, D. P. Curran, M. Robert, L. Fensterbank, M. Malacria and E. Lacôte, Angew. Chem., Int. Ed., 2010, 49, 9166–9169.
38. A. Solovyev, Q. Chu, S. J. Geib, L. Fensterbank, M. Malacria, E. Lacôte and D. P. Curran, J. Am. Chem. Soc., 2010, 132, 15072–15080.
39. S.-H. Ueng, A. Solovyev, X. Yuan, S. J. Geib, L. Fensterbank, E. Lacôte, M. Malacria, M. Newcomb, J. C. Walton and D. P. Curran, J. Am. Chem. Soc., 2009, 131, 11256–11262.
40. M. Yamashita, Angew. Chem., Int. Ed., 2010, 49, 2474–2475.
41. C.-H. Chen and M.-D. Su, Inorg. Chem., 2006, 45, 8217–8226.
42. F. Lavigne, E. Maerten, G. Alcaraz, N. Saffon-Merceron, C. Acosta-Silva, V. Branchadell and A. Baceiredo, J. Am. Chem. Soc., 2010, 132, 8864–8865.
43. C.-S. Wu and M.-D. Su, Dalton Trans., 2012, 3253–3265.
44. H. Meyer, G. Baum, W. Massa, S. Berger and A. Berndt, Angew. Chem., Int. Ed. Engl., 1987, 26, 546–548.
45. H. Meyer, G. Baum, W. Massa and A. Berndt, Angew. Chem., Int. Ed. Engl., 1987, 26, 798–799.
46. A. V. Protchenko, K. H. Birjkumar, D. Dange, A. D. Schwarz, D. Vidovic, C. Jones, N. Kaltsoyannis, P. Mountford and S. Aldridge, J. Am. Chem. Soc., 2012, 134, 6500–6503.
47. M. Z. Kassaee, J. Azarnia and S. Arshadi, J. Mol. Struct.: THEOCHEM, 2004, 686, 115–122.
48. M. Z. Kassaee, B. N. Haerizade and S. Arshadi, J. Mol. Struct.: THEOCHEM, 2003, 639, 187–193.
49. M. Z. Kassaee, Z. S. Hossaini, B. N. Haerizade and S. Z. Sayyed-Alangi, J. Mol. Struct.: THEOCHEM, 2004, 681, 129–135.
50. M. Z. Kassaee, M. R. Nimlos, K. E. Downie and E. E. Waali, Tetrahedron, 1985, 41, 1579–1586.
51. M. Z. Kassaee, S. Z. Sayyed-Alangi and Z. Hossaini, J. Mol. Struct.: THEOCHEM, 2004, 676, 7–14.
52. H. Dürr and F. Werndorff, Angew. Chem., Int. Ed. Engl., 1974, 13, 483–484.
53. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
54. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
55. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Znkrzewski, G. A. Montgomery, R. E. Startmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pamelli, G. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokoma, D. K. Malick, A. D. Rubuck, K. Raghavachari, J. B. Foresman, J. Cioslawski, J. V. Oritz, B. B. Stlefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Comperts, R. L. Martin, P. J. Fox, T. Keith, M. A. Al-laham, C. Y. Peng, A. N. Akkara, C. G. Gonzales, M. C. Combe, P. M. W. Gill, B. Johnson, W. Chem, M. W. Wong, J. L. Andres, C. Gonzales, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, Revision A. 6, Gaussian Inc., Pittsburgh, PA, 1998.
56. ADF2008.01, SCM, Theoretical Chemistry, Vrije University, Amsterdam, the Netherlands, available from: http://www.scm.com.
57. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
58. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
59. M. P. McGrath and L. Radom, J. Chem. Phys., 1991, 94, 511–516.
60. L. A. Curtiss, M. P. McGrath, J. P. Blaudeau, N. E. Davis, R. C. Binning and L. Radom, J. Chem. Phys., 1995, 103, 6104–6113.
61. H. B. Schlegel and M. J. Frisch, Int. J. Quantum Chem., 1995, 54, 83–87.
62. E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
63. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
64. E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953.
65. E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516.
66. E. van Lenthe, R. van Leeuwen, E. J. Baerends and J. G. Snijders, Int. J. Quantum Chem., 1996, 57, 281–293.
67. Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 1849–1868.
68. L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309.
69. W. C. McKee, J. I. Wu, M. Hofmann, A. Berndt and P. v. R. Schleyer, Org. Lett., 2012, 14, 5712–5715.
70. F. Weinhold and C. R. Landis, Valency and Bonding: A Natural Bond Orbital Donor-Acceptor Perspective, Cambridge University Press, 2005.
71. Y. Xiong, S. Yao, S. Inoue, J. D. Epping and M. Driess, Angew. Chem., Int. Ed., 2013, 52, 7147–7150.
72. J.-Y. Chen and M.-D. Su, Dalton Trans., 2011, 7898–7907.
73. B. D. Rekken, T. M. Brown, J. C. Fettinger, F. Lips, H. M. Tuononen, R. H. Herber and P. P. Power, J. Am. Chem. Soc., 2013, 135, 10134–10148.
74. A. A. Tukov, A. T. Normand and M. S. Nechaev, Dalton Trans., 2009, 7015–7028,  10.1039/b906969k.
75. O. Hollóczki, Z. Kelemen and L. Nyulászi, J. Org. Chem., 2012, 77, 6014–6022.
76. M. Veith and M. Grosser, Z. Naturforsch., B: Anorg. Chem., Org. Chem., 1982, 37, 1375–1381.
77. R.-H. Wang and M.-D. Su, J. Phys. Chem. A, 2008, 112, 7689–7698.
78. L. Nyulaszi, T. Veszpremi and A. Forro, Phys. Chem. Chem. Phys., 2000, 2, 3127–3129.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra04911c

---