Cr3+-substitution induced structural reconfigurations in the nanocrystalline spinel compound ZnFe2O4 as revealed from X-ray diffraction, positron annihilation and Mössbauer spectroscopic studies†
Rahul Mundiyaniyil Thankachana,
Jincemon Cyriac‡
a,
B. Raneeshb,
Nandakumar Kalarikkalab,
D. Sanyalc and
P. M. G. Nambissan*d
aSchool of Pure & Applied Physics, Mahatma Gandhi University, Kottayam, Kerala 686560, India. E-mail: rahulmt05@gmail.com; jincemon999@gmail.com; nkkalarikkal@mgu.ac.in
bInternational and Inter University Centre for Nanoscience and Nanotechnology, Mahatma Gandhi University, Kottayam, Kerala 686560, India. E-mail: raneesh.b@gmail.com
cVariable Energy Cyclotron Centre, Department of Atomic Energy, Kolkata 700064, India. E-mail: dirtha@vecc.gov.in
dApplied Nuclear Physics Division, Saha Institute of Nuclear Physics, Kolkata 700064, India. E-mail: pmg.nambissan@saha.ac.in; pmgnambissan@gmail.com; Fax: +91-33-23374637; Tel: +91-33-23375345
First published on 21st July 2015
Abstract
In an earlier work, the substitution of Zn2+ ions at the tetrahedral sites of nanocrystalline zinc ferrite (ZnFe2O4) by Ni2+ ions had been observed to cause a transformation from the normal spinel structure to the inverse one. The present study has been undertaken to explore the possibility of a similar change when the Fe3+ ions at the octahedral sites are replaced by Cr3+ ions. Concomitant lattice contraction and a steady decrease of the sizes of the nanocrystallites preceded and then resulted into the inversion of ZnFe2−xCrxO4 from normal spinel to inverse at x ≥ 0.8. Positron lifetime and coincidence Doppler broadening spectroscopic studies were carried out on the samples and a distinct third positron lifetime component emerged in the range of Cr3+ concentration 0.8 ≤ x ≤ 1.6. The new positron trapping sites were the result of the inversion of the spinel structure wherein the Cr3+ ions which substituted the Fe3+ ions at the octahedral sites got shifted to the tetrahedral sites, interchanging their positions with the Zn2+ ions. The incomplete success of inversion led to the generation of vacancy-type defects, which significantly trapped the positrons and the changes in their lifetimes indicated the occurrence of the process. The continued lattice contraction ensured an inverted spinel structure even for the final ZnCr2O4, which in coarse-grained form and at room temperature is a normal spinel. Mőssbauer spectroscopic studies also supported the idea of spinel inversion above x = 0.8 through definite changes in the isomer and quadrupole shifts.
1. Introduction
The basic crystal structure of bulk zinc ferrite (ZnFe2O4) at room temperature is a complete normal spinel structure with the divalent Zn2+ ions occupying the tetrahedral (A-) sites in four alternative octants of a cubic lattice and the trivalent Fe3+ ions occupying the octahedral (B-) sites in the other four octants.1,2 There are altogether eight divalent and sixteen trivalent cations coordinated respectively in tetrahedral and octahedral geometries with thirty two oxygen ions (O2−) in a unit cell. The anions (i.e., the oxygen ions) are positioned in the same way in all the octants. Each octant contains four oxygen ions on the body diagonals, which form the corners of a tetrahedron as shown in Fig. 1. Thus oxygen ions form an fcc lattice with edge length a/2 where the lattice constant a is the length of each side of the cube. | ||
| Fig. 1 Two octants of the spinel structure. The large spheres represent the oxygen ions. The small black and white spheres represent the metal ions on tetrahedral and octahedral sites respectively.1 | ||
The research on ferrites has received a major boost in recent years since they were observed to exhibit anomalous changes in their fundamental electronic and magnetic properties when reduced to nanocrystallites of sizes of the order of a few (∼1–100) nanometers.3–5 Substitution by other elements of near-ionic radii, changes of the preparation conditions and modulation of the particle sizes etc. are some of the methods to improve the properties of ferrites. There are already a few reports on ferrite systems by various research groups, especially on the changes in structure when substituted with ions of different types and concentrations.6,7 Of the many transition metal ferrites, ZnFe2O4 has drawn the maximum attention due to its promising properties and applications in several areas such as gas sensors, semiconductor photo catalysis, magnetic data storage, ferrofluids, medical imaging, drug delivery and pigments.8
The aim of the present work is to study the effects of substitution of Fe3+ ions on the lattice structure and cation distribution in ZnFe2O4 by the trivalent metallic cation Cr3+ to different concentrations (x = 0.0, 0.2, …, 2.0). While a number of experimental techniques are available for the structural characterization and particle size determination, we also put emphasis on the defects-related structural aspects since they too play a significant role in the ultimate physical and mechanical properties of such materials. Hence positron annihilation spectroscopic investigations have been undertaken in detail to monitor the defects generated and their local interactions with the neighboring ions during the different stages of substitution. The importance and relevance of positron annihilation studies on spinel material systems have been demonstrated in a number of studies reported in literature.9–11 Further, Mössbauer spectroscopic studies have been proved very useful in observing magnetic transitions in such systems especially when there are definite variations in size and composition of the nanocrystallites.12,13
It may not be out of context to mention that normal spinel ferrites undergo inversion under specific experimental conditions. Like temperature, crystallite sizes and composition affecting the cation distribution in spinel materials, the substitution by ions of similar valencies is a commonly adopted method of achieving the inversion. The general chemical formula of an inverse spinel ferrite is Fe(AFe)O4, which means Fe3+ ions are distributed equally among the tetrahedral and the octahedral sites while the divalent ions (Zn2+ in this case) occupy the rest of the octahedral sites. The common factors affecting the cation distribution in spinels are the ionic sizes, site stabilization energies, temperature and the presence and concentration of substitutional impurities. Recent investigations have shown that nanometer sizes of the crystallites also have decisive roles in determining the cation distribution at the different sites in a spinel lattice.14,15
2. Experimental details
In this study, all the samples ZnFe2−xCrxO4 with x = 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4, 1.6, 1.8 and 2.0 were synthesized through the sol–gel technique. Zinc nitrate hexahydrate (Zn(NO3)2·6H2O), ferric nitrate nonahydrate (Fe(NO3)2·9H2O) and chromium nitrate nonahydrate (Cr(NO3)3·9H2O) are used as precursors and polyvinyl alcohol (PVA) as chelating agent. For the synthesis of ZnFe2O4, aqueous solutions of Zn(NO3)2·6H2O and Fe(NO3)2·9H2O of respective strength 0.1 M and 0.2 M are mixed and sonicated. PVA was added to the mixed solution with a weight equal to the weight of the metal ions in the solution. The solution was vigorously stirred until PVA was completely dissolved and then evaporated at 333 K till it gradually turned into a viscous sol and then to a dark brown gel. The dried gels were calcined at 773 K for 2 hours. Similar procedure was repeated for the synthesis of the other samples, the only difference being the change in the molarity of two of the precursor solutions Fe(NO3)2·9H2O and Cr(NO3)3·9H2O and the weight of the PVA in order to keep the stoichiometry and nanocrystalline nature of the products intact. (The molar ratios of the precursor solutions and the corresponding weights and the weight of PVA used for the synthesis of the ZnFe2−xCrxO4 samples are all given in Table 1 in the ESI†).X-ray diffraction (XRD) studies on the synthesized powder samples under dry conditions were carried out using the Phillips X'Pert Pro XRD machine with CuKα radiation (of wavelength 1.5406 Å). Data were collected in the 2θ range 15–85° with a step size of 0.02° and a scan speed of 0.5 second per step at room temperature.
Positron annihilation measurements were carried out using a 22Na source of strength ∼10 μCi taken in the form of a deposition inside a folded Ni foil of thickness 2 mg cm−2. The foil had been annealed before at 1273 K for 2 hours in vacuum (∼10−6 mbar), slowly cooled to room temperature and then cleaned with ethanol and dried to avoid trapping of positrons in any kind of defects or dislocations within the foil. The source prepared in this way is kept immersed in the volume of the powdered sample taken in a glass tube. In order to prevent the annihilation of positrons within the walls of the glass tube, care was taken to fill all sides of the source with sample in thickness more than the range of positrons in it. Also, during the data acquisition, the glass tube containing the source and sample was continuously evacuated to remove air, moisture and absorbed gases otherwise likely to be trapped within the column of the sample. The positron lifetime spectra were recorded using a slow-fast gamma–gamma coincidence set-up which employed BaF2 scintillators coupled to XP2020Q photo multiplier tubes as detectors and the required nuclear electronic modules. The prompt time resolution of this set-up had been initially measured by selecting the photopeaks of the gamma rays from a 60Co source and a full width at half maximum (fwhm) of 140 ps was obtained. The resolution under the 22Na experimental settings (1278 keV and 511 keV photopeaks accepted in the two channels respectively) was obtained as 170 ps. About 106 counts were collected under each spectrum. The spectra were analyzed using the PALSfit program, which incorporated corrections for the contributions from the positron source and the background.16 (ESI†).
The coincidence Doppler broadening spectroscopic (CDBS) measurements were carried out using two high pure germanium (HPGe) detectors.17 They were kept on either side of the source-sample assembly so that both the annihilation gamma rays going in opposite directions can be detected and their energy can be measured. The detectors used in this work had energy resolutions 1.27 keV and 1.33 keV at the positron annihilation gamma ray energy 511 keV. In each experiment, more than 8 × 106 counts were collected. The data were acquired and spectra analyzed using the LAMPS program.18
Room temperature 57Fe Mössbauer spectra for all the samples have been recorded in the transmission configuration with constant acceleration mode.19 While a 10 mCi 57Co isotope embedded in Rh matrix has been used as the Mössbauer source, a gas filled proportional counter has been used for the detection of the 14.4 keV Mössbauer γ-rays. The Mössbauer spectrometer has been calibrated with 95.16% enriched 57Fe2O3 and standard α-57Fe foil. The Mössbauer spectra have been analyzed using a standard least square fitting program NMOSFIT.20
3. Results and discussion
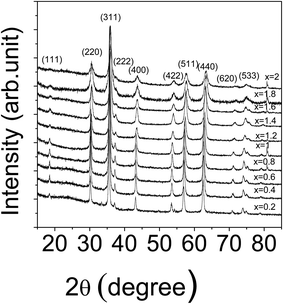
The samples were checked for their purity using X-ray diffraction and the patterns did not show any additional peaks other than those of the ZnFe2−xCrxO4 structure, as illustrated in Fig. 2. The patterns confirmed the formation of ZnFe2−xCrxO4 with spinel structure. The broad reflections are indicative of the formation of crystallites with nanometer sizes. The peaks at 2θ = 18°, 37° and 72°, gradually disappeared at larger values of x indicating the effects of substitution.The lattice constants and the average crystallite sizes of the different samples were calculated from the well-known Bragg's law of X-ray diffraction and the Scherrer equation respectively.21 The effects of a resultant background arising from the high fluorescence arising out of the CuKα radiation has been removed from the estimation by first making measurements on a standard high purity silicon powdered sample and correcting for the instrumental broadening.
The lattice parameters of the samples agreed well with the reported values in the JCPDS cards (card no. 82-1042 for ZnFe2O4 and card no. 22-1107 for ZnCr2O4). The observed lattice parameter showed a continuous decrease with increasing Cr3+ concentration (Fig. 3(a)). The average crystallite sizes of the samples also showed a decrease with increase in Cr3+ concentration (Fig. 3(b)). The observed decrease in the nanocrystallite sizes is to be understood in terms of the substitution of Fe3+ ions (of radius ∼0.67 Å) by Cr3+ ions of slightly smaller radius (∼0.64 Å). The increasing substitution then will lead to reduced crystallite sizes. When the size of the nanocrystallite decreases, the number of atoms within its core decreases and the relative number of atoms on the surface increases. The inward surface tension will then be increasingly effective in bringing the atoms closer and thereby resulting into decreased lattice parameters, as observed earlier in other similar studies also.14 Although the changes in lattice parameter and the nanocrystallite size need not necessarily be interdependent, a plot of the two showed an empirical relation (Fig. 4).
| a = 0.8256 + 0.0006dc | (1) |
 | ||
| Fig. 4 The lattice constant a versus the average crystallite size dc of the Cr3+-doped ZnFe2O4 samples. | ||
Interestingly, such relations have been found holding in some of the nanocrystalline oxides studied recently.22,23
The positron lifetime spectra are composed of extended positron lifetimes and intensities, which are indicative of the presence of defects and defect clusters in the spinel compounds. (ESI.† The peak-normalized raw positron lifetime spectra of all the samples are illustrated).
The individual positron lifetimes and their relative intensities were resolved by analyzing the spectra using the PALSfit program. The spectra of the ZnFe2−xCrxO4 (x = 0.0, 0.2, …, 1.6) samples are fitted using a three lifetime component fit, which gave an acceptable variance of fit (0.90–1.2) but, for the samples with x = 1.8 and 2.0, a two-component fit was found adequate and acceptable. The obtained third components for the samples with x = 0.0, 0.2, 0.4 and 0.6 were large (>1.0 ns) but their relative intensities were very small (<0.3%). So for those samples, only the first two components were selected for interpretation. But for the samples with x = 0.8, 1.0, 1.2, 1.4 and 1.6, the third component appeared to be a physically meaningful lifetime and had a considerable relative intensity too. The variations of the positron lifetimes and their intensities with Cr3+ concentration (x) are shown in the Fig. 5(a) and (b).
The shortest positron lifetime component τ1 is indicative of positron trapping in defects. In fact, the positron lifetime that is characteristic of the defects present in the samples is τ2, which is discussed below. τ1 comes from the relation between the bulk positron lifetime τb and the positron trapping rate κd that is proportional to the concentration of the defects in the solid.24
 | (2a) |
 | (2b) |
τ1 normally comes from the free positron lifetimes, i.e., the lifetimes of positrons annihilating without getting trapped into any defects, and the Bloch state residence time of the trapped positrons. The defect specific positron lifetime τ2 generally stands for the lifetime of positrons trapped in vacancy-type defects. From the magnitude of the lifetime τ2 and its difference from the bulk positron lifetime τb, it is often possible to predict the nature and size of the vacancy-type defect where the positron is trapped before it gets annihilated. τb is normally obtained from the relation24
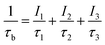 | (3) |
The lifetime τ3 and its intensity I3 are attributed to positron annihilation at the surfaces of the nanocrystallites due to thermal diffusion. They got merged again with the intermediate lifetime τ2 and its intensity I2 (Fig. 5(a) and (b)) when the latter increased at x = 1.8 and 2.0.
Fig. 6 illustrates the behavior of the mean positron lifetime τm defined as
 | (4) |
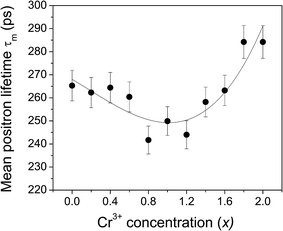 | ||
| Fig. 6 The variation of the mean positron lifetime τm with the Cr3+ concentration in the different samples. | ||
The variation of τm with Cr3+ concentration depicts two distinct stages. There is a steady and well-defined reduction of it from x = 0.0 to 0.8 and then an equally steady increase from x = 0.8 to 2.0. Subsequently, we had seen from the results of coincidence Doppler broadening data analysis discussed later in this paper that the entire process of defect dynamics during the course of substitution of Fe3+ by Cr3+ takes the material characteristics through two such distinct stages.
To understand it more vividly, we estimated the bulk positron lifetime defined by eqn (3) for all the samples and its variation is shown in Fig. 7. The initial reduction of the bulk lifetime by about 20 ps (from 221 ps at x = 0.0 to 201 ps at x = 0.8) is beyond one can comprehend on the basis of a simple lattice contraction shown in Fig. 3(a). We therefore calculated the effect of lattice contraction on the bulk positron lifetime τb following a simple procedure in line with the one described for lattice contraction effects due to the lowering of sample temperature by de la Cruz et al.27 According to this procedure, the annihilation rate of positrons inside a solid is mainly influenced by its electron density. The temperature dependence on the bulk positron lifetime is given by an equation
 | (5) |
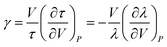 | (6) |
 | (7) |
In analogy with the above, τb in the present work is modified to get the variation of the bulk positron lifetime with change in volume due to the change in concentration (x) of doping of one species atom by another as
 | (8) |
In this work, the observed results show that the increase in concentration of Cr3+ causes a decrease in the lattice volume. So τ is considered as the bulk positron lifetime τb of the sample at a concentration of the dopant material x, τb0 is the bulk positron lifetime at a concentration x = x0 (here x0 = 0.0), γ is the volume coefficient of τb and β(x) is the volume thermal contraction coefficient. The volume coefficient of τ as in the case of eqn (6) is defined as
 | (9) |
 | (10) |
By calculating γ and β(x) for the different values of x, it is possible to predict the change in the corresponding value of the bulk positron lifetime with concentration of Cr3+ ions. This will be helpful to examine the possibility of any other mechanism causing the change in the bulk lifetime other than the lattice contraction effect. The result of this analysis is shown by the curve with open circles in Fig. 7. Barring an insignificant fall initially, the bulk lifetime remained more or less constant throughout the range of doping. This could be due to the fact that Cr3+ has two electrons less in the 3d orbit and hence the enhancement in the local electron density due to the lattice contraction is nullified and the positron lifetime remains unaltered. The solid circles in the figure denote the actual values deduced from the resolved positron lifetimes and their intensities using eqn (3). It demonstrates that the initial reduction of the positron lifetimes are not completely due to the lattice contraction but a concomitant process bringing in a more prominent and predominant reduction in positron lifetimes is taking place during the process of substitution.
On the basis of the earlier works done and reported in literature, the additional decrease and subsequent increase observed in the bulk positron lifetime in addition to that predicted by lattice contraction is attributed to a transformation of the normal spinel structure of ZnFe2O4 to a partly or completely inverted structure of ZnFe2−xCrxO4.11 The following arguments are presented to support this interpretation. It has been demonstrated in earlier studies that the positron lifetimes normally decrease during a normal to inverse spinel transformation and vice versa.10,25 The purpose of this experiment was to explore such a possibility when ions at the B-sites are replaced by other cations. The results seem to favor such an inversion. An identical effect but from inverse to normal spinel transformation had been earlier observed in the case of Cr3+-substitution at the sites of Fe3+ in CoFe2O4.14,28 In a recent study on the effect of Cr3+-substitution at the B-sites of nanocrystalline ZnFe2O4, Kumari et al.29 had reported about the lattice contraction and size reduction of the crystallites and also the change in dielectric properties but had possibly not observed the structural inversion due to the very limited range of substitution, i.e., from x = 0.1 to x = 0.5 only. With the broader range of substitution undertaken in this study, the effect of inversion could be highlighted as it dominates over the competing process of lattice contraction in directly influencing the positron annihilation parameters.
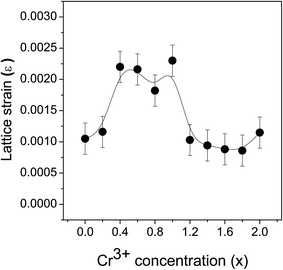
The advent of an inversion of the spinel structure at a Cr3+ concentration of x = 0.8 has come to prominence in an independent estimation of the strain that is built in the ZnFe2−xCrxO4 lattice by the substitution process. The Scherrer formula used in the estimation of the crystallite size shown in Fig. 3(b) is in fact given by21
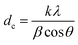 | (11) |
On the other hand, the strain pervading in the powdered nanocrystalline samples due to crystal imperfections, impurities (here the substituted Cr3+ ions) and possibly dislocations too can be evaluated using the formula30–32
 | (12) |
The observed broadening of the X-ray diffraction peaks are therefore considered to emerge from the particle size reduction as well as the induced strain, which are further independent of each other. Hence β can be expressed as the sum of the above two equations to obtain
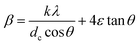 | (13) |
Rearranging the equation, we get
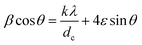 | (14) |
Eqn (14) is the well-known Williamson–Hall equation30 and can be drawn as a linear plot of β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ versus 4
θ versus 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The slope of the plot will give the value of the strain ε generated in the nanomaterial from the crystal imperfections and distortions. The variation of the calculated strain in the ZnFe2−xCrxO4 nanomaterial samples at different levels of Cr3+ concentration is shown in Fig. 8. The noticed lattice strain grows from 0.0010 at x = 0.0 and, with increasing Cr3+ concentration, the rise continues to its maximum of 0.0023 at x = 0.8–1.0. The trend afterwards has reversed and the lattice strain decreased drastically to 0.0011 at x = 2.0. It is obvious that strain has been building up within the lattice due to Cr3+-substitution and, beyond x = 0.8–1.0, it is getting relaxed by the spinel lattice transforming to the inverted phase. The arguments presented earlier in support of this interpretation are strengthened by the present observation.
θ. The slope of the plot will give the value of the strain ε generated in the nanomaterial from the crystal imperfections and distortions. The variation of the calculated strain in the ZnFe2−xCrxO4 nanomaterial samples at different levels of Cr3+ concentration is shown in Fig. 8. The noticed lattice strain grows from 0.0010 at x = 0.0 and, with increasing Cr3+ concentration, the rise continues to its maximum of 0.0023 at x = 0.8–1.0. The trend afterwards has reversed and the lattice strain decreased drastically to 0.0011 at x = 2.0. It is obvious that strain has been building up within the lattice due to Cr3+-substitution and, beyond x = 0.8–1.0, it is getting relaxed by the spinel lattice transforming to the inverted phase. The arguments presented earlier in support of this interpretation are strengthened by the present observation.
Fig. 9 shows the ratio curves (also known as quotient spectra17) generated from the coincidence Doppler broadened spectra of the ZnFe2−xCrxO4 samples with respect to pure (99.999%) Al single crystals annealed at 873 K for 2 hours in high vacuum (∼10−6 mbar). The curves show a prominent peak around pL = 9.5 × 10−3 m0c which is characteristic of positron annihilation with the 2p electrons of O2− ions. What is more noteworthy is the interesting changes in the amplitudes of this peak with increasing replacement of Fe3+ ions by Cr3+ ions (Fig. 10). There is an overall decrease of the amplitude due to the effects of Cr3+-substitution but a remarkable increase intersperses it after x = 0.8, which lasts till x = 1.2. Significantly, this is the region of Cr3+-substitution during which we have earlier observed remarkable changes and even the reversal of trends of variation in the positron lifetime parameters (Fig. 5(a) and (b)–7). It shows positrons are able to sense the changes taking place in the local electron momentum distribution and the said abrupt change points towards a clear redistribution of cations and change of positron trapping sites.
 | ||
| Fig. 9 The ratio curves generated from the CDB spectra of the ZnFe2−xCrxO4 samples with respect to pure annealed Al single crystals. | ||
 | ||
| Fig. 10 The peak amplitudes of the CDBS ratio curves of Fig. 9 plotted against the Cr3+ concentration in the different samples. | ||
To understand this behavior, we note the following. As mentioned earlier, the vacancy type defects which trapped positrons in samples with x = 0.0 to 0.8 are larger in size so that the positron lifetimes in them actually merged with that at the crystallite surfaces whereas the former conspicuously decreased and got delineated from the latter in samples of x = 0.8 to 1.6. This shows that the positron trapping sites in samples of x = 0.8 to 1.6 are smaller in size compared to those in samples of x = 0.0 to 0.8. Since the monovacancies of O2− ions cannot trap positrons, the trapping sites are to be conceived as vacancies of cations. The radii (in Å) of the tetrahedral (A-) and octahedral (B-) sites are calculated using the relations
 | (15a) |
 | (15b) |
 | ||
| Fig. 11 The tetrahedral (square) and octahedral (hexagons) site radii in samples of different Cr3+ concentrations. The solid lines are eye guides only. | ||
It therefore follows from the above explanations that the positron trapping sites in the samples with x = 0.0 to 0.6 are the monovacancies of Fe3+ ions missing from the octahedral sites. These may be vacancies arising out of non-stoichiometry in the composition of the samples and some of them may be even getting filled by the substituted Cr3+ ions. The decreasing probability of annihilation of positrons with the electrons of O2− ions, as reflected by the reducing peak amplitude in Fig. 10, indicates this. After x = 0.8, a spinel inversion seems to occur during which the Zn2+ ions at the A-sites move over to the B-sites and Fe3+/Cr3+ ions at half of the B-sites move over to the A-sites. Zn2+ ions have radius about 0.73 Å,33,34 which is larger than the tetrahedral site radii estimated. This means Zn2+ ions had occupied their sites by “pushing away” the coordinated O2− ions along the body diagonals of the cubic unit cells and the same results in the shrinkage of the octahedral sites to sizes smaller than those indicated by the calculated radii in Fig. 11.1 The radii of the Fe3+ and Cr3+ ions are about 0.67 Å and 0.64 Å respectively and hence they may still easily fit in to the A-sites or the B-sites. On the other hand, due to the shrinkage enforced by the Zn2+ ions, the B-sites may still be inadequate in size for these two ions to occupy and instead they may prefer the A-sites. The spinel inversion will thus help the Cr3+ ions to get easily accommodated at the A-sites. As the inter-ionic distance O-A is less than the O-B distance,1 positron trapping at A-site vacancies will lead to increasing annihilation probability with the O2− electrons and the peak amplitude in Fig. 10 shows accordingly a remarkable increase. Although such an explanation is feasible, it should be pointed out that continued substitution of Fe3+ ions by Cr3+ ions and the inversion do not go unhindered, perhaps owing to the increasing strain associated with the supposed entry of the Zn2+ ions at the B-sites. As a result, it is highly probable to have a large number of B-sites unoccupied and such vacancies will trap positrons. This is one reason that the intensity I2 (Fig. 5(b)) and the lineshape parameter S (see below) have increased in the region of higher concentrations of Cr3+-substitution. The positron lifetime τ2 also interestingly rises back (Fig. 5(a)) and the peak amplitude falls again (Fig. 10). For x = 1.8 and 2.0, we thus obtain an inverted spinel although pure zinc chromite (ZnCr2O4) in bulk coarse-grained form is a normal spinel at room temperature and all the Cr3+ ions are supposed to be at the B-sites.35 Note that the average crystallite size in the sample used here is about 8 nm only and an inversion to the inverted spinel structure is highly probable. In a paper by Vargas-Hernandez et al.,36 it has been pointed out that ZnCr2O4 nanocrystals did indeed undergo inversion giving rise to vacancy type defects at both tetrahedral and octahedral sites and they became responsible for competition and distribution realignment among the ions of Zn and Cr to occupy the sites of each other. Even more recently, Chen et al. have reported about an inversion up to a degree of 0.24 in ZnCr2O4 nanoparticles.37 Although both ZnFe2O4 and ZnCr2O4 are normal spinel in coarse grained composition at room temperature, substitution alone would not have resulted in drastic changes in the lattice constants, crystallite sizes and the positron annihilation parameters. In other words, the conditions for the synthesis of both these compounds with the same lattice constant and crystallite size are not necessarily identical. The inversion is possibly a consequence as we used the same synthesis conditions here. In a few studies reported by us, it had been shown that normal spinel ZnFe2O4 turned to inverse below an average crystallite size of 9 nm and inverse spinel NiFe2O4 turned normal when the constituent crystallites were reduced to sizes below about 5.6 nm.9,10,25 (The starting crystallite size in our present work, as shown in Fig. 3(b), was about 27.5 nm and hence ZnFe2O4 was in its normal spinel configuration.) The vacancy type defects are maximum in number at this stage and the major contributions to τ2 and its intensity I2 again come from those defects. The third component τ3 and its intensity I3 which got separated in the intermediate stage have once again merged with the τ2–I2 component.
The variations of the lineshape parameters S and W with Cr3+ ion concentration (x) are yet other proofs to the interpretations given so far. These variations are given in Fig. 12(a) and (b). The S and W parameters are calculated from the one dimensional projected curves of the CDB spectra as the ratio between the counts under the selected gamma ray energy intervals (ΔE = ±0–0.975 keV for S and ΔE = ±2.125–3.475 keV for W) and the total counts under the full spectra. The variations of these two parameters with Cr3+ ion concentrations are complementary to each other and the S–W plot shown in Fig. 13 depicts the two-stage evolution more vividly. As indicated by the two curves S1–S2 and S2–S3, the positron trapping defects appear to be of two types and they are identified as the two species of cationic vacancies, each predominating over the other in one of the stages, i.e., of lattice contraction and the structural inversion.
 | ||
| Fig. 12 The variation of (a) the S-parameter and (b) the W-parameter with the Cr3+ concentration in the different samples. | ||
 | ||
| Fig. 13 The S–W plot. For clarity, the points on the two lines are shown with two different symbols. | ||
Fig. 14(a) and (b) depict the room temperature Mössbauer spectra of some of the ZnFe2−xCrxO4 samples. It is clear from these figures that all the samples show a doublet type of Mössbauer spectra and no ferromagnetic nature (six line pattern of Mössbauer spectra) has been observed. From the experimental Mössbauer spectra, both the isomer shift (IS) and quadrupole splitting (QS) have been calculated by the standard least square fitting program NMOSFIT.20 Fig. 15 and 16 represent the variation of the isomer shift and the quadrupole splitting with the concentration of Cr3+ in the ZnFe2−xCrxO4 samples. The Fe content of the samples with x > 1.4 gradually decreased to a limit below the sensitivity of the technique and no significant Mőssbauer absorption is observed in the experiments. Hence we have presented the spectra of only samples of x ≤ 1.4.
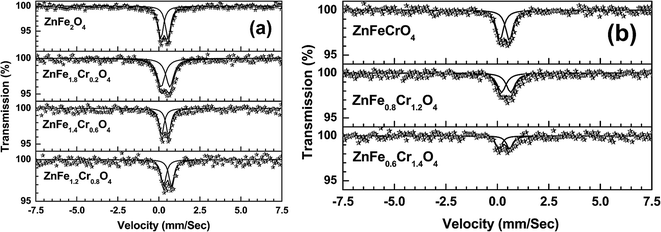 | ||
| Fig. 14 Room temperature Mössbauer spectra of ZnFe2−xCrxO4 ((a) x = 0, 0.2, 0.6, 0.8 and (b) 1.0, 1.2, 1.4) samples. | ||
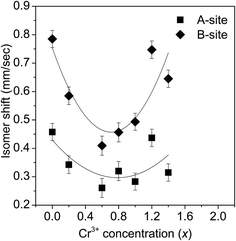 | ||
| Fig. 15 The variation of the isomer shift (IS) with the Cr3+ concentration in the different ZnFe2−xCrxO4 samples. | ||
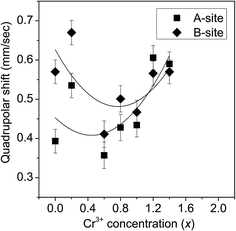 | ||
| Fig. 16 The variation of the quadrupole splitting with the Cr3+concentration in the different ZnFe2−xCrxO4 samples. | ||
To understand the nature of variation of these quantities, we note the following. Bulk ZnFe2O4 is considered to be paramagnetic owing to the complete occupancy of the tetrahedral (A-) sites by the Zn2+ ions and octahedral (B-) sites by the Fe3+ ions. It has been reported in many studies in recent times that ZnFe2O4 particles with nanometer-order sizes tend to be largely ferromagnetic due to cation exchange between the A- and B-sites leading to stronger interactions of the Fe3+ ions at the two sites.38–40 This normally happens when the particle sizes are below ∼10 nm. The Mössbauer spectrum splits into a six line pattern, called sextet, in such cases. Such a sextet is conspicuously absent in the present case since the particle sizes are also above this limit.
Nevertheless, the vivid decrease of the isomer shift during x = 0 to 0.8 as shown in Fig. 15 is indicative of less number of Fe3+ ions occupying the B-sites. It is observed that the variation of isomer shift with x is small as far as the A-site is concerned whereas the variation is more for the B-site. The initial decrease of the isomer shift with x indicates that the 4s electron density decreases with increase in the concentration of Cr3+ ions in the B-site. In other words, an increasing number of Fe3+ ions at the B-sites are being replaced by Cr3+ ions. After x = 0.8, the trend of change of the isomer shift is reversed and there is considerable increase of 4s electron density at the B-sites. This happens when ions of relatively larger size (Zn2+ in this case) replace the Cr3+ ions at the B-sites. Since Zn2+ ion has more number of 4s electrons than Cr3+, the effective 4s electron density at B site increases with x. It is thus yet another proof to the idea of spinel inversion as suggested earlier to explain the anomalous changes of the positron annihilation parameters at this stage.
The variation of the quadrupole splitting with x is almost similar for both the A-sites and B-sites and is slightly increasing in nature. This suggests that the electric field gradient in both the sites increases slightly with x. Thus the addition of Cr3+ in place of Fe3+ seems to alter the spectroscopic character of the ferrite samples to an extent noticeable even in conventional methods of experimentation. The decreasing particle sizes will continue to maintain the inverse spinel structure but with more number of Cr3+ ions at the A-sites instead of Fe3+ ions. In fact, the role played by the decreasing lattice parameter and the crystallite size in causing the inversion and stabilizing the structure against the constraints of site stabilization energies and charge disparities is worth noting. While ZnCr2O4 is a normal spinel in coarse-grained composition, there is no signature of reverting back to a normal spinel after the transformation of the normal ZnFe2O4 to the inverted spinel ZnFe2−xCrxO4 till x ≤ 1.8.
4. Summary and conclusions
It is shown in this paper that the properties of the spinel compound ZnFe2O4 can be significantly altered by cationic interchange at the A- and B-sites and especially by substitution by other cations. The exercise, in most cases, also lead to change of lattice parameter and crystallite sizes although the basic spinel structure may still hold good notwithstanding any possible inversion. It had been proved in earlier studies that ZnFe2O4 can be transformed from a normal spinel configuration to an inverse one through substitution of Zn2+ ions by, for example, Ni2+ ions. The present work is an attempt to explore the possibility of such a change by substituting for the Fe3+ ions which occupy the B-sites. While conventional techniques like X-ray diffraction could not show the occurrence of such changes unambiguously, we get evidences from positron annihilation studies to indicate the effects of cationic substitution through definite changes in the positron lifetimes, intensities and the Doppler broadened gamma ray lineshape parameters. Thus, positron annihilation spectroscopy in such compounds becomes highly promising to understand the effects of substitution as well as to monitor the changes in their electronic structure and properties. The vacancy type defects which are generated as a result of failed occupancy of the A-sites or B-sites due to the mismatch of the available site volume and the ionic sizes serve as strong trapping centres for positrons with distinct lifetimes. The results from lineshape measurements especially through coincidence Doppler broadening spectroscopy also supported the findings. Finally, the results of Mössbauer spectroscopic measurements arguably supported these findings through definite isomer and quadrupole shifts. The study can thus serve as motivation for exploring similar effects when the ions at the A- and B-sites are replaced by other transition metal ions in different concentrations.Acknowledgements
The authors thank Dr Dipankar Das of UGC-DAE Consortium for Scientific Research, Kolkata, India for certain useful suggestions and comments. The help received from Mr Samudrajit Thapa during the experiments is also gratefully acknowledged.References
- J. Smit and H. P. J. Wijn, Intrinsic properties of ferrites with spinel structure, Ferrites - Physical Properties of Ferrimagnetic Oxides in Relation to Their Technical Applications, N. V. Philips' Gloeilampenfabrieken, Eindhoven, The Netherlands, 1959, ch. VIII, pp. 136–176 Search PubMed.
- F. Scordari, Ionic Crystals, Fundamentals of Crystallography, ed. C. Giacovazzo, Oxford University Press, New York, U.S.A., 1992, ch. 6, pp. 403–464 Search PubMed.
- V. A. M. Brabers, Progress in spinel ferrite research, Handbook of Magnetic Materials, ed. K. H. J. Buschow, North-Holland, Amsterdam, 1995, vol. 8, pp. 189–325 Search PubMed.
- D. S. Mathew and R.-S. Juang, Chem. Eng. J., 2007, 129, 51–65 CrossRef CAS PubMed.
- J. J. Thomas, S. Krishnan, K. Sridharan, R. Philip and N. Kalarikkal, Mater. Res. Bull., 2012, 47, 1855–1860 CrossRef CAS PubMed.
- C. Rath, K. K. Sahu, S. Anand, S. K. Date, N. C. Mishra and R. P. Das, J. Magn. Magn. Mater., 1999, 202, 77–84 CrossRef CAS.
- S. Ghosh, P. M. G. Nambissan and R. Bhattacharya, Phys. B, 2004, 353, 75–81 CrossRef CAS PubMed.
- G. Zhang, C. Li, F. Cheng and J. Chen, Sens. Actuators, B, 2007, 120, 403–410 CrossRef CAS PubMed.
- P. M. G. Nambissan, C. Upadhyay and H. C. Verma, Mater. Sci. Forum, 2004, 445–446, 162–164 CrossRef CAS.
- S. Chakraverty, S. Mitra, K. Mandal, P. M. G. Nambissan and S. Chattopadhyay, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 024115 CrossRef.
- P. M. G. Nambissan, O. Mondal, S. Chakrabarty and M. Pal, Mater. Sci. Forum, 2013, 733, 219–223 CrossRef CAS.
- J. J. Thomas, A. B. Shinde, P. S. R. Krishna and N. Kalarikkal, J. Alloys Compd., 2013, 546, 77–83 CrossRef CAS PubMed.
- J. J. Thomas, A. B. Shinde, P. S. R. Krishna and N. Kalarikkal, Mater. Res. Bull., 2013, 48, 1506–1511 CrossRef CAS PubMed.
- K. B. Modi, N. H. Vasoya, V. K. Lakhani, T. K. Pathak and P. M. G. Nambissan, Int. J. Spectrosc., 2013, 2013, 272846 Search PubMed.
- T. Kamayama, K. Haneda, T. Sato, S. Ikeda and H. Asanao, Solid State Commun., 1992, 81, 563–566 CrossRef.
- J. V. Olsen, P. Kirkegaard, N. J. Pedersen and M. Eldrup, Phys. Status Solidi C, 2007, 4, 4004–4006 CrossRef CAS PubMed.
- P. Asoka-Kumar, M. Alatalo, V. J. Ghosh, A. C. Kruseman, B. Nielsen and K. G. Lynn, Phys. Rev. Lett., 1996, 77, 2097–2100 CrossRef CAS.
- A. A. Chatterjee, K. Ramachandran, S. Singh, S. S. Pande and M. D. Ghodgaonkar, Proceedings of the DAE Symp., Nuclear Physics A, 2002, 45, 145–146 Search PubMed.
- M. Chakrabarti, D. Sanyal and A. Chakrabarti, J. Phys.: Condens. Matter, 2007, 19, 236210 CrossRef.
- E. von Meerwall, Comput. Phys. Commun., 1975, 9, 117–128 CrossRef.
- A. Patterson, Phys. Rev., 1939, 56, 978–982 CrossRef CAS.
- S. Deshpande, S. Patil, S. V. N. T. Kuchibhatla and S. Seal, Appl. Phys. Lett., 2005, 87, 133113 CrossRef PubMed.
- A. V. Thorat, T. Ghoshal, J. D. Holmes, P. M. G. Nambissan and M. A. Morris, Nanoscale, 2014, 6, 608–615 RSC.
- B. Bergersen and M. J. Stott, Solid State Commun., 1969, 7, 1203–1205 CrossRef CAS.
- P. M. G. Nambissan, C. Upadhyay and H. C. Verma, J. Appl. Phys., 2003, 93, 6320–6326 CrossRef CAS PubMed.
- P. Hautoj'arvi and C. Corbel, in Positron Spectroscopy of Solids, Proceedings of the International School of Physics “Enrico Fermi”, IOS Press, Amsterdam, 1995, vol. 125, pp. 491–532 Search PubMed.
- R. M. de la Cruz, R. Pareja, A. Segura, V. Munoz and A. Chery, J. Phys.: Condens. Matter, 1993, 5, 971–976 CrossRef CAS.
- P. M. G. Nambissan, V. K. Lakhani and K. B. Modi, Mater. Sci. Forum, 2013, 733, 215–218 CrossRef CAS.
- N. Kumari, V. Kumar and S. K. Singh, J. Alloys Compd., 2015, 622, 628–634 CrossRef CAS PubMed.
- G. K. Williamson and W. H. Hall, Acta Metall., 1953, 1, 22–31 CrossRef CAS.
- V. Biju, N. Sugathan, V. Vrinda and S. L. Salini, J. Mater. Sci., 2008, 43, 1175–1179 CrossRef CAS.
- R. Yogamalar, R. Srinivasan, A. Vinu, K. Ariga and A. C. Bose, Solid State Commun., 2009, 149, 1919–1923 CrossRef CAS PubMed.
- J. Emsley, The Elements, Clarendon Press, Oxford, U.K., 1998 Search PubMed.
- R. G. Burns, Mineralogical applications of crystal field theory, Cambridge Univ. Press, Cambridge, U. K., 1993, pp. 1–551 Search PubMed.
- N. Singh and J. Y. Rhee, J. Korean Phys. Soc., 2010, 57, 1233–1237 CrossRef CAS.
- C. Vargas-Hernandez, O. Almanza and J. F. Jurado, J. Phys.: Conf. Ser., 2009, 167, 012037 CrossRef.
- S. Chen, Y. Wu, P. Cui, W. Chu, X. Chen and Z. Wu, J. Phys. Chem. C, 2013, 117, 25019–25025 CAS.
- T. Sato, K. Haneda, M. Seki and T. Iijima, Appl. Phys. A, 1990, 50, 13–16 CrossRef.
- C. Rath, N. C. Mishra, S. Anand, R. P. Das, K. K. Sahu, C. Upadhyay and H. C. Verma, Appl. Phys. Lett., 2000, 76, 475–477 CrossRef CAS PubMed.
- C. Upadhyay, H. C. Verma, C. Rath, K. K. Sahu, S. Anand, R. P. Das and N. C. Mishra, J. Alloys Compd., 2011, 326, 94–97 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra04516a |
| ‡ Present address (J.C.): Department of Physics, Devamatha College, Kuravilangad, Kottayam, Kerala 686633, India. |
| This journal is © The Royal Society of Chemistry 2015 |