Effect of pulsed electric field with variable frequency on coalescence of drops in oil

Abstract

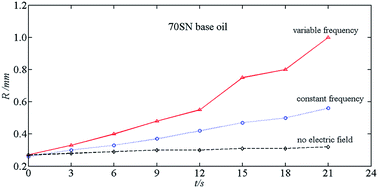
Under a pulsed electric field in oil, drops coalesce and become bigger constantly, leading to a change in the optimal coalescence frequency. A pulsed electric field with variable frequency can resolve this problem. To determine the effect of frequency variation of a pulsed electric field on coalescence, a nonlinear vibration kinetic model of a drop in oil is built to obtain the parametric excitation resonance frequency of the drop, which provides a theoretical basis for studying the effect of the change of the drop size on the optimal coalescence frequency. By utilizing a simple model of coalescence of double drops, the coalescence time is obtained, and then the frequency variation and operating parameters of the pulsed electric field is calculated. Experimental results show that the pulsed electric field with variable frequency has a better effect than that with constant frequency on the coalescence of emulsion drops. This finding has significance for engineering applications.

---

1 Introduction

With high peak value, low overcurrent and high efficiency, a high-voltage pulsed electric field has been applied to the demulsification of water-in-oil (W/O) emulsion oil and achieved a high profile.^1–3 In general, a drop subjected to a pulsed electric field in oil is polarized and generates polarization charges on its surface, and then the periodic electric field force occurs, which leads to the periodic telescopic deformation vibration of the drop.^4–6 The vibration of a drop results in a decrease of its interfacial film mechanical strength and an increase of collision probability between drops, thereby accelerating the coalescence of drops in emulsion and then raising the efficiency of electric field demulsification.⁷ Research has shown that a pulsed electric field had an optimal demulsification frequency and intensity in electro-demulsification. However, varying the electric field intensity may be relatively easy to implement, optimization of demulsification frequency has attracted much attention.^8,9 Zhang Jian et al.⁸ believed that when the electric field frequency was close to the drop's inherent frequency, a drop's resonance occurred and the demulsification effect was the best. Torza et al.¹⁰ discovered that when the electric field frequency was higher, the drop's vibration amplitude was smaller, which was mainly due to the effect of polarized electric field relaxation. Gong et al.⁷ research showed that for a drop with a moderate diameter immersed in oil, the parametric excitation resonance of a drop occurred in a pulsed electric field with low frequency; in addition, the resonance frequency was less than the drop's inherent frequency because of oil viscosity. So the drop resonance exits in the certain condition of pulsed electric field, it happens to be the optimal demulsification.

By subjecting to a continuous pulsed electric field, the size of drops increases rapidly at first, but then changes slowly.¹¹ Given that the change in size of a drop has an effect on the forces on it and the electric field conditions of coalescence are changed,¹² a pulsed electric field with a constant frequency has a limitation on demulsification. Through experiments, Zhang et al.¹³ found that a pulsed electric field with a variable frequency has a better demulsification result than that with a constant frequency. Obviously, the change of pulsed electric field, complying with certain rules, is very beneficial to electro-demulsification. However, related studies about the frequency variation rule of efficient demulsification by pulsed electric field have rarely reported. Based on nonlinear vibration kinetics model of a drop, this paper discusses its resonance frequency and the effect of variable frequency pulsed electric field on coalescence of drops in oil. Result of this study provides a theoretical guidance for engineering practice.

2 Theories and model

2.1 Optimal coalescence frequency

A drop in oil is placed between two parallel electrode plates, on which a high-voltage pulsed electric field is applied. Under the excitation of periodic polarization electric field force, the periodic tensile deformation vibration of a drop occurs in the pulsed electric field. It is assumed that the drop keeps prolate sphere during its deformation. Considering that the right hemisphere of a drop as the research object and keeping the geometric centre unchanged, at some instant, the major semi-axis and minor semi-axis of the vibrating drop are a and b, respectively, and the corresponding deformation velocities are ȧ and ḃ. At this moment, the vibrating drop is subjected to the inertia force F_i, drag force F_r of oil, interfacial restoring force F_h and exciting force F_e of electric field, as shown in Fig. 1. And then, the drop's vibration kinetics model can be expressed as follows:⁸

F_i + F_r + F_h = F_e. (1)

Fig. 1 Forces acting on the right hemisphere of a prolate spherical drop at an instance during its vibration. The major and minor semi-axes of the prolate spherical drop are respectively a and b, and the corresponding deformation velocities are ȧ and ḃ.

According to each force expression of the model in ref. 8, 14 and 15, the differential expression of the drop's nonlinear parametrically excited vibration kinetics model in the pulsed electric field can be obtained as follows:

The expression of pulsed electric field can be written by Fourier transformation. Hence, the function of pulsed electric filed q(t) can be shown as:

In eqn (2), the functions of the drag, interfacial restoring and exciting forces are complicated:

Based on the harmonic balance method,¹⁶ supposing that the drop's first-order approximate solution of fundamental vibration amplitude is χ = χ₀ + χ₁ cos(ωt + ψ₂) and applying the polynomial approximation to φ(χ), f(χ) and e(χ),¹⁷ which are substituted into eqn (2), the following equations can be obtained:

B(χ₀ − 0.12χ₁²−0.24χ₀²) = 2GQ (5)

where the inherent vibration frequency of the drop is ω₀² = 0.25B and Q = 1.47 + 0.2χ₀²− 0.83χ₀ + 0.1χ₁².

From eqn (5), the drop's amplitude can be obtained using χ₀ = p(m,χ₁²) and is substituted into eqn (6) and (7), respectively. By eliminating phase angle ψ₂, we assume that the function relational expression of amplitude component χ₁ is obtained, as given in eqn (8).

Φ(χ₁,ω²/ω₀²,m,n) = 0. (8)

By eqn (4), we can obtain the partial differential of χ₁ to ω. Let ∂χ₁/∂ω = 0, the drop's resonance frequency can be obtained as

ω_reso = Ψ(ω₀,m,n) (9)

where m = 2G/B and .

When the pulsed electric field frequency is equal to ω_reso, the drop's resonance in oil occurs. At this moment, the drop's vibration is most violent, which is advantageous to the collision and coalescence between drops in oil; in addition, the demulsification result is best at this instance, and thus the frequency is the optimal demulsification frequency of pulsed electric field,⁸ which can be obtained by eqn (9). Moreover, the parameters in eqn (9) are related to the size of the drop: the change of size can result in the change of the efficient demulsification frequency.

2.2 Coalescence time of drops

Williams and Urdahl et al.^18,19 studied the effect of the duration time of electric field to the radiuses of drops in oil. They concluded that drops radii increased with the increase of duration time of electric field until reaching a maximum. Atten²⁰ established a simple model to estimate the change of mean size of an emulsified drop over time to test coalescence of drops in pairs in a single diffusion emulsion. The model shows that N drops of radius R coalesce to 0.5N drops of radius 2^1/3R. The evolutionary time is determined by the equation controlling the relative motion between two adjacent drops. The drop's tension can be calculated by Stokes formula, and the attraction between two adjacent drops can be obtained by the polarization formula. Then, the following result can be obtained:

Assuming that the drop's initial spread pattern shows the cubic lattice, then . Time t₁ is only related to volume fraction ϕ:

3 Experimental

3.1 Instruments and samples

The high-voltage pulsed power supply was produced by Tianjin Hui Da Electronic Component Factory. The output is square pulse which range of voltage is 0–20 kV, the output range of frequency is 0.1–5000 Hz and the pulsed duty ratio is adjustable from 10–60%. The Motic series microscope has an objective lens with four magnifications and data acquisition device with high-speed camera. The size of experimental pool is 48 mm × 46 mm × 20 mm and its material is transparent organic glass. The size of pure copper electrodes is 48 mm × 20 mm × 2 mm and the electrode spacing is 20 mm. A Tektronix TDS1001C-SC digital oscilloscope was used for calibration of high-voltage pulsed power supply. In addition, a magnetic stirrer, stopwatches, glass wares, microsyringes and a magnetic stirrer were also used. The experimental setup is shown in Fig. 2.

Fig. 2 Sketch of the experimental devices for observing the coalescence of drops.

Base oils of Ssangyong 70SN, Mobil 100SN and Fushun 150SN were used as experimental oil samples. A BF-03 type kinematic viscosity tester and the BF-18A type density tester, produced by Dalian Northern Analysis Instrument Limited Company, were used to measure the kinematic viscosity (v) and the density (ρ) of the base oils at 20 °C. A JZY-180 type interface tensiometer of Pratt & Whitney was used to measure the interface tensile stress (γ) between oil and water. A WRT27-AYJ type permittivity tester of Zhongxi company was used to measure the relative permittivity (ε₂). A certain amount of distilled water was injected and a small amount of Span 80 was added into the three base oils, which were then stirred for 30 min with a magnetic stirrer to form the W/O emulsion. The volume percentage (ϕ) of water in the emulsion is 2%. By placing emulsion oil samples in the experimental pool, the drops' initial radii in oil were recorded with a microscope and the mean radius (R) was calculated with the image processing software by the manufacturer; the test parameters are shown in Table 1.

Table 1 In experiment, kinematic viscosity (v), density (ρ), interface tensile oil-water (γ) and relative permittivity (ε₂) of three kinds of oil were measured at 20 °C. The mean radius (R) of drops in oils was calculated by software

Oil	v (mm^2 s^−1)	ρ (kg m^−3)	γ (mN m^−1)	ε2	R (mm)
70SN	46.4	825.3	9	2.81	0.270
100SN	48.0	850.2	18	1.95	0.245
150SN	36.8	867.8	12	3.10	0.295

---

According to the relational expression μ = vρ, the kinetic viscosity (μ) of the three kinds of base oil at 20 °C are 38.3 × 10⁻³, 40.8 × 10⁻³ and 31.9 × 10⁻³ Pa s, respectively.

3.2 Experimental operation parameters

After pouring the three emulsion oil samples into the experimental pool, the high-voltage pulsed electric field was applied on the electrode plates; 400 kV m⁻¹ was selected as the amplitude of pulsed electric field intensity and the pulsed duty ratio was 50%. The initial frequency of the applied electric field was determined by eqn (8), and the variable frequencies were determined basing on R, 2^1/3R, 4^1/3R, 2R, 16^1/3R, 32^1/3R, 4R and 128^1/3R. The experimental frequency switching time was determined by eqn (10), and E₀ selected the effective value of pulsed electric field amplitude:¹⁰ . According to the parameters in Table 1, the experimental operation parameters of electric field of the three kinds of emulsion oil are shown in Table 2. By calculating the optimal demulsification frequencies of emulsion oil of 70SN and 100SN, the drop's parametrically excited resonance frequency in emulsion oil does not exist in the initial state, that is, the pulsed electric field is most beneficial to the drops' coalescence. Therefore, the pulsed electric field with a lower frequency (f = 0.1 Hz) was selected to replace the pulsed electric field in the experiment.

Table 2 In the demulsification experiment of three kinds of emulsion oil, the operation frequencies (f) and their action times (t) were selected in the seven kinds of drops radius

		R	2^1/3R	4^1/3R	2R	16^1/3R	32^1/3R	4R	128^1/3R
70SN	f (Hz)	0.1	57	58	47	36	26	18	13
	t (s)	0	3	6	9	12	15	18	21
100SN	f (Hz)	0	60	74	65	51	39	29	21
	t (s)	0.1	4	8	12	16	20	24	28
150SN	f (Hz)	101	86	68	51	37	27	19	14
	t (s)	0	2	4	6	8	10	12	14

---

The coalescence experiment of high-voltage pulsed electric field of each kind of emulsion oil was conducted under the operating conditions in Table 2 and constant initial frequency. A microscope was used to capture areas of the experimental pool randomly; the mean size of drops after coalescence was recorded.

3.3 Experimental results and discussion

In Fig. 3(a), after the emulsion oil of 70SN was fully stirred, the sizes of drops in oil are very small in the initial state. Under the action of variable frequency pulsed electric field, the drops' sizes increase gradually and the coalescence result is obvious, as shown in Fig. 3(a and b). Meanwhile, Fig. 4 shows the coalescence situation of drops in emulsion oil after being subjected to a pulsed electric field with a constant frequency f = 0.1 Hz for 21 s. Although the coalescence result is also obvious, with regard to the sizes of drops after coalescence, the pulsed electric field with a variable frequency has a better result than that with a constant initial frequency. The changes in sizes of the drops of Ssangyong 70SN, Mobil 100SN, and Fushun 150SN under pulsed electric field with a variable frequency and that with a constant frequency are shown in Fig. 5.

Fig. 3 Images of coalesced drops in 70SN emulsion oil were recorded by the action of the pulsed electric field with variable frequencies in time t: (a) 0; (b) 3 s; (c) 6 s; (d) 9 s; (e) 12 s; (f) 15 s; (g) 18 s; and (h) 21 s.

Fig. 4 Images of coalesced drops in 70SN emulsion oil by the action of pulsed electric field with a constant frequency in time t: (a) 0; (b) 21 s.

Fig. 5 Radius change of drops in 70SN, 100SN and 150SN oils under the action of three kinds of condition: (a) pulsed electric field with variable frequency; (b) pulsed electric field with constant frequency; (c) no electric field.

In Fig. 5, the pulsed electric field with a variable frequency has a superior effect on coalescence of drops than that with a constant initial frequency. The change of size can change the optimal demulsification electric field frequency directly, but cannot directly determine the monotonicity variation characteristic. In Table 2, the optimal demulsification frequencies of the experimental oil samples tend to decrease. Although, in this paper, the optimal demulsification frequency and the frequency switching time are obtained using a simple model only, in the experiments, the pulsed electric field with a constant frequency is against the drop's parametrically excited resonance in oil. Moreover, the variable frequency pulsed electric field is more appropriate for the study of effect of the continuous increase of size to the parametrically excited resonance frequency, which has a good promotion effect to the rapid coalescence of drops.

As seen from Fig. 5, the radius of drops in 150SN after coalescence is significantly greater than that in 70SN and 100SN. The main reason is that, under similar initial size and electric field intensity, the permittivity of 150SN is greater than the other two oil samples. As such, higher conductivity of oil results in a more intense forcing vibration of drops, and thus, the coalescence effect is obvious. Given that the permittivity of 100SN is the smallest, the size of drops in 100SN after coalescence is also the smallest. In Table 2, the parametrically excited resonance frequencies of drops in 70SN and 100SN do not exist in the initial state. With the increase of size of drops, the resonance frequency increases initially and then decreases. Therefore, the optimal demulsification frequency peak point exists in the changing process of size for 70SN and 100SN. However, the drop's parametrically excited resonance frequency in 150SN exists in the initial state, and the resonance frequency decreases gradually with the increase of size. The difference in parametrically excited resonance frequencies of drops in three oil samples in the initial state is mainly due to viscosity. In the process of the nonlinear parametrically excited vibration of drops, the viscosity of oil exerts resistance, and when the viscosity is higher, the drop's parametrically excited resonance frequency deviates farther from its free vibration frequency and closer to the zero frequency. In the experiment, the viscosity of 70SN and 100SN is higher than that of 150SN. In the initial state, the sizes of drops in 70SN and 100SN are smaller and their parametrically excited resonance frequencies are over zero; hence, the resonance frequencies do not exist. At this moment, the pulsed electric field has a better coalescence result; thus, f = 0 Hz is the optimal coalescence frequency. The difference on permittivity of oil results in different experimental frequency switching time of each kind of oil. The time interval of frequency switching of 100SN is the longest, which is mainly because its permittivity is the smallest in the experiment. The smaller permittivity entails the smaller polarization force between drops in oil, which affects the speed of migration coalescence of drops and then affects the coalescence time. Therefore, for oils with low permittivity, the coalescence time of drops can be shortened effectively by increasing the intensity of electric field. However, the excessively high intensity of electric field easily results in break-up of drops.⁴

4 Conclusion

Under pulsed electric field, the coalescence of drops in emulsion oil occurs and the sizes of drops increase constantly, resulting in the change of the parametrically excited resonance frequency of the drops. Therefore, utilizing variable frequency pulsed electric field can effectively increase the size and improve coalescence of drops. For oils higher permittivity, the size of drops becomes bigger, the coalescence time is shorter and the coalescence effect is better, which has been confirmed in the coalescence experiment.

Nomenclature

A, B, G	Constants of forces in drop's vibration equations
a	Major semi-axis of drop deformation (m)
ȧ	Deformation velocity along major semi-axis (m s^−1)
b	Minor semi-axis of drop deformation (m)
ḃ	Deformation velocity along minor semi-axis (m s^−1)
d0	Centre distance between two adjacent drops (m)
E	Amplitude of pulse electric field (kV m^−1)
E0	Amplitude effective value of pulse electric field (kV m^−1)
e(χ)	Nonlinear expression of excitation term in drop's vibration equations
Fe	Excitation force acting on vibrating drop (N)
Fh	Restoring force acting on vibrating drop (N)
Fi	Inertia force of vibrating drop (N)
Fr	Drag force to vibration of drop (N)
f	Power frequency of pulse electric filed (Hz)
f(χ)	Nonlinear expression of restoring force in drop's vibration equations
N	Number of drops
M, n	Coefficient ratio variables of forces terms
p(m,χ1^2)	Expression of zero-order amplitude of drop
Q	Calculation function about χ0 and χ1
q(t)	Expression of pulse electric field
R	Initial radius of drop (m)
t	Time (s)
t1	Coalescence time of two drops (s)

Greek letters

γ	Tensile stress at interface between drop and oil (N m^−1)
ε0	Permittivity of vacuum (= 8.8542 × 10^−12 F m^−1)
ε2	Relative permittivity of oil
λ	Drawing ratio of drop
μ	Kinetic viscosity of oil (Pa s)
v	Motion viscosity of oil (mm^2 s^−1)
ρ	Density of drop (kg m^−3)
χ	Amplitude of drop's vibration (= (a − R)/R)
χ0	Zero-order amplitude of drop's vibration
χ1	One-order amplitude of drop's vibration
Ψ(ω0,m,n)	Expression of parametrically excited resonance frequency of drop
ψ2	Initial phase angle of drop's vibration (rad)
φ(χ)	Nonlinear expression of drag force term in drop's vibration equations
τ0	Surface coefficient of prolate spherical drop
ϕ	Volume fraction ratio of water in emulsion oil
ω	Angle frequency of pulse electric field (rad s^−1)
ω0	Natural angular frequency of drop's vibration (rad s^−1)
ωreso	Angular frequency of drop's resonance (rad s^−1)

Acknowledgements

This work was partially supported by grants from the Chinese National Natural Science Foundation (Grant no. 21206204), project of CQ CSTC (Grant no. cstc2012gg-yyjs90011) and project of Scientific and Technological Research Program of Chongqing Municipal Education Commission (Grant no. KJZH14210).

References

1. J. S. Eow and M. Ghadiri, Electrostatic enhancement of coalescence of water droplets in oil:A review of the technology, Chem. Eng. J., 2002, 85, 357–368.
2. Y. Z. Zhang, Y. H. Liu and R. J. Ji, Dehydration efficiency of high-frequency pulsed DC electrical fields on water-in-oil emulsion, Colloids Surf., A, 2011, 373, 130–137.
3. R. Y. Chang, Aviation oil dehydration, Research Department of Air Force Oil, Beijing, 1986.
4. J. S. Eow and M. Ghadiri, Motion, deformation and break-up of aqueous droplets in oils under high electric field strengths, Chem. Eng. Process., 2003, 42, 259–272.
5. Q. Xie and Z. Yan, Study on condition of breakdown emulsion by pulse electric field, Membr. Sci. Technol., 1993, 13, 51–55.
6. X. L. Yang, Drop dynamic of w/o emulsion under the combination of centrifugal field and pulsed electric field, China University of Petroleum, Beijing, 2009.
7. H. F. Gong and Y. Peng, Effect of oil viscidity on optimal demulsion frequency in pulse electric field, Acta Pet. Sin., Pet. Process. Sect., 2013, 29, 168–173.
8. J. Zhang, S. P. Dong and Q. R. Gan, Dynamic model of liquid droplets of water-in-oil emulsions with high-frequency pulsating electrical field, J. Chem. Ind. Eng., 2007, 58, 875–880.
9. J. S. Eow and M. Ghadiri, Electro-hydrodynamic separation of aqueous drops from flowing viscous oil, J. Petro. Sci. Eng., 2007, 55, 146–155.
10. S. Torza, R. G. Cox and S. G. Mason, Electrohydrodynamic deformation and burst of liquid drops, Philos. Trans. R. Soc. London, 1971, 269, 295–319.
11. P. J. Bailes and S. K. L. Larkai, Polarization effects in liquid phase separation by pulsed electric fields, IChemE Symp. Ser., 1984, 94, 235–245.
12. R. S.-H. Kashaev and N. R. Faskchiev, Nuclear (proton) magnetic resonance relaxometry study of the effect of rotating magnetic field on the emulsion structure, Appl. Magn. Reson., 2011, 41, 31–43.
13. Y. Z. Zhang and Y. H. Liu, Application of variable frequency technique on electrical dehydration of water-in-oil emulsion, Colloids Surf., A, 2011, 386, 185–190.
14. H. F. Gong, Y. Q. Tu and Y. G. Shi, Calculation of force acting on flexing and deforming latex particle in oil, CIESC J., 2009, 60, 2191–2196.
15. H. F. Gong, Y. Q. Tu and S. Y. Song, Steady deformation mechanics model of latex particle in emulsion under electric field, Acta Pet. Sin., Pet. Process. Sect., 2010, 26, 600–604.
16. Y. Q. Zhu, Analysis of nonlinear vibrations, Beijing Institute of Technology Press, Beijing, 1996.
17. Y. J. Ren, Numeric analysis and Matlab actualization, Higher Education Press, Beijing, 2007.
18. T. J. Williams, A. G. Bailey and M. T. Thew, The electrostatic destabilisation of water-in-oil emulsions in turbulent flow, Inst. Phys. Conf. Ser., 1995, 143, 13–16.
19. O. Urdahl, T. J. Williams, A. G. Bailey and M. T. Thew, Electrostatic destabilization of water-in-oil emulsions under conditions of turbulent flow, Trans. IChemE, 1996, 74, 158–165.
20. P. Atten, Electro coalescence of water droplets in an insulating liquid, J. Electrostatics, 1993, 30, 259–270.

---