Removal of Pb(II) from aqueous solution by mesoporous silica MCM-41 modified by ZnCl₂: kinetics, thermodynamics, and isotherms

Abstract

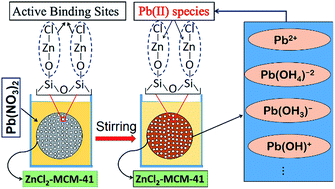
A new hybrid nanostructured sorbent ZnCl₂-MCM-41, was synthesized by a post-synthesis method in toluene as the solvent. To characterize the sorbent, a number of methods were applied, including X-ray diffraction (XRD), nitrogen adsorption–desorption isotherm, Fourier transform infrared spectroscopy (FT-IR), transmission electron microscopy (TEM), and scanning electron microscopy (SEM). Characterization demonstrated that the sorbent particles are of semi-spherical shape, nanostructured with a 754 m² g⁻¹ surface area and a 2.86 nm pore diameter. The Pb(II) removal depended on several parameters, including the pH of solution, temperature, initial Pb(II) concentration, sorbent dosage, ionic strength, and the amount of ZnCl₂ loaded on the MCM-41 surface. The results showed that the pseudo-second-order model describes the kinetics of sorption better than the pseudo-first-order model. The adsorption continuously increased in the pH range of 2.0–7.0, beyond which the adsorption could not be carried out due to the precipitation of the metal ions. The adsorbent had a considerably high Langmuir monolayer capacity of 479 mg g⁻¹. The adsorption process was exothermic at ambient temperature and the computation of the parameters ΔG°, ΔH°, and ΔS° indicated the interactions to be thermodynamically favorable.

---

1. Introduction

Heavy metals are toxic, non-biodegradable, and have a tendency to accumulate in living organisms, causing a number of health problems including various diseases and disorders. Different methods have been developed to remove toxic heavy metals from wastewater – namely, chemical oxidation/reduction, precipitation, ion exchange, electrochemical processes, membrane filtration, and reverse osmosis.¹ These methods are, in general, expensive and potentially risky due to the possibility of generating hazardous by-products, so such methods are not suitable for small-scale industries.^2,3 However, another approach – adsorption – is widely used for metal ion removal because it is simple to operate, cost effective, and has an efficient removal capacity.^4–6 Different adsorbents such as carbon nanotubes,⁷ mesoporous silica (SBA-15),⁸ biomass,⁹ and zeolite¹⁰ have been used for the adsorption of Pb(II) from aqueous solutions. Additionally, mesoporous silica materials have received considerable attention because of their exceptionally large surface area and well-defined pore size and pore shape.^11,12 MCM-41, the adsorbent studied in this research, is one type of mesoporous silica, and has hexagonal arrays of large and uniform pore size, a large surface area, high thermal stability, and mild acidic properties.^13,14 In the previous study,⁵ MCM-41 materials were modified by ZnCl₂ particles in order to remove Hg(II) species from aqueous solutions. This study showed that the adsorption capacity of the ZnCl₂-MCM-41 sorbent for Hg(II) removal from aqueous solutions was sufficiently high (204.1 mg g⁻¹) for justifying future research. In addition, Boudrahem et al.¹⁵ observed that ZnCl₂-activated carbon is an effective adsorbent for the removal of Pb ions from aqueous solutions. However, to the extent of our knowledge, the ability of ZnCl₂-MCM-41 to remove Pb(II) from aqueous solutions has not been investigated previously.

The main purpose of this study was to modify synthesized MCM-41 with ZnCl₂ and apply the modified MCM-41 for the removal of Pb(II) from aqueous solutions. The synthesized ZnCl₂-MCM-41 adsorbent was then characterized using FT-IR, N₂ adsorption–desorption, XRD, TEM, and SEM techniques. Furthermore, the influences of several operating parameters – such as pH, ionic strength, contact time, and temperature – on the sorption capacity of ZnCl₂-MCM-41 were investigated, and the obtained results are reported. Pseudo-first-order, pseudo-second-order, Elovich, and intra-particle kinetic models were used to identify the possible mechanisms of the sorption process, and different isotherm models were used to analyze the sorption equilibrium. Thermodynamic parameters were calculated to determine the nature of the sorption process (i.e., chemisorption or physisorption). Moreover, the desorption of Pb(II) ions from the adsorbent was studied to understand the feasibility of recovering the sorbent and Pb(II) species. Finally, an industrial wastewater sample from a battery production factory was used to study the heavy metal sorption capability of ZnCl₂-MCM-41 sorbent.

The method of least squares is the most widely used technique for predicting the optimum isotherm, and the non-linear regression method is currently the best known way to select the optimum isotherm for experimental data. This non-linear regression method involves the step of minimizing the error distribution between the experimental data and the predicted isotherm: the error distribution between the experimental equilibrium data and the predicted isotherms will be minimized either by minimizing the error function or by maximizing it based on the definition of the error function. In this study, all model parameters were evaluated by nonlinear regression. The optimization procedure was done by seven error functions to measure the goodness of fit, with smaller error function values indicating a better-fitting curve. The non-linear error functions employed in this study are presented in Table S1 (ESI† file). After computing these error functions for each model and calculating the sum of normalized errors (SNE), the optimum isotherm was recognized as the isotherm with the smallest SNE. The calculation method for SNE is presented in the ESI† file.

2. Materials and methods

2.1. Chemicals

Cetyltrimethylammonium bromide (CTAB), tetraethylorthosilicate (TEOS), lead nitrate (Pb(NO₃)₂), ethanol, toluene absolute, zinc chloride (ZnCl₂), sodium hydroxide (NaOH), and hydrochloric acid (HCl) were all supplied by Merck and used without further purification. Aqueous ammonia (25% NH₃) was supplied by Fluka.

2.2. Synthesis of the MCM-41

2.5 g of CTAB was dissolved in 50 g of deionized water. To this surfactant solution, 16.8 g of an ammonia solution (25 wt% in water) and 60 g of ethanol were added. The solution was stirred for 15 min (300 rpm) and then 4.7 g of TEOS were added drop wise. The resulting synthesis gel, with a molar composition of TEOS : CTAB : NH₃ : H₂O : EtOH = 1 : 0.3 : 11 : 144 : 58, was stirred for an additional 2 h at room temperature. The solid product was obtained by filtration, washed with deionized water and ethanol, dried in an oven at 353 K, calcined at 823 K for 8 h with the heating rate of 1 °C min⁻¹, and kept at this temperature for 4 h to remove the CTAB. The outcome of this method is the unmodified version of MCM-41 (throughout this manuscript MCM-41 refers to the calcined MCM-41).

2.3. Synthesis of ZnCl₂-MCM-41

The ZnCl₂-MCM-41 adsorbent was synthesized by post-synthesis method according to Liu et al.¹⁶ In brief, 1.0 g of the calcined MCM-41 was added to a flask containing 50 mL of dried toluene and a specific amount of anhydrous ZnCl₂. To find the maximum adsorption capacity of ZnCl₂-MCM-41 adsorbent for the Pb(II) species, different amounts of ZnCl₂ (0.1–1.0 g) were added to the above-mentioned solution. The mixture was stirred at 35 °C for 6 h (300 rpm). The obtained solid was filtered off, washed completely with dry toluene, and dried at 100 °C for 36 h. Dried powders were washed with 100 mL deionized water to dissolve and remove unreacted Zn²⁺ from mesoporous silica bulk and the filtered solution was analyzed by atomic absorption spectrophotometry (AAS) technique in order to determine the amount of ZnCl₂ loaded on MCM-41. The structure of ZnCl₂-MCM-41 is shown in Fig. 1.

Fig. 1 Schematic structure of MCM-41 and ZnCl₂-MCM-41.

2.4. Preparation of lead solutions

A stock solution of 1.0 M Pb(II) was prepared by dissolving 33.12 g Pb(NO₃)₂ in 100 mL deionized water. Other concentrations, varying between 2 and 200 mg L⁻¹, were also prepared from stock solution. The pH of the working solutions was adjusted to the desired values with 0.1 M HNO₃ or 0.1 M NaOH. Fresh dilutions were used for each experiment.

2.5. Batch adsorption studies

Batch experiments of the Pb(II) adsorption were conducted by placing 10 mg hybrid ZnCl₂-MCM-41 sorbent in a series of Erlenmeyer flasks containing 30 mL of the Pb(II) at the specific initial concentrations and pH. Then the contents of the flasks were magnetically stirred for a specific time at the rate of 300 rpm, with a controlled temperature during adsorption process. The residual concentration of the Pb(II) in the solution was determined by the use of an atomic absorption emission spectrophotometer (Shimadzu AA-670). The amount of Pb(II) sorbed per gram of ZnCl₂-MCM-41 was calculated according to eqn (1):where q_e is the equilibrium Pb(II) concentration on the adsorbent (mg g⁻¹); C_e and C₀ are the equilibrium and initial lead(II) concentrations in the solution, respectively (mg L⁻¹); V is the volume of the solution (L); and m is the mass of dry sorbent used (g). The variables that were investigated for possible effects on adsorption were pH (2–7), contact time (1–60 min), initial ion concentration (2–200 mg L⁻¹), and temperature (20, 30, 40, and 50 °C). All samples were filtered through Whatman no. 42 filter paper and then analyzed with an atomic absorption spectrophotometer.

The metal removal percentage from aqueous solution is calculated using the following equation:

2.6. Characterization of samples

2.6.1. XRD. X-ray powder diffraction patterns were recorded in the 2θ range of 1.5 to 10 deg. at 0.02 deg. steps and 0.4 [s] scan step time on a Philips Analytical X-ray B.V. diffractometer equipped with a Cu-anode (λ = 1.54056 Å).

2.6.2. Nitrogen adsorption. N₂ adsorption isotherms were measured at 77 K on a Micrometrics ASAP 2010 analyzer using standard, continuous procedures. Prior to measurement, all samples were degassed at 573 K for 5 h. The measurements were carried out over relative pressures ranging from ca. 10⁻³ to 0.995. Surface areas and pore size distribution were determined by Brunauer–Emmett–Teller (BET) and Barrett–Joyner–Halenda (BJH) methods, respectively.¹⁷

2.6.3. FT-IR spectroscopy. FT-IR spectra for the produced materials were recorded using a Shimadzu 4300 FT-IR spectrophotometer and a standard KBr technique in the region of 4000–400 cm⁻¹.

2.6.4. TEM and SEM. Transmission electron microscopy (Leo 912 AB, Germany) was used to examine the pore array structure of the ZnCl₂-MCM-41 sorbent. Scanning electron microscopy (KYKY-EM3200 Digital Scanning Electron Microscope) was used to determine the particle morphology and the particle size distribution of the synthesized materials.

3. Results and discussion

3.1. Adsorbent characterization

3.1.1. XRD pattern. XRD patterns of mesoporous MCM-41 and ZnCl₂-MCM-41 are shown in Fig. 2. There are four MCM-41 characteristic peaks at 2.32, 4.05, 4.69, and 6.20 degrees, which could be assigned to (1 0 0), (1 1 0), (2 0 0), and (2 1 0) planes, respectively. These peaks are in good agreement with the XRD patterns obtained by Savidha and Pandurangan.¹⁸ Therefore, it could be inferred that the synthesis procedure of MCM-41 in this work has been done well and the crystalline structure is as expected. The diffraction pattern of the MCM-41 indicated the possession of an ordered structure of hexagonal pore arrays. After ZnCl₂ particles were dispersed into MCM-41, none of the peaks was disappeared. Nevertheless, peak intensities of all planes of the support decreased. Moreover, a slight shift was occurred in the location of the peaks as 2.34, 4.09, 4.71, and 6.28 degrees, which are related to (1 0 0), (1 1 0), (2 0 0), and (2 1 0) planes, respectively. The decrease in peak intensities after incorporation may be explained by reasoning that either: a part of the pore structure is blocked with ZnCl₂;¹⁹ or pore filling reduces the scattering contrast between the pores and walls of mesoporous silica resulting from the formation of “–O–Zn–Cl” sites inside the MCM-41 pores.²⁰ The low intensity and peak broadening observed in the XRD pattern of ZnCl₂-MCM-41 indicate that these materials are not as well ordered as MCM-41; i.e., the hexagonal array of their channels is not quite regular. It should be mentioned that no peaks were observed in the XRD pattern of ZnCl₂-MCM-41 from 10 to 80 degrees, showing that all reactants were either used completely or washed off the surface and hence no unreacted ZnCl₂ left in the obtained sorbent.⁵

Fig. 2 The X-ray diffraction patterns of MCM-41 and ZnCl₂-MCM-41.

3.1.2. N₂ adsorption–desorption isotherm. The nitrogen adsorption–desorption isotherms of MCM-41 and ZnCl₂-MCM-41 samples are shown in Fig. 3a and b. The isotherms of MCM-41 and ZnCl₂-MCM-41 corresponded to type IV based on the IUPAC classification scheme, which is characteristic of MCM-41 materials. The adsorption at low relative pressure (P/P₀ < 0.2) increased considerably due to monolayer adsorption on the external surface. The lower adsorption volume on ZnCl₂-MCM-41 indicated lower surface area. The N₂ adsorption increased again before reaching a nearly constant volume in the relative pressure range of 0.2–0.4, which corresponded to nitrogen adsorption in the mesopores. As indicated in Fig. 3b, the adsorption on the surface of ZnCl₂-MCM-41 decreased in this range, indicating the partial blocking of mesopores by the ZnCl₂ particles. The general and the main feature of adsorption isotherms on MCM-41 is a characteristic step associated with the capillary condensation in pores. It has been shown that, depending on adsorbate, pore size, and temperature, the capillary condensation desorption in MCM-41 may occur both with and without a hysteresis loop.⁵ For both cases, a hysteresis loop occurred in the mesopores. The specific surface areas and pore diameters of both samples are shown in Table 1. The decrease in the surface area of ZnCl₂-MCM-41 indicated that ZnCl₂ particles reduced the pore volume of MCM-41. This may be attributed to the dispersion of ZnCl₂ onto the walls of mesoporous support. In addition, the pore diameters of ZnCl₂-MCM-41 calculated from the BJH equation were in the range of 25–35 Å (figure not presented). This implies that, after ZnCl₂ incorporating into MCM-41 pores, the ZnCl₂-MCM-41 pores are still mesoporous. The long plateau at higher relative pressures indicates that there was a slight pore filling after P/P₀ > 0.40. Textural characteristics of prepared adsorbents were obtained from isotherms using BET and BJH methods, and the results are depicted in Table 1. The specific surface area of MCM-41 was decreased from 1169 to 754 m² g⁻¹ by ZnCl₂ incorporation. After ZnCl₂ loading, a decrease in the V_p and BJH average pore diameter was observed that can be interpreted due to the fact that the ZnCl₂ particles were dispersed onto the MCM-41 mesopores channels.

Fig. 3 N₂ adsorption–desorption isotherm of (a) MCM-41 and (b) ZnCl₂-MCM-41.

Table 1 Physicochemical properties of calcined and ZnCl₂-loaded MCM-41

Samples	SBET (m^2 g^−1)	Vp (cm^3 g^−1)	dBJH (nm)	davg (nm)
MCM-41	1169	0.97	3.25	3.55
ZnCl2-MCM-41	754	0.58	2.86	3.15

---

3.1.3. FT-IR analysis. FT-IR patterns of mesoporous silica materials between 4000 and 400 cm⁻¹ are shown in Fig. 4. Generally, the main feature of the mesoporous silica sample spectra is a large, broad band between 3200 and 3500 cm⁻¹, which is attributed both to –OH bond stretching of the surface silanol groups, and to the remaining adsorbed water molecules. The broad absorption band at around 1030–1240 cm⁻¹ is assigned to the Si–O–Si stretching. The spectrum for the uncalcined MCM-41 (Fig. 4a) shows a group of strong, intense bands at 3396, 2923, 2852, 1639, and 1479 cm⁻¹ and a group of bands in the region below 1400 cm⁻¹. The bands at 3396 and 1639 cm⁻¹ are related to the stretching and bending modes of adsorbed water molecules, while the bands at 2923 and 2854 cm⁻¹ are attributed to the stretching mode of νCH(–CH₃) and νCH(–CH₂–) groups, respectively. The band at 1479 cm⁻¹ is assignable to the bending mode of δCH(–CH₃) and δCH(–CH₂–) groups. The group of bands observed below 1400 cm⁻¹ is related to the framework vibration of MCM-41. For the calcined MCM-41 as shown in Fig. 4b, the band at 2923, 2852 and 1479 cm⁻¹ were disappeared, showing that the CTAB template has been removed completely after calcination. The band at 1058 cm⁻¹ is assigned to ν_as(Si–O–Si); the band at 968 cm⁻¹ is assigned to ν_as(Si–OH); the band at 796 cm⁻¹ is assigned to ν_s(Si–O–Si); and the band at 459 cm⁻¹ is assigned to δ(Si–O–Si). The band at 1634 cm⁻¹ and the broad absorption band centered at 3441 cm⁻¹ are attributed to hydrogen-bonded Si–OH groups perturbed by physically adsorbed water.²¹ For ZnCl₂-MCM-41 (Fig. 4c), the absorption intensity of 3565, 1735, 1614, and 802 cm⁻¹ bands increased and shifted toward greater wave numbers, which could be considered as evidence for the incorporation of ZnCl₂ in the MCM-41 pores. Moreover, there was a change in the intensity and broadening of the 965 cm⁻¹ band, which indicates a structural change for the surface Si–OH group due to the presence of ZnCl₂ species in the MCM-41 material, and might be due to the formation of a new vibration band, ν_as(Si–O–Zn).⁵

Fig. 4 The FT-IR spectra of (a) uncalcined-MCM-41, (b) calcined MCM-41, and (c) ZnCl₂-MCM-41.

3.1.4. TEM images. The TEM image of ZnCl₂-MCM-41 is displayed in Fig. 5. The determined-field image at high magnification of the ZnCl₂-MCM-41 particles shows a mesostructure with a well-defined hexagonal arrangement of uniform pores. The pore size was estimated to be ∼2.7 nm, which is in good agreement with the average pore sizes calculated by the BJH model from N₂ adsorption data. The micrograph confirmed the highly ordered hexagonal arrays and one-dimensional mesoporous parallel channels.

Fig. 5 The TEM image of ZnCl₂-MCM-41.

3.1.5. SEM micrograph. The representative SEM image of the ZnCl₂-MCM-41 is displayed in Fig. 6. From this, it is clear that all of the ZnCl₂-MCM-41 particles have an ovoid morphology without any agglomeration.

Fig. 6 The SEM micrographs for the ZnCl₂-MCM-41.

3.2. Adsorption of Pb(II) species

3.2.1. Effect of ZnCl₂ loading. In order to obtain the maximum adsorption capacity of Pb(II) species by ZnCl₂-MCM-41 sorbent, different amounts of ZnCl₂ (0–7 mmol) were incorporated into 1 g of calcined MCM-41. These samples were used for Pb(II) removal while other operating parameters were kept constant. As shown in Fig. 7, the optimum adsorption was attained when 4 mmol ZnCl₂ was employed for loading onto 1 g of MCM-41. Hence, the rest of the experiments were carried out with the 4 mmol g⁻¹ ZnCl₂-modified MCM-41 sorbent samples. It is worth mentioning that the Pb(II) removal efficiency of the pure MCM-41 was only about 17%, while the modified MCM-41 could remove almost 97% percent of the Pb(II) ions. This significant increase in the Pb(II) removal efficiency of the modified sorbent is attributed to the formation of O–Zn–Cl binding sites by incorporating ZnCl₂ into MCM-41 structure.

Fig. 7 Pb(II) removal efficiency of ZnCl₂-MCM-41 as a function of ZnCl₂ loading (C₀ = 20 mg L⁻¹, T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 60 min, 300 rpm).

3.2.2. Effects of contact time and initial concentration. The sorption data for the uptake of Pb(II) versus contact time at different initial concentrations ranging from 2 to 200 mg L⁻¹ are displayed in Fig. 8. It can be observed that the sorption capacity increased with time and then reached a constant value where no more metal was removed from the solution. At this point, the amount of Pb(II) being sorbed by the sorbent was in a state of dynamic equilibrium with the amount of Pb(II) desorbed from the sorbent. The required contact time for Pb solutions with initial concentrations of 2 to 200 mg L⁻¹ to reach equilibrium was approximately 30 min. Therefore, it can be deduced that the equilibrium time was virtually independent of initial lead concentration. This is because the large pores of the sorbent allow lead species to move through the pores easily and readily access the active binding sites of the sorbent. It was observed that the Pb(II) removal varied with variations in the initial metal concentration. The removal of lead was found to be dependent on the initial concentration; the adsorbed amount increased with increases in the initial concentration. In addition, the adsorption was fast in the early stages, and then attained an asymptotic value for longer contact times. The initial rate of sorption was greater due to higher initial lead concentration; in other words, the resistance to the metal uptake decreased as the mass transfer driving force increased. Equilibrium uptake increased with the increase of initial metal concentration at the range of experimental concentration. This is due to the increase in the driving force – i.e., the concentration gradient. It is also noticed that an increase in the initial lead concentration led to a decrease in the metal removal percentage. This effect can be explained as follows: at low metal/sorbent ratios, there are a number of sorption sites in ZnCl₂-MCM-41 structure, but as the metal/sorbent ratio increases, sorption sites become saturated, resulting in decreases in the sorption efficiency.

Fig. 8 Effect of contact time and initial concentration on the adsorption of Pb(II) onto ZnCl₂-MCM-41 (T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 300 rpm).

3.2.3. Effect of temperature. Fig. 9 shows the amount of lead sorbed versus time at different temperatures. Experimental results showed that the adsorption of Pb(II) ions onto ZnCl₂-MCM-41 was significantly dependent on the temperature until the contact time of 30 min. The adsorption of Pb(II) onto ZnCl₂-MCM-41 at different temperatures showed a decrease in the adsorption capacity with an increase in temperature. As temperature increased from 20 to 50 °C for the equilibrium time, 30 min, the sorption amount decreased from 58.08 to 54.18 mg g⁻¹ for Pb(II). These results indicated the exothermic nature of Pb(II) sorption onto ZnCl₂-MCM-41 pores. The decrease in the sorption of Pb(II) ions resulting from an increase in temperature may be due to an increasing tendency to desorb metal ions from the interface to the solution. Aksu and Kutsal²² have commented that the thickness of the boundary layer decreases at relatively high temperatures, due to the increased tendency of the metal ion to escape from the adsorbent surface to the solution phase, which results in a decrease in adsorption.

Fig. 9 Effect of contact time and temperature on the sorption of Pb(II) onto ZnCl₂-MCM-41 (C₀ = 20 mg L⁻¹; pH = 7; sorbent dosage = 0.333 g L⁻¹; 300 rpm).

As it is evident from Fig. 9, the maximum adsorption capacity is achieved at 20 °C. Therefore, the optimum temperature was selected as 20 °C for further sorption experiments.

3.2.4. Effect of pH. The pH parameter has been identified as one of the most influential parameters on metal sorption, and it strongly influences hydrolysis, complexation by organic and/or inorganic ligands, redox reactions, and precipitation, as well as the speciation and adsorption availability of heavy metals.²³ Additionally, pH is directly related to hydrogen ions' ability to compete with metal ions to occupy active sites on the sorbent surface.²⁴ Several experiments were performed to optimize the pH of the solution for maximum Pb(II) adsorption by ZnCl₂-MCM-41. The initial solution pH was varied at the range of 2–7 in order to avoid precipitation of lead in the form of metal hydroxides and hydrolytic action from metal ions,²⁵ and as pH increased from 2 to 7, the removal of Pb(II) increased from 72.46 to 97.24% (Fig. 10). Lead speciation is great concern in the studies associated with the effect of initial pH of solution. It is known that lead species are present in the forms of Pb²⁺, Pb(OH)⁺, Pb(OH)⁰₂, Pb(OH)₃⁻, and Pb(OH)₄²⁻ at different pH values (Fig. S1†).²⁶ Fig. S1† shows that the predominant speciation of lead ions at pH values higher than 7 is Pb(OH)₂ and therefore in that pH range precipitation occurs. In order to prevent lead precipitation, the pH range of 2–7 was selected for this study. According to the well-known speciation of lead in aqueous solutions, the predominant ionic form at pH < 6 is Pb²⁺. However, at low pH levels, the large amount of H⁺ ions could compete with the Pb²⁺ ions for the binding sites, resulting in low Pb(II) adsorption.

Fig. 10 The effect of pH on the adsorption of Pb(II) ions onto ZnCl₂-MCM-41 (C₀ = 20 mg L⁻¹; T = 20 °C; sorbent dosage = 0.333 g L⁻¹; 300 rpm).

By increasing the pH, the effect of H⁺ competition was decreased, which made the binding sites more accessible to Pb(II) ions. In addition, increasing the pH caused the negative charges on the surface of the adsorbent to increase due to deprotonation of active binding sites. Hence, the electrostatic attraction between ZnCl₂-MCM-41 and Pb(II) was enhanced, further increasing the amount of Pb(II) adsorption. At pH 7–10, the main species of lead are Pb(OH)⁺ and Pb(OH)⁰₂, and thus the removal of lead is possibly accomplished by the simultaneous precipitation of Pb(OH)⁰₂ and sorption of Pb(OH)⁺. Consequently, this condition is often not desirable. Nevertheless, almost 97 percent of lead ions are adsorbed on ZnCl₂-MCM-41 at pH 7, and thereby it is impossible to form precipitation because of the very low concentration of remaining lead in the solution. Therefore, pH 7 was selected as the optimum condition for the sorption of Pb(II) on ZnCl₂-MCM-41. At pH values greater than 10, the predominant lead species are Pb(OH)⁰₂ and Pb(OH)₃⁻, which are difficult to adsorb on the negatively charged surface of the adsorbent.²⁷ (effect of pH on Pb(II) sorption at C₀ = 50 mg L⁻¹ has been presented in Fig. S2†).

3.2.5. Effect of sorbent dosage. The sorption capacity (mg g⁻¹) and sorption efficiency (%) of ZnCl₂-MCM-41 for Pb(II) ions as a function of sorbent dosage was investigated (Fig. 11). The percentage of the sorption increased from 96.7% to 99.9% as the sorbent concentration was increased from 0.01 to 0.05 g (30 mL)⁻¹ solution. This is because of the availability of more binding sites, resulting in greater access to the sorption sites for Pb(II) ions. Further increases in the sorbent concentration did not cause significant improvement in sorption capacity. This may be due to the binding of almost all ions to the sorbent, as well as the establishment of equilibrium between the ions bound to the sorbent and those remaining unsorbed in the solution. The maximum sorption was found to be 99.9% at a ZnCl₂-MCM-41 concentration of 0.05 g (30 mL)⁻¹ solution. On the other hand, the adsorption capacity of Pb(II) on ZnCl₂-MCM-41 decreased gradually with the increase of sorbent dosage. At low adsorbent content, all kinds of surface sites are entirely exposed for adsorption and the surface reaches saturation faster, resulting in a higher adsorption capacity. However, at higher sorbent concentrations the availability of higher energy sites decreases as a larger fraction of lower energy sites is occupied, leading to a lower adsorption capacity.²⁸ Since the lead removal percentage did not change drastically by increasing the sorbent dosage, while the adsorption capacity diminished tremendously, 0.01 g (30 mL)⁻¹ was selected as the optimum sorbent dosage for the rest of the experiments.

Fig. 11 Adsorption of Pb(II) on ZnCl₂-MCM-41 as a function of sorbent dosage (C₀ = 20 mg L⁻¹, T = 20 °C, pH = 7, 60 min, 300 rpm).

3.2.6. Influence of ionic strength. The influence of ionic strength on the adsorption of Pb(II) onto ZnCl₂-MCM-41 is shown in Fig. 12. As can be seen, the adsorption of Pb(II) onto ZnCl₂-MCM-41 was clearly affected by ionic strength. The adsorption decreased steeply with increasing NaNO₃ concentration, which suggests that sodium ions greatly affected Pb(II) adsorption. With increasing Na⁺ concentration in the solution, competition between Pb(II) and Na⁺ for adsorption on the ZnCl₂-MCM-41 surface increases, and thereby the adsorption of Pb(II) on ZnCl₂-MCM-41 decreases. Furthermore, the Na⁺ in solution may influence the double layer thickness and interface potential, and thereby affect the binding of the adsorbed species. Ion exchange and outer-sphere complexes are affected by the variations of ionic strength more easily than are inner sphere complexes, since the background electrolyte ions are placed in the same plane as outer-sphere complexes.

Fig. 12 Influence of ionic strength on the adsorption of Pb(II) onto ZnCl₂-MCM-41 (C₀ = 20 mg L⁻¹, T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 60 min, 300 rpm).

3.3. Adsorption kinetics

To evaluate the adsorption kinetics of Pb(II) ions, four different kinetic models were applied to the experimental data: (1) the pseudo-first order model, (2) the pseudo-second order model, (3) the Elovich model, and (4) the intra-particle diffusion model. Table 2 shows the equations associated with these models. The parameters of the models were calculated by linear and non-linear (using Excel Add-in Solver) regression methods separately. In this study, the coefficient of determination (R²) was used to find the best-fitting kinetic and isotherm models for the experimental data:where q_m is the equilibrium capacity obtained from the model, q_e is the equilibrium capacity obtained from experimental data, and q̄_e is the average of q_e.

Table 2 Equations of the kinetic models

Model	Equation	Ref.
Pseudo-first order	ln(qe − qt) = ln qe − k1t	30
Pseudo-second order		31
Elovich		32
Intra-particle diffusion	qt = kidt^1/2 + ci	33

---

All kinetic parameters and correlation coefficients are listed in Table 3. As can be seen, the pseudo-second order model had the highest R² value at all Pb(II) initial concentrations in both linear and non-linear regression methods. This model assumes that the rate limiting step in the adsorption of Pb(II) species is chemisorption, involving valence forces through the sharing or exchange of electrons between lead ions and active binding sites on the sorbent surface. For all kinetic models, the results obtained from linear regression differ from the results from non-linear regression, especially for the pseudo first-order model. This difference shows that linearization changed the error structure of models and verifies that it is inappropriate to use the coefficient of determination of a linear regression analysis for comparing the best-fitting solution of different isotherms. Detailed explanations about linear and non-linear regression are presented in our previous study.²⁹ For all models, the calculated q_e values are not completely consistent with the experimental data. The R² value of intra-particle diffusion was less than the R² values in other models, which verifies that the diffusion through the sorbent pores is not the rate-limiting step. In fact, the uniform, regular, and large pores of ZnCl₂-MCM-41 allow lead ions to move easily through the pores to access the binding sites without any diffusivity barrier. The Elovich equation does not provide any mechanistic evidence in this study, although previous work has proved that it is suitable for highly heterogeneous systems.²⁹ Consequently, the inability of the Elovich equation to describe the Pb(II) sorption process of the ZnCl₂-MCM-41 sorbent confirms that the sorption system of this study is homogeneous. A comparison of the different kinetic models for the adsorption of Pb(II) onto ZnCl₂-MCM-41 at different initial concentrations is illustrated in Fig. 13.

Table 3 Parameters of the kinetic models for Pb(II) adsorption onto ZnCl₂-MCM-41 (C₀ = 50, 100, and 200 mg L⁻¹, T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 300 rpm)

Kinetic model	Model parameters	Linear regression			Non-linear regression
		50	100	200	50	100	200
Pseudo-first order	qe,meas (mg g^−1)	145.8	287.1	552.4	145.8	287.1	552.4
	qe,model (mg g^−1)	35.3	74.6	110.8	144.3	284.4	548.6
	k1 (min^−1)	0.186	0.223	0.244	0.791	0.743	0.929
	R^2	0.9858	0.9927	0.9875	0.8909	0.9509	0.9255
Pseudo-second order	qe,meas (mg g^−1)	145.8	287.1	552.4	145.8	287.1	552.4
	qe,model (mg g^−1)	149.2	294.1	555.6	148.1	294.5	561.3
	k2 (g mg^−1 min^−1)	0.013	0.007	0.005	0.013	0.0057	0.0047
	R^2	0.9999	0.9999	0.9999	0.9986	0.9880	0.9916
Elovich	a × 10^−8 (g mg^−1 min^−1)	0.011	0.047	2.14	0.011	0.022	0.785
	b (mg g^−1)	0.101	0.045	0.034	0.101	0.042	0.032
	R^2	0.9207	0.8549	0.8591	0.9036	0.8481	0.8499
Intra-particle diffusion	kid (mg g^−1 min^−1/2)	6.06	13.2	17.5	6.5	15.9	21.1
	ci (mg g^−1)	116.6	224.7	469.9	114.1	212.6	453.9
	R^2	0.7921	0.7092	0.7071	0.7933	0.7369	0.7381

---

Fig. 13 Comparison of different kinetic models for Pb(II) adsorption onto ZnCl₂-MCM-41 at three different initial concentrations (a) C₀ = 50 mg L⁻¹, (b) C₀ = 100 mg L⁻¹, and (c) 200 mg L⁻¹ (T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 300 rpm).

3.4. Adsorption isotherm

Three isotherms, namely the Langmuir, Freundlich, and Redlich–Peterson (R–P) models, were fitted to the experimental data to find out more details about the process. These details include maximum theoretical adsorption capacity, process mechanism, physisorption or chemisorption, and monolayer or multilayer adsorption, to name a few. To make a comparison, the isotherm parameters were calculated by linear and nonlinear regression methods. All isotherm equations and their linearized forms are presented in Table S2.†

3.4.1. Linear regression. Linear regression using the method of least squares is the most commonly-used method in determining isotherm parameters. The best-fit isotherm was selected based on the coefficient of determination that produced the minimum error distribution between the predicted and experimental isotherms. The Freundlich, Langmuir, and Redlich–Peterson constants can be obtained from the slope and intercept of the plots between ln(q_e) versus ln(C_e), C_e/q_e versus C_e, and ln(AC_e/q_e − 1) versus ln(C_e), respectively. In the case of the Redlich–Peterson isotherm, the constant A was obtained by maximizing the R² value using a trial and error method in the solver add-in function of Microsoft Excel, Microsoft Corporation. The calculated isotherm parameters at the studied solution conditions, and the corresponding R² values, are shown in Table 4. The R² values were lower for the Freundlich isotherm, which suggests that this isotherm cannot appropriately represent the uptake of Pb(II) by ZnCl₂-MCM-41 particles. In contrast, the very higher R² values for both the Langmuir and the Redlich–Peterson isotherms suggest that these two models can be used for explaining the equilibrium Pb(II) uptake. The Redlich–Peterson isotherm is a hybrid of the Langmuir and Freundlich isotherms into a single equation. Two limiting behaviors exist: the Langmuir form for m = 1 and Henry's law form for m = 0. The m value was 0.693, which indicates that the number of homogeneous active sites on ZnCl₂-MCM-41 was higher than the number of heterogeneous ones. In fact, the higher R² value of the R–P isotherm denotes that both the Langmuir and Freundlich isotherms can describe this sorption process, but most of Pb(II) sorption onto ZnCl₂-MCM-41 takes place according to the assumptions of the Langmuir isotherm. The Freundlich model proposes an adsorption with a heterogeneous energetic distribution of active sites, accompanied by interactions between adsorbed molecules. The Langmuir model suggests that the uptake occurs on a homogeneous surface through monolayer sorption without interaction between adsorbed molecules.³⁴ Thus, according to a linear regression method, most of the Pb(II) uptake is due to monolayer coverage of solute species onto the surface of ZnCl₂-MCM-41. Fig. S1† illustrates the linear behavior of these three isotherm models.

Table 4 The isotherm parameters for the sorption of Pb(II) onto ZnCl₂-MCM-41 obtained by linear regression method (T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 60 min, 300 rpm)

Freundlich			Langmuir			Redlich–Peterson
Kf	1/n	R^2	qm	Ka	R^2	A	B	m	R^2
49.4	0.546	0.9674	454.5	0.110	0.9947	71.3	0.481	0.693	0.9964

---

3.4.2. Non-linear regression. The Freundlich, Langmuir, and Redlich–Peterson isotherm constants and error values were determined by a non-linear regression method based on different error functions. These data are presented in Table S3.† For each isotherm, seven sets of error functions with model parameters were calculated, and then the SNE value of each set was computed. The lowest SNE value indicates the best set of error functions. The S_RE, χ², and ARE sets were obtained as the optimum sets of error functions for the Freundlich, Langmuir, and Redlich–Peterson isotherms, respectively. The optimum sets of the Freundlich and Langmuir models do not have higher R² values than the other sets. Therefore, it is not appropriate to use the coefficient of determination (R²) for comparing the best-fitting isotherms. The parameters obtained by linear regression differ from the non-linear parameters (in the optimum set), especially for the R–P isotherm. This difference verifies that the non-linear method is a better way to obtain the isotherm parameters, since the linearization of non-linear experimental data may distort the error distribution structure of an isotherm.¹⁷ Fig. S3† presents the Langmuir, Freundlich, and R–P isotherms' deviations from experimental data. A comparison of monolayer maximum adsorption capacities (q_max) of some adsorbents for Pb(II) removal from aqueous solution were listed in Table S4.†

3.5. Sorption nature

In addition to the studied isotherms mentioned previously, the equilibrium data were analyzed by the Dubinin–Radushkevitch (D–R) isotherm model to determine whether the adsorption process is physical or chemical. The linear form of the D–R isotherm equation is:⁵

ln q_e = ln q_m − βε² (4)

where q_e is the amount of adsorbate per unit weight of sorbent (mol g⁻¹), q_m is the maximum sorption capacity (mol g⁻¹), β is the activity coefficient related to sorption mean free energy (mol² J⁻²), and ε is the Polanyi potential (ε = RT ln(1 + 1/C_e)). The D–R model parameter values are given in Table 5. The mean free energy (E; kJ mol⁻¹) is defined as follows:

Table 5 The D–R isotherm linear equations and parameters for the adsorption Pb(II) onto ZnCl₂-MCM-41 (T = 20 °C, pH = 7, sorbent dosage = 0.333 g L⁻¹, 60 min, 300 rpm)

ln qm	β (mol^2 J^−2)	E (kJ mol^−1)	R^2
−5.63	6.64 × 10^−9	8.68	0.9845

---

The E (kJ mol⁻¹) value presents information about the adsorption mechanism, describing whether it is occurring physically or chemically. A mean free energy between 8 and 16 kJ mol⁻¹ denotes that an adsorption process takes place chemically, while E < 8 kJ mol⁻¹ shows that an adsorption process proceeds physically. The mean sorption energy was determined as 8.68 kJ mol⁻¹ for the sorption of Pb(II). This result suggests that the sorption process of Pb ions onto ZnCl₂-MCM-41 may be carried out by a chemical mechanism.⁷ However, because of the small difference between 8 and 8.68 kJ mol⁻¹, it could be said that Pb(II) adsorption onto ZnCl₂-MCM-41 might be carried out by a physico-chemical mechanism.

3.6. Thermodynamic study of the adsorption process

Thermodynamic parameters can be determined using the equilibrium constant (K = q_e/C_e), depending on temperature. The Gibbs free energy change (ΔG°) is the fundamental criterion of spontaneity. Reactions occur spontaneously at a given temperature if ΔG° has a negative quantity. The changes in free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°) associated with the adsorption process were calculated using the following equations:²⁹

ΔG° = −RT ln K (6)

The plot of ln K versus 1/T provides the numerical values of ΔH° and ΔS° from slope and intercept, respectively (Fig. 14). The values obtained from eqn (6) and (7) are tabulated in Table 6. A negative value for the standard enthalpy change shows that the adsorption is exothermic. The results indicate that the adsorption of Pb(II) onto ZnCl₂-MCM-41 was favored at low temperatures and blocked at high temperatures. The negative values of ΔG° indicate that the adsorption process had a spontaneous nature. In addition, the negative value of the entropy change (ΔS°) implies that some structural changes occurred in sorbate and sorbent during the adsorption process, which led to a decrease in the disorderedness of the solid–solution system. The thermodynamic analysis derived from temperature-dependent adsorption isotherms shows that the adsorption process of Pb(II) onto ZnCl₂-MCM-41 was spontaneous and exothermic. As the initial concentration of Pb(II) increased from 20 to 200 mg L⁻¹, the free energy change shifted to lower negative values for all studied temperatures. This demonstrates that the adsorption was more spontaneous at low concentrations. From Table 6, it is worth mentioning that the ΔH°, ΔS° and ΔG° obtained at variable initial Pb(II) concentrations are different. The enthalpy change (ΔH°) varied from −29.4 to −10.1 kJ mol⁻¹ in the Pb(II) concentration range of 20–200 mg L⁻¹ while the entropy change (ΔS°) varied from −63.39 to −4.88 J mol⁻¹ K⁻¹. The decrease in enthalpy was in conformity with the exothermic and spontaneous nature of the adsorption process. The distribution of Pb(II) ions in the solution is by nature more chaotic than the distribution of the Pb(II) ions bound to the ZnCl₂-MCM-41 surface, so the binding of Pb(II) ions onto the sorbent surface resulted in a net decrease in entropy. Overall, the values of ΔH°, ΔS°, and ΔG° obtained at variable initial Pb(II) concentrations were different, especially in the case of higher initial Pb(II) concentrations.

Fig. 14 Plot of ln K_D versus 1/T for the determination of thermodynamic parameters.

Table 6 Thermodynamic parameters for the sorption of Pb(II) onto ZnCl₂-MCM-41

C0 (mg g^−1)	ΔG° (kJ mol^−1)				ΔH° (kJ mol^−1)	ΔS° (J mol^−1 K^−1)
	20 °C	25 °C	35 °C	50 °C
20	−10.91	−10.09	−9.46	−9.02	−29.4	−63.39
50	−10.76	−10.05	−9.43	−8.90	−28.9	−62.32
100	−10.12	−9.56	−9.22	−8.70	−23.7	−46.29
200	−8.67	−8.62	−8.53	−8.54	−10.1	−4.88

---

3.7. Adsorbent regeneration and lead recovery

Desorption of the adsorbed Pb(II) ions from ZnCl₂-MCM-41 using different concentrations of HNO₃ was studied. For these studies, different volumes of HNO₃ were used for regenerating 10 mg of the wasted ZnCl₂-MCM-41 adsorbent. The effect of using various volumes of different concentrations of HNO₃ as eluent was investigated in the range of 3–10 mL, the results of which are tabulated in Table 7. The highest recovery for Pb(II) ions was found to be 95% through the use of 10 mL of 1.0 M HNO₃. Furthermore, the adsorbents regenerated by different volumes of 1.0 M HNO₃ were utilized for the uptake of Pb species from 20 mg L⁻¹ Pb(II) solution. This assessment shows that the synthesized sorbents were effectively capable of being regenerated and reutilized, which is of extreme importance in industrial applications. The evaluation of removal efficiency after regenerating the sorbents by HNO₃ is also presented in Table 7.

Table 7 Adsorbent regeneration, Pb(II) recovery, and evaluation of removal efficiency after regeneration by nitric acid

Volume HNO3 (M)	Pb(II) recovery (%)				Pb(II) removal after regeneration by different volumes of 1.0 M HNO3 (%)
	0.3 M	0.5 M	0.8 M	1.0 M
3 mL	47	52	61	68	62
5 mL	49	57	66	73	68
8 mL	56	68	78	91	76
10 mL	72	83	90	95	87

---

3.8. Adsorption ability of ZnCl₂-MCM-41 for an industrial wastewater sample

To examine the performance of ZnCl₂-MCM-41 for the removal of Pb(II) ions in the presence of other cations, the sorbent was added to a 50 mL sample of wastewater from a battery production factory. The sample consists of different heavy metals such as Pb(II), Ni(II), Fe(III), Cr(III), and Zn(II), with different initial concentrations. The results obtained at pH 7, 20 °C, 60 min, and a stirring rate of 300 rpm are listed in Table 8. The results showed that 0.333 g L⁻¹ of sorbent can remove Pb(II) and Fe(III) completely. Moreover, these results illustrated that ZnCl₂-MCM-41 sorbent is capable of considerably adsorbing all contaminants. According to the outcome of these tests, it can be concluded that ZnCl₂-MCM-41 is an effective sorbent for removing a number of heavy metals from aqueous solution.

Table 8 Heavy metal uptake from an industrial wastewater sample onto ZnCl₂-MCM-41

Heavy metal	Initial concentration (μg L^−1)	Removal (%)
Pb(II)	7540	100
Ni(II)	0.575	89.6
Fe(III)	0.76	100
Cr(III)	0.15	91.3
Zn(II)	0.69	88.4

---

4. Conclusion

The present study shows that ZnCl₂-MCM-41 is an effective adsorbent for the removal of Pb(II) ions from aqueous solutions. The SEM and TEM images show that the new synthesized sorbent particles have a spherical morphology with no agglomeration. Other characterization tests indicate that the porosity of particles after modification was preserved. However, the regularity of crystalline structure, surface area, pore volume, and pore diameter was reduced. The adsorption process was a function of ZnCl₂ loading, the solution pH, temperature, adsorbent dose, initial metal concentration, and agitation time. The optimum conditions for the lead removal by ZnCl₂-MCM-41 were 4 mmol ZnCl₂ per gram of MCM-41, pH = 7, 20 °C, and 0.01 g (30 mL)⁻¹ adsorbent dose. Equilibrium was achieved practically in 30 min, but the experiments were done for 1 h to ensure equilibrium. The Freundlich, Langmuir, and Redlich–Peterson isotherms were fitted to the equilibrium sorption data by linear and non-linear regression methods in the following order, according to the SNE values: Redlich–Peterson > Langmuir > Freundlich. According to the analysis results, the non-linear regression method has smaller deviations from the experimental data. Adsorption kinetics followed the pseudo-second order kinetic model. Moreover, the inability of the Elovich equation to describe the sorption process denotes that this process was homogeneous. The influence of ionic strength on the adsorption of Pb(II) onto ZnCl₂-MCM-41 showed that this sorbent was to some degree tolerant against the interference of other ions. The obtained values of ΔH°, ΔG°, and ΔS° indicate that the process was exothermic, spontaneous, and eventually of decreased randomness. Finally, desorption studies using different concentrations of HNO₃ and the adsorption of heavy metals from an industrial wastewater sample demonstrated the feasibility of using this adsorbent for industrial applications.

References

1. F. Luo, Y. Liu, X. Li, Z. Xuan and J. Ma, Chemosphere, 2006, 64, 1122–1127.
2. S. Klimmek, H.-J. Stan, A. Wilke, G. Bunke and R. Buchholz, Environ. Sci. Technol., 2001, 35, 4283–4288.
3. M. Gavrilescu, Eng. Life Sci., 2004, 4, 219–232.
4. M. R. Panuccio, A. Sorgonà, M. Rizzo and G. Cacco, J. Environ. Manage., 2009, 90, 364–374.
5. F. Raji and M. Pakizeh, Appl. Surf. Sci., 2013, 282, 415–424.
6. B. Sen Gupta, M. Curran, S. Hasan and T. Ghosh, J. Environ. Manage., 2009, 90, 954–960.
7. D. Xu, X. Tan, C. Chen and X. Wang, J. Hazard. Mater., 2008, 154, 407–416.
8. Z. L. Yan Liu, J. Gao, J. Dai, J. Han, Y. Wang, J. Xie and Y. Yan, J. Hazard. Mater., 2011, 186, 197–205.
9. T. Akar and S. Tunali, Bioresour. Technol., 2006, 97, 1780–1787.
10. R. Han, W. Zou, H. Li, Y. Li and J. Shi, J. Hazard. Mater., 2006, 137, 934–942.
11. C. Kresge, M. Leonowicz, W. Roth, J. Vartuli and J. Beck, Nature, 1992, 359, 710–712.
12. J. Beck, J. Vartuli, W. Roth, M. Leonowicz, C. Kresge, K. Schmitt, C. Chu, D. Olson and E. Sheppard, J. Am. Chem. Soc., 1992, 114, 10834–10843.
13. S. Morin, P. Ayrault, S. El Mouahid, N. Gnep and M. Guisnet, Appl. Catal., A, 1997, 159, 317–331.
14. N. Kumar, V. Nieminen, L. E. Lindfors, T. Salmi, D. Y. Murzin, E. Laine and T. Heikkilä, Catal. Lett., 2002, 78, 105–110.
15. F. Boudrahem, F. Aissani-Benissad and H. Aït-Amar, J. Environ. Manage., 2009, 90, 3031–3039.
16. J. Liu, D. Yin, L. Qin and D. Yin, Stud. Surf. Sci. Catal., 2005, 156, 815–822.
17. Y.-S. Ho, Carbon, 2004, 42, 2115–2116.
18. R. Savidha and A. Pandurangan, Appl. Catal., A, 2004, 276, 39–50.
19. B. Sun, E. P. Reddy and P. G. Smirniotis, Appl. Catal., B, 2005, 57, 139–149.
20. Y. Shan and L. Gao, Mater. Chem. Phys., 2005, 89, 412–416.
21. K. M. S. Khalil, J. Colloid Interface Sci., 2007, 315, 562–568.
22. Z. Aksu and T. Kutsal, J. Chem. Technol. Biotechnol., 1991, 52, 109–118.
23. M. A. Acheampong, K. Pakshirajan, A. P. Annachhatre and P. N. Lens, J. Ind. Eng. Chem., 2013, 19, 841–848.
24. P. Lodeiro, J. Barriada, R. Herrero and M. Sastre de Vicente, Environ. Pollut., 2006, 142, 264–273.
25. G. Zeng, Y. Pang, Z. Zeng, L. Tang, Y. Zhang, Y. Liu, J. Zhang, X. Lei, Z. Li and Y. Xiong, Langmuir, 2011, 28, 468–473.
26. R. Wang, Q. Li, D. Xie, H. Xiao and H. Lu, Appl. Surf. Sci., 2013, 279, 129–136.
27. Y. Niu, R. Qu, C. Sun, C. Wang, H. Chen, C. Ji, Y. Zhang, X. Shao and F. Bu, J. Hazard. Mater., 2013, 244, 276–286.
28. J. Huang, Y. Liu and X. Wang, J. Hazard. Mater., 2008, 160, 382–387.
29. F. Raji and M. Pakizeh, Appl. Surf. Sci., 2014, 301, 568–575.
30. S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1–39.
31. Y.-H. Li, Z. Di, J. Ding, D. Wu, Z. Luan and Y. Zhu, Water Res., 2005, 39, 605–609.
32. M. K. Aroua, S. Leong, L. Teo, C. Y. Yin and W. M. A. W. Daud, Bioresour. Technol., 2008, 99, 5786–5792.
33. W. Weber and J. Morris, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1963, 89, 31–60.
34. A. Sari, D. Mendil, M. Tuzen and M. Soylak, J. Hazard. Mater., 2009, 162, 874–879.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra01192b

---