A predictive mass transport model for gas separation using glassy polymer membranes
Abstract
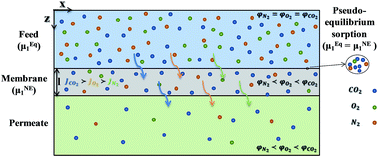
In this work, a predictive mass transfer model was developed based on the solution-diffusion mechanism for gas permeation through glassy polymer membranes. For this purpose, the non-equilibrium lattice fluid (NELF) theory in conjunction with the modified Fick's law and the free volume theory were employed for prediction of gas sorption and permeation and the computational fluid dynamics (CFD) method was used to solve the governing transport equations. This CFD modeling was solved based on the two different cases for the gas diffusion coefficients inside the membrane: (Case 1) concentration dependent diffusion coefficients from the literature and (Case 2) developed diffusion coefficient based on the free volume theory. The proposed models were validated by the experimental data collected in this work as well as the experimental data reported in the literature. The results revealed that the NELF model enables us to predict the sorption behavior of N2, O2, CO2 and CH4 into the polysulfone membrane and the predicted sorption values were in very good agreement with experimental results. Furthermore, the developed mass transport model is able to determine the influence of operating parameters such as temperature and pressure on the separation performance of the membrane and the experimental flux and selectivity were satisfactorily predicted by the proposed model.

 Please wait while we load your content...
Please wait while we load your content...