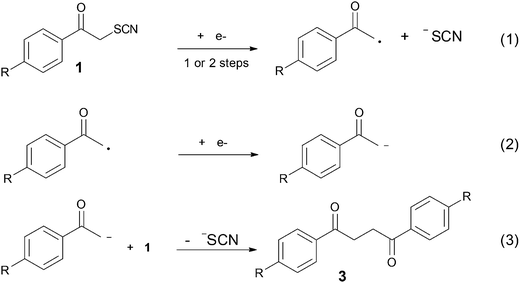
Breaking bonds with electrons: stepwise and concerted reductive cleavage of C–S, C–Se and Se–CN bonds in phenacylthiocyanates and phenacylselenocyanates†
Lydia M. Boucheta,
Alicia B. Peñéñorya,
Marc Robert*b and
Juan E. Argüello*a
aINFIQC-CONICET-UNC, Dpto. de Química Orgánica, Facultad de Ciencias Químicas, Universidad Nacional de Córdoba, Ciudad Universitaria, X5000HUA Córdoba, Argentina. E-mail: jea@fcq.unc.edu.ar; Web: http://www.fcq.unc.edu.ar/infiqc
bUniversité Paris Diderot, Sorbonne Paris Cité, Laboratoired'ElectrochimieMoléculaire, UnitéMixte de RechercheUniversité – CNRS No 7591, Bâtiment Lavoisier, 15 rue Jean de Baïf, 75205 Paris Cedex 13, France. E-mail: robert@univ-paris-diderot.fr
First published on 22nd December 2014
Abstract
The mechanistic aspects of the electrochemical reduction of phenacylthio- and selenocyanates have been studied. With phenacylthiocyanates (1), a change in the reductive cleavage mechanism is observed as a function of the substituent on the phenyl ring. While a stepwise mechanism involving the intermediacy of a radical anion is followed for substrates bearing a strong electron withdrawing group, such as cyano and nitro substituent (1d, 1e), and a concerted mechanism is favoured for compounds bearing an electron-donating or no substituent on the phenyl ring (1a–c). A regioselective bond cleavage leads to the fragmentation of the CH2–S bond with all compounds 1a–e, further yielding the corresponding 1,4-diketone (3) as products. Contrastingly, with phenacylselenocyanates (2), two different reductive cleavages occur involving the breaking of both the CH2–Se and Se–CN bonds. Several products are obtained, all coming from nucleophilic attack at the α (phenacyl) carbon or the selenium atom.
Introduction
The coupling between charge transfer and bond cleavage between two heavy atoms occurs in a large number of chemical, biochemical and catalytic processes, such as cleavage of C–halogen bonds in organic halides, as well as other bonds,1–4 electron transfer activation of small molecules involved in contemporary energy challenges (such as e.g. H2O, O2, N2 and CO2), as well as enzymatic reactions such as dechlorination processes of RX (X = Cl) toxic derivatives within reductive dehalogenases.5 In these reactions, the cleavage accompanying charge transfer may be triggered in various manners, electrochemically, by homogenous electron donors or acceptors, photochemically or using pulse radiolysis.1–3 Charge transfer and bond cleavage reaction may occur concertedly according to a single elementary step (concerted dissociative electron transfer), or in two successive steps, the electron transfer then generating a frangible species that reacts in a distinct, chemical step, as shown in Scheme 1.1–3Potential energy curves describing both reactant and products were modelled by Morse curves, with the assumption that the repulsive interaction of the two fragments formed upon charge transfer is identical to the repulsive part of the reactant Morse curve.6 Solvent reorganization is calculated from the Marcus–Hush model. These two ingredients of the model lead to a quadratic activation (activation free energy: ΔG≠) – driving force (minus standard free energy: −ΔG0) relationship as given in eqn (1):1–3
 | (1) |
 : standard potential of the RX/R˙ + X− couple) is given by
: standard potential of the RX/R˙ + X− couple) is given by
 | (2) |
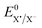 is the standard potential of the X˙/X− redox couple and ΔS0 is the bond dissociation entropy and, when required, additional sources of intramolecular reorganization may be included as an additive term to the intrinsic barrier:
is the standard potential of the X˙/X− redox couple and ΔS0 is the bond dissociation entropy and, when required, additional sources of intramolecular reorganization may be included as an additive term to the intrinsic barrier:
 | (3) |
The homolytic bond dissociation energy DRX represents the kinetic penalty for the concerted reaction as compared to the sequential pathway. The electron transfer rates may then be expressed as in the Marcus–Hush theory (eqn (4)):7–11
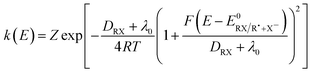 | (4) |
This set of equations have been successfully applied to both homogeneous and heterogeneous concerted dissociative electron transfers (in the former case, the electrode potential in the driving force expression should be replaced by the standard potential of the molecular electron donor), including C–halogen bonds (alkyl and benzyl halides),6,12–14 O–O bonds (alkyl peroxides),15,16 but also N–halogen bonds (N-halogenosultams),17 N–S bonds (sulfonylphthalimides),18 S–C bonds (sulfonium cations)19 or S–Cl bonds in arenesulfenyl chlorides.20,21 It also allowed identifying the competition that exists between the concerted and stepwise pathways, and depends upon intramolecular (structural, electronic) and environmental (solvent, energy of the incoming electron) factors.
Focusing on C–S bonds, the electrochemical reduction of various substituted benzyl thiocyanates showed a change in the cleavage mechanism as a function of the substituent on the benzyl ring.1,22,23 For the p-nitrobenzylthiocyanate, a stepwise dissociative electron transfer mechanism with an anion radical as intermediate takes place, the electron being transitorily located on the π* orbital (largely localized on the nitro groups), before cleavage occurs at the C–S bond. The reduction of the p-cyanobenzylthiocyanate follows a concerted charge transfer-bond breaking mechanism, with the electron going directly into the σ* orbital of the C–S bond. With benzyl thiocyanate, the reduction is also concerted with bond cleavage, but cleavage occurs both at the C–S bond (α-cleavage) and at the S–CN bond (β-cleavage).22,24
In the case of phenacylthiocyanates, it has been proposed that cathodic reduction at a controlled potential releases −SCN as a leaving group and that after a second electron transfer an enolate ion is formed.25 This electrogenerated enolate anion acts as a nucleophile to give a 1,4-diketone as the main product. No mechanistic details have been given about the intimate mechanisms for electron transfer and subsequent reactions, notably the degree of association between charge transfer and bond cleavage. On the other hand, the behaviour of phenacylselenocyanates differ from the corresponding sulphur one because the organic selenocyanates undergo a displacement of the CN group by the attack of nucleophilic reagents. It was suggested that the electrogenerated enolate anion formed after the cleavage of the C–Se bond and reduction with a second electron attacks the phenacylselenocyanate to render the (2-phenacylseleno) acetophenone as the main product.26 Again, no detailed mechanisms were provided.
In this report, we describe the electrochemical reduction of different phenacylthiocyanates (1) and phenacylselenocyanates (2). The SCN and SeCN groups of 1 and 2 may be considered as pseudohalogen groups. These functional groups can also be used as a masked mercapto/seleno group, as wells as precursors toward the synthesis of sulphur/selenium-containing organic compounds. These later compounds possess a broad range of bioactivities with applications as anticancer agents, and their redox behavior is also interesting because some of them exhibit glutathione peroxidase (GPx) activity.27–29
Using both, cyclic voltammetry (CV), theoretical calculations and the model for concerted dissociative electron transfer, we have determined the concerted or stepwise nature of the bond breaking processes and provided a complete analysis of the reduction processes. Various regioselectivity and various mechanisms were encountered. The selected compounds for this study bearing electron donor and withdrawing groups are shown below (Scheme 2).
Results and discussion
Phenacylthiocyanates (1) and phenacylselenocyanates (2) (Scheme 2) were prepared according to standard procedures. Full characterization of new compounds 1d and 2d can be found in the Experimental section and in the ESI† (NMR spectra). The mechanistic analysis was based on the use of the concerted dissociative electron transfer model, in conjunction with insights issued from DFT quantum chemical calculation.Electrochemical reduction of phenacylthiocyanates (1a–e)
The electrochemical reduction of the phenacylthiocyanates (1a–e) was studied by cyclic voltammetry (CV) in N,N′-dimethylformamide (DMF), in the presence of tetrabutylammoniumtetrafluoroborate (TBAF, 0.1 M) at a glassy carbon electrode. In all cases, the first cathodic wave does correspond to the cleavage of the CH2–S bond (see below), showing a remarkable regioselectivity for cleavage in the whole family. The peak characteristics (peak potential (Ep), peak width (Ep − Ep/2), slope of Ep vs. log(v) where v is the scan rate, number of electrons per molecule, and transfer coefficient (αp)) were obtained for all of these compounds and are given in Table 1.30,31| ArCOCH2SCNa | Ep,1b (V vs. SCE) | nc | δEp/δlog (v) sloped | αpe | Ep/2 − Ep (mV) | αpf | Ep,2g (V vs. SCE) | Ep ArCOCH3 |
|---|---|---|---|---|---|---|---|---|
| a In DMF, TBAF (0.1 M), [1a–e] = 1 mM.b First reduction peak potential at 0.1 V s−1.c Number of electrons exchanged per molecule.d mV per unit log(v).e From Ep,1 vs. log(v).f From peak width.g Second reduction peak potential. | ||||||||
| 1a | −1.29 | 1.2 | −63 | 0.47 | 103 | 0.46 | −2.03 | −2.03 |
| 1b | −1.36 | 0.9 | −79 | 0.37 | 102 | 0.46 | −2.10 | −2.13 |
| 1c | −1.39 | 0.9 | −76 | 0.39 | 127 | 0.37 | −2.16 | −2.19 |
| 1d | −0.97 | 1.2 | −59 | 0.5 | 80 | 0.59 | −1.47 | −1.45 |
| 1e | −0.64 | 1 | −39 | 0.75 | 60 | 0.79 | −0.85 | −0.85 |
As an example, the CV of phenacylthiocyanate 1a in DMF displayed an irreversible reduction peak at −1.29 V vs. SCE at low scan rate (Fig. 1a). The peak width had a value of 103 mV and the peak potential varied linearly with log(v) with a slope of 63 mV (Fig. 1b). The transfer coefficient (αp) values, obtained from peak width (0.46) and from the slope of δE/δlog(v) (0.47), were indicative of a slow electron transfer.1,2 This first reduction peak corresponds to the consumption of one electron per molecule (by comparison to the monoelectronic wave of ferrocene and taking into account the slow charge transfer).
 | ||
| Fig. 1 (a) CV of 1a (1 mM) in DMF + TBAF (0.1 M) at a glassy carbon electrode, v = 0.1 Vs−1. (b) Variation of the peak potential (1st reduction wave) with scan rate. | ||
Scanning in the oxidative direction after the first peak allowed observing an oxidation wave (Ep = 0.79 V vs. SCE) similar to the oxidation of +NH4, −SCN (Ep = 0.78 V vs. SCE at low scan rate), showing that the thiocyanate anion was formed, and thus the CH2–S bond was broken during the reduction process. A second reduction peak (reversible) can be seen at lower potentials (−2.03 V vs. SCE at low scan rate, Fig. 1a). As shown in Fig. 2, it may correspond to the reduction of acetophenone or alternatively to the reduction of the dimer 1,4-diphenyl-1,4-butanedione (3a). It has indeed been reported25 that the most likely reduction product of 1a in DMF is the 1,4-diphenyl-1,4-butanedione (3a) because the carbon centred radical formed after the CH2–S fragmentation is immediately reduced at the electrode surface, yielding the corresponding enolate anion, which acts as nucleophile in a subsequent addition process (Scheme 3). This second reduction peak provides a further proof that the CH2–S bond fragments upon reduction.
 | ||
Fig. 2 Cyclic voltammetry of 1a (1 mM,  ) and acetophenone (1 mM, ) and acetophenone (1 mM,  ) in DMF + TBAF (0.1 M) at a glassy carbon electrode, v = 0.1 V s−1. ) in DMF + TBAF (0.1 M) at a glassy carbon electrode, v = 0.1 V s−1. | ||
Compounds 1b and 1c showed similar reduction features with a first, broad, mono electronic reduction peak characterized by slow electron transfer (Fig. S1† and Table 1) and negative reduction potentials (−1.36 to −1.40 V vs. SCE at low scan rates). The transfer coefficient values determined from the peak width and from the slope of Ep vs. log(v) plot were 0.46 and 0.37 for 1b, 0.37 and 0.39 for 1c, respectively. As with 1a, the reduction leads to CH2–S bond fragmentation. The first cathodic peak was followed by a second peak (Table 1), corresponding to the reduction of the 1,4-diketones (1,4-bis(4-tolylbutane-1,4-dione for 1b and 1,4-bis(4-methoxyphenyl)butane-1,4-dione for 1c)) obtained after nucleophilic attack of the electrogenerated enolate onto reactant substrates 1b and c (Scheme 3), similarly to the mechanism followed with 1a.
Compounds 1d and 1e displayed a similar reduction pattern with a first monoelectronic, irreversible reduction peak, but at potentials considerably more positive than those measured with 1a–c (−0.97 V for 1d and −0.64 V vs. SCE for 1e, see Table 1 and Fig. S1†). This first reduction wave was also characterized by considerably smaller peak widths (between 60 mV and 80 mV at low scan rates) and smaller peak potential variations with the scan rate (Table 1), indicative of larger transfer coefficient and faster electron transfer. The CH2–S bond was broken along the reduction wave, as with 1a–c. However CV's characteristics clearly point toward a different mechanism for cleavage. A second and more negative wave was observed (see Table 1) corresponding to the reduction of 1,4-bis(4-cyanophenyl)butane-1,4-dione (3d) and 1,4-bis(4-nitrophenyl)butane-1,4-dione (3e), respectively, again similar to compounds 1a–c (Scheme 3). Further cathodic waves were observed at more negative potentials, due to multielectronic reduction processes of the aromatics (see ESI, Fig. S1†).
Note that in the presence of an excess of phenol, all compounds 1a–e showed a two electrons stoichiometry at the first reduction peak, in agreement with the proposed reaction mechanism (Scheme 3), in which the enolate was intercepted by the acidic phenol before acting as a nucleophilic agent towards a neutral substrate molecule, thus leading to the use of two electrons per reactant molecule (reactions (1) + (2) in Scheme 3). Note also that these results are in agreement with those previously reported.25
Mechanisms for the C–S bond fragmentation
The C–S bond breaking (reaction (1), Scheme 3) may occur in one concerted step or sequentially in two steps through the formation of a transient radical anion, which further undergoes cleavage in a second elementary step. Combining DFT calculations, analysis of CV characteristics and application of the model for concerted dissociative electron transfer allows getting insights in the mechanism as a function of the substituent on the phenyl ring. In the cases of 1a (Fig. 3), 1b and 1c, we were unable to find any minima on the potential energy surface that would correspond to the formation of a radical anion intermediate. Instead, fragmentation occurs at the CH2–S bond, in agreement with experiments, and a loose adduct between the two fragments, the phenacyl radical and the thiocyanate anion, was identified, as shown for 1a in Fig. 3 (left). In contrast, with compounds 1d (Fig. 3, right) and 1e, a minimum was determined prior to bond breaking, that corresponds to the formation of a radical anion intermediate, with the electronic density mainly localized on the electron withdrawing group borne by the phenyl group (CN for 1d, NO2 for 1e). For compounds 1d and 1e, electrochemical data (Table 1) were in agreement with an E + C mechanism, in which a first electron transfer (E) was followed by a fast chemical reaction (C), the breaking of the C–S bond. DFT calculations further confirmed the occurrence of a stepwise mechanism. In other words, reaction (1) (Scheme 3) takes place in two elementary steps. The initial electron was mainly located on the low lying π* orbital of the phenyl ring, owing to the electronic withdrawing substituents (CN, NO2). | ||
| Fig. 3 Left: [phenacyl radical/thiocyanate anion] adduct obtained upon reduction of 1a. Right: 1e˙− radical anion. Gray: carbon; white: hydrogen; red: oxygen; blue: nitrogen; gold: sulphur. | ||
This thermodynamic effect reflects in the peak potentials those were largely positive to the peaks obtained with compounds 1a–c (the positive shift is roughly 400 mV with 1d and 700 mV with 1e as compared to average peak potential values obtained for 1a–c). For compounds 1a–c, DFT calculations suggest a different mechanism, involving a concerted reduction-bond breaking process of the neutral substrate (reaction (1) in Scheme 3 occurs through one single step). The two fragments issued from the cleavage, the phenacyl radical on the one hand and the thiocyanate anion on the other hand were weakly interacting in the gas phase (as illustrated for 1a in Fig. 3). This weak charge–dipole interaction is likely to be washed out in polar DMF. The CV characteristics were compatible with such a mechanism (Table 1), notably the low values for the electron transfer α, suggesting high values for the reorganization energy. However, more evidence needs to be gathered in order to conclude about the exact mechanism. Using the model for concerted dissociative electron transfer, we may evaluate the transfer coefficient values and compare them to the experimental values. Transfer coefficient is defined through eqn (5):
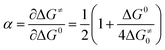 | (5) |
 is the standard potential of the X˙/X− redox couple (X = SCN). This last parameter is equal to 0.75 V vs. SCE.24 λ0, the solvent reorganization energy, could be estimated through the equivalent radii a of the substrate (λ0 ≈ 3/a).1,2 The homolytic bond dissociation energy DRX (C–S bond) and bond dissociation entropy were evaluated by DFT calculations. It also leads to the obtention of the standard free activation energy (intrinsic barrier) through eqn (3). All the data for compounds 1a–c are given in Table 2.
is the standard potential of the X˙/X− redox couple (X = SCN). This last parameter is equal to 0.75 V vs. SCE.24 λ0, the solvent reorganization energy, could be estimated through the equivalent radii a of the substrate (λ0 ≈ 3/a).1,2 The homolytic bond dissociation energy DRX (C–S bond) and bond dissociation entropy were evaluated by DFT calculations. It also leads to the obtention of the standard free activation energy (intrinsic barrier) through eqn (3). All the data for compounds 1a–c are given in Table 2.
With these parameters in hand, we were then able to estimate ΔG0, ΔG≠ at the CV peaks, and then to calculate α. The results obtained at low scan rates are presented in Table 3. A good quantitative match between the experimental (αexp) and calculated (αcalc) values was obtained, thus validating a concerted reductive cleavage mechanism of the C–S bond upon first electron reduction. The electron directly goes into the σ* orbital of the carbon–sulphur bond because no low energy hosting orbital was available for generating a radical anion intermediate, in contrast with what is observed for 1d and 1e. The very negative reduction potentials (as compared to those measured with 1d and 1e) were already clues that the mechanism was likely to be concerted. The single use of DFT calculations cannot lead to the reduction mechanisms, in particular because micro-solvation of the charged species (leaving anion, radical and radical anions) cannot be accurately reproduced, however, they provide a useful tool for confirming that the mechanisms drawn from cyclic voltammetry studies were coherent and plausible.
Electrochemical reduction of phenacylselenocyanates (2)
The electrochemical reduction of the phenacylselenocyanates (2a–e) was studied by CV in DMF + TBAF 0.1 M at a glassy carbon electrode. Characteristics for reductive peaks were determined and the results are summarized in Table 4.| ArCOCH2SeCNa | Eshoulder (V vs. ECS) | Ep1b (V vs. SCE) | δEp/δlog(v)c | Ep/2 − Ep (mV) | Ep2d (V vs. ECS) | Ep3e (V vs. SCE) |
|---|---|---|---|---|---|---|
| a In DMF + TBAF (0.1 M), [2a–e] = 1 mM.b First reduction peak potential.c mV per unit log(v).d Second reduction peak potential.e Third reduction peak potential. | ||||||
| 2a | −0.89 | −1.08 | −85 | — | −1.48 | −2.00 |
| 2b | −0.98 | −1.09 | −155 | — | −1.54 | −2.10 |
| 2c | −1.19 | −1.29 | −65 | — | −1.63 | −2.19 |
| 2d | — | −0.90 | −64 | 125 | −1.27 | −1.48 |
| 2e | — | −0.57 | −54 | 58 | −0.84 | −1.47 |
The CV of phenacylselenocyanate (2a) displayed an irreversible reduction peak at a potential Ep = −1.08 V vs. SCE (Fig. 4), with a shoulder close to −0.89 V vs. SCE (indicated as Eshoulder in Table 4). The irreversible peak observed at −2 V vs. SCE corresponds to the reduction of 1,4-bisphenylbutane-1,4-dione (3a) (or to the reduction of the substituted acetophenone), as observed in the case of thiocyanate analogue. Cleavage of the CH2–Se bond was thus likely to occur at the first reduction peak. That selenocyanate anion as the leaving group was confirmed by the observation of an oxidation wave (Ep = 0.59 V vs. SCE) similar to that of K+, –SeCN (Ep = 0.53 V vs. SCE). The phenacyl radical PhCOCH2˙ obtained after cleavage was reduced at the electrode to the ketone enolate anion (PhCOCH2−) with a second electron, and this enolate ion reacts with a neutral reactant to provide 3a (Scheme 4). Another smaller reduction peak was observed at a potential close to −1.48 V vs. SCE (Table 4 and Fig. 4). It was ascribed to the reduction of the selenide 4a (2-(phenacylseleno)acetophenone), which was identified by comparison with an authentic sample (see ESI, Fig. S5†). This result is in agreement with previous studies,26 in which selenide 4a may come from nucleophilic attack of the enolate at the selenium atom while releasing cyanide ion as leaving group, as shown in Scheme 4. Alternatively, 4a may come from a nucleophilic addition of a selenate anion (PhCOCH2Se−) onto 2a (Scheme 4). Such a selenate anion could be formed upon cleavage of the Se–CN bond (Scheme 4). The observation of a shoulder just before the main, first reduction peak may be the signature of this reductive cleavage (that does not occur in the thiocyanate family of compounds). Breaking of the Se–CN bond may also lead to the dimer compound 5a (2,2′-diselenediylbis(1-phenylethanone), Scheme 4) by a nucleophilic reaction of the selenate anion at the selenium atom of reactant 2a. CV of an authentic sample of diselenide 5a indicated that once formed, it was reduced to 4a (see ESI, Fig. S5†).
In total, the reduction of 2a leads to the cleavage of the CH2–Se bond and to the cleavage of the Se–CN bond, as illustrated in Scheme 4. This non-regioselective reduction process as compared to sulphide analogue 1a may be ascribed to the fact that the Se–CN cleavage, despite the large Se–CN homolytic bond dissociation energy, may be significantly accelerated by in-cage interactions between the fragments PhCOCH2Se˙ and CN− (charge–dipole interaction). Although studies of these interactions stand beyond the scope of this paper, preliminary quantum calculations indicate that a significant attractive interaction (typically in the order of 0.1 eV) does exist between the selenium centred radical and the cyanide anion, while for the CH2–Se bond cleavage, there is no interaction between the phenacyl radical and the selenocyanate anion. Note that a sticky interaction in the order of only 1% of DC–Se will result in a decrease of about 15% of the intrinsic barrier for concerted reductive cleavage.2 Thus, even if the CH2–Se bond breaking is favoured because of a smaller homolytic bond dissociation energy (DCH2–Se = 44 kcal mol−1 ≪ DSe–CN = 90.7 kcal mol−1, estimated by DFT calculations) both cleavages were observed.
Compounds 2b and 2c showed similar peak characteristics (see ESI, Fig. S4†) to compound 2a. In particular they all presented a first reduction peaks with a shoulder at lower potentials (Table 4). This first peak was followed by a second irreversible peak (−1.54 V vs. SCE for 2b and −1.63 V vs. SCE for 2c), in agreement with the reduction of the corresponding selenides with retention of the Se atom (compounds 4b and 4c, Scheme 4). Then, a third irreversible reduction peak corresponding to the reduction of 1,4-bis(4-tolyl)butane-1,4-dione (3b) (starting from 2b) and 1,4-bis(4-methoxyphenyl)butane-1,4-dione (3c) (starting from 2c) could be observed on the CVs. All of these products resulted from nucleophilic attacks as illustrated in Scheme 4. Compound 2d showed comparable characteristic peaks to 2a–c compounds (see ESI, Fig. S4†), except that the two reduction processes on the first cathodic wave (C–Se and Se–CN cleavages) almost merge, thus giving a very large peak width (125 mV). As a consequence, the reduction of 2d led to three products following nucleophilic reactions (Scheme 4).
In this case of p-nitrophenacylselenocyanate (2e), CVs displayed only a first reduction peak corresponding to consumption of one electron per molecule at a potential of −0.57 V vs. SCE (Fig. 5, Table 4), considerably more positive than with compounds 2a–c (typically 300 to 500 mV more positive). At more cathodic potentials, several reduction waves were observed, which correspond to the reduction of 1,4-bis(4-nitrophenyl)butane-1,4-dione (3e) and for the further reduction of the nitrophenyl ring. Fragmentation of the C–Se bond occurred at the first cathodic peak with no cleavage of the Se–CN bond because the reduction was driven to less negative potential due to the nitro substituent on the phenyl ring, making the Se–CN fragmentation non-competitive.
Conclusions
In conclusion, important mechanistic aspects of the electrochemical reduction of phenacylthio- and selenocyanates have been deciphered. With phenacylthiocyanates (1), a striking change in the reductive cleavage mechanism was observed as a function of the substituent on the phenyl ring. In the case of a cyano or a nitro substituent (1d and 1e) a stepwise mechanism involving the intermediacy of the radical anion takes place, while a concerted mechanism is operative with compounds bearing an electron-donating (or no) substituent on the phenyl ring (1a–c). CV characteristics, as well as analysis of the voltammograms in terms of transfer coefficient (α) and theoretical calculations both converge towards these conclusions. Remarkably, a regioselective bond cleavage was observed and reductive fragmentation of the CH2–S bond was followed for all compounds 1a–e, leading to the corresponding 1,4-diketone (3) as products. The latter were formed by an electrochemical-chemical mechanism in which the electrogenerated ketone enolate anions act as nucleophiles in substitution reactions toward 1a–e, with thiocyanate anion as a leaving group. By contrast, for phenacylselenocyanates 2, and except in the case of 2e, which reacts as the sulphur analogue, two different reductive cleavages occur involving breaking of both the C–Se and Se–CN bonds at closely positioned potentials, resulting in the obtention of several products, all coming from nucleophilic attack at the α (phenacyl) carbon or the selenium atom.Experimental section
General methods
1H, 13C and 77Se NMR spectra were recorded at 400.16, 100.62 and 76.32 MHz respectively on a Bruker 400 spectrometer, and chemical shifts were reported in δ (ppm) relative to TMS with CDCl3 as solvent. HRMS were recorded on a MicroTOF Q II equipment, operated with an ESI source and positive mode, using nitrogen as nebulising and drying gas and sodium formate 10 mM as internal calibrant.Chemicals
Dimethylformamide (DMF, Aldrich, >99.8%, extra dry over molecular sieves) was used without further purification. Commercially available reagents were used without further purification. Compounds 1a–e (ref. 32) and 2a–e (ref. 26) were prepared following literature methods.p-Cyanophenacylthiocyanate (1d)
White solid.1H NMR (400.16 MHz, CDCl3, 25 °C, TMS): δ = 8.05 (d, J = 8.8 Hz, 2H); 7.85 (d, J = 8.8 Hz, 2H); 4.69 (s, 2H; CH2). 13C NMR (100.62 MHz, CDCl3, 25 °C, TMS): δ = 189.62; 136.84; 133; 128.89; 118.10; 117.31; 110.94; 42.3(CH2). HRMS (ESI+) calcd for C10H7N2OS [M + H] 203.0274, found: 203.0297.p-Cyanophenacylselenocyanate (2d)
White solid.1H NMR (400.16 MHz, CDCl3, 25 °C, TMS): δ = 8.07 (d, J = 8.8 Hz, 2H); 7.85 (d, 2H, J = 8.4 Hz); 4.88 (s, 2H, CH2). 13C NMR (100.62 MHz, CDCl3, 25 °C, TMS): δ = 192.1; 136.6; 133.0; 129.1; 118.1; 117.4; 101.0; 37.3(CH2). 77Se NMR (76.32 MHz, CDCl3, 25 °C, TMS): δ = 168.59. HRMS (ESI−) calcd for C10H5N2OSe [M − H] 248.9562, found: 248.9560.Cyclic voltammetry
The electrochemical reduction of the phenacylthiocyanates and phenacylselenocyanates (1 mM) were conducted in a three electrode glass cell, thermostated at 25 °C, under a dry nitrogen or argon atmosphere. The working electrode was a 2 mm diameter glassy carbon electrode (Tokai). It was carefully polished and ultrasonically rinsed with ethanol each time. The reference electrode was a SCE separated from the main solution by a fine porosity glass frit. The counter electrode was a platinum wire. A Methrohm Autolab instrument was used. Positive feedback correction was applied to minimize the ohmic drop between the working and reference electrode.Theoretical calculations
Optimizations were carried out using DFT at the B3LYP/6-31+G(d,p) level (and at the B3LYP/6-311+G(d,p) level for the sulphur and selenium atoms).33 We checked that the conformations obtained were minima by running frequency calculations (no imaginary vibrational frequencies were found). Gas phase optimized energies for compounds 1a-c, phenacyl radicals and ˙SCN and ˙SeCN were used to estimate homolytic bond dissociation energy values. LUMO calculation, geometries for one electron reduced compounds were calculated in DMF by using the PCM model. All energy values include zero point correction. The calculations were performed using the Gaussian09 package.34 Z matrix and LUMOs for compounds 1a–e, 2a–e, radicals and radical anions are given in the ESI.†Acknowledgements
Authors acknowledge Ecos-Sud (grant project A10E03), INFIQC-CONICET and Universidad Nacional de Córdoba (UNC). This work was partly supported by MINCyT-ECOS, CONICET, SECyT-UNC and FONCyT. Compound 5a was kindly provided by F.R. Bisogno. LMB acknowledges CONICET for the receipt of a fellowship.Notes and references
- A. Houmam, Chem. Rev., 2008, 108, 2190–2237 CrossRef PubMed.
- C. Costentin, M. Robert and J.-M. Savéant, Chem. Phys., 2006, 324, 40–56 CrossRef CAS.
- J.-M. Savéant, in Advances in Physical Organic Chemistry, ed. T. T. Tidwell, Academic Press, New York, 2000, vol. 35, pp. 117–192 Search PubMed.
- F. W. Maran, D. D. M. Wayner and M. S. Workentin, in Advances in Physical Organic Chemistry, ed. T. T. Tidwell, Academic Press, New York, 2001, vol. 36, pp. 85–116 Search PubMed.
- A. Neumann, H. Scholz-Muramatsu and G. Diekert, Arch. Microbiol., 1994, 162, 295–301 CrossRef CAS PubMed.
- J.-M. Savéant, J. Am. Chem. Soc., 1987, 109, 6788–6795 CrossRef.
- N. S. Hush, Electrochim. Acta, 1968, 13, 1005–1023 CrossRef CAS.
- R. A. Marcus, Electrochim. Acta, 1968, 13, 995–1004 CrossRef CAS.
- N. S. Hush, J. Chem. Phys., 1958, 28, 962–972 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- K. B. Clark and D. D. M. Wayner, J. Am. Chem. Soc., 1991, 113, 9363–9365 CrossRef CAS.
- J.-M. Savéant, J. Am. Chem. Soc., 1992, 114, 10595–10602 CrossRef.
- C. P. Andrieux, A. Le Gorande and J. M. Saveant, J. Am. Chem. Soc., 1992, 114, 6892–6904 CrossRef CAS.
- M. S. Workentin, F. Maran and D. D. M. Wayner, J. Am. Chem. Soc., 1995, 117, 2120–2121 CrossRef CAS.
- S. Antonello, M. Musumeci, D. D. M. Wayner and F. Maran, J. Am. Chem. Soc., 1997, 119, 9541–9549 CrossRef CAS.
- C. P. Andrieux, E. Differding, M. Robert and J. M. Saveant, J. Am. Chem. Soc., 1993, 115, 6592–6599 CrossRef CAS.
- A. Houmam and E. M. Hamed, Chem. Commun., 2012, 48, 11328–11330 RSC.
- M. R. Claude, P. Aodrieux, F. D. Saeva and J.-M. Savéant, J. Am. Chem. Soc., 1994, 116, 7864–7871 CrossRef.
- C. Ji, M. Ahmida, M. Chahma and A. Houmam, J. Am. Chem. Soc., 2006, 128, 15423–15431 CrossRef CAS PubMed.
- C. Ji, J. D. Goddard and A. Houmam, J. Am. Chem. Soc., 2004, 126, 8076–8077 CrossRef CAS PubMed.
- A. Houmam, E. M. Hamed, P. Hapiot, J. M. Motto and A. L. Schwan, J. Am. Chem. Soc., 2003, 125, 12676–12677 CrossRef CAS PubMed.
- A. Houmam, E. M. Hamed and I. W. Still, J. Am. Chem. Soc., 2003, 125, 7258–7265 CrossRef CAS PubMed.
- E. M. Hamed, H. Doai, C. K. McLaughlin and A. Houmam, J. Am. Chem. Soc., 2006, 128, 6595–6604 CrossRef CAS PubMed.
- R. H. B. Batanero, R. Mallmann, M. G. Quintanilla and F. Barba, Electrochim. Acta, 2002, 47, 1761–1764 CrossRef.
- M. A. D. Otero, B. Batanero and F. Barba, Tetrahedron, 2004, 60, 4609–4612 CrossRef CAS.
- A. J. Mukherjee, S. S. Zade, H. B. Singh and R. B. Sunoj, Chem. Rev., 2010, 110, 4357–4416 CrossRef CAS PubMed.
- C. W. Nogueira, G. Zeni and J. B. T. Rocha, Chem. Rev., 2004, 104, 6255–6286 CrossRef CAS PubMed.
- G. Mugesh and H. B. Singh, Chem. Soc. Rev., 2000, 29, 347–357 RSC.
- α = (RT/F)(1.85/Ep/2 − Ep).
- ∂Ep/∂log(v) = −29.5/α at 20 °C.
- F. R. Bisogno, A. Cuetos, I. Lavandera and V. Gotor, Green Chem., 2009, 11, 452–454 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. B. G. Scalmani, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. A. J. A. Yazyev, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra16154h |
| This journal is © The Royal Society of Chemistry 2015 |