Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Calculating the volume of elongated bubbles and droplets in microchannels from a top view image
Michiel
Musterd
,
Volkert
van Steijn
*,
Chris R.
Kleijn
and
Michiel T.
Kreutzer
Department of Chemical Engineering, Delft University of Technology, Julianalaan 136, 2628 BL Delft, The Netherlands. E-mail: v.vansteijn@tudelft.nl
First published on 28th January 2015
Abstract
We present a theoretical model to calculate the volume of non-wetting bubbles and droplets in segmented microflows from given dimensions of the microchannel and measured lengths of bubbles and droplets. Despite the importance of these volumes in interpreting experiments on reaction kinetics and transport phenomena, an accurate model like the one we present here did not yet exist. The model has its theoretical basis in the principle of interfacial energy minimization and is set up such that volume calculations are possible for a wide variety of channel geometries. We successfully validated our model with the 3D numerical energy minimization code SURFACE EVOLVER for the three most commonly used channel geometries in the field of microfluidics and provide accurate user-friendly equations for these geometries.
Introduction
Many microfluidics applications rely on multiphase flow, typically in the form of elongated droplets in a continuous phase.1,2 These droplets can for example be used as small reaction chambers for the synthesis of advanced materials,3–7 the growth and screening of cells,8–12 bacteria13–15 and enzymes,16 the study of mass transfer rates,17–19 and even for DNA sequencing.20 For quantitative analysis it is important to know the volume and surface area of the droplets. This, however, presents a problem as virtually all visualization is done with optical microscopes that only provide two-dimensional top-view images of the droplets, leaving their three-dimensional shape unknown.21,22 A method to accurately determine the volume based on microscope images is therefore of great use.The simplest way to estimate the volume, V, of a confined, non-wetting droplet such as the ones shown in Fig. 1 is to describe its shape as a block that has the length, L, of the droplet and the cross sectional area Ach of the channel, giving V = AchL. For a rectangular channel, with width W and height H, this gives the estimate V = HWL. Many researchers21–23 implicitly use this simple estimate when using the dimensionless length L/W as a proxy for the dimensionless volume V/HW2. A more accurate estimation takes into account the rounded caps at the front and back of the droplet and the fact that the droplet does not invade the corners of the channels. To account for the latter, the cross sectional shape of a non-wetting droplet in rectangular channels is often assumed to consist of two semi-circles with a diameter H, connected by straight lines of length W − H, thus replacing Ach by πH2/4 + H(W − H) in the estimate of the droplet volume. This approximation, however, turns out to be accurate only for shallow channels, where H ≪ W. Moreover, this still does not account for the rounded caps at the front and the back. Although other approximations are reported,18 there is currently no physically sound model to calculate the volume of droplets from two-dimensional micrographs. Additionally, while most previous work focused on channels with a rectangular cross section, no relations have been developed and systematically tested for non-rectangular microchannels like those obtained by isotropic or crystallographic etching.
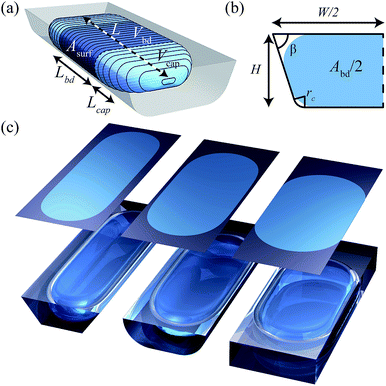
In this paper, we fill this gap by developing a theoretical model that enables the reader to accurately predict volumes of confined non-wetting droplets (contact angle of π) from measured droplet lengths and known channel dimensions. We set up the model such that this volume estimation is possible for a wide variety of channel geometries by considering the generalized channel shape shown in Fig. 1b. This shape is characterized by a channel width W, height H, top corner angle β, and rounded bottom corner with radius rc. We develop solutions of the form V = f(L, H, W, β, rc) for this generalized channel shape and work out simplified approximations for the three most commonly used microchannel geometries shown in Fig. 1c. For the reader who is mainly interested in the final result, we structured the paper such that we directly provide these simplified approximations in eqn (1), followed by full solutions in Fig. 3. After that, we present all the theoretical foundations and the numerical validation. We base our model on quasi-static droplet shapes, which is a valid approach for surface-tension dominated flows where the lubricating film around droplets is much thinner than the height and width of the channel, i.e. for sufficiently low values of the capillary number Ca ≲ 10−3. Readers interested in flows at higher Ca can use the simple extension of our model presented in the discussion section.
The results of this study provide a valuable tool to precisely quantify the volume of droplets from top-view images. This is for example useful to further improve our understanding of the physics of droplet flows, because physical models are often based on volumetric quantities such as flow rates and volumes. From an application point of view, our model enables the precise monitoring of chemical and biotechnological processes in segmented microflows. Mass transfer rates in liquid–liquid extractions and gas–liquid dissolution experiments benefit for example from an accurate method to determine droplet or bubble volumes and surface areas. This information is also important for the design of non-spherical particles for delivery purposes. Also in the field of biotechnology, where the growth of microorganisms inside droplets is tracked by counting the microorganisms in top-view images, accurate knowledge on the volume of the droplets enables the precise calculation of the cell concentration. Lastly, we think that volume calculations from simple length measurements might be useful for point-of-care devices, where it is not possible to integrate expensive measurement techniques like confocal microscopy and absorbance imaging24 or include a collection chamber on the chip where droplets can relax to a sphere such that their volume is easily obtained from the measured diameter.
Summary of the main results
Approximate solutions for common channel geometries, V = f(L, H, W)
As explained later, a good and simple calculation of the droplet volume is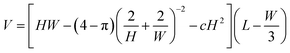 | (1) |
For the three geometries in Fig. 1c, we determined the constant c by fitting eqn (1) over the full range of channel aspect ratios and droplet lengths studied in this work (0.1 ≤ H/W ≤ 1 and 2 ≤ L/W ≤ 9) against droplet volumes calculated with the 3D surface energy minimization of SURFACE EVOLVER.26 We find c = 0.77, c = 0.41, and c = 0, respectively. For droplet lengths L ≥ 3W, volumes calculated by eqn (1) are at least within 5% of the volumes calculated by SURFACE EVOLVER as shown in Fig. 2, and the error is up to an order of magnitude smaller than the error for the simple V = AchL approximation. More accurate solutions and solutions for the generalized channel geometry in Fig. 1b, i.e. for other values of β or rc, are given below.
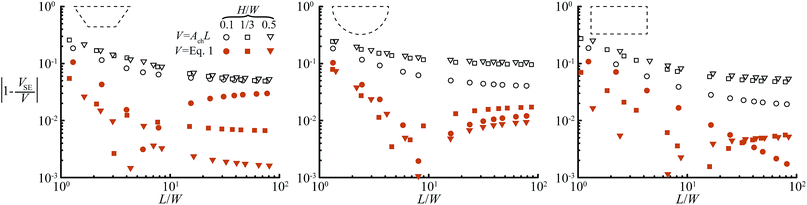 | ||
| Fig. 2 Comparison of the exact droplet volume VSE calculated with SURFACE EVOLVER, with V from eqn (1) (closed symbols) and V from the simple estimate V = AchL (open symbols). The proposed approximation, eqn (1), yields a volume estimate that is at least within 10% of the exact droplet volumes, which is up to 1 order of magnitude better than the simple estimate V = AchL. The minimum in some of the curves of eqn (1) originates from the overestimation of the cap volume and the underestimation of the body volume. The contribution of the body increases with L/W such that for short droplets the total error is positive and for long droplets negative and hence the minimum. | ||
Full solutions for generalized channel geometries, V = f(L, H, W, β, rc)
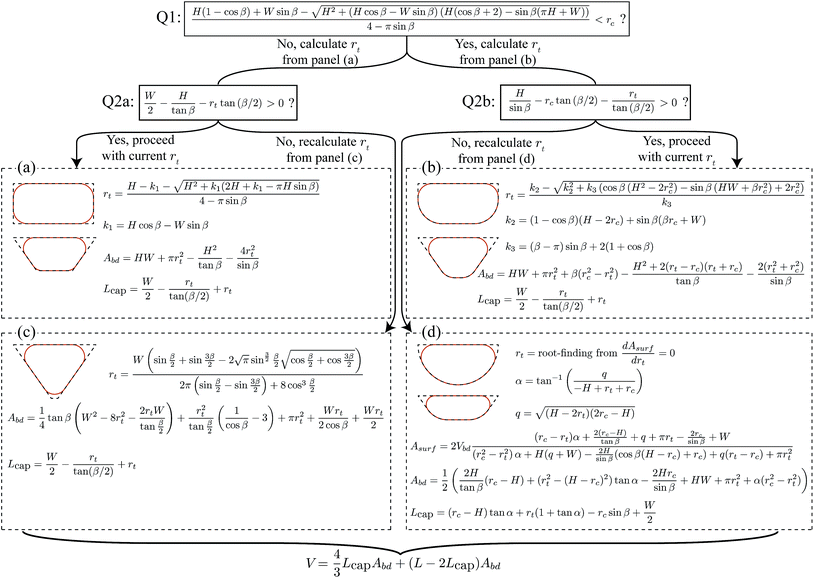
The recipe to calculate droplet volumes from measured droplet lengths and known channel geometries is given in Fig. 3. Depending on the channel geometry, different cross sectional shapes are possible, resulting in different expressions for the droplet volume. The different shapes can be classified based on two questions: (Q1) “does the interface conform to the bottom corners of the channel?” If the answer is “no”, the interface is flattened at the side walls and the remaining question is (Q2a) “is the interface also flattened at the bottom wall?” Yet, if the answer to Q1 is “yes”, the interface is flattened at the bottom wall and the remaining question is (Q2b) “is the interface also flattened at the side walls?” This classification hence leaves four possible interface shapes shown in Fig. 5, with the corresponding expressions for the volume calculation in the four panels of Fig. 3. Selecting which of the panels to use hence starts with answering two questions. Using the corresponding criteria at the top of Fig. 3, this is simply done by filling in the known channel dimensions. Consider for example a channel with a rectangular cross section with straight corners. Then the answer to the first question is “no”, because rc = 0 while the term on the left is always larger than zero. In fact, this term is the radius of curvature, rb, of the interface in the bottom corners of the channel for an unconformed interface. Subsequently calculating the radius of curvature, rt, of the interface in the top corners of the channel, it is straightforward to show that for rectangular channels the answer to Q2a is “yes” irrespective of the values of H and W. This makes sense, because non-wetting droplets in rectangular channels with straight corners do no fill the corners and the curved parts of the interface in the corners are separated by thin flat films on the walls.27 Hence, the expressions in panel (a) should be used to calculate the droplet volume. Importantly, this panel is not exclusive to rectangular channels with straight corners. It, for example, also applies to trapezoidal channels that are sufficiently wide such that the curved corners are separated by flat films. Note that the shapes shown in the other panels are only a few examples of the possible shapes belonging to these panels. Hence, it is recommended to use the two criteria as a guide to select the appropriate panel for the volume calculation.Model validation
We validate our theoretical model with the 3D numerical energy minimization code SURFACE EVOLVER.26 We illustrate the accuracy for the three most commonly used channel geometries shown in Fig. 1c for a wide range of channel aspect ratios (0.1 ≤ H/W ≤ 1) and droplet lengths (2 ≤ L/W ≤ 9). For this entire range, droplet volumes predicted by theory and found in simulations agree within 5% as shown in Fig. 4. The largest deviation is found for shallow channels and short droplets, i.e. H/W = 0.1 and L/W = 2, whereas the difference reduces with larger aspect ratios and droplet lengths to as little as 0.5% for H/W ≥ 0.5 and L/W ≥ 6.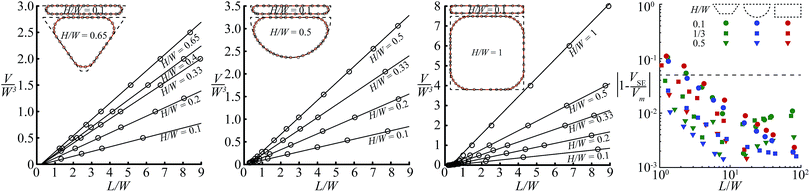 | ||
| Fig. 4 Validation of the theoretical model in Fig. 3 was done by comparing the results from the model (lines) with simulations performed with SURFACE EVOLVER (circles) for the three most commonly used channel geometries. The graphs show the non-dimensional droplet volume V/W3 as a function of the non-dimensional droplet length L/W for a wide range of channel aspect ratios, with some cross-sectional shapes calculated by the model (lines) and SURFACE EVOLVER (circles) in the insets. The direct comparison of the error shown on the right shows that our model agrees with the simulations within 5% (indicated by dashed line) for droplets of length L ≥ 3W, with a reduction in error for larger droplets. | ||
Uncertainty in calculated droplet volume due to experimental inaccuracies
In this section, we briefly explain how to calculate the uncertainty in droplet volume, u(V), for a known uncertainty in the droplet length u(L) and known uncertainties, u(W), u(H), u(β), u(rc), in channel dimensions. Assuming that these uncertainties are independent we can write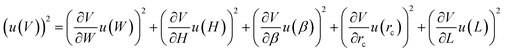 | (2) |
Applying eqn (2) to the desired equation panel in Fig. 3 it is then straightforward to calculate the uncertainty in V from fabrication tolerances and expected errors in droplet length.
To illustrate the use of eqn (2) we work out a typical case for a rectangular microchannel with straight corners with H = 50 ± 2 μm and W = 100 ± 2 μm and a droplet with L = 500 ± 10 μm, i.e. relative errors of 4%, 2%, and 2%. Working out the derivatives of V with respect to W, H, and L (not shown) and filling in the numbers we find V = 2.21 ± 0.11 nL or a relative error of 4.9%.
Full model
Our model describes the shape of quasi-statically moving droplets that do not wet the channel walls. This quasi-static approach is valid for droplets moving at speeds that are sufficiently low to neglect droplet deformations due to viscous and inertial forces. The dimensionless numbers expressing these contributions relative to surface tension are the capillary number, Ca, and the Weber number, We = ReCa, with Re the Reynolds number. For most microfluidic applications, Ca, Re, and hence We are small such that the quasi-static approach is valid. More quantitatively, the calculations of Bretherton28 showed that deformations due to viscous forces are negligible for Ca = μu/γ < 5 × 10−3, with μ the viscosity of the carrier fluid, u the speed of the droplet, and γ the interfacial tension. More recently, Kreutzer et al.29 showed numerically that this boundary can be put somewhat higher at Ca < 10−2. Additionally, Bretherton28 stated that inertial effects can be neglected for We = ρu2W/γ < 1, with ρ the density of the carrier fluid. The droplet shapes calculated in Kreutzer et al.29 confirm that at We ∼ 1, the length of a droplet is appreciably different from the value at We → 0. As Re and Ca are both small in microfluidic flows, the condition We < 1 is met for most applications.Besides droplet deformations due to viscous and inertial forces, we also ignore deformations due to gravity. This is justified, as gravity is generally small compared to surface tension. More quantitatively, the ratio of these forces captured by the Bond number, Bo = ΔρH2g/γ, is typically much smaller than 0.1, where Δρ is the density difference between the fluids and g is the gravitational acceleration.
Under the conditions that (i) surface tension forces are much larger than viscous, inertial, and gravitational forces, and (ii) droplets are surrounded by a thin lubricating film such that there is no direct contact between the droplets and the walls (often achieved by the use of surfactants or surface treatment of the walls), droplets confined by the walls of a channel take the shape for which the surface energy, i.e. surface area, is minimum. This explains why the shape only depends on the channel geometry and droplet volume, and not on fluid parameters. Although we use the word “droplet” throughout this paper, our work hence is equally valid for gas bubbles.
We now derive a relation between the volume and length of a droplet by describing the shape of a droplet with two curved caps connected by a body that is confined by the channel walls as illustrated in Fig. 1a. We first determine the volume of the body based on energy minimization and then propose a description of the caps.
Volume of the body
Considering the droplet shown in Fig. 1a, we define its body as the part that has sides of length Lbd parallel to the channel walls. Along this length, the cross sectional droplet shape is constant and can be described by one of the four possible shapes shown in Fig. 5. Comparing the shapes in (a and c) with those in (b and d), the important difference is the conformation of the interface to the bottom corner of the channel. The shapes in Fig. 5b and d do conform such that the radius of the interface at the bottom equals the radius of the rounded corner, i.e. rb = rc. This leaves the radius at the top, rt, as the only unknown in the description of the cross-sectional droplet shape. By contrast, the bottom interface in Fig. 5a and c does not take the shape of the channel. Because the interface is now free at both the top and the bottom, the curvatures are equal,27i.e. rb = rt. For all four cases, rt is thus the only unknown.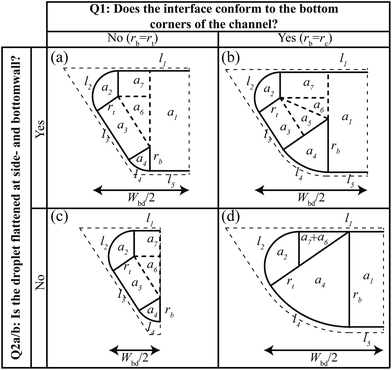 | ||
| Fig. 5 Geometric description of the four possible droplet shapes inside the generalized channel geometry considered in this work. These shapes can be categorized based on the two questions shown at the top and side. All shapes are fully characterized once the radius of curvature at the top, rt, is known, which is found through energy minimization. The resulting expression can be found in the corresponding panels (a)–(d) in Fig. 3. Note that we only present the left side of the channels for display purposes. | ||
The general approach to find the cross-sectional shape, i.e. rt, is to minimize the surface area of the entire body, Asurf, for a fixed body volume, Vbd = AbdLbd, with Abd the cross-sectional area
| Abd = 2∑ai | (3) |
The surface area of the body, Asurf, simply equals the circumference of the cross section, lbd = 2∑li, times the length of the body, i.e. Asurf = 2Lbd∑li. Using elementary geometry, it is straightforward to find expressions for the lengths li and the areas ai for the four cases in Fig. 5. These can be subsequently used to find expressions for Abd, Vbd, and Asurf, which only depend on the unknown radius rt. This radius is found by minimizing the area Asurf for given Vbd, such that the cross-sectional shape is known.
We now illustrate this general approach for the cross-sectional shape shown in Fig. 5a. Using geometry to express the lengths, li, and the areas, ai, in terms of the radii rt and rb and the channel dimensions W, H, β, and rc, we find
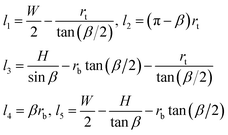 | (4) |
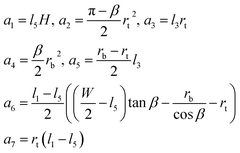 | (5) |
Using rb = rt for the case in Fig. 5a, we hence find the following expressions for the surface area
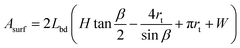 | (6) |
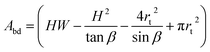 | (7) |
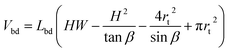 | (8) |
This volume should remain constant when we minimize the surface area. This is simply done by substituting Vbd into Asurf through Lbd, resulting in
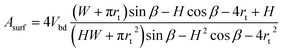 | (9) |
Now minimizing Asurf with respect to the only unknown rt, dAsurf/drt = 0, we find an expression for the radius rt in terms of all known channel dimensions
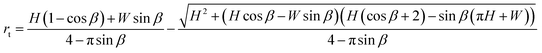 | (10) |
For a rectangular channel, β = 90°, eqn (10) reduces to
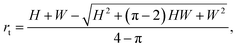 | (11) |
For the other three cases shown in Fig. 5b–d, the analysis is similar. In short, one uses rb = rc instead of rb = rt to obtain the resulting expressions for the case in Fig. 5b, while l5 = 0 should be used in eqn (4) and (5) for the case in Fig. 5c. The case in Fig. 5d needs special attention. For the special case with rc = H shown in Fig. 5d, resulting expressions for rt and Abd are found using rb = rc and l3 = 0. However, for the more generic case where rc ≠ H, finding the root of rt cannot be done analytically and should be done using root finding. For all four cases, the resulting expressions for rt and Abd are summarized in Fig. 3.
Volume of the caps
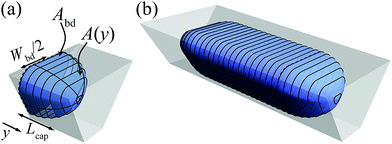
Calculating the shape and volume of the caps could in principle be done using the same energy minimization approach. It, however, involves solving the highly non-linear Young–Laplace equation in 3D, such that it is not possible to obtain an analytical expression for the generalized case. We therefore use a much simpler, but accurate method to reconstruct the shape of the caps. Although this description of the droplet caps is not exact, it is a fair estimate as evidenced by the good match of the droplet volume prediction and the SURFACE EVOLVER simulation shown in Fig. 4. This reconstruction is illustrated in Fig. 6a. We require that the cross-section of the droplet cap continuously and smoothly connects to the body at y = 0 and monotonically decreases to A(y) = 0 at y = Lcap. Additionally, we require A(y) to reproduce a hemispherical cap when viewed from top or bottom, as is commonly found in experiments. The function A(y) = Abd(1 − y2/Lcap2) is the only choice that allows this condition and the other ones. It may be noted that this description results in a shape that looks elliptical from whatever angle the cap is viewed in a 2D projection, thus closely approximating the physically realistic shape as shown in Fig. 6b. The volume of the cap can then simply be calculated as the integral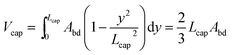 | (12) |
We hereby assume that the length of the cap equals half of the body of the droplet, Wbd/2, thus matching the requirement of a hemispherical cap when viewed from top or bottom. As illustrated for the four shapes in Fig. 5, this width is simply defined as the distance of the side of the droplet to the centerline such that
| Lcap = Wbd/2 = l1 + rt. | (13) |
With l1 and rt determined in the previous section, the cap length can be determined and the resulting expressions are summarized in Fig. 3.
Total droplet volume
The total droplet volume is just the sum of the body volume and the volume of the caps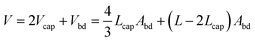 | (14) |
Approximate solutions
Returning to the approximation of the droplet volume postulated in eqn (1), we can now show the origin of this approximation. Substituting the approximation Lcap = W/2 in eqn (14) we obtain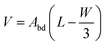 | (15) |
Considering a rectangular channel, the cross sectional area equals Abd = HW − (4 − π)rt2. The unknown radius of curvature, rt, can be found by matching the curvature, 1/rt, of the interface near the corners to the curvature at the front of the droplet, which approximately equals 2/H + 2/W. Using rt ≈ (2/H + 2/W)−1 we find
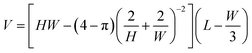 | (16) |
The trapezoidal and round corner channels are clearly far from rectangular such that a correction term is needed. We observe that a simple quadratic correction term, −cH2, for the channel height is sufficient, while higher order terms in W and L do not change the approximation significantly and were left out to keep the approximation as simple as possible. This yields the volume approximation of eqn (1).
Discussion
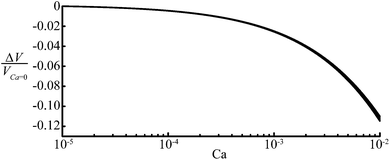
We now address the validity and implications of two important assumptions used in our model. The first assumption is that the droplet is sufficiently long such that it has a straight body. We observed in SURFACE EVOLVER simulations that this assumption breaks down for droplets shorter than L < 2W. Despite this fact, our model is accurate within 12% for droplets with a length W < L < 2W. Shorter droplets either take the shape of a pancake or a sphere, such that their volume is easily calculated using V = πHL2/4 or V = πL3/6 respectively.The second assumption is that the lubricating film around non-wetting droplets is negligibly thin, which is valid for static and slowly moving droplets.30 However, for faster moving droplets the thickness of the lubricating film, δ, should be accounted for. Wong et al.31 showed that this thickness is a complex function of the distance to the droplet caps and channel walls, but on average can be estimated as δ/2W = 0.643rt/W(3Ca)2/3. The assumption in our model that the droplet is separated by an infinitely thin film can be easily modified to take this finite thickness, δ, into account: instead of using H and W, one should use W − 2δ and H − 2δ in the recipe of Fig. 3. Although the right hand side of the expression for rt now depends on rt itself, its value is simply found by solving the equation iteratively. We note that using rt for a zero film thickness to calculate δ without subsequently recalculating rt (valid for small values of Ca for which δ ≪ rt)32 results in a maximum deviation of 2% in the prediction of the volume, which might be sufficiently accurate for some applications. We illustrate the influence of the finite film thickness for rectangular channels with straight corners in Fig. 7. For a measured droplet length of L = 5W, the graph shows the relative difference between the volume of a moving droplet and a static droplet. For the example considered here, the film thickness can be safely neglected for Ca < 10−3, because the 2.5% difference likely falls within experimental error. For relatively large values of Ca, the difference increases to a maximum of 12% for Ca = 10−2. For Ca > 10−3, the film thickness should hence be taken into account as proposed.
Concluding remarks
We have developed a theoretical model to compute the volume of non-wetting bubbles and droplets in a microchannel based on the principle of interfacial energy minimization. The only input to the model is the geometry of the microchannel and the length of the droplet, which can be determined easily from top- or bottom view micrographs. Our model has been validated by comparison with three-dimensional energy minimization calculations using SURFACE EVOLVER. We have illustrated the good agreement between theory and calculations for three most commonly used channel geometries in the field of microfluidics: a rectangular channel, an isotropically etched channel, and a crystallographically etched channel. We expect that the simple theoretical model will be useful for the droplet microfluidics community and aids quantitative analysis and design of droplet microflows.Acknowledgements
We thank Bernhard Righolt for insightful discussions on the geometric calculations. This research was carried out within the framework of the ISPT project HESTRE.References
- S.-Y. Teh, R. Lin, L.-H. Hung and A. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- C. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045 RSC.
- V. Sebastian Cabeza, S. Kuhn, A. A. Kulkarni and K. F. Jensen, Langmuir, 2012, 28, 7007–7013 CrossRef CAS PubMed.
- M. T. Rahman, P. G. Krishnamurthy, P. Parthiban, A. Jain, C. P. Park, D.-P. Kim and S. A. Khan, RSC Adv., 2013, 3, 2897–2900 RSC.
- I. Lignos, L. Protesescu, S. Stavrakis, L. Piveteau, M. J. Speirs, M. A. Loi, M. V. Kovalenko and A. J. deMello, Chem. Mater., 2014, 26, 2975–2982 CrossRef CAS.
- T. Nisisako and T. Torii, Adv. Mater., 2007, 19, 1489–1493 CrossRef CAS PubMed.
- D. Dendukuri, K. Tsoi, T. A. Hatton and P. S. Doyle, Langmuir, 2005, 21, 2113–2116 CrossRef CAS PubMed.
- R. R. Pompano, W. Liu, W. Du and R. F. Ismagilov, Annu. Rev. Anal. Chem., 2011, 4, 59–81 CrossRef CAS PubMed.
- A. Theberge, F. Courtois, Y. Schaerli, M. Fischlechner, C. Abell, F. Hollfelder and W. Huck, Angew. Chem., 2010, 49, 5846–5868 CrossRef CAS PubMed.
- J. J. Agresti, E. Antipov, A. R. Abate, K. Ahn, A. C. Rowat, J.-C. Baret, M. Marquez, A. M. Klibanov, A. D. Griffiths and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 4004–4009 CrossRef CAS PubMed.
- M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146–2155 RSC.
- B. L. Wang, A. Ghaderi, H. Zhou, J. Agresti, D. A. Weitz, G. R. Fink and G. Stephanopoulos, Nat. Biotechnol., 2014, 32, 473–478 CrossRef CAS PubMed.
- S. Jakiela, T. S. Kaminski, O. Cybulski, D. B. Weibel and P. Garstecki, Angew. Chem., 2013, 125, 9076–9079 CrossRef PubMed.
- K. Leung, H. Zahn, T. Leaver, K. M. Konwar, N. W. Hanson, A. P. Pagé, C.-C. Lo, P. S. Chain, S. J. Hallam and C. L. Hansen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7665–7670 CrossRef CAS PubMed.
- J. Cao, D. Kürsten, K. Krause, E. Kothe, K. Martin, M. Roth and J. Köhler, Appl. Microbiol. Biotechnol., 2013, 97, 8923–8930 CrossRef CAS PubMed.
- R. Arayanarakool, L. Shui, S. W. M. Kengen, A. van den Berg and J. C. T. Eijkel, Lab Chip, 2013, 13, 1955–1962 RSC.
- S. G. R. Lefortier, P. J. Hamersma, A. Bardow and M. T. Kreutzer, Lab Chip, 2012, 12, 3387–3391 RSC.
- M. Sauzade and T. Cubaud, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 051001 CrossRef.
- P. Mary, V. Studer and P. Tabeling, Anal. Chem., 2008, 80, 2680–2687 CrossRef CAS PubMed.
- A. R. Abate, T. Hung, R. A. Sperling, P. Mary, A. Rotem, J. J. Agresti, M. A. Weiner and D. A. Weitz, Lab Chip, 2013, 13, 4864–4869 RSC.
- T. Cubaud, M. Sauzade and R. Sun, Biomicrofluidics, 2012, 6, 022002 CrossRef PubMed.
- P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446 RSC.
- M. Abolhasani, M. Singh, E. Kumacheva and A. Gunther, Lab Chip, 2012, 12, 4787–4795 RSC.
- D. Malsch, M. Kielpinski, N. Gleichmann, G. Mayer and T. Henkel, Exp. Fluids, 2014, 55, 1841 CrossRef PubMed.
- P. Abgrall and A.-M. Gué, J. Micromech. Microeng., 2007, 17, R15 CrossRef.
- K. A. Brakke, Exp. Math., 1992, 1, 141–165 CrossRef PubMed.
- H. Wong, S. Morris and C. Radke, J. Colloid Interface Sci., 1992, 148, 317–336 CrossRef CAS.
- F. P. Bretherton, J. Fluid Mech., 1961, 10, 166–188 CrossRef.
- M. T. Kreutzer, F. Kapteijn, J. A. Moulijn, C. R. Kleijn and J. J. Heiszwolf, AIChE J., 2005, 51, 2428–2440 CrossRef CAS PubMed.
- V. S. Ajaev and G. Homsy, Annu. Rev. Fluid Mech., 2006, 38, 277–307 CrossRef.
- H. Wong, C. J. Radke and S. Morris, J. Fluid Mech., 1995, 292, 71–94 CrossRef.
- P. Aussillous and D. Quéré, Phys. Fluids, 2000, 12, 2367–2371 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2015 |