Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational approaches to understanding reaction outcomes of organic processes in ionic liquids
Sinead T. Keaveneya,
Jason B. Harper*a and
Anna K. Croft*b
aSchool of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: j.harper@unsw.edu.au
bDepartment of Chemical and Environmental Engineering, University of Nottingham, University Park, Nottingham, NG7 2RD, UK. E-mail: anna.croft@nottingham.ac.uk
First published on 26th March 2015
Abstract
This review considers how various computational methods have been applied to explain the changes in reaction outcome on moving from a molecular to an ionic liquid solvent. Initially, different conceptual approaches to modelling ionic liquids are discussed, followed by a consideration of the limitations and constraints of these approaches. A series of case studies demonstrating the utility of computational approaches to explain processes in ionic liquids are considered; some of these address the solubility of species in ionic liquids while others examine classes of reaction where the outcome in ionic liquids can be explained through the application of computational approaches. Overall, the utility of computational methods to explain, and potentially predict, the effect of ionic liquids on reaction outcome is demonstrated.
Introduction
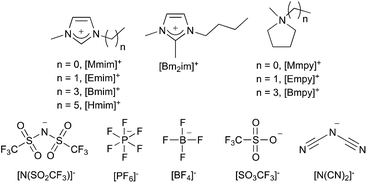
Ionic liquids are defined as salts that are molten below 100 °C;1 the lower melting points of these liquids arise from the bulky, charge diffuse nature of their ions, most commonly the cation.2 Ionic liquids can be composed of many different cations and anions; the ions that make up the ionic liquids discussed in this review are shown in Fig. 1 (including the abbreviations that will be used throughout). These are representative of the types of ions commonly found in these solvents; pyridinium, tetraalkylammonium and tetralkylphosphonium ions are also common.Ionic liquids have many properties that make them attractive alternatives to traditional solvents; negligible vapour pressure3–5 and low flammability,5,6 as well as the prospect of recycling,7 can make them a safer and more environmentally-friendly option than volatile organic compounds. Their tuneable nature and ability to generate reaction outcomes different from those seen in traditional solvents is another factor driving interest in the use of ionic liquids as solvents for organic reactions.2,8–29 For such a replacement to be viable, their effect on reaction outcome needs to be understood and readily predicted, as the limited understanding of ionic liquid solvent effects is hindering further applications.30,31
The focus of this review is to introduce computational simulation techniques, and their underpinning methodologies, that have been able to provide valuable information in understanding the effects of ionic liquids on organic reaction outcomes, particularly when utilised in the context of experimental data. Computational methodologies have been used extensively in recent times to complement experimental studies in the ionic liquid area with a great deal of success. Although there have been a relatively limited number of studies that combine both experimental and computational techniques to understand the effect of ionic liquids on reaction outcome, there are a wealth of studies that have considered basic properties of the ionic liquids themselves, providing important physicochemical data. Due to the size of this emergent field, these underpinning studies will not be covered in this focussed review, except where they are directly related to organic reactions. Such studies include: investigating the existence of ‘nano-domains’ where the polar and non-polar moieties in the ionic liquid group together;32–36 the use of mixtures of different ionic liquids;37–40 the effect of using different chain lengths on the (imidazolium) cation of an ionic liquid;41–45 as well as the use of di-cations.46–48
A number of reviews have been published in recent years addressing both the technical aspects of computational approaches used in ionic liquid modelling,49–52 and the experimental work relating to chemical reaction mechanisms.53 A related review, focussing on the wider issue of chemical reactivity in, and of, ionic liquids, assessed by computational methods, has recently appeared.54 This review covers applications where the ionic liquid takes part directly in the reaction, often due to the acidic or basic nature of the solvent components. A representative example is the involvement of chloroaluminate ionic liquids, where the anion acts in a dual role as both part of the solvent and as a reagent.2,55,56 The applications discussed in the current review will consider reactions where the ionic liquid is acting as a solvent, rather than where the ionic liquid takes part in the reaction. There will be a particular focus on the utility of using a combined experimental and computational approach, when trying to delineate what effect the various interactions within ionic liquid mixtures have on reaction outcomes.
The major computational approaches and associated challenges
In addition to the standard computational considerations for molecular solvents, such as dispersion, π-stacking interactions, accurate reproduction of specific hydrogen-bonding interactions, and other polar interactions, when modelling ionic liquids, strong Coulombic forces also play a dominant role.57–59 Another challenge is that individual components will often have very different electronic distributions, which further adds to the complexity of the interactions present, as well as introducing the possibility of selective aggregation of like components.33,60–64 Overall, it is very difficult to accurately describe the subtle balance of these interactions. This is further complicated by the nature of computational chemistry, for which assumptions need to be made in any molecular description. The extent of the assumptions made is dependent on the theoretical approach taken, as is the ‘computational cost’ of the method; that is, the amount of time and the computing resources required. As such, when modelling an ionic liquid the limitations of the available approaches must be matched with the information required from the simulation to arrive at the optimal technique.When using computational techniques, there are three major conceptual approaches to treating a molecular system; these are depicted in Fig. 2. The first is the use of electronic structure methods, which try to capture the most detailed view of a molecular system, short of solving the Schrödinger equation. Ab initio and semi-empirical calculations are highly accurate and reliable, as they are derived directly from quantum-mechanical principles; the energy is calculated from a wavefunction obtained using approximations of varying quality. As a result of this, there is generally a high computational cost associated with these methods and the simulations are restricted to smaller systems. Density functional theory (DFT), for which the underlying functionals can be either ‘pure’ or rely on parameterisation (i.e. are semi-empirical), is a good compromise between efficiency and accuracy for modelling ionic liquid systems. The energy is now expressed in terms of total electron density and this approach is less computationally demanding than traditional, good-quality ab initio methods of similar accuracy. This allows much larger systems to be handled with reasonable computation times. This is particularly relevant when modelling ionic liquids as it allows multiple ion pairs to be modelled; ionic liquids have a complex mixture of short and long range interactions that can only be accurately captured through models incorporating multiple ion pairs.40,65,66 One of the main limitations of standard DFT methods is the lack of accuracy in describing dispersive interactions, the inclusion of which has been shown to be important for ionic liquid systems,49,67–69 and techniques that circumvent this problem include dispersion-corrected DFT (DFT-D) functionals.
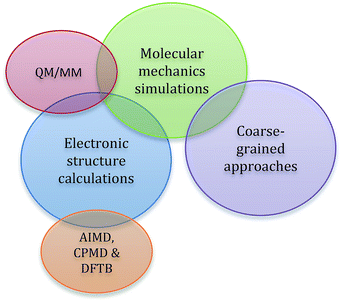 | ||
| Fig. 2 A representation of the three major conceptual approaches to computational chemistry used with ionic liquids, along with subsets of these methods. | ||
In general, ab initio and DFT methods are used on static systems, but with recent advances in computing power, dynamic approaches have been emerging. These ab initio molecular dynamics (AIMD) approaches include the popular Car–Parinello Molecular Dynamics (CPMD) methods. Currently such studies are limited by the size of the system that can be handled due to the quantity of computational power required, but provide a wealth of information not captured by static systems.70–76
Significant reductions in computational time relative to AIMD, whilst retaining DFT-level accuracy, can be achieved with Density Functional Tight Binding (DFTB) calculations,77–79 with this approach being recently pioneered for ionic liquid systems.80–83 Here, some parameterisation of the integrals is used to speed up the calculations, and dispersion corrections in the DFTB3 method help to describe long-range interactions with some accuracy. More importantly, this approach scales well for larger systems, so is able to handle a larger number of ion pairs for accurate calculations (see below). This is an emerging methodology that will no doubt be extremely useful when applied to reactive systems that include ionic liquid solvents.
The second conceptual approach is to use classical, atomistic molecular dynamics (MD) simulations, that rely on molecular mechanics (MM) treatments; this approach is valuable in visualising and interpreting the interactions that exist between both the ions of an ionic liquid and any dissolved solutes, and between the ions themselves.50,84 The MM treatment considers whole atoms, rather than the electrons, as discrete units, so is able to reduce computational time significantly at the cost of accuracy for systems where electronic interactions are less important.84 The electronic properties of each atom are represented through a force field that characterises charges, interactions, bonds, angle bending and dihedral rotation using a series of parameters. The main factor that determines the accuracy of a molecular dynamics simulation is the quality of the force field that is used. There are currently a relatively limited number of force fields available that adequately describe all the physical and chemical properties of a wide range of ionic liquids,85–89 with many being specific for the ionic liquid (or class of ionic liquids) they are parametrised for (see Table 8 below).
To gain the best of both worlds and utilise both of the above conceptual frameworks, the hybrid approach of Quantum Mechanics/Molecular Mechanics (QM/MM) can be used to describe the core reactive centres using electronic structure (ab initio, DFT) approaches, with the impact of the ionic liquid environment described using molecular-mechanics based force fields.90,91 An alternative approach is to use ReaxFF (reactive force field), which has an accuracy similar to semi-empirical calculations. Here, a specifically parameterised force field is used with a bond order approach, allowing bond-breaking and bond-making to be simulated.92 This methodology has been utilised in the ionic liquid field for examining carbon dioxide absorption,93 and may have future applicability for reactions in ionic liquids.
Coarse-grained approaches form the third conceptual model. These are variations of classical molecular dynamics simulations, where atoms are grouped together into ‘beads’ or ‘grains’.94 These beads are typically parameterised from atomistic MD simulations, with the concomitant loss of chemical resolution, but greatly improved calculation times. This methodology has not yet been utilised for organic reactions in ionic liquids (and thus will not be described further in this review), but has been successfully applied to ionic liquids themeselves95,96 and in areas such as biomass dissolution, where very large molecular systems need to be considered.97,98 Based on work in the biomolecular simulation field,99 coarse-grained methods show significant promise for future applications in multiscale systems, where they can be combined with atomistic models to look at reactions on large systems and for the long time-scales that are required for proper treatment of slowly-diffusing ionic liquids.
Methodological limitations and considerations
Currently there is a strong focus on developing accurate and reliable computational techniques that can precisely model the static and transport properties of ionic liquids. Work in this area often involves complex parameterisation for each ion combination used, and is very computationally demanding. Other areas are focused on the development of force fields for use in classical (non-polarisable) molecular dynamics, with an emphasis on transferability and efficiency, at the expense of accuracy.85 Whilst these methods may not be able to reproduce the exact transport properties of specific ionic liquids, they can still be very useful for gaining a basic understanding of what is happening at the molecular level, and can provide the rationalisation needed to complement experimental work. It is arguable whether computationally intensive and exact simulations are always necessary, and the different computational approaches discussed can be useful for certain applications, as long as the limitations of the technique are taken into account.Ab initio and DFT studies
The primary limitation of ab initio and DFT studies is that they are computationally ‘expensive’ for systems of more than a few atoms; that is, they require substantial amounts of computer time because they generate a detailed electronic description of the system under study. As such, the primary motivation when using these methods is on delineating which specific interactions play a governing role in determining ionic liquid properties and in influencing reactivity. This information can also be fed forward into improving force field parameters. An example interaction that requires electronic detail is hydrogen bonding, which is known to be heavily involved in directing a number of reactions and solvent properties.23,100–103 Such interactions require a full quantum mechanical treatment, as the nuances behind them are not always fully captured in molecular dynamics force fields.68,102,104An interesting method that has emerged in recent years is DFTB.78,79 While there will be a decrease in the accuracy of the calculations relative to ab initio methods, due to the greatly improved calculation times it is possible to perform calculations on multiple ion pairs. In a recent study investigating protic ionic liquids using DFTB systems containing up to 20 ion pairs were able to be modelled.80 Another study was able to model clusters of imidazolium nitrate ionic liquids containing up to 15 ion pairs using DFTB, and found that the structure and stability of the ionic liquids could be accurately modelled using this technique.83
One further approach to reducing the complexity of including a number of ion pairs is to utilise a continuum method (sometimes referred to as implicit solvent method) to mimic the bulk phase. This is driven by a static dielectric parameter, and leaves a minimum number of molecules to be fully calculated. Such continuum models provide a computationally cheap way to rapidly screen systems by providing the bulk of the forces to be experienced by the molecules of interest, but do not allow for specific interactions to be modelled beyond those explicitly described. For some systems, however, this approach will be adequate to qualitatively assess the impact of the ionic liquid on reaction barriers and energies.52,54 Particularly notable is the proprietary COSMO-RS model, which has been simplified and parameterised to be numerically more efficient than standard polarisable continuum models and has proven popular in the ionic liquid field. However, it has not been extensively used for reaction mechanism studies, with only a few examples highlighted in the literature.107,108 Use of this model has, however, highlighted the difference in charge transfer experienced by ions, relative to non-application of a continuum,109 and this will have an impact on the properties and solvation of substrates, products and transition states.
In terms of polarisable continuum models, the General Ionic Liquid solvation model (SMD-GIL) has recently demonstrated that small mean unsigned errors can be achieved for solvation free energies in a range of ionic liquids.110 The utility of this approach for exploring reaction pathways in more detail has been shown for the DABCO-enhanced reaction of the [Bmim]+ cation with benzaldehyde,111 and the acid-catalysed hydrolysis of lignin using standard DFT approaches.112
Calculations of the standard molar enthalpy of formation for [Bmim][N(CN)2] also highlighted the limitations of DFT methods; the G3MP2 calculated value of 359.63 kJ mol−1 was much closer to the experimental value of (363.4 ± 2.7) kJ mol−1, when compared to the more poorly performing B3LYP/6-31+G(d,p) method, which gave a calculated value of 345.5 kJ mol−1.113 Further, another investigation found that B3LYP calculations were sufficient to calculate bond length and angles for [Bmim][Cl] that were in good agreement with X-ray data, yet calculations of the interaction energies were very dependent on the method and basis set of choice (Table 2).117
While it can be generally concluded that the use of ab initio and composite approaches is desirable, as mentioned earlier, the use of multiple ion pairs is also necessary to model the nano-scale structure of the bulk phase of ionic liquids. This leads to a trade off between accuracy and system size, as calculations of multiple ion pairs using either ab initio or DFT methods are often too computationally demanding to be practical. As discussed above, DFTB is a promising alternative that allows multiple ion pairs to be modelled relatively accurately with a lowered computational cost relative to traditional ab initio and DFT methods.
Another interesting approach is the use of DFT-D, which works by including an additional dispersive term in a standard DFT functional, so can better describe the weak interactions that are core to hydrogen bonding and π-interactions. Although this adds an overhead to calculation time, it has been shown to produce much improved results,122,123 and such functionals have been applied with some success, particularly in the ionic liquid field.122–125
Molecular dynamics simulations
MD simulations provide a balance of accuracy and system size, where interactions that do not involve electron transfer from one component to another are to be considered. Underpinning the accuracy of such simulations are (i) the parameters used to generate the system, which themselves are often now based upon ab initio and DFT calculations, and (ii) the simulation conditions used.There are two major established methodologies to predict partial atomic charges; the one-particle density matrix method and the one-particle electron density method. The one-particle density matrix approach calculates the atomic partial charge by comparing the number of electrons residing in the ground state of a neutral, free atom and the atomic population on the atom within the molecule. The most commonly used methods that are based on this scheme are the Mulliken Population Analysis (MPA),129 Löwdin Population Analysis (LPA)130 and Natural Population Analysis (NPA)131 methods. While initially these methods were very popular, they are relatively inaccurate and considered somewhat dated; most studies now use the electron density approach.132 In these schemes the atomic partial charge is calculated by deriving the electrostatic potential of the system using ab initio methods, followed by fitting of the atomic charges to reproduce this electrostatic potential. These RESP techniques are now the method of choice in the calculation of ionic liquid partial charges.127
A comprehensive study compared a number of commonly used atomic partial charge schemes and assessed their effectiveness.127 The general conclusion was that all the methods had drawbacks, but the RESP methods performed considerably better than all of the population analysis schemes. There was also a surprisingly large variation in the calculated partial charges between the different methods; for example, the partial charge on the chlorine atom in [Mmim][Cl] varied from the commonly used value of −1, to as low as −0.63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 when calculated by CPMD using the Blöchl method; chloride partial charges calculated using a variety of different methods are shown in Table 3.66,105,133–136
105 when calculated by CPMD using the Blöchl method; chloride partial charges calculated using a variety of different methods are shown in Table 3.66,105,133–136
Another study calculated the partial charges on [Bmim][Br] using RESP, Natural Bonding Orbitals (NBO) and Shared Electron Number (SEN) methods, and found that the calculated charges within the imidazolium ring were very dependent on the method used.137 For example, the charge on the nitrogen atom adjacent to the butyl chain was calculated to be three markedly different values; +0.07, −0.35 and +0.21; using three different methods. It is clear that when wanting to compare a number of ionic liquids, using the same method for the partial charge calculations will at least allow for a degree of internal consistency within the set.
Most partial charge calculations are currently done using a single ion in the gas phase, mainly due to the computational expense of modelling bulk systems; arguments for and against this approach have been published.76,119,136 Recently, the use of ionic liquid-based continuum methods has indicated that significant improvements can be obtained in the calculated charges over single ion pairs in the gas phase.109 Many studies suggest that, due to the presence of short and long range interactions, multiple ion pairs are required to accurately model both the electronic environment and the distribution of ions in ionic liquids.40,65,66,138 This necessity to use multiple ion pairs is further reinforced by calculations which have demonstrated that different conformers of an ion pair can give markedly different partial charges (Table 4); in other words, the position of the ions relative to each other affects the resultant partial charge.135,136 Clearly as the position of the ion affects the partial charge, having a number of ion pairs is best as it will allow for a more accurate average partial charge to be calculated, and the most accurate representation of the bulk liquid environment.
Another advantage of using multiple ion pairs is the charge transfer information that can be obtained from these calculations; the importance of considering extents of charge transfer between ions will be discussed further below. The detailed study mentioned above highlighted the need to use clusters of ions to represent charge transfer within the ionic liquid, but also identified issues with this approach due to insufficient charge fitting, as some atoms were being ‘buried’ within the cluster of ions.127 Despite this, the advantages that ion pair(s) confer in partial charge calculations, with respect to capture of charge transfer information, has seen calculations utilising ion pair(s) becoming more prevalent than those of a single ion.66,76,105,139–143
There are two ways in which this method has been used: (i) by applying a relatively arbitrary scaling factor to the partial charges (either calculated or directly from the force field being used) to match a set of target experimental data;144–151 and (ii) by determining the reduced charges for a particular anion-cation combination from quantum calculations of the ion pair(s).66,76,105,139–143 In the majority of these studies, the transport properties of the ionic liquid are significantly closer to experimental values when reduced charges are used. The validity of this method has been supported by a number of experimental studies, where charge transfer between ions was reported in studies using X-ray Photoelectron Spectroscopy (XPS)40,164–166 and Nuclear Magnetic Resonance (NMR) spectroscopy.166 It has generally been found that the difference in the extent of charge transfer is more marked when changing the anion, than when changing the cation.76,140 This observation highlights that when modelling a range of different ionic liquids it might be more important to consider the different charge transfer effects when varying the anion, than when the cation is varied. Overall, charge scaling is an effective way to introduce a degree of ‘polarisability’, although it is not as robust as the use of true polarisable models.167
The OPLS-AA based CL&P85,87–89,173 force field is one of the most widely used and transferable force fields for ionic liquids currently available. As many ionic liquids are based on general organic moieties, many of the repulsive, angle and bond parameters could be transferred directly from the OPLS-AA to the CL&P force field. However, given the charged nature of ionic liquids, the focus was on re-parametrisation of the partial charges and dihedral angles so that ionic liquids were more accurately described.85 This approach has been very successful, providing an adequate force field to be used for modelling a range of ionic liquids.85,87–89,173 The advantages and limitations of this framework lie in its transferability: while it can be used for multiple systems, the ‘generic’ nature of its parameters meant that a number of approximations were made, reducing its accuracy in describing specific ionic liquids.
There have been other ionic liquid force fields developed, e.g. an all atom force field based on the AMBER force field for use with imidazolium based ionic liquids,159 as well as many other force fields for use with specific ionic liquids. Table 8 lists a number of the available ionic liquid force fields (although it is not comprehensive), and includes the force field framework on which the developed force field was based, the cations and anions contained in the force field, whether it is an all atom or united atom model, whether it is polarisable or non-polarisable, and for the non-polarisable cases whether the sum of the partial charges have been scaled below unity or not.
| Force field | Basis | Cations included | Anions included | Typea | Chargesb |
|---|---|---|---|---|---|
| a Where AA = all atom, UA = united atom, non-P = non-polarisable and P = polarisable.b Indicates whether the sum of the partial charge on each ion is equal to 1 (unity), or is below 1 (scaled), either through calculation or ‘arbitrary’ scaling. | |||||
| CL&P85,87–89,173,197 | OPLS-AA | Many imidazolium, pyridinium, ammonium and phosphonium based cations | Halides, [NO3]−, [N(CN)2]−, [SO3CF3]−, phosphate, and alkylsulfate, alkylsulfonate, fluoroalkylfluorophoshate and bis(sulfonyl)imide based anions | AA, non-P | Unity |
| Acevedo et al.162 | OPLS-AA | 1-Alkyl-3-methylimidazolium and N-alkylpyridinium cations, choline | [Cl]− [NO3]−, [PF6]−, [BF4]−, [AlCl4]−, [Al2Cl7]−, [SO3CF3]−, saccarinate and acesulfamate | AA, non-P | Unity |
| LHW AA159,198 | AMBER | 1-Alkyl-3-methylimidazolium cations | [Cl]−, [BF4]− and [PF6]− | AA, non-P | Unity |
| LHW UA154 | Liu et al. AA159 | 1-Alkyl-3-methylimidazolium cations | [BF4]− and [PF6]− | UA, non-P | Unity |
| Maginn et al.199 | CHARMM | Triazolium cations | [NO3]− and [ClO4]− | AA, non-P | Unity |
| Maginn et al.200 | CHARMM | Pyridinium cations | [N(SO2CF3)2]− | AA, non-P | Unity |
| Maginn et al.201 | CHARMM | [Bmim]+ | [PF6]− | AA, non-P | Unity |
| Maginn et al.202 | CHARMM | [Emim]+ | [CH3CH2SO4]− | AA, non-P | Unity |
| Maginn et al.203 | CHARMM | Hydrazinium based cations | [NO3]− | AA, non-P | Unity |
| Ludwig et al.180 | CL&P | 1-Alkyl-3-methylimidazolium catons | [N(SO2CF3)2]− | AA, non-P | Unity |
| Ludwig et al.204 | Ludwig et al.180 | 1-Alkyl-3-methylimidazolium cations | [N(SO2CF3)2]− | UA, non-P | Unity |
| Soares et al.205 | GROMOS | [Bmim]+ | [NO3]− and [PF6]− | UA, non-P | Unity |
| Stassen et al.206 | AMBER | [Emim]+ | [AlCl4]− | AA, non-P | Unity |
| Stassen et al.158 | AMBER | [Bmim]+ | [AlCl4]− and [BF4]− | AA, non-P | Unity |
| Zhang et al.207 | AMBER | 1,1,3,3-Tetramethylguanidium | Formate, lactate, [ClO4]−, [SO3CF3]−, [CF3COO]− | AA, non-P | Unity |
| Zhang et al.179 | AMBER | Cyclic guanidium based cations | [NO3]− | AA, non-P | Unity |
| Zhang et al.208 | AMBER | Guanidium cations | [Cl]−, [BF4]− and [PF6]− | AA, non-P | Unity |
| Zhang et al.209 | AMBER | Guanidium cations | [NO3]− and [ClO4]− | UA, non-P | Unity |
| Zhang et al.210 | AMBER | Tetrabutylphosphonium | Amino acids | AA, non-P | Unity |
| Zhang et al.211 | AMBER | Phosphonium cations | [N(SO2CF3)2]− | AA, non-P | Unity |
| Zhang et al.212 | AMBER | 1-Allyl-3-methylimidazolium | [Cl]− | AA, non-P | Unity |
| Youngs et al.213 | OPLS-AA | [Mmim]+ | [Cl]− | AA, non-P | Unity |
| Li et al.214 | OPLS-AA | 1,1,3,3-Tetramethylguanidium | Lactate | AA, non-P | Unity |
| Voth et al.215 | AMBER | [Emim]+ | [NO3]− | AA, non-P | Unity |
| Voth et al.94 | Yan et al.175 | 1-Alkyl-3-methylimidazolium cations | [NO3]− | UA, non-P | Unity |
| Hu et al.216 | AMBER | [Emim]+ | Lactate | UA, non-P | Unity |
| Singh et al.217 | AMBER | [Emim]+ | [CH3COO]− | AA, non-P | Unity |
| Smit et al.218 | AMBER and OPLS | Triazolium cations | [N(SO2CF3)2]− | AA, non-P | Unity |
| Laaksonen et al.219 | AMBER and DREIDING | Tetraalkylphosphonium cations | Chelated orthoborate anions | AA, non-P | Unity |
| Chaban et al.142 | LHW AA159 | [Emim]+ and [Bmim]+ | [BF4]− | AA, non-P | Scaled |
| Chaban et al.220 | CL&P | N-Butylpyridinium | [BF4]−, [N(SO2CF3)2]−, [PF6]−, [N(CN)2]−, [SO3CF3]− and [Cl]− | AA, non-P | Scaled |
| Balasubramanian et al.150 | CL&P | [Bmim]+ | [PF6]− | AA, non-P | Scaled |
| Balasubramanian et al.140 | CL&P | 1-Alkyl-3-methylimidazolium cations | [Cl]−, [BF4]−, [NO3]−, [PF6]−, [SO3CF3]− and [N(SO2CF3)2]− | AA, non-P | Scaled |
| Han et al.221 | CHARMM | [Bmim]+ | [PF6], [SO3CF3]−, [CF3COO]−, [C3F7COO]− and [C4F9SO3]− | AA, non-P | Scaled |
| Lisal et al.143,222 | CHARMM | Chiral imidazolium based cations | [Br]− | AA, non-P | Scaled |
| Youngs et al.151 | Youngs et al.213 | [Mmim]+ | [Cl]− | AA, non-P | Scaled |
| Economou et al.41 | CHARMM | 1-Alkyl-3-methylimidazolium cations | [N(SO2CF3)2]− | AA, non-P | Scaled |
| Economou et al.223 | AMBER and DREIDING | [Emim]+ | [B(CN)4]− | UA, non-P | Scaled |
| Maginn et al.201 | CHARMM | [Bmim]+ | [PF6]− | AA, non-P | Scaled |
| Smit et al.224 | AMBER | 1-Alkyl-3-methylimidazolium cations | [Cl]− | UA, non-P | Scaled |
| Liu et al.225 | OPLS and AMBER | 1-Alkyl-3-methylimidazolium cations | [BF4]−, [PF6]−, [SO3CF3]−, [SO3CH3]−, [CF3COO]−, [CH3COO]− and [N(SO2CF3)2]− | UA, non-P | Scaled |
| Holm et al.139 | CL&P | 1-Alkyl-3-methylimidazolium cations | [Cl]−, [N(CN)2]− and [SCN]− | AA, non-P | Scaled |
| Chaban et al.226 | CHARMM | [Emim]+ | Amino acid based anions | AA, non-P | Scaled |
| APPLE&P189 | Many imidazolium, pyridinium, ammonium, morpholinium and phosphonium cations | [PF6]−, [NO3]−, and many fluoroborate, cyano and bis(sulfonyl)imide based anions | AA, P | — | |
| Wu et al.227 | Wu et al.195 | 1-Alkyl-3-methylimidazolium cations | Glycine | AA, P | — |
| Wu et al.228 | OPLS-AA | Guanidium cations | [NO3]− and [ClO4]− | AA, P | — |
| Wu et al.195 | AMBER | [Emim]+ | Glycine | AA, P | — |
| AMOEBA229 | [Mmim]+ | [F]−, [Cl]−, [BF4]−, [NO3]− | AA, P | — | |
| Margulis et al.230 | OPLS-AA | 1-Methoxyethylpyridinium | [N(CN)2]− | AA, P | — |
| Yan et al.175 | Voth et al.215 | [Emim]+ | [NO3]− | AA, P | — |
| Yan et al.181,182 | AMBER | [Emim]+ | [NO3]− | AA, P | — |
| Steinhauser et al.192 | AMBER and CL&P | [Emim]+ | [SO3CF3]− | AA, P | — |
| Yethiraj et al.231 | Schmidt et al.232 | [Bmim]+ | [BF4]− | AA, P | — |
| Johnson et al.93 | ReaxFF92 | Tetrabutylphosphonium | Glycinate | ReaxFF | — |
There are two main types of polarisable models: point induced dipoles, many of which are based on the Thole model,183 where a smeared charge distribution is used both on the atom and on ‘off atom’ sites; and Drude oscillators, which mimic dipoles by attaching a fixed point charge on an harmonic spring to each atom location.184 Both methods have had some success. Studies using point induced dipoles have found that the calculated transport properties were much closer to experimental values than those calculated using classical MD,175,181,182 and found that long range ordering185 and the formation of ion cages186 in ionic liquids is important. A recent study calculated a number of anisotropic ionic polarisabilities, based on the Thole model, for a wide range of anions and cations, which can be utilised in MD simulations.187 Recent efforts have also been made to develop a polarisable force field, based on the Thole model, that can be used for a wide range of ionic liquids, known as the Atomistic Polarisable Potential for Liquids, Electrolytes and Polymers (APPLE&P) force field.188–191
There have also been a number of studies that have utilised the Drude oscillator model;167,192–194 one demonstrated that the dynamics, dipole moments and dielectric constants are dependent on the extent of polarisation used when modelling the ionic liquid [Emim][SO3CF3].192 Another study found that relatively long lived, heterogeneous ion cages formed within the ionic liquid.193
Another method, which is becoming more popular, is the Electronegativity Equalisation Method (EEM) (which can then be combined with molecular mechanics), where the polarisability of a system is mimicked by allowing the atomic partial charges to fluctuate.195,196 Such an approach accounts for changes in the electrostatic potential of atoms in response to different environments, and can also represent hydrogen bonding interactions.195
The results obtained from polarisable models describe properties that are important for explaining reactivity, and in the coming years it is likely that the use of polarisable force fields will become more widespread in investigating the impact of ionic liquids on reaction outcome.
Case studies: the utility of combining computational and experimental approaches
General solubility studies
Solubility studies are important as they highlight some of the underpinning concepts regarding the use of ionic liquids as solvents, along with helping to shape our understanding of ionic liquid mixtures. Having a sound understanding of the range of interactions and microscopic phenomena within ionic liquids, and their mixtures with solutes, is necessary before embarking on any analysis of their effects on reaction outcome. As will be discussed later, interactions between the ionic liquid and species along the reaction coordinate (that is, the starting materials and transition state) are important in directing the outcome of many reactions.Ionic liquids have been found to be surprisingly good at dissolving a range of compounds. Early work examined the solubility of aromatic compounds, particularly benzene, when compared to their aliphatic counterparts (for benzene, this is cyclohexane).177,233–238 A classical molecular dynamics study concluded that the high solubility of aromatics is due to the local electrostatic interactions between the ionic liquid (specifically [Mmim][Cl] and [Mmim][PF6] in this case) and the quadrupole moment of the aromatic species,235 analogous to cation–π interactions.239 A subsequent study looking at the solubility of benzene and hexafluorobenzene in the ionic liquid [Mmim][PF6], found that the specific grouping of the ions is dependent on the orientation of the quadrupole moment; in benzene, which has a region of electron density above and below the molecule and positive charge about the equator, the cations grouped above and below the plane of the solute whilst the anions were found about the equator. Hexafluorobenzene has an inverted quadrupole moment relative to benzene due to the electron withdrawing substituents; that is, positive regions above and below the ring, and electron density about the equator; resulting in opposite grouping of the ions.233 A similar molecular dynamics study, looking at a range of fluorinated benzenes, found that when both quadrupole and dipole moments exist there is an antagonistic effect; the solubility will be decreased when both exist, with higher solubilities found when there are solely either quadrupole or dipole moments within the compound.236
The importance of considering the dipole and quadrupole moments of solutes was also highlighted when looking at the solubility of gases in ionic liquids; this area has gained much attention in recent years, mainly focused around capture and storage of greenhouse gases.240–243 A classical molecular dynamics study investigated the solubility of a number of different gases in the ionic liquid [Emim][N(SO2CF3)2]; they found that both hydrogen sulphide (which has a significant dipole moment) and carbon dioxide (no dipole moment but with a large quadrupole moment), were highly soluble. In contrast, molecular hydrogen and nitrogen, with no dipole or quadrupole moments, were much less soluble. This trend was supported by experimental work, and reinforces the importance of considering the overall electronic distribution of species dissolved in ionic liquids.244
It has also been demonstrated that the nature of the cation and anion is important; a number of experimental and computational studies on the solubility of carbon dioxide and sulfur dioxide have generally found that the solubility of the gas is more dependent on the anion than the cation, and that the anion-carbon dioxide (and anion-sulfur dioxide245) interactions reduce the extent of anion-cation interactions within the mixture.70,116,120,246–249 The anion–solute interactions thus disrupt the ordering of the ionic liquid components, which results in a decreased viscosity of the solution and an increase in the diffusion coefficients of both the ionic liquid components and the dissolved gas.241,242,247,249 This brings about another important point of reflection; considering the balance of ion–solute and ion–ion interactions within the mixture. In the cases described here, the balance of these interactions resulted in a disruption in ordering of the ionic liquid upon dissolution of the gas.
Another area which has received considerable attention is the dissolution of lignocellulosic biomass in ionic liquids; lignocellulosic biomass is defined as any material obtained from currently or previously living flora, and its dissolution is an area of increasing interest due to the possibility of utilising waste materials for energy production and as a source of aromatic starting materials.250 A number of studies have demonstrated that lignin, cellulose and other biomass components are much more soluble in ionic liquids than traditional solvents.251–254 A range of computational studies in this area have sought to understand the role of the anion and cation in the dissolution process.255,256 A combination of experimental and DFT studies found that the greater the hydrogen bond accepting ability of the anion, the greater the solubility of lignin (a highly complex, aromatic species). Interestingly it was found that there was a subtle balance between the ionic liquid ions interacting with themselves, and with the biomass components; increasing the coordinating ability of the anion would result in an increase in both these interactions.256 An experimental study found that the nature of the cation also had an effect on lignin solubility,257 with the importance of π–π interactions between an aromatic cation and lignin also demonstrated through DFT calculations.125
For cellulose, a series of classical molecular dynamics simulations found that the ionic liquid cations interact more with the non-polar regions of cellulose, whilst the anions interact with the polar regions.255 The general conclusion of this study is that the solvation of cellulose is driven by the strong interaction between the anion and the polar regions of cellulose; this idea is supported by other computational258,259 and experimental260 studies where it has been concluded that the anion disrupts the intermolecular forces between the cellulose polymers, resulting in increased solubility.
Highlighted by the examples above, there are some important considerations that become apparent when beginning to analyse the effects of ionic liquids on reaction outcome. These include consideration of: interactions between the ionic liquid and specific sites on the species along the reaction coordinate based on electronic distribution (such as charged species, and dipole and quadrupole moments); the competing interactions between the ions themselves and between ions and any dissolved species; the existence of hydrogen bonding interactions, if any; and disruption of the ordering in the system, whether it be disruption of the ionic liquid ordering or of any strong interactions that exist with the reagents. The following discussion will be with reference to, and in the context of, these points.
Studies on reaction outcome
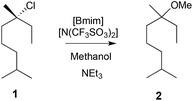 | ||
| Scheme 1 The methanolysis reaction of the chloride 1 to give the ether 2. The rate constant was found to vary when the mole fraction of [Bmim][N(SO2CF3)] in methanol was changed.8,9 | ||
It was found that on addition of a small amount of [Bmim][N(SO2CF3)2] to methanol (χIL ca. 0.02) there was a two-fold increase in the rate constant. Further increases in the ionic liquid concentration resulted in a decreased rate constant, and at χIL 0.72 the rate constant was half that found in methanol.8 These observations were rationalised using activation parameter data determined from temperature-dependent kinetic experiments, molecular dynamics simulations, and by considering the electrostatic interactions that act to stabilise the incipient charges in the transition state.9 At low concentrations, this charge stabilisation results in a faster rate through a lowering of the enthalpy of activation – an enthalpic benefit. With increasing amounts of ionic liquid there is a degree of solvent organisation when moving to the transition state, resulting in a decrease in the entropy of activation – an entropic cost. At higher concentrations this substantial entropic cost outweighs the enthalpic benefit, causing an overall decrease in reaction rate. It is interesting to note that in both kinetic16 and experimental262 studies on unimolecular substitution reactions that involve less charge localisation in the transition state, the use of ionic liquids increased the reaction rate relative to molecular solvents.
Classical molecular dynamics simulations were used to further investigate the microscopic origin of these effects found for the reaction shown in Scheme 1. Geometry optimisations were performed at the B3LYP/6-31G(d) level to obtain the substrate and intermediate structures, and the simulations were done using the CL&P force field. [Mmim][PF6] (an ionic liquid comparable to [Bmim][N(SO2CF3)2], used because it was small and tractable) was modelled about both the chloride 1 and the carbocation intermediate of the process. The simulations showed a significant increase in ordering about the intermediate, specifically organisation of the ionic liquid cation about the chloride leaving group, and the anion of the ionic liquid about the carbocation intermediate, when compared to the non-dissociated species 1.9 This is consistent with the experimental observations.
It should be noted that the above case involves consideration of the intermediate in the process, not the transition state, due to computational limitations in modelling a transition state. This is not an unreasonable approximation (consider Hammond's postulate), given that how the transition state would vary between solvents would be hard to model.
A few reports have also examined the effect of ionic liquids on reactions involving a charged nucleophile;263–266 these studies all focused on a dediazoniation reaction, where it was found that the non-nucleophilic anion [N(SO2CF3)2]− was reacting in preference to the more nucleophilic halide reagents (Scheme 2), with the product 6 forming predominantly.
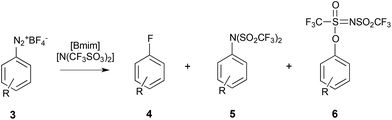 | ||
| Scheme 2 The fluorodediazoniation of the diazonium salt 3 to give either product 4 due to reaction with the fluoride nucleophile, or products 5 and 6 due to reaction with the anion of the ionic liquid either at the nitrogen or at the oxygen, respectively.263 | ||
DFT calculations showed that the product 6 was also less thermodynamically stable, indicating that the selectivity was kinetically driven.264 Further work265,266 was able to demonstrate that the apparent ‘increased nucleophilicity’ of [N(SO2CF3)2]− is actually a result of a decrease in the relative nucleophilicity of the halide in the ionic liquid. The charge dense and coordinating halides interact more strongly with the [Bmim]+ cation, relative to [N(SO2CF3)2]−; as a result there is much more ‘free’ [N(SO2CF3)2]− available to react with the aromatic diazonium salt 3, hence the apparent increase in the nucleophilicity of [N(SO2CF3)2]−. This concept is supported by a number of computational105,139,140 and experimental40,166 studies that show that more coordinating anions will interact more strongly with, and will have a greater degree of charge transfer to, the cation, when compared to less coordinating anions. This reinforces the importance of considering the competing interactions between the components of the ionic liquid themselves, and the ions and reagent.
Overall, studies so far on unimolecular substitution processes have revealed two key points: firstly, the importance of considering the electrostatic interactions between the ionic liquid and the charge-separated transition state, leading to the ionic intermediate. The magnitude of such an interaction has a marked effect on the reaction rate when compared to molecular solvents; with studies suggesting that strong intermediate–ionic liquid interaction can decrease the rate constant,8,9 while lessened extents of intermediate–ionic liquid interaction can have a positive influence on the rate constant.16,262 Secondly, that having an understanding of the different coordination strength of the ions in the reaction mixture is essential, as when using a mixture of ionic species there can be preferential interaction of ionic components.263–266
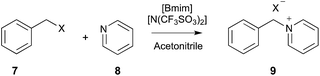 | ||
| Scheme 3 The bimolecular substitution reaction between benzyl halide 7 (where X = Cl or Br) and pyridine 8, performed in different mole fractions of [Bmim][N(SO2CF3)] in acetonitrile.12,15,16,19 | ||
This trend suggests that there is an increase in disorder on moving to the transition state, with the increased enthalpy arising from either stabilisation of the starting materials or destabilisation of the transition state. Given the high solubility of aromatic compounds in ionic liquids (as discussed previously), it was initially suspected that the increased entropy was due to ordering about the delocalised π systems of reagents 7 and 8.12 A series of deconvolution and classical molecular dynamics studies using the CL&P force field showed that, whilst there is a significant cation–quadrupole interaction, the extent of organisation about the starting material 8 does not change significantly with the removal of the delocalised π system.15 Hence, the organisation about the nucleophilic nitrogen centre in the amine 8 was key as, on moving to the transition state, interaction with this centre is no longer possible.
In a study on a similar Menschutkin reaction (Scheme 4),267 the effect of a selection of ionic liquids on the rate constant was found to be comparable to that discussed above. DFT calculations of a series of single ion pairs, using the B3LYP/CEP-121G(d,p) level of theory, were used to investigate interactions with the transition state. This study found that the primary interaction in the transition state was that between the ionic liquid cation and the halide leaving group.
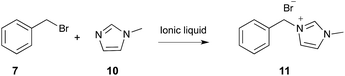 | ||
| Scheme 4 The bimolecular substitution reaction between benzyl bromide 7 and N-methylimidazole 10, performed in a range of ionic liquids.267 | ||
By considering both of these studies12,15,267 it is clear that whilst the cation interacts with both the nucleophile starting material and the anionic leaving group in the transition state, the trend in the activation parameters indicates that organisation about, and stabilisation of, the nucleophile is more substantial, resulting in the significant entropic benefit responsible for the increased rate constant.14,184
Another aspect that is interesting to consider is the effect that changing the ionic liquid itself has on reaction outcome. Whilst many experimental studies have focussed on these, there is less related computational data.
The effect of changing both the cation and anion on the substitution reaction between benzyl bromide 7 and pyridine 8 has been investigated in a range of ionic liquids.18,20 An important outcome when altering the cation was that, when systemically replacing the imidazolium ring hydrogens with methyl groups, there was no change in the enthalpy of activation, indicating that there is no directional interaction between the ring hydrogens and the nucleophile 8.18 This is supported by calculations on imidazolium and methylated imidazolium ionic liquids,100,103,268 along with other computational studies, suggesting that all the ring hydrogens, as well as the methylene and methyl protons in the alkyl substituents, are capable of hydrogen bonding, and therefore methyl substitution has little effect.102,269
The condensation reaction between 4-methoxybenzaldehyde 12 and hexylamine 13 (Scheme 5) is not a substitution process, but the first step involves nucleophilic attack on a carbonyl centre and, hence, it is mechanistically related to the previous examples. Further, it is affected by ionic liquids in the same manner as the substitution case shown in Scheme 3, with a comparable interaction between the cation and the nitrogen lone pair on the amine 13 inferred by the enthalpic benefit and entropic cost on moving to the ionic solvent.21 This case was more affected by modification of the ionic liquid cation; this was rationalised by the fact that, due to the less bulky nature of the nucleophile 13 when compared to the more rigid pyridine 8, the nucleophile can better access the charged cationic centre.
 | ||
| Scheme 5 The condensation reaction between 4-methoxybenzaldehyde 12 and hexylamine 13, performed in a range of different ionic liquids where the charge accessibility and density of the cation, and the coordinating ability of the anion, was varied.21,270 | ||
An interesting result from this work was that the extent of cation–nucleophile interaction could be controlled in a systematic fashion by varying the nature of both the cation21 and anion.270 Generally the more accessible and charge dense the cation, and the lower the coordinating ability of the anion, the larger the associated enthalpy and entropy of activation.21,270 A more subtle observation was that the enthalpy of activation was slightly less for [Bm2im][N(SO2CF3)2] than [Bmim][N(SO2CF3)2], due to the steric bulk of the methyl group inhibiting access to the charged centre. Yet the entropy of activation was the same for both ionic liquids, rather than [Bmim][N(SO2CF3)2] being higher as would be expected.
These results can be explained by the numerous computational studies on [Bmim]+ and [Bm2im]+ based systems, aimed at explaining the anomalous melting points and viscosities found for [Bm2im]+ ionic liquids.100,101,103,268,271,272 Methyl substitution at the C2 position was anticipated to decrease the extent of hydrogen bonding in the ionic liquid, causing a decrease in the melting point and viscosity. Yet [Bm2im]+ ionic liquids have higher melting points and viscosities than their [Bmim]+ counterparts.101,271,272 A number of quantum chemical calculations (B3LYP and MP2) of clusters of ionic liquids found that the C2-methylated systems have fewer stable configurations than their protonated versions, with larger energy differences between the stable conformers when compared to the protonated cases. This restricts movement of the anion and results in the observed increased viscosities and melting points, as there is an increase in ordering of the system.100,103,268 The main conclusion from these studies is that entropy is more significant for the C2 methylated ionic liquids than for the corresponding unsubstituted cases.
Linking this back to the condensation reaction discussed above, the similar entropies can now be explained by the increased solvent ordering in [Bm2im][N(SO2CF3)2], compared to [Bmim][N(SO2CF3)2]. Ordering within the [Bm2im][N(SO2CF3)2] solvent shell about the nucleophile 13 will be more substantial than expected if only considering the ordering caused by cation–nucleophile interaction. When moving to the transition state, where the cation will move away from the nucleophile, the ordering within this solvent shell will be disrupted significantly. This change in ordering is greater than what would be expected if only considering the extent of cation–nucleophile interaction, resulting in the entropies of activation for [Bm2im][N(SO2CF3)2] and [Bmim][N(SO2CF3)2] being comparable.
There have also been studies on bimolecular substitution processes that involve charged reagents; of particular interest here is the reaction of methyl p-nitrobenzenesulfonate 15 with a number of charged nucleophiles, which has been investigated both experimentally25,273–275 and computationally.276 When performed in molecular solvents this process can proceed through either the discrete anion, where the nucleophile is not coordinated to a counterion, or as an ion pair when a higher reagent concentration is used.277 When using an ionic liquid solvent it was found that the reaction proceeded faster than when in the highly polar, protic hexafluoropropan-2-ol but slower than the relatively non-polar solvent dichloromethane. The activation parameters for the reaction with a chloride anion (Scheme 6) were determined in a number of ionic liquids, and compared with both the ion pairing and discrete anion mechanism in dichloromethane to gain an understanding of the microscopic origin of this effect.25
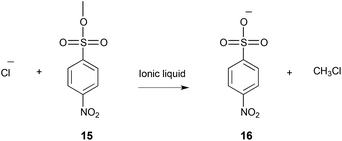 | ||
| Scheme 6 The reaction of p-nitrobenzenesulfonate 15 with chloride to give the product 16, performed in a number of molecular solvents and ionic liquids.25,273,276 | ||
It was found that the entropy of activation for the ionic liquid cases was close to that of the free ion in dichloromethane, while the enthalpy of activation more closely resembled the ion pairing mechanism.25 A QM/MM study276 investigated this reaction further in [Bmim][PF6], and found that the [Bmim]+ cations are strongly associated with the chloride nucleophile; such an interaction would stabilise the nucleophile and introduce an enthalpic cost, resulting in an enthalpy of activation comparable to the ion pairing mechanism, as an ion will need to be ‘removed’ from the nucleophile for the reaction to proceed. It was also suggested that there is a hydrogen-bonding interaction between the ionic liquid cation and [Cl]−;276 this idea is supported by the experimental work that found that the rate constant increased as the hydrogen bond donor ability of the cation decreased.25 Further, the computational study suggested that this interaction was entropically favourable as the [Bmim]+–[Cl]− distance increased on moving to the transition state, yet this was offset by interaction between [Bmim]+ and the leaving group in the transition state, resulting in the entropy of activation more closely resembling that of the free ion in dichloromethane. In other words, the entropic benefit will be minimal as the ionic liquid cation can interact with both the charged nucleophile and the charge separated transition state.
For these bimolecular processes the importance of the extent of electrostatic interactions between the ionic liquid components and the species along the reaction coordinate, as seen for the unimolecular case, is once again demonstrated. Interestingly, the combination of experimental and computational work has provided significant insight into the subtle interactions between the ionic liquid and the reagents' lone pair, and the effect that ordering within the ionic liquid itself can have on reaction outcome. Importantly, when using a neutral nucleophile use of an ionic liquid resulted in an entropically driven rate increase, yet when using a charged nucleophile the enthalpic barrier for the process was higher due to the strong interactions with the charged nucleophile. Further, for the charged nucleophile cases there was significant interaction between the ionic liquid and the more charge-separated transition state, resulting in any entropic effects being minimal.
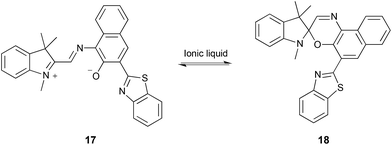 | ||
| Scheme 7 Cyclisation of the merocyanine 17 to give the spiroxazine 18.278–281 | ||
Whilst it generally appears that the decreased rate is due to an increased enthalpy of activation, partially offset by an increased entropy of activation, when compared to polar aprotic molecular solvents, no uncertainties in the data were reported and the activation parameters covered a large range of values for different ionic liquids.278 They also noted that the observed effects could not be correlated with any measured solvent parameters. Through a combined UV-Vis and computational (ab initio and DFT) approach on a related system, it was suggested that the nature of both the cation280 and the anion281 played a role. It was found that the ionic liquid cation could interact with the phenolate oxygen, stabilising the derivative of 17 and shifting the equilibrium position to the left.280 Considering this cation–phenolate interaction, and the increased enthalpy and entropy of activation for the reaction in Scheme 7 when using an ionic liquid, it is likely that there is a similar effect to that discussed above for the bimolecular substitution cases. Interaction between the cation and the phenolate on 17 would stabilise this reagent, decreasing its nucleophilicity and hence increase the enthalpic barrier for the reaction. Whilst there is an entropic benefit associated with such an interaction, due to the increased disorder on moving to the transition state and considering that the rate constant is decreased relative to molecular solvents, the entropic advantage for this reaction is not sufficient to offset the enthalpic cost (in contrast to what was seen for the reactions in Schemes 3–5, and again emphasises the importance of the balance of these interactions).
The ethanolysis of 1-fluoro-2,4-dinitrobenzene 19 (Scheme 8) was conducted in ethanol and the ionic liquid [Bmim][N(SO2CF3)2] (χIL ca. 0.5) across a range of temperatures to allow the activation parameters to be determined. When using the ionic liquid, there was a small enthalpic cost that was offset by a more substantial entropic benefit when compared to ethanol, with an overall increase in the rate constant.14
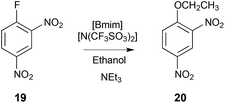 | ||
| Scheme 8 The nucleophilic aromatic substitution reaction between the substituted benzene 19 and ethanol, to give the product 20.14 | ||
Molecular dynamics simulations, using the CL&P force field for the ionic liquid components, were performed on the starting material 19 and the corresponding Meisenheimer intermediate with either [Bmim][N(SO2CF3)2] or ethanol. The radial distribution functions showed that [Bmim][N(SO2CF3)2] was more ordered about the starting material than the intermediate, and that ethanol showed little organisation about either species under the same simulation conditions. Particularly, it was noted that the anion–π interaction was most significant, with a decreased extent of ordering about the intermediate, whilst the extent of ordering of the cation changed little. The importance of the anion–π interaction can be rationalised by recognising that the inclusion of electron-withdrawing substituents will reorient the quadruple moment of the aromatic system relative to benzene, resulting in grouping of the anion above and below the plane of the reagent 19, and the cations about the equator.233 This phenomena is reflected in the molecular dynamics simulations of this fluoro- and nitro-substituted benzene, and confirms that the trend in the activation parameters is due to increased ordering of the anion about the delocalised π-system of the reagent, relative to the disrupted π-system of the transition state.14
This work was extended to investigate the effect of changing the cation and anion of the ionic liquid.17 Generally, there were minimal changes in the activation parameters when varying the cation; a logical result given the localisation of cations about the aromatic-equator, an interaction that is unlikely to be largely affected by a disruption in aromaticity.14,233 It was anticipated that changing the coordinating ability of the anion would have a more significant effect on the activation parameters, due to the likely ordering above and below the plane of the aromatic species 19. This expected trend did hold for single ionic liquid systems, but not for binary mixtures of ionic liquids.14
Another interesting example is the amination of activated thiophenes 21 using a series of different secondary cyclic amines 22 (for example, piperidine, pyrrolidine and morpholine), shown in Scheme 9.27 It was found that the reaction proceeded faster in the ionic liquids [Bmim][BF4], [Bmim][PF6] and [Bm2im][BF4] than it did in molecular solvents. The experimentally-determined activation parameters indicated that this rate enhancement was enthalpically driven, and it was suggested that this was due to greater stabilisation of the transition state by the ionic liquids, when compared to molecular solvents. Interestingly, it was also suggested that the situation was likely more complex, and factors such as differing extents of nucleophile solvation needed to be taken into account.27
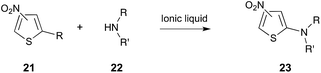 | ||
| Scheme 9 The nucleophilic aromatic substitution reaction between the substituted thiophenes 21 and a number of cyclic, secondary amines 22 (for example, R/R′ = –(CH2)4–, –(CH2)5–, –(CH2)2O(CH2)2–).27,282 | ||
A recent QM/MM study has appeared, which aimed to provide further insight into the microscopic origin of the rate changes described above for the reaction in Scheme 9. The calculated activation parameters closely matched the experimentally derived parameters, once again concluding that the rate increase was due to an enthalpic benefit.282 The computational work also suggested an increased amine nucleophilicity in the ionic liquids, compared to methanol, as well as significant π–π interactions between the [Bmim]+ cation and nitrothiophene 21 substrate. Interestingly, they also found that the transition state in the ionic liquid more closely resembled the Meisenheimer complex than it did in methanol, and that there was a significant increase in the electrostatic interactions between the ionic liquid and the transition state, compared to the reagents. This increased interaction with the transition state, when using an ionic liquid, resulted in the enthalpic benefit and entropic cost seen.282
The main points to take away from studies on nucleophilic aromatic substitution processes are that: firstly, (again) the importance of considering electrostatic interactions between the ionic liquid and charged species along the reaction coordinate, similar to that seen for unimolecular substitution processes, is identified. And secondly, for processes that involve a change in aromaticity in the rate-determining step, differing extents of solvation of these aromatic species along the reaction pathway can affect reaction outcome when using ionic liquids. This concept links to the solubility studies discussed earlier, where the importance of ion-quadrupole and ion–dipole interactions have been realised.233,235,236,244
A detailed study on the reaction between cyclopentadiene 24 and methyl acrylate 25a (Scheme 10) in a number of ionic liquids concluded that the increased rate and selectivity for isomer 26 over isomer 27, when compared to a non-polar solvent, is due to hydrogen bonding between the ionic liquid and the dienophile 25. The greater the extent of hydrogen bonding with the dienophile 25, the more selective the reaction was and the more the reaction was accelerated.23
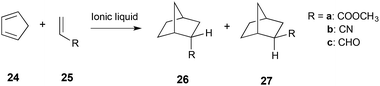 | ||
| Scheme 10 The Diels–Alder reaction between cyclopentadiene 24 and a number of dienophiles 25.23,286 | ||
The complex balance between the ions interacting with themselves, and with the dienophile, was also highlighted and has been raised by many authors.247,249,265,285 The highest selectivity and rate were achieved when using a cation with a strong hydrogen bond donating ability, and an anion that is a poor hydrogen bond acceptor.23 Attempts to develop Linear Solvation Energy Relationships (LSERs) when using dienophiles 25a, 25b and 25c (Scheme 10) found that whilst the selectivity fit was quite good, correlation with the rate constant was not as successful.286 The limitations of this approach were also highlighted in a study on an intramolecular case, where simple use of LSERs was not sufficient to describe the observed rate constants and selectivity, and much better fits were seen when viscosity was taken into account.287
A number of computational studies have been used to further investigate the observed selectivity and reactivity; DFT calculations (B3LYP/cep-121g(d,p)) of the cation with the reagents, transition state and product were performed on the reaction between 24 and dienophiles 25 (Scheme 10).288 There were two key conclusions from this work; first, that the cation coordinates to the dienophile, which could activate it towards cycloaddition as has previously been suggested;289 and second, that the dienophile is held rigid due to this interaction. This essentially ‘clamps’ the dienophile in place, increasing the probability of dienophile-diene stacking that is necessary for the reaction to proceed.285,288 The interaction of the dienophile and the cation supports the hydrogen bonding argument discussed above. Further investigations (using KS-DFT/3D-RISM-SCF290,291) of the reaction of cyclopentadiene 24 and acrolein 25c in the ionic liquid [Mmim][PF6] showed that coordination of the cation was not essential, and in some cases the preferential interaction of the ionic liquid components with each other were responsible for the changes in reaction outcome.292 Interestingly, it was noted that interactions between the carbonyl oxygen of acrolein 25c and the C4, C5 and methyl hydrogens of the cation [Mmim]+ were more significant than interaction with the C2 hydrogen, reinforcing the idea that interaction with the C2 proton is not fundamental.18,269 Overall, the solvent effects of the Diels Alder reaction are complex, and a complete understanding of the role that an ionic liquid plays in dictating reaction outcome is still developing.
In summary, the extensive experimental and computational work over recent years has contributed significantly to the understanding of ionic liquids, and their effect on the outcome of organic processes. The major interactions identified so far as governing ionic liquid solvent effects are: (1) the electrostatic interactions between the ionic liquid and charged species along the reaction coordinate; (2) interactions between the ionic liquid, and dipole and quadrupole moments of the reagents; and (3) interactions between the ionic liquid and lone pairs, particularly in reagents. Once these features have been identified, careful consideration of the magnitude of these different interactions, as well as their position along the reaction coordinate, can allow for predictions to be made about how the ionic liquid will affect the activation parameters for the process, and hence the rate constant. While such a predictive framework is by no means comprehensive and is still developing, the growing interest in this area is bringing us closer to having a full understanding of ionic liquid solvent effects.
Conclusions
This review has summarised the major computational techniques that can be used to investigate ionic liquid solvent effects, and identifies both the utility and limitations of the computational approaches commonly used. There are many different forms of computational studies that can be used to compliment experimental work; whether it be studies focusing on the nature of ionic liquids themselves, such as the complex landscape of interactions that exist in ionic liquids; or on interactions between ionic liquids and dissolved species. The combination of experimental and computational work has greatly increased our fundamental understanding of ionic liquids as solvents, and has contributed substantially to the developing predictive framework for using ionic liquids as solvents for organic reactions. The increasing popularity of computational approaches, as well as advancing computing technologies, will hopefully see the emergence of more combined computational and experimental studies, as such an approach is crucial for gaining a thorough understanding of ionic liquid media and their effect on reaction outcome.Acknowledgements
STK acknowledges the support of the Australian government through the receipt of an Australian Postgraduate Award. JBH acknowledges financial support from the Australian Research Council through the Discovery Project Funding Scheme (Project DP130102331). AKC is grateful for support through the European Union COST CM1206 EXIL (Exchange in Ionic Liquids) Network. All authors thank Dr Ron Haines (University of New South Wales) for helpful discussions on the content of this manuscript.Notes and references
- S. Z. El Abedin and F. Endres, Acc. Chem. Res., 2007, 40, 1106–1113 CrossRef CAS PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- K. R. Seddon, Kinet. Catal., 1996, 37, 693–697 CAS.
- C. L. Hussey, Pure Appl. Chem., 1988, 60, 1763–1772 CrossRef CAS.
- M. J. Earle, J. M. S. S. Esperanca, M. A. Gilea, J. N. Canongia Lopes, L. P. N. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831–834 CrossRef CAS PubMed.
- D. M. Fox, J. W. Gilman, A. B. Morgan, J. R. Shields, P. H. Maupin, R. E. Lyon, H. C. De Long and P. C. Trulove, Ind. Eng. Chem. Res., 2008, 47, 6327–6332 CrossRef CAS.
- B. Wu, W. Liu, Y. Zhang and H. Wang, Chem.–Eur. J., 2009, 15, 1804–1810 CrossRef CAS PubMed.
- B. Y. W. Man, J. M. Hook and J. B. Harper, Tetrahedron Lett., 2005, 46, 7641–7645 CrossRef CAS.
- H. M. Yau, S. A. Barnes, J. M. Hook, T. G. A. Youngs, A. K. Croft and J. B. Harper, Chem. Commun., 2008, 3576–3578 RSC.
- C. E. Rosella and J. B. Harper, Tetrahedron Lett., 2009, 50, 992–994 CrossRef CAS.
- H. M. Yau, S. J. Chan, S. George, J. Hook, A. Croft and J. Harper, Molecules, 2009, 14, 2521–2534 CrossRef CAS PubMed.
- H. M. Yau, A. G. Howe, J. M. Hook, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2009, 7, 3572–3575 CAS.
- S. R. D. George, G. L. Edwards and J. B. Harper, Org. Biomol. Chem., 2010, 8, 5354–5358 CAS.
- S. G. Jones, H. M. Yau, E. Davies, J. M. Hook, T. G. A. Youngs, J. B. Harper and A. K. Croft, Phys. Chem. Chem. Phys., 2010, 12, 1873–1878 RSC.
- H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371 RSC.
- S. T. Keaveney and J. B. Harper, RSC Adv., 2013, 3, 15698–15704 RSC.
- E. E. L. Tanner, R. R. Hawker, H. M. Yau, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 7516–7521 CAS.
- E. E. L. Tanner, H. M. Yau, R. R. Hawker, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 6170–6175 CAS.
- H. M. Yau, S. T. Keaveney, B. J. Butler, E. E. L. Tanner, M. S. Guerry, S. R. D. George, M. H. Dunn, A. K. Croft and J. B. Harper, Pure Appl. Chem., 2013, 85, 1979 CrossRef CAS.
- S. T. Keaveney, D. V. Francis, W. Cao, R. S. Haines and J. B. Harper, Aust. J. Chem., 2015, 68, 31–35 CrossRef CAS.
- S. T. Keaveney, K. S. Schaffarczyk McHale, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2014, 12, 7092 CAS.
- B. J. Butler and J. B. Harper, New J. Chem., 2015, 39, 213–219 RSC.
- A. Aggarwal, N. L. Lancaster, A. R. Sethi and T. Welton, Green Chem., 2002, 4, 517–520 RSC.
- T. Fischer, A. Sethi, T. Welton and J. Woolf, Tetrahedron Lett., 1999, 40, 793–796 CrossRef CAS.
- N. L. Lancaster, P. A. Salter, T. Welton and G. B. Young, J. Org. Chem., 2002, 67, 8855–8861 CrossRef CAS PubMed.
- I. Newington, J. M. Perez-Arlandis and T. Welton, Org. Lett., 2007, 9, 5247–5250 CrossRef CAS PubMed.
- F. D'Anna, V. Frenna, R. Noto, V. Pace and D. Spinelli, J. Org. Chem., 2006, 71, 5144–5150 CrossRef PubMed.
- F. D'Anna, V. Frenna, V. Pace and R. Noto, Tetrahedron, 2006, 62, 1690–1698 CrossRef.
- F. D'Anna, S. La Marca, P. Lo Meo and R. Noto, Chem.–Eur. J., 2009, 15, 7896–7902 CrossRef PubMed.
- S. T. Keaveney, R. S. Haines and J. B. Harper, in Encyclopedia of Physical Organic Chemistry, ed. U. Wille, Wiley, in press Search PubMed.
- M. J. Earle, S. P. Katdare and K. R. Seddon, Org. Lett., 2004, 6, 707–710 CrossRef CAS PubMed.
- Y. Wang and G. A. Voth, J. Am. Chem. Soc., 2005, 127, 12192–12193 CrossRef CAS PubMed.
- K. Shimizu, C. E. S. Bernardes, A. Triolo and J. N. Canongia Lopes, Phys. Chem. Chem. Phys., 2013, 15, 16256–16262 RSC.
- A. B. Pereiro, M. J. Pastoriza-Gallego, K. Shimizu, I. M. Marrucho, J. N. C. Lopes, M. M. Piñeiro and L. P. N. Rebelo, J. Phys. Chem. B, 2013, 117, 10826–10833 CrossRef CAS PubMed.
- K. Shimizu, C. E. S. Bernardes and J. N. Canongia Lopes, J. Phys. Chem. B, 2013, 118, 567–576 CrossRef PubMed.
- B. Schwenzer, S. N. Kerisit and M. Vijayakumar, RSC Adv., 2014, 4, 5457–5464 RSC.
- G. Chatel, J. F. B. Pereira, V. Debbeti, H. Wang and R. D. Rogers, Green Chem., 2014, 16, 2051–2083 RSC.
- H. Niedermeyer, J. P. Hallett, I. J. Villar-Garcia, P. A. Hunt and T. Welton, Chem. Soc. Rev., 2012, 41, 7780–7802 RSC.
- R. S. Payal and S. Balasubramanian, Phys. Chem. Chem. Phys., 2013, 15, 21077–21083 RSC.
- I. J. Villar-Garcia, K. R. J. Lovelock, S. Men and P. Licence, Chem. Sci., 2014, 5, 2573–2579 RSC.
- G. E. Logotheti, J. Ramos and I. G. Economou, J. Phys. Chem. B, 2009, 113, 7211–7224 CrossRef CAS PubMed.
- G. Adamova, J. N. Canongia Lopes, L. P. N. Rebelo, L. M. N. B. Santos, K. R. Seddon and K. Shimizu, Phys. Chem. Chem. Phys., 2014, 16, 4033–4038 RSC.
- S. M. Urahata and M. C. C. Ribeiro, J. Chem. Phys., 2004, 120, 1855–1863 CrossRef CAS PubMed.
- E. Androulaki, N. Vergadou and I. G. Economou, Mol. Phys., 2014, 1–13 Search PubMed.
- S. P. Verevkin, D. H. Zaitsau, V. N. Emel'yanenko, A. V. Yermalayeu, C. Schick, H. Liu, E. J. Maginn, S. Bulut, I. Krossing and R. Kalb, J. Phys. Chem. B, 2013, 117, 6473–6486 CrossRef CAS PubMed.
- S. Li, K. L. Van Aken, J. K. McDonough, G. Feng, Y. Gogotsi and P. T. Cummings, J. Phys. Chem. C, 2014, 118, 3901–3909 CAS.
- S. Yeganegi, A. Soltanabadi and D. Farmanzadeh, J. Phys. Chem. B, 2012, 116, 11517–11526 CrossRef CAS PubMed.
- Z. Fei, D.-R. Zhu, N. Yan, R. Scopelliti, S. A. Katsuba, G. Laurenczy, D. M. Chisholm, J. S. McIndoe, K. R. Seddon and P. J. Dyson, Chem.–Eur. J., 2014, 20, 4273–4283 CrossRef CAS PubMed.
- F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, ChemPhysChem, 2012, 13, 1625–1637 CrossRef CAS PubMed.
- E. J. Maginn, J. Phys.: Condens. Matter, 2009, 21, 373101 CrossRef CAS PubMed.
- M. Salanne, Phys. Chem. Chem. Phys., 2015 10.1039/c1034cp05550k.
- B. Kirchner, O. Hollóczki, J. N. Canongia Lopes and A. A. H. Pádua, WIRES Comput. Mol. Sci., 2015, 5, 202–214 CrossRef CAS.
- C. D. Hubbard, P. Illner and R. van Eldik, Chem. Soc. Rev., 2011, 40, 272–290 RSC.
- C. Chiappe and C. S. Pomelli, Phys. Chem. Chem. Phys., 2013, 15, 412–423 RSC.
- J. S. Wilkes, J. A. Levisky, R. A. Wilson and C. L. Hussey, Inorg. Chem., 1982, 21, 1263–1264 CrossRef CAS.
- K. R. Seddon, J. Chem. Technol. Biotechnol., 1997, 68, 351–356 CrossRef CAS.
- K. Fumino and R. Ludwig, J. Mol. Liq., 2014, 192, 94–102 CrossRef CAS.
- R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3238–3253 RSC.
- S. Zahn, M. Brehm, M. Brüssel, O. Hollóczki, M. Kohagen, S. Lehmann, F. Malberg, A. S. Pensado, M. Schöppke, H. Weber and B. Kirchner, J. Mol. Liq., 2014, 192, 71–76 CrossRef CAS.
- S. Puttick, A. L. Davis, K. Butler, L. Lambert, J. El harfi, D. J. Irvine, A. K. Whittaker, K. J. Thurecht and P. Licence, Chem. Sci., 2011, 2, 1810–1816 RSC.
- C. C. Weber, A. F. Masters and T. Maschmeyer, Angew. Chem., Int. Ed., 2012, 51, 11483–11486 CrossRef CAS PubMed.
- J. N. A. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 3330–3335 CrossRef CAS PubMed.
- A. Triolo, O. Russina, B. Fazio, R. Triolo and E. Di Cola, Chem. Phys. Lett., 2008, 457, 362–365 CrossRef CAS.
- T. Pott and P. Meleard, Phys. Chem. Chem. Phys., 2009, 11, 5469–5475 RSC.
- F. Dommert, J. Schmidt, C. Krekeler, Y. Y. Zhao, R. Berger, L. Delle Site and C. Holm, J. Mol. Liq., 2010, 152, 2–8 CrossRef CAS.
- J. Schmidt, C. Krekeler, F. Dommert, Y. Zhao, R. Berger, L. D. Site and C. Holm, J. Phys. Chem. B, 2010, 114, 6150–6155 CrossRef CAS PubMed.
- W. T. Borden and E. R. Davidson, Acc. Chem. Res., 1996, 29, 67–75 CrossRef CAS.
- P. A. Hunt and I. R. Gould, J. Phys. Chem. A, 2006, 110, 2269–2282 CrossRef CAS PubMed.
- E. Rezabal and T. Schäfer, J. Phys. Chem. B, 2012, 117, 553–562 CrossRef PubMed.
- B. L. Bhargava and S. Balasubramanian, J. Phys. Chem. B, 2007, 111, 4477–4487 CrossRef CAS PubMed.
- M. Brussel, M. Brehm, T. Voigt and B. Kirchner, Phys. Chem. Chem. Phys., 2011, 13, 13617–13620 RSC.
- K. Wendler, M. Brehm, F. Malberg, B. Kirchner and L. Delle Site, J. Chem. Theory Comput., 2012, 8, 1570–1579 CrossRef CAS.
- D. S. Firaha and B. Kirchner, J. Chem. Eng. Data, 2014, 59, 3098–3104 CrossRef CAS.
- M. Brehm, H. Weber, A. S. Pensado, A. Stark and B. Kirchner, Phys. Chem. Chem. Phys., 2012, 14, 5030–5044 RSC.
- M. G. Del Pópolo, R. M. Lynden-Bell and J. Kohanoff, J. Phys. Chem. B, 2005, 109, 5895–5902 CrossRef PubMed.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. B, 2012, 116, 10036–10048 CrossRef CAS PubMed.
- P. Koskinen and V. Mäkinen, Comput. Mater. Sci., 2009, 47, 237–253 CrossRef CAS.
- M. Elstner and G. Seifert, Density functional tight binding, 2014 Search PubMed.
- A. F. Oliveira, G. Seifert, T. Heine and H. A. Duarte, J. Braz. Chem. Soc., 2009, 20, 1193–1205 CrossRef CAS.
- M. A. Addicoat, R. Stefanovic, G. B. Webber, R. Atkin and A. J. Page, J. Chem. Theory Comput., 2014, 10, 4633–4643 CrossRef CAS PubMed.
- T. Carstens, R. Gustus, O. Höfft, N. Borisenko, F. Endres, H. Li, R. J. Wood, A. J. Page and R. Atkin, J. Phys. Chem. C, 2014, 118, 10833–10843 CAS.
- A. J. Page, A. Elbourne, R. Stefanovic, M. A. Addicoat, G. G. Warr, K. Voitchovsky and R. Atkin, Nanoscale, 2014, 6, 8100–8106 RSC.
- M. A. Addicoat, S. Fukuoka, A. J. Page and S. Irle, J. Comput. Chem., 2013, 34, 2591–2600 CrossRef CAS PubMed.
- E. J. Maginn, in Reviews in Computational Chemistry, John Wiley & Sons, Inc., 2009, pp. 421–493 Search PubMed.
- J. Canongia Lopes and A. H. Pádua, Theor. Chem. Acc., 2012, 131, 1129 CrossRef.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 11250 CrossRef.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- J. N. Canongia Lopes and A. A. H. Pádua, J. Phys. Chem. B, 2006, 110, 19586–19592 CrossRef CAS PubMed.
- J. N. Canongia Lopes, A. A. H. Pádua and K. Shimizu, J. Phys. Chem. B, 2008, 112, 5039–5046 CrossRef CAS PubMed.
- A. Warshel and M. Levitt, J. Mol. Biol., 1976, 103, 227–249 CrossRef CAS PubMed.
- M. J. Field, P. A. Bash and M. Karplus, J. Comput. Chem., 1990, 11, 700–733 CrossRef CAS.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- B. Zhang, A. C. T. van Duin and J. K. Johnson, J. Phys. Chem. B, 2014, 118, 12008–12016 CrossRef CAS PubMed.
- Y. Wang, S. Feng and G. A. Voth, J. Chem. Theory Comput., 2009, 5, 1091–1098 CrossRef CAS.
- Y. Wang, W. Jiang, T. Yan and G. A. Voth, Acc. Chem. Res., 2007, 40, 1193–1199 CrossRef CAS PubMed.
- B. L. Bhargava, R. Devane, M. L. Klein and S. Balasubramanian, Soft Matter, 2007, 3, 1395–1400 RSC.
- J. Wohlert and L. A. Berglund, J. Chem. Theory Comput., 2011, 7, 753–760 CrossRef CAS.
- C. A. López, A. J. Rzepiela, A. H. de Vries, L. Dijkhuizen, P. H. Hünenberger and S. J. Marrink, J. Chem. Theory Comput., 2009, 5, 3195–3210 CrossRef.
- S. Riniker, J. R. Allison and W. F. van Gunsteren, Phys. Chem. Chem. Phys., 2012, 14, 12423–12430 RSC.
- P. A. Hunt, J. Phys. Chem. B, 2007, 111, 4844–4853 CrossRef CAS PubMed.
- K. Fumino, T. Peppel, M. Geppert-Rybczynska, D. H. Zaitsau, J. K. Lehmann, S. P. Verevkin, M. Kockerling and R. Ludwig, Phys. Chem. Chem. Phys., 2011, 13, 14064–14075 RSC.
- I. Skarmoutsos, D. Dellis, R. P. Matthews, T. Welton and P. A. Hunt, J. Phys. Chem. B, 2012, 116, 4921–4933 CrossRef CAS PubMed.
- Y. Zhang and E. J. Maginn, Phys. Chem. Chem. Phys., 2012, 14, 12157–12164 RSC.
- I. Skarmoutsos, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3675–3685 RSC.
- K. Wendler, S. Zahn, F. Dommert, R. Berger, C. Holm, B. Kirchner and L. Delle Site, J. Chem. Theory Comput., 2011, 7, 3040–3044 CrossRef CAS.
- S. Kossmann, J. Thar, B. Kirchner, P. A. Hunt and T. Welton, J. Chem. Phys., 2006, 124, 174506 CrossRef PubMed.
- M. Gonzalez-Miquel, M. Talreja, A. L. Ethier, K. Flack, J. R. Switzer, E. J. Biddinger, P. Pollet, J. Palomar, F. Rodriguez, C. A. Eckert and C. L. Liotta, Ind. Eng. Chem. Res., 2012, 51, 16066–16073 CrossRef CAS.
- J. Völkl, K. Müller, L. Mokrushina and W. Arlt, Chem. Eng. Technol., 2012, 35, 579–583 CrossRef.
- O. Holloczki, F. Malberg, T. Welton and B. Kirchner, Phys. Chem. Chem. Phys., 2014, 16, 16880–16890 RSC.
- V. S. Bernales, A. V. Marenich, R. Contreras, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2012, 116, 9122–9129 CrossRef CAS PubMed.
- X. Wei and D. Zhang, Comput. Theor. Chem., 2013, 1014, 24–28 CrossRef CAS.
- B. G. Janesko, Phys. Chem. Chem. Phys., 2014, 16, 5423–5433 RSC.
- V. N. Emel'yanenko, S. P. Verevkin and A. Heintz, J. Am. Chem. Soc., 2007, 129, 3930–3937 CrossRef PubMed.
- P. A. Hunt, B. Kirchner and T. Welton, Chem.–Eur. J., 2006, 12, 6762–6775 CrossRef CAS PubMed.
- P. Nockemann, B. Thijs, K. Driesen, C. R. Janssen, K. Van Hecke, L. Van Meervelt, S. Kossmann, B. Kirchner and K. Binnemans, J. Phys. Chem. B, 2007, 111, 5254–5263 CrossRef CAS PubMed.
- C. S. Pomelli, C. Chiappe, A. Vidis, G. Laurenczy and P. J. Dyson, J. Phys. Chem. B, 2007, 111, 13014–13019 CrossRef CAS PubMed.
- Y. Wang, H. Li and S. Han, J. Chem. Phys., 2005, 123, 174501 CrossRef PubMed.
- Y. Wang, H. Li and S. Han, J. Phys. Chem. B, 2006, 110, 24646–24651 CrossRef CAS PubMed.
- C. Krekeler, J. Schmidt, Y. Y. Zhao, B. Qiao, R. Berger, C. Holm and L. Delle Site, J. Chem. Phys., 2008, 129, 174503 CrossRef PubMed.
- B. L. Bhargava and S. Balasubramanian, Chem. Phys. Lett., 2007, 444, 242–246 CrossRef CAS.
- E. I. Izgorodina, U. L. Bernard and D. R. MacFarlane, J. Phys. Chem. A, 2009, 113, 7064–7072 CrossRef CAS PubMed.
- E. I. Izgorodina, D. Golze, R. Maganti, V. Armel, M. Taige, T. J. S. Schubert and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2014, 16, 7209–7221 RSC.
- S. Grimme, W. Hujo and B. Kirchner, Phys. Chem. Chem. Phys., 2012, 14, 4875–4883 RSC.
- S. Zahn, D. R. MacFarlane and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 13664–13675 RSC.
- B. G. Janesko, Phys. Chem. Chem. Phys., 2011, 13, 11393–11401 RSC.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2006, 110, 11481–11490 CrossRef CAS PubMed.
- J. Rigby and E. I. Izgorodina, Phys. Chem. Chem. Phys., 2013, 15, 1632–1646 RSC.
- Y. Dai, Y. Qu, S. Wang and J. Wang, Chem. Phys. Lett., 2014, 608, 366 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- P. O. Löwdin, J. Chem. Phys., 1950, 18, 365–375 CrossRef.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- F. Martin and H. Zipse, J. Comput. Chem., 2005, 26, 97–105 CrossRef CAS PubMed.
- M. Bühl, A. Chaumont, R. Schurhammer and G. Wipff, J. Phys. Chem. B, 2005, 109, 18591–18599 CrossRef PubMed.
- R. M. Lynden-Bell, Phys. Chem. Chem. Phys., 2010, 12, 1733–1740 RSC.
- Z. Liu, T. Chen, A. Bell and B. Smit, J. Phys. Chem. B, 2010, 114, 4572–4582 CrossRef CAS PubMed.
- K. Wendler, F. Dommert, Y. Y. Zhao, R. Berger, C. Holm and L. Delle Site, Faraday Discuss., 2012, 154, 111–132 RSC.
- M. Kohagen, M. Brehm, J. Thar, W. Zhao, F. Müller-Plathe and B. Kirchner, J. Phys. Chem. B, 2010, 115, 693–702 CrossRef PubMed.
- E. Bodo, S. Mangialardo, F. Ramondo, F. Ceccacci and P. Postorino, J. Phys. Chem. B, 2012, 116, 13878–13888 CrossRef CAS PubMed.
- F. Dommert, K. Wendler, B. Qiao, L. Delle Site and C. Holm, J. Mol. Liq., 2014, 192, 32–37 CrossRef CAS.
- A. Mondal and S. Balasubramanian, J. Phys. Chem. B, 2014, 118, 3409–3422 CrossRef CAS PubMed.
- W. Beichel, N. Trapp, C. Hauf, O. Kohler, G. Eickerling, W. Scherer and I. Krossing, Angew. Chem., Int. Ed., 2014, 126, 3207–3210 CrossRef.
- V. V. Chaban, I. V. Voroshylova and O. N. Kalugin, Phys. Chem. Chem. Phys., 2011, 13, 7910–7920 RSC.
- M. Lísal, Z. Chval, J. Storch and P. Izák, J. Mol. Liq., 2014, 189, 85–94 CrossRef.
- M. A. Carignano, J. Phys. Chem. B, 2013, 117, 15176–15183 CAS.
- F. Chen, L. Jin, S. W. de Leeuw, J. M. Pringle and M. Forsyth, J. Chem. Phys., 2013, 138, 244503–244513 CrossRef CAS PubMed.
- H. Liu, Z. Zhang, J. E. Bara and C. H. Turner, J. Phys. Chem. B, 2013, 118, 255–264 CrossRef PubMed.
- C. M. Tenney, M. Massel, J. M. Mayes, M. Sen, J. F. Brennecke and E. J. Maginn, J. Chem. Eng. Data, 2014, 59, 391–399 CrossRef CAS.
- D. T. Bowron, C. D'Agostino, L. F. Gladden, C. Hardacre, J. D. Holbrey, M. C. Lagunas, J. McGregor, M. D. Mantle, C. L. Mullan and T. G. A. Youngs, J. Phys. Chem. B, 2010, 114, 7760–7768 CrossRef CAS PubMed.
- Z. L. Terranova and S. A. Corcelli, J. Phys. Chem. B, 2013, 117, 15659–15666 CrossRef CAS PubMed.
- B. L. Bhargava and S. Balasubramanian, J. Chem. Phys., 2007, 127, 114510 CrossRef CAS PubMed.
- T. G. A. Youngs and C. Hardacre, ChemPhysChem, 2008, 9, 1548–1558 CrossRef CAS PubMed.
- F. Dommert, J. Schmidt, B. Qiao, Y. Zhao, C. Krekeler, L. Delle Site, R. Berger and C. Holm, J. Chem. Phys., 2008, 129, 224501 CrossRef PubMed.
- C. E. Resende Prado and L. C. Gomide Freitas, J. Mol. Struct.: THEOCHEM, 2007, 847, 93–100 CrossRef CAS.
- Z. Liu, X. Wu and W. Wang, Phys. Chem. Chem. Phys., 2006, 8, 1096–1104 RSC.
- S. Zhang, N. Sun, X. He, X. Lu and X. Zhang, J. Phys. Chem. Ref. Data, 2006, 35, 1475–1517 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS.
- H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600 CrossRef CAS PubMed.
- J. de Andrade, E. S. Böes and H. Stassen, J. Phys. Chem. B, 2002, 106, 13344–13351 CrossRef CAS.
- Z. Liu, S. Huang and W. Wang, J. Phys. Chem. B, 2004, 108, 12978–12989 CrossRef CAS.
- A. Noda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2001, 105, 4603–4610 CrossRef CAS.
- A. Deyko, K. R. J. Lovelock, J.-A. Corfield, A. W. Taylor, P. N. Gooden, I. J. Villar-Garcia, P. Licence, R. G. Jones, V. G. Krasovskiy, E. A. Chernikova and L. M. Kustov, Phys. Chem. Chem. Phys., 2009, 11, 8544–8555 RSC.
- S. V. Sambasivarao and O. Acevedo, J. Chem. Theory Comput., 2009, 5, 1038–1050 CrossRef CAS.
- W.-G. Xu, L. Li, X.-X. Ma, J. Wei, W.-B. Duan, W. Guan and J.-Z. Yang, J. Chem. Eng. Data, 2012, 57, 2177–2184 CrossRef CAS.
- B. B. Hurisso, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 17737–17748 RSC.
- S. Men, K. R. J. Lovelock and P. Licence, Phys. Chem. Chem. Phys., 2011, 13, 15244–15255 RSC.
- T. Cremer, C. Kolbeck, K. R. J. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H.-P. Steinrück, Chem.–Eur. J., 2010, 16, 9018–9033 CrossRef CAS PubMed.
- C. Schroder, Phys. Chem. Chem. Phys., 2012, 14, 3089–3102 RSC.
- S. Gabl, C. Schröder and O. Steinhauser, J. Chem. Phys., 2012, 137, 94501 CrossRef PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- G. Kaminski and W. L. Jorgensen, J. Phys. Chem., 1996, 100, 18010–18013 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- A. Bagno, F. D'Amico and G. Saielli, J. Mol. Liq., 2007, 131–132, 17–23 CrossRef CAS.
- T. Yan, C. J. Burnham, M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 11877–11881 CrossRef CAS.
- C. E. R. Prado, M. G. D. Pópolo, T. G. A. Youngs, J. Kohanoff and R. M. Lynden-Bell, Mol. Phys., 2006, 104, 2477–2483 CrossRef CAS.
- R. M. Lynden-Bell, M. G. Del Pópolo, T. G. A. Youngs, J. Kohanoff, C. G. Hanke, J. B. Harper and C. C. Pinilla, Acc. Chem. Res., 2007, 40, 1138–1145 CrossRef CAS PubMed.
- F. Dommert and C. Holm, Phys. Chem. Chem. Phys., 2013, 15, 2037–2049 RSC.
- X. Liu, G. Zhou, S. Zhang, G. Wu and G. Yu, J. Phys. Chem. B, 2007, 111, 5658–5668 CrossRef CAS PubMed.
- T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2007, 8, 2464–2470 CrossRef PubMed.
- T. Yan, Y. Wang and C. Knox, J. Phys. Chem. B, 2010, 114, 6905–6921 CrossRef CAS PubMed.
- T. Yan, Y. Wang and C. Knox, J. Phys. Chem. B, 2010, 114, 6886–6904 CrossRef CAS PubMed.
- B. T. Thole, Chem. Phys., 1981, 59, 341–350 CrossRef CAS.
- F. Wang and K. D. Jordan, J. Chem. Phys., 2001, 114, 10717–10724 CrossRef CAS.
- T.-M. Chang and L. X. Dang, J. Phys. Chem. A, 2009, 113, 2127–2135 CrossRef CAS PubMed.
- T. Taylor, M. Schmollngruber, C. Schröder and O. Steinhauser, J. Chem. Phys., 2013, 138, 204119–204128 CrossRef PubMed.
- Y. Gu and T. Yan, J. Phys. Chem. A, 2012, 117, 219–227 CrossRef PubMed.
- O. Borodin and G. D. Smith, J. Phys. Chem. B, 2006, 110, 6279–6292 CrossRef CAS PubMed.
- O. Borodin, J. Phys. Chem. B, 2009, 113, 11463–11478 CrossRef CAS PubMed.
- D. Bedrov, O. Borodin, Z. Li and G. D. Smith, J. Phys. Chem. B, 2010, 114, 4984–4997 CrossRef CAS PubMed.
- J. B. Hooper, O. N. Starovoytov, O. Borodin, D. Bedrov and G. D. Smith, J. Chem. Phys., 2012, 136, 194506/194501–194506/194507 CrossRef PubMed.
- C. Schröder and O. Steinhauser, J. Chem. Phys., 2010, 133, 154511 CrossRef PubMed.
- C. Schröder, J. Chem. Phys., 2011, 135, 24502–24512 CrossRef PubMed.
- C. Schroder, T. Sonnleitner, R. Buchner and O. Steinhauser, Phys. Chem. Chem. Phys., 2011, 13, 12240–12248 RSC.
- Y. Wu, Y. Li, N. Hu and M. Hong, Phys. Chem. Chem. Phys., 2014, 16, 2674–2685 RSC.
- A. d. O. Cavalcante, M. C. C. Ribeiro and M. S. Skaf, J. Chem. Phys., 2014, 140, 144108–144117 CrossRef PubMed.
- K. Shimizu, D. Almantariotis, M. F. C. Gomes, A. A. H. Padua and J. N. Canongia Lopes, J. Phys. Chem. B, 2010, 114, 3592–3600 CrossRef CAS PubMed.
- X. Wu, Z. Liu, S. Huang and W. Wang, Phys. Chem. Chem. Phys., 2005, 7, 2771–2779 RSC.
- C. Cadena and E. J. Maginn, J. Phys. Chem. B, 2006, 110, 18026–18039 CrossRef CAS PubMed.
- C. Cadena, Q. Zhao, R. Q. Snurr and E. J. Maginn, J. Phys. Chem. B, 2006, 110, 2821–2832 CrossRef CAS PubMed.
- T. I. Morrow and E. J. Maginn, J. Phys. Chem. B, 2002, 106, 12807–12813 CrossRef CAS.
- M. S. Kelkar, W. Shi and E. J. Maginn, Ind. Eng. Chem. Res., 2008, 47, 9115–9126 CrossRef CAS.
- K. E. Gutowski, B. Gurkan and E. J. Maginn, Pure Appl. Chem., 2009, 81, 1799–1828 CrossRef CAS.
- T. Köddermann, D. Reith and R. Ludwig, ChemPhysChem, 2013, 14, 3368–3374 CrossRef PubMed.
- N. M. Micaelo, A. M. Baptista and C. M. Soares, J. Phys. Chem. B, 2006, 110, 14444–14451 CrossRef CAS PubMed.
- J. de Andrade, E. S. Boees and H. Stassen, J. Phys. Chem. B, 2002, 106, 3546–3548 CrossRef CAS.
- X. Liu, S. Zhang, G. Zhou, G. Wu, X. Yuan and X. Yao, J. Phys. Chem. B, 2006, 110, 12062–12071 CrossRef CAS PubMed.
- X. Liu, G. Zhou and S. Zhang, Fluid Phase Equilib., 2008, 272, 1–7 CrossRef CAS.
- X. M. Liu, X. C. Zhang, G. H. Zhou, X. Q. Yao and S. J. Zhang, Sci. China: Chem., 2012, 55, 1573–1579 CrossRef CAS.
- G. Zhou, X. Liu, S. Zhang, G. Yu and H. He, J. Phys. Chem. B, 2007, 111, 7078–7084 CrossRef CAS PubMed.
- X. Liu, Y. Zhao, X. Zhang, G. Zhou and S. Zhang, J. Phys. Chem. B, 2012, 116, 4934–4942 CrossRef CAS PubMed.
- Y. Zhao, X. Liu, J. Wang and S. Zhang, ChemPhysChem, 2012, 13, 3126–3133 CrossRef CAS PubMed.
- T. G. A. Youngs, M. G. Del Popolo and J. Kohanoff, J. Phys. Chem. B, 2006, 110, 5697–5707 CrossRef CAS PubMed.
- Y. Wang, H. Pan, H. Li and C. Wang, J. Phys. Chem. B, 2007, 111, 10461–10467 CrossRef CAS PubMed.
- M. G. Del Pópolo and G. A. Voth, J. Phys. Chem. B, 2004, 108, 1744–1752 CrossRef.
- Y. Hu, H. Jiang, X. Zhang, Z. Liu, J. Ren and R. Liu, J. Mol. Struct.: THEOCHEM, 2009, 915, 132–140 CrossRef CAS.
- H. Liu, K. L. Sale, B. M. Holmes, B. A. Simmons and S. Singh, J. Phys. Chem. B, 2010, 114, 4293–4301 CrossRef CAS PubMed.
- F. Yan, M. Lartey, K. Damodaran, E. Albenze, R. L. Thompson, J. Kim, M. Haranczyk, H. B. Nulwala, D. R. Luebke and B. Smit, Phys. Chem. Chem. Phys., 2013, 15, 3264–3272 RSC.
- Y.-L. Wang, F. U. Shah, S. Glavatskih, O. N. Antzutkin and A. Laaksonen, J. Phys. Chem. B, 2014, 118, 8711–8723 CrossRef CAS PubMed.
- I. V. Voroshylova and V. V. Chaban, J. Phys. Chem. B, 2014, 118, 10716–10724 CrossRef CAS PubMed.
- S. U. Lee, J. Jung and Y.-K. Han, Chem. Phys. Lett., 2005, 406, 332–340 CrossRef CAS.
- M. Lísal, J. Chem. Phys., 2013, 139, 214701 CrossRef PubMed.
- T. Koller, J. Ramos, N. M. Garrido, A. P. Froba and I. G. Economou, Mol. Phys., 2012, 110, 1115–1126 CrossRef CAS.
- Z.-P. Liu, T. Chen, A. Bell and B. Smit, J. Phys. Chem. B, 2010, 114, 4572–4582 CrossRef CAS PubMed.
- X. Zhong, Z. Liu and D. Cao, J. Phys. Chem. B, 2011, 115, 10027–10040 CrossRef CAS PubMed.
- E. E. Fileti and V. V. Chaban, Chem. Phys. Lett., 2014, 616–617, 205–211 CrossRef CAS.
- Y. Wu, N. Hu, L. Yue, L. Wei and W. Guan, J. Chem. Phys., 2015, 142, 064503 CrossRef PubMed.
- M. Klahn, A. Seduraman and P. Wu, J. Phys. Chem. B, 2008, 112, 10989–11004 CrossRef CAS PubMed.
- O. N. Starovoytov, H. Torabifard and G. A. Cisneros, J. Phys. Chem. B, 2014, 118, 7156–7166 CrossRef CAS PubMed.
- Z. Hu, X. Huang, H. V. R. Annapureddy and C. J. Margulis, J. Phys. Chem. B, 2008, 112, 7837–7849 CrossRef CAS PubMed.
- E. Choi, J. G. McDaniel, J. R. Schmidt and A. Yethiraj, J. Phys. Chem. Lett., 2014, 5, 2670–2674 CrossRef CAS PubMed.
- J. G. McDaniel and J. R. Schmidt, J. Phys. Chem. A, 2013, 117, 2053–2066 CrossRef CAS PubMed.
- J. B. Harper and R. M. Lynden-Bell, Mol. Phys., 2004, 102, 85–94 CrossRef CAS.
- L. A. Blanchard and J. F. Brennecke, Ind. Eng. Chem. Res., 2000, 40, 287–292 CrossRef.
- C. G. Hanke, A. Johansson, J. B. Harper and R. M. Lynden-Bell, Chem. Phys. Lett., 2003, 374, 85–90 CrossRef CAS.
- K. Shimizu, M. F. Costa Gomes, A. A. H. Pádua, L. P. N. Rebelo and J. N. Canongia Lopes, J. Phys. Chem. B, 2009, 113, 9894–9900 CrossRef CAS PubMed.
- M. B. Shiflett and A. Yokozeki, J. Chem. Eng. Data, 2008, 53, 2683–2691 CrossRef CAS.
- J. Lachwa, J. Szydlowski, A. Makowska, K. R. Seddon, J. M. S. S. Esperanca, H. J. R. Guedes and L. P. N. Rebelo, Green Chem., 2006, 8, 262–267 RSC.
- D. J. Cram and M. Goldstein, J. Am. Chem. Soc., 1963, 85, 1063–1074 CrossRef CAS.
- X. Zhang, X. Zhang, H. Dong, Z. Zhao, S. Zhang and Y. Huang, Energy Environ. Sci., 2012, 5, 6668–6681 CAS.
- Z. Lei, C. Dai and B. Chen, Chem. Rev., 2013, 114, 1289–1326 CrossRef PubMed.
- A. Maiti, Int. J. Quantum Chem., 2014, 114, 163–175 CrossRef CAS.
- E. Torralba-Calleja, J. Skinner and D. Gutirrez-Tauste, J. Chem., 2013, 2013, 16 Search PubMed.
- H. Liu, S. Dai and D.-e. Jiang, J. Phys. Chem. B, 2014, 118, 2719–2725 CrossRef CAS PubMed.
- M. Mohammadi and M. Foroutan, J. Mol. Liq., 2014, 193, 60–68 CrossRef CAS.
- S. N. V. K. Aki, B. R. Mellein, E. M. Saurer and J. F. Brennecke, J. Phys. Chem. B, 2004, 108, 20355–20365 CrossRef CAS.
- J. Xu, S. Wang, W. Yu, Q. Xu, W. Wang and J. Yin, Chin. J. Chem. Eng., 2014, 22, 153–163 CrossRef CAS.
- C. Cadena, J. L. Anthony, J. K. Shah, T. I. Morrow, J. F. Brennecke and E. J. Maginn, J. Am. Chem. Soc., 2004, 126, 5300–5308 CrossRef CAS PubMed.
- T. C. Lourenço, M. F. C. Coelho, T. C. Ramalho, D. van der Spoel and L. T. Costa, Environ. Sci. Technol., 2013, 47, 7421–7429 Search PubMed.
- A. Brandt, J. Grasvik, J. P. Hallett and T. Welton, Green Chem., 2013, 15, 550–583 RSC.
- D. A. Fort, R. C. Remsing, R. P. Swatloski, P. Moyna, G. Moyna and R. D. Rogers, Green Chem., 2007, 9, 63–69 RSC.
- L. Kyllonen, A. Parviainen, S. Deb, M. Lawoko, M. Gorlov, I. Kilpelainen and A. W. T. King, Green Chem., 2013, 15, 2374–2378 RSC.
- L. J. A. Conceicao, E. Bogel-Lukasik and R. Bogel-Lukasik, RSC Adv., 2012, 2, 1846–1855 RSC.
- M. M. Hossain and L. Aldous, Aust. J. Chem., 2012, 65, 1465–1477 CrossRef CAS.
- B. D. Rabideau, A. Agarwal and A. E. Ismail, J. Phys. Chem. B, 2014, 118, 1621–1629 CrossRef CAS PubMed.
- N. Sun, R. Parthasarathi, A. M. Socha, J. Shi, S. Zhang, V. Stavila, K. L. Sale, B. A. Simmons and S. Singh, Green Chem., 2014, 16, 2546–2557 RSC.
- W. E. S. Hart, J. B. Harper and L. Aldous, Green Chem., 2015, 17, 214 RSC.
- N. P. Novoselov, E. S. Sashina, V. E. Petrenko and M. Zaborsky, Fibre Chem., 2007, 39, 153–158 CrossRef CAS.
- Z. Jarin and J. Pfaendtner, J. Chem. Theory Comput., 2014, 10, 507–510 CrossRef CAS.
- J. Zhang, H. Zhang, J. Wu, J. Zhang, J. He and J. Xiang, Phys. Chem. Chem. Phys., 2010, 12, 1941–1947 RSC.
- X. Creary, E. D. Willis and M. Gagnon, J. Am. Chem. Soc., 2005, 127, 18114–18120 CrossRef CAS PubMed.
- L.-y. Liu, B. Wang, H.-m. Yang, W.-x. Chang and J. Li, Tetrahedron Lett., 2011, 52, 5636–5639 CrossRef CAS.
- K. K. Laali and V. J. Gettwert, J. Fluorine Chem., 2001, 107, 31–34 CrossRef CAS.
- K. K. Laali, T. Okazaki and S. D. Bunge, J. Org. Chem., 2007, 72, 6758–6762 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, E. Marmugi and D. Pieraccini, Chem. Commun., 2006, 897–899 RSC.
- R. Bini, O. Bortolini, C. Chiappe, D. Pieraccini and T. Siciliano, J. Phys. Chem. B, 2007, 111, 598–604 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, C. S. Pomelli and B. Parisi, J. Org. Chem., 2009, 74, 8522–8530 CrossRef CAS PubMed.
- E. I. Izgorodina, R. Maganti, V. Armel, P. M. Dean, J. M. Pringle, K. R. Seddon and D. R. MacFarlane, J. Phys. Chem. B, 2011, 115, 14688–14697 CrossRef CAS PubMed.
- O. Acevedo, W. L. Jorgensen and J. D. Evanseck, J. Chem. Theory Comput., 2007, 3, 132–138 CrossRef CAS.
- S. T. Keaveney, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2015, 3771–3780 CAS.
- Y. Yoshida, O. Baba, C. Larriba and G. Saito, J. Phys. Chem. B, 2007, 111, 12204–12210 CrossRef CAS PubMed.
- Z. Ren, A. S. Ivanova, D. Couchot-Vore and S. Garrett-Roe, J. Phys. Chem. Lett., 2014, 5, 1541–1546 CrossRef CAS PubMed.
- N. L. Lancaster, T. Welton and G. B. Young, J. Chem. Soc., Perkin Trans. 2, 2001, 2267–2270 RSC.
- N. L. Lancaster and T. Welton, J. Org. Chem., 2004, 69, 5986–5992 CrossRef CAS PubMed.
- L. Crowhurst, R. Falcone, N. L. Lancaster, V. Llopis-Mestre and T. Welton, J. Org. Chem., 2006, 71, 8847–8853 CrossRef CAS PubMed.
- G. M. Arantes and M. C. C. Ribeiro, J. Chem. Phys., 2008, 128, 114503 CrossRef PubMed.
- S. Alunni, A. Pero and G. Reichenbach, J. Chem. Soc., Perkin Trans. 2, 1998, 1747–1750 RSC.
- S. Coleman, R. Byrne, S. Minkovska and D. Diamond, Phys. Chem. Chem. Phys., 2009, 11, 5608–5614 RSC.
- S. Zhang, Q. Zhang, B. Ye, X. Li, X. Zhang and Y. Deng, J. Phys. Chem. B, 2009, 113, 6012–6019 CrossRef CAS PubMed.
- R. Byrne, K. J. Fraser, E. Izgorodina, D. R. MacFarlane, M. Forsyth and D. Diamond, Phys. Chem. Chem. Phys., 2008, 10, 5919–5924 RSC.
- R. Byrne, S. Coleman, K. J. Fraser, A. Raduta, D. R. MacFarlane and D. Diamond, Phys. Chem. Chem. Phys., 2009, 11, 7286–7291 RSC.
- C. Allen, B. W. McCann and O. Acevedo, J. Phys. Chem. B, 2014, 743–752 Search PubMed.
- D. A. Jaeger and C. E. Tucker, Tetrahedron Lett., 1989, 30, 1785–1788 CrossRef CAS.
- S. Tiwari and A. Kumar, Angew. Chem., Int. Ed., 2006, 45, 4824–4825 CrossRef CAS PubMed.
- C. Chiappe, M. Malvaldi and C. S. Pomelli, Green Chem., 2010, 12, 1330–1339 RSC.
- R. Bini, C. Chiappe, V. L. Mestre, C. S. Pomelli and T. Welton, Org. Biomol. Chem., 2008, 6, 2522–2529 CAS.
- S. Tiwari, N. Khupse and A. Kumar, J. Org. Chem., 2008, 73, 9075–9083 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, V. Mestre, C. Pomelli and T. Welton, Theor. Chem. Acc., 2009, 123, 347–352 CrossRef CAS.
- H. Sun, D. Zhang, C. Ma and C. Liu, Int. J. Quantum Chem., 2007, 107, 1875–1885 CrossRef CAS.
- A. Kovalenko and F. Hirata, Chem. Phys. Lett., 1998, 290, 237–244 CrossRef CAS.
- A. Kovalenko and F. Hirata, J. Chem. Phys., 1999, 110, 10095–10112 CrossRef CAS.
- C. Chiappe, M. Malvaldi and C. S. Pomelli, J. Chem. Theory Comput., 2010, 6, 179–183 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |