High-temperature creep properties of TATB-based polymer bonded explosives filled with multi-walled carbon nanotubes
Abstract
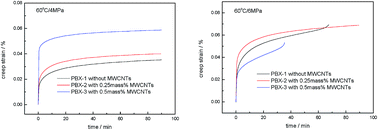
In order to investigate the effects of multi-walled carbon nanotubes (MWCNTs) content and loading stress on the high-temperature creep properties of 1,3,5-triamino-2,4,6-trinitrobenzene (TATB)-based polymer bonded explosives (PBXs), three-point bending creep behavior was studied by dynamic mechanical analyzer at 60 °C. The experimental results showed that under low stress (4 MPa), the constant creep strain rates of the MWCNTs modified formulation reduced with MWCNT concentration. However, due to the agglomeration of MWCNTs, the existence of intertube sliding or stick-slip resulted in an increase in creep strain. Under higher stress (6 MPa and 7 MPa), with only 0.25 mass% of MWCNTs, the creep resistance of TATB-based PBX could be significantly improved with reduced constant creep strain rate. Additionally, compared with TATB-based PBX without MWCNTs, the creep lifetime of the nanocomposites with a content of 0.25 mass% MWCNTs had been considerably extended by over 33.3% and 750% under 6 MPa and 7 MPa, respectively. The nanocomposites with a content of 0.5 mass% MWCNTs displayed a lower creep resistance compared to that of the TATB-based PBX without MWCNTs. The creep resistance of the TATB-based PBXs depends significantly on loading stress. A six-element model could be used to simulate the high-temperature creep behaviors of the TATB-based PBXs with and without MWCNTs. The constitutive equations of the creep curves under different stresses at 60 °C were obtained. Among the fitting parameters, the elastic modulus of high elastic deformation E3 and the viscosity of Voigt units η3 were sensitive and promising for the evaluation of the creep strain of the TATB-based PBXs.

 Please wait while we load your content...
Please wait while we load your content...