Tug-of-war between corrugation and binding energy: revealing the formation of multiple moiré patterns on a strongly interacting graphene–metal system

Abstract

The formation of multidomain epitaxial graphene on Rh(111) under ultra-high vacuum (UHV) conditions has been characterized by scanning tunnelling microscopy (STM) measurements and density functional theory (DFT) calculations. At variance with the accepted view for strongly interacting graphene–metal systems, we clearly demonstrate the formation of different rotational domains leading to multiple moiré structures with a wide distribution of surface periodicities. Experiments reveal a correlation between the STM apparent corrugation and the lattice parameter of the moiré unit cell, with corrugations of just 30–40 pm for the smallest moirés. DFT calculations for a relevant selection of these moiré patterns show much larger height differences and a non-monotonic behaviour with the moiré size. Simulations based on non-equilibrium Green's function (NEGF) methods reproduce quantitatively the experimental trend and provide a detailed understanding of the interplay between electronic and geometric contributions in the STM contrast of graphene systems. Our study sheds light on the subtle energy balance among strain, corrugation and binding that drives the formation of the moiré patterns in all graphene/metal systems and suggests an explanation for the success of an effective model only based on the lattice mismatch. Although low values of the strain energy are a necessary condition, it is the ability of graphene to corrugate in order to maximize the areas of favourable graphene–metal interactions that finally selects the stable configurations.

---

Introduction

The growth of graphene is of paramount importance for a forthcoming new technology based on this two dimensional material.^1–4 Among all the different techniques, the epitaxial growth of graphene (G) on transition metals has been swiftly developed as a quick method for the large scale production of high quality graphene.⁵ Scanning tunnelling microscopy (STM) has already played a fundamental role in the characterization of these systems. STM confirmed the formation of moiré patterns as a consequence of the different lattice parameters of the graphene and the metal underneath and the relative angle between them. The G–metal interaction not only induces structural changes but also can modify and tune the remarkable electronic properties of G.^6–10 According to the strength of the interaction between the carbon layer and the metallic substrate, two subgroups were defined: those systems in which the graphene is barely coupled to the substrate, like graphene on Pt(111),¹¹ Ir(111)¹² or Cu(111),¹³ where the electronic properties of graphene remain almost unchanged except for a small charge transfer with the metal underneath;^7,9,11,14 and those like Ru(0001),¹⁵ Re(0001)¹⁶ and Rh(111),¹⁷ in which the hybridization of the π band of the graphene with the d band of the metal leads to a strong coupling that dramatically modifies the electronic structure from that of free-standing graphene.⁷ In the first subgroup, and as a consequence of the low interaction between graphene and the metal underneath, several rotational domains are stable on the surface,^{10,14,18–20} while in the strongly interacting systems, the opposite case, just one orientation, leading to only one moiré pattern, has been mainly observed.^{10,16,17,21,22}

The highly interacting graphene on the Rh(111) system is one of the cases where both experiments and density functional theory (DFT) calculations have shown the formation of a commensurate (12 × 12)_G on a (11 × 11) Rh(111) superstructure in which both atomic layers are aligned with the moiré.^17,23,24 According to DFT calculations,^23,24 this pattern is highly corrugated, with a difference in height among the topmost and the bottom C atom larger than 100 pm. This variation in the graphene–metal distance along the moiré unit cell gives rise to a significant change in the interaction between them and a gradual shift in the chemical environment of the C atoms as it was proved by photoelectron spectroscopy.⁷ This pattern of large geometrical corrugations seems to be characteristic of the strongly interacting systems. In contrast, the buckling of the graphene sheet in the weakly coupled graphene/metal group is much lower and the distances between both layers are higher in every region. DFT calculations¹¹ for the graphene on Pt(111) have concluded that the geometric buckling is very low, less than 3 pm. STM experiments seem to confirm these trends, with apparent corrugations of ∼100 pm for highly interacting systems and one order of magnitude lower, ∼10 pm, for systems with weak G–metal coupling. However, care must be taken when attempting a direct quantitative comparison between the real geometry and the apparent STM corrugation, where both electronic and structural contributions play a role. G/Pt(111) is a paradigmatic example where the STM images exhibit an anticorrugation of one order of magnitude larger than the height difference among the C atoms due to subtle changes in the electronic structure induced by the metal interaction.¹¹

In this study, we report on the growth of graphene on Rh(111) under ultra-high vacuum conditions and challenge some of the main ideas assumed so far for strongly interacting G–metal systems. We clearly demonstrate the formation of several rotational domains and therefore different moiré structures with a wide distribution of surface periodicities. Experiments reveal a monotonous correlation between the STM apparent corrugation and the lattice parameter of the moiré unit cell, with corrugations of just 30–40 pm for the smallest moirés. The structure of a relevant selection of these moiré patterns has been determined with DFT. These calculations show much larger height differences and a non-monotonic behaviour with the moiré size. Simulations of the STM current based on non-equilibrium Green's function (NEGF) methods, in which the electronic current between the tip and the sample is correctly addressed,²⁵ reproduce quantitatively the experimental trend and provide a detailed understanding of the interplay between electronic and geometric contributions in the contrast formation of the graphene systems. Finally, based on this agreement between theory and experiment, we discuss how the balance between the relative contributions of strain, corrugation and G–metal binding energies stabilizes the observed moirés. This detailed study sheds light on the general understanding of the lattice-mismatched graphene/metal systems.

Results

Growth of graphene on Rh(111) and characterization of the new moirés

We have grown high quality graphene monolayers on Rh(111) under ultra-high vacuum conditions via in situ chemical vapour deposition (CVD) of low pressure ethylene (C₂H₄). The surface is mostly covered by the already known (12 × 12)_G moiré^17,24 in which both the carbon and rhodium atomic lattices are aligned with the superstructure (Fig. 1a), but some large areas with different rotational orientations are also found (Fig. 1c). Fig. 1a and b display a combination of STM images and DFT structures (see Methods and the ESI† for details) in which the “usual” moiré is characterized. It is formed by 11 per 11 rhodium atoms aligned with 12 per 12 carbon atoms. DFT calculations clearly show that the graphene–metal distance varies within the moiré unit cell depending on the position of the carbon atoms with respect to the rhodium atoms underneath, giving rise to a geometrical corrugation from the lowest carbon atom to the highest one of about 121 pm, in agreement with the previous DFT calculations.^23,24

Fig. 1 (a) 7.5 × 10.5 nm² atomically resolved STM image (V_S = −0.4 V, I_T = 2.0 nA) of 1 ML graphene on Rh(111) where the structure of the (12 × 12)_G moiré is observed. The DFT calculated atomic positions are overlaid on the bottom part of the image. (b) Ball and stick model of the DFT structure for the same moiré pattern. This side view highlights the large corrugation of the graphene layer (121 pm). (c) 63 × 96 nm² STM image (V_S = 0.8 V, I_T = 0.9 nA) of 1 ML graphene grown by UHV-CVD on Rh(111). Two different rotational domains are observed in the same terrace: the (12 × 12)_G moiré is observed in the top while a different moiré pattern (highlighted in green) is resolved in the bottom.

The graphene grown on Rh(111) by our CVD method forms one complete monolayer. As we could not experimentally observe the metallic surface after the graphene growth, the orientation of the new moirés was obtained by comparing them with the orientation of the aligned (12 × 12)_G superstructure. Fig. 2a illustrates the procedure to identify and characterize the new moirés. On the top part, the (12 × 12)_G moiré (from now on moiré 0) has been drawn while on the bottom part, there is an arbitrary moiré (X) with a lattice parameter L. Due to the alignment of the moiré 0 with both the G and the Rh atomic lattices, the characteristic angles, Ω and Φ, could be easily obtained for the new superstructure: Ω is the angle between the Rh(111) lattice and the moiré pattern and was extracted by measuring the rotation between both moirés. Φ is the angle between both atomic lattices, i.e. Rh(111) and graphene, and was obtained by either comparing the relative orientation of the graphene atomic lattice in each domain or by measuring the angle between the new graphene flake and the moiré 0. In order to do so, we needed STM images (like Fig. 2b) where the two superstructures could be observed. Figs. 2c–e show three different atomically resolved STM images where five new moiré patterns and the aligned moiré 0 can be observed. Models for each of these five new moirés are displayed in Fig. 2f. Below each model, their parameters are described with respect to the graphene layer using Wood's notation. Table 1 shows the relevant data for all the observed moiré patterns.

Fig. 2 Procedure to determine the new moirés’ parameters: (a) schematic model in which both the “usual” (12 × 12), moiré 0, and a new one (X) are compared. (b) 15 × 15 nm² STM image (V_S = 0.3 V, I_T = 18.7 nA) where both the moiré 0 and the new one appear together. The new moirés’ parameters, characterized by the angles Ω and Φ (see text), are obtained by comparing them with those already known from the moiré 0. (c–e) 12 × 12 nm² atomically resolved STM images where five moirés different from moiré 0 are shown. The corresponding numbers of these moirés are consistent with Table 1. (c) On the bottom part of the image (V_S = 38 mV, I_T = 11.1 nA), the (5 × 5)_G moiré (labeled as 16 in the figure) is observed; (d) the [(√91 × √91) − R27°]_G moiré is on the bottom-left of the image (named as 8) while the [(6√3 × 6√3) − R24.5°]_G moiré (labelled as 7) is on the top-left (V_S = 0.3 V, I_T = 18.7 nA); (e) on the bottom part of the image, the moiré number 17 corresponds to the (4 × 4)_G superperiodicity, while number 2, in the top part, corresponds to [(√133 × √133) − R17.5°]_G (V_S = 0.7 V, I_T = 15.7 nA). (f) Schematic models of the moirés obtained by STM measurements in the figures on top.

Table 1 Table of the different moiré superstructures observed on graphene on Rh(111). The parameters have been obtained with the geometric model and are in agreement with those observed experimentally. L is the moiré periodicity, Φ the angle between the graphene layer and Rh(111), Ω the angle between the moiré and Rh(111), and γ the angle between the moiré and graphene. The mismatch is referred to the graphene lattice parameter while the strain is referred to the moiré supercell. The Φ angles of the moirés marked with * could not be determined from the corresponding experimental STM images. They were obtained from the geometrical model. In these cases, there are two different values of Φ compatible with all the other parameters

Moiré	Superstructure		L (Å)	Φ (°)	Ω (°)	γ (°)	Mismatch (%)	Strain (%)
	Relative to Rh(111)	Relative to graphene
0	(11 × 11)	(12 × 12)G	29.6	0	0	0	1.5	0.1
1*	(2√29 × 2√29) − R13.9°	[(√139 × √139) − R12.7°]G	28.9	1.1/26.6	13.9	12.7	2.5	0.2
2	(4√7 × 4√7) − R19.1°	[(√133 × √133) − R17.5°]G	28.4	1.6	19.1	17.5	2.7	0.2
3*	(4√7 × 4√7) − R4.7°	[(√133 × √133) − R17.5°]G	28.4	22.2/12.7	4.7	17.5	−2.5	−0.2
4*	(6√3 × 6√3) − R24.5°	[(√129 × √129) − R22.4°]G	27.9	2.1/13.1	24.5	22.4	4.6	0.4
5	(2√26 × 2√26) − R9.8°	[(2√31 × 2√31) − R8.9°]G	27.4	18.7	9.8	8.9	−5	−0.5
6	(√94 × √94) − R21°	[(4√7 × 4√7) − R19.1°]G	26.1	19.8	21	19.1	−4.9	−0.5
7	(√91 × √91) − R27°	[(6√3 × 6√3) − R24.5°]G	25.6	2.5	27	24.5	2.1	0.3
8	(2√19 × 2√19) − R23.4°	[(√91 × √91) − R27°]G	23.4	3.6	23.4	27	−1.7	−0.2
9*	(√66 × √66) − R12.2°	[(√79 × √79) − R17°]G	21.8	29.2/4.8	12.2	17	5.2	0.6
10*	(√61 × √61) − R26.3°	[(√73 × √73) − R5.8°]G	21	20.5/27.8	26.3	5.8	−1.3	−0.2
11	(2√14 × 2√14) − R6.6°	[(√67 × √67) − R12.2°]G	20.1	5.6	6.6	12.2	6.1	0.7
12*	(√53 × √53) − R13.9°	[(3√7 × 3√7) − R19.1°]G	19.6	5.2/27	13.9	19.1	−6.1	−0.8
13*	(√43 × √43) − R7.6°	[(2√13 × 2√13) − R13.9°]G	17.6	21.5/6.3	7.6	13.9	−4.9	−0.7
14	(6 × 6)	[(√43 × √43) − R7.6°]G	16.1	7.6	0	7.6	−0.4	−0.1
15*	(√31 × √31) − R9°	[(√37 × √37) − R25.3°]G	15	25.7/16.3	9	25.3	−0.2	−0
16	(√21 × √21) − R10.9°	(5 × 5)G	12.3	10.9	10.9	0	0.5	0.1
17	(√13 × √13) − R13.9°	(4 × 4)G	9.7	13.9	13.9	0	−6.2	−1.5

---

Geometric analysis of the moiré patterns

Once the superstructures were experimentally characterized, all the resulting data have been compared with a purely geometrical model, first proposed by Merino et al.¹⁸ to identify the possible moiré patterns in G/Pt(111) and other weakly interacting graphene/metal systems. In ref. 18 they argued that the lattice parameter and the orientation of the observed moiré structures are related to the values that minimize the mismatch, δ, between the G and the metal atomic lattices.

We have applied this model to our graphene on Rh(111). The mismatch, δ, is defined as a percentage of the difference vector between the graphene and Rh(111) lattices, i.e., 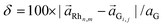, where and are vectors of the Rh(111) and graphene lattices, respectively, and a_G is the undistorted graphene lattice parameter. We have used the experimental lattice parameters a_G = 2.46 Å and a_Rh = 3.80 Å.

Our results show that this model seems to work also on this strongly interacting G–metal system, as the experimentally found moiré patterns correspond to those superstructures in which the mismatch between both atomic lattices is a minimum value (see the ESI†). The experimental results with their corresponding mismatch values are shown in Table 1. Here we follow the commonly employed sign convention (opposite to the one used in ref. 18) for δ: the stretching of the graphene () is expressed by a positive sign, while a negative sign indicates its compression.

A good agreement between the model and the experimental data indicates that the energy cost of deforming the G lattice to match it with the metallic substrate plays a relevant role not only in the case of weakly coupled systems as graphene on Pt(111),¹⁸ but also for the strongly interacting graphene on Rh(111). However, it has to be noticed that the physical quantity that characterizes the elastic energy associated with the change in the in-plane C–C distances is not the mismatch δ but the strain 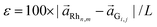, where L is the periodicity of the corresponding moiré unit cell. Values of the strain for the observed moiré patterns can also be found in Table 1, using the same sign convention as for the mismatch. Furthermore, due to its two-dimensional character, graphene easily deforms in the normal direction, changing the corrugation of the layer. Based on our DFT calculations, we show below how the interplay of the energy cost associated with strain and corrugation is balanced by the G–metal binding interaction in order to stabilize the observed moirés, and suggest an explanation for the success of the effective model based on the lattice mismatch.

Changes in the experimental apparent corrugation of the moiré patterns

As is well known, the STM topography is a combination of geometric and electronic contributions.^{15,23,26–28} This combined vertical modulation is called apparent corrugation. During the experimental measurements we also observed relevant changes in the moirés’ apparent corrugation as a function of the moiré periodicity. The profile taken from the STM image in Fig. 3a shows how the corrugation amplitude significantly decreases from a larger moiré to a smaller one. In order to confirm this first evidence, large data sets of STM images presenting both the (12 × 12)_G and another different moiré were acquired and from these data, the apparent corrugations were measured. In Fig. 3b, the apparent corrugations as a function of the moirés’ periodicities are plotted. An important trend emerges from this plot: apparent corrugation increases as the moiré periodicity increases. This trend could be related to the corrugation energy cost in a highly interacting graphene on a metal layer, and to its dependence on the periodicity. However, as already stated, electronic effects could overwhelm the geometry in STM measurements.²² Thus, prior to extracting further conclusions regarding the energetics of G/Rh(111), we need to assess the validity of such experimental findings by first-principles calculations. These calculations will be discussed in detail in the following sections.

Fig. 3 Variation of the corrugation with the moirés’ periodicity: (a) 19 × 13 nm² atomically resolved STM image of two different moirés; tunnelling parameters, V_S = 40 mV, I_T = 11 nA; inset: profile taken from the STM image where the difference in the corrugation amplitude in both moirés can be easily observed. (b) Plot of the apparent corrugation of several moirés as a function of their periodicity parameter (L). The apparent corrugations have been taken from measurements performed with the bias voltage in the range between −1.1 and −1.8 V. See the ESI† for more details on measurements performed under other tunnelling conditions.

Discussion

DFT and STM simulations: real topography and STM apparent corrugation

Although graphene is considered to be strongly coupled to Rh, our STM measurements presented above have uncovered the existence of large rotational domains. Furthermore, we have characterized the dependency between the measured corrugation and the moiré size. This experimental information promotes G/Rh as an ideal system to investigate the underlying mechanisms that control the formation of moiré patterns on G on metals. To tackle this goal we have combined the above experimental results with DFT calculations using the VASP code²⁹ with the PBE³⁰ exchange–correlation potential supplemented by van der Waals interactions as described by the Grimme's D2 approach.³¹ We have used a plane wave basis set with a cutoff of 400 eV and PAW pseudopotentials^32,33 (see the Methods section for details).

We have simulated four moiré patterns: (12 × 12)_G, [(√91 × √91) − R27.0°]_G, [(√43 × √43) − R7.6°]_G and (5 × 5)_G (see Fig. 4) built using the theoretical lattice parameters and the experimental strain (see the ESI†). They correspond to moirés 0, 8, 14 and 16 of Table 1. With this set, that covers the whole experimental range in the system size (L = 2.9 nm, 2.3 nm, 1.6 nm and 1.2 nm), we can explore the relationship between apparent corrugation and the moiré size unveiled in the experiments. These results are shown in Fig. 5 (red dots). The largest system, moiré 0, yields a geometrical corrugation of 121 pm (similar to previous results of 107 pm^23,24). For the smallest moiré pattern, we have found a significantly smaller corrugation of 92 pm. Thus the simulations follow the experimental trend – an increase in the corrugation with the system size – but, at variance with the experiments, the behaviour is not monotonous and the geometrical corrugation saturates for large moirés. The corrugation for moiré 8 (L = 2.3 nm) is 126 pm, slightly larger than the 121 pm of the largest pattern, moiré 0 (L = 2.9 nm).

Fig. 4 (top) Color maps (in Å) of the graphene heights obtained in the DFT simulations for the four different moiré patterns. Note that all images have the same dimensions and color scale. (bottom) Constant current profiles along the high symmetry path marked in the corresponding top panels for different values of the current (different average heights). Profiles are calculated using a NEGF formalism at a voltage of −1.0 V and taking as reference the current calculated in the initial position with the tip placed at a z₀ height above the highest carbon atom.

Fig. 5 Variation of the corrugation with the moirés’ periodicity: both the experimental and the theoretical results have been plotted in this figure. Despite the fact that geometrical values for the corrugation are higher (red circles) than the apparent corrugation measured in the STM experiments (black squares), accurate transport simulations of constant current STM profiles using a NEGF formalism yield apparent corrugations (blue triangles, extracted from the profiles at z₀ = 5 Å in Fig. 4) in excellent agreement with the experiments.

This general trend can be understood in terms of the elastic properties of 2D materials like graphene: the energy cost for out of plane deformations on layered materials increases upon reduction in the deformation areas.³⁴ For the largest system sizes (moiré 0 and moiré 8), this general effect saturates and subtle differences associated with the nature of the strain induced on the G to fit with the moiré superperiodicity, stretching for moiré 0 vs. compression for moiré 8, play a role (see the ESI†).

Although we can explain the observed trend, Fig. 5 clearly shows that the absolute value of the corrugation is always underestimated in the STM measurements. It is well known that STM experiments are not a direct measure of the real topography of the sample as electronic and tip effects control the electronic current. We have unveiled the effects that rule the apparent corrugation measured by STM carrying out simulations of constant current STM profiles. We have used Non-Equilibrium Green's Function (NEGF) techniques to calculate the STM current²⁵ (see Methods for details). In our calculations we mimic the tip apex with an atom with a d_z² orbital and allow the electrons to directly tunnel not only to the G layer but also to the first metal layer.¹¹ The calculated STM profiles are shown in Fig. 4 (bottom). The apparent corrugation is reduced with respect to the real topography for all system sizes with only small variations in the tip–G distance.

The reduction of the apparent corrugation measured by the STM comes from two main effects: (i) the spatial distribution of the current density – on G the current not only comes from the carbon closer to the tip, but also from an area around the tip position, therefore non-planar layers yield smaller measured corrugations; and (ii) the effect of the metal – at the areas where the G is closer to the metal, a significant fraction of the current flows through the Rh, further reducing the measured corrugation (see Fig. S8†). The simulated STM apparent corrugation (Fig. 5, blue triangles) not only reproduces the behaviour with system size but also yields absolute values in quantitative agreement with the experimental measurements. We have to stress that this agreement requires an approach, like our NEGF method, that correctly addresses the electronic transport between the tip and all the atoms in the sample. The common Tersoff–Hamann approximation³⁵ clearly overestimates the corrugation (see Fig. S8†). Furthermore, NEGF simulations that do not include the tunnelling through the Rh atoms still yield slightly higher apparent corrugations.

Stability of the moiré patterns

The agreement between the calculations and the measurements provides confidence on our results and allows us to study the subtle energy balance that favours some of the possible moiré patterns. The stability of the moiré patterns is characterized by the adsorption energy, E_ad = E(GRh) − E(Rh_ideal) − E(G_ideal), the difference in total energies between the whole G/Rh system and the two ideal and isolated subsystems, graphene and rhodium. The results in Table 2 from DFT simulations show that adsorption energies for moirés with quite different sizes are all in the 127–131 meV per C atom range, with differences of just a few meV per C atom and without a clear trend with the system size. This striking similarity, completely consistent with the multitude of experimentally observed moirés (see Table 1), is at odds with the dominance of a single moiré expected for a strongly interacting G–metal system.

Table 2 Energy balance in the formation of the moiré patterns from the DFT simulations: the stability of the moiré patterns is characterized by the adsorption energy, E_ad = E(GRh) − E(Rh_ideal) − E(G_ideal), the difference in total energies between the whole G/Rh system and the two ideal and isolated subsystems, graphene and rhodium. A remarkable similarity in E_ad for the different moirés results from a subtle balance between the deformation energies ΔE(G) and ΔE(Rh), the energies needed to corrugate (E_corr) and to stretch/compress (E_strain) the graphene sheet and the rhodium surface respectively, and E_int, the interaction energy between the metal and the graphene sheet calculated as the difference between the whole system and the distorted subsystems

Energy (meV per C atom)	moiré 0	moiré 8	moiré 14	moiré 16
E ad	−131	−127	−128	−129
ΔE(G) (Estrain, Ecorr)	17 (<1, 17)	18 (<1, 18)	24 (<1, 24)	40 (<1, 40)
ΔE(Rh) (Estrain, Ecorr)	28 (25, 3)	29 (26, 3)	28 (25, 3)	32 (25, 7)
E int	−176	−174	−180	−201

---

The stability of the G on metals is determined by the competition between the graphene–metal interaction E_int, and the energy required to deform both the G layer, and the Rh surface, ΔE(G) and ΔE(Rh). These deformation energies include both strain and corrugation contributions associated with the necessary stretch/compression of the lattice parameter and the out-of-plane deformations – that, for G, include all the deformations in the layer different from the stretching/compression of the flat layer – respectively. With the help of DFT simulations we can determine each of these quantities and analyse the corresponding energy balance for each of the four moiré patterns. Deformation energies can be separated into strain and corrugation contributions, e.g. ΔE(G) = E_strain(G) + E_corr(G), and each of them is calculated as the differences in total energy between the atomic configuration in the G/Rh system, the strained flat layer, and the ideal structure: E_strain(G) = E_strain(G_{flat,strained}) − E_strain(G_ideal), E_corr(G) = E_corr(G_{on GRh atomic configuration}) − E_corr(G_{flat,strained}). Finally, E_int, the G–Rh interaction energy between the metal and the graphene sheet, can be obtained from the total energy difference between the whole system and the distorted subsystems, i.e. E_int = E(GRh) − E(Rh_{on GRh atomic configuration}) − E(G_{on GRh atomic configuration}).

The values of these energy contributions (collected in Table 2) explain a similar stability of all the moiré patterns. The deformation energies, ΔE(G) + ΔE(Rh), are significantly larger for our two smaller systems (moiré 14 and moiré 16): 7 and 27 meV per C atom more repulsive than in the moiré 0. These variations mainly come from graphene, and in particular, from its corrugation energy, as the strain contribution is less than 1 meV per C atom for all the cases (see the ESI†). This energy cost is compensated by the G–Rh interaction energy, 4 and 25 meV per C atom more attractive than in the moiré 0. The large absolute value in moiré 16 is particularly surprising. The results shown in Fig. 4 help to understand this behaviour: smaller moirés show a larger percentage of C atoms in “low”, attractive, areas than the larger moirés, increasing the average interaction (see the ESI†). Therefore, our results show that the existence of several moiré patterns in G on Rh is possible as the G–Rh interaction balances the energy required to corrugate small size moirés.

We are now in a position to discuss the main driving force for the formation of the moiré patterns and the ability of the simple model proposed in ref. 18, based on the lattice mismatch, to predict the structures observed in the experiments. The extremely low values of the strain energy confirm that this is a necessary condition. However, it is the ability of graphene to corrugate in order to maximize the areas of favourable G–metal interaction that finally selects the stable configurations. Thus, the interplay between corrugation and binding, behaving in opposite directions with the system size, plays a key role in the moiré stability.

A model that minimizes the lattice mismatch δ, and not the strain ε (related through δ = εL/a_G), favours moirés with smaller sizes, effectively capturing the trend of larger binding energies found for the small moirés. However, this phenomenological model has its limitations. For example, in ref. 18, it was reported that the structures with large compressive strains predicted for G/Pt(111) were not observed in the experiments. We speculate that this is due to the fact that compression would induce a corrugation of the G layer that is particularly unfavourable because of the lack of a strong G–metal interaction to compensate it in this weakly coupled system.

Finally, we address the preference of one particular moiré pattern, the (12 × 12)_G in the G/Rh case, frequently observed in the experiments. The differences in stability shown by the adsorption energies slightly favour the (12 × 12)_G structure but are not large enough to justify its dominance. A possible explanation comes from boundary effects associated with the growth process. Recent work on G on Pt has shown that the interaction of the G edges with Pt steps plays an important role in the moiré pattern formation.³⁶ The particular alignment of the (12 × 12)_G moiré with the Rh crystallographic directions may be responsible for the observed preference.

Methods

Experimental set-up and sample preparation

All the experiments and sample preparations were carried out under ultra-high vacuum (UHV) conditions with a base pressure of 1 × 10⁻¹⁰ Torr. The UHV system is equipped with a homemade variable temperature scanning tunnelling microscope (VT-STM)^37,38 and a four-grid LEED/Auger optics.

Two rhodium single crystals from different companies^39,40 were used for this experiment and both gave similar results. The sample preparation was carried out following two different methods on both crystals. In the first method, the Rh(111) surface was cleaned by cycles of argon sputtering at room temperature and annealing while keeping the sample under an oxygen atmosphere to avoid carbide formation at the surface from carbon segregation from the bulk (T_sample = 950 °C; P_oxygen = 2 × 10⁻⁷ Torr). The graphene monolayer was grown via chemical vapour deposition (CVD) of low pressure (P = 3 × 10⁻⁷ Torr) ethylene (C₂H₄) while flashing the sample at 850 °C. As a result, we always obtain one monolayer of high quality graphene mostly aligned with the Rh(111) surface highest symmetry directions together with some other rotational domains leading to different moiré patterns. The second method to grow graphene was just annealing the sample at 900 °C for several minutes with neither oxygen nor ethylene in order to segregate carbon atoms from the bulk. As a result, the metallic surface was covered by imperfect graphene patches. For this reason, this second method was not used further and all the results shown here have been obtained from samples (of both crystals) prepared by the first method, i.e. UHV-CVD (see the ESI†). The resulting preparation was checked with the LEED equipment before transferring the sample to the VT-STM. STM measurements were then performed in an ample sample temperature range varying from 40 K to room temperature. STM data acquisition and image processing were performed with the WSxM software from Nanotec Electrónica S.L.⁴¹

DFT method

In this work all DFT simulations have been carried out using plane-wave basis sets as implemented in the VASP code.²⁹ The cutoff for the plane-wave basis was set to 400 eV to ensure convergence and the PAW method^32,33 was used to construct the pseudopotentials for carbon and rhodium. We have performed several ionic relaxations following a conjugate gradient algorithm and the convergence criterion was that forces upon atoms had to be less than 0.01 eV Å⁻¹. The super-cells were different for each moiré pattern but we always considered a four-layer metallic slab. Atoms belonging to the two deepest layers were kept fixed while all of the rest were allowed to relax in order to find their equilibrium positions. The reciprocal space was sampled using Monkhorst and Pack grids⁴² with different number of k-points according to the size of the cell (see the ESI†). Our C–C equilibrium distance in free graphene was 1.4248 Å, so in all cases we apply the experimental strain to the graphene layer and then the lattice parameter of the Rh is fitted to avoid the mismatch and obtain exact periodic boundary conditions. The exchange and correlation functional was a Generalized Gradient Approximation by Perdew, Burke and Ernzerhof (PBE)³⁰ with the semi-empirical correction by S. Grimme (D2)³¹ in order to take into account van der Waals interactions. In this particular system, if these interactions are neglected misleading results are obtained in the corrugation values.^17,43 Moreover, we have tested the results with a more accurate description of the van der Waals interaction, DFT+DF(optB86b),⁴⁴ for the smallest moiré patterns, obtaining very similar results, with corrugation increases smaller than 0.12 Å.

STM simulations

STM profiles were calculated using a NEGF formalism²⁵ in which the electronic current between the tip and the sample is correctly addressed. In this case the moiré patterns were characterized using DFT but with localized orbital basis sets. The OpenMX software was employed using single-ζ basis of its numerical pseudoatomic orbitals^45,46 with cutoff radii for carbon and rhodium of 6.0 and 7.0 au respectively.

Conclusions

In summary, we have reported, in contrast to earlier predictions, the coexistence of several moiré patterns on the G on Rh(111), a prototypical system for strong graphene–metal coupling. Combining DFT calculations, STM simulations and STM experiments we have unveiled the atomic structure of these patterns and found that the corrugation of the G sample increases with the system size and saturates in the larger structures. Our results also show that the STM apparent corrugation underestimates the real deformation of the graphene layer due to electronic effects. We have also shown that the stability of the different moiré patterns is the result of a subtle energy balance between the energy required to corrugate the graphene, that increases upon system size reduction, but it is compensated by the interaction energy between the G and the metal allowing the coexistence of multiple patterns even in the case of highly interacting G–metal systems. This suggests that the preference of some of the energetically possible patterns should be governed by the growth process or boundary effects. We deem that these conclusions can be extended to G grown on different metals including both weak and strong interacting G–metal systems.

Conflict of interest

The authors declare no competing financial interest.

Acknowledgements

We acknowledge financial support from Spanish grants MAT2013-41636-P, MAT2011-23627, MAT2011-26534, CSD2010-00024 (MINECO, Spain) and S2009/MAT-1467 (CAM, Spain). A.J.M.G. was supported by a Marie Curie action under the Seventh Framework Programme. P.P. was supported by the Ramón y Cajal Program. Computer time provided by the Spanish Supercomputing Network (RES) in the Barcelona Supercomputer Center (MareNostrum III) is gratefully acknowledged.

Notes and references

1. A. K. Geim, Science, 2009, 324, 1530–1534.
2. S. Bae, H. Kim, Y. Lee, X. F. Xu, J. S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. R. Kim, Y. I. Song, Y. J. Kim, K. S. Kim, B. Ozyilmaz, J. H. Ahn, B. H. Hong and S. Iijima, Nat. Nanotechnol., 2010, 5, 574–578.
3. H. Yang, J. Heo, S. Park, H. J. Song, D. H. Seo, K. E. Byun, P. Kim, I. Yoo, H. J. Chung and K. Kim, Science, 2012, 336, 1140–1143.
4. K. C. Yung, W. M. Wu, M. P. Pierpoint and F. V. Kusmartsev, Contemp. Phys., 2013, 54, 233–251.
5. X. S. Li, W. W. Cai, J. H. An, S. Kim, J. Nah, D. X. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314.
6. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
7. A. B. Preobrajenski, M. L. Ng, A. S. Vinogradov and N. Martensson, Phys. Rev. B: Condens. Matter, 2008, 78, 073401.
8. A. L. V. de Parga, F. Calleja, B. Borca, M. C. G. Passeggi, J. J. Hinarejos, F. Guinea and R. Miranda, Phys. Rev. Lett., 2008, 100, 056807.
9. G. Giovannetti, P. A. Khomyakov, G. Brocks, V. M. Karpan, J. van den Brink and P. J. Kelly, Phys. Rev. Lett., 2008, 101, 026803.
10. M. Batzill, Surf. Sci. Rep., 2012, 67, 83–115.
11. M. M. Ugeda, D. Fernandez-Torre, I. Brihuega, P. Pou, A. J. Martinez-Galera, R. Perez and J. M. Gomez-Rodriguez, Phys. Rev. Lett., 2011, 107, 116803.
12. I. Pletikosic, M. Kralj, P. Pervan, R. Brako, J. Coraux, A. T. N'Diaye, C. Busse and T. Michely, Phys. Rev. Lett., 2009, 102, 056808.
13. A. J. Martinez-Galera, I. Brihuega and J. M. Gomez-Rodriguez, Nano Lett., 2011, 11, 3576–3580.
14. P. Sutter, J. T. Sadowski and E. Sutter, Phys. Rev. B: Condens. Matter, 2009, 80, 245411.
15. B. Borca, S. Barja, M. Garnica, M. Minniti, A. Politano, J. M. Rodriguez-Garcia, J. J. Hinarejos, D. Farias, A. L. V. de Parga and R. Miranda, New J. Phys., 2010, 12, 093018.
16. E. Miniussi, M. Pozzo, A. Baraldi, E. Vesselli, R. R. Zhan, G. Comelli, T. O. Mentes, M. A. Nino, A. Locatelli, S. Lizzit and D. Alfe, Phys. Rev. Lett., 2011, 106, 216101.
17. B. Wang, M. Caffio, C. Bromley, H. Fruchtl and R. Schaub, ACS Nano, 2010, 4, 5773–5782.
18. P. Merino, M. Svec, A. L. Pinardi, G. Otero and J. A. Martin-Gago, ACS Nano, 2011, 5, 5627–5634.
19. A. T. N'Diaye, R. van Gastel, A. J. Martinez-Galera, J. Coraux, H. Hattab, D. Wall, F. J. M. zu Heringdorf, M. Horn-von Hoegen, J. M. Gomez-Rodriguez, B. Poelsema, C. Busse and T. Michely, New J. Phys., 2009, 11, 113056.
20. A. J. Martinez-Galera and J. M. Gomez-Rodriguez, J. Phys. Chem. C, 2011, 115, 23036–23042.
21. A. Martín-Recio, A. J. Martínez-Galera and J. M. Gómez-Rodríguez, J. Phys. Chem. C, 2015, 119, 401–406.
22. D. Stradi, S. Barja, C. Diaz, M. Garnica, B. Borca, J. J. Hinarejos, D. Sanchez-Portal, M. Alcami, A. Arnau, A. L. V. de Parga, R. Miranda and F. Martin, Phys. Rev. Lett., 2011, 106, 186102.
23. M. Iannuzzi and J. Hutter, Surf. Sci., 2011, 605, 1360–1368.
24. E. N. Voloshina, Y. S. Dedkov, S. Torbrugge, A. Thissen and M. Fonin, Appl. Phys. Lett., 2012, 100, 241606.
25. J. M. Blanco, F. Flores and R. Perez, Prog. Surf. Sci., 2006, 81, 403–443.
26. R. Cortes, D. P. Acharya, C. V. Ciobanu, E. Sutter and P. Sutter, J. Phys. Chem. C, 2013, 117, 20675–20680.
27. S. K. Hamalainen, M. P. Boneschanscher, P. H. Jacobse, I. Swart, K. Pussi, W. Moritz, J. Lahtinen, P. Liljeroth and J. Sainio, Phys. Rev. B: Condens. Matter, 2013, 88, 201406.
28. M. Ondracek, P. Pou, V. Rozsival, C. Gonzalez, P. Jelinek and R. Perez, Phys. Rev. Lett., 2011, 106, 176101.
29. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
31. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
32. P. E. Blochl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775.
34. C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
35. J. Tersoff and D. R. Hamann, Phys. Rev. Lett., 1983, 50, 1998–2001.
36. P. Merino, L. Rodrigo, A. L. Pinardi, J. Mendez, M. F. Lopez, P. Pou, R. Perez and J. A. Martin-Gago, ACS Nano, 2014, 8, 3590–3596.
37. O. Custance, S. Brochard, I. Brihuega, E. Artacho, J. M. Soler, A. M. Baro and J. M. Gomez-Rodriguez, Phys. Rev. B: Condens. Matter, 2003, 67, 235410.
38. A. J. Martinez-Galera and J. M. Gomez-Rodriguez, J. Phys. Chem. C, 2011, 115, 11089–11094.
39. MaTeck GmbH, http://www.mateck.de.
40. SPL, http://www.spl.eu.
41. I. Horcas, R. Fernandez, J. M. Gomez-Rodriguez, J. Colchero, J. Gomez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705.
42. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
43. B. Wang and M. L. Bocquet, J. Phys. Chem. Lett., 2011, 2, 2341–2345.
44. J. Klimes, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
45. T. Ozaki, Phys. Rev. B: Condens. Matter, 2003, 67, 155108.
46. T. Ozaki and H. Kino, Phys. Rev. B: Condens. Matter, 2004, 69, 195113.

---

Footnotes

† Electronic supplementary information (ESI) available: Growth of graphene on Rh(111). Geometric model for the moiré patterns of G on Rh(111). Apparent corrugation of graphene on Rh(111) in STM experiments. G/Rh moiré patterns used in the DFT simulations. Apparent corrugation of graphene on Rh(111) in STM simulations. See DOI: 10.1039/c5nr00825e

‡ Present address: II. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany.

---