Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Origin of the large dispersion of magnetic properties in nanostructured oxides: FexO/Fe3O4 nanoparticles as a case study†
Marta
Estrader
*ab,
Alberto
López-Ortega
c,
Igor V.
Golosovsky
*de,
Sònia
Estradé
f,
Alejandro G.
Roca
g,
German
Salazar-Alvarez
 b,
Lluís
López-Conesa
f,
Dina
Tobia
h,
Elin
Winkler
h,
José D.
Ardisson
i,
Waldemar A. A.
Macedo
i,
Andreas
Morphis
j,
Marianna
Vasilakaki
j,
Kalliopi N.
Trohidou
j,
Arsen
Gukasov
k,
Isabelle
Mirebeau
k,
O. L.
Makarova
l,
Roberto D.
Zysler
h,
Francesca
Peiró
f,
Maria Dolors
Baró
m,
Lennart
Bergström
b and
Josep
Nogués
gn
b,
Lluís
López-Conesa
f,
Dina
Tobia
h,
Elin
Winkler
h,
José D.
Ardisson
i,
Waldemar A. A.
Macedo
i,
Andreas
Morphis
j,
Marianna
Vasilakaki
j,
Kalliopi N.
Trohidou
j,
Arsen
Gukasov
k,
Isabelle
Mirebeau
k,
O. L.
Makarova
l,
Roberto D.
Zysler
h,
Francesca
Peiró
f,
Maria Dolors
Baró
m,
Lennart
Bergström
b and
Josep
Nogués
gn
aDepartament de Química Inorgànica, Universitat de Barcelona, Diagonal 645, E-08028, Barcelona, Spain. E-mail: martaestrader@gmail.com
bDepartment of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, 10691 Stockholm, Sweden
cINSTM and Dipartimento di Chimica “U. Schiff”, Università degli Studi di Firenze, Via della Lastruccia 3, Sesto Fiorentino, I-50019 Firenze, Italy
dNational Research Center “Kurchatov Institute”, B.P. Konstantinov, St. Petersburg Nuclear Physics Institute, 188300, Gatchina, Russia. E-mail: golosov@pnpi.spb.ru
eA.F. Ioffe Physico-Technical Institute RAS, 194021, St. Petersburg, Russia
fLENS-MIND-IN2UB, Departament d'Electrònica, Universitat de Barcelona, Martí i Franquès 1, E-08028 Barcelona, Spain
gICN2 – Institut Catala de Nanociencia i Nanotecnologia, Campus UAB, E-08193 Bellaterra (Barcelona), Spain
hCentro Atómico Bariloche, CNEA-CONICET, 8400 S.C. de Bariloche, Río Negro, Argentina
iLaboratório de Física Aplicada, Centro de Desenvolvimento da Tecnologia Nuclear, 31270-901Belo Horizonte, Minais Gerais, Brazil
jINN-Institute of Nanoscience and Nanotechnology, NCSR “Demokritos”, 153 10 Aghia Paraskevi, Attiki, Greece
kLaboratoire Leon Brillouin, CEA/CNRS, F-91191 Gif-sur-Yvette Cedex, France
lNational Research Center “Kurchatov Institute”, 123182 Moscow, Russia
mDepartament de Física, Universitat Autònoma de Barcelona, E-08193 Bellaterra (Barcelona), Spain
nInstitució Catalana de Recerca i Estudis Avançats (ICREA), Barcelona, Spain
First published on 31st December 2014
Abstract
The intimate relationship between stoichiometry and physicochemical properties in transition-metal oxides makes them appealing as tunable materials. These features become exacerbated when dealing with nanostructures. However, due to the complexity of nanoscale materials, establishing a distinct relationship between structure-morphology and functionalities is often complicated. In this regard, in the FexO/Fe3O4 system a largely unexplained broad dispersion of magnetic properties has been observed. Here we show, thanks to a comprehensive multi-technique approach, a clear correlation between the magneto-structural properties in large (45 nm) and small (9 nm) FexO/Fe3O4 core/shell nanoparticles that can explain the spread of magnetic behaviors. The results reveal that while the FexO core in the large nanoparticles is antiferromagnetic and has bulk-like stoichiometry and unit-cell parameters, the FexO core in the small particles is highly non-stoichiometric and strained, displaying no significant antiferromagnetism. These results highlight the importance of ample characterization to fully understand the properties of nanostructured metal oxides.
Introduction
Transition metal oxides are extremely versatile given the well-established dependence of their physicochemical properties on the oxidation state.1–3 Interestingly, this effect is dramatically enhanced at the nanoscale, since their reactivity may result in local differences in the oxidation state of the material which may lead to novel properties.4 However, as the size is reduced down to a few nanometers, the characterization of these sophisticated systems should not solely rely on a few techniques as is usually done for bulk materials. Namely, the fine, yet critical, structural alterations which often occur at the nanoscale may be easily overlooked or misinterpreted if not properly analyzed.5–8 For instance, in tantalum oxides TaO2−x (Ta+4) is conducting whereas Ta2O5−x (Ta+5) is insulating. Notably, an in-depth electron microscopy analysis demonstrated the presence of a TaO1−x nanoscale layer which was, in part, responsible for the observation of a new resistance-switching phenomenon.4 A similar case is also found for nanostructured perovskite manganites, where, for example, a gradual transition from antiferromagnetism to ferromagnetism contrasts with the sharp one exhibited in bulk.9 A widely studied transition metal system is iron oxide, FexOy.10–14 Among iron oxide materials, wüstite (FexO) is a particularly interesting material. In bulk, wüstite is not stable under ambient conditions and disproportionates into α-Fe and magnetite (Fe3O4). However, metastable non-stoichiometric FexO can be obtained by high temperature quenching. Moreover, FexO can be stable in nanoparticle form.15–18 FexO can oxidize into Fe3O4 and subsequently into maghemite (γ-Fe2O3), which at the nanoscale may give rise to FexO/Fe3O4 core/shell particles.10,19–37 FexO/Fe3O4 systems have been proposed for diverse applications, including magnetic bioassays, microwave absorbers, anode materials for Li-ion batteries or solar hydrogen production via water-splitting.35,38–41From a magnetic point of view FexO is antiferromagnetic (AFM) whereas Fe3O4 is ferrimagnetic (FiM), which gives rise to a rich set of magnetic properties in this system.10,19–37 In particular, exchange coupling between the AFM-core and the FiM-shell, which strongly depends on the core size, shell thickness or shape, should result in an exchange bias, i.e., the shift of the hysteresis loop in the field axis after field cooling (HE).42–47 Remarkably, in FexO/Fe3O4 core/shell nanoparticles an unusually broad spectrum of magnetic properties has been reported, even for nominally comparable particles. For instance, Kavich et al. showed an exchange bias in 14 nm FexO/Fe3O4 particles whereas the ones of 13 nm reported by Lak et al. show HE = 0, thus claiming the absence of a FexO core.22,27 On the other hand, an exchange bias was observed in single phase Fe3−δO4 nanoparticles, after the complete oxidation of the FexO phase, which was ascribed to the presence of antiphase boundaries formed during the oxidation process. These antiphase boundaries were also claimed to be responsible for the observed reduced saturation magnetization (MS) compared to bulk values, although Benitez et al. attributed an analogous MS reduction (in similar 20 nm particles) to the occurrence of small amounts of FexO.25,32 Further, some groups report obvious features of the FexO AFM transition at its Néel temperature, TN (e.g., a sharp downturn of magnetization around TN) while others find the temperature dependence of magnetization, M(T), featureless around TN.22,27,32,34,36,37 Similarly, although in some cases the nanoparticles have been shown to exhibit a clear Verwey transition, TV (typical of bulk Fe3O4),28,36 similar particles show no characteristics of this transition.22,25,27
To address the origin of these diverse magnetic behaviours, in this work we present an in-depth systematic study of two different FexO/Fe3O4 core/shell systems, with significantly different overall sizes of 9 and 45 nm. These particle sizes are among the smallest and largest sizes of core–shell FexO/Fe3O4 nanoparticles, respectively, with a well-defined size and shape reported in the literature. Diverse techniques have been employed to accurately characterize both compositionally and magnetically the core/shell structure. The results show that the spread of magnetic responses in the FexO/Fe3O4 core/shell systems stems from a combination of factors such as size effects, the composition x of the FexO core or the strains in both the core and the shell.
Results
Structural and morphological characterization
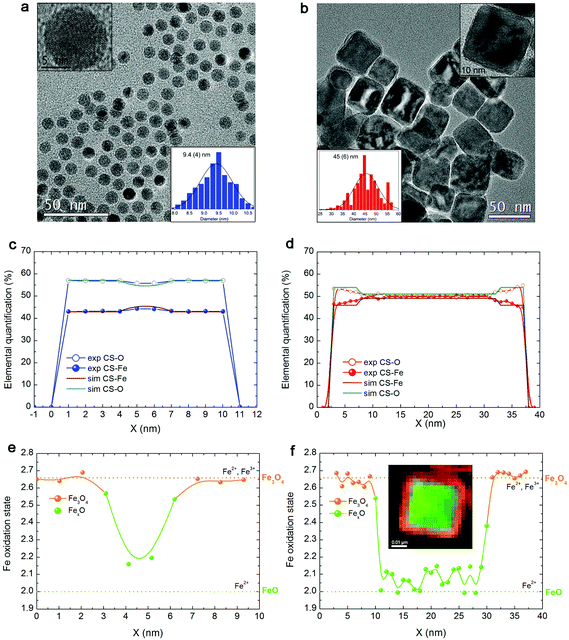
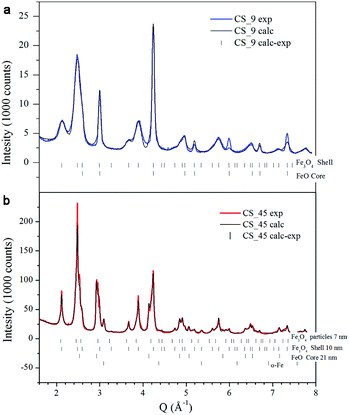
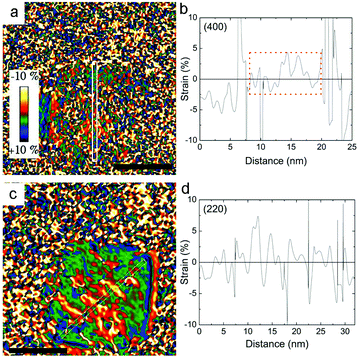
Fig. 1a, b show the transmission electron microscopy (TEM) images of small spherical, CS_9, and large cubic-shaped, CS_45, nanoparticles, respectively. The corresponding volume–weight particle size histograms, depicted in the insets, follow a Gaussian distribution with mean sizes of 9.4(4) nm and 45(6) nm for the CS_9 and CS_45 nanoparticles, respectively. The HRTEM images (insets of Fig. 1a, b) clearly show the crystallinity of the particles, although the presence of a core/shell morphology cannot be completely identified. To elucidate the composition of the nanoparticles, local electron energy loss spectra (EELS) analysis across the whole particle was performed. The Fe/O ratio confirms a core/shell structure (diameter/thickness) of FexO(3 nm)/Fe3O4(3.5 nm) for CS_9 and FexO(20 nm)/Fe3O4(8 nm) for CS_45 (Fig. 1c, d). Further, the iron oxidation state (Feox.st) was obtained both for the shell (orange colour in the graphs) and the core (represented in green) by a quantitative analysis of the EELS data (Fig. 1e, f). Note that to obtain the oxidation state of the core the Fe3O4-shell contribution was subtracted. As can be seen in Fig. 1e, f, for both the CS_9 and CS_45 particles, in the shell region Feox.st is +2.6, which exactly corresponds to Fe3O4. In contrast, while for CS_45 particles the FexO-core has an average Feox.st = +2.05 which denotes a Fe0.95O composition, the CS_9 particles have a Feox.st = +2.2. This implies that the core of the small particles has a highly defected wüstite phase with a Fe0.80O stoichiometry. As shown in the inset of Fig. 1f, the FexO/Fe3O4 core/shell structure of the large particles, CS_45, is further confirmed by an EELS mapping using the Fe2+ and Fe3+ oxidation states.8The profile refinement of the X-ray patterns indicates two dominant phases in the samples: magnetite (Fe3O4), with a spinel structure, and wüstite (FexO), with a NaCl structure (Fig. 2). The analysis has also revealed that the CS_45 sample contains some impurities: a small fraction of 7 nm Fe3O4 particles and some α-Fe particles (Fig. 2b and ESI Table S1†). To analyze the morphology of the core/shell particles, while the core size is obtained from the crystallite size obtained from the FexO peak broadening, the shell size is the calculated effective thickness of a uniform layer covering the core from the refined scale factors, which are proportional to the scattering volumes. This analysis leads to a FexO-core/Fe3O4-shell structure with dimensions of 10.1(5)/2.0(2) nm and 21(1)/8.8(3) nm for CS_9 and CS_45 nanoparticles, respectively, consistent with the microscopy results. The study of the Fe3O4-shell composition shows refined oxygen parameter values, 0.252(4)-CS_9 and 0.257(4)-CS_45 and unit cell values, 0.8395(1) nm CS_9 and 0.8391(2) nm CS_45, close to the 0.2548 and 0.8394 nm values of bulk stoichiometric magnetite. This implies that the Fe3O4-shell is, in both types of samples, rather stoichiometric (in agreement with EELS). The lattice parameter is very similar to bulk values, but larger than typical values observed in nanoparticles, which may indicate that the Fe3O4 may be slightly strained. Owing to the strong correlation between x and the Debye factor, to perform the FexO-core profile refinement the x parameter was fixed according to the EELS data of Fe0.80O-CS_9 and Fe0.95O-CS_45. The lattice parameters obtained from the fit for FexO are rather different for both particles, with 0.42190(8) nm for CS_9 and 0.42986(1) nm for CS_45. Interestingly, given that in bulk FexO the unit cell and the x parameters are directly related by the formula aFexO = 0.3856 + 0.478x,26,48 we have calculated the x values of our particles using the refined unit cell parameters, leading to Fe0.76(1)O-CS_9 and Fe0.92(1)O-CS_45, which are consistent with the EELS results. The small discrepancy between the x values obtained from EELS and the lattice parameter may indicate that apart from non-stoichiometry, the FexO cell may be compressed with respect to bulk samples with the same x. Unfortunately, given the overlap of the XRD peaks of the two phases the use of the Williams–Hall plot analysis is rather unreliable to obtain information about the strains in the system. Hence, to assess the internal strains in the nanoparticles geometric phase analysis (GPA) was used for the CS_45 particles. Notably, GPA allows for the determination and quantification of crystal lattice deformations from high-resolution TEM images.25 The strains existing in two different sublattices, i.e., the (220) lattice plane associated with the cations in the tetrahedral positions (spinel phase only) and the (400Spinel and 200wüstite) lattice plane associated with both the spinel and wüstite phases were studied through the phase imaging of these reflections upon applying GPA (see the Methods section and ESI Fig. S1†). The deformation maps along g200(wüstite)/g400(spinel) and g220(spinel) (Fig. 3a,c) clearly indicate a core with compressive, positive strains and a shell with tensile, negative strains. This becomes particularly evident in Fig. 3c; the central part of the particle (i.e., the core) is predominantly red-yellow (compressive strains), whereas the boundary of the particle (i.e., the shell) is mainly green-blue (i.e., expansive strains). The quantification of the strains originating from these defects is shown in Fig. 3b,d. The strain analysis along g200(wüstite)/g400(spinel) (Fig. 3b) unambiguously shows highly strained regions due to mismatch dislocations, which are likely located at the core–shell interface. The stressed interface arises from mismatched dislocations owing to the lattice differences between the wüstite (core) and spinel (shell) phases, as previously demonstrated in this type of system.25 An analogous study of CS_9 nanoparticles reveals a similar strained structure (see ESI Fig. S2†). However, these particles are exceedingly small to carry out a reliable quantitative GPA analysis.
Neutron diffraction
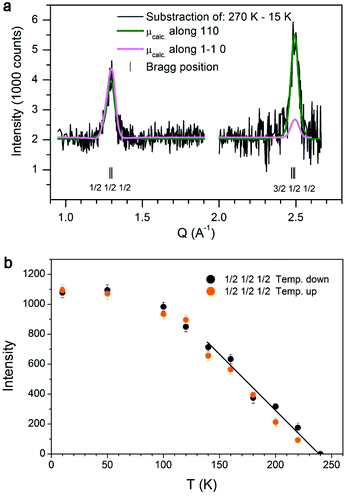
The magnetic structure of both the FexO-core and the Fe3O4-shell for the two core/shell samples was determined by neutron diffraction (ESI Fig. S3†). The refined average magnetic moments in the shell for CS_9 and CS_45 are 3.8(6)μB and 4.2(3)μB, respectively. Concerning the magnetic structure of the FexO-core remarkable opposite features between the CS_9 and CS_45 samples are manifested. Firstly, in the CS_9 particles, the absence of all the expected magnetic reflections indicates a lack of magnetic order in the FexO-core. On the other hand, the scenario for the CS_45 particles is completely different, since not only they present the usual (3/2, 1/2, 1/2) magnetic reflection, but they also exhibit the forbidden (1/2, 1/2, 1/2) reflection.49 This implies that although the FexO core is magnetic, the moments in the FexO-core deviate from the [111] direction observed in bulk.49 Remarkably, the refinement of the magnetic reflections unambiguously demonstrates that the core is AFM with the magnetic moments aligned along the [110] axis (Fig. 4a).Magnetic measurements
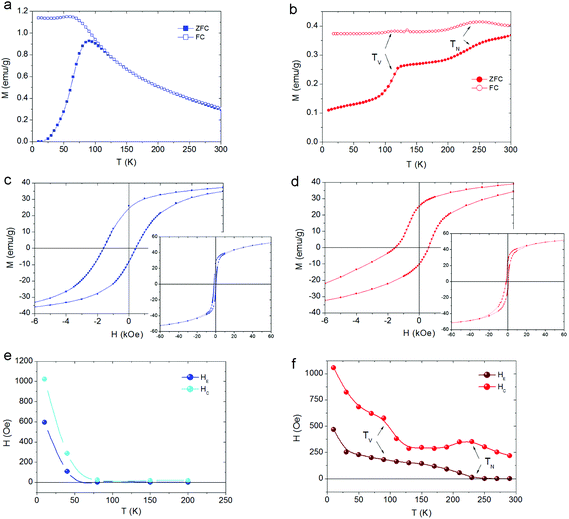
The zero field cooled–field cooled (ZFC–FC) magnetization curves for the CS_9 sample (Fig. 5a) exhibit the characteristics of superparamagnetic systems50 with a maximum in the ZFC magnetization, Tmax = 90 K associated with the FiM Fe3O4-shell. This maximum is related to the blocking temperature (TB) distribution due to the particle-size (or energy barrier) distribution. Notably, the ZFC–FC curves for the CS_45 particles (Fig. 5b) are markedly different. First, they do not merge at high temperatures, implying that the shell remains blocked (i.e., FiM) at room temperature. Moreover, the kink at 120 K is attributed to the Verwey transition51 of the Fe3O4-shell, i.e., TV ∼ 120 K. The second feature at 240 K is attributed to the magnetic ordering of the FexO core, i.e., TN = 240 K (somewhat larger than the bulk TN of FexO, TN ∼ 200 K13,52). Importantly, the enhancement of TN with respect to the bulk values is supported by the temperature dependence of the intensity of the (1/2, 1/2, 1/2) magnetic reflection, which shows that the magnetic order of the FexO core is maintained up to roughly TN ∼ 240 K (Fig. 4b). To confirm that we are dealing with thermodynamic transitions and not blocking temperatures, we performed M(T) measurements at different applied fields. As can be seen in the ESI Fig. S4† the TV and TN transition temperatures are virtually independent of the field, as expected. Shown in the insets of Fig. 5c, d are the hysteresis loops of the samples at 10 K after FC in 20 kOe from 300 K. The reduced saturation magnetization, MS, values (obtained by subtracting the weight of the surfactant from the total mass), MCS_9S = 46 emu g−1 and MCS_45S = 52 emu g−1, with respect to bulk magnetite (MS = 90 emu g−1)53 are in line with the presence of FexO. The enlarged loops of both samples exhibit exchange bias (HE) and increased coercivities (HC), as expected from the AFM/FiM exchange coupling.42 However, bearing in mind that, according to neutron diffraction, for the CS_9 particles the FexO-core is not antiferromagnetically ordered, the observed HE (∼600 Oe) and HC (∼1000 Oe) should arise from other effects. For example, surface effects in metal oxide nanoparticles are known to result in HE and enhanced HC.54,55 However, the large HE and HC observed for CS_9 indicate that, even if the FexO-core is non-magnetic, the uncompensated spins of the Fe3O4-shell at the FexO/Fe3O4 interface may also contribute to the exchange bias properties. In fact, Monte Carlo simulations demonstrate that a core/shell nanoparticle with a paramagnetic (PM) core can have a rather large exchange bias (ESI Fig. S5†). The temperature dependence of HE and HC (Fig. 5e) show that both quantities decrease rather fast, vanishing below TB. Thus, there is no indication of the presence of a Verwey or Néel transitions, which is again consistent with the non-magnetic character of the FexO core. On the other hand, for the CS_45 particles the temperature dependence of both HE and HC exhibits a rather intricate behaviour (Fig. 5f). When decreasing T, at about 230 K, HE starts to increase while HC exhibits a maximum. These are well known effects of the onset of AFM/ferromagnetic (FM) exchange bias.56,57 Hence, HC(T) and HE(T) also support the enhanced TN of the core. As the temperature is lowered further, at about T = 120 K, HC exhibits a steep increase while HE shows a subtle change of a slope. These features can be linked to the changes in the magnetocrystalline anisotropy (both in the intensity and the easy axis direction58) associated with the Verwey transition. Indeed, the strong temperature dependence of HC around TV is corroborated by Monte Carlo simulations. When assuming the known strong temperature dependence of the anisotropy of Fe3O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58 for the shell anisotropy, KSH (see the inset of ESI Fig. S6†), and a reorientation of the easy axis from (111) to (100), the simulations clearly show that while HC has a rather steep change at TV, HE changes more smoothly (ESI Fig. S6†), in concordance with the experimental results (Fig. 5f). Finally, at very low temperatures there is an additional increase in HC and HE. This is probably related to the fraction of small Fe3O4 nanoparticles observed in CS_45 by XRD and TEM.
58 for the shell anisotropy, KSH (see the inset of ESI Fig. S6†), and a reorientation of the easy axis from (111) to (100), the simulations clearly show that while HC has a rather steep change at TV, HE changes more smoothly (ESI Fig. S6†), in concordance with the experimental results (Fig. 5f). Finally, at very low temperatures there is an additional increase in HC and HE. This is probably related to the fraction of small Fe3O4 nanoparticles observed in CS_45 by XRD and TEM.
Ferromagnetic resonance
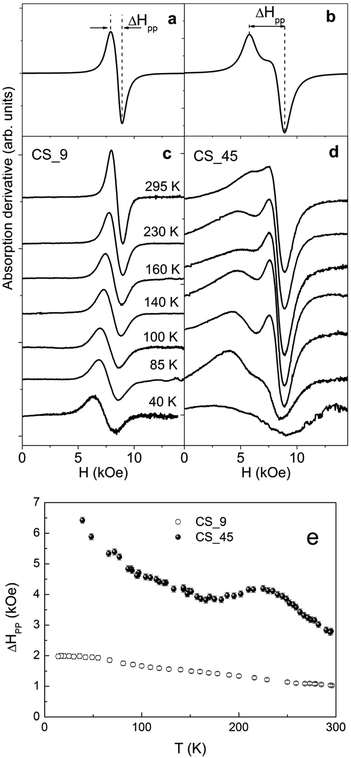
The CS_9 nanoparticles show, at room temperature, a single isotropic resonance line centered at the resonance field Hr = 8.49(4) kOe, with a peak-to-peak linewidth, ΔHpp = 1.03(4) kOe, which grows smoothly up to ∼2 kOe as the temperature decreases (Fig. 6c, e). The results are analogous to the ones measured in low anisotropy Fe3O4 nanoparticles59–62 and show no evidence of either TN of FexO or a Verwey transition, in agreement with the temperature dependence of HC (Fig. 5e), which is also featureless.The large CS_45 nanoparticles show a very broad and asymmetric spectrum with a secondary peak located at lower fields (Fig. 6d). At room temperature ΔHpp is 2.79(8) kOe. Notably, the expected linewidth at room temperature for random oriented single phase Fe3O4 nanoparticles with cubic magnetocrystalline anisotropy (K1 ∼ −1 × 105 erg cm−3 and MS ∼ 55 emu g−1) leads to ΔHpp = 5/3(2 K/MS) ∼ 1.1 kOe.58,59,63,64 This value is almost three times smaller than the value obtained for the CS_45 nanoparticles, which suggests the presence of other significant contributions besides magnetocrystalline anisotropy. In line with this, the simulated profiles (Fig. 6a, b) confirm that the effective anisotropy of the large particles is considerably enhanced with respect to the small ones (see ESI† for details on the simulation parameters).
As can be seen in Fig. 6e, in contrast to the CS_9 particles, the temperature dependence of the FMR linewidth for CS_45 particles exhibits a markedly non-monotonic behavior. Namely, ΔHpp has a peak at around T ∼ 230 K. At about T ∼ 150 K ΔHpp increases moderately again. Finally, at low T there is a rather sharp increase in ΔHpp. The peak in ΔHpp at 230 K can be correlated with the increases in anisotropy expected in AFM/FM systems at the AFM TN,56 and is consistent with HC(T) (Fig. 5f). Further, ΔHpp(T) once again confirms the enhanced TN of the FexO core. Similarly, the upturn in ΔHpp of CS_45 at moderate temperatures can be correlated with the evolution of the system to a phase of lower crystalline symmetry at TV, consistent with the HC behavior. However, a more direct correlation between the line shape and the anisotropy constants is rather difficult since (i) bulk Fe3O4 presents a complex temperature evolution of the magnetocrystalline contribution (i.e. due to a change in the crystal symmetry, from cubic to monoclinic, and the easy axis reorientation at TV),58 (ii) we are dealing with nanoparticle systems with a distribution of anisotropy constants arising from the particle size distribution, different degrees of crystallinity and magnetic disorder, and (iii) the particular morphology of the core/shell system can induce additional anisotropy terms like AFM/FiM exchange coupling, surface, shape or strain anisotropy.
Mössbauer spectroscopy
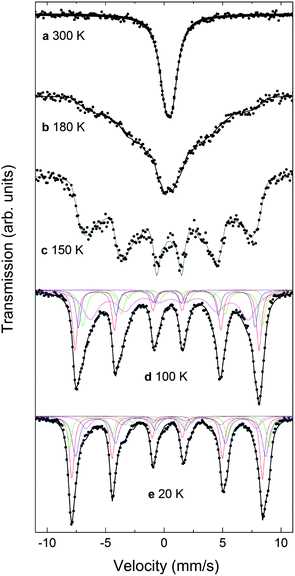
Mössbauer spectra for the CS_9 and CS_45 samples at different temperatures from 20 K to 300 K are shown in Fig. 7 and 8. The 300 K spectrum of the CS_9 (9 nm) particles (Fig. 7a) shows only a broad peak centered at 0.44 mm s−1, while the spectrum of the CS_45 particles (45 nm) at the same temperature (Fig. 8a) shows well resolved sextets in addition to a central peak at around 1.0 mm s−1.For CS_9 while the spectrum in Fig. 7a is typical of superparamagnetic Fe-oxide nanoparticles, a small fraction of paramagnetic FexO (less than 10%) cannot be completely ruled out (although, this value is considerably smaller than the 40% observed for CS_9 from EELS, XRD or neutrons). At 150 K (Fig. 7c) resolved Zeeman sextets start to appear. The spectra measured at 20 K and at 100 K (Fig. 7e, d), i.e., below the Verwey temperature of bulk magnetite, were fitted using five components for Fe3O4, in agreement with other studies and indicate the presence of only Fe3O4 (see ESI†), without a clear evidence of FexO in the sample.65–67 For this sample, Mössbauer spectroscopy suggests a blocking temperature TB close to 180 K, although some magnetic relaxation is still present at 100 K, as can be seen from the significant broadening of the spectral lines when compared to the spectrum at 20 K. The difference of TB between Mössbauer and magnetometry stems from the difference in the characteristic measuring times between both techniques.68 The obtained Mössbauer parameters of the fitting for the 20 K CS_9 spectrum are shown in Table S2 in ESI.†
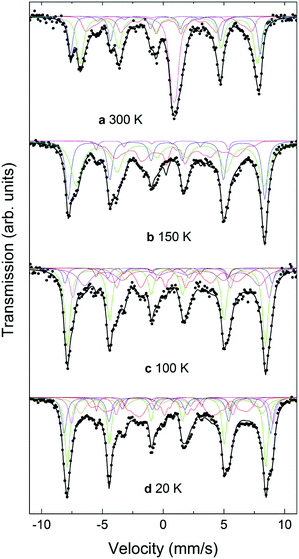
For the CS_45 particles, the fit of the T = 300 K spectrum (Fig. 8a) allows the clear identification of Fe3O4 (ferrimagnetic at room temperature) as the main component (see ESI†). Moreover, the spectrum shows a broad paramagnetic central peak, with an isomer shift of 1.04(2) mm s−1 (20% of the spectral area), which can be assigned to paramagnetic FexO (i.e., above TN). Although the Mössbauer spectrum of non-stoichiometric FexO at room temperature typically consists of a sum of singlets and doublets, depending strongly on the defect concentration in the lattice (where different fitting methods have been applied to describe it69–72), due to the low resolution of the spectrum (broad velocity range, ±12 mm s−1) and lines superposition, the 300 K FexO peak was fitted to just one doublet (ESI Table S2†). A comparison of these Mössbauer parameters with weighted average values from ref. 75 and 77 suggests x > 0.95 for the FexO core, in agreement with EELS and X-ray results. The fitting results at T = 300 K indicate about 20% of FexO in the CS_45 particles, consistent also with the X-ray fits (ESI Table S2†). The spectra measured at 20 K and at 100 K, i.e., below the Verwey temperature of bulk magnetite, were fitted using five components for Fe3O4. Thus, the fact that a higher number of sextets are needed to fit the low temperature spectra (with respect to high temperatures) clearly indicates a Verwey transition. As shown in Table S2,† the obtained Mössbauer parameters are in reasonable agreement with previous studies on magnetite.66,67,73–77 Concerning the FexO subspectrum, it can be seen that at low temperatures (≤150 K, Fig. 8b–d) the high temperature paramagnetic peak opens into a resolved complex spectrum, indicating that the FexO core becomes magnetic. However, the complexity of the FexO spectrum (which in the fit is taken into account by an additional BHF distribution), hinders obtaining accurate magnetostructural details. The resulting magnetic hyperfine field distribution (ESI Table S2†) is fully consistent with an antiferromagnetic FexO core.35,72 Additionally, Mössbauer spectroscopy indicates an ordering transition (i.e., TN) close to 220 K (ESI Fig. S7†) for this phase, in agreement with the neutron, ferromagnetic resonance and magnetometry results.
Discussion
Some of the contrasting properties observed in the two types of nanoparticles stem from different factors, including: (i) size effects, (ii) the exact stoichiometry of the FexO core and (iii) the strains related to the core/shell structure. It is well known that as the size is reduced a number of effects occur in magnetic nanoparticles such as superparamagnetism or reduction of the transition temperatures.50,78 Further, it is well established that in bulk the magnetic properties of FexO are strongly dependent on the exact stoichiometry of FexO.79,80 Finally, another important aspect to be taken into account is the lattice mismatch between the core and the shell counterparts, which can induce significant strains (compressive or tensile) on both the core and the shell,25 which can affect their physicochemical properties. This effect, combined with the strong dependence of the magnetic properties of FexO on pressure,48,77,81,82 can help to understand some of the properties.The enhanced TN with respect to bulk values observed in the large particles can be certainly explained from the combined effects of non-stoichiometry, x, and the internal pressure induced by the Fe3O4 shell. Notably, in bulk it has been shown that TN depends strongly on x,80,83,84 where the less stoichiometric samples have a larger TN. Thus, from the estimation of x in the core/shell nanoparticles, obtained from the EELS analysis, x ∼ 0.95, a higher TN than in bulk is indeed plausible. However, TN ∼ 240 K is probably exceedingly large to be explained solely by non-stoichiometry. Additionally, neutron diffraction and Mössbauer studies have established that the TN of FexO increases with pressure for moderate pressures.81,85 Since the lattice parameter of Fe3O4 is smaller than twice the one of FexO, the lattice mismatch at the core/shell interface generates a compressive strain on the FexO core, as indicated by the GPA analysis. Consequently, the large TN observed experimentally is probably also influenced by the internal pressure, as observed previously in MnO/Mn3O4 core/shell particles,47,86 although proximity effects due to the Fe3O4 shell cannot be ruled out.87,88 However, it is difficult to determine the relative importance of the effects of stoichiometry and strains (and proximity effects) on TN.
An additional novel effect observed in the large particles is that the magnetic moments of the Fe ions in the FexO core are aligned along the [110] and not along the [111] direction as in the bulk phase.49 This effect may again be related to both stoichiometry and strains. Theoretical calculations have shown that although the [111] direction appears to be an easy axis for FexO, small changes (e.g., trigonal asymmetries or deviations of the orbital moments) may change the easy axis to the (111) plane.89–91 This implies that perturbations from the ideal FexO structure may affect the effective easy axis of the system. Experimentally, in bulk it has been observed that the easy axis can significantly deviate from the [111] direction.91–93 It has been argued that this deviation is related to a different magnetic ordering around the defects caused by non-stoichiometry,91,93 which is in the (111) plane.94 As the non-stoichiometry increases, the number of defect clusters grows, a higher tendency to (111) plane orientation of the moments would increase. Given that in the CS_45 samples we have x ∼ 0.95, a reorientation of the easy axis is conceivable. Moreover, it has been theoretically predicted that a compressive strain could reorient the magnetic moments from [111] to the (111) plane due to orbital moments.89 Therefore, the internal pressure observed in the deformation maps obtained by GPA is potentially also contributing to the observed easy axis reorientation. Interestingly, for CoO epitaxial thin films (with a similar spin structure) and Co/CoO core/shell nanoparticles it has been demonstrated that the epitaxial strain can induce reorientations of the easy axis,95,96 similar to the ones observed in the FexO/Fe3O4 nanoparticles. Therefore, once again the combination of stoichiometry and strains appears to control the magnetic properties of the FexO core. However, magnetic effects like perpendicular coupling and easy axis reorientation in FM/AFM systems97–99 may also contribute to the observed [110] easy axis (i.e., in the (111) plane).
Another appealing effect observed in the large particles is the bulk-like Verwey transition51 of the Fe3O4 shell, TV ∼ 120 K, since it has been shown that in nanoparticles TV is significantly affected by size effects. For example, nanoparticles in the range of 20–50 nm already show depleted TV transitions100,101 and smaller particles usually show no signs of TV.102 Although our nanoparticles with ∼40 nm are at the high end of the size effects, it should be taken into account that Fe3O4 comprises only the shell with a rather reduced thickness (∼9 nm). Hence, size effects would be somewhat expected. Moreover, TV is also affected by stoichiometry and small deviations from Fe3O4 quickly suppress the transition.103 Thus, the rather sharp Verwey transition at ∼120 K shows an excellent stoichiometry of the Fe3O4 shell in concordance with EELS and XRD results. In the case of TV, it is known that the pressure (i.e., compressive stress) quickly decreases the transition temperature. However, since the lattice parameter of Fe3O4 is smaller than twice the one of FexO, a tensile stress is expected in the shell from the core (opposing the compressive strain on the FexO core). Thus, perhaps the tensile epitaxial strain favours the stability of the low temperature phase. Another factor to take into account is that the particles are rather cubic in shape and are consequently less prone to magnetic and structural surface effects which may influence TV.54,104
Concerning the small particles, their M(T) shows the typical shape of a superparamagnetic transition, indicating that due to their small size and moderate anisotropy, K, the anisotropy energy, KV, is rather low leading to a superparamagnetic behaviour.50,78,102 However, the most striking feature of these particles is that, while structurally the presence of FexO is confirmed by XRD and neutron diffraction, magnetically (magnetometry, neutron diffraction, FMR and Mössbauer) there is no clear sign of FexO, except for the presence of an exchange bias. The first idea would be to relate the absence of a magnetic signal of FexO to size effects. It is well known that the TN in AFM nanoparticles is substantially reduced for small enough particles.105–108 However, although this could explain the neutron diffraction results, a paramagnetic FexO would lead to an unsplitted central peak in the Mössbauer spectrum,77 as observed for the CS_45 particles at 300 K, which is virtually absent in our data. The large non-stoichiometry of the small particles suggests another origin for the observed effects. The cation deficiency in the FexO structure leads to defects. Interestingly, in FexO these defects tend to cluster forming in some cases Fe3O4-like structures.109 These defect structures should have Mössbauer signatures similar to the Fe3O4 shell, since Mössbauer measures the short-range magnetic order rather than the long-range order measured by neutron diffraction. Consequently, a larger non-stoichiometry should lead to higher number of defects and hence weaker FexO signs in the Mössbauer spectrum. In particular, the progressive oxidation of FexO takes place by oxidizing the Fe2+ ions into Fe3+ ions. This should lead to the progressive appearance of higher magnetic hyperfine field components (absent in nearly stoichiometric FexO) in the Mössbauer spectrum, similar to Fe3O4, as x decreases.69,77 Nevertheless, in line with the large particles, another effect to take into account is pressure, particularly since the small particles probably have larger strains than the larger particles, as evidenced by their smaller lattice parameters. Although the effect of pressure on the magnetic properties of bulk FexO is somewhat controversial,77,81,110 it has been shown that the Mössbauer spectra tend to develop high hyperfine field components as the pressure is increased,77,110 probably due to the fact that the defect clusters start approaching each other. This would contribute to the overlapping of the FexO and Fe3O4 Mössbauer components, and a small fraction of FexO could be “hidden” in the 20 K CS_9 spectrum. Thus, similar to non-stoichiometry the strain effects should also tend to decrease the typical features of FexO in the Mössbauer spectra for the small particles. The combination of neutrons and Mössbauer seems to indicate that the FexO is not magnetic (due to size effects) and that any Mössbauer signal arising from the core is a sign of local magnetism of the defect clusters rather than a true long range magnetic order of FexO.111 Notably, the presence of a sizable exchange bias can be explained without the need of an AFM counterpart. Although it is known that surface effects can give rise to an exchange bias,54 Monte Carlo simulations indicate that the presence of a core/shell interface (even when the core is paramagnetic) can also contribute significantly to the exchange bias properties (ESI Fig. S5†). This exchange bias is in a sense similar to the exchange bias observed in hollow γ-Fe2O3 nanoparticles,112 although in FexO/Fe3O4 the interphase is probably magnetically less disordered than the inner shell in hollow structures.
Finally, note that in the small particles TV of the Fe3O4 shell is lacking. Given the rather small size of the particles, this is probably due to the finite size effects.78
Conclusions
In summary, we have shown that the combination of diverse factors (i.e., non-stoichiometry, core/shell strains and size effects) can shed some light on the broad range of properties exhibited by transition metal oxides at the nanoscale. Importantly, to clarify all these effects, a detailed, multi-technique, characterization is usually required. In particular, we have performed an exhaustive magneto-structural investigation of the smallest and largest FexO/Fe3O4 core/shell nanoparticles (9 nm and 45 nm) reported in the literature. The results reveal a highly non-stoichiometric FexO phase (x ∼ 0.80) for the smaller particles which leads to the non-magnetic character of the FexO core. On the other hand, the larger ones, with x ∼ 0.95, exhibit an antiferromagnetic behaviour. Commonly, in transition metal oxides x depends on the synthesis and post-synthesis conditions as well as on the size, since smaller particles are more reactive thus more prone to oxidation and the reduced number of atoms in the particles implies a higher difficulty to reach a long-range crystal order. Similarly, the internal pressure is determined by several factors like the overall size of the particles, the thickness of the shell, the diameter of the core and shape. Furthermore, in the case of the FexO phase since the lattice parameter depends significantly on x, the strain caused by the lattice mismatch will also depend on x. Hence, our results establish that although some of the overall properties of the FexO/Fe3O4 nanoparticles can be similar (e.g., the presence of an exchange bias or reduced magnetization), the exact features (the presence of TV, enhanced TN, or non-monotonic HE and HC dependence) will depend on the exact structure (e.g., stoichiometry and internal strains) and morphology of the samples (e.g., size or shape).Methods
Synthesis of FexO/Fe3O4 core/shell nanoparticles
All starting materials were purchased from Sigma-Aldrich, except oleic acid (99% of purity) that was acquired from TCI, and used without further purification. In the first step, the iron(III) oleate precursor was synthesized following the procedure described by Park et al.113The small nanoparticles (CS_9) were obtained by dissolving 2 g (1.95 mmol) of iron(III) oleate and 0.09 g (0.32 mmol) of oleic acid in 20 mL of 1-octadecene. The reaction system was degassed at 100 °C under magnetic stirring by carrying out cycles of vacuum/argon. Subsequently, the mixture was heated up to 320 °C (at 7–8 °C min−1) in argon and kept for 30 min.
To synthesize the larger nanoparticles (CS_45), the previous method was slightly modified according to the procedure proposed by Wetterskog et al.25 Namely, 10.25 g (10 mmol) of iron(III) oleate were dissolved in 34 mL of eicosane together with 1.44 g (5.12 mmol) of oleic acid and 1.56 g (5.12 mmol) of sodium oleate. After being degassed under a nitrogen atmosphere, the solution was heated at 100 °C for 2 h to dissolve the sodium oleate. The temperature was then increased to 350 °C using a 3 °C min−1 heating rate. The mixture was maintained at this temperature for 30 min. For both systems the slurry was exposed to air after removing it from the heating source and allowed to cool down to room temperature. The nanoparticles were washed by several cycles of coagulation with ethanol, centrifugation at 2000g, disposal of supernatant solution and re-dispersion in hexane and n-heptane for CS_9 and CS_45, respectively.
Structural and morphological characterization
Transmission electron microscopy (TEM) images were obtained using a Jeol JEM-2100 with a LaB6 filament. High-angle annular dark-field (HAADF) imaging and electron energy loss spectra (EELS) were collected using a Jeol J2010F (S)TEM operating at 200 kV and coupled to a GIF spectrometer and in an FEI Titan operated at 80 kV fitted with a CEOS Probe Corrector and a Gatan Tridiem Energy Filter. EEL data were acquired at about every 1 nm along the diameter of the nanoparticles at an energy range containing the Fe–L2,3 and O–K edges with an energy resolution of 0.8 eV. Fe/O quantification was performed using Gatan Digital Micrograph commercial software. The Fe oxidation state was obtained from a homemade script (“Oxide Wizard”) for Gatan Digital Micrograph software,8 where the required iron oxide reference data were obtained from Schmid et al.114 X-ray diffraction patterns were collected at 300 K at the ID31 beamline of the European Synchrotron Radiation Facility (ESRF) with a wavelength of 0.4 Å for the CS_9 particles and at the BL04-MSPD of the ALBA Synchrotron Light Facility with a wavelength of 0.62 Å for the CS_45 sample.Geometric phase analysis
The geometric phase analysis (GPA) was carried out using the GPA plugin by HREM Research Inc. In this case, e.g., a 1D case (deformation mapping), only one spot corresponding to a given crystallographic interplanar spacing was chosen (see ESI Fig. S1†). Details of the analysis can be found in ref. 25.In the GPA analysis a cosine mask was used on g200(wüstite)/g400(spinel) and g220(spinel), where the size of the mask corresponded to a resolution of 0.9 nm and 1.2 nm, respectively. The width of the integration profiles shown in Fig. 3 was chosen to match the lateral resolution of the images.
Neutron diffraction
Neutron diffraction measurements were carried out at 10 K using a D20 diffractometer of the Institute Laue-Langevin with a neutron wavelength of 1.5 Å for the CS_9 particles and in the temperature range from 15 to 270 K both using the 6T2 and G61 diffractometers of the Laboratoire Léon Brillouin with a neutron wavelength of 2.34 and 4.74 Å, respectively, for the CS_45 sample. All diffraction patterns were analyzed using FullProf115 based on the known crystal and magnetic structures of FexO and Fe3O4.Magnetic measurements
The magnetic properties were measured on tightly packed powdered samples using a superconducting quantum interference device (SQUID, Quantum Design) magnetometer with a 70 kOe maximum field. The measurements of the temperature dependence of magnetization, M(T), were carried out at 20 Oe after either zero field cooling (ZFC) or field cooling (FC) in 20 Oe from 300 K to 10 K. Some M(T) measurements were also carried out at different applied fields (200 and 2000 Oe). Hysteresis loops, M(H), were obtained after FC in 20 kOe from 300 to 10 K. The loops were obtained sequentially at increasing fixed temperatures.Ferromagnetic resonance measurements
Ferromagnetic resonance spectra were recorded with a commercial Bruker ESP300 spectrometer at a frequency of ν = 24 GHz (K-band) in the 5–300 K temperature range.Mössbauer measurements
Transmission 57Fe Mössbauer spectroscopy measurements were conducted at different temperatures ranging from 20 to 300 K, using a closed cycle cryostat, a conventional constant acceleration transducer and a 57Co/Rh source. The Normos least-squares fit program116 was employed for data evaluation and identical recoil-free fractions were assumed for all phases and lattice sites. The isomer shift values are quoted relative to α-Fe at room temperature.Monte Carlo simulations
To model the large particles, CS_45, we consider cubic nanoparticles on a simple cubic (sc) lattice, consisting of an AFM core with an edge length (LC = 12) and a FiM shell (tSH = 3), surrounding the core. The spins in the particles interact with the nearest neighbour's Heisenberg exchange interaction, and at each crystal site they experience a uniaxial anisotropy. In the presence of an external magnetic field, the total energy of the system is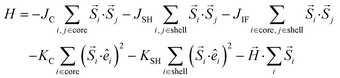 | (1) |
Here Si is the atomic spin at site i and 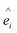 is the unit vector in the direction of the easy axis at site i. We consider the magnitude of the atomic spins in the two AFM sublattices equal to 1 and in the two FiM sublattices of the shell to be equal to 1 and 1.5, respectively. The first term in eqn (1) gives the exchange interaction between the spins in the AFM core; the second term gives the exchange interaction between the spins in the FiM shell. We consider the exchange coupling constant of the core as JC = −0.5JFM and that of the shell as JSH = −1.5JFM, where JFM is considered to be the exchange coupling constant of a pure ferromagnet (FM), JFM = 1 is taken as the reference value. The third term gives the exchange interaction at the interface between the core and the shell. The interface includes the last layer of the AFM core and the first layer of the FiM shell. The exchange coupling constant of the interface JIF is taken to be equal to that of the shell JSH. The fourth term gives the anisotropy energy of the AFM core, KC = 0.05JFM. Based on our neutron diffraction results, KC is assumed to be along the [110] direction and constant in the whole temperature range studied. If the site i lies in the outer layer of the AFM core then KiC = KIF_C, and KiC = KC elsewhere. The core and the shell interface anisotropies are the same as the shell anisotropy for all temperatures. The fifth term gives the anisotropy energy of the FiM shell. To account for the strong non-monotonic temperature dependence of the K of Fe3O4 around the Verwey transition,58 we have set a different KSH value at each simulated temperature (see the inset in Fig. S6 in ESI†). If i lies in the outer layer of the shell (i.e., the surface) then the anisotropy is taken to be random and smoothly changing with T from KS = 3.0JFM (T = 0.01JFM/kB) to 1.6JFM (T = 0.5JFM/kB). Importantly, based on the literature results for Fe3O4 around TV,51,58 two different directions are considered for the shell anisotropy, along the [100] direction for T < TV and along the [111] direction for T > TV. Note that in concordance with the literature values, TV is taken to be about 1/7 of the ferrimagnetic transition temperature of the shell (TC ∼ 1.75JFM/kB), i.e., TV = 0.25JFM/kB. Moreover, from the parameters used in the simulation the TN of the core is established to be TN = 0.7JFM/kB. The last term in eqn (1) is the Zeeman energy.
is the unit vector in the direction of the easy axis at site i. We consider the magnitude of the atomic spins in the two AFM sublattices equal to 1 and in the two FiM sublattices of the shell to be equal to 1 and 1.5, respectively. The first term in eqn (1) gives the exchange interaction between the spins in the AFM core; the second term gives the exchange interaction between the spins in the FiM shell. We consider the exchange coupling constant of the core as JC = −0.5JFM and that of the shell as JSH = −1.5JFM, where JFM is considered to be the exchange coupling constant of a pure ferromagnet (FM), JFM = 1 is taken as the reference value. The third term gives the exchange interaction at the interface between the core and the shell. The interface includes the last layer of the AFM core and the first layer of the FiM shell. The exchange coupling constant of the interface JIF is taken to be equal to that of the shell JSH. The fourth term gives the anisotropy energy of the AFM core, KC = 0.05JFM. Based on our neutron diffraction results, KC is assumed to be along the [110] direction and constant in the whole temperature range studied. If the site i lies in the outer layer of the AFM core then KiC = KIF_C, and KiC = KC elsewhere. The core and the shell interface anisotropies are the same as the shell anisotropy for all temperatures. The fifth term gives the anisotropy energy of the FiM shell. To account for the strong non-monotonic temperature dependence of the K of Fe3O4 around the Verwey transition,58 we have set a different KSH value at each simulated temperature (see the inset in Fig. S6 in ESI†). If i lies in the outer layer of the shell (i.e., the surface) then the anisotropy is taken to be random and smoothly changing with T from KS = 3.0JFM (T = 0.01JFM/kB) to 1.6JFM (T = 0.5JFM/kB). Importantly, based on the literature results for Fe3O4 around TV,51,58 two different directions are considered for the shell anisotropy, along the [100] direction for T < TV and along the [111] direction for T > TV. Note that in concordance with the literature values, TV is taken to be about 1/7 of the ferrimagnetic transition temperature of the shell (TC ∼ 1.75JFM/kB), i.e., TV = 0.25JFM/kB. Moreover, from the parameters used in the simulation the TN of the core is established to be TN = 0.7JFM/kB. The last term in eqn (1) is the Zeeman energy.
We performed our simulations on isolated, cubic (AFM) core/(FiM) shell nanoparticles using the MC simulation technique with the implementation of the Metropolis algorithm.117 A hysteresis loop is calculated after a field cooling procedure starting at temperature T = 2.0JFM/kB down to Tf = 0.01JFM/kB, at a constant rate under a static magnetic field Hcool = 6.0JFM/gμB. To account for the experimental random distribution of nanoparticles,7 the cooling fields have been applied in different directions defined by spherical coordinates (θ,φ), where θ = 0, 15,…, 180 and φ = 0, 15,…, 345 degrees. The final hysteresis loop is calculated by averaging the hysteresis loops for each magnetic field direction according to the equation:
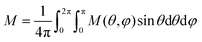 | (2) |
The hysteresis loop shift on the field axis gives the exchange field HE = −(Hright + Hleft)/2. The coercive field is defined as HC = (Hright − Hleft)/2. Hright and Hleft are the points where the loop intersects the field axis. The fields H, HC and HE are given in dimensionless units of JFM/gμB, the temperature T in units JFM/kB and the anisotropy coupling constants K in units of JFM. We have used 104 MC steps per spin (MCSS) at each field step and the results were averaged over 50–200 different samples (namely random numbers) depending on the fluctuations in the calculated values. The small nanoparticles, CS_9 are simulated using a spherical morphology with an FiM shell (tSH = 3) and a core size of three lattice spacings in diameter (dC = 3). The material parameters for the shell are the ones used above for the large particles at low T (JSH = JIF_SH = −1.5JFM, KSH = KIF_SH = 0.3). The surface anisotropy is taken at random with KS = 3.0JFM. However, four different types of cores are considered in this case:
(1) AFM core with the same parameters as for CS_45, i.e., JC = −0.5JFM, and KC = 0.05.
(2) Paramagnetic core with JC = 0.00, KC = 0.00.
(3) FiM core with the same parameters as the shell (i.e., a homogeneous FiM particle).
(4) No core (i.e., a hollow nanoparticle).
Notably, the internal surface of the particle is also assumed to have a random anisotropy with the same KS as the external surface. Since we are only interested in the trends, for simplicity, the anisotropy and magnetic fields are assumed to be along the z-axis, thus no angular hysteresis loop averaging is performed.
Acknowledgements
This work was supported by the 2014-SGR-1015 and 2009-SGR-35 projects of the Generalitat de Catalunya, by the MAT2010-20616-C02, MAT2011-27380-C02-01, MAT2010-16407, MAT2013-48628-R and CSD2009-00013 projects of the Spanish Ministerio de Economía y Competitividad (MINECO), the ONDA and COEFNANO projects (no. FP7-PEOPLE-2009-IRSES-247518 and no. FP7-PEOPLE-2012-IRSES-318901) of the European Union, the Russian grants RFBR 13-02-00121, 13-02-12429 and RG 14.B25.31.0025, the Brazilian grants CNPq-304368/2010-5 and FAPEMIG-PPM 00319-11, the Argentine grants PIP 1333 (CONICET) and SECTyP 06/C404 (Univ. Nac. de Cuyo) and the Swedish Research Council (VR). Research at NCSR “D” was supported by the HSF-EU program ARISTEIA, grant COMANA/22. GSA was partially supported by the Knut and Alice Wallenberg Foundation (Project: 3DEM-NATUR). I.V.G. thanks the Generalitat de Catalunya for his sabbatical fellowship (2010 PIV 00096). M.D.B. was partially supported by an ICREA Academia award. M.E. acknowledges the Spanish Ministry of Science and Innovation through the Juan de la Cierva Program. A. G. Roca would like to thank Generalitat de Catalunya for financial support under the Beatriu de Pinós fellowship program (2011 BP_B 00209). ICN2 acknowledges support from the Severo Ochoa Program (MINECO, grant SEV-2013-0295). We also acknowledge the European Synchrotron Radiation Facility (ESRF, Grenoble, France) and the ALBA Synchrotron Light Facility for the provision of synchrotron beam time and the Institute Laue-Langevin (ILL) and Laboratoire Léon Brillouin (LLB) for the provision of neutron beam time.References
- M. T. Greiner, L. Chai, M. G. Helander, W. M. Tang and Z.-H. Lu, Adv. Funct. Mater., 2012, 22, 4557–4568 CrossRef CAS.
- P. Poizot, S. Laruelle, S. Grugeon, L. Dupont and J. M. Tarascon, Nature, 2000, 407, 496–499 CrossRef CAS PubMed.
- Y. Tokura, Rep. Prog. Phys., 2006, 69, 797–851 CrossRef CAS.
- G. S. Park, Y. B. Kim, S. Y. Park, X. S. Li, S. Heo, M. J. Lee, M. Chang, J. H. Kwon, M. Kim, U. I. Chung, R. Dittmann, R. Waser and K. Kim, Nat. Commun., 2013, 4, 2382 Search PubMed.
- A. Juhin, A. López-Ortega, M. Sikora, C. Carvallo, M. Estrader, S. Estradé, F. Peiró, M. D. Baró, P. Sainctavit, P. Glatzel and J. Nogués, Nanoscale, 2014, 6, 11911–11920 RSC.
- K. L. Krycka, J. A. Borchers, G. Salazar-Alvarez, A. López-Ortega, M. Estrader, S. Estradé, E. Winkler, R. D. Zysler, J. Sort, F. Peiró, M. D. Baró, C. Kao and J. Nogués, ACS Nano, 2013, 7, 921–931 CrossRef CAS PubMed.
- A. López-Ortega, M. Estrader, G. Salazar-Alvarez, S. Estradé, I. V. Golosovsky, R. K. Dumas, D. J. Keavney, M. Vasilakaki, K. N. Trohidou, J. Sort, F. Peiró, S. Suriñach, M. D. Baró and J. Nogués, Nanoscale, 2012, 4, 5138–5147 RSC.
- L. Yedra, E. Xuriguera, M. Estrader, A. López-Ortega, M. D. Baró, J. Nogués, M. Roldan, M. Varela, S. Estradé and F. Peiró, Microsc. Microanal., 2014, 20, 698–705 CrossRef CAS PubMed.
- T. Zhang, X. P. Wang, Q. F. Fang and X. G. Li, Appl. Phys. Rev., 2014, 1, 031302 Search PubMed.
- F. X. Redl, C. T. Black, G. C. Papaefthymiou, R. L. Sandstrom, M. Yin, H. Zeng, C. B. Murray and S. P. O'Brien, J. Am. Chem. Soc., 2004, 126, 14583–14599 CrossRef CAS PubMed.
- S. Sun and H. Zeng, J. Am. Chem. Soc., 2002, 124, 8204–8205 CrossRef CAS PubMed.
- P. Guardia, A. Labarta and X. Batlle, J. Phys. Chem. C, 2011, 115, 390–396 CAS.
- R. Cornell and U. Schwertmann, The Iron Oxides: Structure, Properties, Reactions, Occurences and Uses, New York, 2nd edn, 2003 Search PubMed.
- P. Tartaj, M. P. Morales, T. Gonzalez-Carreño, S. Veintemillas-Verdaguer and C. J. Serna, Adv. Mater., 2011, 23, 5243–5249 CrossRef CAS.
- A. Glaria, M. L. Kahn, P. Lecante, B. Barbara and B. Chaudret, ChemPhysChem, 2008, 9, 776–780 CrossRef CAS PubMed.
- H. Si, C. Zhou, H. Wang, S. Lou, S. Li, Z. Du and L. S. Li, J. Colloid Interface Sci., 2008, 327, 466–471 CrossRef CAS PubMed.
- M. Yin, Z. Chen, B. Deegan and S. O'Brien, J. Mater. Res., 2011, 22, 1987–1995 CrossRef.
- Y. Hou, Z. Xu and S. Sun, Angew. Chem., Int. Ed., 2007, 46, 6329–6332 CrossRef CAS PubMed.
- L. M. Bronstein, X. Huang, J. Retrum, A. Schmucker, M. Pink, B. D. Stein and B. Dragnea, Chem. Mater., 2007, 19, 3624–3632 CrossRef CAS.
- H. T. Hai, H. T. Yang, H. Kura, D. Hasegawa, Y. Ogata, M. Takahashi and T. Ogawa, J. Colloid Interface Sci., 2010, 346, 37–42 CrossRef CAS PubMed.
- M. I. Bodnarchuk, M. V. Kovalenko, H. Groiss, R. Resel, M. Reissner, G. Hesser, R. T. Lechner, W. Steiner, F. Schäffler and W. Heiss, Small, 2009, 5, 2247–2252 CrossRef CAS PubMed.
- D. W. Kavich, J. Dickerson, S. Mahajan, S. Hasan and J. H. Park, Phys. Rev. B: Condens. Matter, 2008, 78, 174414 CrossRef.
- C. J. Chen, R.-K. Chiang, H. Y. Lai and C. R. Lin, J. Phys. Chem. C, 2010, 114, 4258–4263 CAS.
- H. T. Hai, H. Kura, M. Takahashi and T. Ogawa, J. Colloid Interface Sci., 2010, 341, 194–199 CrossRef CAS PubMed.
- E. Wetterskog, C. Tai, J. Grins, L. Bergström and G. Salazar-Alvarez, ACS Nano, 2013, 7, 7132–7144 CrossRef CAS PubMed.
- B. P. Pichon, O. Gerber, C. Lefevre, I. Florea, S. Fleutot, W. Baaziz, M. Pauly, M. Ohlmann, C. Ulhaq, O. Ersen, V. Pierron-Bohnes, P. Panissod, M. Drillon and S. Begin-Colin, Chem. Mater., 2011, 23, 2886–2900 CrossRef CAS.
- A. Lak, M. Kraken, F. Ludwig, A. Kornowski, D. Eberbeck, S. Sievers, F. J. Litterst, H. Weller and M. Schilling, Nanoscale, 2013, 5, 12286–12295 RSC.
- H. Khurshid, W. Li, S. Chandra, M.-H. Phan, G. C. Hadjipanayis, P. Mukherjee and H. Srikanth, Nanoscale, 2013, 5, 7942–7952 RSC.
- K. Simeonidis, S. Mourdikoudis, I. Tsiaoussis, N. Frangis, M. Angelakeris, O. Kalogirou, A. Delimitis and C. Dendrinou-Samara, Mod. Phys. Lett. B, 2007, 21, 1143–1151 CrossRef CAS.
- A. Corrias, G. Mountjoy, D. Loche, V. Puntes, A. Falqui, M. Zanella, W. J. Parak and M. F. Casula, J. Phys. Chem. C, 2009, 113, 18667–18675 CAS.
- S. K. Sharma, J. M. Vargas, K. R. Pirota, S. Kumar, C. G. Lee and M. Knobel, J. Alloys Compd., 2011, 509, 6414–6417 CrossRef CAS PubMed.
- M. J. Benitez, D. Mishra, P. Szary, G. A. Badini Confalonieri, M. Feyen, A. H. Lu, L. Agudo, G. Eggeler, O. Petracic and H. Zabel, J. Phys.: Condens. Matter, 2011, 23, 126003 CrossRef CAS PubMed.
- H. T. Hai, H. Kura, M. Takahashi and T. Ogawa, J. Appl. Phys., 2010, 107, 09E301 CrossRef PubMed.
- R. Chalasani and S. Vasudevan, J. Phys. Chem. C, 2011, 115, 18088–18093 CAS.
- A. Lak, J. Dieckhoff, F. Ludwig, J. M. Scholtyssek, O. Goldmann, H. Lünsdorf, D. Eberbeck, A. Kornowski, M. Kraken, F. J. Litterst, K. Fiege, P. Mischnick and M. Schilling, Nanoscale, 2013, 5, 11447–11455 RSC.
- X. Sun, N. F. Huls, A. Sigdel and S. Sun, Nano Lett., 2012, 12, 246–251 CrossRef CAS PubMed.
- H. Khurshid, S. Chandra, W. Li, M. H. Phan, G. C. Hadjipanayis, P. Mukherjee and H. Srikanth, J. Appl. Phys., 2013, 113, 17B508 CrossRef PubMed.
- A. Stamatiou, P. G. Loutzenhiser and A. Steinfeld, Chem. Mater., 2010, 22, 851–859 CrossRef CAS.
- L. Xiao, S. Y. Wu and Y.-R. Li, Renewable Energy, 2012, 41, 1–12 CrossRef PubMed.
- L. Shi, Y. D. He, X. H. Xia, Z. M. Jian and H. B. Liu, J. Iran Chem. Soc., 2010, 7, 721–726 CrossRef CAS.
- J. Zheng, Z. Yu, G. Ji, X. Lin, H. Lv and Y. Du, J. Alloys Compd., 2014, 602, 8–15 CrossRef CAS PubMed.
- J. Nogués, J. Sort, V. Langlais, V. Skumryev, S. Suriñach, J. S. Muñoz and M. D. Baró, Phys. Rep., 2005, 422, 65–117 CrossRef PubMed.
- W. H. Meiklejohn and C. Bean, Phys. Rev., 1956, 102, 1413–1414 CrossRef.
- J. Nogués, V. Skumryev, J. Sort, S. Stoyanov and D. Givord, Phys. Rev. Lett., 2006, 97, 157203 CrossRef.
- G. Margaris, K. N. Trohidou and J. Nogués, Adv. Mater., 2012, 24, 4331–4336 CrossRef CAS PubMed.
- G. Salazar-Alvarez, J. Sort, S. Suriñach, M. D. Baro and J. Nogués, J. Am. Chem. Soc., 2007, 129, 9102–9108 CrossRef CAS PubMed.
- A. López-Ortega, D. Tobia, E. Winkler, I. V. Golosovsky, G. Salazar-Alvarez, S. Estradé, M. Estrader, J. Sort, M. A. González, S. Suriñach, J. Arbiol, F. Peiró, R. D. Zysler, M. D. Baró and J. Nogués, J. Am. Chem. Soc., 2010, 132, 9398–9407 CrossRef PubMed.
- C. A. McCammon and L. Liu, Phys. Chem. Miner., 1984, 10, 106–113 CrossRef CAS.
- W. Roth, Phys. Rev., 1958, 110, 1333–1341 CrossRef CAS.
- M. Knobel, W. Nunes, L. Socolovsky, E. De Biasi, J. M. Vargas and J. Denardin, J. Nanosci. Nanotechnol, 2008, 8, 2836–2857 CAS.
- F. Walz, J. Phys.: Condens. Matter, 2002, 14, R285–R340 CrossRef CAS.
- G. Srinivasan and M. S. Seehra, Phys. Rev. B: Condens. Matter, 1983, 28, 6542–6544 CrossRef CAS.
- A. G. Roca, M. P. Morales, K. O'Grady and C. J. Serna, Nanotechnology, 2006, 17, 2783–2788 CrossRef CAS.
- G. Salazar-Alvarez, J. Qin, V. Sepelák, I. Bergmann, M. Vasilakaki, K. N. Trohidou, J. D. Ardisson, W. A. A. Macedo, M. Mikhaylova, M. Muhammed, M. D. Baró and J. Nogués, J. Am. Chem. Soc., 2008, 130, 13234–13239 CrossRef CAS PubMed.
- N. Rinaldi-Montes, P. Gorria, D. Martínez-Blanco, A. B. Fuertes, L. Fernández Barquín, J. Rodríguez Fernández, I. de Pedro, M. L. Fdez-Gubieda, J. Alonso, L. Olivi, G. Aquilanti and J. A. Blanco, Nanoscale, 2014, 6, 457–465 RSC.
- J. Nogués and I. K. Schuller, J. Magn. Magn. Mater., 1999, 192, 203–232 CrossRef.
- C. Leighton, M. Fitzsimmons, A. Hoffmann, J. Dura, C. F. Majkrzak, M. S. Lund and I. K. Schuller, Phys. Rev. B: Condens. Matter, 2002, 65, 064403 CrossRef.
- S. Chikazumi , in AIP Conf. Proc., AIP, 1976, vol. 29, pp. 382–387.
- N. Guskos, E. A. Anagnostakis, V. Likodimos, T. Bodziony, J. Typek, M. Maryniak, U. Narkiewicz, I. Kucharewicz and S. Waplak, J. Appl. Phys., 2005, 97, 024304 CrossRef PubMed.
- E. De Biasi, E. Lima, C. A. Ramos, A. Butera and R. D. Zysler, J. Magn. Magn. Mater., 2013, 326, 138–146 CrossRef CAS PubMed.
- S. Pal, P. Dutta, N. Shah, G. P. Huffman and M. S. Seehra, IEEE Trans. Magn., 2007, 43, 3091–3093 CrossRef CAS.
- Y. Köseoglu and H. Kavas, J. Nanosci. Nanotechnol., 2008, 8, 584–590 CrossRef PubMed.
- E. Lima, A. L. Brandl, A. D. Arelaro and G. F. Goya, J. Appl. Phys., 2006, 99, 083908 CrossRef PubMed.
- A. H. Morrish, The Physical Principles of Magnetism, New York, NY, 2001 Search PubMed.
- R. S. Hargrove and W. Kündig, Solid State Commun., 1970, 8, 303–308 CrossRef CAS.
- F. J. Berry, S. Skinner and M. F. Thomas, J. Phys.: Condens. Matter, 1998, 10, 215–220 CrossRef CAS.
- A. G. Roca, J. F. Marco, M. P. Morales and C. J. Serna, J. Phys. Chem. C, 2007, 111, 18577–18584 CAS.
- M. Popovici, M. Gich, A. Roig, L. Casas, E. Molins, C. Savii, D. Becherescu, J. Sort, S. Suriñach, J. S. Muñoz, M. D. Baró and J. Nogués, Langmuir, 2004, 20, 1425–1429 CrossRef CAS.
- N. N. Greenwood and A. T. Howe, J. Chem. Soc., Dalton Trans., 1972, 110–116 RSC.
- C. Wilkinson, A. K. Cheetham, G. J. Long, P. D. Battle and D. A. O. Hope, Inorg. Chem., 1984, 23, 3136–3141 CrossRef CAS.
- T. Yoshikawa, Y. Kanke, H. Yanagihara, E. Kita, Y. Tsunoda, K. Siratori and K. Kohn, Hyperfine Interact., 2012, 205, 135–138 CrossRef CAS.
- C. A. McCammon and D. C. Price, Phys. Chem. Miner., 1985, 11, 250–254 CrossRef CAS.
- I. Dézsi, C. Fetzer, A. Gombkötő, I. Szűcs, J. Gubicza and T. Ungár, J. Appl. Phys., 2008, 103, 104312 CrossRef PubMed.
- T. J. Daou, G. Pourroy, S. Bégin-Colin, J. M. Grenèche, C. Ulhaq-Bouillet, P. Legaré, P. Bernhardt, C. Leuvrey and G. Rogez, Chem. Mater., 2006, 18, 4399–4404 CrossRef CAS.
- A. C. Doriguetto, N. G. Fernandes, A. I. C. Persiano, E. N. Filho, J. M. Grenèche and J. D. Fabris, Phys. Chem. Miner., 2003, 30, 249–255 CAS.
- N. A. Fellenz, L. A. Cano, J. F. Bengoa, I. de Souza Azevedo, R. C. Mercader and S. G. Marchetti, Hyperfine Interact., 2011, 202, 17–24 CrossRef CAS.
- S. Nasu, Hyperfine Interact., 1994, 90, 59–75 CrossRef CAS.
- X. Batlle and A. Labarta, J. Phys. D: Appl. Phys., 2002, 35, R15–R42 CrossRef CAS.
- R. M. Hazen and R. Jeanloz, Rev. Geophys., 1984, 22, 37–46 CrossRef CAS.
- F. B. Koch and M. E. Fine, J. Appl. Phys., 1967, 38, 1470–1471 CrossRef CAS PubMed.
- I. Kantor, L. Dubrovinsky, C. Mccammon, N. Dubrovinskaia, I. Goncharenko, A. Kantor, A. Kuznetsov and W. Crichton, Phase Transitions, 2007, 80, 1151–1163 CrossRef CAS.
- S. V. Ovsyannikov, V. V. Shchennikov, M. A. Shvetsova, L. S. Dubrovinsky and A. Polian, Phys. Rev. B: Condens. Matter, 2010, 81, 060101 CrossRef.
- M. S. Seehra and G. Srinivasan, J. Phys. C: Solid State Phys., 1984, 17, 883–892 CrossRef CAS.
- A. Pattek-Janczyk, B. Sepioł, J. C. Grenier and L. Fournès, Mater Res. Bull., 1986, 21, 1083–1092 CrossRef CAS.
- K. Glazyrin, L. Dubrovinsky, S. Klotz, M. Uhlarz, J. Wosnitza, T. Hansen and N. Dubrovinskaia, J. Appl. Phys., 2011, 110, 026109 CrossRef PubMed.
- N. J. O. Silva, M. Karmaoui, V. S. Amaral, I. Puente-Orench, J. Campo, I. da Silva, A. Ibarra, R. Bustamante, A. Millán and F. Palacio, Phys. Rev. B: Condens. Matter, 2013, 87, 224429 CrossRef.
- I. V. Golosovsky, G. Salazar-Alvarez, A. López-Ortega, M. González, J. Sort, M. Estrader, S. Suriñach, M. Baró and J. Nogués, Phys. Rev. Lett., 2009, 102, 247201 CrossRef CAS.
- P. K. Manna and S. M. Yusuf, Phys. Rep., 2014, 535, 61–99 CrossRef PubMed.
- I. V. Solovyev, A. I. Liechtenstein and K. Terakura, J. Magn. Magn. Mater., 1998, 185, 118–120 CrossRef CAS.
- A. Schrön and F. Bechstedt, J. Phys.: Condens. Matter, 2013, 25, 486002 CrossRef PubMed.
- H. Fjellvåg, F. Grønvold, S. Stølen and B. Hauback, J. Solid State Chem., 1996, 124, 52–57 CrossRef.
- H. Fjellvåg, B. C. Hauback, T. Vogt and S. Stølen, Am. Mineral, 2002, 87, 347–349 Search PubMed.
- P. J. Saines, M. G. Tucker, D. A. Keen, A. K. Cheetham and A. L. Goodwin, Phys. Rev. B: Condens. Matter, 2013, 88, 134418 CrossRef.
- P. D. Battle and A. K. Cheetham, J. Phys. C: Solid State Phys., 1979, 12, 337–345 CrossRef CAS.
- S. Csiszar, M. Haverkort, Z. Hu, A. Tanaka, H. Hsieh, H. J. Lin, C. Chen, T. Hibma and L. Tjeng, Phys. Rev. Lett., 2005, 95, 187205 CrossRef CAS.
- S. Inderhees, J. Borchers, K. Green, M. Kim, K. Sun, G. Strycker and M. Aronson, Phys. Rev. Lett., 2008, 101, 117202 CrossRef CAS.
- E. Jiménez, J. Camarero, J. Sort, J. Nogués, N. Mikuszeit, J. García-Martín, A. Hoffmann, B. Dieny and R. Miranda, Phys. Rev. B: Condens. Matter, 2009, 80, 014415 CrossRef.
- T. J. Moran, J. Nogués, D. Lederman and I. K. Schuller, Appl. Phys. Lett., 1998, 72, 617–619 CrossRef CAS PubMed.
- J. Zhu, Q. Li, J. X. Li, Z. Ding, J. H. Liang, X. Xiao, Y. M. Luo, C. Y. Hua, H. J. Lin, T. W. Pi, Z. Hu, C. Won and Y. Z. Wu, Phys. Rev. B: Condens. Matter, 2014, 90, 054403 CrossRef.
- G. F. Goya, T. S. Berquó, F. C. Fonseca and M. P. Morales, J. Appl. Phys., 2003, 94, 3520–3528 CrossRef CAS PubMed.
- J. Santoyo Salazar, L. Perez, O. de Abril, L. Truong Phuoc, D. Ihiawakrim, M. Vazquez, J. M. Greneche, S. Begin-Colin and G. Pourroy, Chem. Mater., 2011, 23, 1379–1386 CrossRef CAS.
- P. Dutta, S. Pal, M. S. Seehra, N. Shah and G. P. Huffman, J. Appl. Phys., 2009, 105, 07B501 Search PubMed.
- Ö. Özdemir, D. J. Dunlop and B. M. Moskowitz, Geophys. Res. Lett., 1993, 20, 1671–1674 CrossRef.
- Y. Hwang, S. Angappane, J. Park, K. An, T. Hyeon and J. G. Park, Curr. Appl. Phys., 2012, 12, 808–811 CrossRef PubMed.
- X. Zheng, C. Xu, K. Nishikubo, K. Nishiyama, W. Higemoto, W. Moon, E. Tanaka and E. Otabe, Phys. Rev. B: Condens. Matter, 2005, 72, 014464 CrossRef.
- S. Sako and K. Ohshima, J. Phys. Soc. Jpn., 1995, 64, 944–950 CrossRef CAS.
- S. Sako, K. Ohshima, M. Sakai and S. Bandow, Surf. Rev. Lett., 1996, 03, 109–113 CrossRef CAS.
- S. Thota, J. H. Shim and M. S. Seehra, J. Appl. Phys., 2013, 114, 214307 CrossRef PubMed.
- C. R. A. Catlow and B. E. F. Fender, J. Phys. C: Solid State Phys., 1975, 8, 3267–3279 CrossRef CAS.
- M. Pasternak, R. Taylor, R. Jeanloz, X. Li, J. Nguyen and C. McCammon, Phys. Rev. Lett., 1997, 79, 5046–5049 CrossRef CAS.
- Y. Ding, J. Xu, C. T. Prewitt, R. J. Hemley, H. Mao, J. A. Cowan, J. Zhang, J. Qian, S. C. Vogel, K. Lokshin and Y. Zhao, Appl. Phys. Lett., 2005, 86, 052505 CrossRef PubMed.
- A. Cabot, A. Alivisatos, V. Puntes, L. Balcells, Ò. Iglesias and A. Labarta, Phys. Rev. B: Condens. Matter, 2009, 79, 094419 CrossRef.
- J. Park, K. An, Y. Hwang, J. G. Park, H. J. Noh, J. Y. Kim, J. H. Park, N. M. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895 CrossRef CAS PubMed.
- H. K. Schmid and W. Mader, Micron, 2006, 37, 426–432 CrossRef CAS PubMed.
- J. Rodríguez-Carvajal, Physica B, 1993, 192, 55–69 CrossRef.
- R. A. Brand, Nucl. Instrum. Methods Phys. Res., Sect. B, 1987, 28, 398–416 CrossRef.
- K. Binder, Applications of Monte Carlo Methods in Statistical Physics, Springer-Verlag, Berlin, Germany, 1984 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4nr06351a |
| This journal is © The Royal Society of Chemistry 2015 |