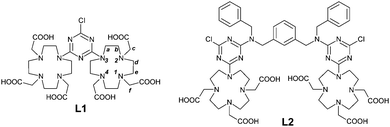
Solution thermodynamics, computational and relaxometric studies of ditopic DO3A-based Mn(II) complexes

Abstract

Mn(II)-complexes are experiencing renewed interest as MRI contrast agents due to safety concerns related to the use of Gd(III)-chelates. While the preparation of oligomeric and polymeric Gd(III)-chelates is widely employed to multiply their efficiency, scarce examples of this strategy are reported for the corresponding Mn(II)-complexes. Two novel ditopic DO3A-based ligands were designed and synthesized and their Mn(II)-complexes evaluated in order to shed more light on the correlation of the paramagnetic properties of the resultant dinuclear complexes with their structural features. The stability of these complexes was assessed by potentiometric titration, while modelling was adopted to gain the structural features. A detailed relaxometric characterization provided a defined picture of the paramagnetic properties of these dinuclear chelates, paving the way for the design of Mn(II)-based multimeric MRI contrast agents.

---

Introduction

Magnetic Resonance Imaging (MRI) is a diagnostic technique widely employed to provide images of living bodies with an unsurpassed definition. A considerable percentage of the MRI scans is registered after injection of specific contrast agents (CAs), usually paramagnetic chelates whose effect is to accelerate the relaxation rate of water protons, the latter being responsible for the signal employed in the image construction.¹ Complexes of Gd(III) are the most popular CAs due to the optimal properties of this lanthanide ion (seven unpaired electrons, long electronic relaxation time and the ability to form stable complexes with polyaminopoly-carboxylic ligands).² Recent reports of toxic effects due to slow release of Gd(III)-ions from acyclic ligands³ led to a resurgence of interest in less toxic paramagnetic metal ions such as Fe(III) and Mn(II).

Mn(II) ions with 5 unpaired electrons provide a viable alternative to Gd(III) ions, although with intrinsically lower magnetic properties. Nevertheless, manganese is an essential element to human life and its eventual release (in limited amounts) is tolerated and even demonstrated to be involved in the contrast mechanism of Mn-based chelates.⁴ In the last decade several novel Mn(II)-complexes were examined as potential CAs for MRI; a detailed list along with the corresponding characterization can be found in recent dedicated reviews.^5–7 Nevertheless, few Mn-based CAs have reached the clinical stages; the reason underlying this shortage could be identified in the difficulties in the design of Mn(II)-complexes, gathering the efficiency required for MRI applications with the stability required for in vivo administration. This is quite easily obtained with the lanthanide Gd(III), for which a stable coordination could be gained with macrocyclic octadentate⁸ or even with selected heptadentate^9,10 ligands, while it is more difficult to achieve with the usually hexacoordinating Mn(II) ion. Few ligands form Mn(II)-complexes with high thermodynamic stabilities (log K_MnL > 20)¹¹ leading to a lack of a reference coordinating platform. Even in the restricted number of stable Mn(II)-chelates the relaxivity values are lower than those of Gd-based CAs, as a result of the lower hydration and resulting in the lack of a “gold standard” Mn-based MRI CA. To overcome the low relaxivity values of Mn(II)-chelates, a collection of multiple units in a single oligomeric molecule¹² may be useful. Paramagnetic oligomers and polymers experience a multiplication of the effect of the single metallic centers, further enhanced by the slowing down of the rotational motion due to the increase in the overall molecular size; the efficiency of this approach leads to a wide range of applications in the research field of Gd-based CAs. While several dimeric Mn(II)-complexes were studied, for example as SOD-mimics,¹³ scarce reports in the literature of oligomeric Mn(II)-complexes as MRI CAs have appeared, involving complexation of the paramagnetic metal ion by DOTA/NOTA ligands conjugated to nanoglobular dendrimers with a silsesquioxane core¹⁴ or by DTPA residues linked to chitosan oligosaccharides.¹⁵

The need for a systematic study of the influence of factors such as the nuclearity, the molecular rigidity and the overall size on the relaxivity of Mn(II)-based oligo- and polymeric assemblies led us to explore low nuclearity members of this class. In this work, we designed two original ditopic ligands, able to form dinuclear Mn(II)-complexes. The ligand units were derived from the well known macrocyclic DO3A platform. The choice of DO3A units was driven by the high value of the stability constant of Mn(II)–DO3A,¹⁶ overcoming demetallation issues; an additional advantage stems: (i) from the expected formation of non-hydrated complexes (q = 0), avoiding the treatment of hydration equilibria, and (ii) from the straightforward functionalization of the secondary amino-group of DO3A. A symmetric arrangement of both coordinating units in the homoditopic ligands ensures homogeneous behaviour of the paramagnetic metal ions and a more simple analysis of their properties.

Results and discussion

Synthesis

The dimeric DO3A-like ligands (L1 and L2) employed for the formation of paramagnetic complexes of this work are depicted in Scheme 1.

Scheme 1 Structures of the two dimeric ligands (L1 and L2) employed in this work.

Two DO3A coordinating subunits were connected by reaction with cyanuryl chloride, leading to the ligand L1, where the s-triazine heterocyclic residue plays the role of the linker and the spacer of the macrocyclic cages. The ligand L2 is designed to share the local coordinating environments of L1 but is separated by a rigid and longer spacer moiety, represented by N,N′-dibenzyl-m-xylylenediamine. The reason of the difference in the distance stems from the intention to explore the eventual proximity effect (i.e.: magnetic coupling) between the paramagnetic transition metal ions. The presence of two benzyl groups is devised to induce non-covalent interaction with plasma proteins such as HSA, further increasing the molecular weight and making an additional positive contribution to the relaxivity.¹⁷ The preparation of L1 and L2 is reported in Scheme 2.

Scheme 2 Synthesis of L1 and L2. (a) Ref. 18; (b) DIPEA, acetonitrile, r.t., 18 h, 72%; (c) TFA, DCM, r.t., 18 h; (d) DIPEA, acetonitrile, reflux, 1 h, 78%; (e) DIPEA, acetonitrile, r.t., 18 h, 81%; and (f) TFA, DCM, r.t., 18 h.

The tri-t-butyl ester of DO3A (1, DO3A(tBu)₃) was prepared according to the literature procedure using cyclen and t-butyl bromoacetate.¹⁸ The direct alkylation of cyanuryl chloride with an excess of DO3A(tBu)₃ under basic conditions afforded the hexaester of L1 (2, L1(tBu)₆); the deprotection of the esters by treatment with trifluoroacetic acid, gave the dimeric ligand L1. The spacer between the two macrocyclic rings of L2 was firstly obtained by the reaction of 1,3-bis[(N-benzyl)aminomethyl]benzene with an excess of cyanuryl chloride under basic conditions, affording the 1,3-bis{[N-benzyl-N-(3,5-dichloro-2,4,6-triazino)]aminomethyl}benzene (3). The alkylation of 3 with an excess of DO3A(tBu)₃ under basic conditions afforded the hexa-t-butyl ester of L2 (4, L2(tBu)₆), further deprotected with trifluoroacetic acid to give the dimeric ligand L2.

Molecular modelling

As the crystal structures of the two Mn(II)-complexes could not be properly obtained, we chose to assess their structural parameters by undertaking ab initio calculations. Keeping in mind the information from the X-ray crystal structures of other Mn(II) macrocyclic complexes and starting from the low energy structures obtained for the free ligands, we undertook full geometry optimization at the ab initio HF level of theory, using the effective core potential (ECP) standard basis set LanL2DZ¹⁹ for manganese and the full-electron standard basis set 3-21G*²⁰ for all other atoms. Selected calculated bond lengths and angles for the complexes are collected in Table 1.

Table 1 Selected calculated bond lengths and angles for Mn₂L1 and Mn₂L2

		Mn2L1		Mn2L2
		Mn1	Mn2	Mn1	Mn2
Bond dist. (Å)	Mn–N	2.3057	2.3454	2.3014	2.3234
		2.2778	2.3187	2.2837	2.2894
		2.3179	2.2856	2.3422	2.2977
		2.3499	2.3070	2.2665	2.2467
	Mn–O	2.2122	2.1975	2.2020	2.2265
		2.2420	2.2489	2.2158	2.2245
		2.2252	2.2466	2.2207	2.2060
Bond angles (°)	N–Mn–N	85.16	85.04	78.34	77.49
		80.12	80.06	83.00	85.11
		82.98	83.54	80.19	79.05
		79.45	77.43	85.31	86.62
	O–Mn–O	68.31	68.25	73.91	77.19
		73.87	74.96	66.77	75.52
		72.81	74.05	76.34	66.87

---

Fig. 1 shows the optimized structures obtained for Mn₂L1 and Mn₂L2. The common feature of both complexes is the hepta-coordination of the Mn(II) ions, coordinated by the four amine nitrogen atoms of the macrocyclic ring as well as by three oxygen atoms of the pendant carboxylate groups. The molecular geometry around the metal ions is somewhat distorted but could be best described as a capped trigonal prism in which the oxygen atom of one pendant carboxylate group caps the rectangular face defined by two nitrogen and two oxygen atoms. Several other structurally characterized 7-coordinate Mn(II)-complexes are based on capped trigonal prismatic geometries²¹ although pentagonal bi-pyramidal structures have been observed, too.²² The Mn–N bond lengths are in the expected range, while the Mn–O bond lengths are shorter. This behaviour may be rationalized by considering the balance between the increased electrostatic attraction of the negatively charged carboxylate groups and the steric demands in the 7-coordinate complex. Furthermore, the coordination spheres of the Mn(II) ions are quite irregular, probably because of the geometric constraints imposed by the triazine ring. In fact, in the free ligands the triazine ring is oriented to be almost coplanar with the macrocycle. The complexation with the Mn(II) metal ion induces a rotation of the triazine ring which move to match the vacated coordination site, where it exerts a steric effect on the pendant carboxylate groups of the macrocycle. These conformational changes, along with the different charge distribution of the triazine ring, represent the only significant differences observed between the free ligands and the complexes.

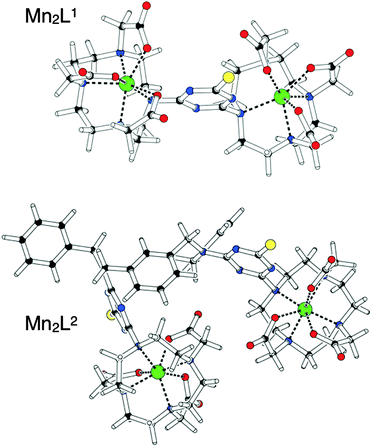Fig. 1 Schematic representation of Mn₂L1 and Mn₂L2 as obtained after full geometry optimization at the HF/3-21G* level of theory, using the LanL2DZ basis set for Mn(II) ions.

Solution thermodynamic study of L1 and L2 ligands

Protonation equilibria of L1 and L2. The protonation constants of H₆L1 and H₆L2 (log K^H_i), listed in Table 2, were determined by both pH-potentiometric titrations and pH ¹H-NMR spectroscopic titrations (Fig. S1–S3, ESI†) in 0.1 M KCl solution at 25 °C (the definitions and equations used for the evaluation of the equilibrium data are summarized in the ESI†).

Table 2 Protonation constants of H₆L1, H₆L2, H₄DOTA and H₃DO3A (0.1 M KCl, 25 °C)

I	H6L1		H6L2	H4DOTA^a	H3DO3Aa
	0.1 M KCl		0.1 M KCl	0.1 M KCl	0.1 M KCl
	pH-pot.	^1H-NMR	pH-pot.	pH-pot.	pH-pot.
a Ref. 23.
log K^H1	13.03 (1)	13.01 (8)	12.86 (1)	11.41	11.99
log K^H2	11.51 (1)	11.77 (5)	11.08 (2)	9.83	9.51
log K^H3	7.54 (1)	7.36 (7)	7.16 (2)	4.38	4.30
log K^H4	6.78 (1)	6.47 (5)	6.42 (2)	4.63	3.63
log K^H5	4.19 (1)	4.41 (4)	4.08 (2)	1.92	1.84
log K^H6	3.44 (1)	3.65 (3)	3.54 (2)	1.58	—
log K^H7	2.48 (1)	2.85 (4)	2.67 (2)	—	—
log K^H8	1.71 (2)	—	1.81 (3)	—	—
∑log K^Hi	50.72		49.61	33.75	31.26

---

Ligands H₆L1 and H₆L2 have the similar protonation behaviour and the protonation sequence of H₆L1 was studied by following the pH-dependence of ¹H-NMR chemical shifts of non-labile protons. Only the protonation scheme of H₆L1 will be described in detail. The first two protonation processes of L1⁶⁻ result in a downfield shift of the signals of the (b–f) protons whereas the signals of the protons (a) do not change significantly. According to these results, it can be assumed that the first and second protonation processes take place at the N-atoms (1) of the macrocyclic rings. In the pH range of 5–8, in parallel with the occurrence of the third and fourth protonation processes, the signals corresponding to the protons (a–e) undergo a downfield shift, while the proton signals of (f) are slightly shifted to lower frequencies. This confirms that the log K^H₃ and log K^H₄ are related to the protonation of the N-atoms (2 or 4) of the macrocyclic ring, whereas the first proton is concomitantly transferred to the non-protonated N-atoms (2 or 4) of the DO3A units because of the electrostatic repulsion between protonated ring nitrogen atoms. Further lowering of pH resulted in the downfield shift of the proton signals of (f) indicating that the log K^H₅ and log K^H₆ values are related to the protonation of carboxylate groups in the pH range of 2–5. Finally, further protonation occurs at the non-protonated carboxylate pendant arms. The log K^H_i values obtained from the ¹H-NMR study agree well with the data determined by pH-potentiometric titrations (Table 2).

By taking into account the structures of dimeric L1 and L2 ligands, it can be assumed that the protonation of the identical donor atoms of two DO3A units takes place simultaneously and separately. However, the log K^H_i values of the same donor atoms of the separated DO3A units (log K^H₁ − log K^H₂, log K^H₃ − log K^H₄ and log K^H₅ − log K^H₆) indicate that the presence of the second macrocycle affects the protonation in the donor atoms of the individual macrocycle. This is especially true for the first protonation constants of L1 and L2, which are about 1 log K unit higher than that of DO3A (Table 2). This might be attributed to the effect of the H-bond formation between the two macrocyclic rings through protonated and unprotonated N-atoms probably due to the “U” conformation of both ligands. The result of such H-bond formation increases the basicity of one macrocycle and slightly decreases the basicity of the other one (i.e.: the non-protonated ring N-atom of the other macrocycle). The protonation constants of the second ring nitrogen atoms (log K^H₃ and log K^H₄ for L1 and L2; log K^H₂ for DOTA and DO3A) of L1 and L2 are significantly lower than those of DOTA and DO3A. The basicity of the second ring N-atoms in L1 and L2 might be influenced by four potential effects: (i) the electron withdrawing effect of the aromatic group reducing the basicity of the nitrogen donor atoms; (ii) the stereochemical rigidity of the ligands which is caused by the aromatic linker between the DO3A units; (iii) electrostatic repulsion between protonated ring nitrogen atoms; and (iv) the formation of a H-bonding interaction between a protonated nitrogen atom and a carboxylate group increasing the basicity of the macrocyclic N-atoms. The simultaneous contribution of these processes could be responsible of the lower log K^H_i values of the second ring nitrogen donor atoms of L1 and L2. The acidity of the carboxylic groups is indeed comparable with the corresponding log K values of DOTA and DO3A. The ∑log K^H_i values (total basicity), presented in Table 2, indicate that the total basicity of the L1 and L2 is significantly higher than that of DOTA and DO3A. However, the half of the ∑log K^H_i values of dimeric ligands (L1: 25.36; L2: 24.81) are lower than the total basicity of DOTA and DO3A due to the lower second protonation constants (log K^H₃ and log K^H₄) of L1 and L2.

Stability and protonation constants of the Mn(II)-complexes formed with L1 and L2. The stability and protonation constants of Mn(II)-complexes of L1 and L2 were investigated by pH-potentiometric titration performed at 1 : 1 and 2 : 1 Mn(II)-to-ligand concentration ratios (25 °C, 0.1 M KCl). The titration curves are shown in Fig. S2 and S3 (ESI†), and the calculated stability and protonation constants are reported in Table 3. For a direct comparison, the pMn values have also been calculated (pMn = −log[Mn(II)]_free).²⁴ (The equations used for the evaluation of the equilibrium data are summarized in the ESI.†)

Table 3 Stability and protonation constants of Mn(II)-complexes formed with L1, L2, DOTA and DO3A ligands (25 °C)

	L1	L2	DOTA^a	DO3A^a
I	0.1 M KCl
a Ref. 23. b pMn calculated for [Mn(II)] = 1 mM, [L] = 10 mM, pH = 7.4 (ref. 24).
log KMnL	14.89 (2)	14.05 (4)	19.44	19.43
log KMnHL	11.03 (2)	10.81 (4)	3.96	3.37
log KMnH2L	7.29 (1)	6.92 (2)	3.70	—
log KMnH3L	4.05 (4)	3.62 (3)	—	—
log KMnH4L	4.02 (2)	3.54 (3)	—	—
log KMn2L	14.56 (3)	13.98 (3)	—	—
log KMn2HL	4.07 (4)	4.10 (4)	—	—
log KMn2H2L	3.95 (3)	3.84 (4)	—	—
pMn^b	10.50	10.53	14.05	13.70

---

The log K_MnL values of MnL1 and MnL2 are lower by 5 log K units than those of Mn (DOTA) and Mn (DO3A) because of the lower second protonation constant of the L1 and L2. Under acidic conditions the free donor atoms of MnL1 and MnL2 complexes can be protonated with the formation of several protonated complexes (MnHL, MnH₂L, MnH₃L and MnH₄L) which indicates that the Mn(II) ion is coordinated by one of the DO3A units in MnL1 and MnL2.

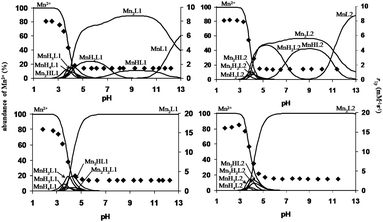
Because of the dimeric structure of the L1 and L2 ligands, the formation of the dinuclear Mn₂L complexes was also investigated. The pH-potentiometric titration curves of the systems obtained at a 2 : 1 Mn(II)-to-ligand concentration ratio (Fig. S2 and S3, ESI†) indicate one equivalent more base consumption than the titration curves of the 1 : 1 Mn(II)-to-ligand systems in the pH range of 4–11. This finding can be explained by the release of all protons from L1 and L2 due to the coordination of two Mn(II) ions and the formation of Mn₂L species. Interestingly, the stability constants of the dinuclear Mn₂L complexes (log K_Mn2L) are identical to those of the mononuclear MnL complexes (log K_MnL). This behaviour of the L1 and L2 ligands can be explained by the similar affinity of the Mn(II) ion to the donor atoms of both DO3A units (the two DO3A units of L1 and L2 ligands cannot be distinguished) resulting in the formation of the Mn₂L species even at a 1 : 1 Mn(II)-to-ligand concentration ratio. Moreover, the protonation constants of the Mn₂HL and Mn₂H₂L species (log K_Mn2HL and log K_Mn2LH2) are also identical, which indicates the protonation of similar carboxylate donor groups of the two DO3A units in the Mn₂L1 and Mn₂L2 complexes.

To obtain some information about the kinetic inertness of the ditopic DO3A-based Mn(II) complexes, the transmetallation reactions of Mn₂L1 with the Zn(II)-ion have been investigated (eqn (1)) by ¹H-NMR relaxometry. In order to maintain pseudo-first-order conditions, the release of the Mn(II) ion has been investigated in the presence of a 10-fold excess of exchanging Zn(II)-ion.

Mn₂L1 + Zn²⁺ ⇌ Zn₂L1 + Mn²⁺ (1)

The pseudo-first-order rate constant (k_d) was calculated by fitting the relaxivity values to eqn (2):

r_t = (r₀ − r_e)e^(−k_dt) + r_e (2)

where r₀, r_e and r_t are the relaxivity values at the starting point (t = 0 s), at equilibrium and at the time t of the reaction, respectively. The kinetic data of the transmetallation reaction of Mn₂L1 with Zn(II)-ions are reported in Fig. S4 (ESI†). The k_d pseudo-first-order rate constant characterizing the transmetallation reaction is 2.6(±0.1) × 10⁻⁵ s⁻¹. This k_d value, obtained under similar experimental conditions, is comparable to that of Mn(NOTA) and 20 times higher than for Mn(DOTA) (Mn(NOTA): k_d = 2.5 × 10⁻⁵ s⁻¹; Mn(DOTA): k_d = 1.4 × 10⁻⁶ s⁻¹; [MnL] = 1.0 mM, [Zn(II)] = 10 mM, pH = 4.6),²⁵ respectively. This result indicates that the kinetic inertness of Mn₂L1 is quite similar to that of Mn(NOTA), but significantly lower than of Mn(DOTA). The faster transmetallation reaction of Mn₂L1 as compared to Mn(DOTA) might be explained by a weaker interaction between the Mn(II) ion and the ring nitrogen atom linked to the triazine, due to its lower basicity resulting in relatively fast dissociation and transmetallation processes.

Relaxometric characterization of Mn(II)-complexes

1/T₁ NMRD profiles of Mn₂L1 and Mn₂L2 complexes. The relaxivity values of the Mn(II) complexes with the ligands L1 and L2 and their trends in aqueous solution as a function of pH are quite similar, thus indicating the occurrence of identical microscopic behaviour (Table 4). To obtain a detailed description of the relaxometric properties of the systems, we measured the relaxivity dependence at 298 K from the applied magnetic field (Nuclear Magnetic Resonance Dispersion, NMRD) by considering a wide range of values, from 0.00024 to 1.65 T (corresponding to 0.01–70 MHz proton Larmor frequencies). The amplitude and shape of a NMRD profile are determined by the combination and the relative weight of the various possible contributions to the relaxivity: those resulting from the water molecule(s) belonging to the inner-(IS) and outer coordination spheres (OS) of the metal complex.^2b The IS contribution to r_1p essentially depends on the number q of bound water molecules and their rate of exchange (k_ex = 1/τ_M), on the rate of molecular tumbling (1/τ_R), and on the electronic relaxation times (T_1,2e) of Mn(II). The OS component is determined by T_1,2e, the relative diffusion coefficient of solvent and solute molecules (D) and their distance of minimum approach, a. The relaxivity values and the NMRD profiles of Mn₂L1 and Mn₂L2 are quite typical of pure outer sphere complexes (q = 0), with a relaxivity plateau in the range 0.01 to 2 MHz (r_1p ∼ 2.2 mM⁻¹ s⁻¹) and a dispersion about 12–15 MHz (Fig. 2). This is further confirmed by the close similarity with the corresponding profile of [Mn(DO3A)]⁻, a q = 0 complex.²⁶

Table 4 Best fit parameters obtained from analysis of the NMRD profiles (298 K, pH = 7)

	Mn2L1	Mn2L2	[Mn(DO3A)]^−^a
a Ref. 26. b Fixed in the fitting procedure.
^20 r 1p [mM^−1 s^−1]	1.45	1.45	1.3
q	0	0	0
Δ ^2 [s^−2 × 10^19]	7.3 ± 0.3	6.7 ± 0.2	7.4 ± 0.9
τ V [ps]	23 ± 4	17 ± 3	18.1± 1.6
a [Å]	3.6	3.6	3.6
D [cm^2 s^−1]	2.24^b	2.24^b	2.35 ± 0.03

---

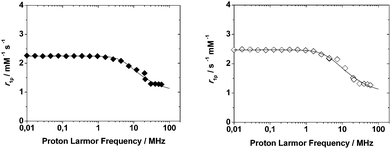Fig. 2 1/T₁ NMRD profiles of Mn₂L1 (left, filled diamonds) and Mn₂L2 (right, open diamonds) complexes at 298 K and pH = 7. The curves are calculated with the best-fit parameters reported in Table 4, as described in the text.

Then, the relaxometric data confirm the identical coordination geometry of Mn(II) in these highly symmetrical ditopic chelators. The experimental NMRD data were fitted according to the established theory of paramagnetic relaxation expressed in terms of the Freed's^27,28 equation for the outer-sphere proton relaxation mechanism. For the data fitting it is useful to make a reasonable estimate of some of the relaxation parameters: a and D were set to 3.6 Å and 2.24 × 10⁻⁵ cm² s⁻¹ (at 298 K), respectively. The best fit parameters are listed in Table 4 and compared with those of the related parent complex [Mn(DO3A)]⁻.²⁶

Relaxivity of the Mn(II)–L1 and Mn(II)–L2 systems as a function of pH. In order to confirm the presence in solution of the species observed by pH-potentiometry, the relaxivity of the MnL1 and MnL2 systems was measured as a function of pH at 1 : 1 and 2 : 1 metal-to-ligand concentration ratios and at 20 MHz and 298 K. The pH dependency of r_1p is shown in Fig. 3. To compare the relaxivity and the species distribution of the MnL1 and MnL2 systems, the relaxivity of the Mn–DOTA and Mn–DO3A systems was also measured as a function of pH at a 1 : 1 Mn(II)-to-ligand concentration ratio. The species distribution and the relaxivity values of Mn–DOTA and Mn–DO3A systems as a function of pH are shown in Fig. S5 and S6 (ESI†), respectively. The r_1p values for both Mn(II)–L1 and Mn(II)–L2 systems are very similar over the pH range of 2–12. In the case of a 1 : 1 Mn(II)-to-ligand concentration ratio, the relaxivity increases from 1.4 to 8.04 mM⁻¹ s⁻¹ in the pH range of 6 to 2, reflecting the formation of various protonated forms of the mononuclear MnL1, MnL2 and the dinuclear Mn₂L1, Mn₂L2 complexes. In the region 6 < pH < 12, the complete formation of the mononuclear-(MnL1, MnL2), the dinuclear-complexes (Mn₂L1, Mn₂L2) and the disappearance of the protonated species are not associated with relaxivity changes. In the cases of the Mn–DOTA and Mn–DO3A systems, the relaxivity increases from 1.32 to 7.90 mM⁻¹ s⁻¹ following the formation of protonated forms of the Mn(DOTA) and Mn(DO3A) complexes over the pH range of 5–2. Because of their higher stability, the formation of the Mn(DOTA) and Mn(DO3A) complexes takes place under more acidic conditions than for MnL1 and MnL2. The pH dependency of the r_1p values observed at 2 : 1 and 1 : 1 metal-to-ligand concentration ratios is very similar. The relaxivity increases from 2.9 to 15.9 mM⁻¹ s⁻¹ in the pH range of 6–2 as a result of the formation of the protonated mononuclear MnL1 and MnL2 species and of the dinuclear Mn₂H₂L1, Mn₂HL1, Mn₂L1, Mn₂H₂L2, Mn₂HL2 and Mn₂L2 complexes. In the pH region 5 to 8, the Mn₂L1 and Mn₂L2 complexes predominate and their relaxivities assume the identical value of 1.45 mM⁻¹ s⁻¹ (per Mn). Of course, the relaxivity per complex (Mn₂L1 and Mn₂L2) is simply twice as large, and then r_1p = 2.9 mM⁻¹ s⁻¹. Since the relaxivity of the 1 : 1 Mn(II)-to-L1 and Mn(II)-to-L2 systems is 1.4 mM⁻¹ s⁻¹, it can be assumed that the coordination environment of both Mn(II) ions in the Mn₂L1 and Mn₂L2 complexes is identical and very similar to that of the Mn(DOTA) and Mn(DO3A) complexes. These assumptions are confirmed by the fact that the relaxivity values of Mn(II)–L1 and Mn(II)–L2 systems are independent of the concentration of the Mn(II) containing species formed in the 1 : 1–2 : 1 metal to ligand concentration ratios at pH = 6.5 (Fig. S7, ESI†). According to the r_1p values of the Mn₂L1, Mn₂L2, Mn(DOTA) and Mn(DO3A) complexes (Mn₂L1 and Mn₂L2: r_1p = 2.9 mM⁻¹ s⁻¹; Mn(DOTA) and Mn(DO3A): r_1p = 1.3 mM⁻¹ s⁻¹; pH = 7.0, 20 MHz and 25 °C) it can be assumed that there are no water molecules in the inner-sphere of the Mn(II) ions. Thus, the relaxivity of the Mn₂L1 and Mn₂L2 complexes is only determined by the outer-sphere contribution, as previously found for Mn(DOTA) and Mn(DO3A).²⁶

Fig. 3 Relaxivity vs. pH and species distribution diagrams for Mn(II)-complexes of L1 (left) and L2 (right) at 1 : 1 (top) and 2 : 1 metal-to-ligand concentration ratios.

Serum protein binding. The presence in the ligand L2 of two benzyl groups enables the ability of hydrophobic interactions of the corresponding metal complex with serum proteins such as human serum albumin (HSA). The non-covalent interaction of paramagnetic complexes (q > 0) with macromolecules reduces the tumbling rate of the metal complex (increase τ_R) and boosts the relaxivity to higher values, leading to better contrast and to use lower doses of the agent.²⁹ Also in the case of q = 0 chelates relaxivity enhancement has been observed and explained on the basis of the presence of exchangeable protons on the protein, dipolarly coupled with the paramagnetic complex, and of a network of hydrogen-bonded water molecules defining a second coordination sphere.³⁰ The interaction of Mn₂L2 with HSA was measured by relaxometric titration at 20 MHz and 298 K and the results are reported in Fig. 4.

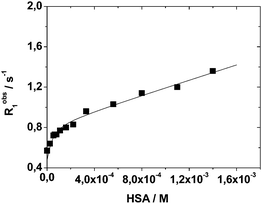Fig. 4 Longitudinal water proton relaxation rate (R^obs₁) as a function of HSA concentration for a 0.13 mM solution of Mn₂L2 at neutral pH, 298 K and 20 MHz.

Data analysis indicates the presence of two strong binding sites associated with an affinity constant of 2.0 (±0.6) × 10⁴ M⁻¹ and a bound relaxivity of 6.9 ± 0.3 mM⁻¹ s⁻¹. The observed values are in line with a related Mn-complex embodying HSA-interacting benzyloxymethyl pendant groups.³¹

Conclusions

The preparation of two novel DO3A-based ditopic ligands and a detailed study of the structure, thermodynamic and relaxometric properties of the corresponding Mn(II) complexes were accomplished in this work. The ligands host the Mn(II) ion in a symmetric arrangement, heptacoordinated by the macrocyclic moieties and the carboxymethyl side arms. A reasonable stability is observed, even if somewhat lower than that showed with the DO3A parent structure, as a result of the reduced availability of the lone pair of the macrocyclic nitrogen atom linked to the heteroaromatic triazine ring. The absence of coordinated water molecules is supported by the relaxometric measurements, showing once more a highly symmetrical coordination of the paramagnetic ions, closely retaining the properties observed in the parent Mn (DO3A). These results will be useful to direct the future design of oligonuclear Mn(II) complexes as potential alternatives to Gd-based MRI contrast agents.

Experimental

General

Reagents were obtained from Aldrich or Alfa-Aesar and used without further purification. ¹H and ¹³C NMR spectra were recorded on a Jeol Eclipse ECP300 spectrometer at 300 MHz and 75.4 MHz, respectively. Mass spectra were recorded using a Thermo Finnigan LCQ-Deca XP-PLUS, operating in ESI-MS mode.

Compound 2

DO3A-tBu₃·HBr¹⁸ (5.00 g, 8.4 mmol) was dissolved in 20 mL of acetonitrile. Cyanuryl chloride (465 mg, 2.5 mmol, 0.3 eq.) and DIPEA (2.17 g, 16.8 mmol, 2 eq.) were added in one portion at room temperature. The resultant reaction mixture was stirred at room temperature overnight. The solvent was removed by evaporation under reduced pressure. The resultant oil was redissolved with dichloromethane and washed thrice with a saturated solution of sodium bicarbonate and twice with a saturated solution of sodium chloride. The organic layer was dried over anhydrous sodium sulfate, filtered and the solvent was removed by evaporation under reduced pressure. The product was purified by gravimetric chromatography on a silica-gel column (dichloromethane/methanol 9 : 1), affording 2.06 g of compound 2 (1.8 mmol, 72%) as a brownish oil. ¹H-NMR (CDCl₃, 300 MHz, 298 K) δ: 3.66 (bs, 4H), 3.23 (bs, 16H), 2.92 (bs, 8H), 2.66 (bs, 16H), 1.34 (s, 54H). ¹³C-NMR (CDCl₃, 75.4 MHz, 298 K) δ: 173.0 (C), 170.9 (C), 169.1 (C), 164.5 (C), 80.9 (C), 80.7 (C), 57.6 (CH₂), 56.1 (CH₂), 53.2 (CH₂), 52.2 (CH₂), 47.7 (CH₂), 46.9 (CH₂), 28.2 (CH₃), 27.9 (CH₃). ESI⁺-MS: 1140.5 [M + H]⁺, 570.99 [M + 2H]²⁺.

Synthesis of L1

Compound 2 (1.00 g, 0.96 mmol) was dissolved in 2 mL of dichloromethane and the resultant solution was added dropwise to 10 mL of trifluoroacetic acid. The resultant reaction mixture was stirred overnight at room temperature. The solvent was evaporated and the product was purified by dissolution in MeOH and precipitation with diethylether. This procedure was repeated 2–3 times, affording 950 mg of L1 as a white hygroscopic solid. ¹H-NMR (D₂O/K₂CO₃, 300 MHz, 343 K) δ: 3.76 (bs, 8H), 3.48 (s, 4H), 3.43 (s, 4H), 3.39 (s, 4H), 3.23 (bs, 8H), 3.05 (s, 16H). ¹³C-NMR (D₂O/K₂CO₃, 75.4 MHz, 343 K) δ: 176.6 (C), 169.9 (C), 169.2 (C), 168.8 (C), 168.2 (C), 55.8 (CH₂), 55.5 (CH₂), 52.7 (CH₂), 52.3 (CH₂), 51.3 (CH₂), 51.1 (CH₂), 50.6 (CH₂), 50.0 (CH₂), 47.1 (CH₂), 44.2 (CH₂). ESI⁺-MS: 804.4 [M + H]⁺; 826.4 [M + Na]⁺.

Compound 3

1,3-Bis[(N-benzyl)aminomethyl]benzene (900 mg, 2.84 mmol) was dissolved in 25 mL of acetonitrile. Cyanuryl chloride (1.57 g, 8.53 mmol, 3 eq.) and DIPEA (1.47 g, 11.36 mmol, 4 eq.) were added and the resultant mixture was stirred at reflux for 1 hour. The solvent was partially evaporated under reduced pressure until a white solid precipitated. The solution was heated to redissolve the precipitate, then cooled to –4 °C. The formed precipitate was filtered, washed with cold acetonitrile, and the residual solvent was removed under reduced pressure, affording 1.35 g of 1,3-bis{[N-benzyl-N-(3,5-dichloro-2,4,6-triazin-1-yl)]aminomethyl}benzene 3 (2.21 mmol, 78%) as a white amorphous solid. ¹H-NMR (CDCl₃, 300 MHz, 298 K) δ: 7.38–7.28 (m, 7H), 7.23–7.15 (m, 6H), 7.06 (bs, 1H), 4.79 (s, 4H), 4.76 (s, 4H). ¹³C-NMR (CDCl₃, 75.4 MHz, 298 K) δ: 170.6 (2C), 165.7 (4C), 136.3 (2C), 135.3 (2C), 129.5 (CH), 129.0 (4CH), 128.3 (2CH), 128.2 (4CH), 128.1 (CH), 127.9 (2CH), 49.6 (2CH₂), 49.3 (2CH₂). ESI⁺-MS: 611.2/613.2/615.2 [M + H]⁺.

Compound 4

1,3-Bis{[N-benzyl-N-(3,5-dichloro-2,4,6-triazin-1-yl)]aminomethyl}benzene 3 (500 mg, 0.82 mmol) and DO3A-tBu₃ hydrobromide (1.40 g, 2.46 mmol, 3 eq.) were dissolved in 10 mL of acetonitrile. DIPEA (420 mg, 3.28 mmol, 4 eq.) was added and the resultant reaction mixture was stirred at room temperature overnight. The solvent was removed under reduced pressure and the brownish oil obtained was redissolved with dichloromethane and washed thrice with a saturated solution of sodium carbonate and twice with a saturated solution of sodium chloride. The organic phase was dried over anhydrous sodium sulphate, filtered and the filtrate was washed with dichloromethane. The solvent was removed under reduced pressure, affording a brownish oil purified by gravimetric chromatography on a silica gel column (petroleum ether/ethyl acetate 9 : 1). 1.04 g of compound 4 (0.66 mmol, 81%) was obtained as a yellowish oil. ¹H-NMR (CDCl₃, 300 MHz, 333 K) δ: 7.31–7.02 (m, 13H), 6.96 (s, 1H), 4.80–4.56 (m, 6H), 3.86–3.56 (m, 8H), 3.29 (bs, 8H), 3.18–2.54 (m, 24H), 1.42 (s, 36H), 1.34 (bs, 9H), 1.32 (bs, 9H). ¹³C-NMR (CDCl₃, 75.4 MHz, 333K) δ: 171.2 (C), 169.5 (C), 169.4 (C), 169.1 (C), 165.6 (C), 164.9 (C), 137.9 (C), 137.4 (C), 128.9 (CH), 128.6 (CH), 128.3 (CH), 127.5 (CH), 127.3 (CH), 127.0 (CH), 82.5 (C), 82.3 (C), 56.6 (CH₂), 56.2 (CH₂), 54.5 (bs, CH₂), 53.9 (bs, CH₂), 52.7 (CH₂), 49.6 (CH₂), 47.6 (bs, CH₂), 46.9 (bs, CH₂), 28.2 (CH₃), 28.1 (CH₃). ESI⁺-MS: 1569.56 [M + H]⁺, 784.51 [M + 2H]²⁺.

Synthesis of L2

Compound 4 (670 mg, 0.43 mmol) was dissolved in 2 mL of DCM and the resultant solution was added dropwise at room temperature to 10 mL of trifluoroacetic acid. The solution was stirred for 12 hours at room temperature. The solvent was evaporated and the product was purified by dissolution in MeOH and precipitation with diethylether. This procedure was repeated 2–3 times, affording 370 mg of L2 as a white hygroscopic solid. ¹H-NMR (D₂O, 300 MHz, 363 K) δ: 7.31–6.88 (m, 13H), 6.66 (bs, 1H), 4.71–4.50 (m, 8H), 4.29–4.11 (m, 8H), 3.93–3.72 (m, 12H), 3.67–3.02 (m, 24H). ESI⁺-MS: 1231.50 [M + H]⁺.

Computational study

The three-dimensional structures of the free ligands L1 and L2 were built and energy-minimized using Avogadro, an open-source molecular builder and visualization tool (http://avogadro.openmolecules.net/, Version 1.1.0).³² The conformational space was completely explored using the molecular-dynamics module of TINKER.^33,34 The Fortran software sources for TINKER were recompiled using the 64-bit optimizations, to suit our 64-bit and SMP CPU architecture. Every compound was soaked in a water box composed of TIP3P water molecules and then simulated for 1.0 ns at a constant temp. of 298 K. The time step was 1.0 fs, and the system was saved every 1.0 ps, giving rise to a set of 1000 conformations, which were then optimized with respect to all the torsion angles, and convergence was assumed when the energy change in two subsequent cycles of the minimization procedure was less than 0.5 kcal mol⁻¹. MM2 Force-field^35,36 was used for the conformational energies. The resultant geometries of the minimum-energy conformations thus located were used to build the starting macrocyclic complexes. A full optimization of the macrocyclic complexes (Mn₂L1 and Mn₂L2) was performed at the ab initio HF level of theory using the GAMESS programs.³⁷ The effective core potential (ECP) standard basis set LanL2DZ,¹⁹ was utilized for manganese. The full-electron standard basis set 3-21G*²⁰ was used for all other atoms. The solvation energy was obtained by using the Polarizable Continuum Model (PCM) as implemented in GAMESS to take into account the strong influence of water on the behaviour of these compounds.³⁸

Equilibrium measurements

The stock solutions of MnCl₂ were prepared by dissolving MnCl₂ (Fluka 99.9%) in water. The concentration of the MnCl₂ solution was determined by complexometric titrations with standardized Na₂H₃DTPA and eriochrome black T as indicators. The concentration of the H₆L1 and H₆L2 solutions was determined by pH-potentiometric titrations in the presence and absence of a 40-fold excess of Ca(II). The pH-potentiometric titrations were performed with standardized 0.2 M KOH.

All the equilibrium measurements were conducted at a constant ionic strength maintained by 0.1 M KCl at 25 °C. For determining the protonation constants of H₆L1 and H₆L2 three parallel pH-potentiometric titrations were performed with 0.2 M KOH in 0.002 M ligand solutions. The protonation and the stability constants of Mn(II)-complexes formed with L1 and L2 were determined by pH-potentiometric titrations. The Mn(II)-to-ligand concentration ratios were 1 : 1 and 2 : 1 (the concentration of the ligand was generally 0.002 M). For the calculation of the equilibrium constants the mL base – pH data were used, obtained in the pH range of 1.7–11.5.

The pH-potentiometric titrations were carried out using a 702SM Titrino titration workstation with the use of a Metrohm-6.0233.100 combined electrode. The titrated solution (10 mL) was thermostated at 25 °C. The samples were stirred with a magnetic stirrer and to avoid the effect of CO₂, N₂ gas was bubbled through the solutions. The titrations were performed in the pH range of 1.7–11.7. For the calibration of the pH meter, KH-phthalate (pH = 4.005) and borax (pH = 9.177) buffers were used. For the calculation of the H⁺ concentration from the measured pH values, the method proposed by Irving et al. was used.³⁹ A 0.01 M HCl (0.1 M KCl or KNO₃) solution was titrated with the 0.2 M KOH and the difference between the measured and calculated pH values was used to calculate the [H⁺] from the pH values determined in the titration experiments. For the calculation of the equilibrium constants the PSEQUAD program was used.⁴⁰

¹H relaxometry

The water proton longitudinal relaxation rates were measured using a Stelar Spinmaster Spectrometer (Mede, PV, Italy) on about 0.5–2.5 mM manganese solutions in non-deuterated water. The exact concentrations of manganese were determined by measurement of bulk magnetic susceptibility shifts of a tBuOH signal and/or by ICP-OES. The ¹H T₁ relaxation times were acquired by the standard inversion recovery method with a typical 90° pulse width of 3.5 μs, from 16 experiments of 4 scans. The reproducibility of the T₁ data was ±5%. The temperature was controlled with a Stelar VTC-91 airflow heater equipped with a calibrated copper-constantan thermocouple (uncertainty of ±0.1 °C). The proton 1/T₁ NMRD profiles were measured on a fast field-cycling Stelar SmartTracer relaxometer over a continuum of magnetic field strengths from 0.00024 to 0.25 T (corresponding to 0.01–10 MHz proton Larmor frequencies). The relaxometer operates under computer control with an absolute uncertainty in 1/T₁ of ±1%. Additional data points in the range of 15–70 MHz were obtained on a Stelar Relaxometer equipped with a Bruker WP80 NMR electromagnet adapted to variable-field measurements (15–70 MHz proton Larmor frequency).

NMR experiments

¹H-NMR spectra of L1 were collected using a Bruker DRX 400 (9.4 T) NMR spectrometer equipped with a Bruker VT-1000 thermocontroller and a BB inverse z gradient probe (5 mm). For these experiments, 0.01 M solution of the L1 was prepared in H₂O (D₂O was added to the samples in a capillary). The pH was adjusted by stepwise addition of a solution of KOH and HCl. At pH > 12, the pH was adjusted by solid KOH and the pH was calculated from the [OH⁻] values. The calculations were performed by using the computer program Micromath Scientist.⁴¹

Acknowledgements

This research was supported by the European Union and the State of Hungary, co-financed by the European Social Fund in the framework of TÁMOP 4.2.4. A/2-11-1-2012-0001 ‘National Excellence Program' (grant no. A2-MZPD-12-0038) (Zs. B). The authors also thank the Hungarian Scientific Research Fund (OTKA K109029 and K84291) and ENVIKUT project (grant no. TÁMOP-4.2.2.A-11/1/KONV-2012-0043) implemented through the New Hungary Development Plan, co-financed by the European Social Fund and the European Regional Development Fund for financial support. The Italy-Hungary Intergovernmental S&T Cooperation Program (HU11MO2-TET_10-1-2011-0202) is also gratefully acknowledged.

Notes and references

1. (a) The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging, ed. A. Merbach, L. Helm and E. Toth, Wiley, New York, 2nd edn, 2013; (b) C. F. G. C. Geraldes and S. Laurent, Contrast Media Mol. Imaging, 2009, 4, 1–23.
2. (a) P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Chem. Rev., 1999, 99, 2293–2352; (b) S. Aime, M. Botta and E. Terreno, Adv. Inorg. Chem., 2005, 57, 173–237.
3. (a) P. H. Kuo, A. Abu-Alfa, R. Bucala, J. Griffith, K. Carlson, M. Girardi, J. Weinreb and S. Cowper, Appl. Radiol., 2009, 38, 22–33; (b) A. Kribben, O. Witzke, U. Hillen, J. Barkhausen, A. E. Daul and R. Erbel, J. Am. Coll. Radiol., 2009, 53, 1621–1628; (c) S. K. Morcos and J. Haylor, World J. Radiol., 2010, 2, 427–433.
4. B. Gallez, G. Bacic and H. M. Swartz, Magn. Reson. Med., 1996, 35, 14–19.
5. D. Oan, A. H. Schmieder, S. A. Wickline and G. M. Lanza, Tetrahedron, 2011, 67, 8431–8444.
6. B. Drahoš, I. Lukeš and E. Tóth, Eur. J. Inorg. Chem., 2012, 1975–1986.
7. M. Kueny-Stotz, A. Garofalo and D. Felder-Flesch, Eur. J. Inorg. Chem., 2012, 1987–2005.
8. A. Bianchi, L. Calabi, F. Corana, S. Fontana, P. Losi, A. Maiocchi, L. Paleari and B. Valtancoli, Coord. Chem. Rev., 2000, 204, 309–393.
9. Z. Baranyai, F. Uggeri, G. B. Giovenzana, A. Bènyei, E. Brücher and S. Aime, Chem. – Eur. J., 2009, 15, 1696–1705.
10. Zs. Baranyai, M. Botta, M. Fekete, G. B. Giovenzana, R. Negri, L. Tei and C. Platas-Iglesias, Chem. – Eur. J., 2012, 18, 7680–7685.
11. A. E. Martell and R. M. Smith, Critical Stability Constants, Plenum Press, New York, 1974, vol. 4.
12. (a) S. Aime, D. Delli Castelli, S. Geninatti Crich, E. Gianolio and E. Terreno, Acc. Chem. Res., 2009, 42, 822–831; (b) S. Aime, S. Geninatti Crich, E. Gianolio, G. B. Giovenzana, L. Tei and E. Terreno, Coord. Chem. Rev., 2006, 250, 1562–1579.
13. D. Lieb, F. C. Friedel, M. Yawer, A. Zahl, M. M. Khusniyarov, F. W. Heinemann and I. Ivanović-Burmazović, Inorg. Chem., 2013, 52, 222–236.
14. (a) M. Tan, X. Wu, E.-K. Jeong, Q. Chen, D. L. Parker and Z.-R. Lu, Mol. Pharmaceutics, 2010, 7, 936–943; (b) M. Tan, Z. Ye, E.-K. Jeong, X. Wu, D. L. Parker and Z.-R. Lu, Bioconjugate Chem., 2011, 22, 931–937.
15. Y. Huang, X. Zhang, Q. Zhang, X. Dai and J. Wu, Magn. Reson. Imaging, 2011, 29, 554–560.
16. A. Bianchi, L. Calabi, C. Giorgi, P. Losi, P. Mariani, D. Palano, P. Paoli, P. Rossi and B. Valtancoli, J. Chem. Soc., Dalton Trans., 2001, 917–922.
17. (a) P. Caravan, Acc. Chem. Res., 2009, 42, 851–862; (b) J. S. Troughton, M. T. Greenfield, J. M. Greenwood, S. Dumas, A. J. Wiethoff, J. Wang, M. Spiller, T. J. McMurry and P. Caravan, Inorg. Chem., 2004, 43, 6313–6323.
18. D. A. Moore, Org. Synth., 2008, 85, 10–14.
19. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
20. K. D. Dobbs and W. J. Hehre, J. Comput. Chem., 1987, 8, 880–893.
21. C. H. Hureau, S. Blanchard, M. Nierlich, G. Blain, E. Rivière, J.-J. Girerd, E. Anxolabéhère-Mallart and G. Blondin, Inorg. Chem., 2004, 43, 4415–4426.
22. A. Dees, A. Zahl, R. Puchta, N. J. R. van Eikema Hommes, F. W. Heinemann and I. Ivanovićc-Burmazović, Inorg. Chem., 2007, 46, 2459–2470.
23. A. Takács, R. Napolitano, M. Purgel, A. Bényei, L. Zékány, E. Brücher, I. Tóth, Zs. Baranyai and S. Aime, Inorg. Chem., 2014, 53(6), 2858–2872.
24. E. Balogh, Z. He, W. Hsieh, S. Liu and É. Tóth, Inorg. Chem., 2007, 46, 238–250.
25. B. Drahoš, V. Kubicek, C. S. Bonnet, P. Hermann, I. Lukes and E. Toth, Dalton Trans., 2011, 40, 1945–1951.
26. G. A. Rolla, C. Platas-Iglesias, M. Botta, L. Tei and L. Helm, Inorg. Chem., 2013, 52, 3268–3279.
27. L. P. Hwang and J. H. Freed, J. Chem. Phys., 1975, 63, 4017–4025.
28. J. H. Freed, J. Chem. Phys., 1978, 69, 4034–4037.
29. S. Aime, M. Botta, M. Fasano, S. Geninatti Crich and E. Terreno, JBIC, J. Biol. Inorg. Chem., 1996, 1, 312–319.
30. (a) S. Aime, A. S. Batsanov, M. Botta, J. A. K. Howard, D. Parker, K. Senanayake and G. Williams, Inorg. Chem., 1994, 33, 4696–4706; (b) M. Botta, Eur. J. Inorg. Chem., 2000, 399–407.
31. S. Aime, P. L. Anelli, M. Botta, M. Brocchetta, S. Canton, F. Fedeli, E. Gianolio and E. Terreno, JBIC, J. Biol. Inorg. Chem., 2002, 7, 58–67.
32. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
33. (a) P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947; (b) P. Ren and J. W. Ponder, J. Comput. Chem., 2002, 23, 1497–1506.
34. R. V. Pappu, R. K. Hart and J. W. Ponder, J. Phys. Chem. B, 1998, 102, 9725–9742.
35. J. C. Tai and N. L. Allinger, J. Am. Chem. Soc., 1988, 110, 2050–2055.
36. J. C. Tai, J. H. Lii and N. L. Allinger, J. Comput. Chem., 1989, 10, 635–647.
37. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
38. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
39. H. M. Irving, M. G. Miles and L. Pettit, Anal. Chim. Acta, 1967, 38, 475–488.
40. L. Zékány and I. Nagypál, in Computational Method for Determination of Formation Constants, ed. D. J. Legett, Plenum, New York, 1985, p. 291.
41. Micromath Scientist, v. 2.01, MicroMath Inc, Salt Lake City, UT, USA, 1995.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the determination of the protonation and stability constants; the ¹H-NMR titration curve of L1; titration curves; relaxivity of the Mn₂L1–Zn(II) reacting system; species distribution with relaxivity values of the Mn(II)–DO3A and Mn(II)–DOTA systems; and relaxivity values of Mn(II)–L1 and Mn(II)–L2 systems as a function of the Mn(II)/L ratio. See DOI: 10.1039/c4nj01571a

---