A dihydrogen phosphate selective anion receptor based on acylhydrazone and pyrazole

Abstract

A novel chromogenic anion receptor 1 based on acylhydrazone and pyrazole has been designed and synthesized. Chromogenic anion receptor 1 forms stable 1 : 1 complexes with dihydrogen phosphate (H₂PO₄⁻) and other halide (Cl⁻, Br⁻) anions in DMSO solution, as shown by UV-vis, fluorescence and ¹H NMR spectroscopic experiments. The pyrazole containing host 1 in the optimized geometry of the complex has been noted as planar. The planarity of the host with the H₂PO₄⁻ anion resulted from four strong N–H⋯O and two weak C–H⋯O types of H-bonding. In total six H-bonding and the planarity of the host in the complex are responsible for the high binding energy. The addition of an excess of more basic anions (F⁻ and CH₃COO⁻) induces stepwise deprotonation, an event signalled by the appearance of a bright yellow color. The intensity of the fluorescence spectrum increases when hydrogen bonding occurs and decreases when deprotonation occurs, which is evidenced by fluorescence titrations.

---

Introduction

Phosphate-binding receptors have become highly favourable targets in molecular recognition chemistry due to the importance of biological and environmental roles of phosphate. For example, phosphate is an essential component of chemotherapeutic and antiviral drugs.^1–3 Moreover, phosphate is becoming the main water pollutant in many countries, and is causing serious environmental problems.^4–7 Therefore, several systems designed to selectively coordinate phosphate have been reported.^8–10

As anions display a wide range of geometries, the design and synthesis of artificial receptors that exhibit high binding affinity and selectivity to a targeted anion still remain great challenges. Among various noncovalent interactions, hydrogen-bonding interactions are particularly useful and effective in this regard. To achieve high binding affinity and good selectivity, hydrogen bonding moieties are arranged in space in a rigid and convergent manner. In addition, receptors bearing multiple hydrogen bonding moieties have been shown to be useful to promote cooperative binding, which would result in enhanced binding affinity.^11,12 Previously we have achieved selective and cooperative hydrogen bonding for dihydrogen phosphate utilizing acylhydrazone and indole.¹³ Recently, we also found that similar selective and cooperative hydrogen bonding for dihydrogen phosphate could be achieved by introducing the pyrazole group instead of the indole group. From modeling, we found that six H-bonding resulting from four strong N–H⋯O and two weak C–H⋯O types of H-bonding and the planarity of the host in the complex are responsible for the high binding energy. Here we would like to report the synthesis and the anion binding phenomena of receptor 1. The binding phenomena of receptor 1 could be monitored by UV-vis, fluorescence and ¹H NMR spectra.

Experimental section

Materials

Tetra-n-butylammonium hydroxide (TBAOH), tetra-n-butylammonium fluoride (TBAF), tetra-n-butylammonium dihydrogen phosphate (TBAH₂PO4), tetra-n-butylammonium acetate (TBAA), and tetra-n-butylammonium bromide (TBABr), tetra-n-butylammonium chloride (TBACl) tetra-n-butylammonium hydrogen sulphate (TBAHSO₄) were purchased from Sigma-Aldrich Chemical Co., Inc., and used as received.

Measurements

Absorption spectra were recorded using a biochrom Libra S70 spectrophotometer (Biochrom Ltd, England). NMR spectra were recorded using a BRUKER spectrometer operated at 500 MHz. ESI MS spectra were obtained using a JMS 700 (Jeol, Japan) double focusing magnetic sector mass spectrometer. All measurements were carried out at room temperature (298 K).

Synthesis

3-(4-Nitrophenyl)-1H-pyrazole-5-carbohydrazide was prepared according to the previous literature protocol.¹⁴

Receptor 1 was synthesized by reacting anthracene-1,8-dicarbaldehyde¹⁵ and 3-(4-nitrophenyl)-1H-pyrazole-5-carbohydrazide in ethanol using acetic acid as a catalyst with a yield of 49%.

3-(4-Nitrophenyl)-1H-pyrazole-5-carbohydrazide

A mixture of 0.285 g (1.09 mmol) ethyl 3-(4-nitrophenyl)-1H-pyrazole-5-carboxylate and 0.462 mL (0.0148 mmol) of hydrazine hydrate in 10 mL of ethanol was refluxed for 36 h then cooled. The solid collected by filtration, washed with water, and dried in vacuo, gave the desired product (0.269 g, 74.3%) ¹H NMR (500 MHz, DMSO-d₆) δ 14.01 (br, 1H), δ 9.84 (s, 1H), δ 8.31 (d, J = 8.5, 2H), δ 8.02 (d, J = 8.5, 2H), δ 7.35 (s, 1H), δ 4.54 (br, 2H) ¹³C NMR (500 MHz, DMSO-d₆) δ 158.44, 148.60, 146.64, 139.47, 137.92, 125.91, 124.34, 102.77.

Receptor 1

Anthracene-1,8-dicarbaldehyde (70 mg, 0.3 mmol), 3-(4-nitrophenyl)-1H-pyrazole-5-carbohydrazide (147 mg, 0.6 mmol) and three drops of acetic acid were dissolved in 25 mL ethanol. The above mixed solution was heated to reflux for overnight and then cooled to room temperature. The formed precipitate was filtered off and washed with ethanol to afford (101 mg, 49%) of receptor. ¹H NMR (500 MHz, DMSO-d₆) δ 11.28 (s, 1H), δ 9.46 (s, 2H), δ 8.77 (s, 1H), δ 8.25 (d, J = 8.5, 2H), δ 8.03 (d, J = 6.9, 8H), δ 7.82 (br, 2H), δ 7.69 (t, J = 7.5, 2H), δ 7.39 (br, 2H) ¹³C NMR (500 MHz, DMSO-d₆) ¹³C NMR (500 MHz, DMSO-d₆) δ 147.55, 146.39, 131.16, 130.29, 129.89, 128.54, 127.19, 125.69, 125.32, 123.90, 123.54, 104.63. HRMS (FAB, double focusing mass sector) calcd for C₃₆H₂₄O₆N₁₀Na [M + Na]⁺: 715.1778, found: 715.1779.

Results and discussion

Interactions with dihydrogen phosphate

The ability of receptor 1 to recognize dihydrogen phosphate was first studied in DMSO using UV-vis titration spectra. Receptor 1 displayed absorption bands at 268, 299, 407, and 433 nm. Upon the addition of increasing amounts of H₂PO₄⁻, moderate increases and decreases in absorption at different wavelengths (Fig. 1), and multiple isosbestic points were observed at 285, 306, 380, 398, 414, 427, and 438 nm, suggesting typical hydrogen bonding complex formation between receptor 1 and dihydrogen phosphate.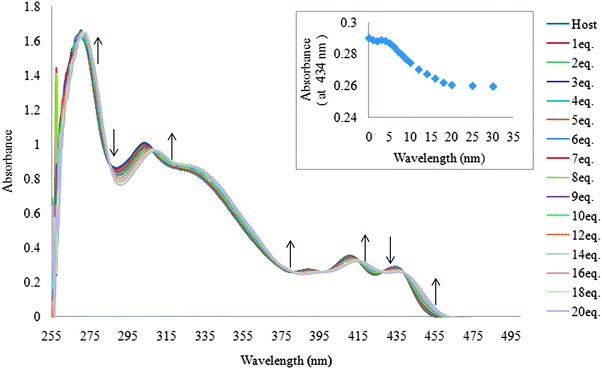

Fig. 1 Family of spectra recorded over the course of titrating a 20 μM DMSO solution of receptor 1 with increasing amounts of tetrabutylammonium dihydrogen phosphate.

Receptor 1 showed a strong fluorescence emission spectrum in DMSO as expected. The excitation wavelength was 394 nm and emission wavelengths were 422, 452 and 475 nm. The intensity of the emission spectrum from 20 μM solution of receptor 1 gradually increased as the concentration of tetrabutylammonium dihydrogen phosphate salts was increased (1–23 equiv.), which also indicates the association between receptor 1 and dihydrogen phosphate (Fig. 2).

Fig. 2 The change in fluorescence spectra over the course of titration of 20 μM DMSO solutions of receptor 1 when tetrabutylammonium dihydrogen phosphate was added. The change in the fluorescence of the intensity measured at 475 nm.

Hydrogen bond formation was also confirmed by ¹H NMR titration. In the ¹H NMR of receptor 1, not only amide N–H and pyrazole N–H peaks but also imine C–H peak is broad probably due to the slow rotation of two pyrazole arms. When dihydrogen phosphate was added, two N–H peaks showed intense broadening and the imine C–H peak (H_i) showed a downfield shift (Fig. 3). We believe that these phenomena were caused by a slow equilibrium between receptor 1 and dihydrogen phosphate as well as the complexation of added dihydrogen phosphate by receptor 1 through amide N–H, pyrazole N–H, and imine C–H hydrogen bond formation.^16–18 Furthermore, anthracene 9-H(H₉) showed an upfield shift. In fact, two effects are expected as a result of hydrogen bond formation between receptor 1 and the anion. (i) A through-bond propagation increases the electron density in the anthracene ring, which causes a shielding effect and promotes an upfield shift; (ii) a through-space effect increases a polarization of C–H bonds, which causes deshielding and promotes a downfield shift. In this case, the through-bond propagation dominates, and an upfield shift is observed for the anthracene 9-H peak.

Fig. 3 ¹H NMR spectra of 2 mM of receptor 1 containing increasing amounts of tetrabutylammonium dihydrogen phosphate (0–6.6 equiv.) in DMSO-d₆.

The stoichiometry between receptor 1 and dihydrogen phosphate was determined to be 1 : 1 using a UV-vis Job plot in DMSO-d₆ (Fig. 4). A Benesi–Hildebrand plot¹⁹ by the use of change at 433 nm in the UV-vis spectrum and at 475 nm in the fluorescence spectrum gave the association constants for dihydrogen phosphate. The calculated association constants for dihydrogen phosphate were 1.2 × 10⁴ by UV-vis titration and 1.1 × 10⁴ by fluorescence titration.

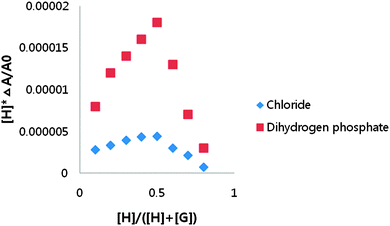Fig. 4 Job plots of receptor 1 with tetrabutylammonium dihydrogen phosphate and tetrabutylammonium chloride obtained by the UV-vis spectrum in DMSO.

Interactions with halides

The abilities of receptor 1 to recognize halides were also studied in DMSO using UV-vis titration spectra. When the amount of chloride was increased, a moderate decrease in absorbance was observed throughout most of the spectrum. However, moderate increases in absorbance were observed above 443 nm with an isosbestic point at this wavelength (Fig. 5), suggesting typical hydrogen bonding complex formation between receptor 1 and chloride.

Fig. 5 A family of spectra recorded over the course of titrating a 20 μM DMSO solution of receptor 1 with increased amounts of tetrabutylammonium bromide.

The existence of the isosbestic point for UV-vis titrations of receptors 1 with chloride suggests a 1 : 1 complexation, and this was also confirmed by Job's plot analysis (Fig. 4).

In fluorescence titration with chloride, the intensity of the emission spectrum gradually increased as the concentration of tetrabutylammonium chloride salts was increased (1–150 equiv.), which also indicates hydrogen bonding between receptor 1 and chloride (Fig. 6).

Fig. 6 The change of fluorescence spectra over the course of titration of 20 μM DMSO solutions of receptor 1 when tetrabutylammonium chloride was added.

The association constants calculated for chloride were 8.0 × 10² for UV-vis titration and 5.7 × 10² for fluorescence titration. Other halides such as bromide showed similar behaviors toward chloride; calculated binding constants for other anions are summarized in Table 1.

Table 1 Association constants (M⁻¹) of receptor 1 with various anions in DMSO

Anion	UV	Fluorescence
DP – deprotonation.
H2PO4^−	1.2 × 10^4	1.1 × 10^4
HSO4^−	1.1 × 10^3	1.2 × 10^3
Cl^−	8.0 × 10^2	5.7 × 10^2
Br^−	5.3 × 10^2	5.2 × 10^2
CH3COO^−	DP	DP
F^−	DP	DP

---

The selective sensing ability of receptor 1 for tetrahedral shaped anions such as dihydrogen phosphate and hydrogen sulfate could be seen from fluorescence intensity change with binding anions. No significant fluorescence intensity changes were observed upon the addition of 22 equiv. of halides such as chloride and bromide (Fig. 7). This result shows that receptor 1 has an optimum geometry for dihydrogen phosphate.

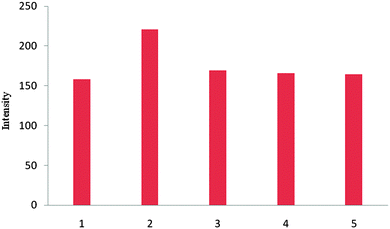Fig. 7 Fluorescence intensity changes of 1 (20 μM) upon the addition of various anions (22 equiv.) in DMSO at λ_ex = 460 nm 1, host 1 alone; 2, H₂PO₄⁻; 3, HSO₄⁻; 4, Cl⁻; 5, Br⁻.

Interactions with hydroxide, fluoride and acetate

In order to discriminate between H-bonding and deprotonation, the UV-vis titration of receptor 1 with tetrabutylammonium hydroxide was carried out (Fig. 8). Changes in the absorbance spectra in the presence of hydroxide were clearly different from those observed for dihydrogen phosphate. Furthermore, only one isosbestic point was observed at 362 nm, which differed from those observed in the presence of dihydrogen phosphate. In addition, UV-vis spectral changes upon adding excessive fluoride were almost identical to those induced by hydroxide.

Fig. 8 Family of UV-vis spectra recorded over the course of titrating a 20 μM DMSO solution of receptor 1 with increasing amounts of tetrabutylammonium hydroxide (a) and tetrabutylammonium fluoride (b).

In UV-vis titration with acetate, a similar phenomenon was observed with an isosbestic point at 343 nm. In fluorescence titration with acetate, the intensity of the emission spectrum from 20 μM solution of receptor 1 gradually decreased as the concentration of tetrabutylammonium acetate salts was increased (1–80 equiv.). The decrease of fluorescence intensity was also observed with hydroxide (see ESI†). Therefore, it could be concluded that only deprotonation occurred with acetate. It was not easy to figure out which hydrogen is deprotonated first between pyrazole N–H(H₂₉, H₅₇) and amide N–H(H₄₅, H₇₂) from receptor 1 as both peaks are too broad. Therefore we tried the ¹H NMR titration of 3-(4-nitrophenyl)-1H-pyrazole-5-carbohydrazide, which showed the pyrazole peak and the amide peak clearly. When we added 0.5 equivalents of tetrabutylammonium fluoride, we observed that the pyrazole peak disappeared first (Fig. 9). From this experiment, we suggest that pyrazole N–H(H₂₉, H₅₇) would be deprotonated first from receptor 1 although we cannot see the deprotonation phenomena of receptor 1 clearly through ¹H NMR.

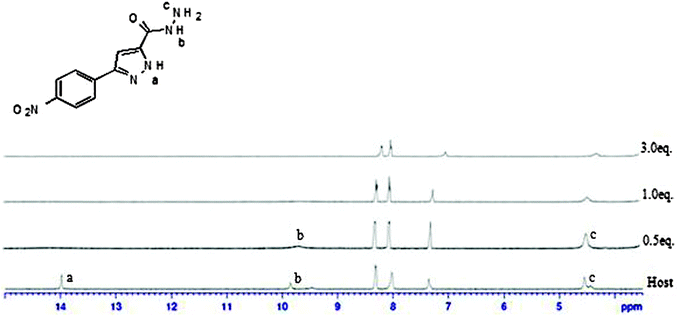Fig. 9 ¹H NMR spectra of 2 mM of 3-(4-nitrophenyl)-1H-pyrazole-5-carbohydrazide containing increasing amounts of tetrabutylammonium fluoride (0–3 equiv.) in DMSO-d₆.

Fig. 10 shows color change of solutions of receptor 1 after adding various anions in DMSO. Color changes from light green to purple or intense yellow were observed in the presence of hydroxide, fluoride or acetate, whereas dihydrogen phosphate did not induce any color change. UV-vis titration results and these color changes suggest that deprotonation events occurred due to hydroxide, fluoride and acetate but hydrogen bonding occurs between dihydrogen phosphate and receptor 1.

Fig. 10 Color changes of receptor 1 at 100 μM in DMSO when treated with 80 equivalents of various anions.

The other anions did not induce any color changes even when added in excess. The examples of selectively sensing acetate from dihydrogen phosphate are relatively limited due to the similarity of their basicity. However, they were able to be differentiated by considering the different color responses observed.

Binding energy studies

In the present study the computational modeling using the DFT (density functional theory) method has been carried out for the pyrazole containing receptor with dihydrogen phosphate, Br⁻, Cl⁻ and HSO₄⁻ anion complexes. The common hybrid B3LYP method is chosen for this study.

The B3LYP hybrid functional consists of Becke's exchange functional, the Lee–Yang–Parr correlation functional, and a Hartree–Fock exchange term. The DFT has been successfully used to study hydrogen-bonded complexes,²⁰ even for the most weakly bonded systems.²¹ The calculated binding energy is corrected for the basis set superposition error (BSSE) using the counter poise method.²² The experimental binding constant of a newly synthesized compound shows similarity to the previously reported receptors,¹³ which was unexpected because the present receptor seems to be formed possibly by four strong N–H⋯O and two weak C–H⋯O types of H-bonding. So, we have decided to investigate the binding process more accurately using the state-of-the-art density functional theory. Fig. 11 shows the optimized structure of the host and its H₂PO₄⁻ complex optimized at the B3LYP level^23–26 using the 6-31g(d) basis set. The binding energies of experimental and theoretical values are reported in Table 2.

Fig. 11 Most stable structure of the host·H₂PO₄⁻ complex in the solvent phase (DMSO as a solvent) optimized using B3LYP/6-31g(d) in Gaussian 09. Dashed lines denote the hydrogen bonds (strong and weak). See Table 3 for geometrical parameters and Mulliken charges. Atom numbering included. Atom colors: grey-carbon; red-oxygen; blue-nitrogen; white-hydrogen; orange-phosphorus.

Table 2 Experimental and computational binding energies (BE) of the host with anion complexes^a

	BE
Anions	Exp. (UV)	Calc. (DFT)
a Units are in kcal mol^−1. Experimental binding energy is derived from the UV binding constant. DFT calculations are performed at (B3LYP/6-31G(d)) using a polarizable continuum model in DMSO. The basis set superposition error is corrected.
H2PO4^−	−5.56	−24.96
HSO4^−	−4.15	−16.27
Cl^−	−3.96	−13.04
Br^−	−3.71	−11.69

---

The experimental binding energy is derived from the binding constant (UV experiments). For the solvent effect the DMSO is considered using the PCM (polarizable continuum model).²⁷ The binding energy calculation and computational details have been described in the ESI.† All calculations have been computed by using the Gaussian 09 suite of programs.²⁸

To obtain the complex structure, several geometries have been considered for optimization. Here, we chose the lowest-energy structure as a representative one. All geometries of the host, the guest and the complex have been optimized without any stringent optimization criteria. We could not perform the second derivatives due to the size of the system and the limitation of computational resources. We assume that the experimental binding energies should correlate with the calculated binding energy value (see Table 2). When we compare the calculated binding energy with the experimental binding energy, we noted the difference between the theory and the experiment. The divergence is not unexpected due to the crude solvation model used in the theoretical calculation and the host–anion complex interactions are rather complicated. The chronological order of binding energies derived from the theoretical calculation for host–anion complexes is consistent with the experimental results (see Table 2). Furthermore, the results have been focused on the host·H₂PO₄⁻ complex due to its large binding energy and specific binding properties towards the pyrazole receptor in the current study.

Theoretically the calculated structure contains all experimentally observed H-bonding elements (Fig. 11). The remarkable result of the computed binding configuration of the host–H₂PO₄⁻ complex reveals that all the N–H protons have acted as donors for H₂PO₄⁻. Overall, four N–H⋯O types of H-bonding have been observed in the host–H₂PO₄⁻ complex. Moreover, two additional weak C–H⋯O types of H-bonding have also been observed. The newly introduced pyrazole group instead of the indole group in our previous report shows the strong binding with H₂PO₄⁻ due to the strong four N–H⋯O types of H-bonding. And, the pyrazole containing host in the optimized geometry of the complex has been interestingly noted to be planar, which is not the case in the indole containing host optimized geometry of the complex in our previous report.¹³ The planarity of the host with a strong H-bonding has produced the highest binding energy for the presently investigated pyrazole containing host complex. The bond angle of ∠N₄₈H₂₉O₇₈ is observed to be 160.9° in the complex. All hydrogen atoms in the cage of the pyrazole containing host point towards the oxygen of the H₂PO₄⁻ anion and form H-bonding in the complex. We have also attempted to optimize the geometry to form the H-bonding with O–H₈₃ in the H₂PO₄⁻ anion with N₄₉ in the pyrazole ring. But the optimized results give a similar type of geometry as shown in Fig. 11 of the present study, due to the long distance between O–H₈₃ and N₄₉, 4.834 Å, which is too far for H-bonding. The hydrogen bonding configurations are denoted by dashed lines in Fig. 11 and the corresponding H-bonding lengths are listed in Table 3. In general the X–H⋯B H-bonding length is longer than that of corresponding individual monomers. Once the H-bonding becomes shortened it strengthens the complex.

Table 3 Charges and geometries of the host and its H₂PO₄⁻ complexes (cx)

		cx	Host
Mulliken atomic charges (e)
	H40	0.1669	0.167
	H15	0.1617	0.1578
	H73	0.1914	0.167
	H29	0.4084	0.3833
	H45	0.4185	0.3632
	H57	0.4174	0.3833
	H72	0.4255	0.3632
Heavy atom distance (Å)
	C23–O77	3.848
	C7–O77	3.774
	C50–O77	3.474
	N48–O78	2.752
	N25–O78	2.874
	N59–O79	2.761
	N52–O79	2.866
H-bond distance (Å)
	H40⋯O77	2.771
	H15⋯O77	2.939
	H73⋯O77	2.521
	H29⋯O78	1.758
	H45⋯O78	1.848
	H57⋯O79	1.762
	H72⋯O79	1.838
Bond angle (deg)
	C23H40O77	168.5
	C7H15O77	134.4
	C50H73O77	145.5
	N48H29O78	160.9
	N25H45O78	172.5
	N59H57O79	133.2
	N52H72O79	174.0

---

TD-DFT results

To further support the experimental observations of the host–anion interactions and to provide a better insight into fundamental H-bonded cavity and anion binding interaction, TD-DFT calculations were carried out. The HOMO–LUMO and TD-DFT results are listed in Table 4. The B3LYP optimized structure of the host⋯H₂PO₄⁻ complex and its electronic delocalization of the frontier molecular orbitals (FMOs) can be seen in Fig. 12. We predicted that the addition of anions might change the electronic distribution such that the HOMO is corresponding to the anthracene part and the LUMO is corresponding to the anion interaction of the pyrazole parts. Indeed, we found this to be the case as shown in Fig. 12 and Fig. S6(a–d) (ESI†). These definitive observations are consistent with the above ¹H NMR measurements. Moreover, to provide the extended conjugations in the current system we employed the DFT and TD-DFT calculations. The predicted absorption wavelengths, oscillator strength (f) and the configuration description of the singlet excited states are shown in Table 4. The energy minimized host⋯anion complexes (Br⁻, Cl⁻ and HSO₄⁻) and their electronic delocalization of the frontier molecular orbitals (FMOs) can be seen in Fig. S6(b–d) (ESI†).

Table 4 Calculated HOMO, LUMO, HOMO–LUMO gaps (HLGs), wavelength (λ_abs) and oscillator strength (f) for Ho⋯H₂PO₄⁻, Ho⋯Br⁻, Ho⋯Cl⁻ and Ho⋯HSO₄⁻ complexes in the solvent phase

Complex	HOMO (eV)	LUMO (eV)	HLG^a (eV)	TD-DFT calculated data^b
				E	λ abs,cal (nm)	f	Conf.^d	Wt (%)
a HOMO, LUMO, and HOMO–LUMO gaps (HLG) are calculated by the B3LYP/6-31G(d) method. b Absorption energies are calculated by the TD-DFT method at the B3LYP/6-31G(d) level. c Oscillator strength. d H and L stand for the predicted HOMO and LUMO, respectively. Ho stands for the host.
Ho⋯H2PO4^−	−4.47	−2.20	2.27	S1	503	0.0237	H → L	69
Ho⋯Br^−	−4.53	−2.21	2.32	S1	491	0.0203	H → L	84
Ho⋯Cl^−	−4.54	−2.21	2.33	S1	489	0.0256	H → L	84
Ho⋯HSO4^−	−4.49	−2.21	2.28	S1	499	0.014	H → L	74

---

Fig. 12 Molecular orbital distribution plots of HOMO and LUMO states in the ground state of the host⋯H₂PO₄⁻ complex.

For the host–H₂PO₄⁻ anion complex (see Fig. 12), the lowest energy singlet transitions are mainly from the HOMO to the LUMO. For other anion complexes reported here, they also show the similar results as HOMO to LUMO singlet transitions. The HOMO–LUMO gaps (HLGs) have also been calculated and reported in Table 4. Among the anions H₂PO₄⁻ shows the lowest HLGs supporting the selective binding as confirmed from our experimental results. For both anthracene and pyrazole units FMOs are delocalized over the entire structure. To envision the above observations and the trend we carried out the TD-DFT calculations and results are listed in Table 4. In all the anion complexes the transition energies result mainly from the HOMO to the LUMO.

Conclusion

In DMSO the H₂PO₄⁻ anion was complexed with the presently reported pyrazole containing host via N–H⋯O and C–H⋯O types of H-bonding. The pyrazole containing host in the optimized geometry of the complex has been interestingly noted as planar, which is not the case for the indole containing host in the optimized geometry of the complex in our previous report.¹³ The planarity of the host with the H₂PO₄⁻ anion resulted from four strong N–H–O and three weak C–H⋯O types of H-bonding. In total seven H-bonding and the planarity of the host in the complex are responsible for the high binding energy. The bond angle of ∠N₄₈H₂₉O₇₈ has been observed to be 160.9° in the complex. The N–H⋯O type of H-bonding appeared to be strong and the C–H⋯O type of H-bonding appeared to participate in molecular recognition. From the aforementioned discussions, we concluded that the currently investigated pyrazole containing host has a comparable affinity towards the H₂PO₄⁻ anion as compared with the previously reported receptor.¹³

Acknowledgements

This research was supported by the Basic Science Research Program of the Korean National Research Foundation funded by the Korean Ministry of Education, Science and Technology (#2010-0021333).

References

1. P. A. Furman, J. A. Fyfe, M. H. St. Clair, K. Weinhold, J. L. Rideout and G. A. Freeman, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 8333–8337.
2. V. Král and J. L. Sessler, Tetrahedron, 1995, 51, 539–554.
3. A. Ojida, Y. Mito-oka, K. Sada and I. Hamachi, J. Am. Chem. Soc., 2004, 126, 2454–2463.
4. P. D. Beer, Chem. Commun., 1996, 689–696.
5. L. Fabbrizzi, G. Francese, M. Licchelli, A. Perotti and A. Taglietti, Chem. Commun., 1997, 581–582.
6. L. Deng, L. Wang, J. Huo, Q.-H. Tan, Q. Yang, H.-J. Yu, H.-Q. Gao and J. F. Wang, J. Phys. Chem. B, 2008, 112, 5333–5337.
7. F. Zapata, A. Caballero, A. Espinosa, A. Tarraga and P. J. Molina, J. Org. Chem., 2008, 73, 4034–4044.
8. P. A. Gale, J. R. Hiscock, S. J. Moore, C. Caltagirone, M. B. Hursthouse and M. E. Light, Chem. – Asian J., 2010, 5, 555–561.
9. P. A. Gale, J. R. Hiscock, N. Lalaoui, M. E. Light, N. J. Wells and M. Wenzel, Org. Biomol. Chem., 2012, 10, 5909–5915.
10. S. Kondo and R. Takai, Org. Lett., 2013, 15, 538–541.
11. M. S. Wong, P. F. Xia, X. L. Zhang, P. K. Lo, Y.-K. Cheng, K.-T. Yeung, X. Guo and S. Shuang, J. Org. Chem., 2005, 70, 2816–2819.
12. A. T. Wright and E. V. Anslyn, Org. Lett., 2004, 61341–61344.
13. T. S. Pandian, S. J. Cho and J. Kang, J. Org. Chem., 2013, 78, 12121–12127.
14. D. Wu, F. Jin, W. J. Zhu, C. Li, W. Wang, Y. Tang, H. Jiang, J. Huang, G. Liu and J. Li, J. Chem. Biol. Drug Des., 2012, 79, 897–906.
15. T. Iwasawa, R. J. Hooley and J. Jr. Rebek, Science, 2007, 317, 493–496.
16. Y. Choi and J. Kang, J. Inclusion Phenom. Macrocyclic Chem., 2014, 79, 95–102.
17. S. R. Beeren and J. K. M. Sanders, Chem. Sci., 2011, 2, 1560–1567.
18. Y.-M. Zhang, Q. Lin, T.-B. Wei, X.-P. Qin and Y. Lin, Chem. Commun., 2009, 6074–6076.
19. H. Benesi and H. Hildebrand, J. Am. Chem. Soc., 1949, 71, 2703–2707.
20. V. Srinivasadesikan, P. K. Sahu and S. H. Lee, J. Phys. Chem. B, 2012, 116, 11173–11179.
21. S. D. Wetmore, R. Schofield, D. M. Smith and L. Radom, J. Phys. Chem. A, 2001, 105, 8718–8726.
22. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
23. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
24. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
25. A. D. Becke, J. Chem. Phys., 1997, 107, 8554.
26. H. L. Schmider and A. D. Becke, J. Chem. Phys., 1998, 108, 9624.
27. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian Inc., Wallingford, CT, 2009.

---

Footnote

† Electronic supplementary information (ESI) available: ¹H, ¹³C, and HRMS spectra and binding energy calculations for the optimized host–anion complexes. See DOI: 10.1039/c4nj01063a

---