 Open Access Article
Open Access ArticleS100A4 and its role in metastasis – computational integration of data on biological networks†
Antoine
Buetti-Dinh
*abc,
Igor V.
Pivkin
bd and
Ran
Friedman
*ac
aDepartment of Chemistry and Biomedical Sciences, Linnæus University, Kalmar, Sweden. E-mail: antoine.buetti@lnu.se; ran.friedman@lnu.se
bInstitute of Computational Science, Faculty of Informatics, Università della Svizzera Italiana, Lugano, Switzerland
cCentre of Excellence for Biomaterials Chemistry, Linnæus University, Kalmar, Sweden
dSwiss Institute of Bioinformatics, Lausanne, Switzerland
First published on 23rd June 2015
Abstract
Characterising signal transduction networks is fundamental to our understanding of biology. However, redundancy and different types of feedback mechanisms make it difficult to understand how variations of the network components contribute to a biological process. In silico modelling of signalling interactions therefore becomes increasingly useful for the development of successful therapeutic approaches. Unfortunately, quantitative information cannot be obtained for all of the proteins or complexes that comprise the network, which limits the usability of computational models. We developed a flexible computational framework for the analysis of biological signalling networks. We demonstrate our approach by studying the mechanism of metastasis promotion by the S100A4 protein, and suggest therapeutic strategies. The advantage of the proposed method is that only limited information (interaction type between species) is required to set up a steady-state network model. This permits a straightforward integration of experimental information where the lack of details are compensated by efficient sampling of the parameter space. We investigated regulatory properties of the S100A4 network and the role of different key components. The results show that S100A4 enhances the activity of matrix metalloproteinases (MMPs), causing higher cell dissociation. Moreover, it leads to an increased stability of the pathological state. Thus, avoiding metastasis in S100A4-expressing tumours requires multiple target inhibition. Moreover, the analysis could explain the previous failure of MMP inhibitors in clinical trials. Finally, our method is applicable to a wide range of biological questions that can be represented as directional networks.
1 Introduction
1.1 Modelling biological networks
Being able to predict the behaviour of signalling networks by simulation is fundamental for studying complex diseases as it enables the prediction of the consequences of defective gene functions,1,2 as well as the effect of drugs in different cell types.3 While the mathematical formalism for integrating kinetic data in quantitative models is well established (e.g., Michaelis–Menten formalism), the probabilistic nature of biological signalling can make models of highly intricate and redundant networks inefficient. In fact, due to the large number of microscopic parameters necessary to set up network models, assumptions and simplifications are necessary to make models tractable.The information required for setting up large-scale models is available through current experimental technologies (e.g., high-throughput sequencing). Various methods based on Bayesian probability or information theory, such as Bayesian network inference, can be used to infer on gene regulatory networks by utilising data from diverse data sources.4–7 Such methods are used to integrate datasets from omic technologies into networks representing the main biological features of a system.8–11 Reconstructed networks can subsequently be analysed for the development of therapeutic strategies.12,13
Numerous different approaches exist to simulate biological signalling networks, from very specific models integrating high level of details (e.g., mass-action kinetics) to more approximate ones (e.g., Boolean networks, Petri nets) based on more general principles that allow broader applicability to diverse biological systems.14 In highly accurate models, details on microscopic reaction rates have to be provided by kinetic experiments. This is challenging to achieve when working with biological components in vitro, and substantially more difficult when trying to obtain the same information in vivo. Partially missing information can however be extrapolated computationally through optimization based on the available parameters and using incomplete experimental data.12,13,15 Importantly, biomolecular interaction is strongly determined by its in vivo context, whereas in vitro experiments sometimes fail to determine quantitative information about regulatory processes.16–19 In the absence of detailed description of the system, approximate models can provide qualitative or semi-quantitative information. Such models rely on simple and quite general principles, and thus require a smaller number of parameters. They also can be implemented into computer programs that automatically build a simulation system from the network configuration in a flexible manner according to few control parameters.20–22 These approaches are very well suited to investigate the effect of network components at the qualitative level, with the drawback of poorly describing the system quantitatively.
The computational method we developed combines flexibility and broad applicability to diverse networks, together with quantitative predictive power. The method quantifies the effect of variable network parameters through an automated multidimensional sensitivity analysis with respect to each network component. Every network component (or network node) is represented through a reduced set of parameters. Model parameters assume value ranges reflecting the information available for a given node or interaction and provide a corresponding sensitivity map that takes into consideration the effects associated to experimental uncertainties and heterogeneity in cellular populations. Signalling in cellular populations is modelled through a steady-state interaction network, where continuous functions express activation and inhibition that involves the network's components. Interacting components are treated phenomenologically through a system of ordinary differential equations (ODEs) that are generated per system and condition, thereby setting the basis for flexibility and applicability of the approach to various biological systems. At the same time, our approach facilitates the processing, comparison and modification of different simulated systems making it particularly suited to study partially described signalling networks. We demonstrate its usability by studying a protein network involving the metastasis promoter S100A4.
1.2 S100A4 and its role in metastasis
S100A4 is involved in multiple signalling pathways bridging metastasis and angiogenesis, two cooperating processes that are crucially important for tumour malignancy.23 The protein is used as a prognostic marker in a number of human cancers and correlates to metastatic tumours.24–26 Animal and cellular studies suggest that S100A4 is not only a marker but an active mediator of cancer progression27 and that tumour growth is reduced when extracellular S100A4 is targeted with monoclonal antibodies.28 Metastasizing S100A4-expressing tumour cells can induce cells of the invaded tissues to express S100A4.29Despite a wealth of experimental data, the molecular mechanisms underlying metastasis formation are largely unknown. The involvement of S100A4 in different pathways of cancer-related processes makes it an interesting target for therapeutic strategies and underscores the importance of studying metastasis from a system perspective. This is efficiently achieved here by representing S100A4 in the context of its signalling interactions using a network model to explore the role of S100A4 in view of potential therapeutic strategies.
Current cancer therapies apply evolutionary pressure that dynamically shapes the genomic landscapes of tumours.30,31 Tumour heterogeneity plays a crucial role in such processes32–36 where resistant cells are selected for their capacity to sustain tumour growth utilizing alternative pathways, that eventually lead to treatment resistance. Our method provides means to quantitatively investigate such effects by considering parameters of the signalling interactions over defined ranges, thereby accounting for the tumour's heterogeneous character that leads to resistance to therapy.
2 Methods
2.1 Network representation
We prepared a signalling network model of S100A4 based on the experimental evidence found in the literature (see text ESI 1,†) and illustrated in Fig. 1 using cytoscape.37 Different biological systems can be simulated and investigated by control analysis through a network representation, where the components and type of interaction (activation or inhibition) constitute the only required information. The general principles underlying the presented method enable the application of our modelling framework to diverse biological systems that can be represented by an activation/inhibition network and at the same time facilitate the integration of experimentally accessible information.2.2 Computational workflow
Here we present a quantitative phenomenological modelling framework applied to the case of the S100A4 network. The program performs efficient sensitivity analysis of biological networks at the steady-state and at the same time permits the integration of the available experimental data, to test hypotheses on network regulation as well as to understand the influence of specific components on the dynamics of the system. The program can therefore be used to derive from and integrate in the model new information in an iterative way.A network model is initially built from an input file and read by the main program module. Input files contain node names and the types of interactions between them. A simulation is performed according to a program-defined set of parameters corresponding to the processed network. Interactions between nodes are assumed to occur through continuous, regulatory functions. The dynamical properties of the system are determined by a set of parameters. In practice, this is achieved by setting up a specific value or a range of values for each component, that represents its biological activity. Parameters of interest and their variation ranges are user-defined and determine the subsequent simulation and analysis procedures. The first part of the program workflow consists of generating steady-state values corresponding to the node's activity. Accordingly, a set of ODEs describing the dynamics of the signalling network is automatically built using Hill-type transfer functions as interaction links between nodes.38,39 The different conditions corresponding to the user-defined parameter space are simulated by numerically solving the system of ODEs. In the second part, analysis of the simulated conditions is carried out based on sensitivity and principal component analysis (PCA). The numerical procedure that is coded in C++ relies on the GNU Scientific Library (GSL, version 1.15)40 and is optimized for fast execution. Moreover, the parameter space is automatically split using MPI-based processing in order to make use of parallel architectures thereby enabling the screening of a large number of conditions (see Fig. ESI 3 and ESI 4,† for details on the workflow, and text ESI 2,† for details on computational performance and model scalability).
2.3 Model details
The system is described as a network of interacting components evolving in time according to the ODEs. Every component in the network is represented by a node. The nodes are connected by links, where each link is a regulatory function that represents either activation or inhibition. Every node in the model is parametrized by the parameters β and δ and every link by α, γ and η (see Table 1).| Parameter name | Description |
|---|---|
| β | Basal level of a node's activity |
| δ | Decay constant of a node |
| γ | Interaction strength between two nodes (affinity) |
| η | Nonlinearity in signalling interaction (Hill coefficient) |
| α | Multiplicative scaling factor applied to the regulatory function |
 | (1) |
2.4 Control analysis
Sensitivity analysis is used to identify parameter combinations responsible for the relevant dynamical properties of the system. Each parameter change in the combinatorial parameter space is processed according to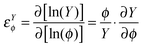 | (2) |
 | (3) |
where ϕ is an input parameter or variable and Y an output variable. Eqn (2) expresses the relative change of activity in the nodes as a function of a variation in the parameter set. In the computational procedure, two conditions (i and j) are evaluated at each step of the sensitivity analysis according to eqn (3). The conditions are defined by vectors of steady-state values (Yi and Yj) corresponding to the nodes' activities and are determined by the parameter sets (ϕi and ϕj). Parameter sets processed by eqn (3) differ in a single parameter by a finite factor determined in the parameter interval sampling. The infinitesimal interval in the denominator of eqn (2) is therefore approximated to a finite multiplicative factor and the numerator computed by the logarithm of the ratio between the corresponding simulated steady-state values.
Multivariate analysis is included as the final step of the procedure providing graphical and quantitative information on the controllability of the system. The prcomp function of R is used to carry out PCA. It is applied to both steady-state and sensitivity datasets in order to reveal co-activity and co-regulatory patterns between the nodes, respectively (see Fig. ESI 4,† for details).
3 Results
3.1 Determination of parameter space regions of interest
Sensitivity analysis can be used to quantify the contribution of certain nodes (components) to the phenomenological output of the system. Here we use two parameters, namely cell dissociation and capillary growth, to characterize pathological phenotypes. Moreover, the sensitivity calculated with respect to specific nodes enables the assessment of their controllability by other components of the network.| Parameter name | Range of variation (fold-variation step) |
|---|---|
| β(MMPs) | 10−4–10+3(1.2) |
| β(TIMPs) | 10−4–10+3(1.2) |
| β(S100A4_int) | 10−3–10+1(100) |
| β(S100A4_ext) | 10−3 |
| β(BCat) | 10−2 |
| β(ECadh) | 10−2 |
| β(Myo9) | 10−2 |
| β(EGFR) | 10−3 |
| β(NFKB) | 10−3 |
| β(OPN) | 10−3 |
| β(uPA_uPAR) | 10−3 |
| β(EphrA1) | 10−3 |
| β(Plasmin) | 10−3 |
| β(CellDiss) | 10−3 |
| β(CapGrowth) | 10−3 |
By simulating the model we obtained surfaces representing the sensitivities of cell dissociation with respect to the biological activities of MMPs (convex surfaces) and TIMPs (concave surfaces), (see Fig. 2). Interestingly, we could identify regions with pronounced sensitivity values (positive for εCellDissMMPs and negative for εCellDissTIMPs). The overlap of these regions defines a subspace of high controllability with respect to the variables: for example, in the range of MMPs activities between 0.1–1 and of TIMPs activity >5, small variations in the activities of MMPs and TIMPs are predicted to have a decisive effect on cell dissociation. This suggests that a therapeutic window exists where the system could be influenced but also deteriorate, not unlike transition states in chemistry. In addition to the combinatorial variation of MMPs and TIMPs, the effect of S100A4 was investigated by applying three different activity levels of S100A4. An increased concentration of active S100A4 affects the system in two principal ways: (i) the activities of MMPs and TIMPs shift to higher steady-state values, the first of which is supposed to be a hallmark of metastasis (see the bottom projections in Fig. 2). (ii) The system loses sensitivity of cell dissociation to MMPs/TIMPs activity (see the 3D upper surfaces in Fig. 2). Taken together, our simulations indicate that once the system is driven to a metastatic regime (high steady-state values of cell dissociation) characterized by high proteinase activity, the system becomes less sensitive to MMPs and TIMPs, i.e., it loses the potential of reverting to a normal physiological state.
 | ||
Fig. 3 Sensitivity of capillary growth. Sensitivity surfaces calculated in response to variation of MMPs activity  are shown in light colours and in response to variation of TIMPs activity are shown in light colours and in response to variation of TIMPs activity  in dark colours. Projections in the lower planes represent the activity ranges (steady-state values) of MMPs and TIMPs (higher projections are identical to Fig. 2, colour code corresponding to the sensitivity surfaces). The lowest projection represents the steady-state values of capillary growth at low S100A4 activity. in dark colours. Projections in the lower planes represent the activity ranges (steady-state values) of MMPs and TIMPs (higher projections are identical to Fig. 2, colour code corresponding to the sensitivity surfaces). The lowest projection represents the steady-state values of capillary growth at low S100A4 activity. | ||
 | ||
| Fig. 4 PCA (loading plots) of simulation datasets of the S100A4 network with varying S100A4 activity. MMPs and TIMPs variation; PCA calculations were carried for low (A and D), medium (B and E), high (C and F) activities of S100A4. The top scheme (A–C) is the PCA of steady-state values whereas the scheme at the bottom (D–F) is the PCA of sensitivity values. The dataset used for PCA is generated according to section “Determination of parameter space regions of interest”. The full names of the variables are found in Fig. 1. | ||
3.2 Global parameter variation: basal activity (β)
We extended the procedure described above by including a broader parameter variation. To this end, we evaluated the robustness of the previous results by taking into account the variable nature of basal activity due to cell heterogeneity. A numerical range was therefore assigned to the basal activity parameter (β) for those network components previously set to a single initial value. Ranges of 10-fold increase in basal activities (0.001–0.1) were combinatorially tested for all nodes except for S100A4 which was varied as in the previous section; MMPs and TIMPs, which were varied within same ranges as in the previous section in 10-fold steps; and the nodes CellDiss and CapGrowth that were assumed to have low initial activity (β = 0.001). The resulting combinatorial set of simulation conditions was subsequently averaged and the resulting mean sensitivity surfaces were consistent with previous outcomes (see Fig. 5 compared with Fig. 2 and Fig. 6 compared with Fig. 3). This indicates that the effects of S100A4 low, medium and high activity levels are not an artefact of an arbitrary choice of basal activities for the nodes but a genuine feature of the interaction network. As in the previous section, PCA was applied to this dataset. Only the sensitivity data differed significantly compared to the PCA in section “Determination of parameter space regions of interest”. Previously, a group of variables composed of S100A4, EGFR and NFKB progressively merged together with CellDiss and CapGrowth as S100A4 activity increased. Here instead, two groups are distinguishable at low S100A4, one consisting of S100A4, EGFR and NFKB and one including CellDiss and CapGrowth that merge in a single compact cluster only at intermediate S100A4 activity and remain grouped by subsequent increase of S100A4 activity. This indicates that with a more variable basal expression of the network components, the regulation of the variables CellDiss and CapGrowth is still driven by S100A4 over a certain threshold of S100A4 activity (compare Fig. 4 to Fig. ESI 2,†). | ||
| Fig. 5 Sensitivity of cell dissociation (global β variation). (A) Sensitivity landscape plotted against variable β values. (B) Sensitivity landscape plotted against steady-state values of MMPs and TIMPs (as a consequence of the variation of β(MMPs) and β(TIMPs), respectively). Logarithmic binning is applied for specific β values (A) or for the corresponding ranges of steady-state values (B). Note that the regions of high sensitivity and high variability (high standard deviation values) over the global parameter variation surfaces are comparable to the regions of high sensitivity of Fig. 2. | ||
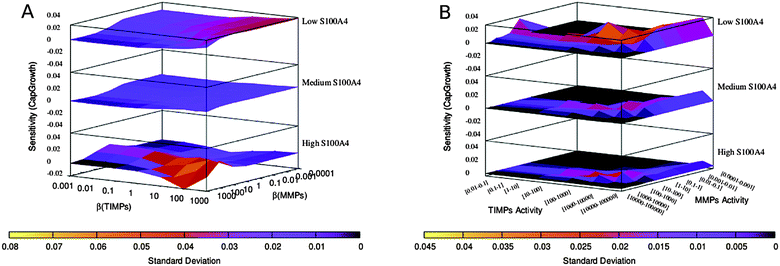 | ||
| Fig. 6 Sensitivity of capillary growth (global β variation). (A) Sensitivity landscape plotted against variable β values. (B) Sensitivity landscape plotted against steady-state values of MMPs and TIMPs (as a consequence of the variation of β(MMPs) and β(TIMPs), respectively). Logarithmic binning is applied for specific β values (A) or for the corresponding ranges of steady-state values (B). Note that the regions of high sensitivity and high variability (high standard deviation values) over the global parameter variation surfaces are comparable to the regions of high sensitivity of Fig. 3. | ||
4 Discussion
Properties of the S100A4 model under variable activities of MMPs and TIMPs
We first devised a network model of S100A4 based on the available knowledge including information on interacting biomolecules and principal processes involved in angiogenesis and metastasis formation (Fig. 1). On the basis of this model, simulations were initially run under standard parametrization and regulatory features of interest were subsequently validated in a more general, computationally-intensive context accounting for global parameter variation. MMPs and their natural inhibitors TIMPs are typically deregulated in metastatic tumours. Therefore, we simulated the system over a broad activity range of MMPs and TIMPs and analysed the sensitivity of cell dissociation and capillary growth, i.e., whether these outcomes can be influenced under certain conditions. Indeed, we could identify regions of high controllability in the space defined by the activities of MMPs and TIMPs. Furthermore, under these conditions, we could distinguish two features of relevance driven by S100A4. On the one hand, by increasing the activity of S100A4, MMPs and TIMPs steady-state values were predicted to shift to higher activities consistent with experimental data (Fig. 2 and 3). On the other hand, sensitivity analysis outlines two different scenarios for cell dissociation and capillary growth. The sensitivity of cell dissociation presents a barrier separating the normal and metastatic regimes (defined according to proteinases activity). Beyond a certain threshold in MMPs activity, the system gains stability at the high metastatic regime: it looses any sensitivity to external control of MMPs and TIMPs, hence reducing its potential to return to a normal physiological state. This explains why tumours expressing S100A4 show poor prognosis. S100A4's activity has however a different effect on capillary growth. In addition to an overall decrease of sensitivity, the sensitivity landscape (Fig. 3) is characterised by multiple regions separated by near-zero, buffering sensitivity boundaries that rearrange dynamically with increasing activity of S100A4 suggesting multistable equilibria. This implies different phenotypic responses depending on the activity of S100A4 and could explain the formation of aggressive tumours with limited sensitivity to therapy.Despite the partial description of the network considered, the simulations could reproduce recent experimental findings by showing that the activity of S100A4 dramatically reduced the sensitivity of cell dissociation to MMPs and their natural inhibitors TIMPs, thereby driving a metastatic phenotype. It also suggests that, in order to prevent the emergence of a metastatic phenotype, MMPs inhibitors may only be useful in cells with low S100A4 activity, potentially explaining the failure of an MMP inhibitor (Marimastat) in clinical trials.46–48 Our results suggest that blockage of MMPs alone is not sufficient to prevent cell dissociation. Rather, it appears that combined inhibition of different targets is required to combat metastasis when it is about to emerge, unless some of the components are not expressed in the tumour.
5 Conclusions
In this article we discuss a steady-state simulation framework that integrates partial information on biological networks and through sensitivity analysis identifies control points of interest for targeted therapeutic intervention. Similarly to mass-action kinetics models, our approach assumes continuous regulation between nodes and can therefore provide quantitative insights on the studied system. It however requires only minimal information to set up simpler qualitative boolean models. Steady-state relationships between the network's components enable the user to supplement pre-existing settings with experimentally retrieved information. In addition, lack of information can be compensated by efficient sampling using parallel computing architectures. Such an approach is especially useful in the case of S100A4: the high connectivity between different regulatory processes needs to be considered simultaneously in order to understand phenomena underlying drug resistance and be able to design appropriate therapeutic strategies. Despite large amount of data, the precise biological role of S100A4 as a metastasis promoter still remains unclear; our approach allows efficient integration of the sparse information which is available. The outcome of different simulated conditions can be tested with different available in vivo and in vitro models. Our results suggest that it would be instructive to assess the efficacy of inhibitors that previously failed clinical trials in cell lines with naturally low or no activity of S100A4. Finally, the general design of the modelling enables a flexible application of the tool to diverse problems as long as the scientific question can be described by an activation/inhibition network.Acknowledgements
We acknowledge Prof. Gunhild M. Mælandsmo together with her staff for helpful discussions and Kirill Lykov for technical help with computational infrastructures. The calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at Lunarc, centre for scientific and technical computing for research at Lund University and by the Swiss National Supercomputing Centre (CSCS). I.V.P. acknowledges the support from Swiss National Science Foundation and Swiss Platform for Advanced Scientific Computing. This work was supported by Holcim Foundation (Switzerland, to AB) and Crafoord Foundation (Sweden, grant application numbers 20120856 and 20130787, to RF).References
- P. Kreeger, R. Mandhana, S. Alford, K. Haigis and L. Da, Cancer Res., 2009, 69(20), 8191–8199 CrossRef CAS PubMed.
- T. Zhang, P. Brazhnik and J. Tyson, Biophys. J., 2009, 97(2), 415–434 CrossRef CAS PubMed.
- S. Pingle, Z. Sultana, S. Pastorino, P. Jiang, R. Mukthavaram, Y. Chao, I. Bharati, N. Nomura, M. Makale, T. Abbasi, S. Kapoor, A. Kumar, S. Usmani, A. Agrawal, S. Vali and S. Kesari, J. Transl. Med., 2014, 12, 128 CrossRef PubMed.
- J. Tegner, M. K. Yeung, J. Hasty and J. J. Collins, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(10), 5944–5949 CrossRef CAS PubMed.
- J. Yu, V. A. Smith, P. P. Wang, A. J. Hartemink and E. D. Jarvis, Bioinformatics, 2004, 20(18), 3594–3603 CrossRef CAS PubMed.
- X. Solé, N. Bonifaci, N. López-Bigas, A. Berenguer, P. Hernández, O. Reina, C. A. Maxwell, H. Aguilar, A. Urruticoechea, S. de Sanjosé, F. Comellas, G. Capellá, V. Moreno and M. A. Pujana, PLoS One, 2009, 4(2), e4544 Search PubMed.
- N. S. Watson-Haigh, H. N. Kadarmideen and A. Reverter, Bioinformatics, 2010, 26(3), 411–413 CrossRef CAS PubMed.
- A. Crombach, K. R. Wotton, D. Cicin-Sain, M. Ashyraliyev and J. Jaeger, PLoS Comput. Biol., 2012, 8(7), e1002589 CAS.
- L. Salvatori, F. Caporuscio, A. Verdina, G. Starace, S. Crispi, M. R. Nicotra, A. Russo, R. A. Calogero, E. Morgante, P. G. Natali, M. A. Russo and E. Petrangeli, PLoS One, 2012, 7(2), e31467 CAS.
- S. Crispi, R. A. Calogero, M. Santini, P. Mellone, B. Vincenzi, G. Citro, G. Vicidomini, S. Fasano, R. Meccariello, G. Cobellis, S. Menegozzo, R. Pierantoni, F. Facciolo, A. Baldi and M. Menegozzo, PLoS One, 2009, 4(9), e7016 Search PubMed.
- K. Sachs, O. Perez, D. Pe'er, D. A. Lauffenburger and G. P. Nolan, Science, 2005, 308(5721), 523–529 CrossRef CAS PubMed.
- B. Schoeberl, E. A. Pace, J. B. Fitzgerald, B. D. Harms, L. Xu, L. Nie, B. Linggi, A. Kalra, V. Paragas, R. Bukhalid, V. Grantcharova, N. Kohli, K. A. West, M. Leszczyniecka, M. J. Feldhaus, A. J. Kudla and U. B. Nielsen, Sci. Signaling, 2009, 2(77), ra31 CrossRef PubMed.
- W. W. Chen, B. Schoeberl, P. J. Jasper, M. Niepel, U. B. Nielsen, D. A. Lauffenburger and P. K. Sorger, Mol. Syst. Biol., 2009, 5, 239 Search PubMed.
- S. Ghosh, Y. Matsuoka, Y. Asai, K. Y. Hsin and H. Kitano, Nat. Rev. Genet., 2011, 12(12), 821–832 CAS.
- M. Tigges, T. T. Marquez-Lago, J. Stelling and M. Fussenegger, Nature, 2009, 457(7227), 309–312 CrossRef CAS PubMed.
- C. J. Wienken, P. Baaske, U. Rothbauer, D. Braun and S. Duhr, Nat. Commun., 2010, 1(7), 100 CrossRef PubMed.
- A. Bancaud, S. Huet, N. Daigle, J. Mozziconacci, J. Beaudouin and J. Ellenberg, EMBO J., 2009, 28(24), 3785–3798 CrossRef CAS PubMed.
- A. Magno, A. Caflisch and R. Pellarin, J. Phys. Chem. Lett., 2010, 1(20), 3027–3032 CrossRef CAS.
- M. A. Savageau, J. Theor. Biol., 1995, 176(1), 115–124 CrossRef CAS PubMed.
- A. Feiglin, A. Hacohen, A. Sarusi, J. Fisher, R. Unger and Y. Ofran, Bioinformatics, 2012, 28(21), 2811–2818 CrossRef CAS PubMed.
- D. Ruths, M. Muller, J. T. Tseng, L. Nakhleh and P. T. Ram, PLoS Comput. Biol., 2008, 4(2), e1000005 Search PubMed.
- G. Karlebach and R. Shamir, Nat. Rev. Mol. Cell Biol., 2008, 9(10), 770–780 CrossRef CAS PubMed.
- D. Hanahan and R. A. Weinberg, Cell, 2000, 100(1), 57–70 CrossRef CAS.
- A. M. Platt-Higgins, C. A. Renshaw, C. R. West, J. H. Winstanley, S. De Silva Rudland, R. Barraclough and P. S. Rudland, Int. J. Cancer, 2000, 89(2), 198–208 CrossRef CAS.
- K. Boye and G. M. Mælandsmo, Am. J. Pathol., 2010, 176(2), 528–535 CrossRef CAS PubMed.
- H. Chen, C. Xu, Q. Jin and Z. Liu, Am. J. Cancer Res., 2014, 4(2), 89–115 Search PubMed.
- S. C. Garrett, K. M. Varney, D. J. Weber and A. R. Bresnick, J. Biol. Chem., 2006, 281(2), 677–680 CrossRef CAS PubMed.
- J. L. Hernández, L. Padilla, S. Dakhel, T. Coll, R. Hervas, J. Adan, M. Masa, F. Mitjans, J. M. Martinez, S. Coma, L. Rodrguez, V. Noé, C. J. Ciudad, F. Blasco and R. Messeguer, PLoS One, 2013, 8(9), e72480 Search PubMed.
- C. Xue, D. Plieth, C. Venkov, C. Xu and E. G. Neilson, Cancer Res., 2003, 63(12), 3386–3394 CAS.
- R. Friedman, PLoS One, 2013, 8(12), e82059 Search PubMed.
- J. Foo and F. Michor, J. Theor. Biol., 2014, 355(0), 10–20 CrossRef PubMed.
- B. Vogelstein, N. Papadopoulos, V. E. Velculescu, S. Zhou, L. A. J. Diaz and K. W. Kinzler, Science, 2013, 339(6127), 1546–1558 CrossRef CAS PubMed.
- A. Kreso, C. A. O'Brien, P. van Galen, O. Gan, F. Notta, A. M. Brown, K. Ng, J. Ma, E. Wienholds, C. Dunant, A. Pollett, S. Gallinger, J. McPherson, C. G. Mullighan, D. Shibata and J. E. Dick, Science, 2012, 339(6119), 543–548 CrossRef PubMed.
- P. B. Gupta, C. M. Fillmore, G. Jiang, S. D. Shapira, K. Tao, C. Kuperwasser and E. S. Lander, Cell, 2011, 146(4), 633–644 CrossRef CAS PubMed.
- E. C. de Bruin, N. McGranahan, R. Mitter, M. Salm, D. C. Wedge, L. Yates, M. Jamal-Hanjani, S. Shafi, N. Murugaesu, A. J. Rowan, E. Grnroos, M. A. Muhammad, S. Horswell, M. Gerlinger, I. Varela, D. Jones, J. Marshall, T. Voet, P. Van Loo, D. M. Rassl, R. C. Rintoul, S. M. Janes, S.-M. Lee, M. Forster, T. Ahmad, D. Lawrence, M. Falzon, A. Capitanio, T. T. Harkins, C. C. Lee, W. Tom, E. Teefe, S.-C. Chen, S. Begum, A. Rabinowitz, B. Phillimore, B. Spencer-Dene, G. Stamp, Z. Szallasi, N. Matthews, A. Stewart, P. Campbell and C. Swanton, Science, 2014, 346, 251–256 CrossRef CAS PubMed.
- J. Zhang, J. Fujimoto, J. Zhang, D. C. Wedge, X. Song, J. Zhang, S. Seth, C.-W. Chow, Y. Cao, C. Gumbs, K. A. Gold, N. Kalhor, L. Little, H. Mahadeshwar, C. Moran, A. Protopopov, H. Sun, J. Tang, X. Wu, Y. Ye, W. N. William, J. J. Lee, J. V. Heymach, W. K. Hong, S. Swisher, I. I. Wistuba and P. A. Futreal, Science, 2014, 346, 256–259 CrossRef CAS PubMed.
- P. Shannon, A. Markiel, O. Ozier, N. S. Baliga, J. T. Wang, D. Ramage, N. Amin, B. Schwikowski and T. Ideker, Genome Res., 2003, 13(11), 2498–2504 CrossRef CAS PubMed.
- Z. Cheng, F. Liu, X. P. Zhang and W. Wang, FEBS Lett., 2008, 582(27), 3776–3782 CrossRef CAS PubMed.
- H. Song, P. Smolen, E. Av-Ron, D. A. Baxter and J. H. Byrne, Biophys. J., 2007, 92(10), 3407–3424 CrossRef CAS PubMed.
- M. Galassi, J. Davies, J. Theiler, B. Gough, G. Jungman, P. Alken, M. Booth and F. Rossi, GNU Scientific Library Reference Manual, Network Theory Limited, United Kingdom, ISBN 0954612078, 3rd edn, 2009 Search PubMed.
- A. V. Hill, J. Physiol., 1910, 40, 4–7 Search PubMed.
- K. Bjørnland, J. O. Winberg, O. T. Odegaard, E. Hovig, T. Loennechen, A. O. Aasen, O. Fodstad and G. M. Mælandsmo, Cancer Res., 1999, 59(18), 4702–4708 Search PubMed.
- G. Che, J. Chen, L. Liu, Y. Wang, L. Li, Y. Qin and Q. Zhou, Neoplasma, 2006, 53(6), 530–537 CAS.
- J. Melendez-Zajgla, L. Del Pozo, G. Ceballos and V. Maldonado, Mol. Cancer, 2008, 21;7, 85 CrossRef PubMed.
- R. Milo, P. Jorgensen, U. Moran, G. Weber and M. Springer, Nucleic Acids Res., 2010, 38, D750–D753 CrossRef CAS PubMed.
- C. M. Overall and O. Kleifeld, Nat. Rev. Cancer, 2006, 6(3), 227–239 CrossRef CAS PubMed.
- J. A. Sparano, P. Bernardo, P. Stephenson, W. J. Gradishar, J. N. Ingle, S. Zucker and N. E. Davidson, J. Clin. Oncol., 2004, 22(23), 4683–4690 CrossRef CAS PubMed.
- W. P. Steward and A. L. Thomas, Expert Opin. Invest. Drugs, 2000, 9(12), 2913–2922 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5mb00110b |
| This journal is © The Royal Society of Chemistry 2015 |




