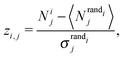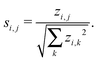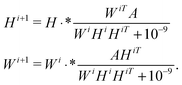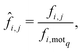Network motif frequency vectors reveal evolving metabolic network organisation†
Nicole
Pearcy
,
Jonathan J.
Crofts
* and
Nadia
Chuzhanova
School of Science and Technology, Nottingham Trent University, Nottingham, NG11 8NS, UK. E-mail: jonathan.crofts@ntu.ac.uk; Tel: +44 (0)115 848 8419
First published on 2nd October 2014
Abstract
At the systems level many organisms of interest may be described by their patterns of interaction, and as such, are perhaps best characterised via network or graph models. Metabolic networks, in particular, are fundamental to the proper functioning of many important biological processes, and thus, have been widely studied over the past decade or so. Such investigations have revealed a number of shared topological features, such as a short characteristic path-length, large clustering coefficient and hierarchical modular structure. However, the extent to which evolutionary and functional properties of metabolism manifest via this underlying network architecture remains unclear. In this paper, we employ a novel graph embedding technique, based upon low-order network motifs, to compare metabolic network structure for 383 bacterial species categorised according to a number of biological features. In particular, we introduce a new global significance score which enables us to quantify important evolutionary relationships that exist between organisms and their physical environments. Using this new approach, we demonstrate a number of significant correlations between environmental factors, such as growth conditions and habitat variability, and network motif structure, providing evidence that organism adaptability leads to increased complexities in the resultant metabolic networks.
Introduction
Many biological systems can be described using the techniques of network science,1,2 which provides a powerful set of tools for analysing the underlying connectivity structures that naturally arise within all living organisms.3,4 At the cellular level, networks emerge via interacting proteins, and other macro-molecules, resulting in various biochemical nets, such as gene regulatory networks,5,6 protein–protein interaction networks7 and protein residue networks.8,9 In this regards, the metabolic process in particular plays a fundamental role, providing the building blocks (nucleic acids and amino acids) that enable genes to interact effectively, and thus for the cell to function properly. Moreover, recent evidence suggests that the interaction patterns described by metabolic networks reflect the evolutionary origins of important functional changes,10–12 and thus understanding their topological organisation promises to unravel important features of biological organisation at the systems level.Metabolic networks have been the focus of a large number of studies (see, for example, the review by Lacroix et al.13 and references therein) and several important structural characteristics have been evidenced. For example, modularity, i.e. the propensity for a network to organise into nearly-independent structural units, has been shown to be a prevalent feature within metabolic networks,14,15 and has, for example, been related to important biological properties such as robustness16,17 and evolvability.10,11,16 However, metabolic networks are by no means perfectly modular; their inter-module connectivity is relatively high, leading some authors to conclude that these networks are better described as being hierarchically structured,14 that is metabolic networks may be considered to possess fractal-like properties, such as self-similarity. Indeed, the existence of many small highly integrated units, which then group together to form larger modules and so on, provides one possible explanation for the high level of inter-modular connectivity observed in these networks.
Another popular approach for analysing metabolic networks is provided by network motifs,18i.e. recurrent, statistically significant subgraphs. Motifs are of particular interest since they are typically associated with certain biological functions, and their relative over-abundance is considered to be an evolutionary result reflecting their “importance” to the organisms involved.19,20 Moreover, they constitute the basic structural units from which complex metabolic networks are formed, and thus provide a simplified framework for probing large-scale topologies. For example, in a recent study Shellman et al.21 successfully captured key evolutionary differences between metabolic networks from the six different kingdoms of life, employing network motif analysis. Another example, highlighting the considerable potential of such an approach, is provided by the work of Asgari and colleagues,22 in which the authors employ recent advances in the theory of network controllability as a method for improving drug–target discovery techniques. In particular, they suggest that network motifs provide ideal ‘driver’ candidates, which can be employed to manoeuvre the system of interest into certain desirable states.
Here, we introduce a novel technique for comparing biological networks of varying size based on local network structure. In particular, we propose a new embedding technique based on low order network motifs. In our approach, each network is mapped to a point in a high-dimensional vector space, the dimension of which depends on the number of motifs considered (n = 212 in our work as we consider all 3 and 4 node motifs23). By using a suitably defined low-rank approximation, we are able to combine the 212 motif frequency scores into a single network specific measurement, which allows us to compare and contrast networks in terms of just a single parameter. Using this new measure we investigated 383 bacterial metabolic networks with identified growth conditions, as well as a smaller subset of 115 networks classified according to the amount of variability present within their natural habitats, and found a number of significant correlations between network motif structure and fluctuations in environmental conditions.
A new graph embedding approach
Motivated by the prominent role that network motifs have played to date in the analysis of biological networks (see, for example, the book of Alon3 and references therein), we propose a new, lossy graph embedding technique based on low-order motifs. The proposed technique is lossy in the sense that the original network cannot be recovered from the corresponding vector-space representation. Importantly, such an approach takes a difficult and unwieldy problem, i.e. the analysis of many large, complex biological networks of differing order, and replaces it by one which is ‘easier’ to manipulate – a plethora of tools and techniques from statistical machine learning24,25 already exist for the analysis of the resultant embedded data.Motif frequency vectors
Motif frequencies can be used to directly compare different metabolic networks as they provide a ‘unique’ network signature.21 Alternatively, networks can be compared by calculating a feature vector of z-score's, computed in the usual way, i.e.where here, Nij denotes the rate of recurrence of the jth motif within the ith network whilst
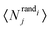 and
and 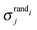 denotes the mean and standard deviation of the rate of recurrence of the jth motif in an ensemble of randomised networks.3
denotes the mean and standard deviation of the rate of recurrence of the jth motif in an ensemble of randomised networks.3
In this way, for each network of interest we can compute a feature vector, zi, whose elements are the z-scores of each network motif. For example, if, as in this work, we consider all 3- and 4-node motifs then the result is a vector zi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 212 representing the ith network.
212 representing the ith network.
Note that it is typically the case that the networks we wish to compare are of varying order and as such we need to take care that network size does not bias any results. To handle this issue one can consider instead of the z-scores defined above, a so-called significance profile26 defined by
In the work presented here, we threshold the network significance profiles such that any entries si,j > 0 are set to zero as we are only interested in those motifs that are over represented. Motifs that are under represented are known as anti-significant motifs, or anti-motifs, and although we do not consider them in this study, the approach forwarded here can easily be extended to that case. This results in a matrix
| S = [s1,…,sm]T ≥ 0, |
To analyse the matrix S we use a matrix decomposition to compute a low-rank approximation of the data.25 Since our data is non-negative, it is natural to decompose it using a non-negative matrix factorisation27 (NNMF) (for algorithmic details see the Methods section). Such an approach is akin to a principal component analysis, that reduces the dimension of the problem, thus allowing us to detect important network features. Mathematically, we approximate S as follows:
| S ≈ WH, | (1) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×k and H ∈
m×k and H ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) k×212 are non-negative matrices. Here, k is the rank of the approximation and m the number of networks being considered. Importantly, both the columns of W and the rows of H can be used to reveal important network features.28,29 Note, that in all of our experiments, the factorisation in (1) was carried out using k = 3, and W, H were chosen so as to minimise the residual25
k×212 are non-negative matrices. Here, k is the rank of the approximation and m the number of networks being considered. Importantly, both the columns of W and the rows of H can be used to reveal important network features.28,29 Note, that in all of our experiments, the factorisation in (1) was carried out using k = 3, and W, H were chosen so as to minimise the residual25| ||S − WH||F. |
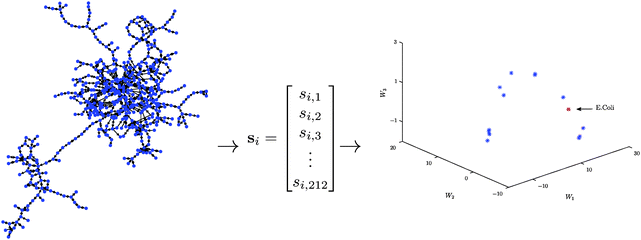
The approach can be concisely summarised into the following three basic steps (see Fig. 1 for a schematic description):
Step 1: For each metabolic network compute the significance profile, si ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 212, consisting of the normalised significance scores for each of the 212 three- and four-node motifs.
212, consisting of the normalised significance scores for each of the 212 three- and four-node motifs.
Step 2: Compute a low-dimensional (k ≪ 212) representation of the thresholded matrix of significance scores, S = [s1,…,sm]T, using a non-negative matrix factorisation.
Step 3: Use the columns/rows of W/H to determine important network features.
Global and local motif significance scores
In order to determine the relative importance of the jth motif in the ith network we construct the following local motif significance score:| P(i,j) = si,j · h1,j. | (2) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m×212 (m = 115 or m = 383 here), whose rows encapsulate the network motif structure of each metabolic network, and whose columns provide information pertaining to the relative importance of specific motifs across the network ensemble.
m×212 (m = 115 or m = 383 here), whose rows encapsulate the network motif structure of each metabolic network, and whose columns provide information pertaining to the relative importance of specific motifs across the network ensemble.
In the experiments in the next section, we derive a global significance score for each network by summing the rows of P as follows
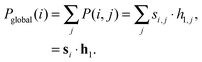 | (3) |
Results and discussion
In this section we present the results of applying the approach described in the previous section to a large cohort of metabolic networks. We begin by giving a brief description of the organisms studied, and details of the network construction process.Metabolic networks
The metabolic data in this study is the same as used by Takemoto,30 and was derived from the KEGG database31 on May 20th, 2011. In total, we studied upto 383 bacterial species (see Tables 1 and 2 for an overview of some basic network properties), each being characterised by a number of shared biological features (e.g. environmental variability, oxygen requirements and genome size), using graph theoretical techniques. A complete list of all the bacterial species used in our analysis is provided in the ESI.†| Environment | Number of nodes | Number of edges | ||||
|---|---|---|---|---|---|---|
| Min | Median | Max | Min | Median | Max | |
| Obligate (34) | 78 | 273 | 620 | 91 | 340 | 840 |
| Specialised (5) | 442 | 480 | 541 | 566 | 641 | 692 |
| Aquatic (4) | 541 | 580 | 647 | 700 | 751 | 868 |
| Facultative (41) | 90 | 652 | 809 | 101 | 890 | 1160 |
| Multiple (28) | 430 | 615 | 800 | 560 | 821 | 1119 |
| Terrestrial (3) | 557 | 689 | 693 | 779 | 944 | 966 |
| Total (115) | 78 | 541 | 809 | 91 | 730 | 1160 |
| Environment | Number of nodes | Number of edges | ||||
|---|---|---|---|---|---|---|
| Min | Median | Max | Min | Median | Max | |
| Aerobic (154) | 65 | 605 | 892 | 74 | 809 | 1210 |
| Facultative (180) | 78 | 602 | 816 | 91 | 825 | 1168 |
| Anaerobic (49) | 307 | 488 | 681 | 381 | 645 | 969 |
| Total (383) | 65 | 581 | 892 | 74 | 789 | 1210 |
Metabolic processes can be modelled using simple graphs in a number of ways33 and it is important to choose an appropriate representation. The most common representation is the substrate–product graph whereby nodes and edges correspond to metabolites and reactions, respectively. Note, that a potential caveat of such an approach is that it can lead to the detection of erroneous pathways (see, for example, the discussion in Montañez et al.34). However, since we are not considering a path analysis here and for the ease of comparability with related studies, we consider the substrate–product representation in all of our experiments. Moreover, ubiquitous metabolites such as H2O, ATP and NADH were removed from the analysis as they tend not to be involved in higher order functions, and if included, typically lead to physiologically meaningless pathways. Finally, to further simplify the analysis, we consider only the largest connected component for each network. This avoids, for example, issues that arise when constructing randomised networks through the rewiring of metabolic networks consisting of a number of disconnected components. For further details of the network construction the interested reader is referred to the papers of Takemoto and colleagues.11,30,35
It is worth noting that, in addition to the modelling issues touched upon above, there are general limitations to any complex network study of metabolism due to noisy and incomplete metabolic maps (e.g. missing/spurious links), the omission of reaction stoichiometry data and incomplete reaction reversibility data. Nevertheless, the approach taken here is standard within the field and provides a global picture of the biochemical systems under investigation.
As an illustration of the approach introduced in the previous section, we carried out two experiments with the aim of testing the hypothesis that organism adaptability is manifested via the network motif structure of the corresponding metabolic networks.
Habitat variability and network motif structure
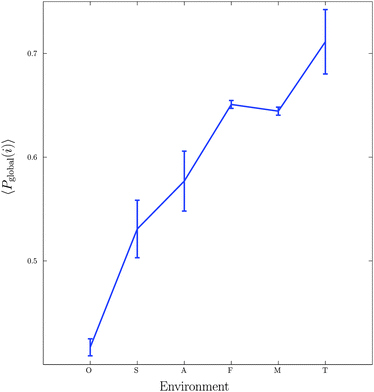
The first experiment undertaken considered 115 metabolic networks, each being categorised according to their environmental habitat (see Table 1). The organisms can be found in a variety of conditions, ranging from highly specialised (e.g. symbiotic bacteria living within a host), to extremely heterogeneous conditions such as soil, and thus have evolved under very different selective pressures.Fig. 2 shows a plot of the mean global significance score, 〈Pglobal〉, versus environmental variability for the 115 different bacterial networks. Note that the average here is taken over each of the six environmental classes: obligate, specialised, aquatic, facultative, multiple and terrestrial. Importantly, we found that motif frequency, and thus network complexity, increased significantly with environmental variability. The lowest motif frequency was found for the bacteria within the obligate class, followed by a relatively steep increase to the specialised and aquatic classes, then higher again for the facultative and multiple classes, and then highest for the terrestrial class. The group differences shown in Fig. 2 are statistically significant (Kruskal–Wallis test, p < 10−9).
This result provides evidence supporting the view that variability in an organisms habitat has important consequences for the topology of the resultant metabolic networks, and is consistent with previous studies10,12,36,37 that have demonstrated important links between the metabolic networks of organisms and their biochemical environments. In the current context, these results can be understood as an evolutionary effect due to the greater uncertainty that accompanies an increasingly fluctuating environment: greater numbers of 3- and 4-node motifs lead to larger numbers of cycles, i.e. closed paths, and thus to increased redundancy in the metabolic network, which in turn promotes greater adaptability and robustness.
The effect of oxygen requirement on network structure
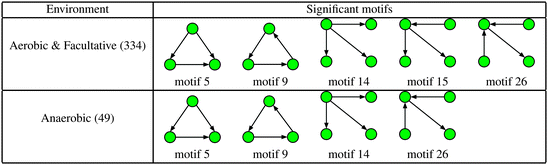
Next, we considered the effect of oxygen requirements on metabolic network structure. We studied 383 bacterial species which were categorised into three groups: 154 aerobes, 180 facultative aerobes and 49 anaerobes.Fig. 3 shows a plot of the mean global significance scores versus growth conditions for the 383 different bacterial species. Interestingly, we found that networks that have evolved in the presence of oxygen, i.e. aerobes and facultative aerobes, have a significantly larger number of network motifs. The group differences shown in Fig. 3 were found to be significant (Kruskal–Wallis test, p < 10−4).
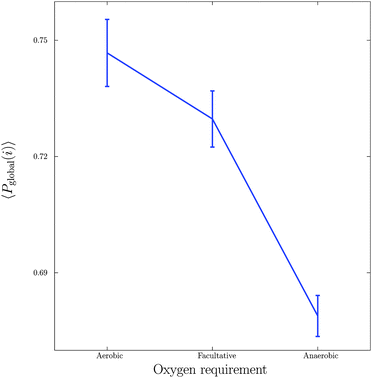 | ||
| Fig. 3 Relationship between growth conditions, in particular oxygen requirements, and mean global significance score 〈Pglobal〉. Vertical bars represent standard errors. | ||
The results shown in Fig. 3 are in agreement with recent studies (see, for example, the paper by Raymond and Segré38) demonstrating that bacterial networks that are exposed to oxygen are able to form additional pathways, compared to those that are oxygen deprived. In particular, the study by Raymond and Segrè38 found that aerobic bacteria have approximately a 1.5 fold increase in the number of reactions and metabolites relative to anaerobic bacteria, resulting in the expansion of metabolic networks evolving in the presence of oxygen, and thus supporting the view of oxygen induced network complexity.
Motifs responsible for the observed differences
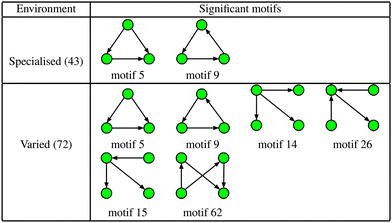
To determine the specific motifs driving the observations of the previous section, we considered the quantity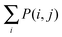 , that is, the column sum of the matrix P defined in eqn (2) – recall that the columns of P contain information specific to individual motifs. Moreover, by restricting the sum above to a particular subgroup of interest (specialised, obligate, multiple, etc.), it is possible to detail the extent to which any particular motif featured within that group. In the following we consider a motif to be significant within a particular group, if the mean local significance score of that motif (restricted to the group of interest) is at least 2 standard deviations greater than the mean score across the entire network ensemble. Note that a list of all 3- and 4-node motifs is provided in the ESI.†
, that is, the column sum of the matrix P defined in eqn (2) – recall that the columns of P contain information specific to individual motifs. Moreover, by restricting the sum above to a particular subgroup of interest (specialised, obligate, multiple, etc.), it is possible to detail the extent to which any particular motif featured within that group. In the following we consider a motif to be significant within a particular group, if the mean local significance score of that motif (restricted to the group of interest) is at least 2 standard deviations greater than the mean score across the entire network ensemble. Note that a list of all 3- and 4-node motifs is provided in the ESI.†
The increased numbers of network motifs present within the varied class indicates a potentially significant growth in network redundancy within those organisms inhabiting fluctuating environments, and can be considered as further evidence of so-called functional redundancy mediated robustness,40 that is, the observed perseverance of systems level redundancies prevalent in metabolic, as well as more general, cellular networks. More specifically, of the 4 additional significant motifs found in the varied class, motifs 14 and 15 may be considered variants of the single-input motif, motif 62 a bi-parallel fan, and motif 26 a multi-input motif, all of which have been implicated as potential indicators of network redundancy. For example, in the context of metabolism the single-input motif consists of a substrate X that is consumed in multiple reactions, the result of which are the products Y, Z,…; whilst the bi-parallel fan implies the presence of multiple, or compensatory, pathways whose efficiencies may vary according to alterations in environmental conditions. Indeed, these findings are in agreement with a number of recent studies relating genetic robustness and organism adaptability,40,41 and suggest that bacteria that live in more variable environments typically display a greater abundance of redundant metabolic reactions.
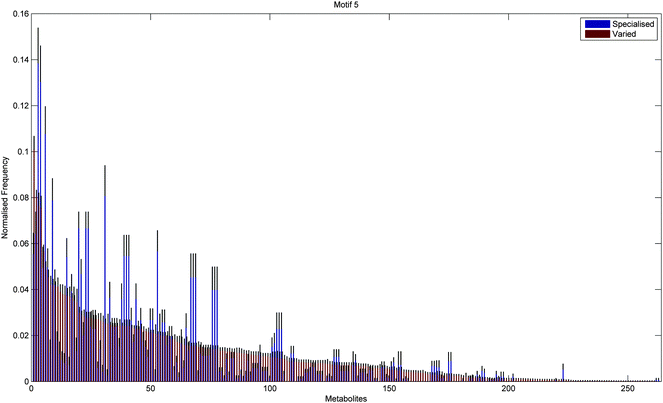
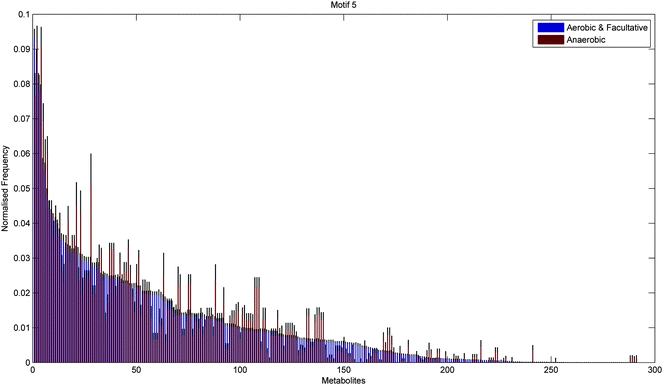
In addition to the topological differences observed between varied and specialised bacteria, we found that the distribution of those metabolites occurring within motif structures present across the entire network ensemble, i.e. motifs 5 and 9, also differed significantly. Fig. 4 and 5 show the mean frequency for metabolites occurring within motif 5 for the 115 metabolic networks, again grouped into the specialised (blue bars) and varied classes (red bars). Note that the frequencies plotted in Fig. 4 and 5 have been normalised to remove any bias due to network size (see Methods section for further details), and metabolites are displayed in decreasing order according to the varied class. Fig. 4 displays the distribution for those 263 metabolites that occurred at least once within motif 5 across the two classes under consideration. Interestingly, we see that the distribution for the varied class is relatively broad, with a large number of metabolites occurring with a relatively low frequency, whereas the distribution for the specialised class is more akin to a scale-free or power-law distribution, consisting of a small set of relatively high frequency metabolites. Note that similar results were found for motif 9 (see ESI†).
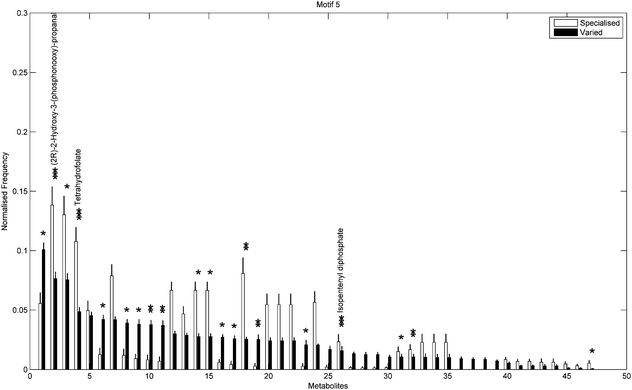
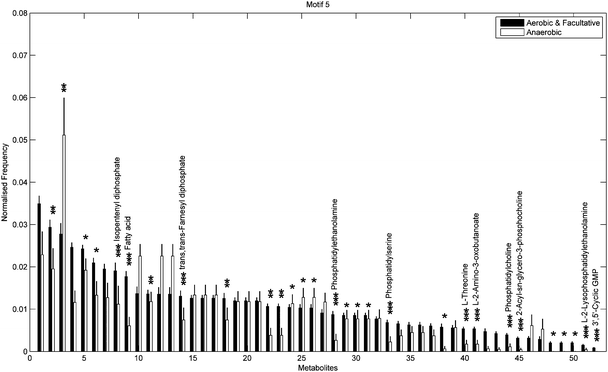
Next we used a Chi-square test (Fisher's Exact test, p < 0.01) to explore the differences in proportions of the individual metabolites between the two groups. Fig. 5 shows the 47/263 metabolites for which a significant difference in proportions was found, again displayed according to decreasing frequency of the varied class. Metabolites displaying the most significant differences (Fisher's Exact test, p < 10−5) included (2R)-2-hydroxy-3-(phosphonooxy)-propanal, tetrahydrofolate and isopentenyl diphosphate, all of which were overrepresented in the specialised group compared to the varied group. Note that the aforementioned overrepresented metabolites are required for biosynthesis of various amino acids, folates and terpenoids and are also responsible for the regulation of carbohydrate metabolism in many bacterial species.
Fig. 6 and 7 show the distribution of metabolites across motif 5 for the two groups, ordered according to decreasing metabolite frequency for the aerobic class (blue bars). Note, that the aerobic class exhibits a fairly broad distribution, whilst the anaerobic distribution tails off slightly quicker, in a similar but less pronounced manner to that displayed by the specialised bacteria in Fig. 4. Fig. 7 shows those metabolites that displayed a significant group difference. Interestingly, the majority of metabolites, some 37/52, were found to be overrepresented in the aerobic group compared to the anaerobic group, the most significant of which were isopentenyl diphosphate, fatty acid, trans,trans-farnesyl diphosphate, phosphatidylethanolamine, phosphatidylserine, L-threonine, L-2-amino-3-oxobutanoate, phosphatidylcholine, 2-acyl-sn-glycero-3-phosphocholine, L-2-lysophosphatidylethanolamine, 3′,5′-cyclic GMP (Fisher's Exact test, p < 10−5). These metabolites are known to be involved in the biosynthesis of a range of amino acids and secondary metabolites. Again, similar results where found for motif 9 (see ESI†).
Conclusions
In this work, we have introduced a new graph embedding approach for studying large numbers of networks, of possibly differing order, and employed it to investigate the effect of environmental variability on the metabolic network structure of a large cohort of bacterial species. Using the new technique, we found evidence supporting the view that organisms that evolve in more uncertain environments exhibit more complex metabolic connectivity structures than those evolving under more stable conditions. Note, that the motif based approach forwarded here strongly supports the view that environmental conditions play a pivotal role in shaping the resultant metabolic networks, and is robust in the sense that the patterns described in Fig. 2 and 3 are reproducible in both the latest and older, less complete versions of the data42 (data not shown). This is in contrast to recent studies in which network features that were found to correlate with environmental variability (e.g. modularity) disappeared when tested on newer versions of the data.30,43 These findings suggest that alterations in the motif signature provide a robust indicator of adaptability and evolvability in bacterial metabolic networks.Methods
Detection of network motifs and the choice of null model
Network motif frequencies were computed using the open-source software mfinder.23,44 To determine significance, motif frequencies were compared against frequency distributions for some 1000 random graphs, chosen so as to preserve both the in- and out degree, as well as (n − 1)-node motifs. Note that the latter condition ensures that the enrichment of n-node motifs is not simply due to the presence of highly significant subgraphs.Non-negative matrix factorisation
There are many different variants of the non-negative matrix factorisation algorithm.28 In our work we used the Multiplicative Update algorithm which is included in the MATLAB statistics toolbox.‡ Starting with initial guesses W0, H0, typically random matrices, the method computes a rank-k approximation to the data matrix A ≈ WH (here A ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×m, W ∈
n×m, W ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×k and H ∈
n×k and H ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) k×m) via successive iterations of the equations
k×m) via successive iterations of the equationsHere · * denotes point-wise multiplication.
Note that due to the iterative nature of the scheme, the resulting decomposition can vary depending upon (a) the choice of initial matrices W0, H0; (b) the choice of the parameter k, which is usually not obvious a priori, and tends to be based on heuristics such as the number of expected clusters in the data, or a visual inspection of the scree plot. In our experiments, we ran the algorithm with 100 different random initial conditions, choosing as our factorisation the matrices W, H for which the residual ||A − WH||F was minimised, according to the Frobenius norm. Moreover, we repeated the experiments for a range of different k values (up to and including k = 25) to test the robustness of our results. We found the effects of varying k to be inappreciable, in the sense that the patterns reported were reproduced for most values of k.
Determining significant metabolites
When considering the differences between the frequency of metabolites occurring in a motif of interest (5 or 9 in our case) care must be taken to eliminate the influence of network size on the analysis. This bias is due to the increased number of motifs exhibited by larger networks which naturally leads to greater frequencies of metabolites. Thus, given a network i and a metabolite j, we denote by fi,j the frequency with which metabolite j appears within the motif of interest, motif q say, for the ith network. Now, in order to remove any bias due to network size we normalise the statistic fi,j by dividing it by the frequency with which motif q appears in network i, which we denote by fi,motq. This then leads to the following normalised statistic:describing the relative importance of metabolites via their participation within specific motifs.
Acknowledgements
We thank Kazuhiro Takemoto for generously providing the metabolic data used in this study and for a number of useful discussions. NP is grateful to Nottingham Trent University for support via an RAE funded PhD scholarship.References
- M. E. J. Newman, Networks: An Introduction, Oxford University Press, 2010 Search PubMed.
- E. Estrada, The Structure of Complex Networks: Theory and Applications, Oxford University Press, 2011 Search PubMed.
- U. Alon, An Introduction to Systems Biology: Design Principles of Biological Circuits, Chapman and Hall/CRC, 2010 Search PubMed.
- M. Buchanan, Networks in Cell Biology, Cambridge University Press, 2010 Search PubMed.
- E. Davidson and M. Levin, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 4935 CrossRef CAS PubMed.
- G. Karlebach and R. Shamir, Nat. Rev. Mol. Cell Biol., 2008, 9, 770–780 CrossRef CAS PubMed.
- A. Zhang, Protien Interaction Networks: Computational Analysis, Cambridge University Press, 2009 Search PubMed.
- A. Gursoy, O. Ksekin and R. Nussinov, Biochem. Soc. Trans., 2008, 36, 1398–1403 CrossRef CAS PubMed.
- N. T. Doncheva, K. Klein, F. S. Domingues and M. Albrecht, Trends Biochem. Sci., 2011, 36, 179–182 CrossRef CAS PubMed.
- M. Parter, N. Kashtan and U. Alon, BMC Evol. Biol., 2007, 7, 169 CrossRef PubMed.
- K. Takemoto and S. Borjigin, PLoS One, 2011, 6, e25874 CAS.
- J. J. Crofts and E. Estrada, J. Math. Chem., 2014, 52, 675–688 CrossRef CAS.
- V. Lacroix, L. Cottret, P. Thebault and M. Sagot, IEEE/ACM Trans. Comput. Biol. Bioinf., 2008, 5, 594–617 CrossRef PubMed.
- E. Ravasz, A. L. Somera, D. A. Mongru, Z. N. Oltvai and A. Barabsi, Science, 2002, 297, 1551–1555 CrossRef CAS PubMed.
- R. Guimera and L. A. N. Amaral, Nature, 2005, 895–900 CrossRef CAS PubMed.
- A. Hintze and C. Adami, PLoS Comput. Biol., 2008, 4, e23 Search PubMed.
- P. Holme, PLoS One, 2011, 6, e16605 CAS.
- U. Alon, Nat. Rev. Genet., 2007, 8, 450–461 CrossRef CAS PubMed.
- Y. Asgari, A. Salehzadeh-Yazdi, F. Schreiber and A. Masoudi-Nejad, Nat. Genet., 2003, 35, 176–179 CrossRef PubMed.
- N. Kashtan and U. Alon, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13773–13778 CrossRef CAS PubMed.
- E. R. Shellman, C. F. Burant and S. Schnell, Mol. BioSyst., 2013, 9, 352–360 RSC.
- Y. Asgari, A. Salehzadeh-Yazdi, F. Schreiber and A. Masoudi-Nejad, PLoS One, 2013, 8, e79397 Search PubMed.
- R. Milo, S. Shen-Orr, S. Itzkovitz, N. Kashtan, D. Chklovskii and U. Alon, Science, 2002, 298, 824–827 CrossRef CAS PubMed.
- C. M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006 Search PubMed.
- D. B. Skillicorn, Understanding Complex Datasets: Data Mining with Matrix Decompositions, Chapman and Hall/CRC, 2007 Search PubMed.
- R. Milo, S. Itzkovitz, N. Kashtan, R. Levitt, S. Shen-Orr, I. Ayzenshtat, M. Sheffer and U. Alon, Science, 2004, 303, 1538–1542 CrossRef CAS PubMed.
- D. D. Lee and H. S. Seung, Science, 1999, 401, 788–791 CAS.
- C. Lee, D. J. Higham, D. Crowther and J. K. Vass, Monografias de la Real Academia de Ciencias de Zaragoza, 2010, 33, 39–53 Search PubMed.
- Y. Li and A. Ngom, Source Code Biol. Med., 2013, 8, 1–15 CrossRef PubMed.
- K. Takemoto, PLoS One, 2013, 8, e61348 CAS.
- M. Kanehisa, S. Goto, Y. Sato, M. Furumichi and M. Tanabe, Nucleic Acids Res., 2011, 40, 109–114 CrossRef PubMed.
- Entrez Genome Project, http://www.ncbi.nlm.nih.gov/genomes/lproks.cgi.
- P. Holme, J. R. Soc., Interface, 2011, 6, 1027–1034 CrossRef PubMed.
- R. Montañez, M. A. Medina, R. V. Solé and C. Rodrguez-Caso, BioEssays, 2010, 32, 246–256 CrossRef PubMed.
- K. Takemoto, J. C. Nacher and T. Akutso, BMC Bioinf., 2007, 8, 303 CrossRef PubMed.
- A. Kreimer, E. Borenstein, U. Gophna and E. Ruppin, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 6976–6981 CrossRef CAS PubMed.
- S. C. Janga and M. M. Babu, Genome Biol., 2008, 9, 1–5 CrossRef PubMed.
- J. Raymond and D. Segrè, Science, 2006, 311, 1764–1767 CrossRef CAS PubMed.
- A. A. Apte, J. W. Cain, D. G. Bonchev and S. S. Fong, J. Biol. Eng., 2008, 2, 1–12 CrossRef PubMed.
- Z. Wang and J. Zhang, Genome Biol. Evol., 2009, 1, 23–33 CrossRef PubMed.
- R. Harrison, B. Papp, C. Pal, S. Oliver and D. Delneri, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 2307–2312 CrossRef CAS PubMed.
- H. W. Ma and A. P. Zeng, Bioinformatics, 2003, 19, 270–277 CrossRef CAS PubMed.
- W. Zhou and L. Nakhleh, BMC Evol. Biol., 2012, 12, 181 CrossRef PubMed.
- N. Kashtan, S. Itzkovitz, R. Milo and U. Alon, Bioinformatics, 2004, 20, 1746–1758 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4mb00430b |
| ‡ http://www.mathworks.com/ |
| This journal is © The Royal Society of Chemistry 2015 |