Open Access Article
Open Access ArticleWater's tensile strength measured using an optofluidic chip†
Z. G.
Li
*a,
S.
Xiong
a,
L. K.
Chin
a,
K.
Ando
b,
J. B.
Zhang
a and
A. Q.
Liu
a
aSchool of Electrical and Electronic Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798. E-mail: lizh0018@ntu.edu.sg
bDepartment of Mechanical Engineering, Keio University, Yokohama 223-8522, Japan
First published on 18th March 2015
Abstract
In this paper, for the first time, the tensile strength of water is directly measured using an optofluidic chip based on the displacement of air–water interface deformation with homogeneous nucleation. When water in a microchannel is stretched dynamically via laser-induced shock reflection at the air–water interface, the shock pressures are determined by measuring the displacements of the deformed interface. Observation of the vapor bubbles is used as a probe to identify the cavitation threshold with a critical distance, and the tensile strength of water at 20 °C is measured to be −33.3 ± 2.8 MPa. This method can be extended to investigate the tensile strength of other soft materials such as glycerol, which is measured to be −59.8 ± 10.7 MPa at 20 °C.
The characterization of mechanical properties of soft materials, such as water, tissue, cells and gel, is becoming an important topic in today's engineering and biomedical research, ranging from artificial human cells and tissue to flexible display screens. Tensile strength is one of the most important and fundamental mechanical properties. It has long been known that water is in a metastable state with respect to liquid plus vapour when it is under tension (negative pressure). A further reduction of the pressure will cause the water to rupture and form vapour cavities. The threshold pressure for cavitation inception is termed as tensile strength. So far the measurement of tensile strength has been difficult to perform and most of the outputs deviate from the theoretical prediction. A simple and accurate method is needed to measure this nature of water for both fundamental studies and engineering applications.1–4 Additionally, it offers a fascinating approach to investigate similar properties of other soft materials.
Measurements of tensile strength originate in the work of Berthelot in which water is stretched and ruptured in a sealed tube as the vessel cooled down.5 In later studies, capillary tubes,6 shock reflectors7,8 and acoustic waves9 are used to create negative pressure for water rupture. However, a great discrepancy exists between these experimental results and the theoretical value due to unavoidable heterogeneous nucleation in a large volume of water.10,11 Even if water has a theoretical tensile strength of approximately 130 MPa, most experimental values are below 30 MPa. The only exception is the mineral inclusion method. Evidence shows that high tension exists in microscopic aqueous inclusion in minerals, which is close to the theoretical limit of 140 MPa at 42 °C.12 However, the experiments are complex, which require high temperature (300–400 °C) for sample preparation and an autoclave at a desired combination of pressure and temperature within the inclusions. In addition, the tensile strength is indirectly measured by extrapolating from an equation of state, which involves limitation and unreliable quantities in the simulation. The development of microfluidics provides another solution to realize homogenous nucleation by controlling the water volume.13 Although the tensile strengths of water and ethanol are successfully measured by comparing the bubble distribution with the simulated pressure field, this method is not suitable for high-viscosity liquids such as oil and glycerol, due to the fact that the simulation is based on the assumption of inviscid flow.
In this paper, a new experimental approach is demonstrated to directly measure the tensile strength of water with the advancement of optofluidic techniques. Water is stretched via the interaction between a laser-induced shock wave and an air–water interface in a microchannel. By investigating the statistics of cavitation nucleation with different distances between the laser spot and the air–water interface, the reproducible cavitation threshold, as the tensile strength, is obtained. The microscopic confinement effectively reduces the probability of the heterogeneous nucleation and significantly decreases the experimental time to hundreds of nanoseconds. This method gets rid of the burdensome dependence on the simulation and complex experimental procedures, which offers the feasibility of investigating the tensile strength of various soft materials. In addition, the low-cost optofluidic chip not only facilitates temperature and fluidic controls, but also is easy to be integrated into complete and functional systems. It can be widely used in different field-deployable applications for testing a large number of samples rapidly.
Fig. 1 shows the schematic illustration of the rupture of water caused by the interaction of the shock wave and the air–water interface. A laser pulse is focused in the microchannel partially filled with water and creates a shock wave. Its strength depends on the absorption process and the optical breakdown.14 The negative pressure is generated by the reflection of the shock wave on an air–water interface. The pressure value is clearly identified by measuring the propagation of the shock wave and the interface displacement. When the negative pressure is larger than tensile strength, the rupture of the water can be detected from the nucleation of vapour bubbles near the air–water interface. The tensile strength of water can be identified by varying the standoff distance, which is the distance from the focal point of the laser pulse to the air–water interface.
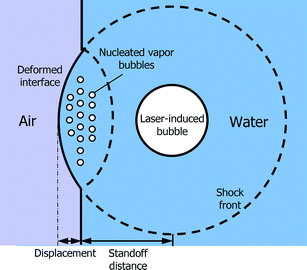 | ||
| Fig. 1 Schematic illustration of the nucleation process triggered by the reflection of the shock by the air–water interface. | ||
The temporal evolution of the laser-induced shock and its interaction with the air–water interface in the microchannel are shown in Fig. 2. Since the contact angle between water and PDMS surface is approximately 90°, the air–water interface is fairly flat. After the laser is triggered, an optical breakdown in water is induced in proximity to the air–water interface with a standoff distance of 138.6 μm. A spherical shock wave is generated due to the rapid expansion of the hot plasma after the optical breakdown. The shock front is identified as a dark fringe in images. A spherical bubble is created after the plasma recombination, which can be clearly observed at t = 48.0 ns (see Fig. 2(a)). When the shock wave reaches the air–water interface (Fig. 2(b)), it is reflected as a tensile wave due to the acoustic impedance mismatch between air and water in the microchannel. A region with high negative pressure is created between the interface and the reflected shock front, which is termed as the nucleation region and pseudo-colored in yellow as shown in Fig. 2. A cloud of vapor bubbles, as the direct indicator of water rupture, arises in this region at t = 97.9 ns. The number of the nucleated bubbles increases with the propagation of the reflected shock wave as shown in Fig. 2(c) and (d).
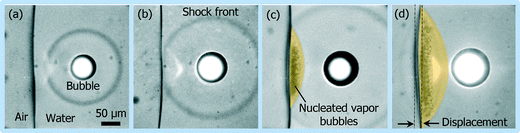 | ||
| Fig. 2 Evolution of the shock interacting with the air–water interface: (a) 48.0, (b) 74.2, (c) 97.9 and (d) 108.1 ns after the laser shooting. | ||
It is noted that the air–water interface is deformed when water is under tension. The distance between the original location of the interface and the point of maximum curvature on the deformed interface is termed as the displacement of the air–water interface deformation as shown in Fig. 2(d). Velocity of the interface v is expressed as
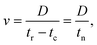 | (1) |
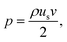 | (2) |
Fig. 3 shows the rupture of water with different standoff distances of 34.0, 51.1, 75.7, 117.8, 135.3 and 159.9 μm, respectively. To keep the tension time tn = 40 ns, different lengths of optical fibers are chosen for different standoff distances, since the green illumination laser pulse is guided by the optical fibers (ESI†). It is observed that larger displacement of the air–water interface deformation is obtained when the standoff distance is shorter, which is consistent with the predicted fast decay of the shock pressure. The bright light spot in proximity to the interface is due to the deformed polymer channel wall. Since the displacement of the air–water interface deformation can be directly measured from captured images with tn = 40 ns, the velocities of the interface with various standoff distances are easily calculated using eqn (1) and plotted in Fig. 4. Then the shock speeds are measured with different standoff distances, which change from 2.8 to 1.6 km s−1. Thereafter, the velocities of the interface, the shock speeds and water density (998 kg m−3, 20 °C) are put into eqn (2) to estimate the shock pressure. Measured shock pressures are compared with the simulation results as shown in Fig. 4. In the range of the standoff distance from 30 to 300 μm, it can be expressed as P(r) = 5.0 × 104r−1.25, where r is the standoff distance in micrometer. With the increase in the standoff distance, the shock pressure decreases from 765 to 33 MPa.
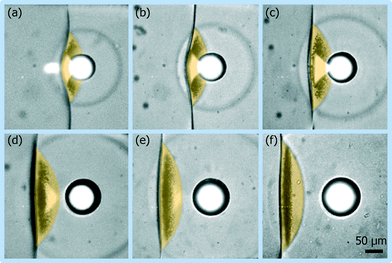 | ||
| Fig. 3 Images of the nucleation induced by the shock reflection with standoff distances of (a) 34.0, (b) 51.1, (c) 75.7, (d) 117.8, (e) 135.3 and (f) 159.9 μm. | ||
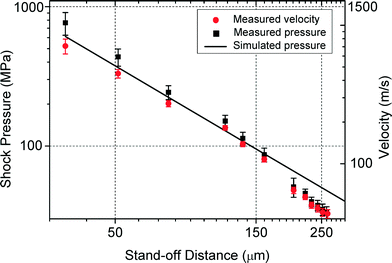 | ||
| Fig. 4 Measured velocity of the interface and shock peak pressure values with various stand-off distances compared with the simulation results. | ||
In the measurement of the shock pressure, the velocity of the deformed interface v is calculated as the average velocity for the whole tension time tn. Therefore, its value becomes higher with a shorter reflection time and it is underestimated for all experimental results in Fig. 4. The presence of the nucleated vapor bubbles is another important factor, which induces the overestimation of the displacement D. This effect increases with increasing shock peak pressure. As a result, the shock pressure is overestimated especially with short standoff distance. These two factors partially cancel off each other and reduce the measurement deviation.
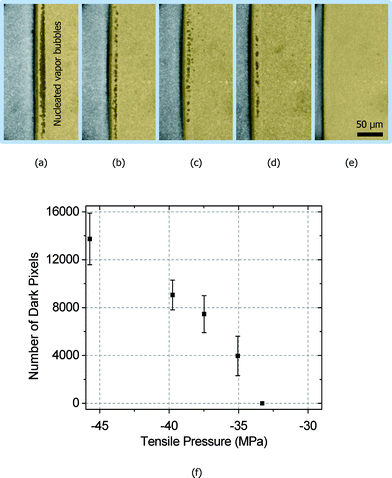
The tensile strength of water can be determined by measuring the shock pressure at a critical standoff distance. When the standoff distance is larger than the critical value, the water is not ruptured. The homogeneous nucleation in the reflected shock region decreases obviously and eventually disappears when the standoff distance increases from 220.7 to 260.2 μm as shown in Fig. 5(a)–(e). A clearer tendency of the nucleation is shown in Fig. 5(f), where the number of dark pixels in the nucleation region is plotted as a function of the tensile pressure to represent the cavitation yields. In this case, the critical standoff distance is determined to be 260.2 μm, and the corresponding shock speed and the velocity of interface are 1573.3 m s−1 and 42.4 m s−1, respectively. The tensile strength is equal to the shock pressure calculated from eqn (2). As a result, the tensile strength of DI water at room temperature (20 °C) is −33.3 ± 2.8 MPa.
This method is extended to measure the tensile strength of glycerol (99+%, Aldrich) with a viscosity of 1.412 Pa s as described in the ESI.† The tensile strength is measured to be −59.8 ± 10.7 MPa at room temperature (20 °C), while the most negative value in earlier research is −85 MPa.16 This measurement shows the potential applications of this method in the determination of tensile strengths of various liquids, despite the limitations of theoretical modelling.
In conclusion, an optofluidic chip is proposed to measure the tensile strength of water by visualizing the displacement of air–water interface deformation. By detecting shock pressure at the critical standoff distance, the tensile strength of water at room temperature (20 °C) is measured to be −33.3 ± 2.8 MPa. In addition, this method can be extended to investigate the properties of high-viscosity materials such as glycerol with a measured tensile strength of −59.8 ± 10.7 MPa (20 °C).
Experimental section
The experimental setup for shock wave generation and imaging is described in the ESI.† In short, an infrared (IR) laser pulse (1064 nm) of 1.84 ± 0.05 mJ is used to create shock in a polydimethylsiloxane microchannel with a width of 400 μm and a height of 85 μm, which is partially filled with air-saturated DI water (Thermo Scientific) to form an air–water interface. Images from the top of the microchannel are recorded by a CCD camera with a single exposure (7.5 ns) of a green laser pulse (632 nm). The IR and green lasers are triggered at the same time. The recording time of the image is determined by the time delay between the IR and green laser pulses due to the different optical paths. For example, the green pulse arrives at the detector with a time delay of 149.2 ± 0.2 ns when it propagates through a 30 m optical fiber.Acknowledgements
This work is supported by the Environmental and Water Industry Development Council of Singapore (Research project Grant No. 1102-IRIS-05-04) and the AcRF Tier 1 grant from the Minister of Education of Singapore (Research project Grant No. M4010891.120, RG45/09).References
- T. D. Wheeler and A. D. Stroock, Nature, 2008, 455, 208 CrossRef CAS PubMed.
- S. J. Henderson and R. J. Speedy, J. Phys. E., 1980, 13, 778 CrossRef CAS.
- J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318 CrossRef CAS PubMed.
- Y. Guan and D. G. Fredlund, Can. Geotech. J., 1997, 34, 604 CrossRef.
- M. Berthelot, Ann. Chim. Phys., 1850, 30, 232 Search PubMed.
- L. J. Briggs, J. Appl. Phys., 1950, 21, 721 CrossRef CAS PubMed.
- D. A. Wilson, J. W. Hoyt and J. W. Mckune, Nature, 1975, 253, 723 CrossRef CAS.
- P. R. Williams and R. L. Williams, Mol. Phys., 2004, 102, 2091 CrossRef CAS.
- E. Herbert, S. Balibar and F. Caupin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 041603 CrossRef.
- J. C. Fisher, J. Appl. Phys., 1948, 19, 1062 CrossRef PubMed.
- M. Blander and J. Kartz, AIChE J., 1975, 21, 833 CrossRef CAS.
- Q. Zheng, D. J. Durben, G. H. Wolf and C. A. Angell, Science, 1991, 254, 829 CAS.
- K. Ando, A. Q. Liu and C. D. Ohl, Phys. Rev. Lett., 2012, 109, 044501 CrossRef.
- A. Vogel1, J. Noack, G. Huttman and G. Paltauf, Mechanisms of femtosecond laser nanosurgery of cells and tissues, Appl. Phys. B: Lasers Opt., 2005, 81, 1015 CrossRef PubMed.
- H. Kolsky, Stress Waves in Solids, Dover Publications Inc., 1964 Search PubMed.
- G. A. Carlson and H. S. Levine, J. Appl. Phys., 1975, 46, 1954 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5lc00048c |
| This journal is © The Royal Society of Chemistry 2015 |